Turbidity Currents Carrying Shallow Heat Invading Stable Deep-Water Areas May Be an Unrecognized Source of “Pollution” in the Ocean
Abstract
1. Introduction
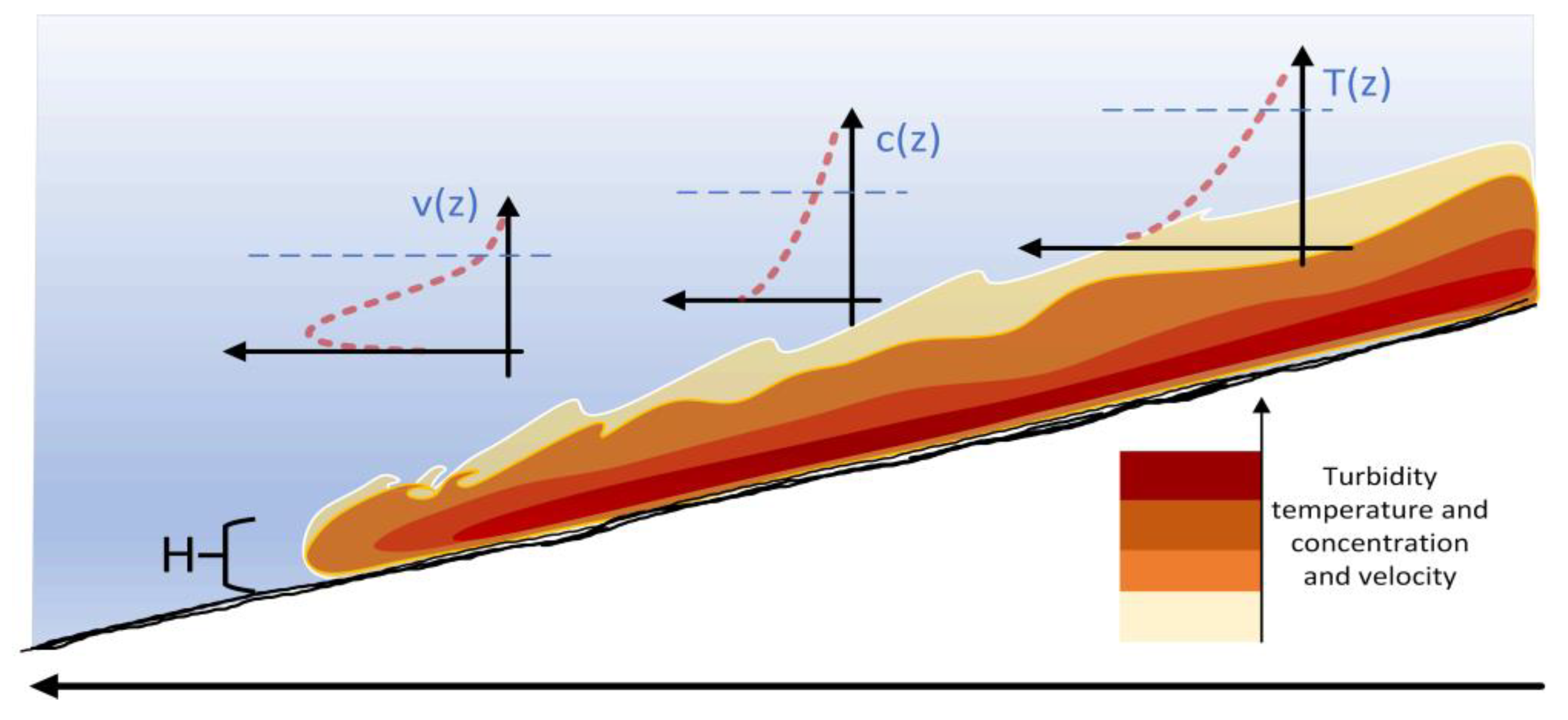
2. Theory
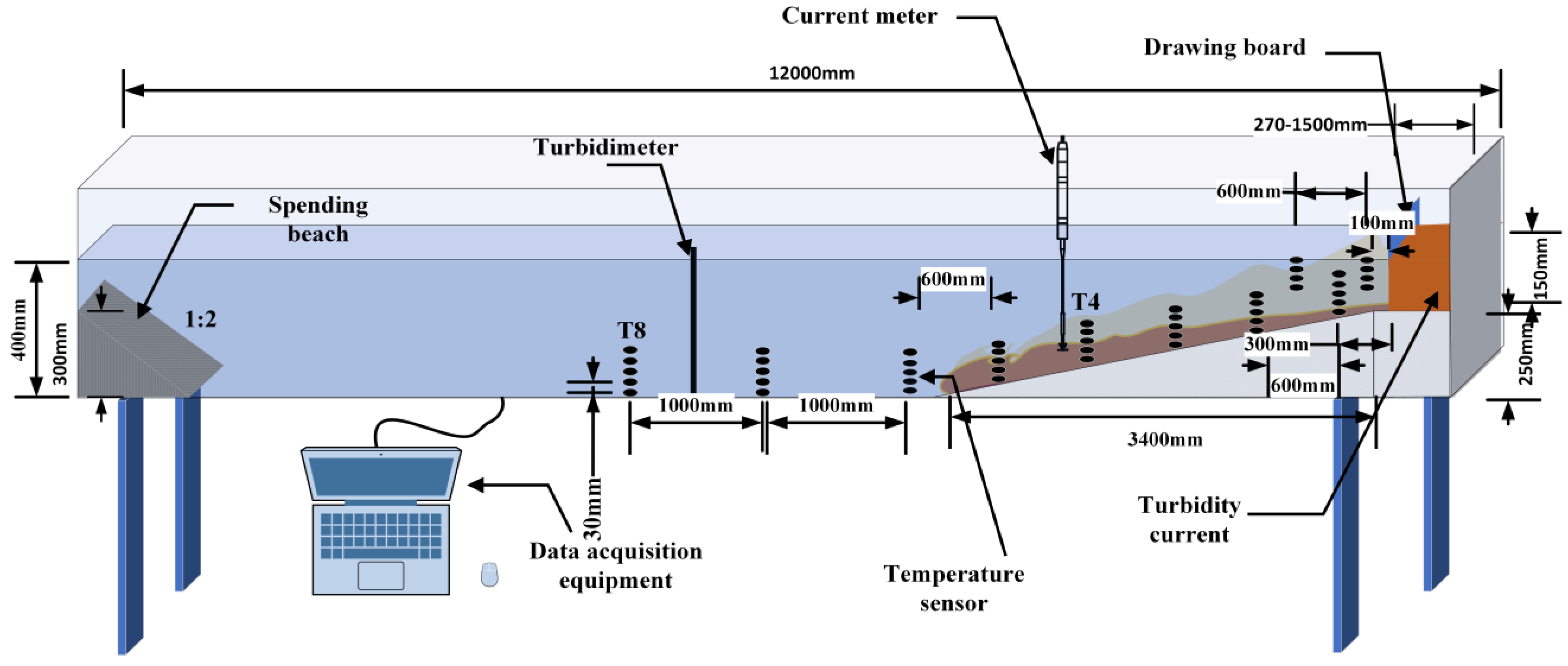
3. Experimental Design
4. Experimental Results
4.1. Temperature Monitoring of Vertical Structural Changes
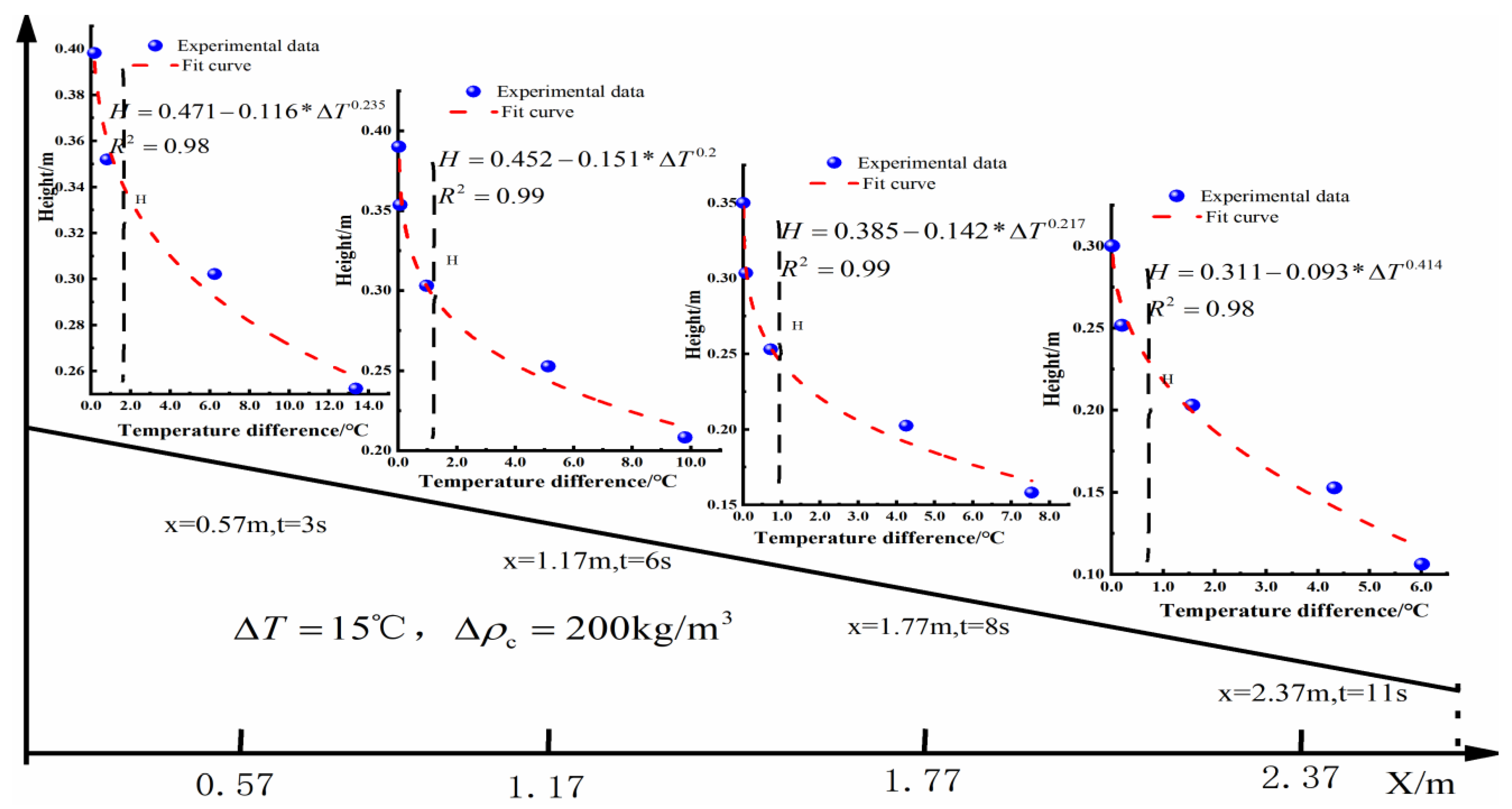
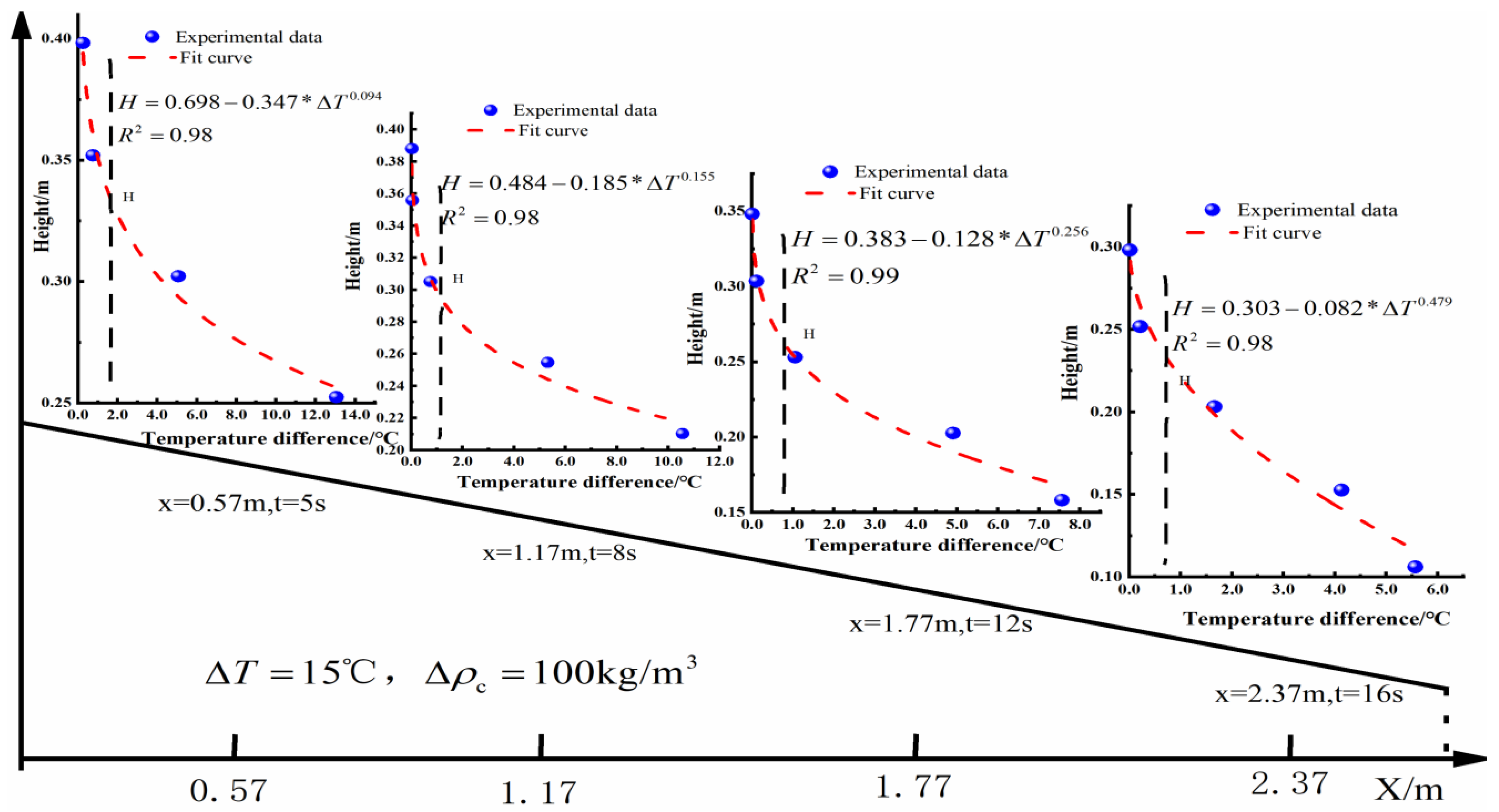
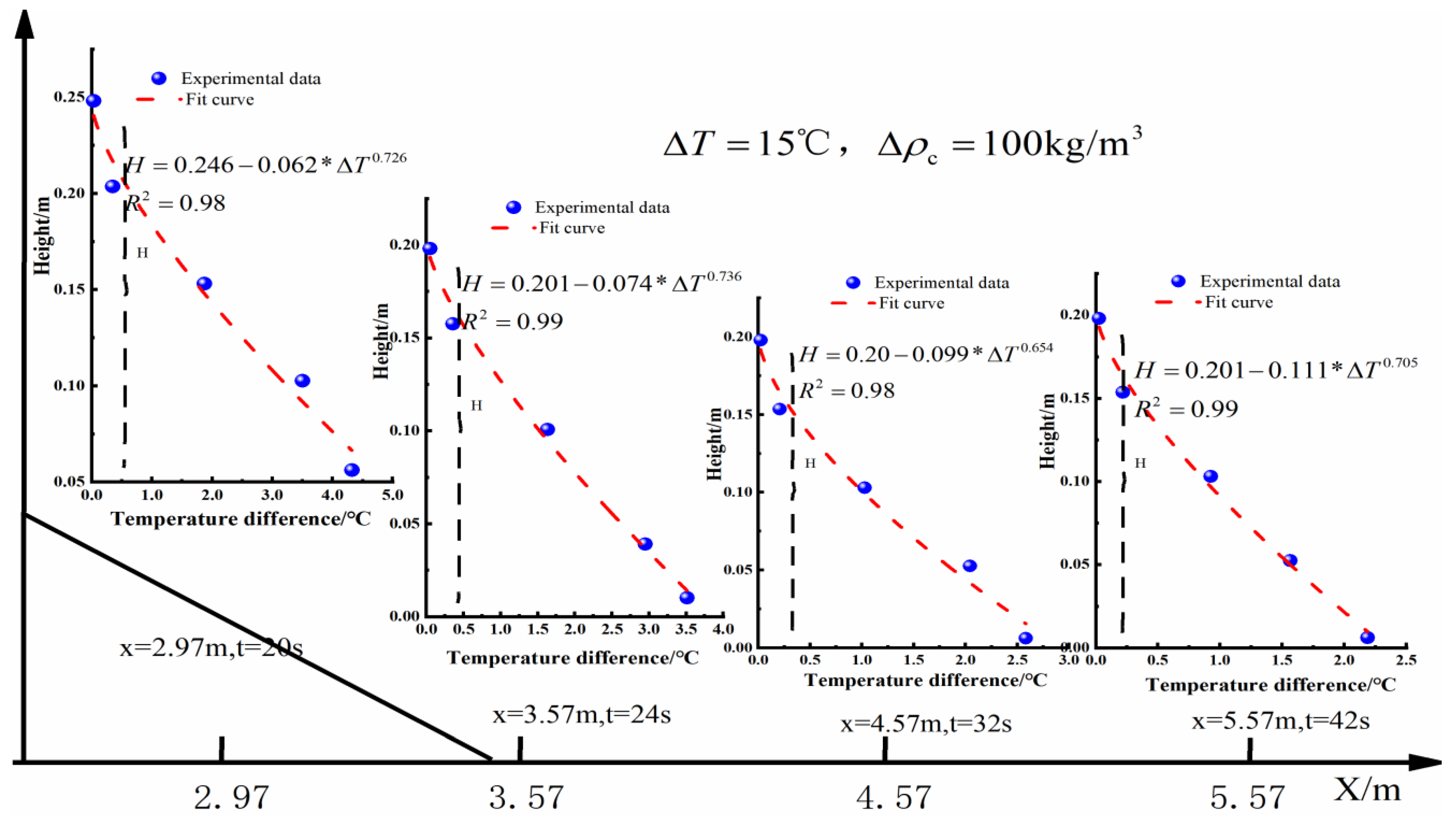
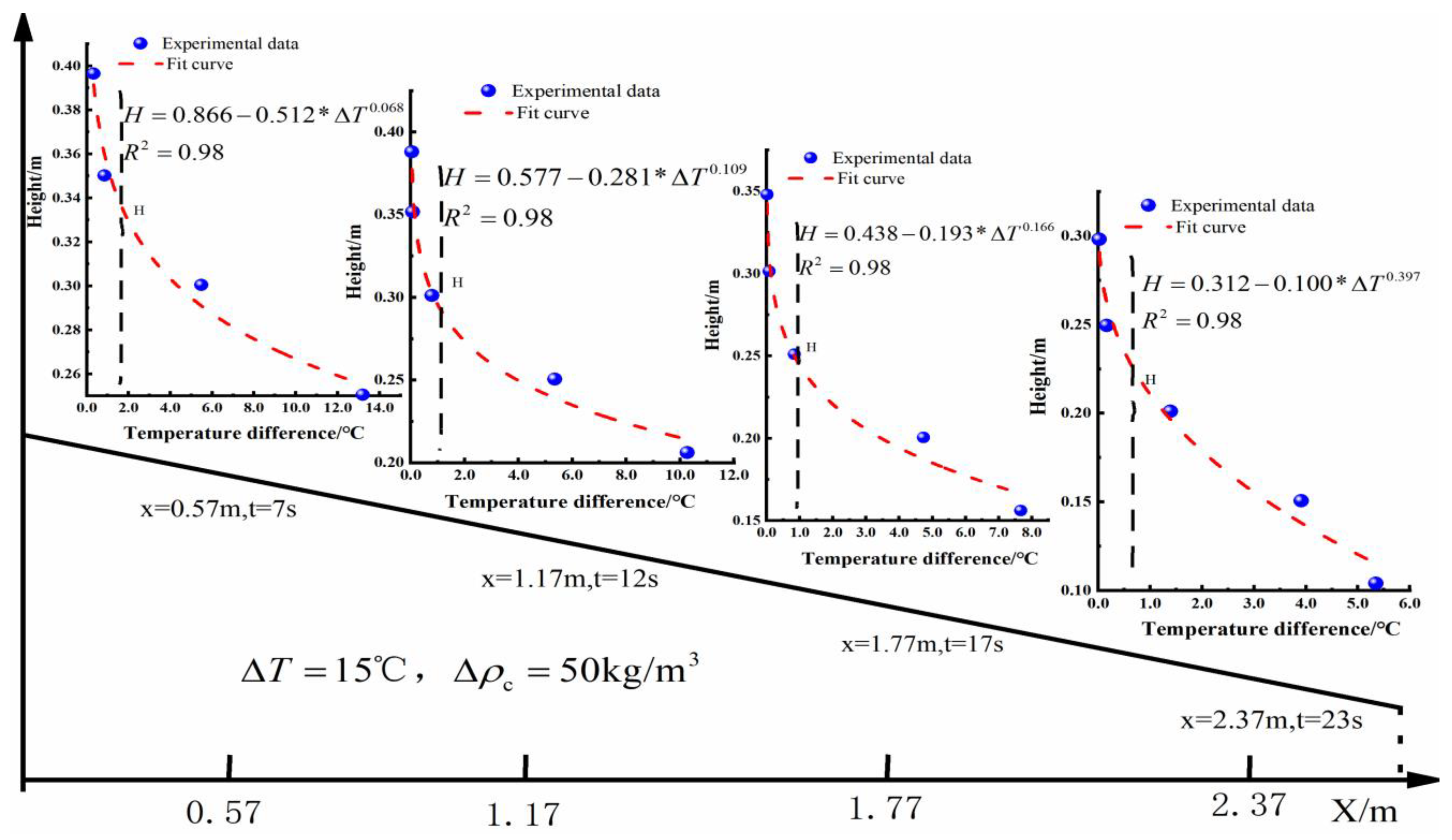
4.2. Monitoring the Impact of Temperature on Turbidity Current Motion
5. Discussion
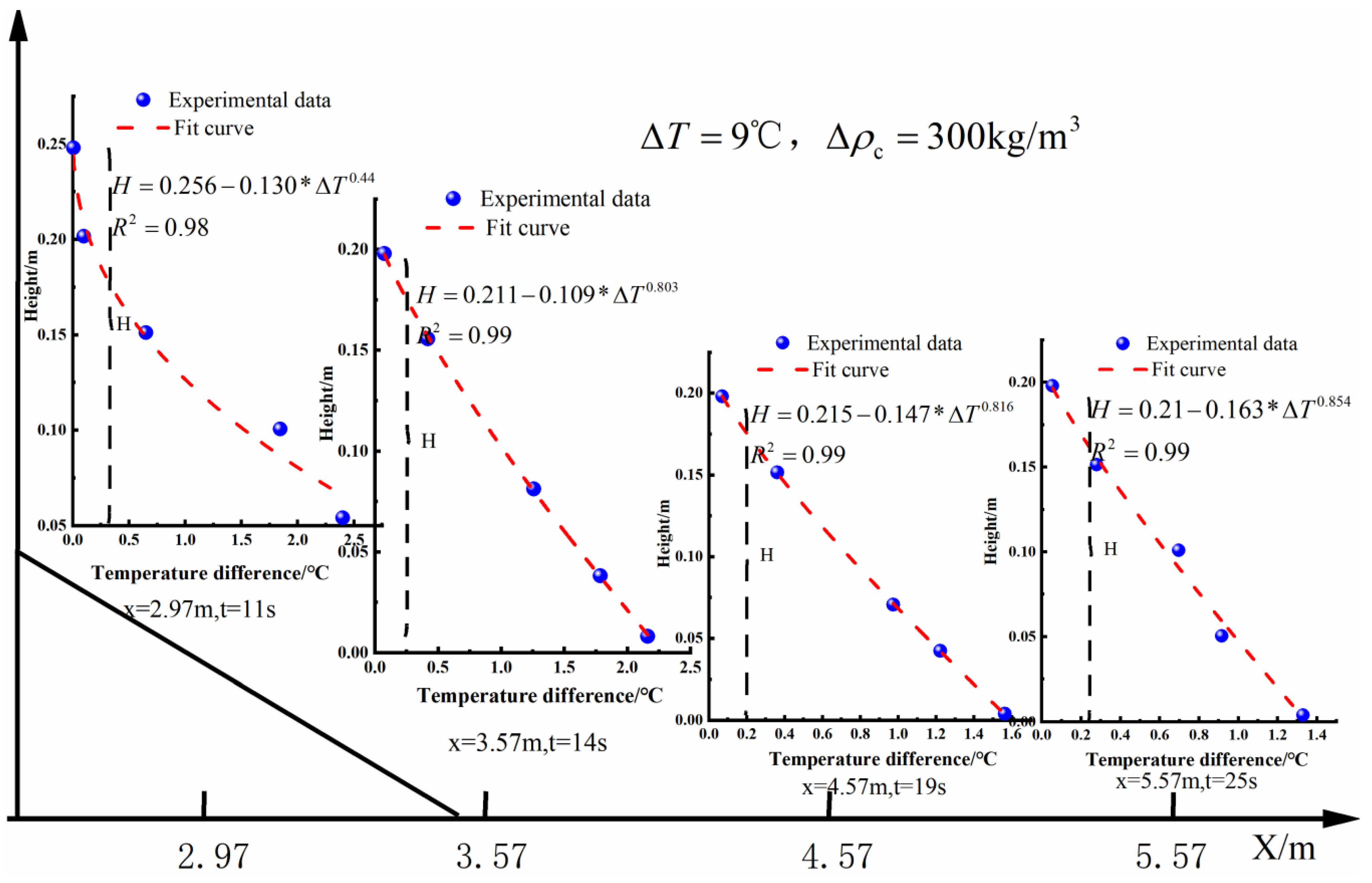
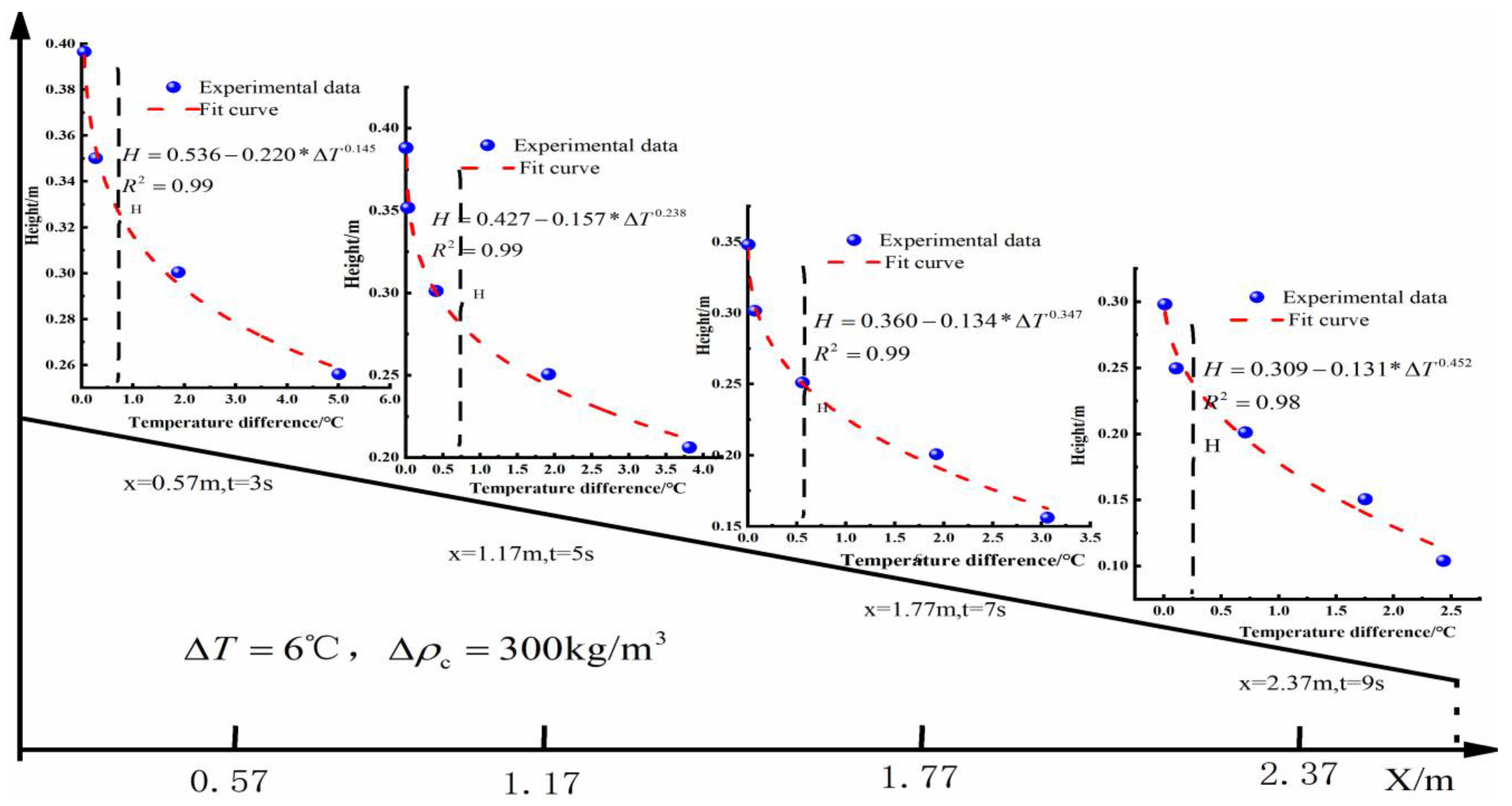
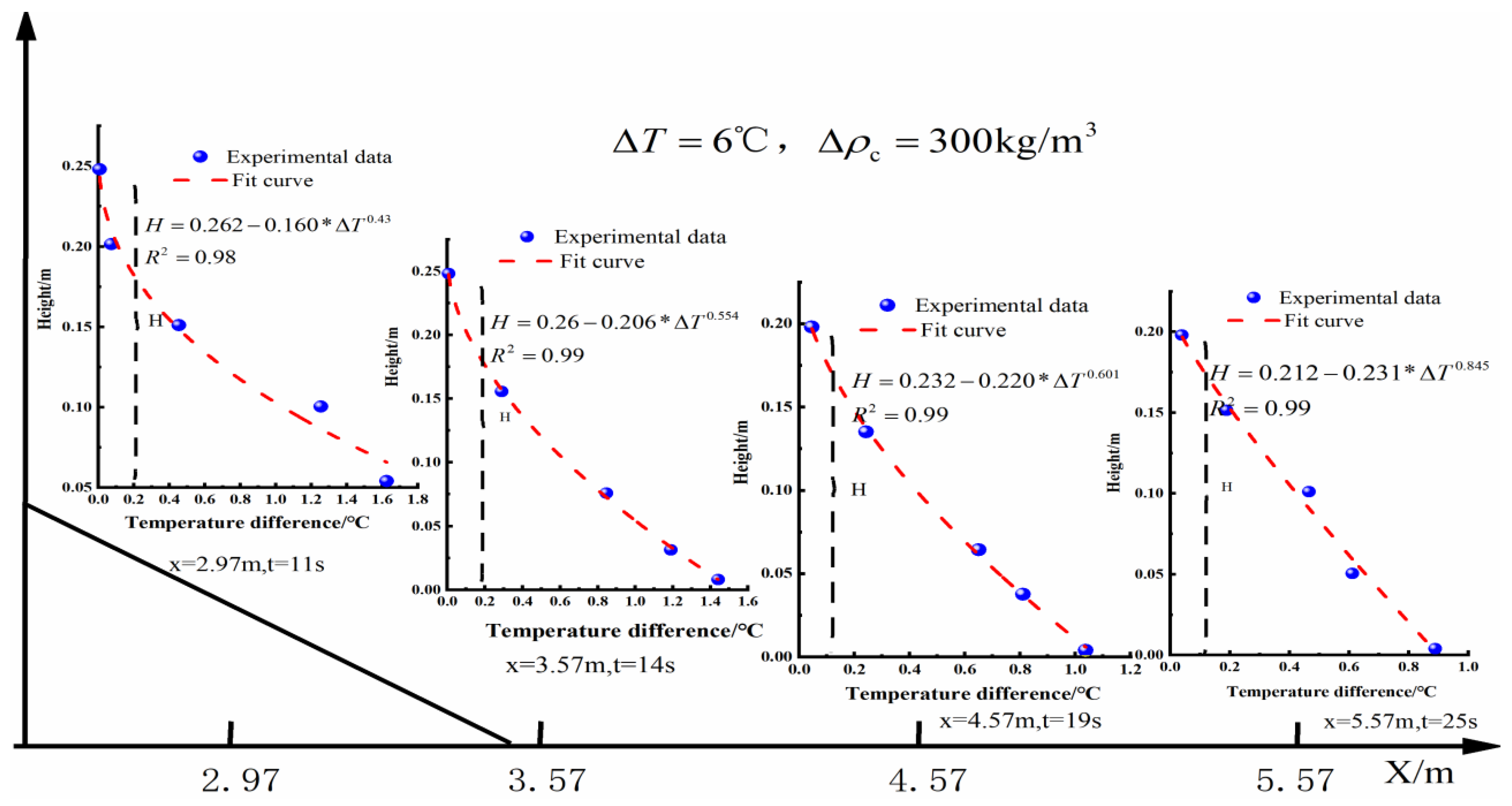
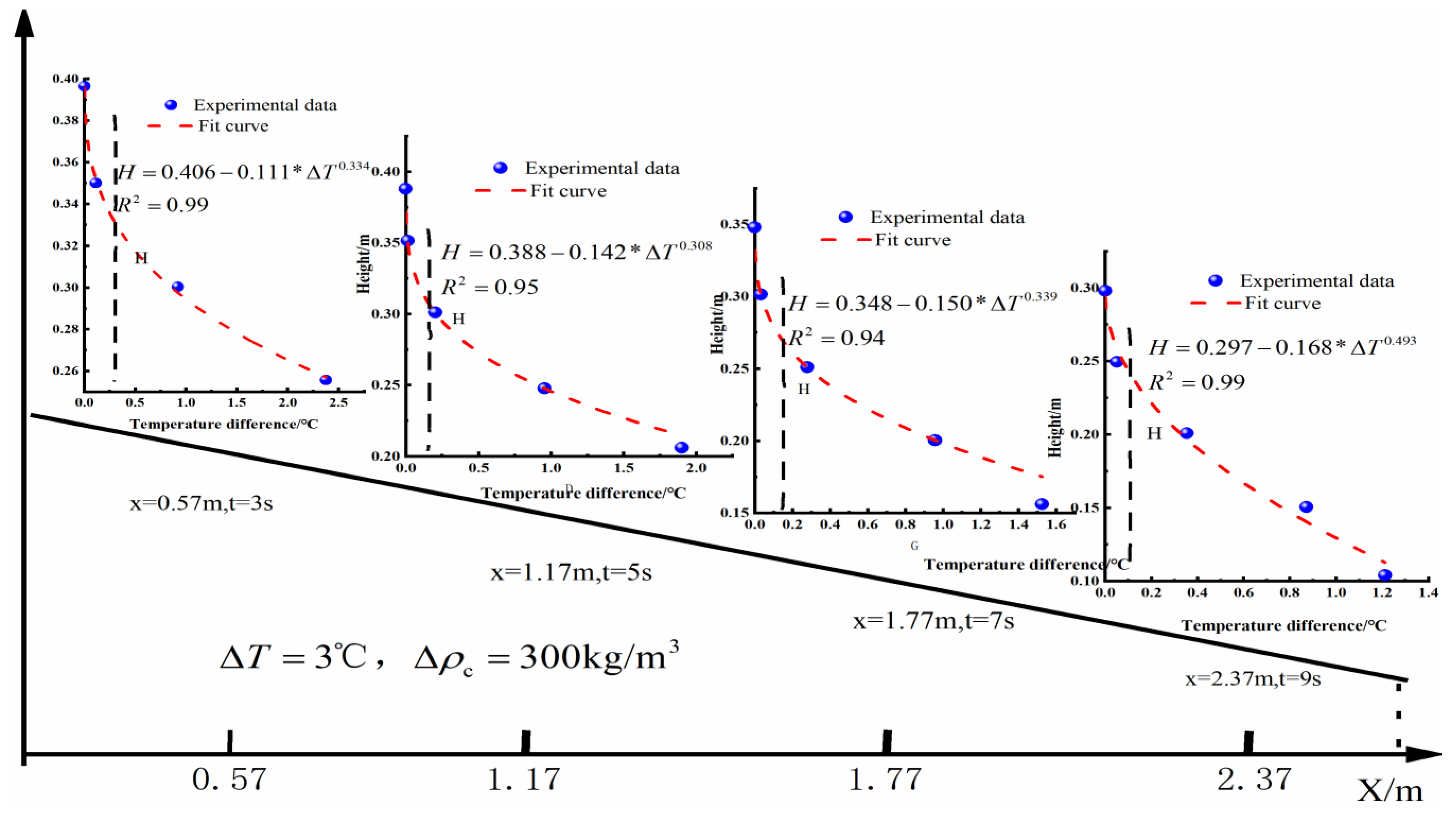
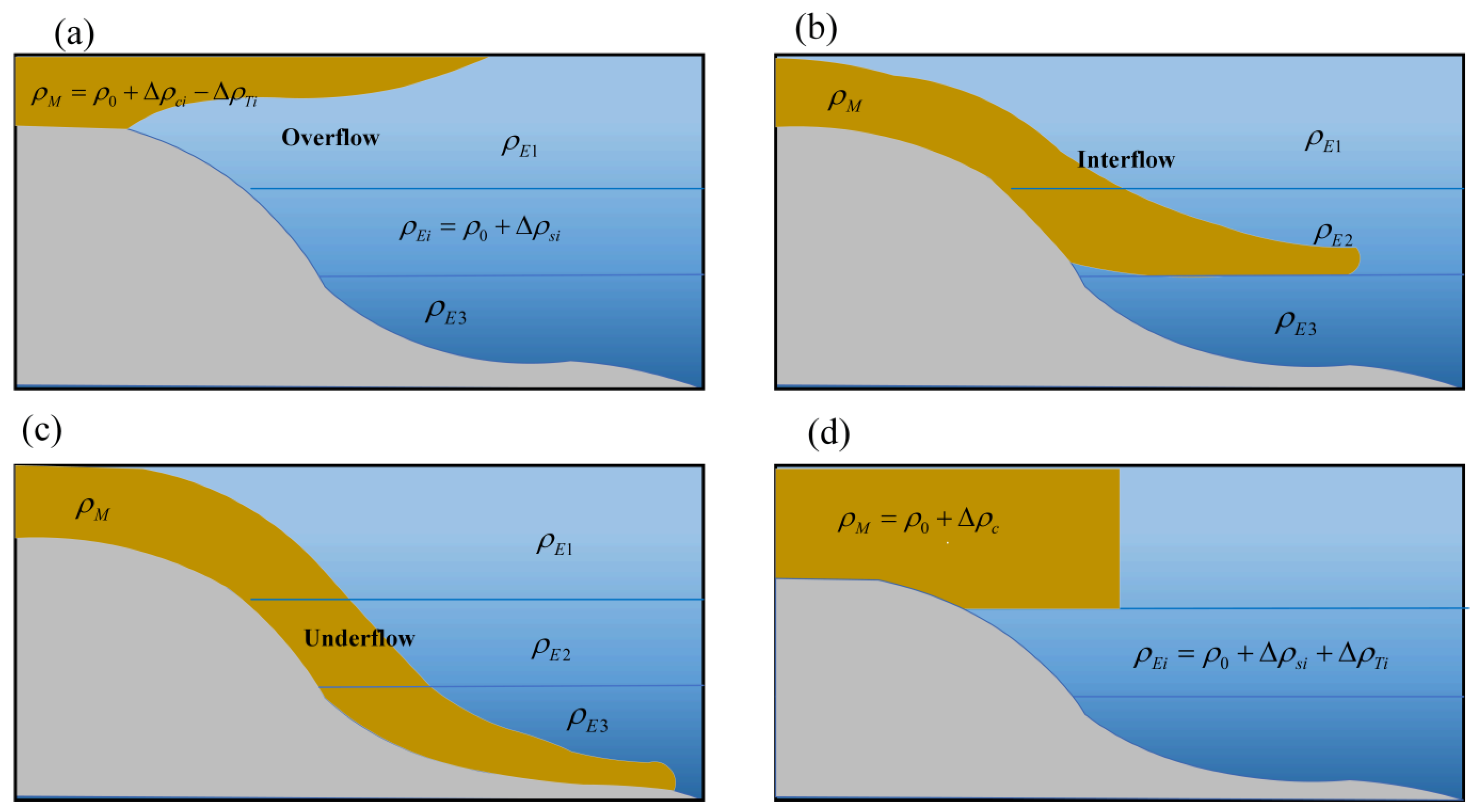
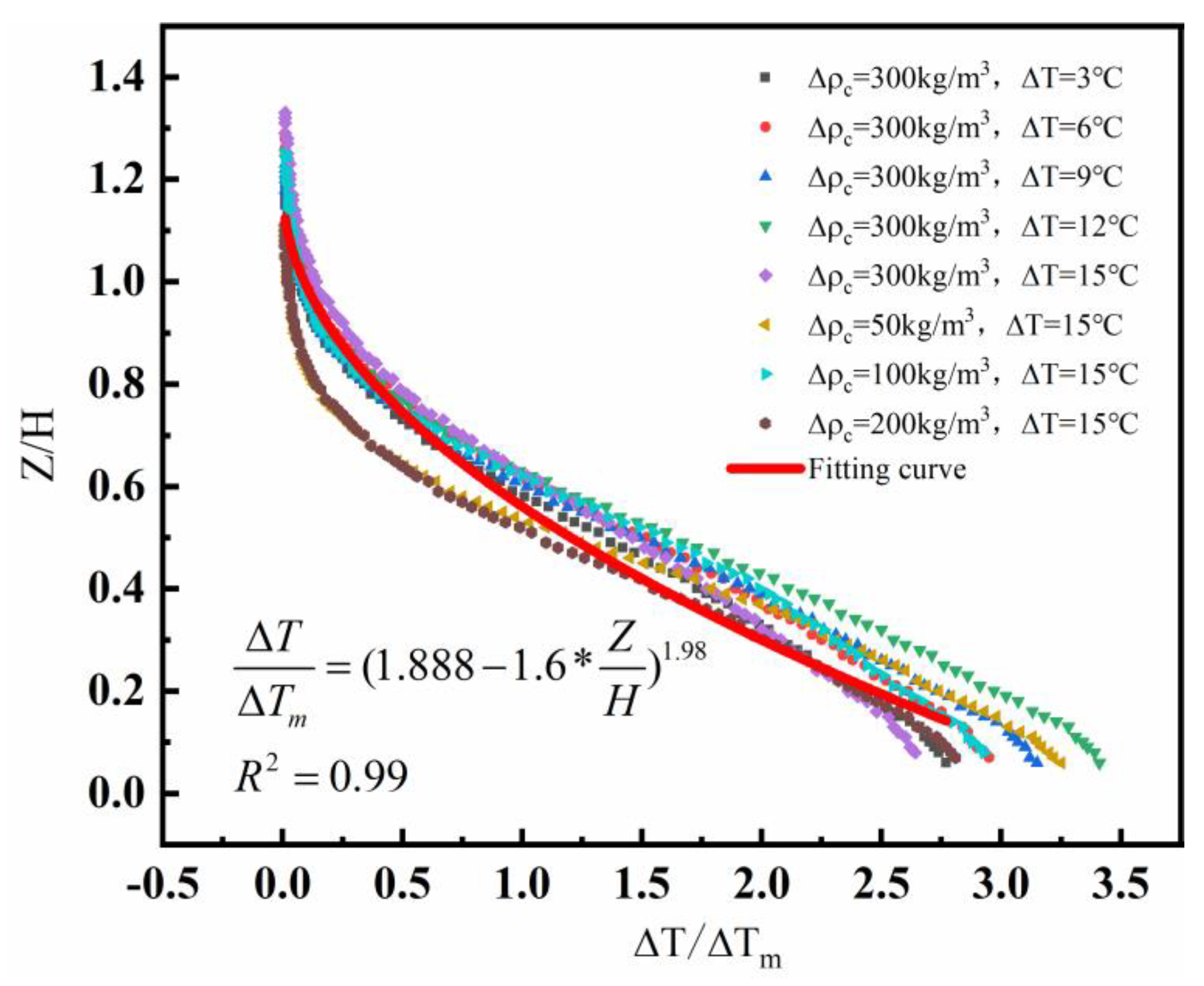
5.1. Vertical Temperature Distribution in Turbidity Current
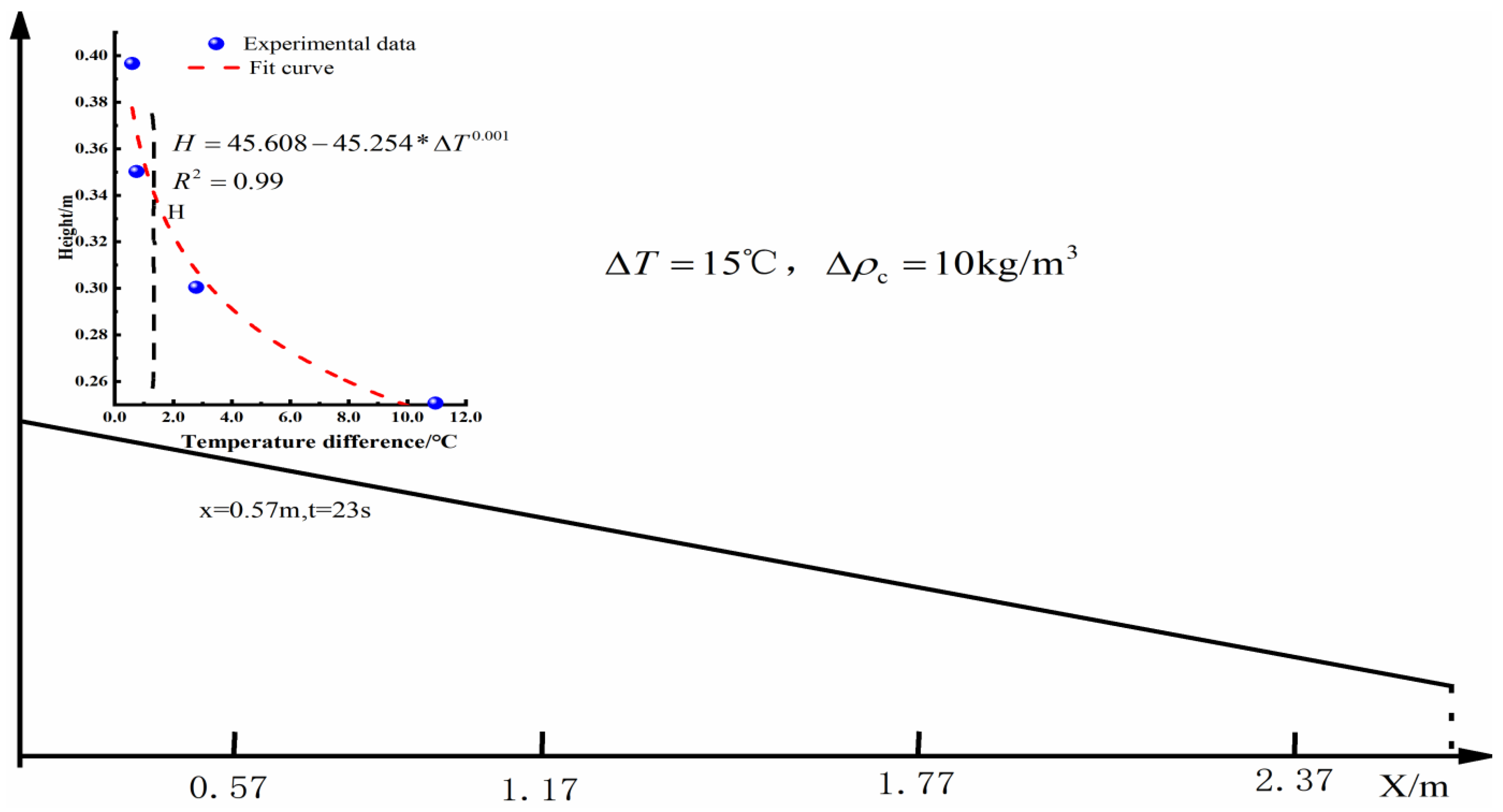
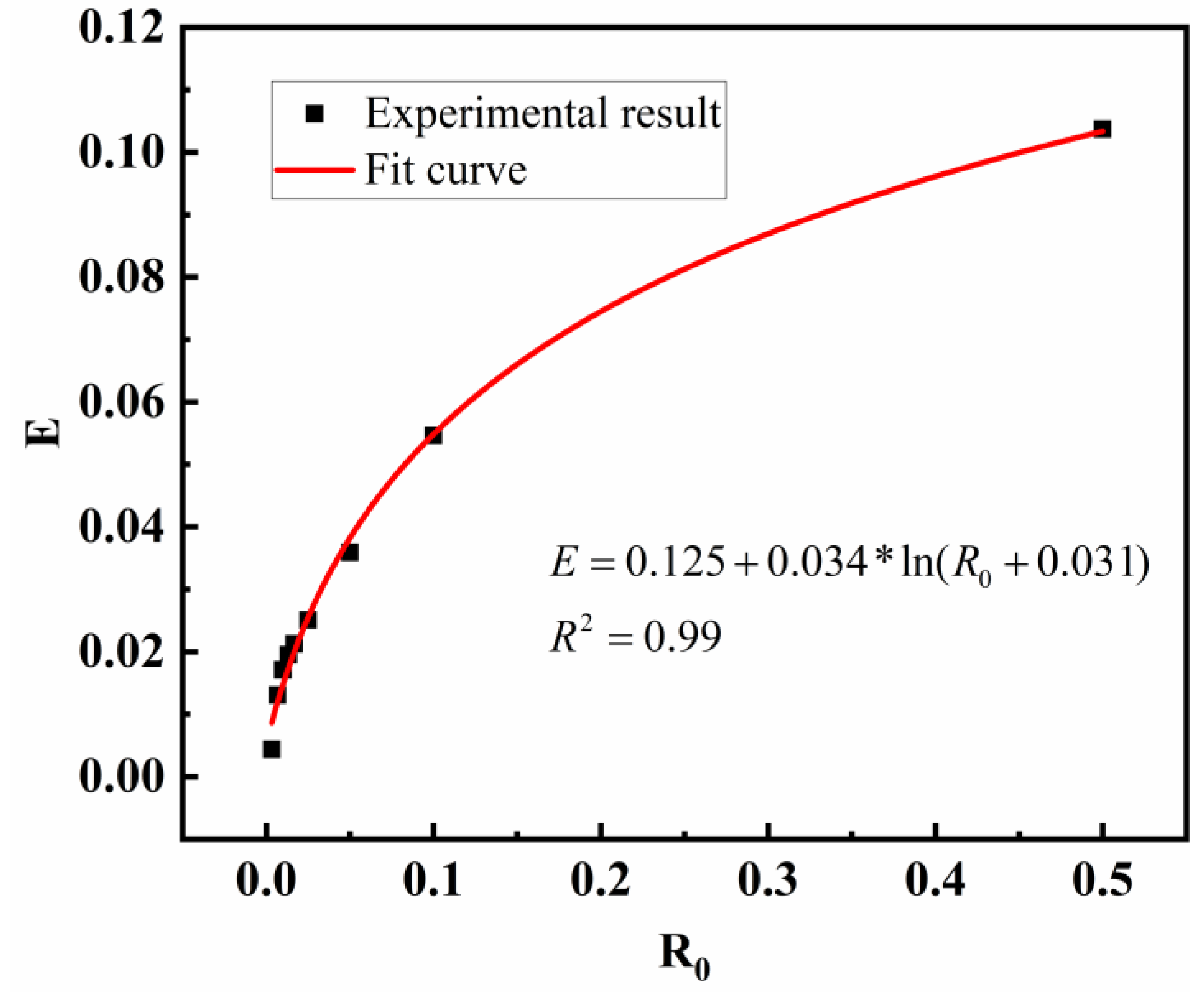
5.2. The Relationship Between and
5.3. The Relationship Between and
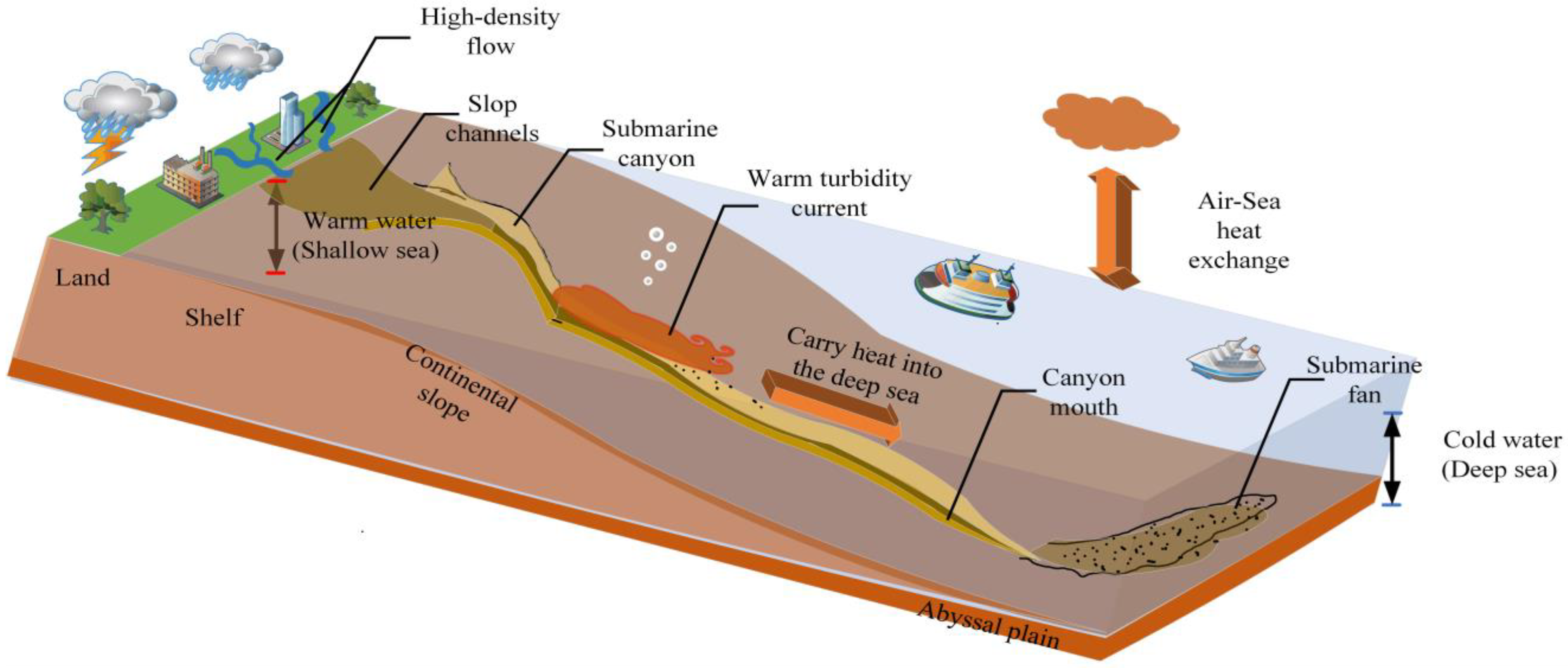
5.4. Implications and Hypotheses of Turbidity Currents in Marine Environments
6. Conclusions
- We quantitatively describe the convection and environmental mixing dynamics of shallow high-temperature turbidity currents at different sediment concentrations using the environmental entrainment coefficient and summarize the relationship between the environmental entrainment function and considering temperature effects: . Two simple dimensionless parameters effectively describe flow factors and flow patterns during turbidity current motion. These two parameters quantify the ratio of temperature, salinity, and sediment content, summarize the relationship between the dimensionless density ratio reflecting turbidity current convection and environmental mixing and the environmental entrainment number : and describe the impact of upper warm turbidity currents on the stable stratification of lake or coastal marine environments.
- During the heat transport process of turbidity currents, the temperature distribution in the vertical direction is exponential: , and 70% of the heat is concentrated in the lower half of the turbidity current for rapid transport, making the turbidity current efficiently store transported heat, reducing the vertical convective heat transfer loss, and facilitating the long-range transport of heat carried by turbidity. The continuous input of the turbidity current will be accompanied by a large amount of energy transfer, which will affect the temperature distribution in the regional marine environment.
- Heat transfer at the sea–air interface has difficulty changing the energy distribution in the deep sea, and the effect of turbidity currents is opposite to the effect of river-to-ocean heat transfer or ocean surface-to-bottom heat transfer, directly affecting the thermal distribution of the internal or underpart of the ocean environment. The introduction of upper-layer heat into the deep sea by turbidity currents is an important component of the global heat transfer system that cannot be ignored, and it is also a complement to the heat transfer process of the global heat transfer system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
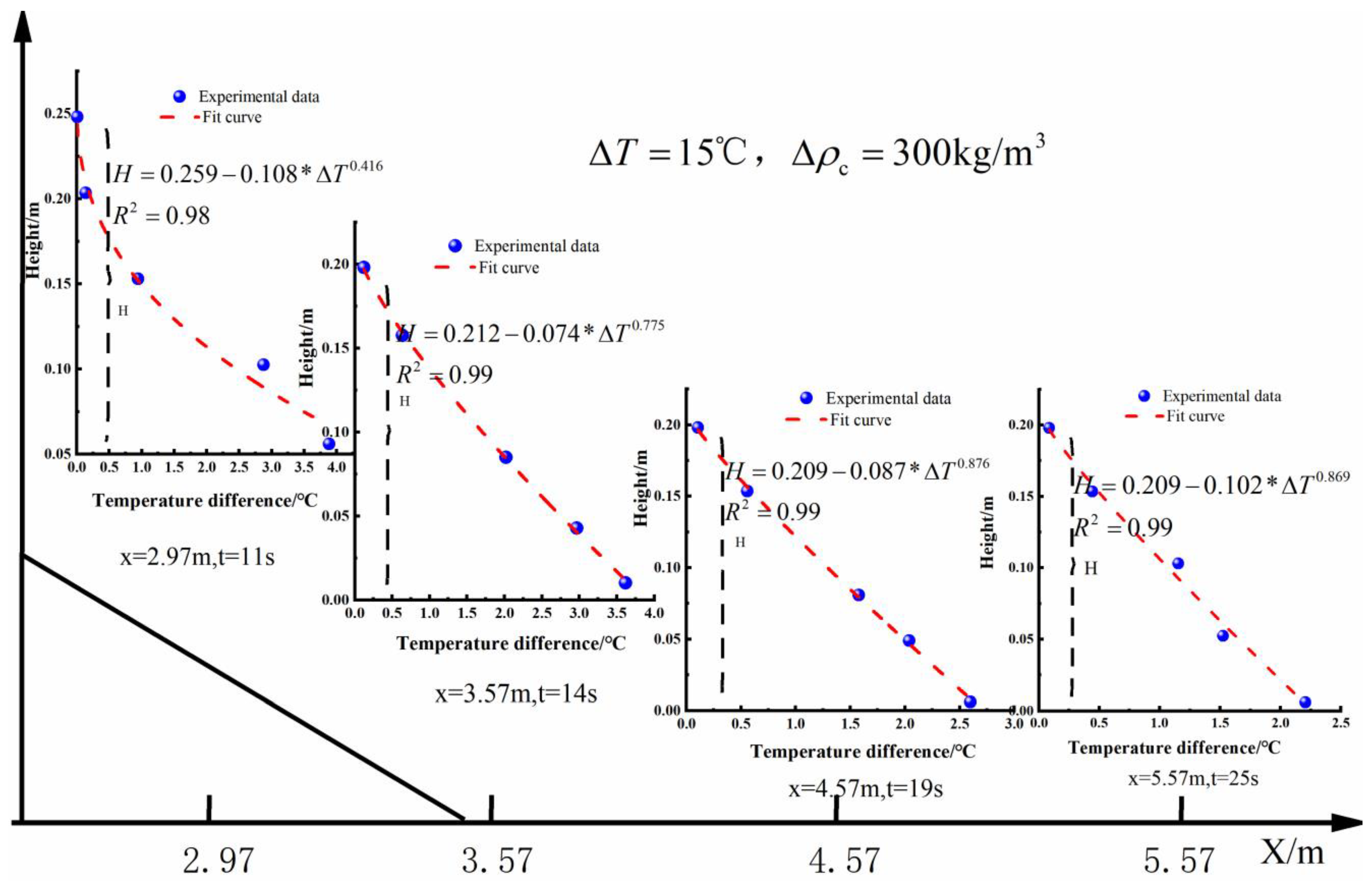

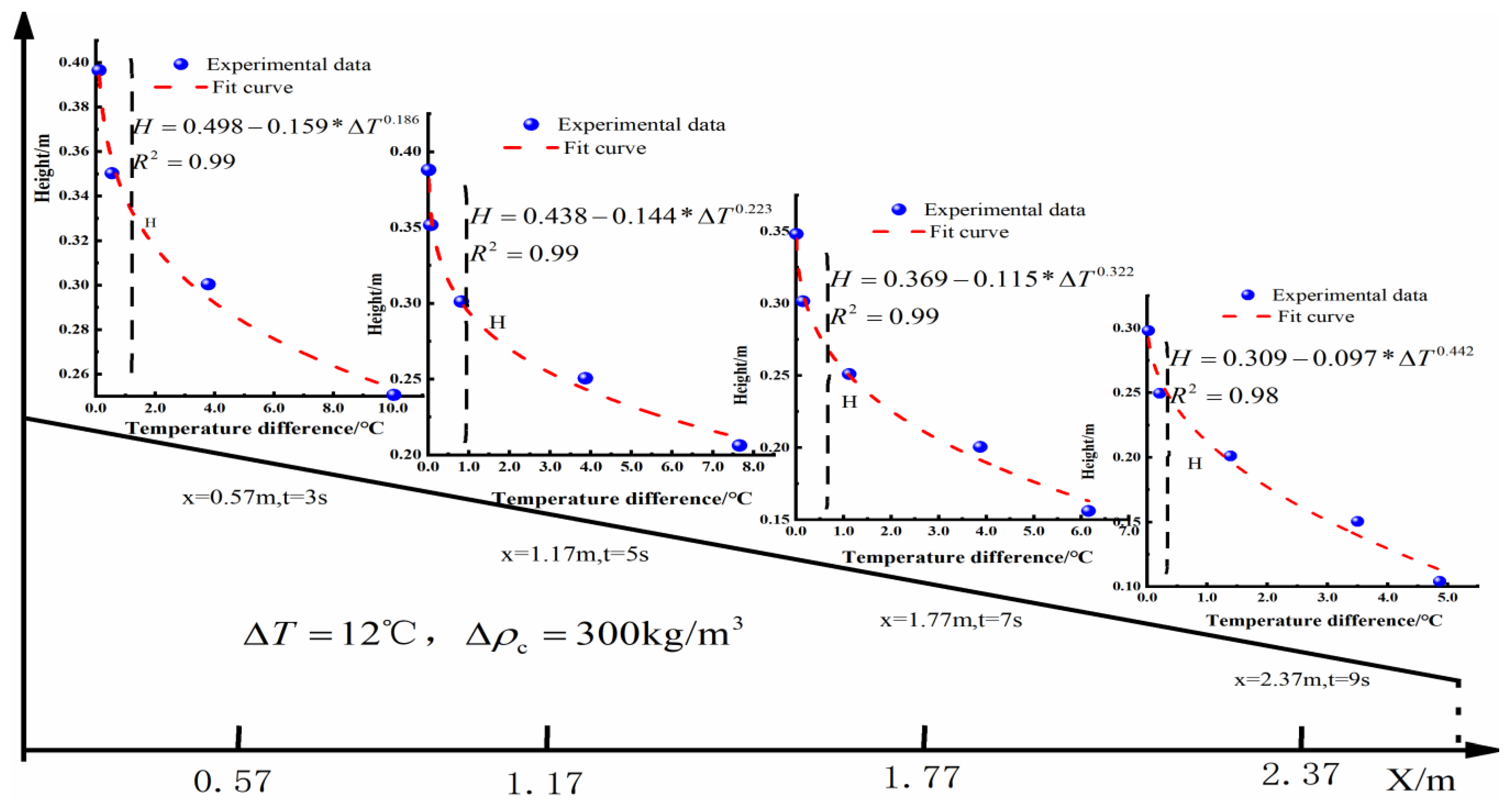
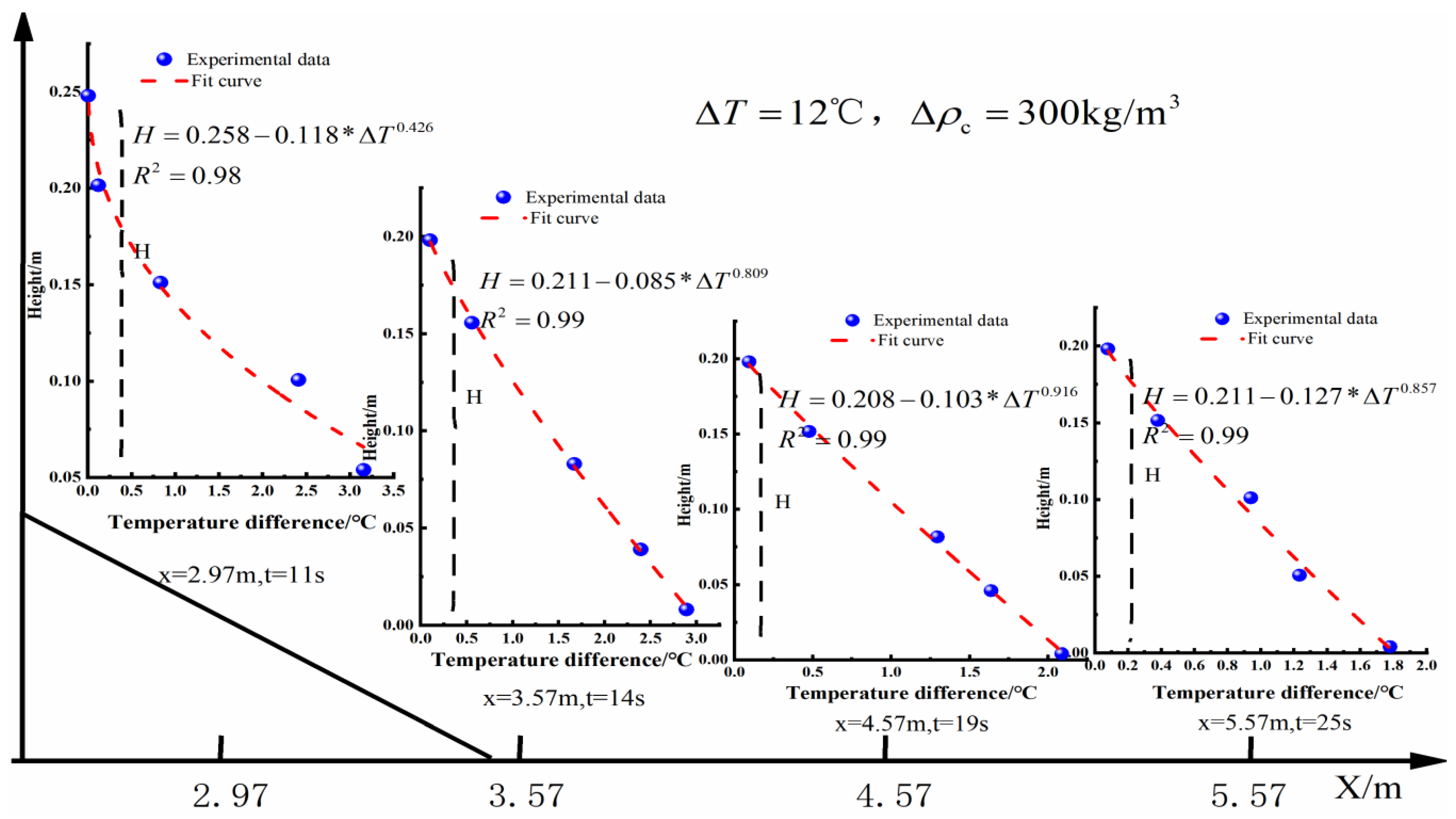
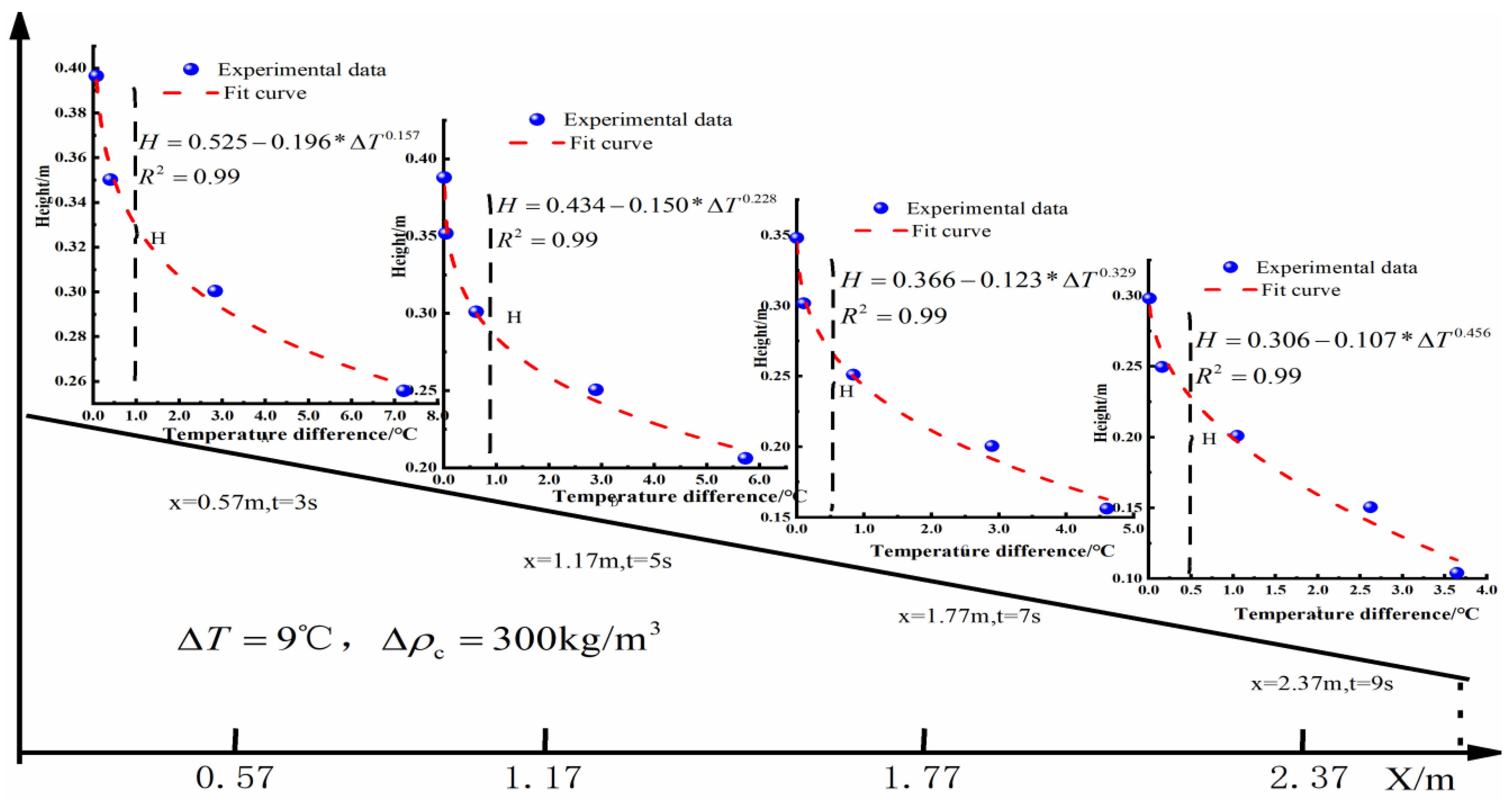

References
- Khripounoff, A.; Vangriesheim, A.; Babonneau, N.; Crassous, P.; Dennielou, B.; Savoye, B. Direct observation of intense turbidity current activity in the Zaire submarine valley at 4000 m water depth. Mar. Geol. 2003, 194, 151–158. [Google Scholar] [CrossRef]
- Piper, D.J.; Normark, W.R. Processes that initiate turbidity currents and their influence on turbidites: A marine geology perspective. J. Sediment. Res. 2009, 79, 347–362. [Google Scholar] [CrossRef]
- Talling, P.J.; Masson, D.G.; Sumner, E.J.; Malgesini, G. Subaqueous sediment density flows: Depositional processes and deposit types. Sedim 2012, 59, 1937–2003. [Google Scholar] [CrossRef]
- Xu, J.; Noble, M.; Rosenfeld, L.K. In-situ measurements of velocity structure within turbidity currents. GeoRL 2004, 31. [Google Scholar] [CrossRef]
- Tian, Z.; Huang, J.; Xiang, J.; Zhang, S. Suspension and transportation of sediments in submarine canyon induced by internal solitary waves. PhFl 2024, 36, 022112. [Google Scholar] [CrossRef]
- Dalrymple, R.W.; Mackay, D.A.; Ichaso, A.A.; Choi, K.S. Processes, morphodynamics, and facies of tide-dominated estuaries. Princ. Tidal Sedimentol. 2012, 79–107. [Google Scholar] [CrossRef]
- Hage, S.; Galy, V.; Cartigny, M.; Acikalin, S.; Clare, M.; Gröcke, D.; Hilton, R.; Hunt, J.; Lintern, D.; McGhee, C. Efficient preservation of young terrestrial organic carbon in sandy turbidity-current deposits. Geo 2020, 48, 882–887. [Google Scholar] [CrossRef]
- Kane, I.A.; Clare, M.A. Dispersion, accumulation, and the ultimate fate of microplastics in deep-marine environments: A review and future directions. Front. Earth Sci. 2019, 7, 80. [Google Scholar] [CrossRef]
- Pohl, F.; Eggenhuisen, J.T.; Kane, I.A.; Clare, M.A. Transport and burial of microplastics in deep-marine sediments by turbidity currents. Environ. Sci. Technol. 2020, 54, 4180–4189. [Google Scholar] [CrossRef]
- Tian, H.; Ren, Y.; Chen, Z.; Tao, W.; Wu, H.; Xu, G. Numerical Study of the Transport Process of Shallow Heat Carried by Turbidity Currents in Deep-Sea Environments. J. Geophys. Res. Ocean. 2023, 128, e2022JC019478. [Google Scholar] [CrossRef]
- Danovaro, R.; Bianchelli, S.; Gambi, C.; Mea, M.; Zeppilli, D. α-, β-, γ-, δ-and ε-diversity of deep-sea nematodes in canyons and open slopes of Northeast Atlantic and Mediterranean margins. Mar. Ecol. Prog. Ser. 2009, 396, 197–209. [Google Scholar] [CrossRef]
- Lambshead, P.J.D. Marine Nematode Biodiversity; Volume 1: Nematode morphology, physiology, and ecology; CABI Publishing: Wallingford, UK, 2004; pp. 438–468. [Google Scholar]
- Heip, C.; Vincx, M.; Vranken, G. The ecology of marine nematodes. Oceanogr. Mar. Biol. 1985, 23, 399–489. [Google Scholar]
- Danovaro, R.; Dell’Anno, A.; Pusceddu, A. Biodiversity response to climate change in a warm deep sea. Ecol. Lett. 2004, 7, 821–828. [Google Scholar] [CrossRef]
- Paull, C.K.; Talling, P.J.; Maier, K.L.; Parsons, D.; Xu, J.; Caress, D.W.; Gwiazda, R.; Lundsten, E.M.; Anderson, K.; Barry, J.P. Powerful turbidity currents driven by dense basal layers. Nat. Commun. 2018, 9, 4114. [Google Scholar] [CrossRef]
- Simmons, S.; Azpiroz-Zabala, M.; Cartigny, M.; Clare, M.; Cooper, C.; Parsons, D.; Pope, E.; Sumner, E.; Talling, P. Novel acoustic method provides first detailed measurements of sediment concentration structure within submarine turbidity currents. J. Geophys. Res. Ocean. 2020, 125, e2019JC015904. [Google Scholar] [CrossRef]
- Hage, S.; Cartigny, M.J.; Sumner, E.J.; Clare, M.A.; Hughes Clarke, J.E.; Talling, P.J.; Lintern, D.G.; Simmons, S.M.; Silva Jacinto, R.; Vellinga, A.J. Direct monitoring reveals initiation of turbidity currents from extremely dilute river plumes. Geophys. Res. Lett. 2019, 46, 11310–11320. [Google Scholar] [CrossRef]
- Kelly, R.; Dorrell, R.; Burns, A.; McCaffrey, W. The structure and entrainment characteristics of partially confined gravity currents. J. Geophys. Res. Ocean. 2019, 124, 2110–2125. [Google Scholar] [CrossRef]
- Traer, M.; Hilley, G.; Fildani, A.; McHargue, T. The sensitivity of turbidity currents to mass and momentum exchanges between these underflows and their surroundings. J. Geophys. Res. Earth Surf. 2012, 117, 7. [Google Scholar] [CrossRef]
- Gill, A.E. Atmosphere-Ocean Dynamics; Academic Press: Cambridge, MA, USA, 1982; Volume 30. [Google Scholar]
- Hwang, J.-S.; Souissi, S.; Dahms, H.-U.; Tseng, L.-C.; Schmitt, F.G.; Chen, Q.-C. Rank-abundance allocations as a tool to analyze planktonic copepod assemblages off the Danshuei river estuary (Northern Taiwan). Zool. Stud. 2009, 48, 49–62. [Google Scholar]
- Sparkes, R.B.; Lin, I.-T.; Hovius, N.; Galy, A.; Liu, J.T.; Xu, X.; Yang, R. Redistribution of multi-phase particulate organic carbon in a marine shelf and canyon system during an exceptional river flood: Effects of Typhoon Morakot on the Gaoping River–Canyon system. Mar. Geol. 2015, 363, 191–201. [Google Scholar] [CrossRef]
- Wang, R.-M.; You, C.-F.; Chu, H.-Y.; Hung, J.-J. Seasonal variability of dissolved major and trace elements in the Gaoping (Kaoping) River Estuary, Southwestern Taiwan. J. Mar. Syst. 2009, 76, 444–456. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Zhao, Y.; Colin, C.; Zhang, X.; Wang, M.; Zhao, S.; Kneller, B.J.G. Long-term in situ observations on typhoon-triggered turbidity currents in the deep sea. Geo 2018, 46, 675–678. [Google Scholar] [CrossRef]
- Puig, P.; Ogston, A.S.; Mullenbach, B.; Nittrouer, C.; Parsons, J.; Sternberg, R. Storm-induced sediment gravity flows at the head of the Eel submarine canyon, northern California margin. J. Geophys. Res. Ocean. 2004, 109, C03019. [Google Scholar] [CrossRef]
- Xu, J.; Sequeiros, O.E.; Noble, M.A. Sediment concentrations, flow conditions, and downstream evolution of two turbidity currents, Monterey Canyon, USA. Deep Sea Res. Part I 2014, 89, 11–34. [Google Scholar] [CrossRef]
- Bailey, L.P.; Clare, M.A.; Rosenberger, K.J.; Cartigny, M.J.; Talling, P.J.; Paull, C.K.; Gwiazda, R.; Parsons, D.R.; Simmons, S.M.; Xu, J. Preconditioning by sediment accumulation can produce powerful turbidity currents without major external triggers. Earth Planet. Sci. Lett. 2021, 562, 116845. [Google Scholar] [CrossRef]
- Azpiroz-Zabala, M.; Cartigny, M.J.; Talling, P.J.; Parsons, D.R.; Sumner, E.J.; Clare, M.A.; Simmons, S.M.; Cooper, C.; Pope, E.L. Newly recognized turbidity current structure can explain prolonged flushing of submarine canyons. Sci. Adv. 2017, 3, e1700200. [Google Scholar] [CrossRef]
- Descy, J.P.; Darchambeau, F.; Lambert, T.; Stoyneva-Gaertner, M.P.; Bouillon, S.; Borges, A.V. Phytoplankton dynamics in the Congo River. Freshw. Biol. 2017, 62, 87–101. [Google Scholar] [CrossRef]
- Barats, A.; Féraud, G.; Potot, C.; Philippini, V.; Travi, Y.; Durrieu, G.; Dubar, M.; Simler, R. Naturally dissolved arsenic concentrations in the Alpine/Mediterranean Var River watershed (France). Sci. Total Environ. 2014, 473, 422–436. [Google Scholar] [CrossRef]
- Khripounoff, A.; Crassous, P.; Bue, N.L.; Dennielou, B.; Jacinto, R.S. Different types of sediment gravity flows detected in the Var submarine canyon (northwestern Mediterranean Sea). Prog. Oceanogr. 2012, 106, 138–153. [Google Scholar] [CrossRef]
- Palanques, A.; de Madron, X.D.; Puig, P.; Fabres, J.; Guillén, J.; Calafat, A.; Canals, M.; Heussner, S.; Bonnin, J. Suspended sediment fluxes and transport processes in the Gulf of Lions submarine canyons. The role of storms and dense water cascading. Mar. Geol. 2006, 234, 43–61. [Google Scholar] [CrossRef]
- Halbwachs, M.; Sabroux, J.C.; Grangeon, J.; Kayser, G.; Tochon-Danguy, J.C.; Felix, A.; B’eard, J.C.; Villevieille, A.; Vitter, G.; Richon, P. Degassing the “killer lakes” Nyos and Monoun, Cameroon. Eos Trans. Am. Geophys. Union 2004, 85, 281–285. [Google Scholar] [CrossRef]
- Sparks, R.S.J.; Bonnecaze, R.T.; Huppert, H.E.; Lister, J.R.; Hallworth, M.A.; Mader, H.; Phillips, J. Sediment-laden gravity currents with reversing buoyancy. Earth Planet. Sci. Lett. 1993, 114, 243–257. [Google Scholar] [CrossRef]
- Cantelli, A.; Johnson, S.; White, J.; Parker, G. Sediment sorting in the deposits of turbidity currents created by experimental modeling of explosive subaqueous eruptions. J. Geol. 2008, 116, 76–93. [Google Scholar] [CrossRef]
- Gladstone, C.; Pritchard, D. Patterns of deposition from experimental turbidity currents with reversing buoyancy. Sedim 2010, 57, 53–84. [Google Scholar] [CrossRef]
- Hizzett, J.L.; Hughes Clarke, J.E.; Sumner, E.J.; Cartigny, M.; Talling, P.; Clare, M. Which triggers produce the most erosive, frequent, and longest runout turbidity currents on deltas? GeoRL 2018, 45, 855–863. [Google Scholar] [CrossRef]
- Kineke, G.; Woolfe, K.; Kuehl, S.; Milliman, J.D.; Dellapenna, T.; Purdon, R. Sediment export from the Sepik River, Papua New Guinea: Evidence for a divergent sediment plume. Cont. Shelf. Res. 2000, 20, 2239–2266. [Google Scholar] [CrossRef]
- Steel, E.; Buttles, J.; Simms, A.R.; Mohrig, D.; Meiburg, E. The role of buoyancy reversal in turbidite deposition and submarine fan geometry. Geo 2017, 45, 35–38. [Google Scholar] [CrossRef]
- Steel, E.; Simms, A.R.; Warrick, J.; Yokoyama, Y. Highstand shelf fans: The role of buoyancy reversal in the deposition of a new type of shelf sand body. Bulletin 2016, 128, 1717–1724. [Google Scholar] [CrossRef]
- Lu, G.; Wells, M.; van Strygen, I.; Hecky, R.E. Intrusions of sediment laden rivers into density stratified water columns could be an unrecognized source of mixing in many lakes and coastal oceans. Sedim 2022, 69, 2228–2245. [Google Scholar] [CrossRef]
- Morton, B.; Taylor, G.I.; Turner, J.S. Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 234, 1–23. [Google Scholar] [CrossRef]
- Jacobson, M.; Testik, F.Y. Turbulent entrainment into fluid mud gravity currents. Environ. Fluid Mech. 2014, 14, 541–563. [Google Scholar] [CrossRef]
- Han, D.; He, Z.; Lin, Y.T.; Wang, Y.; Guo, Y.; Yuan, Y. Hydrodynamics and sediment transport of downslope turbidity current through rigid vegetation. Water Resour. Res. 2023, 59, e2023WR034421. [Google Scholar] [CrossRef]
- He, Z.; Zhao, L.; Lin, T.; Hu, P.; lv, Y.; Ho, H.-C.; Lin, Y.-T. Hydrodynamics of gravity currents down a ramp in linearly stratified environments. J. Hydraul. Eng. 2017, 143, 04016085. [Google Scholar] [CrossRef]
- Carter, L.; Gavey, R.; Talling, P.J.; Liu, J.T. Insights into submarine geohazards from breaks in subsea telecommunication cables. Oceanography 2014, 27, 58–67. [Google Scholar] [CrossRef]
- Talling, P.J.; Clare, M.L.; Urlaub, M.; Pope, E.; Hunt, J.E.; Watt, S.F. Large submarine landslides on continental slopes: Geohazards, methane release, and climate change. Oceanography 2014, 27, 32–45. [Google Scholar] [CrossRef]
- Tanaka, M.; Girard, G.; Davis, R.; Peuto, A.; Bignell, N. Recommended table for the density of water between 0 C and 40 C based on recent experimental reports. Metro 2001, 38, 301. [Google Scholar] [CrossRef]
- Kneller, B.; Nasr-Azadani, M.M.; Radhakrishnan, S.; Meiburg, E. Long-range sediment transport in the world’s oceans by stably stratified turbidity currents. J. Geophys. Res. Ocean. 2016, 121, 8608–8620. [Google Scholar] [CrossRef]
- Giorgio Serchi, F.; Peakall, J.; Ingham, D.; Burns, A. A unifying computational fluid dynamics investigation on the river-like to river-reversed secondary circulation in submarine channel bends. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Sequeiros, O.E.; Spinewine, B.; Beaubouef, R.T.; Sun, T.; García, M.H.; Parker, G. Characteristics of velocity and excess density profiles of saline underflows and turbidity currents flowing over a mobile bed. J. Hydraul. Eng. 2010, 136, 412–433. [Google Scholar] [CrossRef]
- Hiscott, R.N. Loss of capacity, not competence, as the fundamental process governing deposition from turbidity currents. J. Sediment. Res. 1994, 64, 209–214. [Google Scholar] [CrossRef]
- Sumner, E.J.; Amy, L.A.; Talling, P.J. Deposit structure and processes of sand deposition from decelerating sediment suspensions. J. Sediment. Res. 2008, 78, 529–547. [Google Scholar] [CrossRef]
- Johnson, H.P.; Miller, U.K.; Salmi, M.S.; Solomon, E.A. Analysis of bubble plume distributions to evaluate methane hydrate decomposition on the continental slope. Geochem. Geophys. Geosyst. 2015, 16, 3825–3839. [Google Scholar] [CrossRef]
- Phrampus, B.J.; Hornbach, M.J. Recent changes to the Gulf Stream causing widespread gas hydrate destabilization. Nature 2012, 490, 527–530. [Google Scholar] [CrossRef]
- Dorrell, R.; Peakall, J.; Sumner, E.; Parsons, D.; Darby, S.; Wynn, R.; Özsoy, E.; Tezcan, D. Flow dynamics and mixing processes in hydraulic jump arrays: Implications for channel-lobe transition zones. Mar. Geol. 2016, 381, 181–193. [Google Scholar] [CrossRef]
- Meiburg, E.; Kneller, B. Turbidity currents and their deposits. AnRFM 2010, 42, 135–156. [Google Scholar] [CrossRef]
- Turner, J. Turbulent entrainment: The development of the entrainment assumption, and its application to geophysical flows. JFM 1986, 173, 431–471. [Google Scholar] [CrossRef]
- Imran, J.; Khan, S.M.; Pirmez, C.; Parker, G. Froude scaling limitations in modeling of turbidity currents. Environ. Fluid Mech. 2017, 17, 159–186. [Google Scholar] [CrossRef]
- Akan, A.O.; Iyer, S.S. Open Channel Hydraulics; Butterworth-Heinemann: Oxford, UK, 2021. [Google Scholar]
- Task Committee on Hydraulic Modeling of the Environmental; Water Resources Institute of ASCE. Hydraulic Modeling: Concepts and Practice; ACSE: Reston, VA, USA, 2000. [Google Scholar]
- Marino, M.; Stagnitti, M.; Stancanelli, L.M.; Musumeci, R.E.; Foti, E. Dynamics of wave-supported gravity currents in intermediate water. Cont. Shelf. Res. 2023, 267, 105082. [Google Scholar] [CrossRef]
- Monaghan, J. Gravity currents and solitary waves. Phys. D Nonlinear Phenom. 1996, 98, 523–533. [Google Scholar] [CrossRef]
- Tian, Z.; Liu, C.; Jia, Y.; Song, L.; Zhang, M. Submarine trenches and wave-wave interactions enhance the sediment resuspension induced by internal solitary waves. J. Ocean Univ. China 2023, 22, 983–992. [Google Scholar] [CrossRef]
- Falcini, F.; Fagherazzi, S.; Jerolmack, D. Wave-supported sediment gravity flows currents: Effects of fluid-induced pressure gradients and flow width spreading. Cont. Shelf. Res. 2012, 33, 37–50. [Google Scholar] [CrossRef]
- Tian, Z.; Huang, J.; Xiang, J.; Zhang, S.; Wu, J.; Liu, X.; Luo, T.; Yue, J. Interaction between internal solitary waves and the seafloor in the deep sea. Deep. Undergr. Sci. Eng. 2024, 3, 149–162. [Google Scholar] [CrossRef]
- Piper, D.J.; Cochonat, P.; Morrison, M.L. The sequence of events around the epicentre of the 1929 Grand Banks earthquake: Initiation of debris flows and turbidity current inferred from sidescan sonar. Sedim 1999, 46, 79–97. [Google Scholar] [CrossRef]
- Rothwell, R.; Thomson, J.; Kähler, G. Low-sea-level emplacement of a very large Late Pleistocene ‘megaturbidite’in the western Mediterranean Sea. Nature 1998, 392, 377–380. [Google Scholar] [CrossRef]
- Talling, P.; Wynn, R.; Masson, D.; Frenz, M.; Cronin, B.; Schiebel, R.; Akhmetzhanov, A.; Dallmeier-Tiessen, S.; Benetti, S.; Weaver, P. Onset of submarine debris flow deposition far from original giant landslide. Nature 2007, 450, 541–544. [Google Scholar] [CrossRef]
- Milliman, J.D.; Syvitski, J.P. Geomorphic/tectonic control of sediment discharge to the ocean: The importance of small mountainous rivers. J. Geol. 1992, 100, 525–544. [Google Scholar] [CrossRef]
- Kao, S.; Dai, M.; Selvaraj, K.; Zhai, W.; Cai, P.; Chen, S.; Yang, J.; Liu, J.; Liu, C.; Syvitski, J. Cyclone-driven deep sea injection of freshwater and heat by hyperpycnal flow in the subtropics. Geophys. Res. Lett. 2010, 37, L21702. [Google Scholar] [CrossRef]
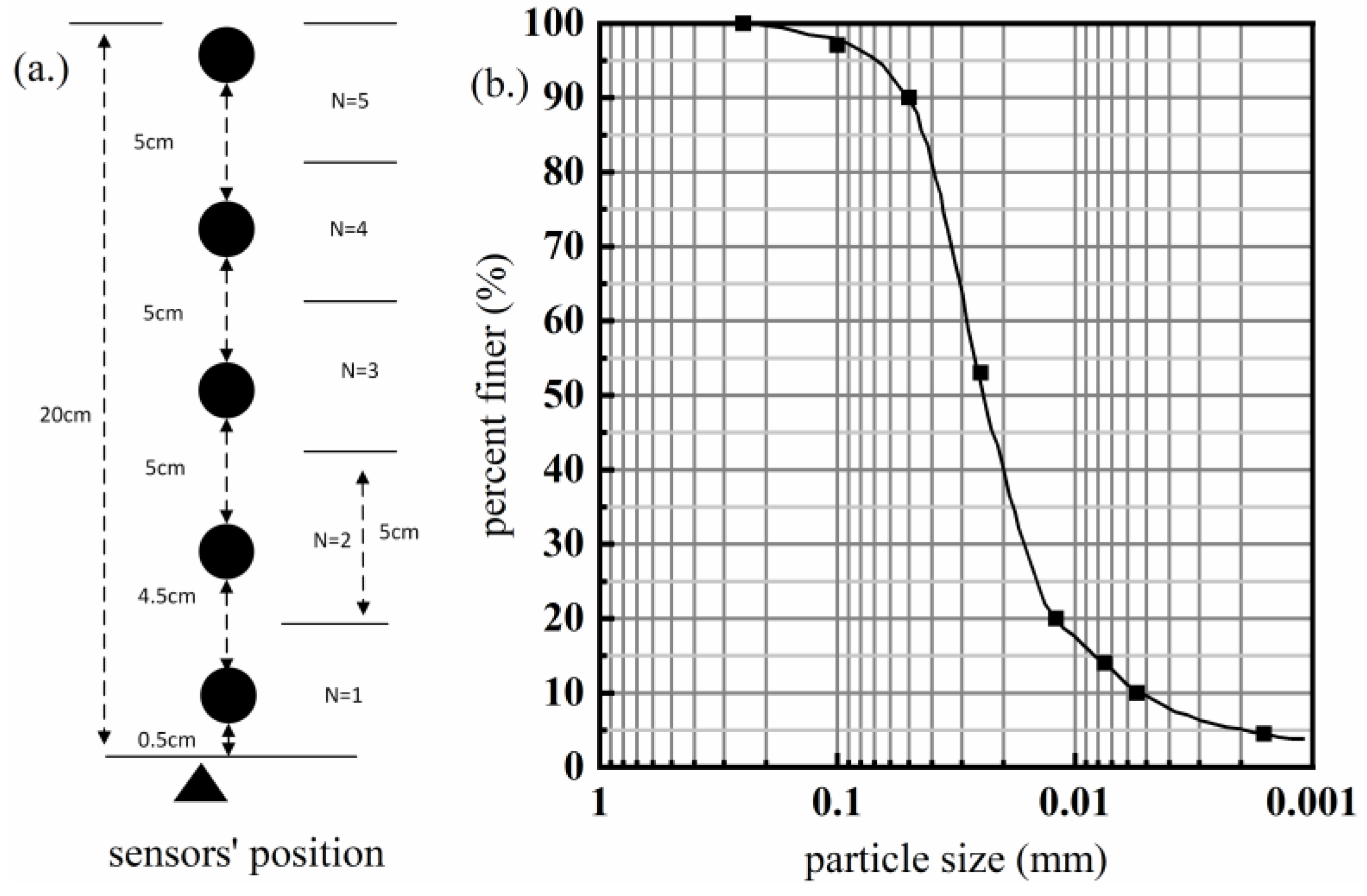

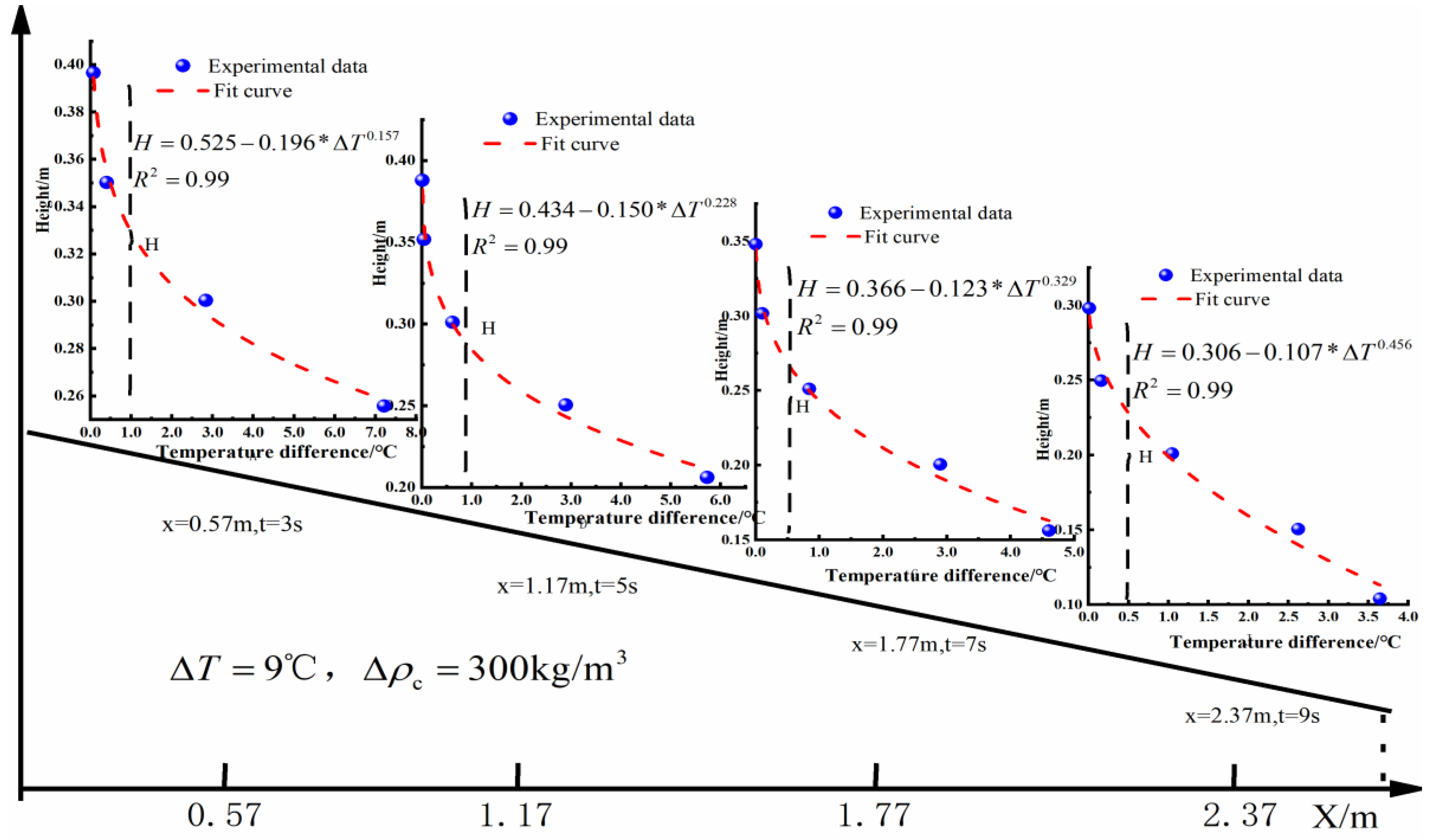
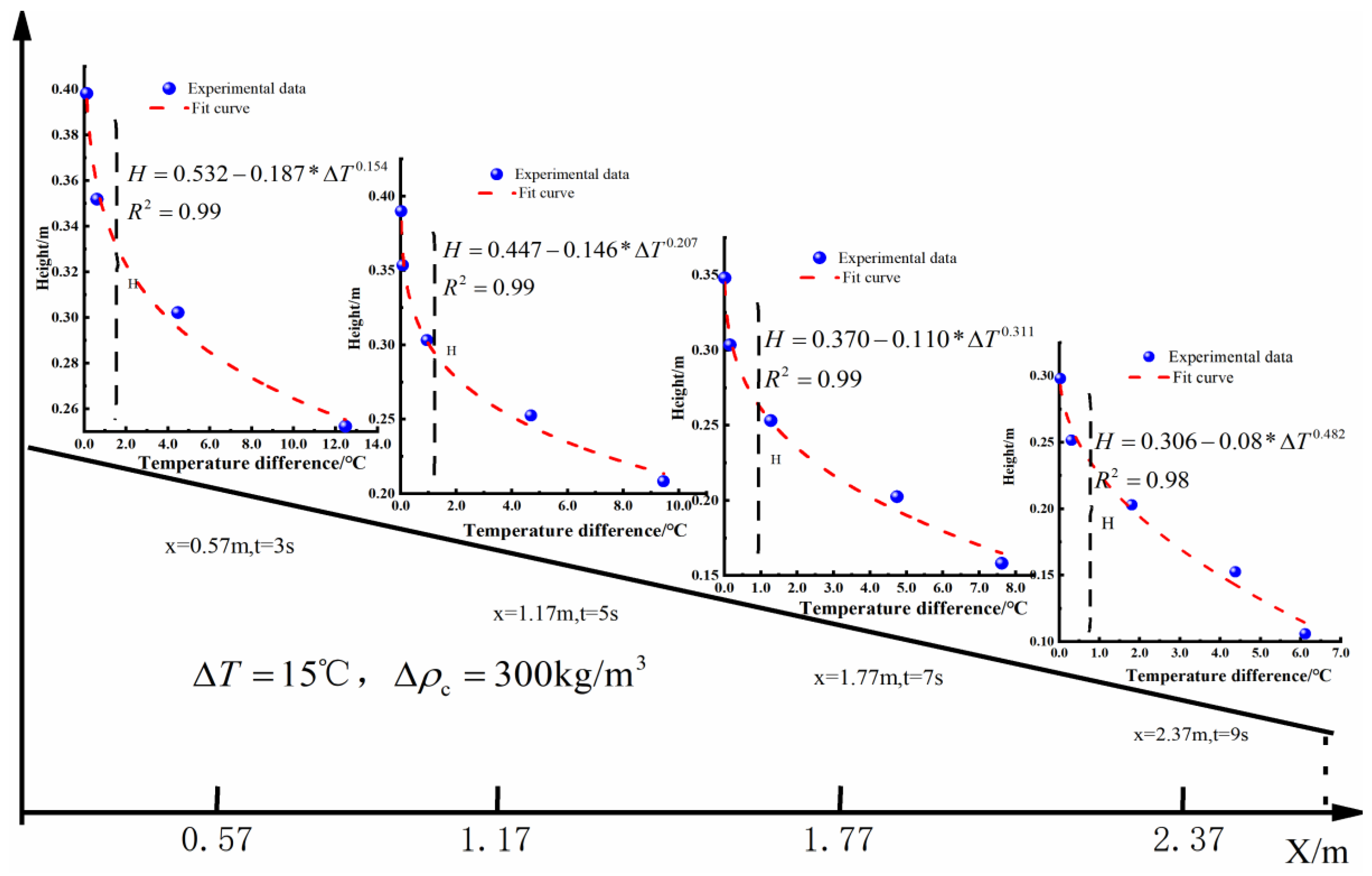
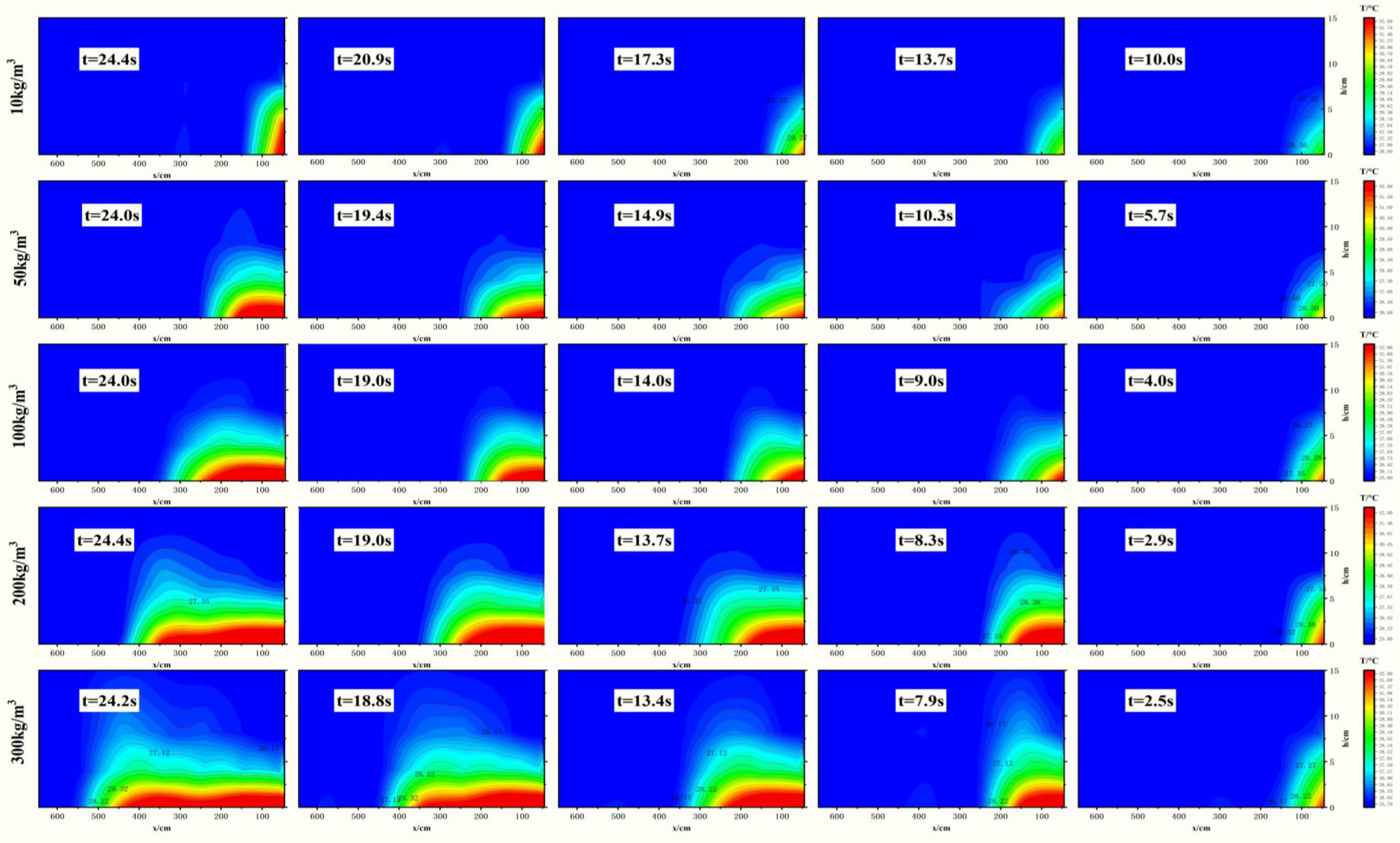

| Location of Turbidity Current | Time | Trigger Mechanism | Trigger Source Temperature | Ambient Temperature of Water Body Along the Movement of Turbidity Currents | Source |
|---|---|---|---|---|---|
| Gaoping Canyon | 7–10 August 2009 | Storms cause high-density floods | Gaoping River temperature: above 28 °C | Sea area: 0–200 m: 30–15 °C 200–500 m: 15–8 °C 500–1000 m: 8–5 °C 1000–4000 m: 5–3 °C | [21,22] |
| Gaoping Canyon | 14–17 September 2016 | Storms cause high-density floods | Gaoping River temperature: above 28 °C | Sea area: 0–200 m: 30–15 °C 200–500 m: 15–8 °C 500–1000 m: 8–5 °C 1000–4000 m: 5–3 °C | [23,24] |
| Eel Bay Canyon | 12 January–3 April 2000 | Storms, not directly related to river floods | 0–100 m: 14–10 °C | Sea area: 100–200 m: 10–9 °C 200–400 m: 9–7 °C 400–1500 m: 7–3 °C | [25,26] |
| Monterey Canyon | 17–19 December 2002 | Highly consistent with the storm activity | 0–200 m: 14–9 °C | Sea area: 200–500 m: 9–5 °C 500–1500 m: 5–3 °C | [26] |
| Monterey Canyon | Winter | Failure of canyon head or slope due to sediment accumulation | 0–200 m: 14–9 °C | Sea area: 200–500 m: 9–5 °C 500–1500 m: 5–3 °C | [26,27] |
| Congo Canyon | December 2019–March 2010 | Increased flow of high-density rivers | Congo River water temperature: above 26 °C | Sea area: 0–200 m: 30–15 °C, 200–500 m: 15–8 °C Under 500 m: 8–3 °C | [28,29] |
| Val Canyon | 17–19 December 2008 5–8 February 2009 | High-density flow during river flooding and some local storms | Annual average temperature of Val River: 17–25 °C | Sea area: 0–510 m: 25–13 °C 510–1280 m: 13–3 °C | [30,31] |
| Lion Bay Canyon | 12 November 2003 | Rivers flooded during the storm | 0–100 m: 17–16 °C | Sea area: 100–200 m: 16–15 °C 200–300 m: 15–13 °C Under 300 m: 13–3 °C | [32] |
| Sediment Concentration/ | V/L | Turbidity Water Temperature/°C | Ambient Water Temperature/°C | / | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0.500 | 0.006 | 10.00 | 20 | 40.80 | 992.20 | 25.80 | 997.20 | 15.0 | 5.0 |
| 0.100 | 0.030 | 50.00 | 20 | 40.80 | 992.20 | 25.80 | 997.20 | 15.0 | 5.0 |
| 0.050 | 0.062 | 100.00 | 20 | 40.80 | 992.20 | 25.80 | 997.20 | 15.0 | 5.0 |
| 0.025 | 0.124 | 200.00 | 20 | 40.80 | 992.20 | 25.80 | 997.20 | 15.0 | 5.0 |
| 0.017 | 0.186 | 300.00 | 20 | 40.80 | 992.20 | 25.80 | 997.20 | 15.0 | 5.0 |
| 0.013 | 0.186 | 300.00 | 20 | 37.80 | 993.20 | 25.80 | 997.20 | 12.0 | 4.0 |
| 0.010 | 0.186 | 300.00 | 20 | 34.80 | 994.20 | 25.80 | 997.20 | 9.0 | 3.0 |
| 0.007 | 0.186 | 300.00 | 20 | 31.80 | 995.20 | 25.80 | 997.20 | 6.0 | 2.0 |
| 0.003 | 0.186 | 300.00 | 20 | 28.80 | 996.20 | 25.80 | 997.20 | 3.0 | 1.0 |
| 0.010 | 0.186 | 300.00 | 40 | 34.80 | 994.20 | 25.80 | 997.20 | 9.0 | 3.0 |
| 0.010 | 0.186 | 300.00 | 60 | 34.80 | 994.20 | 25.80 | 997.20 | 9.0 | 3.0 |
| 0.010 | 0.186 | 300.00 | 80 | 34.80 | 994.20 | 25.80 | 997.20 | 9.0 | 3.0 |
| 0.010 | 0.186 | 300.00 | 100 | 34.80 | 994.20 | 25.80 | 997.20 | 9.0 | 3.0 |
| Migration Distance/m | Time/s | Turbidity Current Height/m | ||||||
|---|---|---|---|---|---|---|---|---|
| 3.0 | 5.52 | 24.0 | 0.23 | 1297.00 | 2.996 | 56.421 | 4.231 | 0.004 |
| 6.0 | 5.52 | 24.0 | 0.23 | 1296.00 | 2.986 | 56.233 | 4.217 | 0.013 |
| 9.0 | 5.52 | 24.0 | 0.23 | 1295.00 | 2.976 | 56.044 | 4.203 | 0.017 |
| 12.0 | 5.52 | 24.0 | 0.23 | 1294.00 | 2.966 | 55.855 | 4.189 | 0.019 |
| 15.0 | 5.52 | 24.0 | 0.23 | 1293.00 | 2.956 | 55.667 | 4.175 | 0.021 |
| 15.0 | 4.80 | 24.0 | 0.20 | 1193.00 | 1.954 | 49.275 | 3.695 | 0.025 |
| 15.0 | 3.36 | 24.0 | 0.14 | 1093.00 | 0.952 | 45.961 | 3.447 | 0.036 |
| 15.0 | 2.40 | 24.0 | 0.10 | 1043.00 | 0.451 | 44.701 | 3.352 | 0.055 |
| 15.0 | 1.44 | 24.0 | 0.06 | 1003.00 | 0.050 | 15.682 | 1.176 | 0.104 |
| 9.0 | 6.72 | 24.0 | 0.28 | 1295.00 | 2.976 | 0.0750 | 4.203 | 0.018 |
| 9.0 | 7.68 | 24.0 | 0.32 | 1295.00 | 2.976 | 0.0753 | 4.203 | 0.017 |
| 9.0 | 8.40 | 24.0 | 0.35 | 1295.00 | 2.976 | 0.0751 | 4.203 | 0.016 |
| 9.0 | 8.88 | 24.0 | 0.37 | 1295.00 | 2.976 | 0.0756 | 4.203 | 0.015 |
| U | E | ||||
|---|---|---|---|---|---|
| 0.0033 | 5.3000 | 4.8463 | 0.2304 | 0.0010 | 0.0044 |
| 0.0067 | 5.3000 | 4.8463 | 0.2304 | 0.0030 | 0.0131 |
| 0.0100 | 5.3000 | 4.8463 | 0.2304 | 0.0039 | 0.0171 |
| 0.0134 | 5.3000 | 4.8463 | 0.2304 | 0.0045 | 0.0195 |
| 0.0167 | 5.3000 | 4.8463 | 0.2304 | 0.0049 | 0.0213 |
| 0.0250 | 4.5700 | 0.5254 | 0.1987 | 0.0050 | 0.0250 |
| 0.0500 | 3.3100 | 0.3935 | 0.1439 | 0.0052 | 0.0359 |
| 0.1000 | 2.3100 | 0.2915 | 0.1004 | 0.0055 | 0.0546 |
| 0.5000 | 1.3000 | 0.1753 | 0.057 | 0.0059 | 0.1037 |
| Turbidity Volume/ | Heat Transport Efficiency/ | ||||||
|---|---|---|---|---|---|---|---|
| 20 | 1295 | 3 | 4182 | 1182 | 286.791 | 38.717 | 0.135 |
| 20 | 1295 | 6 | 4182 | 1182 | 573.581 | 115.8637 | 0.202 |
| 20 | 1295 | 9 | 4182 | 1182 | 860.372 | 212.512 | 0.247 |
| 20 | 1295 | 12 | 4182 | 1182 | 1147.163 | 308.587 | 0.269 |
| 20 | 1295 | 15 | 4182 | 1182 | 1433.953 | 559.242 | 0.39 |
| 40 | 1295 | 9 | 4182 | 1182 | 1720.744 | 578.170 | 0.336 |
| 60 | 1295 | 9 | 4182 | 1182 | 2581.116 | 1022.122 | 0.396 |
| 80 | 1295 | 9 | 4182 | 1182 | 3441.488 | 1369.712 | 0.398 |
| 100 | 1295 | 9 | 4182 | 1182 | 4301.860 | 1772.366 | 0.412 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, H.; Xu, G.; Zhao, J.; Ren, Y.; Wu, H. Turbidity Currents Carrying Shallow Heat Invading Stable Deep-Water Areas May Be an Unrecognized Source of “Pollution” in the Ocean. Water 2024, 16, 3521. https://doi.org/10.3390/w16233521
Tian H, Xu G, Zhao J, Ren Y, Wu H. Turbidity Currents Carrying Shallow Heat Invading Stable Deep-Water Areas May Be an Unrecognized Source of “Pollution” in the Ocean. Water. 2024; 16(23):3521. https://doi.org/10.3390/w16233521
Chicago/Turabian StyleTian, Hao, Guohui Xu, Jingtao Zhao, Yupeng Ren, and Hanru Wu. 2024. "Turbidity Currents Carrying Shallow Heat Invading Stable Deep-Water Areas May Be an Unrecognized Source of “Pollution” in the Ocean" Water 16, no. 23: 3521. https://doi.org/10.3390/w16233521
APA StyleTian, H., Xu, G., Zhao, J., Ren, Y., & Wu, H. (2024). Turbidity Currents Carrying Shallow Heat Invading Stable Deep-Water Areas May Be an Unrecognized Source of “Pollution” in the Ocean. Water, 16(23), 3521. https://doi.org/10.3390/w16233521





