Peroxydisulfate Persistence in ISCO for Groundwater Remediation: Temperature Dependence, Batch/Column Comparison, and Sulfate Fate

Abstract

The persistence of peroxydisulfate anion (S₂O₈²⁻) in soil is a key factor influencing the effectiveness of in situ chemical oxidation (ISCO) treatments, which use S₂O₈²⁻ (S₂O₈²⁻ based ISCO) to remediate contaminated groundwater. However, only a few studies have addressed aspects of S₂O₈²⁻ persistence, such as the effect of temperature and the fate of sulfates (SO₄²⁻) generated by S₂O₈²⁻ decomposition in real soil and/or aquifer materials. Additionally, there are no studies comparing batch and dynamic column tests. To address these knowledge gaps, we conducted batch tests with varying temperatures (30–50 °C) and initial S₂O₈²⁻ concentrations (2.7 g/L and 16.1 g/L) along with dynamic column experiments (40 °C, 16.1 g/L) with comprehensively characterized real soil/aquifer materials. Furthermore, the principal component analysis (PCA) method was employed to investigate correlations between S₂O₈²⁻ decomposition and soil material parameters. We found that S₂O₈²⁻ decomposition followed the pseudo-first-order rate law in all experiments. In all tested soil materials, thermal dependence of S₂O₈²⁻ decomposition followed the Arrhenius law with the activation energies in the interval 65.2–109.1 kJ/mol. Decreasing S₂O₈²⁻ concentration from 16.1 g/L to 2.7 g/L led to a several-fold increase (factor 2–11) in bulk S₂O₈²⁻ decomposition rate coefficients (k′) in individual soil/aquifer materials. Although k′ in the dynamic column tests showed higher values compared to the batch tests (factor 1–3), the normalized S₂O₈²⁻ decomposition rate coefficients to the total BET surface were much lower, indicating the inevitable formation of preferential pathways in the columns. Furthermore, mass balance analysis of S₂O₈²⁻ decomposition and SO₄²⁻ generation suggests the ability of some systems to partially accumulate the produced SO₄²⁻. Principal Component Analysis (PCA) identified total organic carbon (TOC), Ni, Mo, Co, and Mn as key factors influencing the decomposition rate under varying soil conditions. These findings provide valuable insights into how S₂O₈²⁻ behaves in real soil and aquifer materials, which can improve the design and operation of ISCO treatability studies for groundwater remediation.

1. Introduction

Groundwater is a vital resource that supports drinking water supplies, agriculture, and industrial processes, making its protection and remediation critical for environmental and human health [1]. However, contamination from organic pollutants has become a pressing global challenge, necessitating the development of effective remediation techniques. ISCO is a well-established technique for groundwater remediation involving the injection of chemical oxidants to degrade organic pollutants [2]. Among the various oxidants employed, peroxydisulfate anion (S₂O₈²⁻) has gained prominence due to (i) the excellent water solubility and the relatively low cost of the source salt Na₂S₂O₈, (ii) its relative persistence in subsurface environments, and (iii) capacity to generate non-specific reactive oxidant species (ROS) through activation, primarily producing sulfate radicals (SO₄^•−) and indirectly generating hydroxyl radicals (^•OH), among others depending on specific subsurface conditions, which enables transformation of organic pollutants via various mechanisms [3,4,5].

Various methods have been explored to activate S₂O₈²⁻ [6,7,8], including heat [9] and UV radiation (Equation (1)) [10], base activation (Equation (2)) [11], dissolved transition metal ions (Equation (3)) [12], zerovalent Fe [13], ultrasound [14], carbonaceous materials [15,16], electrochemical systems [17,18], and minerals [19].

$$S_2{O}_8^{2-}\stackrel{∆}{\to }2{SO}_4^{•-}$$

(1)

$$2S_2{O}_8^{2-}+{2H}_{2}O\stackrel{{OH}^{-}}{\to }S{O}_4^{\bullet -}+3S{O}_4^{2-}+4H^{+}+O_2^{\bullet -}$$

(2)

$${M^{n+}+S}_2{O}_8^{2-}\to M^{(n+1)+}+{SO}_4^{•-}+{SO}_4^{2-}$$

(3)

While these techniques demonstrate the versatility of S₂O₈²⁻ activation, many are impractical for soil and/or groundwater remediation due to engineering challenges and/or logistical constraints [20]. For instance, UV radiation cannot penetrate soil effectively; metal catalysts, such as Co, may pose environmental risks or form insoluble compounds (e.g., Fe(II) oxidized to insoluble Fe(III) oxides) [21]. Base activation is commonly used in field applications, but it requires large quantities of alkaline substances [4], and thermal activation shows promise for soil/groundwater remediation but requires significant energy input [22].

Groundwater contamination often involves a mixture of pollutants and dissolved species that influence remediation processes. In addition to organic pollutants, aquifers commonly contain dissolved oxygen (DO), ammonium (NH₄⁺), nitrate (NO₃⁻), and dissolved organic carbon (DOC), which can interact with remediation agents and alter their behavior [23]. Regarding S₂O₈²⁻ activation by minerals, several studies have shown the potential of using naturally occurring ≡Fe(III) and ≡Mn(IV) containing minerals (Equations (4) and (5), where ≡M represents the surface site of the corresponding metal integral to the mineral structure) [22,24,25,26,27,28,29] and soil organic matter (SOM) [30,31,32] to interact with S₂O₈²⁻ as activators. Based on these principles, the sole S₂O₈²⁻, complementarily enhanced by elevated temperatures, has been recently successfully applied at bench scale to degrade/transform organic pollutants in aquifer/soil materials, such as 1,4-dioxane [33], triphenyl phosphate [34,35], aniline [20], PAHs [36,37], and sulfamethoxazole [38].

$${\equiv M\left(n\right)+S}_2{O}_8^{2-}\to \equiv M(n-I)+{S_{2}O}_8^{•}$$

(4)

$${\equiv M(n-I)+S}_2{O}_8^{2-}\to \equiv M\left(n\right)+{SO}_4^{•-}+{SO}_4^{2-}$$

(5)

To efficiently design, model, and implement ISCO systems using sole/thermally enhanced S₂O₈²⁻ at full scale, it is essential to analyze the persistence of S₂O₈²⁻ in aquifer/soil materials through bench- or pilot-scale treatability tests [39,40,41]. This analysis is critical to determine the required amount of S₂O₈²⁻ needed to reach targeted polluted zones and to ensure that these zones are exposed to S₂O₈²⁻ for sufficient residence times.

Despite its importance, the nature of S₂O₈²⁻ persistence in real aquifer/soil materials has been exclusively the subject of only a few studies, see Figure 1. Some researchers hypothesized that S₂O₈²⁻ behaved similarly to permanganate in terms of finite stable natural oxidant demand (NOD) determined by the amount of nontarget oxidizable substances by S₂O₈²⁻ (Fe- and Mn-containing minerals and SOM) [42,43,44]. On the contrary, the remaining investigations successfully approximated S₂O₈²⁻ consumption in real aquifer/soil materials by continuous pseudo-first-order kinetics [22,45,46,47,48]. Besides the nature and the quantification of S₂O₈²⁻ persistence, some other related aspects have also been investigated, such as potential metal leaching [42], variations in SOM and mineral composition throughout the S₂O₈²⁻ exposure [43,47], effect on microbial activity [43], mechanism of heterogeneous S₂O₈²⁻ decomposition [22,45,47], influence of organic pollutants presence on S₂O₈²⁻ decomposition [22], identification of ROS [45], and effects of pH and matrix anions [44].

However, as far as we are aware, insufficient or no attention has been dedicated to the temperature influence on S₂O₈²⁻ persistence in systems containing soil or aquifer materials, despite the widespread adoption of the thermal S₂O₈²⁻ activation method. Moreover, the role of the experimental setup (batch versus dynamic column tests) and the fate of SO₄²⁻ generated by S₂O₈²⁻ decomposition have often been overlooked. To investigate these aspects, we conducted batch tests under varying thermal conditions (30 °C–50 °C), initial S₂O₈²⁻ concentrations (2.7 g·L⁻¹ and 16.1 g·L⁻¹), and dynamic column experiments (40 °C, 16.1 g·L⁻¹) with comprehensively characterized natural aquifer and soil materials. Furthermore, the principal component analysis (PCA) method was employed to investigate correlations between S₂O₈²⁻ decomposition and soil/aquifer material parameters. This approach allowed a more thorough understanding of overlooked but still very important aspects of S₂O₈²⁻ persistence in real soil/aquifer materials.

2. Materials and Methods

2.1. Chemicals

All the chemicals were of reagent grade and were used without further purification. Sodium peroxydisulfate (PDS, Na₂S₂O_8, p.a., Penta, Prague, Czech Republic), sodium hydroxide (NaOH 1 N, Agilent, Santa Clara, CA, USA), sodium molybdate (Na₂MoO₄, p.a., Sigma Aldrich, St. Louis, MO, USA), Agilent Inorganic Ions Buffer pH 7.7, hydrochloric acid (HCl; Lach-Ner, Neratovice, Czech Republic), nitric acid (HNO₃; Lach-Ner, Czech Republic), phosphoric acid (H₃PO₄; Lach-Ner, Czech Republic). Demineralized water (DW) was used to set up the experiments (OmniaTap-W, StakPure GmbH, Niederahr, Germany).

2.2. Soil and Aquifer Materials

Soil samples were collected from four sites in the Czech Republic, targeting various soil horizons and aquifer materials during excavation. Sampling depths ranged from 30 cm (soil material denoted as E) and 150 cm (soil materials denoted C, D) to 4 m (aquifer materials denoted as A, B) as part of a geological survey. The collected soil samples were homogenized, dried at room temperature for 24–48 h until a constant weight was achieved, and subsequently sieved through a 3.55 mm mesh.

2.3. Soil Characterization

To assess the influence of soil/aquifer materials on S₂O₈²⁻ persistence, their elemental composition and physical properties were characterized. The moisture content was determined in accordance with ISO 17892-1:2014 [51]. Bulk density (ρ_b) and soil particle density (ρ_s) were measured using the core method and the pycnometer method, respectively. Porosity (ε) was then calculated using the equation ε = (1 – ρ_b/ρ_s) × 100 [49,50]. The specific surface area and total pore volume of the soil/aquifer materials were evaluated using Brunauer–Emmett–Teller (BET) analysis (COULTER SA 3100). The total inorganic carbon (TIC) content of the soil materials was determined by acidification using H₃PO₄ (5 g of samples + 20 mL of H₃PO₄) till the constant weight was achieved. The total carbon content (TC) was determined using the dry combustion method on a Vario El Cube with TCD detection (Elementar), followed by TOC calculation by subtracting TIC values from TC values. To determine the elements that could be potentially leached from the soils due to the S₂O₈²⁻ exposure, extraction of individual soil samples using aqua regia was performed. Specifically, 5 g of soil was weighed into a beaker, mixed with 20 mL of aqua regia and 100 mL of water, and heated on a hotplate for 3 h. After cooling, the mixture was filtered, and the resulting mineral extract was analyzed using the ICP-OES GBC Integra 6000 instrument, equipped with a fully thermostated, 0.75 m Czerny–Turner monochromator with nitrogen-purged optics. The wavelength range was 160–800 nm, using 1800 g·mm⁻¹ holographic grating. The instrument employs a dual photomultiplier system, including an R1754 solar-blind tube for UV detection and a wideband R928 tube for visible light detection. Argon was used as the carrier gas, with plasma gas at 10 L·min⁻¹, auxiliary gas at 0.5 L·min⁻¹, and nebulizer gas at 0.5 L·min⁻¹. The system is equipped with multitasking Windows software GBC ICP Quantima version 3.1 that controls all gases, utilizing a built-in wavelength database. In this study, the methods used were QUANT for 15 elements (Al, As, Ba, Cd, Co, Cr, Cu, Mn, Mo, Ni, Pb, Se, Sr, Zn, K) at concentrations from 0.05 to 5 mg, and QUANT for Fe, Hg, Na, Mg, and Ca at concentrations from 0.5 to 25 mg.

2.4. S₂O₈²⁻ and SO₄²⁻ Analysis

The concentrations of S₂O₈²⁻ and SO₄²⁻ were determined using a LUMEX CAPEL-205 capillary electrophoresis (CE) system equipped with a fused silica capillary (inner diameter: 75 μm, length: 55 cm) and UV detection system. Sample preparation involved extracting 500 μL of the reaction mixture into 2 mL plastic vials using a pipette, followed by centrifugation using Vitrum WiseSpin CF-10 to separate the dispersed soil material. Subsequently, 200 μL of the supernatant was first diluted with DW and then mixed with a pre-cooled (4 °C) internal standard stock solution (SS-IS) containing molybdate anions (c(MoO₄²⁻) = 50 mg·L⁻¹) to achieve a concentration of S₂O₈²⁻ appropriate for the CE calibration range (the dilution factor varied within the interval 40–200 as required). After the dilution, the volume of 800 μL was transferred to 2 mL plastic vials and stirred on a shaker for 10 s prior to CE analysis. Before each CE analysis, the capillary was conditioned sequentially with 0.5 M HCl for 3 min, DW for 5 min, 0.5 M NaOH for 3 min, DW for 5 min, and the electrolyte for 10 min. Prior to each sample run, the capillary was flushed with 0.25 M NaOH for 20 s, followed by the electrolyte for 80 s, a 1-minute blank analysis (−30 kV), and a final flush with the electrolyte for an additional 2 min. This analysis was carried out under the following conditions: applied voltage of −30 kV; the electrolyte was Agilent Inorganic Ions Buffer (pH 7.7); the capillary temperature was set at 20 °C; hydrodynamic injection at 10 mbar for 5 s; inverted UV detection at a wavelength of 245 nm, with a total analysis duration of 5 min.

2.5. Experimental Setup

2.5.1. Batch Experiments

Batch experiments were conducted in 100 mL Erlenmeyer flasks sealed with glass stoppers and parafilm. Each flask contained 50 g of soil sample and 40 mL of DW. The prepared reactors were placed in a thermostat (IF75, Memmert GmbH) on an orbital shaker (GS-20, Hangzhou Miu Instruments, Hangzhou, China). After 24 h of agitation and equilibration, 10 mL of NaS₂O₈ stock solution (100 g·L⁻¹ or 16.4 g·L⁻¹) was added to achieve an initial NaS₂O₈ concentration of 20 g·L⁻¹ or 3.27 g·L⁻¹ in each system according to the experimental design and final soil concentration of 1 g·mL⁻¹. Homogenous control (HC) samples consisting of only S₂O₈²⁻ (50 mL) without soil/aquifer materials were prepared alongside the soil samples. Most conditions were tested in triplicate.

2.5.2. Column Experiments

The column experiments were performed using Plexiglas columns (inner diameter: 4.8 cm; length: 40 cm; Figure S1). All tubing was either Tygon or Teflon. A peristaltic pump (Ismatec 123) was used to deliver DW and S₂O₈²⁻ solution into the columns. Each column was packed wet with approximately 1060 g of dry soil, aiming for a bulk density (dry soil weight in kg/soil volume in L) of around 1.47 kg·L⁻¹. The pore volume (PV), 180–185 mL, was calculated as the water required for packing the columns. The experiments were conducted in a thermostat (MLR-351, Sanyo, Tokyo, Japan) controlled environment, in the dark, at a temperature of 40 °C. Initially, the columns were flushed with DW for 24 h before introducing the S₂O₈²⁻ solution to achieve a concentration of 16.1 g·L⁻¹.

3. Results and Discussions

3.1. Characterization of Soil/Aquifer Materials

Table 1. Summary of soil/aquifer materials properties.

Parameters	Material A	Material B	Material C	Material D	Material E
Soil texture
pH	7.3	7.5	6.4	6.3	7.2
moisture content/% (weight)	1.01	5.02	5.55	6.69	3.56
BET surface area/m2·g−1	9.361	14.323	4.802	4.769	12.033
Total pore volume/mL·g−1	0.024	0.024	0.027	0.017	0.016
Bulk density/kg·L−1	1.06	1.12	1.20	1.26	1.23
Particle density/g·mL−1	2.05	1.92	2.08	1.81	2.09
Porosity/-	0.482	0.420	0.423	0.303	0.414
Total carbon (TC)/%	0.071	0.080	0.289	0.820	1.630
Total organic carbon (TOC)/%	0.062	0.080	0.289	0.703	1.610
Total inorganic carbon (TIC)/%	0.007	0.008	0.014	0.117	0.026
Pore distribution [nm]
<6/%	13.7	45.1	7.06	10.5	50.2
6–8/%	6.72	11.8	1.06	4.3	7.43
8–10/%	6.16	7.45	2.08	3.95	5.09
10–12/%	6.43	6.05	2.2	4.33	4.5
12–16/%	8.75	5.77	2.97	6.02	5.02
16–20/%	9.14	4.64	3.39	6.45	4.55
20–80/%	39.2	15.2	47.0	44.9	18.1
>80/%	9.91	4.02	34.3	19.5	5.09
Metal content [mg·kg−1]
Fe	1347.14	4279.55	6239.24	6932.75	1465.61
Mn	12.82	126.95	251.50	130.29	266.31
Cu	9.59	3.50	3.53	21.48	7.80
Al	3166.12	5387.39	17,671.09	4292.67	2992.34
Co	1.32	2.33	4.56	3.57	4.14
As	6.56	nd *	0.85	nd	31.23
Mo	0.28	nd	0.26	nd	7.20
Zn	11.15	9.39	39.47	43.30	24.62
Pb	16.30	2.69	9.22	25.25	12.76
Cr	5.07	6.19	24.21	10.72	6.55
Na	50	115	83	164	62
Ca	525	510	1023	4384	7571
K	2556	6395	20,292	725	10,910
Mg	138	696	1540	785	1236

Note: * nd—not detected.

summarizes soil/aquifer materials properties used within this study. The pH values range from slightly acidic to neutral, with materials C and D being mildly acidic, while materials A, B, and E are close to neutral. BET surface area shows considerable variation, with material B having the highest value at 14.323 m²·g⁻¹ and materials C and D being the lowest at around 4.8 m²·g⁻¹. Total pore volume is relatively consistent across all materials, ranging from 0.016 to 0.027 mL·g⁻¹. Bulk density increases gradually from material A (1.06 kg·L⁻¹) to material D (1.26 kg·L⁻¹), while particle density remains consistent across all materials, ranging from 1.81 to 2.09 g·mL⁻¹. Porosity is highest in material A at 0.482 and lowest in material D at 0.303. The TOC content is lowest in materials A and B, which were extracted from an aquifer, and material C also shows low TOC typical of deeper soil layers (corresponding to a fraction of organic carbon (f_oc) ˂ 0.005). By contrast, materials D and E display relatively higher TOC, especially material E, with a value of 1.61%.

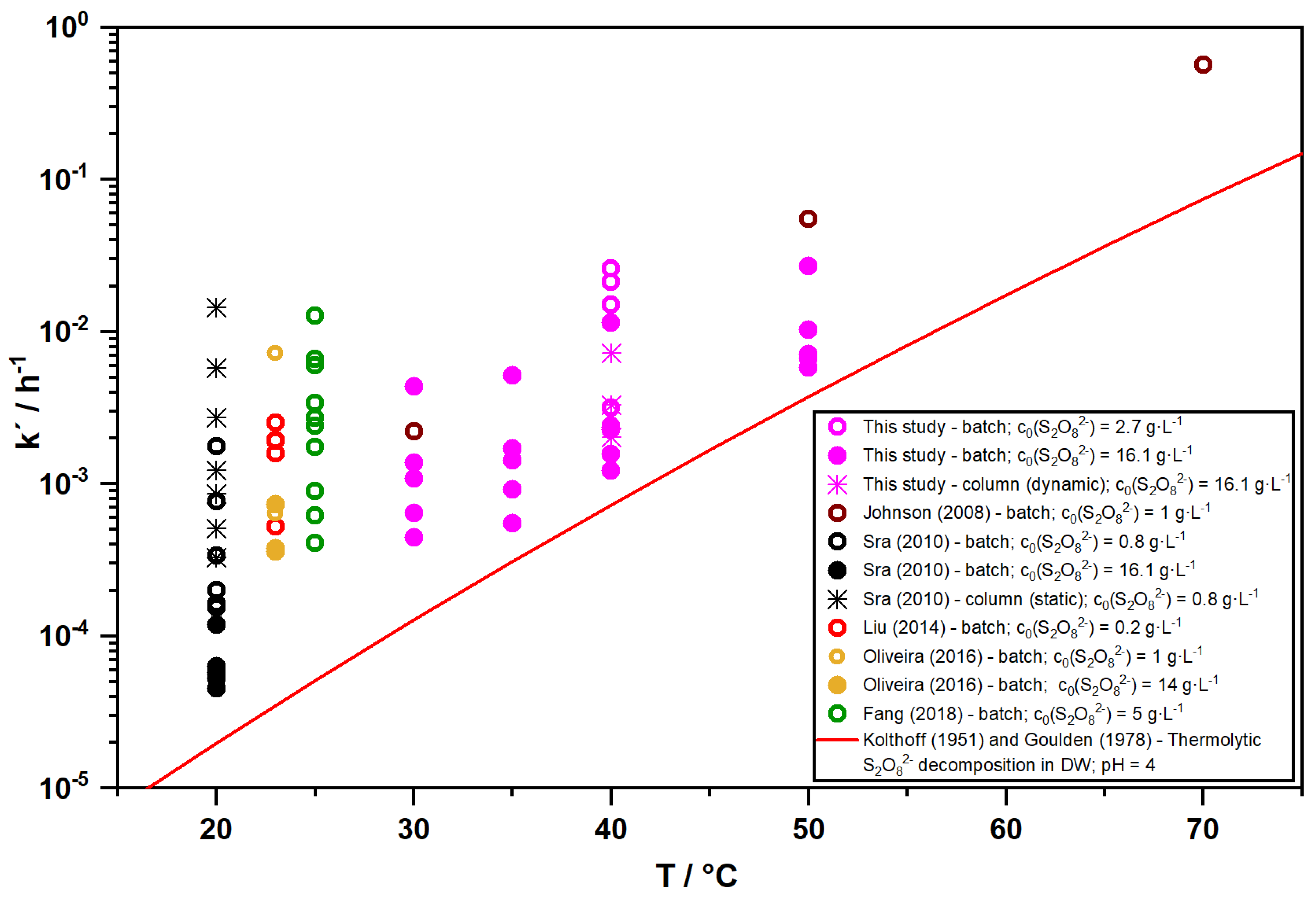
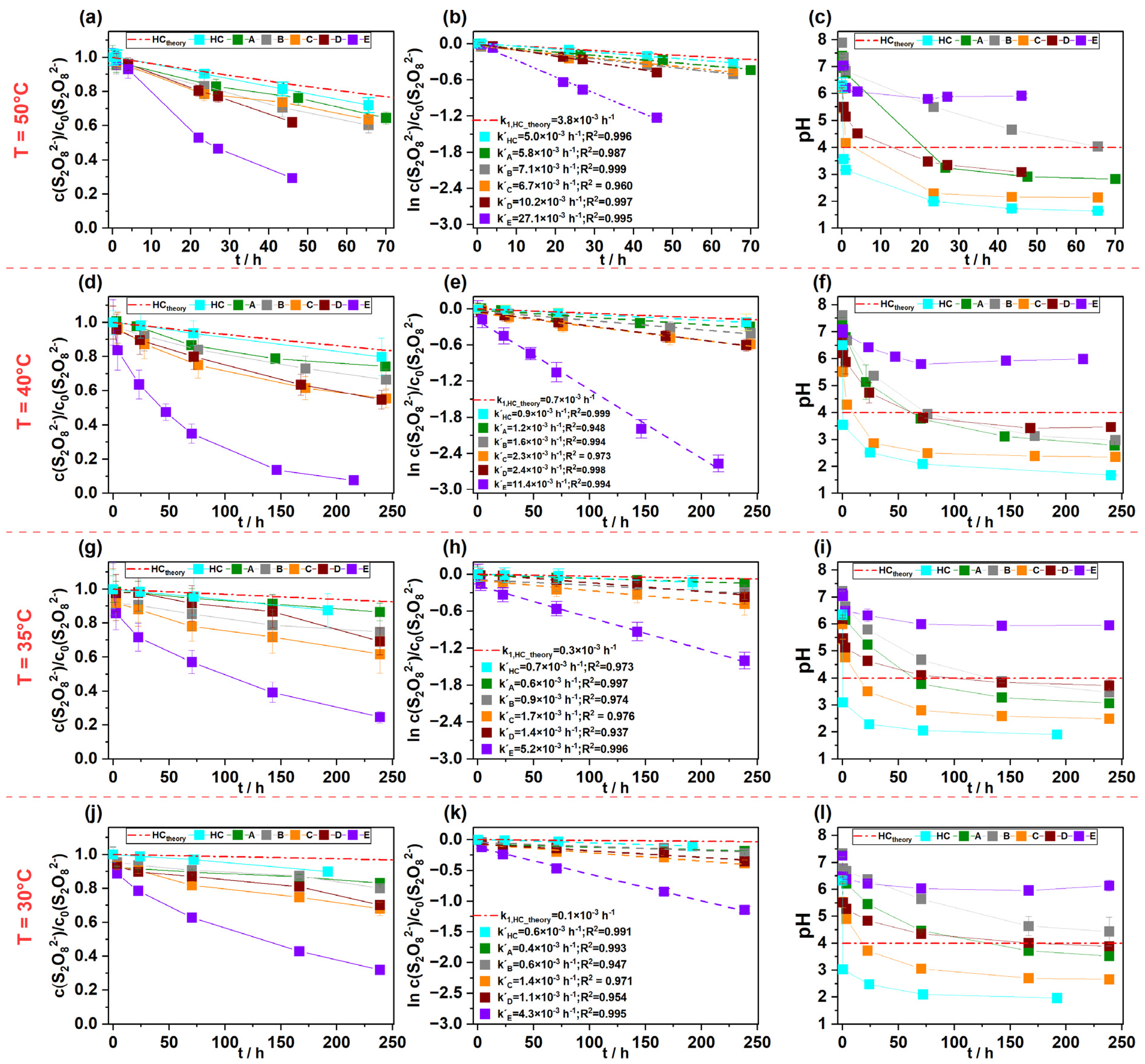
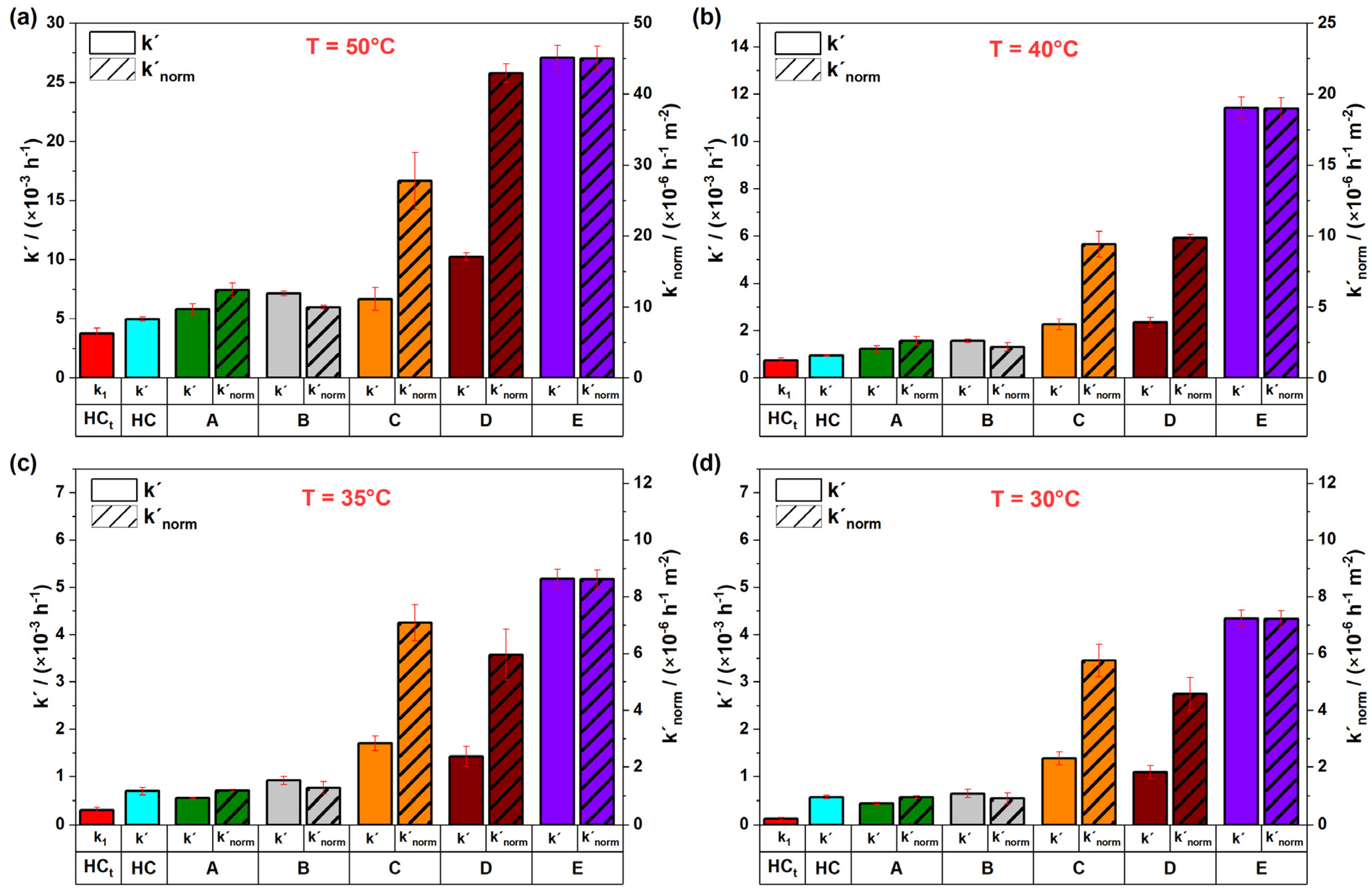
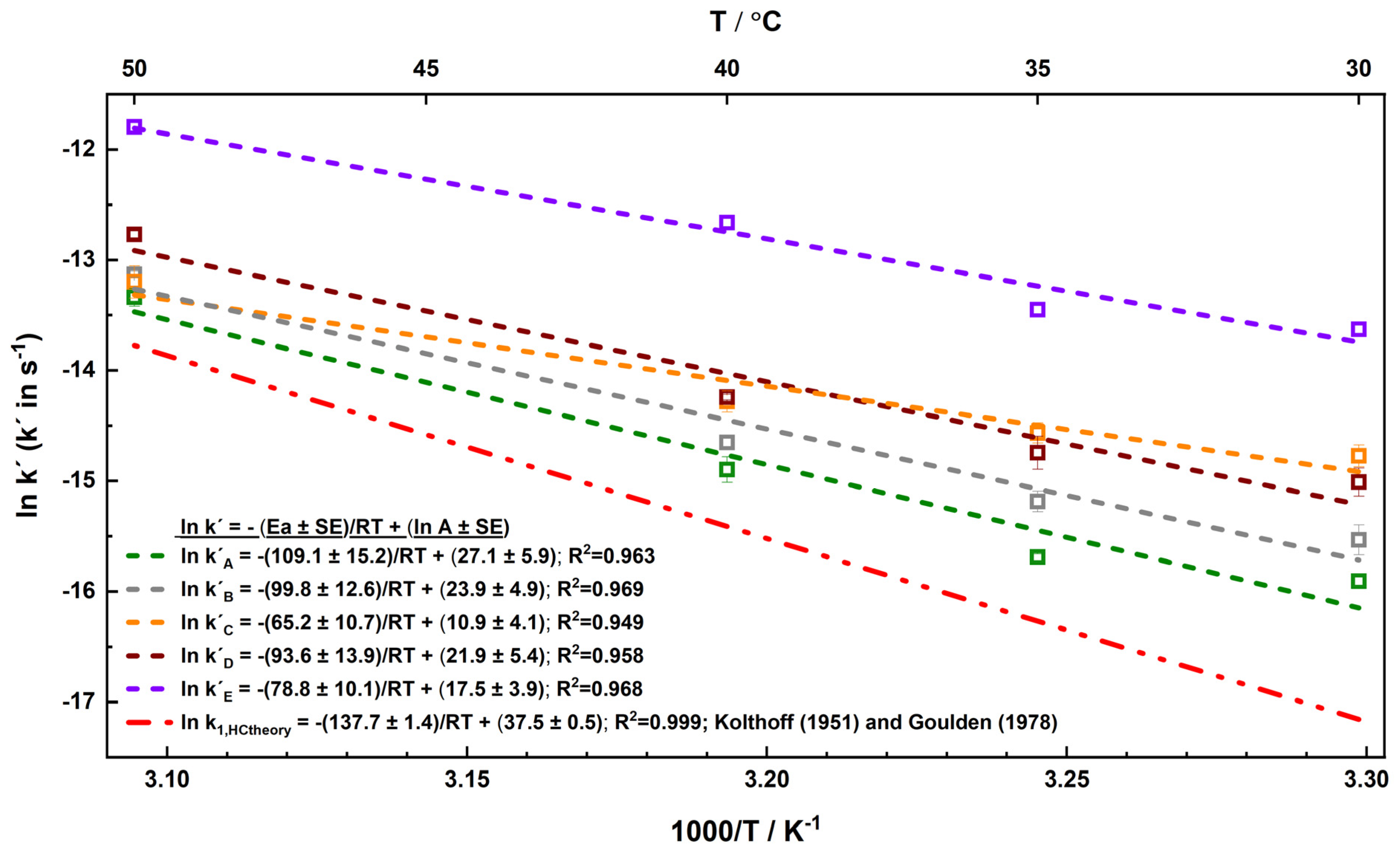
3.2. Influence of Temperature on S₂O₈²⁻ Persistence in Soil/Aquifer Materials

To examine the effect of temperature on S₂O₈²⁻ persistence in natural soil materials, we performed a series of batch experiments with five real soil/aquifer materials (systems A–E) at four temperatures: 50 °C; 40 °C; 35 °C; and 30 °C.

The normalized concentrations (c/c₀), natural logarithms of normalized concentrations (ln c/c₀), and pH in individual systems for selected temperatures throughout the experiments are depicted in Figure 2, which also includes theoretical S₂O₈²⁻ consumption (Figure S2) at fixed pH = 4 not considering the acidic decomposition of S₂O₈²⁻ (Equation (8)). Significant decreases (5–10%) in S₂O₈²⁻ concentrations were observed within the first 3–4 h for 30 °C, 35 °C, and 40 °C and the first 1 h in the case of 50 °C in all systems (Figure 2a,d,g,j). These decreases were likely due to reactions between S₂O₈²⁻ and readily oxidizable substances leached in solution during the equilibration period (24 h) preceding experiments. Therefore, the initial concentration data points (t = 0 h) were not considered in the following regression analysis of S₂O₈²⁻ decomposition rates. Finite NOD was not observed in any of the experiments. S₂O₈²⁻ decomposition was continuous and followed pseudo-first-order kinetics at given conditions in all systems (Figure 2b,e,h,k). This behavior can be approximated by Equation (6)–(7) [48], where k′ is the observed bulk pseudo-first-order reaction rate constant of S₂O₈²⁻ decomposition. The rate constant k′ is influenced by several specific reaction pathways. These include k_1, the first-order reaction rate constant of S₂O₈²⁻ thermolysis (Equation (1)); k_2, the second-order reaction rate constant of acid-catalyzed S₂O₈²⁻ hydrolysis (Equation (8)); and k₃, the second-order reaction rate constant of base-catalyzed S₂O₈²⁻ hydrolysis (Equation (2)); k_cat is the minerals catalyzed reaction rate constant, and k_SOM is the SOM catalyzed reaction rate constant.

$${\displaystyle \frac{d\left[S_2{O}_8^{2-}\right]}{dt}}=-k^{\prime }\left[S_2{O}_8^{2-}\right]$$

(6)

$$k^{\prime }=k_1+k_2\left[H^{+}\right]+k_3\left[{OH}^{-}\right]+k_{cat}{\left[C_{cat}\right]}^{n_{cat}}+k_{SOM}{\left[C_{SOM}\right]}^{n_{SOM}}$$

(7)

$$S_2{O}_8^{2-}+H_{2}O\stackrel{H^{+}}{\to }{H}_{2}S{O}_5+S{O}_4^{2-}$$

(8)

Except for system E, showing only a slight decrease in pH from an initial value of ~7 to a final pH of ~6, the other systems showed a more significant decrease in pH values from an initial 6.0–8.0 to a final 2.1–4.4 throughout the experiments, reflecting the different buffering capacities of soil/aquifer materials (Figure 2c,f,i,l). In general, the lowest pH values were observed in systems with soil C (pH_final ≈ 2.1–2.7) and A (pH_final ≈ 2.8–3.5) and alternately followed by the set of systems with material D (pH_final ≈ 3.1–3.9) and B (pH_final ≈ 3.0–4.4) at the end of experiments.

From the perspective of S₂O₈²⁻ decomposition rates in terms of k′ (Figure 3), system E exhibited substantially higher values, 27.1∙10⁻³ h⁻¹, 11.4∙10⁻³ h⁻¹, 5.2∙10⁻³ h⁻¹, and 4.3∙10⁻³ h⁻¹ at 50 °C, 40 °C, 35 °C, and 30 °C, respectively, compared to other systems, thus showing the lowest S₂O₈²⁻ persistence. Except for system B at 50 °C, system E was generally followed by the set of systems C (6.7∙10⁻³ h⁻¹, 2.3∙10⁻³ h⁻¹, 1.7∙10⁻³ h⁻¹, and 1.4∙10⁻³ h⁻¹ at 50 °C, 40 °C, 35 °C, and 30 °C, respectively) and D (10.2∙10⁻³ h⁻¹, 2.4∙10⁻³ h⁻¹, 1.4∙10⁻³ h⁻¹, and 1.1∙10⁻³ h⁻¹ at 50 °C, 40 °C, 35 °C, and 30 °C, respectively) in alternate order, and then by systems B (7.1∙10⁻³ h⁻¹, 1.6∙10⁻³ h⁻¹, 0.9∙10⁻³ h⁻¹, and 0.6∙10⁻³ h⁻¹ at 50 °C, 40 °C, 35 °C, and 30 °C, respectively) and A (5.8∙10⁻³ h⁻¹, 1.9∙10⁻³ h⁻¹, 0.6∙10⁻³ h⁻¹, and 0.4∙10⁻³ h⁻¹ at 50 °C, 40 °C, 35 °C, and 30 °C, respectively) in alternate order.

Apart from system A at 30 °C, determined k′ values of individual systems were higher than that of system HC with unbuffered pH and of k₁ theoretical value in DW (HC_theory) at fixed pH = 4 (Figure S2), indicating the significant influence of soil/aquifer materials presence on higher S₂O₈²⁻ decomposition, i.e., lower S₂O₈²⁻ persistence. Although in the case of system A at 30 °C (pH_final ≈ 3.5) and 35 °C (pH_final ≈ 3.1), determined k′ values (k′_A,30°C = 0.4∙10⁻³ h⁻¹ and k′_A,35°C = 0.6∙10⁻³ h⁻¹) are lower than that of HC (k′_HC,30°C = 0.6∙10⁻³ h⁻¹ and k′_HC,35°C = 0.7∙10⁻³ h⁻¹) with pH_final ≈ 2.0, these are still higher than that of k′ theoretical value in DW at fixed pH = 4 (k_{1,HCtheory,30°C} = 0.1∙10⁻³ h⁻¹ and k_{1,HCtheory,30°C} = 0.3∙10⁻³ h⁻¹). The lower rate of S₂O₈²⁻ decomposition in system A compared to HC does not automatically imply the non-reactivity of material A toward S₂O₈²⁻ but indicates the significant influence of acid-catalyzed S₂O₈²⁻ decomposition (Equation (8)) in HC.

The normalized S₂O₈²⁻ decomposition rate (k′_norm), adjusted to the total BET specific surface area, is defined in Equation (9), where BET refers to the specific surface area of the soil/aquifer material, and m_soil is the mass of the material in the given system. The order of decomposition rates observed for k′_norm aligns with that of the bulk S₂O₈²⁻ decomposition rates (k′), including data at 50 °C. Notably, the observed differences between system E and the set of systems C and D are relatively minor. In contrast, the differences between the set of systems C and D and the set of systems A and B are more significant.

$$k_{norm}^{\prime }={\displaystyle \frac{k^{\prime }}{BET·m_{soil}}}$$

(9)

As can be seen in Figure 4, determined ln k′ values of S₂O₈²⁻ decomposition rates as a function of temperature fit relatively well the linearized form of the Arrhenius equation (Equation (10)):

$${\ln k}^{\prime }=-{\displaystyle \frac{E_a}{\mathrm{R}\mathrm{T}}}+\ln A$$

(10)

where ln k′ is the natural logarithm of S₂O₈²⁻ bulk decomposition rate constant (k′ in s⁻¹); E_a is the activation energy (kJ∙mol⁻¹); R = 8.314∙10⁻³ kJ∙K⁻¹∙mol⁻¹ is the universal gas constant; T is the temperature (K), and ln A is the natural logarithm of pre-exponential factor (A in s⁻¹). The determined values of the activation energies (109.1 ± 15.2) kJ∙mol⁻¹, (99.8 ± 12.6) kJ∙mol⁻¹, (65.2 ± 10.7) kJ∙mol⁻¹, (93.6 ± 13.9) kJ∙mol⁻¹, and (78.8 ± 10.1) kJ∙mol⁻¹ for systems A, B, C, D, and E, respectively, were significantly lower than the only one previously published value of (120 ± 7) kJ∙mol⁻¹ by Johnson et al. [46], who tested S₂O₈²⁻ decomposition in a system with sand of basaltic origin (TOC~0.3%) and used initial S₂O₈²⁻ concentration of 1 g∙L⁻¹ and soil concentration of 1 g∙mL⁻¹. The significantly lower E_a compared to the E_a of homolytic S₂O₈²⁻ decomposition in water for less reactive soils with S₂O₈²⁻, such as A, B, C, and D, has significant implications for heat-assisted ISCO using S₂O₈²⁻ since, as also suggested by Johnson et al. [46], at higher temperatures, the S₂O₈²⁻decomposition is mostly due to homolytic S₂O₈²⁻ decomposition in water and not activation/consumption by soil/aquifer materials. For instance, in systems with soil materials A, B, C, D, and E, homolytic S₂O₈²⁻ decomposition would dominate at temperatures higher than ~57.7 °C, ~62.2 °C, ~54.5 °C, ~67.0 °C, and ~81.1 °C, respectively, according to the determined regression parameters of the linearized form of Arrhenius equation.

This suggests that in specific practical applications of thermally assisted ISCO, using S₂O₈²⁻ at elevated temperatures, in which soil/aquifer materials demonstrate relatively low reactivity with S₂O₈²⁻ and have lower E_a compared to that of k₁, S₂O₈²⁻ persistence may primarily be governed by its homolytic cleavage.

3.3. Influence of Initial S₂O₈²⁻ Concentration on Its Persistence in Soil Materials

To examine the influence of initial S₂O₈²⁻ concentration on its persistence in natural soil/aquifer materials, additional batch experiments were conducted at a reduced initial concentration c₀(S₂O₈²⁻) = 2.7 g∙L⁻¹ at 40 °C. This concentration is lower than the initial concentration used in Section 3.2, where c₀(S₂O₈²⁻) = 16.1 g∙L⁻¹. Figure 5 presents normalized concentrations (c/c₀), natural logarithms of normalized concentrations (ln c/c₀), and pH in individual systems for the lower S₂O₈²⁻ initial concentration. Additionally, it compares the determined S₂O₈²⁻ decomposition rate constants obtained for c₀(S₂O₈²⁻) = 2.7 g∙L⁻¹ with those determined at the higher initial concentration of c₀(S₂O₈²⁻) = 16.1 g∙L⁻¹ at 40 °C (Figure 2).

Similarly to the higher S₂O₈²⁻ initial concentration at 40 °C (Figure 2d,e), no finite NOD value was observed at the lower S₂O₈²⁻ initial concentration, but a gradual S₂O₈²⁻ decrease according to pseudo-first-order kinetics was observed in all systems (Figure 5a,b). This decrease was again accompanied by a drop in pH (Figure 5c), but of much lesser significance than in the case of the higher S₂O₈²⁻ initial concentration (Figure 2f), when only system C dropped below pH = 4 from all systems at the end of this experiment.

In terms of k′ (Figure 5d) and k′_norm (Figure 5e), when the initial S₂O₈²⁻ concentration was reduced from 16.1 g∙L⁻¹ to 2.7 g∙L⁻¹, there was a several-fold increase in the individual systems, specifically about 2-fold in the case of systems A, B and E and about 7-fold and 11-fold in systems C and D, respectively. A comparable enhancing effect of reducing the initial S₂O₈²⁻ concentration on its decomposition in the presence of aquifer/soil materials was also observed by Sra et al. [48] and Oliveira et al. [47], who observed a 3–12 fold and 2–10 fold increase in k′, respectively, for their tested aquifer materials, when the initial S₂O₈²⁻ concentration was lowered from 16.1 g∙L⁻¹ to 0.8 g∙L⁻¹ and from 14 g∙L⁻¹ to 1 g∙L⁻¹, respectively. The variations in the rate constants as a function of initial S₂O₈²⁻ concentration can be principally attributed to the detrimental effect of ionic strength on interactions between S₂O₈²⁻ and minerals and/or SOM [47,48].

The high sensitivity of S₂O₈²⁻ decomposition to variations in ionic strength, primarily controlled by elevated concentrations of S₂O₈²⁻ (g∙L⁻¹) and, subsequently, by generated SO₄²⁻ from S₂O₈²⁻ decomposition, presents potential for optimization in full-scale ISCO applications using the sole or thermally enhanced S₂O₈²⁻. For example, when modeling and designing ISCO applications for soils/aquifers with the high sensitivity of S₂O₈²⁻ decomposition to ionic strength, such as materials C and D (Figure 5d), it is possible to adjust the S₂O₈²⁻ persistence by choosing injected S₂O₈²⁻ concentration to optimally reach the target contaminated zones. Moreover, based on our results, it might be suggested that high S₂O₈²⁻ concentrations (high ionic strength) could also negatively affect the extent of S₂O₈²⁻ activation by soil/aquifer materials and, consequently, pollutant removal efficiency. For instance, Qutob et al. [37] have recently observed only a marginal increase in PAH removal efficiency from soil samples when increasing S₂O₈²⁻ concentration from 1 g∙L⁻¹ to 2.5 g∙L⁻¹. However, on the other hand, Dong et al. [35] and Mustapha et al. [20] still observed increases in the removal efficiencies of triphenyl phosphate and aniline, respectively, in soil materials when the S₂O₈²⁻ concentration increased from 9.6 g∙L⁻¹ to 19.2 g∙L⁻¹ and from 3.8 g∙L⁻¹ to 9.6 g∙L⁻¹, respectively. The impact of ionic strength on S₂O₈²⁻ interactions with soil/aquifer materials should be considered in assessing pollutant removal efficiency and included in bench- or pilot-scale tests.

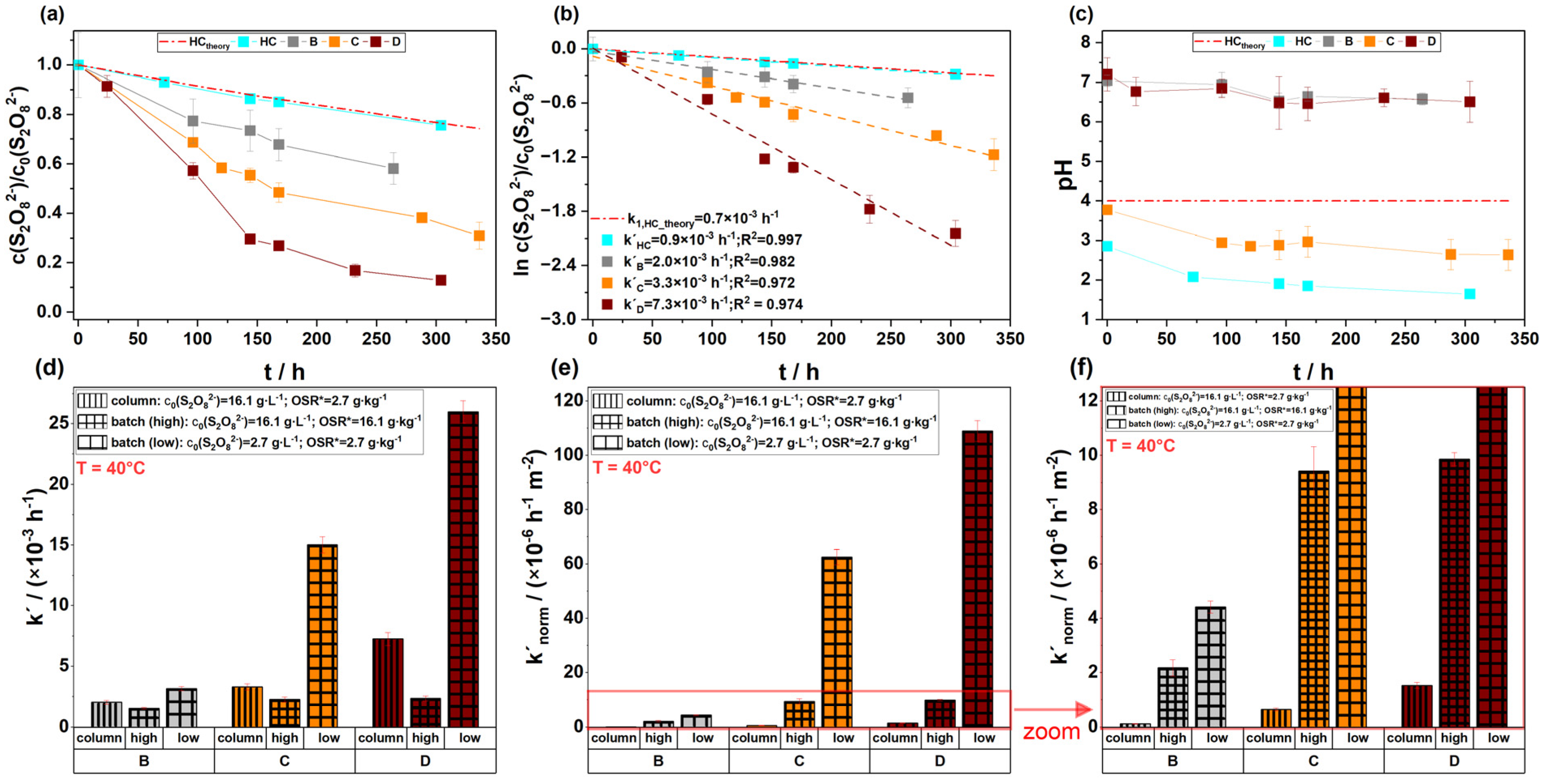
3.4. Comparison of Experimental Designs: Batch Versus Dynamic Column Tests

In addition to the standard batch experimental setup, dynamic column tests were conducted with soil/aquifer materials B, C, and D at 40 °C with initial S₂O₈²⁻ concentration 16.1 g∙L⁻¹ and oxidant-to-soil mass ratio (OSR) 2.7 g∙kg⁻¹. Materials A and E were excluded from these tests due to their extremely low permeability, which precluded reaching a dynamic state, as revealed through preliminary testing. Figure 6 illustrates the normalized concentrations (c/c₀), natural logarithms of normalized concentrations (ln c/c₀), and pH values for individual column systems. Furthermore, Figure 6d,e,f compares S₂O₈²⁻ decomposition rate constants determined in column systems and previous batch experiments at 40 °C at both examined initial S₂O₈²⁻ concentrations 2.7 g∙L⁻¹ with OSR 2.7 g∙kg⁻¹ (Figure 5b) and 16.1 g∙L⁻¹ with OSR 16.1 g∙kg⁻¹ (Figure 3b). S₂O₈²⁻ decomposition followed pseudo-first-order kinetics, consistent with the batch tests, and bulk decomposition rate constants (k′) determined in this setup were higher than those observed in the batch experiments at equivalent initial S₂O₈²⁻ concentrations (c₀(S₂O₈²⁻) = 16.1 g∙L⁻¹), with increases of 1.3-, 1.5-, and 3-fold in systems B, C, and D, respectively. However, when compared to batch tests conducted with an identical OSR of 2.7 g/kg, i.e., batch systems with c₀(S₂O₈²⁻) = 2.7 g∙L⁻¹, the determined S₂O₈²⁻ decomposition rate constants were significantly lower in the dynamic column tests. Specifically, the bulk rate constants (k′) were 1.6, 4.5, and 3.6 times lower for systems B, C, and D, respectively. In the only other study addressing S₂O₈²⁻ persistence in a column arrangement, though using static stop–flow column tests, Sra et al. [48] similarly observed an increase in bulk S₂O₈²⁻ decomposition rate constants compared to batch experiments with the same initial S₂O₈²⁻ concentrations (c₀(S₂O₈²⁻) = 0.8 g∙L⁻¹). However, Sra et al. [48] observed a consistent ca. eight-fold increase in bulk S₂O₈²⁻ decomposition rates across all tested aquifer materials when comparing static stop–flow column tests to batch experiments. This inconsistency likely stems from the fundamental differences between dynamic (present study) and static stop–flow column tests. As demonstrated in Figure 6e,f, the normalized S₂O₈²⁻ degradation constants to the total BET surfaces (k′_norm) are significantly lower compared to batch systems with identical initial concentrations (c₀(S₂O₈²⁻) = 16.1 g∙L⁻¹). This observation suggests limited accessibility of soil/aquifer materials reactive surfaces to the aqueous solution compared to batch tests, indicating the probable formation of preferential flow paths in column systems despite meticulous column test preparation, particularly during the gradual filling process accompanied by progressive water saturation of the column.

Given the labor-intensive preparation of dynamic column tests, their unsuitability for low-permeability materials, and the complex interpretation of obtained data due to uncertainties regarding preferential flow path formation, batch tests, or static stop–flow column tests, such as those employed by Sra et al. [48], are recommended for bench-scale S₂O₈²⁻ persistence tests in ISCO applications.

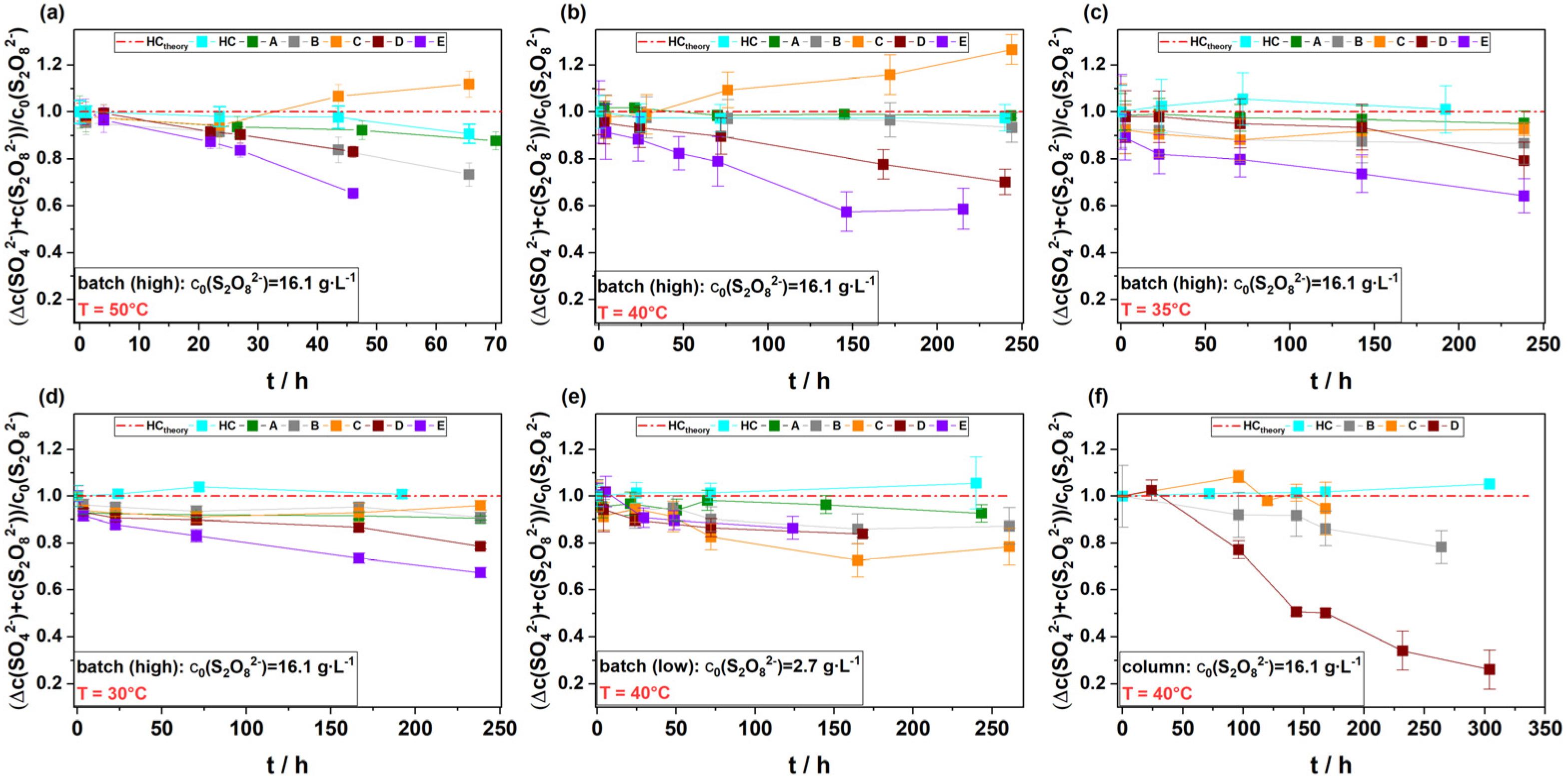
3.5. Fate of Generated SO₄²⁻ in the Experimental Systems

The full-scale implementation of ISCO using S₂O₈²⁻ induces significant alterations in subsurface biogeochemistry, primarily through acid and SO₄²⁻ generation. After the typical S₂O₈²⁻ solution injection, SO₄²⁻ concentrations can elevate to concentrations ≥1 g∙L⁻¹, substantially surpassing the secondary drinking water standard of 250 mg∙L⁻¹. Moreover, under reducing conditions, SO₄²⁻ can undergo microbial reduction to sulfide (HS⁻), potentially compromising water quality and facilitating sulfide mineral precipitation [4].

Given these considerations, we concurrently monitored SO₄²⁻ concentrations alongside the S₂O₈²⁻ concentration and pH profiles. The normalized mass balance of SO₄²⁻ generated from S₂O₈²⁻ decomposition (NMB(S₂O₈²⁻/SO₄²⁻) defined in Equation (11)) for all tests conducted in this study and illustrated in Figure 7. NMB(S₂O₈²⁻/SO₄²⁻) enables the comparison of individual soil-containing systems with the HC_theory, where the value of NMB(S₂O₈²⁻/SO₄²⁻) equals unity.

$$NMB\left(S{O}_4^{2-}\right)={\displaystyle \frac{c\left(S{O}_4^{2-}\right)-c_0\left(S{O}_4^{2-}\right)}{c_0\left(S_2{O}_8^{2-}\right)}}+{\displaystyle \frac{c\left(S_2{O}_8^{2-}\right)}{c_0\left(S_2{O}_8^{2-}\right)}}={\displaystyle \frac{\mathsf{\Delta }c\left(S{O}_4^{2-}\right)-c\left(S_2{O}_8^{2-}\right)}{c_0\left(S_2{O}_8^{2-}\right)}}$$

(11)

As shown in Figure 7a–d, the batch tests at higher S₂O₈²⁻ concentrations (c₀(S₂O₈²⁻) = 16.1 g∙L⁻¹) exhibit a general trend of decreased NMB(S₂O₈²⁻/SO₄²⁻) for systems containing aquifer/soil materials E and D, reaching approximately 30–40% and 15–30%, respectively, across all temperatures. This NMB(S₂O₈²⁻/SO₄²⁻) decline might be attributed to the precipitation of sulfate salts, such as gypsum (CaSO₄·2H₂O), which has a solubility of around 4 g∙L⁻¹ in the temperature range of 30–50 °C and ionic strength of 0.5 mol∙L⁻¹ [52], corresponding roughly to the average conditions in the systems upon 40% S₂O₈²⁻ decomposition. Additionally, the sorption of SO₄²⁻ onto soil particles may also contribute to this decline, as soil components can act as sorbents for anions under certain conditions [53]. For systems A and B, this decrease remains within a negligible 10% except in the 50 °C tests for system B, where the decline reaches ≈25%. Notably, the systems containing material C exhibited intriguing behavior, with NMB(S₂O₈²⁻/SO₄²⁻) increasing by approximately 10% and 25% at 50 °C and 40 °C, respectively. This phenomenon is likely attributable to the pronounced pH decrease in system C, reaching levels around 2. This substantial acidification likely facilitated the subsequent dissolution of SO₄²⁻-containing salts/minerals that did not occur during the 24-h equilibration period in DW prior to these experiments. At the lower temperatures of 30 °C and 35 °C, the aforementioned effect was not observed for system C, and the NMB(S₂O₈²⁻/SO₄²⁻) decreases were aligned with the levels seen for the system containing material A. This might be attributed to the higher pH conditions at these temperatures, in combination with the relatively lower ionic strength, leading to reduced dissolution intensity of SO₄²⁻-containing substrates.

Comparing batch systems with higher (c₀(S₂O₈²⁻) = 16.1 g∙L⁻¹; Figure 7b) and lower (c₀(S₂O₈²⁻) = 2.7 g∙L⁻¹; Figure 7e) initial S₂O₈²⁻ concentrations at 40 °C shows that the combination of reduced ionic strength and generally higher pH in the aqueous solutions resulted in approximately half the decrease in NMB(S₂O₈²⁻/SO₄²⁻) for systems D and E. In contrast, system C exhibited the most significant reduction in NMB(S₂O₈²⁻/SO₄²⁻) among all soils. Systems A and B demonstrated comparable decreases in NMB(S₂O₈²⁻/SO₄²⁻), again up to ≈10%.

In the case of column tests conducted at 40 °C (Figure 7f), the reduction in NMB(S₂O₈²⁻/SO₄²⁻) was more pronounced compared to its batch counterpart. Notably, material D exhibited a surprising decrease in NMB(S₂O₈²⁻/SO₄²⁻) of up to 70%. These more substantial reductions might be attributed to the leaching of higher concentrations of Ca²⁺ during the process, likely due to the higher material-to-water ratio employed in the column tests.

Generally, these results indicate highly complex and diverse SO₄²⁻ behavior within the context of ISCO using PDS. However, a more profound understanding and description of the occurring phenomena extend beyond the scope of the current research work. A comprehensive explanation of these processes would necessitate detailed studies specifically dedicated to these phenomena.

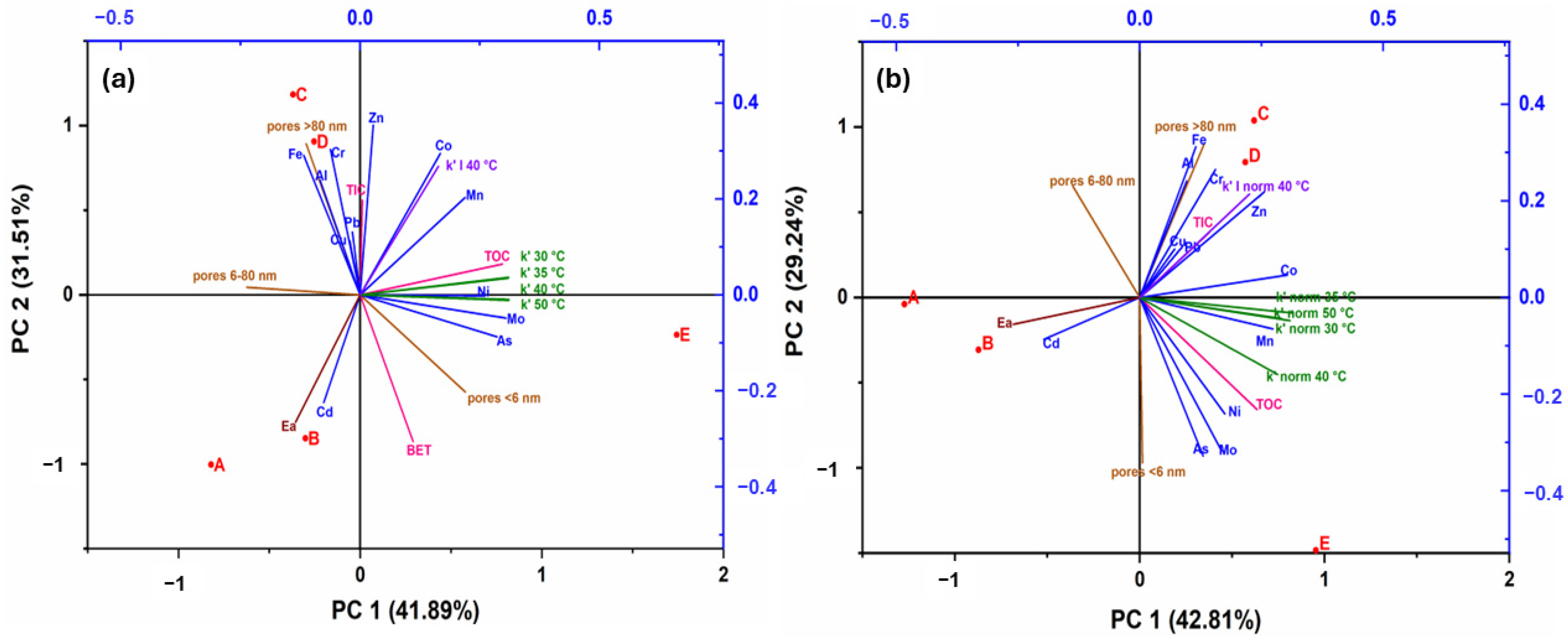
3.6. PCA Analysis

The PCA analyses reveal consistent patterns, indicating the robustness of relationships among determined S₂O₈²⁻ decomposition rate constants (k′ in Figure 8a and k′_norm Figure 8b) of batch experiments, elemental concentrations, and material characteristics. The optimal number of principal components (PCs) was determined based on eigenvalues from the correlation matrix, with both PC1 and PC2 exhibiting eigenvalues greater than 6.7. In each analysis, these two components collectively explain a similar proportion of the variance: 73.40% for a dataset with k′ (41.89% for PC1 and 31.51% for PC2) and 72.05% for data containing k′_norm (42.81% for PC1 and 29.24% for PC2). This suggests that using the dataset with k′_norm has minimal impact on the original data structure.

In both analyses, strong correlations are evident, with green vectors representing rate constants of batch experiments at higher concentrations (c₀(S₂O₈²⁻) = 16.1 g∙L⁻¹ denoted as k′ in Figure 8) and temperatures between 30 °C and 50 °C closely aligning with TOC, Ni, and Mo. In contrast, at a lower concentration (c₀(S₂O₈²⁻) = 2.7 g∙L⁻¹) and a temperature of 40 °C, rate constant k′ (denoted as “k′ l 40 °C” with purple color in Figure 8) aligns with Co and Mn, indicating a strong association under these conditions. Material clustering patterns are consistent across analyses: materials A and B cluster in the lower left quadrant, showing negative correlations with most variables, while materials C and D cluster together, shifting slightly to the upper right quadrant in the analysis of the dataset containing k′_norm and associating with large pore sizes (>80 nm), Fe, Al, Cr, Zn, and “k′ l 40 °C”. Additionally, the distinct positioning of material E along the positive PC1 axis in the analysis of the dataset using the k′_norm highlights unique characteristics that were less evident in the analysis of the dataset with k′. These consistent patterns across analyses confirm the core associations within the data, while the analysis dataset containing the total BET normalization of S₂O₈²⁻ decomposition rate constant highlights specific sample characteristics, particularly for material E, without disrupting the primary trends and correlations.

4. Implications for Environmental Applications

This study examined the persistence and reactivity of S₂O₈²⁻ across a range of soil materials using batch and dynamic column experiments, revealing critical insights for optimizing S₂O₈²⁻-based ISCO. Key findings include the following:

• Soil characteristics, especially TOC, strongly influence S₂O₈²⁻ decomposition rates;
• Lower initial concentrations of S₂O₈²⁻ increased decomposition rates across most soil systems, likely due to reduced ionic strength, thus, enhanced interaction with soil/aquifer minerals and SOM. This concentration-dependent reactivity suggests that adjusting the initial oxidant dose could optimize decomposition rates;
• Differences in E_a among the materials indicate varied thermal requirements for S₂O₈²⁻ activation, suggesting that materials with higher E_a may necessitate additional heat input to drive effective decomposition. This underscores the potential for temperature modulation as a control measure for S₂O₈²⁻ persistence in practical applications;
• While batch tests yielded higher S₂O₈²⁻ decomposition rates normalized to the total BET surfaces, dynamic column tests revealed that limited reactive surface accessibility and the formation of preferential flow paths may reduce the reliability of this setup in representing in situ conditions. Therefore, using batch or static stop–flow column tests may be more suitable for the evaluation of S₂O₈²⁻ persistence during bench-scale treatability tests;
• The main parameters affecting the decomposition rate of S₂O₈²⁻ were closely related to TOC, Ni, and Mo concentrations, particularly at higher concentrations (c₀(S₂O₈²⁻) = 16.1 g∙L⁻¹) and temperatures between 30 °C and 50 °C. Additionally, at a lower concentration (c₀(S₂O₈²⁻) = 2.7 g∙L⁻¹) and a temperature of 40 °C, the decomposition rate was more strongly associated with Co and Mn.

These findings underscore the necessity of tailoring ISCO treatments to specific soil properties such as TOC, the presence of different elements, and buffering capacity. Based on these factors, adjusting S₂O₈²⁻oxidant concentration and temperature has the potential to improve ISCO efficiency, minimize overall oxidant consumption, and reduce potential adverse effects on groundwater quality.