Abstract
When using a differential evolution algorithm to solve the joint flood optimization scheduling problem of cascade reservoirs, a greedy random optimization strategy is prone to premature convergence. Therefore, a new, improved Elite Conservative Differential Evolution Algorithm (ECDE) was proposed in this study. This algorithm divides a population into elite and general populations. The elite population does not undergo differential mutation, whereas the general population uses an adaptive differential mutation strategy based on successful historical information to participate in differential mutation. This elite conservative strategy effectively improves the diversity of the population evolution process and enhances convergence accuracy and stability. In a numerical experiment involving 10 test functions, the proposed ECDE performed the best overall (seven functions had the best stable convergence solution, while the remaining three performed the best), while in the single-objective flood control optimization scheduling problem of cascade reservoirs in the middle reaches of the Gan River, some algorithms could not even stably converge to feasible solutions (taking the 1973 inflow as an example, the peak shaving rate of the ECDE calculation results was 3.4%, 13.72%, and 11.73% higher than those of SHADE, SaDE, and GA, respectively). The proposed ECDE algorithm outperformed the SHADE, SaDE, GA, PSO, and ABC algorithms in terms of both convergence accuracy and stability. Finally, ECDE was used to analyze the multi-objective flood control scheduling problem of cascade reservoirs in the middle reaches of the Gan River, and it was found that the weight setting in multi-objective optimization should follow an upstream priority program or equilibrium programs. Adopting a downstream priority program results in poor upstream flood control performance. The above analysis fully verifies the superiority of the proposed algorithm, which can be used to solve and analyze the joint optimization scheduling problem of cascade reservoirs.
1. Introduction
Reservoir scheduling is an important and effective method for the optimal allocation of water resources and can regulate runoff and effectively alleviate regional flooding [1]. As many reservoirs are built and put into operation, the rational operation and management of reservoir clusters to maximize the comprehensive benefits of gradient reservoir clusters have been increasingly emphasized [2]. Establishing a joint optimal scheduling model for reservoir groups is an effective method to solve this problem [3]. The joint optimal scheduling of reservoir groups is a decision optimization problem that mathematically transforms complex reservoir scheduling problems in the actual process into abstract optimization problems, transforms these problems into different constraints, and seeks an optimal solution based on these constraints [4]. Because reservoir flood control and scheduling involves many factors, such as natural, social, economic, and technical factors, it is a complex, high-dimensional, nonlinear, strongly coupled multi-objective optimization problem, which has been researched by many scholars [5,6].
Currently, research on multi-objective optimal scheduling of reservoir groups mainly focuses on the establishment of mathematical models for multi-objective optimal scheduling, multi-objective evolutionary algorithms and their improvements, and multi-objective competitive relationship analyses [7]. The solution methods mainly include direct solutions using multi-objective evolution algorithms (MOEAs) [8] and the idea of converting the multi-objective problems arising in the process of flood control and scheduling into single-objective problems for solving through the idea of weighting methods [5,9]. Earlier studies focused on the theoretical areas of linear programming (LP), dynamic programming (DP), and progressive optimization algorithms (POA) based on the principles of operations research [10,11,12,13]. In recent years, with the broadening of mathematical theories and the popularization of computer hardware, intelligent optimization algorithms have been widely used in the field, and the common underlying models, including Genetic Algorithms (GA), Particle Swarm Algorithms (PSO), and Jaya Algorithms, etc., have been widely used for solving the multi-objective optimization scheduling problem [14,15,16,17,18]. Dash proposed an algorithm based on SWAT, HEC-ResSim, and a GA optimization framework (SWAT-HEC-ResSim-GA) for developing an optimal scheduling plan for dams in the Kansabati River Basin in eastern India [19]. Yu et al. developed a multi-objective robust optimization method, which is mainly used for real-time scheduling of reservoir flood control under prediction uncertainty, and established a multi-objective robust optimization scheduling model that integrates upstream and downstream safety, which improves the efficiency of reservoir utilization while reducing the flood risk [20]. These heuristic algorithms employ intelligent, bionic, and heuristic strategies to guide the search process, and are therefore more flexible and efficient than traditional optimization methods. However, they also face the challenge of balancing the local convergence and global search.
Storn and Price [21] proposed the Differential Evolution (DE) algorithm in 1997. Because of its simplicity and ease of implementation compared to other algorithms, it has shown good performance in various fields, such as image processing and optimization scheduling. Qin et al. [22] proposed a multi-objective differential evolution algorithm based on adaptive Cauchy mutation, which overcomes the problem of DE falling into local optima when solving multi-extremum problems and effectively avoids premature convergence, improving convergence accuracy. He et al. [23] proposed an improved DE algorithm with partition parameter adaptive update strategy, which can effectively improve the comprehensive benefits of water resources in the upstream of the Yangtze River when applied to the joint scheduling of cascade reservoirs in the lower reaches of the Jinsha River. Bilal [24] combined metaheuristic algorithms, improved heuristic algorithms, and the classical DP algorithm, among which the DP-FCADE2 algorithm performed the best and was applied to finding the optimal scheduling strategy for the Mula reservoir. Ahmadianfa et al. [25] developed an Adaptive Differential Evolution based on Particle Swarm Optimization algorithm, which uses new mutation and crossover mechanisms to improve both global and local search capabilities. In addition, there are algorithms such as CoDE [26], SaDE [27], JaDE [28], and SHADE [29], etc., all of which have made improvements in differential evolution strategies or parameter updates. The above-mentioned improved algorithms have, to some extent, improved the computational speed and solution accuracy of reservoir optimization scheduling problems. However, they suffer from poor stability and are prone to local optima. Further research is needed on algorithm parameter update mechanisms and search strategies.
To address these issues, this study proposes effective improvements to the traditional DE algorithm. Each generation was divided into an elite population and general population during the differential mutation process in the ECDE. The elite population preserves excellent genes without using mutation strategies, whereas individuals in the general population evolve with various mutation strategies based on successful historical information during the evolution process. Subsequently, the effectiveness of the proposed ECDE in this study was verified through numerical experiments and engineering case analysis.
2. Research Area and Data
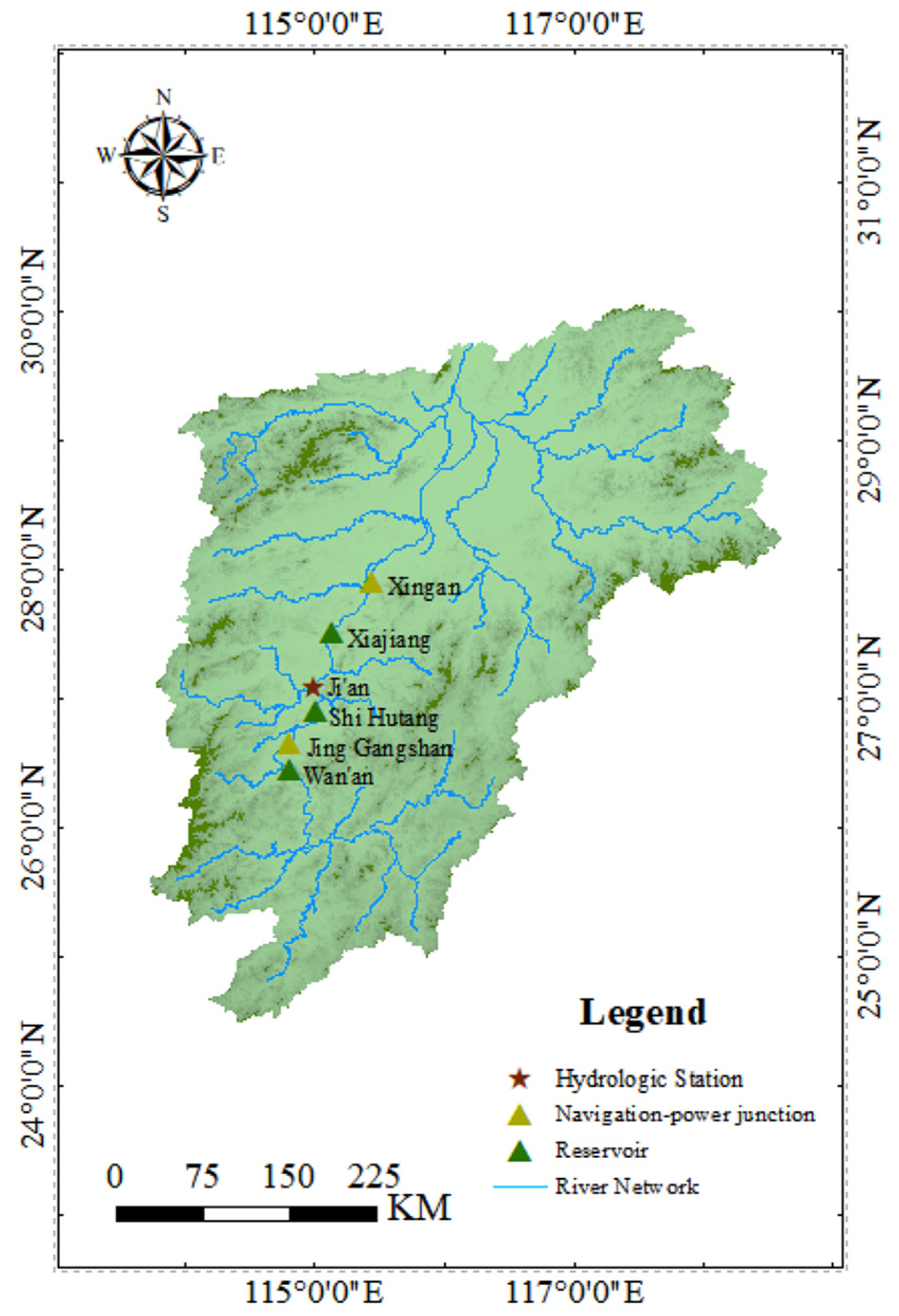
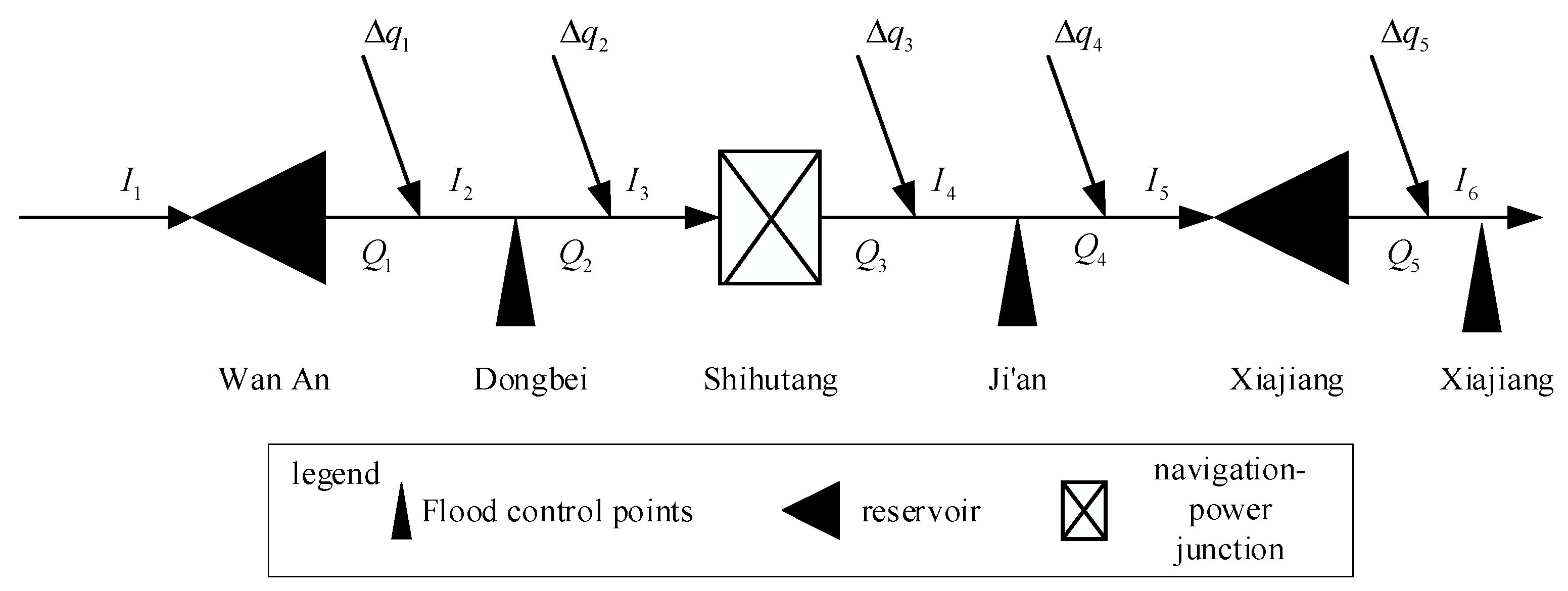
The Ganjiang River is located in Jiangxi Province, China, Asia. It is one of the main tributaries of the Yangtze River. It runs through the north and south of Jiangxi Province and finally flows into Poyang Lake (see as Figure 1). The Gan River has a total length of 766 km and a watershed area of 83,500 square kilometers, accounting for more than half of the area of Jiangxi Province, and there are water conservancy projects in the middle reaches of the Gan River (see as Figure 2), such as Wan’an, Shihutang, and Xiajiang, etc.; the main parameters of the group of stepped reservoirs in the analysis of the engineering examples are given in Table 1. In addition, there is an important flood control point (Ji’an Hydrological Station) located downstream of Shihutang Reservoir and upstream of Xiajiang Reservoir, which is used for flood warning in Ji’an City.
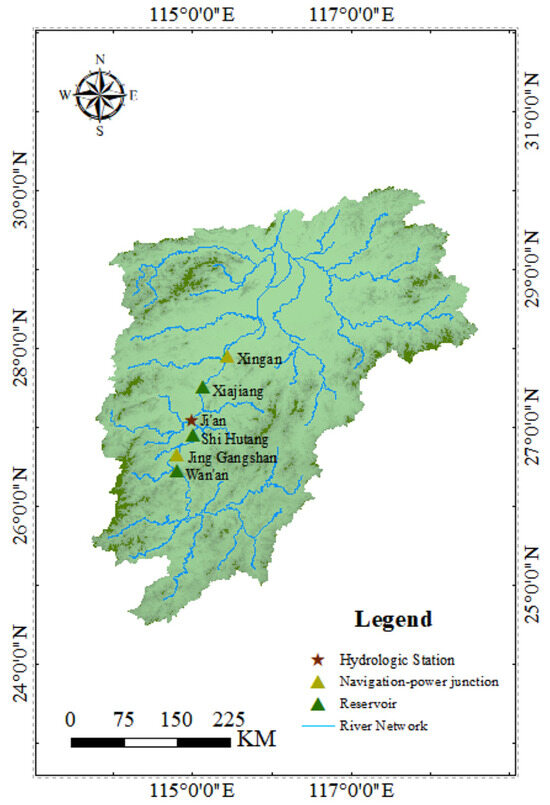
Figure 1.
Overview map of the research area (cascade reservoirs in the middle reaches of the Ganjiang River).
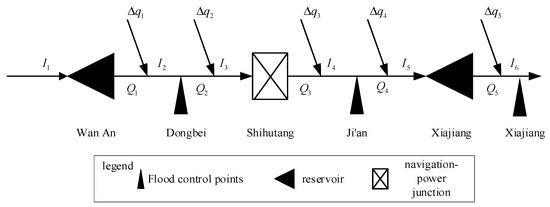
Figure 2.
Topological map of the cascade reservoir in the middle reaches of Ganjiang River.

Table 1.
The main parameters of hydropower stations in research area.
3. Optimization and Operation Model for Flood Control of Cascade Reservoirs in the Middle Reaches of Ganjiang River
This study focuses on the joint multi-objective flood optimization scheduling problem of the cascade reservoir group in the middle reaches of the Gan River to simultaneously meet the flood control requirements of different objectives in the watershed while ensuring the flood safety of the reservoirs themselves. It establishes a joint flood optimization scheduling model for the Wan’an, Shihutang, and Xiajiang reservoirs.
3.1. Objective Function
When flood control safety downstream of the cascade reservoir is considered as the protection object, the maximum peak shaving criterion is used as the flood control objective. Therefore, minimizing the discharge process of Xiajiang Reservoir and reducing the flood control pressure in the downstream protection zone will be considered as the scheduling objective. The objective function for minimizing the sum of squares of the outflow of Xiajiang Reservoir is shown in the following equation:
Currently, reservoir flood control scheduling tasks mainly include three aspects: the dam’s own flood safety, reservoir area flood safety, and downstream flood protection zone flood safety. There is a conflict between upstream and downstream flood control objectives. Therefore, multi-objective scheduling of reservoirs requires algorithms to optimize multiple objectives simultaneously. The objectives for joint multi-objective flood scheduling of the reservoir group are as follows: (1) Minimize the flood control point discharge; (2) Minimize the outflow from the Wan’an Reservoir; (3) Minimize the outflow from the Xiajiang Reservoir. To optimize these flood control objectives simultaneously, a widely used weighted method [30] was employed to combine the three objectives mentioned above. The weight values for each flood control objective can be set by decision makers based on the importance of the objectives and requirements of the actual scheduling process. The model objective function was formulated as follows:
where and , respectively, represent the single objective and multi-objective function values for joint optimization and scheduling of cascade reservoirs. , , and , respectively, represent the outflow of Wan’an Reservoir, Shihutang Reservoir, and Xiajiang Reservoir in period t, and represents the flow of Ji’an Hydrological Station in period t. and , respectively, represent the maximum outflow of Wan’an Reservoir and Xiajiang Reservoir in this optimization scheduling, and represents the maximum flow at Ji’an Hydrological Station to ensure flood control safety. a, b, and c represent the weights of the three flood control objectives, respectively. represents the number of scheduling periods.
3.2. Constraints
- Water balance constraint.
- Water level upper and lower bound constraint.
- Water level variation constraint.
- Flood control point discharge constraint.
- Outflow constraint.where represents the serial number of reservoir, with w, s, and x from upstream to downstream, representing Wan’an Reservoir, Shihutang Reservoir, and Xiajiang Reservoir, respectively. and , respectively, represent initial and final storage of the m-th reservoir at period . , , and , respectively, represent the inflow, outflow, and local inflow of the m-th reservoir at period . and , respectively, represent the water level and maximum water level variation of the m-th reservoir at period . and , respectively, represent the lowest water level and highest water level of the m-th reservoir at period . and , respectively, represent the minimum outflow and maximum outflow of the m-th reservoir at period . In addition, the Muskingum method was used to calculate the river flood routing; detailed information can be found in the literature [31,32,33].
4. The Details of ECDE
4.1. Classical Differential Evolution Algorithm
Intelligent optimization algorithms have been widely promoted and applied in the field of reservoir scheduling. Among them, Differential Evolution (DE) is a primary algorithm for continuous domain intelligent optimization; the specific steps of the algorithm can be found in reference [21]. The key operations include initialization, differential variation, crossover, and selection. The differential variation strategies include rand/1, rand/2, best/1, best/2, current to best/1, etc., and each mutation strategy has its optimization characteristics. Their abilities in global and local searches vary. The choice of strategy significantly affects the convergence speed of the algorithm [34].
4.2. Adaptive Differential Mutation and Elite Conservative Strategy
Elite populations are widely used in intelligent optimization algorithms but are generally used to retain optimal or better individuals, thereby guiding other individuals in the population to accelerate the optimization process and improve the convergence speed of the algorithm. But as is well known, intelligent algorithms not only face the problem of slow convergence speed, but also the problem of premature local convergence. In practical problems, the convergence speed of algorithms is obviously not as important as the convergence accuracy. Therefore, research has found that adopting a conservative strategy for elite populations without evolving them can increase the population diversity and improve the convergence accuracy of the algorithm. Meanwhile, one can also refer to the adaptive differential mutation strategy and choose multiple functional differential mutation operators (such as those with strong local or global search capabilities) combined with the elite population conservative strategy to improve the convergence performance of the algorithm.
4.2.1. Elite Conservative Strategy
In previous differential evolution, elite populations tended to participate preferentially in greedy differential operators, accelerating convergence and making it easier for the population to quickly approach elite populations, resulting in a sharp decrease in population diversity. Therefore, research suggests that conservative strategies can be adopted by elite populations to reduce their participation in evolution, thereby enhancing population diversity.
Specifically, the specific implementation of the conservative strategy for elite populations is as follows: (1) First, the population is ranked in descending order of fitness; (2) An elite population ratio parameter , is set, where the top individuals in the sorted population are considered elite populations and the remaining individuals are considered general populations; (3) Individuals in elite populations do not participate in differential variation, while individuals in general populations normally participate in differential variation.
4.2.2. Adaptive Differential Mutation Strategy
The adaptive differential mutation strategy and parameter adaptive updating are common improvement strategies in differential evolution algorithm [35,36].
SaDE (Self-adaptive DE) [35] is an improved differential evolution algorithm that selects differential strategies for each generation based on the success rate of individuals generated using each differential strategy. However, this method cannot fully leverage the advantages of the different strategies at different stages of evolution. Among the various mutation strategies, “DE/rand/2” has the strongest global search capability, but it converges relatively slowly, which is not conducive to the rapid convergence of the population. The mutation strategy “current-to-pbest/1” has a relatively strong local search capability and can rapidly cause the population to converge [37]. However, its search range is narrow, which can lead to premature convergence or becoming stuck in a local optimum.
Therefore, to enable the algorithm to converge quickly while maintaining global exploration capabilities, the ECDE algorithm, inspired by the “current-to-pbest/1” strategy, extends “rand/1” and “rand/2” by replacing two randomly selected individuals in the operator with the (k + 1)-th individual in the current generation and individuals randomly selected from both the current generation and external archive. This leads to the creation of “current-to-rand/1” and “current-to-rand/2” strategies for the differential mutation operators. A strategy collection was established using the “current-to-pbest/1”, “rand/2”, “current-to-rand/1”, and “current-to-rand/2” differential mutation operators. Among these, the “current-to-pbest/1” strategy introduces a control parameter, , to control the greediness of “current-to-pbest/1” strategy toward pbest. Smaller values of enhance local search capability and accelerate convergence but may result in local convergence and premature convergence.
The ECDE algorithm dynamically adjusts the probabilities of the four mutation strategies based on the differences in the benefits to individuals using each strategy in the previous generation. In the initial evolution stage, the four mutation strategies are assigned equal probabilities. After each generation completes the evolution, the probabilities are recalculated based on the differences in the benefits before and after evolution for each strategy’s individuals. In the next generation, individuals randomly select mutation strategies based on historical information regarding successful evolution. The differential mutation strategies were as follows:
- “rand/2”:
- “current-to-rand/1”:
- “current-to-rand/2”:
- “current-to-pbest/1”:where is the number of population generations; is the -th solution or individual in the -th generation population of differential evolution; is the -th mutated individual generated by the -th generation parent through the mutation strategy; is the individual with the best performance in the fitness evaluation index of the -th generation population; is randomly selected from the top individuals with better fitness evaluation in the -th generation population, where the control parameter is a random number that obeys a uniform distribution within the range of . is the individual randomly selected from the -th generation population and the external archive set after mixing; in the random selection process, the index numbers , , ~ of the individuals are required to be different, in which the index numbers ~ of the individuals represent randomly selected in the range of .
The formula for the probability of selecting the -th mutation strategy during the evolution of the -generation population is as follows.
where represents the probability of the -th mutation strategy being selected during the evolution of the -generation population. represents the set of individuals that successfully evolved after adopting the -th mutation strategy in the -generation population. Therefore, represents the difference in objective function between this generation and the previous generation for all individuals in the set .
The ECDE algorithm adapts its parameters using a similar approach to that of SHADE and JADE algorithms [28,29]. It creates an archive set to store the and values that have participated in successful evolution, and updates the archive set using the history of successful evolution parameters. The archive set is set with a size of , and parameters are updated using both Cauchy and normal distribution methods.
4.3. Crossover and Selection
The crossover and selection operations in ECDE are similar to those in classical DE. The binomial Crossover is the most commonly used crossover operator in DE. It crosses the parent and the mutant vector to generate trial vector . For each dimension j, it is implemented as follows:
where is a decision variable index which is uniformly randomly selected from .
After all trial vectors have been generated, a selection process determines the survivors for the next generation. The selection operator in standard DE compares each individual against its corresponding trial vector , keeping the better individual in the population.
In the selection process, the trial individual is compared with the parent individual based on fitness evaluation criteria. When the trial individual’s evaluation was better than that of the parent individual, it was recorded as a successful evolution. And in unsuccessful evolution, those individuals that were not chosen to enter the next generation will be stored in an external archive set , the size of which is determined by the population size and the parameter , . If, after a population evolution, becomes larger than , all individuals in are sorted based on their fitness and some of the individuals with lower fitness are removed to ensure that the size of meets the condition.
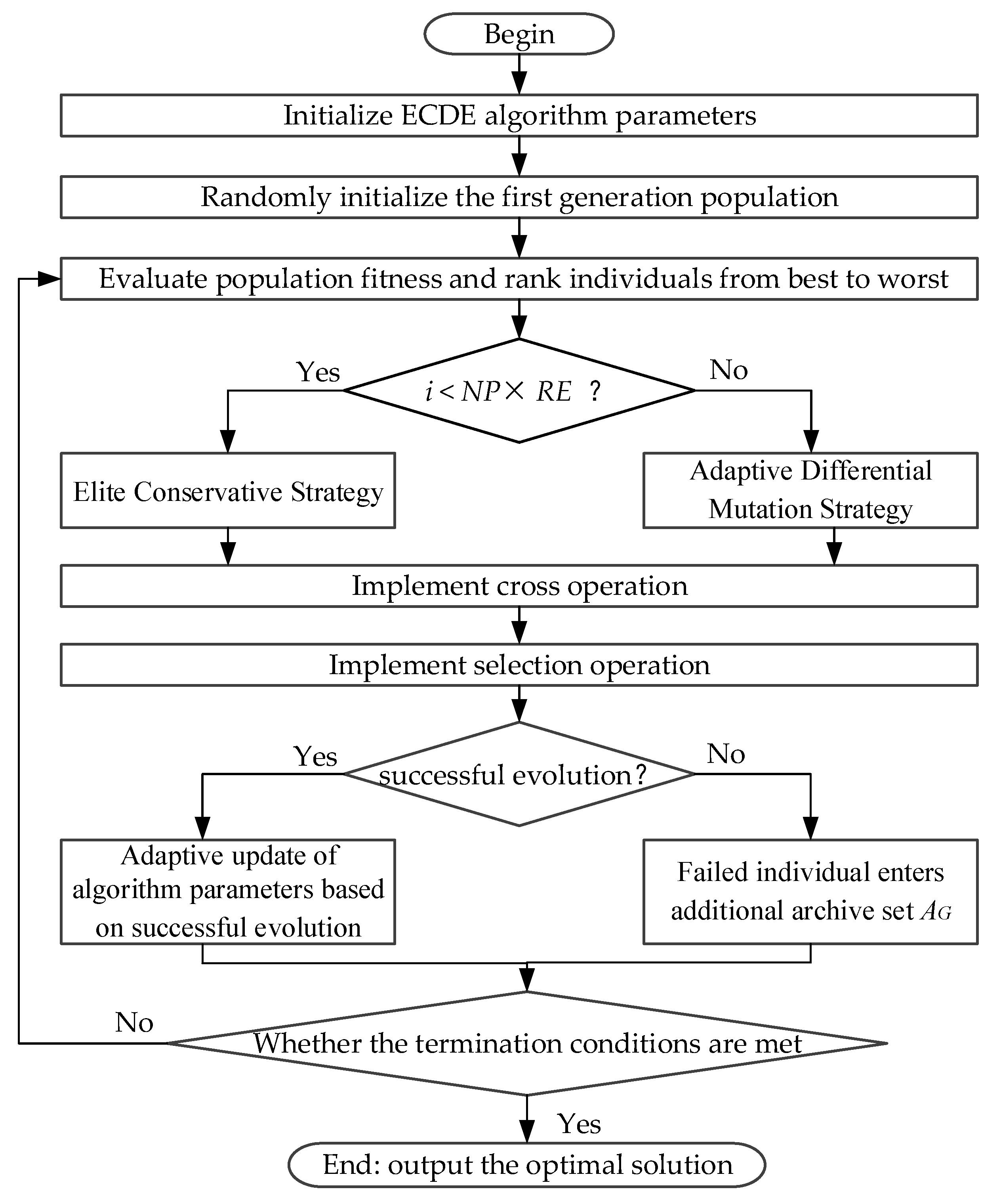
The calculation flowchart for the ECDE algorithm is illustrated in Figure 3.
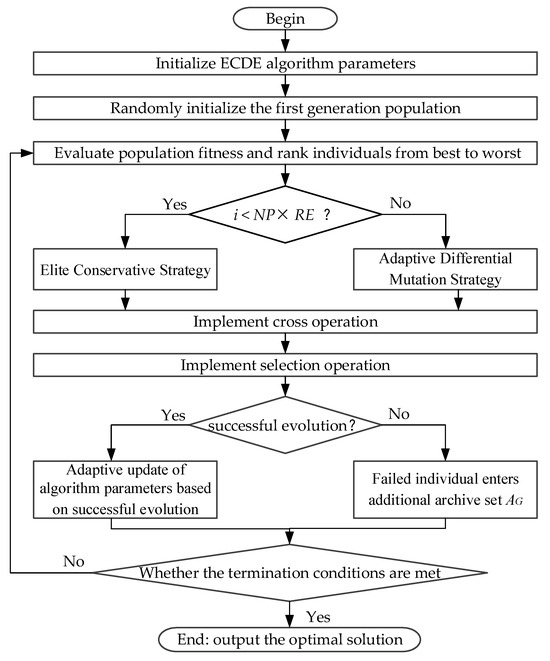
Figure 3.
Calculation flowchart of the ECDE algorithm.
5. Numerical Experiment
To assess the ECDE’s local quick convergence and global search capabilities, experiments were conducted using ten different evaluation functions, which are presented in Table 2. The experiments included five single-peaked optimization functions (, , , and ) primarily to evaluate the algorithm’s local quick convergence capabilities. The other five functions were multi-peaked optimization problems used to assess global exploration capabilities [23]. The algorithm’s final optimization results were compared to the optimal values of these functions, considering the solution as optimal when the difference was less than .

Table 2.
Details of benchmark problems.
To enhance the reliability and rigor of the experiments and better evaluate the convergence performance of ECDE, this study compares ECDE with other improved differential evolution algorithms (SHADE, SaDE, DE) vertically and then with other optimization algorithms (GA, PSO) horizontally through test function experiments. To ensure the scientificity of the experiment, the six optimization algorithms were solved independently with dimensions D = 100 for each of the 10 test functions. The experimental results of each algorithm on each test function are counted, and the evaluation indexes are set to assess the convergence ability and convergence stability of the algorithms; the four evaluation indexes are the optimal value of the convergence error, the mean, the standard deviation, and the number of successes (the number of times of reaching the optimal solution); and the test parameters are set as follows: , . The experimental results for the test functions are listed in Table 3.

Table 3.
Experimental results of solving high-dimensional test functions using ECDE and other optimization algorithms.
From the analysis of the results in Table 3, it can be seen that the optimization algorithms, such as DE, GA, and PSO, cannot converge to the optimal solution in ten function tests. SHADE and SaDE can obtain optimal solutions for the three functions. ECDE obtains the optimal solutions of seven functions, and also performs the best among the remaining three functions (, , and ). Especially in the functions and , ECDE algorithm’s number of successes, optimal values, etc., are much better than other algorithms. In summary, the ECDE algorithm is a competitive, improved differential evolutionary algorithm with a better convergence performance and stability than other optimization algorithms in high-dimensional function test results.
6. Case Study
6.1. Steps of DE Solving the Flood Control Scheduling Problem of Cascade Reservoirs
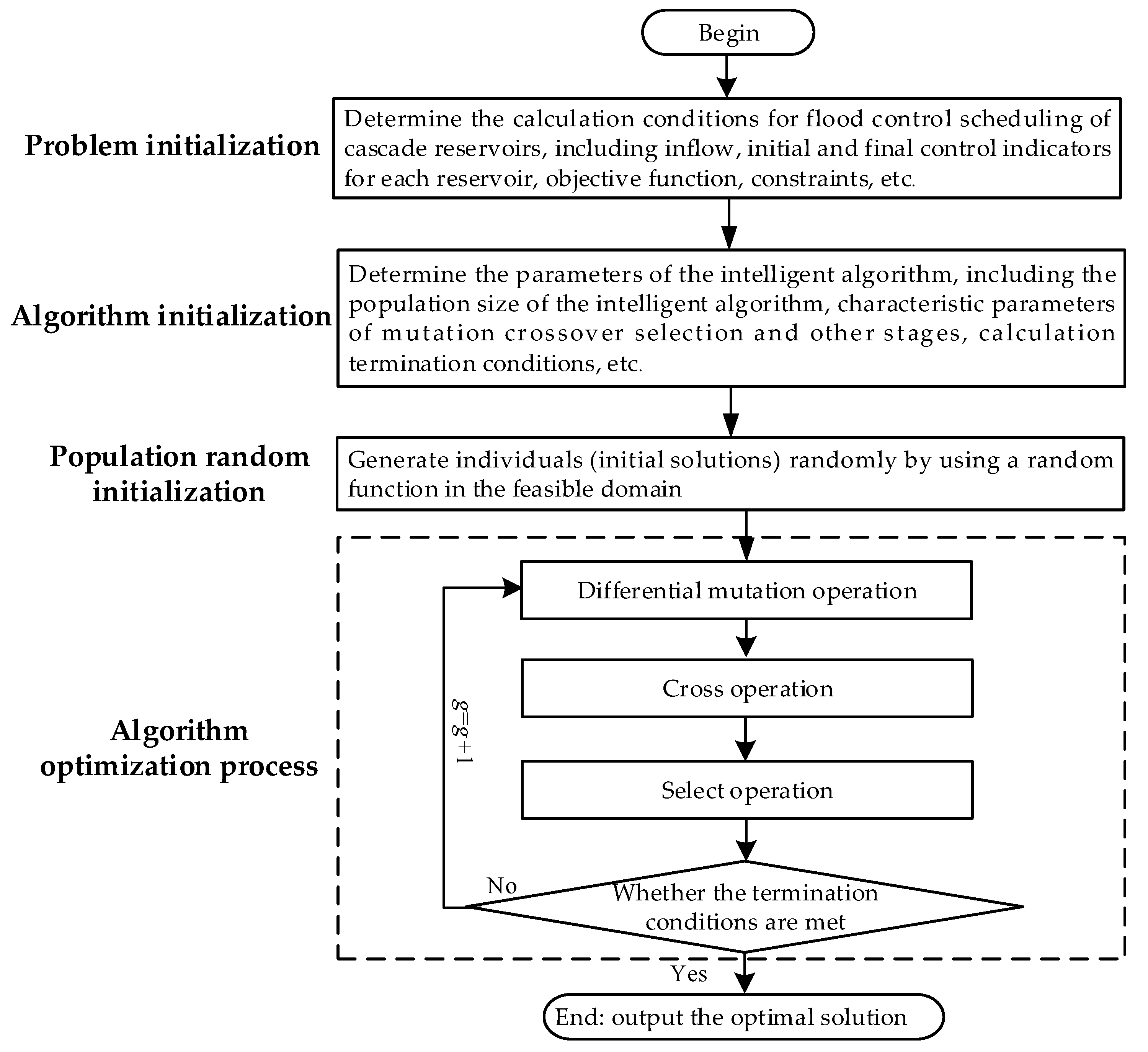
To test the application performance of ECDE in practical engineering, a case study was conducted using cascade reservoirs in the middle reaches of the Gan River as an example. The brief steps for using intelligent algorithms to solve the flood control and scheduling problem of cascade reservoirs (see Figure 4) are as follows.
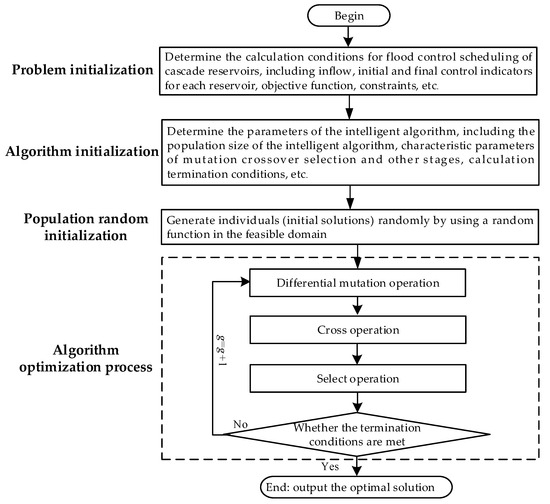
Figure 4.
Flowchart for optimal scheduling of multi-objective flood control.
Step 1: Determine the calculation conditions for the flood control scheduling problem of cascade reservoirs, including the inflow, initial, and final control indicators for each reservoir, objective function, and constraints.
Step 2: Determine the parameters of the intelligent algorithm, including the population size of the intelligent algorithm, characteristic parameters of the mutation crossover selection and other stages, and calculation termination conditions.
Step 3: Randomly generate individuals (initial solutions) using a random function in the feasible domain.
Step 4: Randomly initialize the first-generation population of the algorithm.
Step 5: Iterate optimization based on the mutation, crossover, and selection strategies of the algorithm until the termination conditions for the calculation are met.
Step 6: Select the best performing individual from the last generation population as the solution to the problem
6.2. Case Study 1: Comparison of Different Algorithms
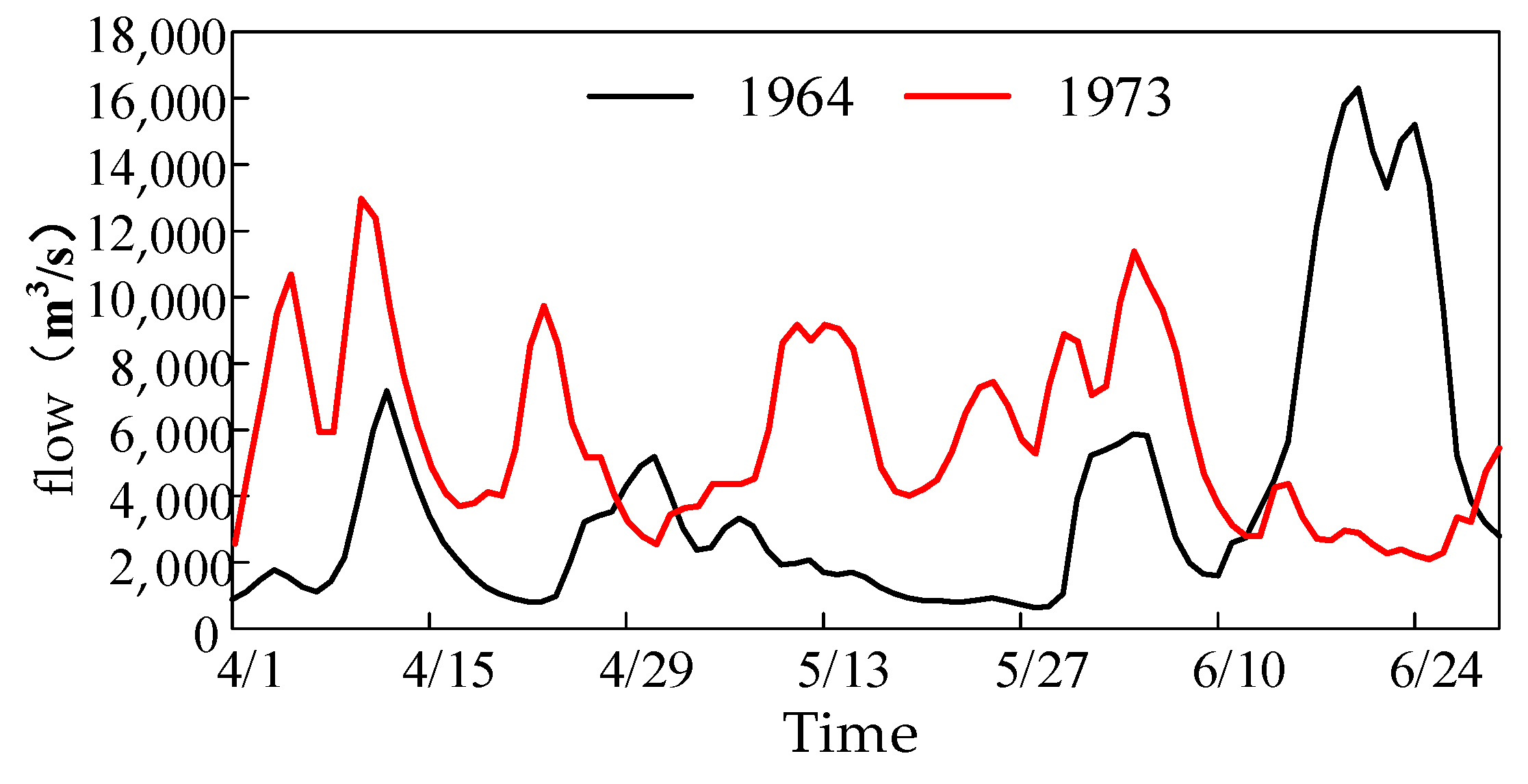
Numerical experiments verified that the proposed ECDE algorithm is superior to the other algorithms in terms of numerical optimization problems. This section further combines the single objective (Formula (1)) for the flood control scheduling problem of cascade reservoirs established in Section 3 to conduct a case study analysis. This case study also used six algorithms from numerical experiments for solving with the same parameter settings as in the numerical experiments. The termination condition fitness evaluation was set to 300,000 times. The typical historical floods of 1964 and 1973 are selected as the inputs of inflow conditions, which are single-peak floods and multi-peak floods, respectively, as shown in Figure 5. The peak flow rates of Xiajiang Station were 16,300.00 m3/s and 13,000.00 m3/s, respectively. The calculation period of the model was from April to July with a calculation time step of 6 h.
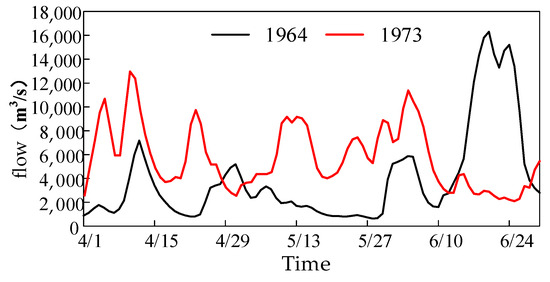
Figure 5.
Historical flood processes in 1964 and 1973.
Table 4 presents the calculation results of the peak flow and peak shaving rates at Xiajiang Station using the various optimization algorithms. As shown in Table 4, the ECDE, SHADE, and GA algorithms achieved a success rate of 100% in solving feasible solutions for cascade reservoir flood control scheduling problems in 50 independent repeated experiments of historical floods in 1964 and 1973. The SaDE algorithm had a success rate of 100% in the 1973 historical flood but only succeeded nine times in the 1964 historical flood. However, the PSO and DE algorithms were unable to obtain feasible solutions under the two flood conditions.

Table 4.
Statistical results of peak discharge and peak shaving rate at Xiajiang Station.
Under the historical flood in 1964, the average value of peak discharge flow at Xiajiang station of the ECDE algorithm for 50 independent repeated experiments was 13,402.71 m3/s, and the average peak shaving rate reached 17.8%. In terms of the peak shaving rate, ECDE increased by 0.90% and 2.43% compared to SHADE and GA, respectively. In the optimal and worst solutions, the ECDE results are significantly better than those of SHADE and GA.
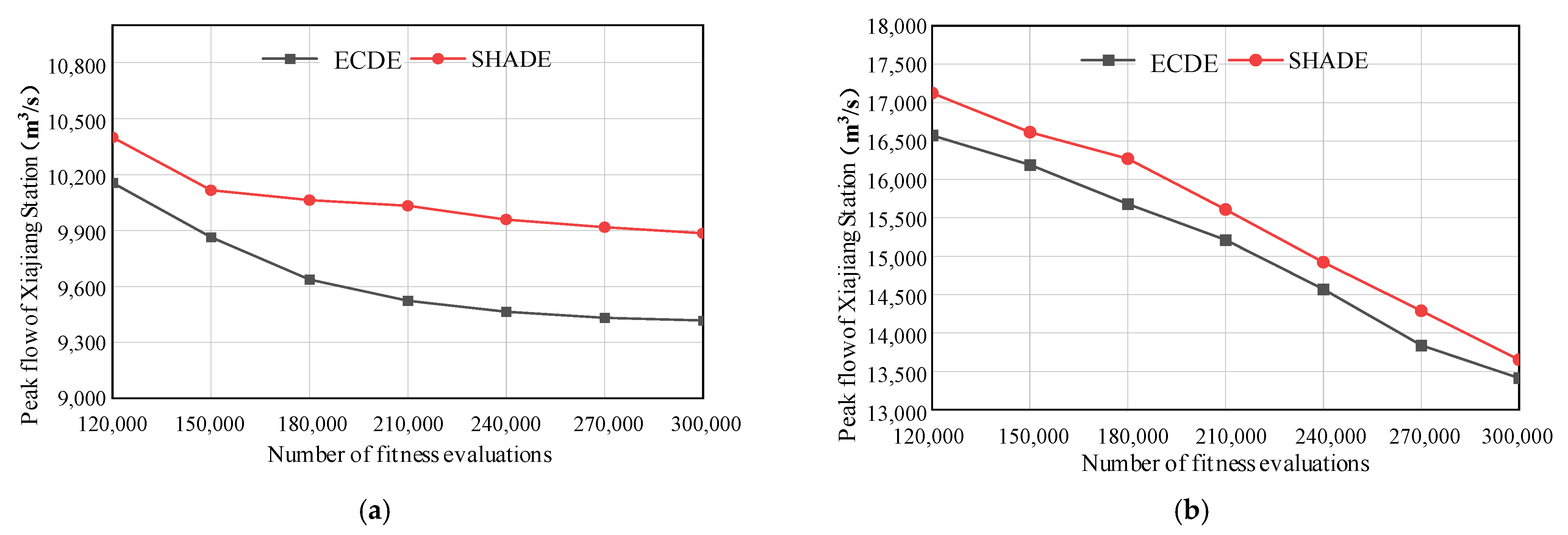
In addition, the flood control scheduling problem of cascade reservoirs not only requires algorithms with strong optimization capabilities, but also crucial convergence stability. Therefore, the stability of the algorithm was evaluated based on two indicators: the range and standard deviation. During the historical flood process of 1964, the ECDE algorithm had a range of 135.72 m3/s and standard deviation of 47.15 m3/s. Compared with the SHADE algorithm, the range decreased by 286.19 m3/s and the standard deviation decreased by 147.03 m3/s. During the 1973 historical flood process, the ECDE algorithm performed better than SHADE, SaDE, GA, and other algorithms in terms of range and standard deviation indicators. Figure 6 shows the convergence process of the ECDE and SHADE algorithms, and it is evident that ECDE has a better convergence speed and accuracy than SHADE under two historical flood conditions.
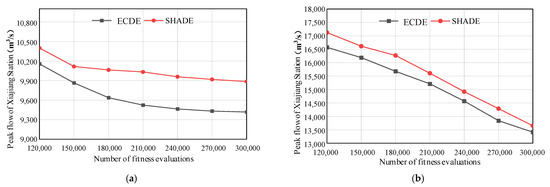
Figure 6.
The convergence process of ECDE and SHADE during historical flood processes. (a) The 1964 historical flood; (b) The 1973 historical flood.
In summary, the ECDE proposed in this study adopts an elite conservative strategy and improves the two basic differential strategies by selecting four mutation strategies for probabilistic adaptive selection. This enhances the global search capability of the ECDE and improves population diversity during the evolutionary process. Compared with SHADE, SaDE, GA, and other algorithms, it performs the best in terms of convergence feasible solutions, convergence accuracy, convergence stability, and convergence speed indicators and can be used as an efficient and stable solution tool for the flood control scheduling problem of cascade reservoirs.
6.3. Case Study 2: Multi-Objective Flood Control Optimization Scheduling of Cascade Reservoirs
This case study further combines the multi-objective function (Formula (2)) established in Section 3 to analyze the relationship between the different weights, inflow, and flood control objectives of each reservoir. A 50-year design flood in 1983 was selected as input. Table 5 presents the multi-objective flood control optimization scheduling results of the cascade reservoirs under the five weight design programs. Among the five weight design programs, programs A, B, and C focus on the flood control objectives of Wan’an Reservoir, Ji’an Hydrological Station, and Xiajiang Reservoir, respectively, whereas programs D and E can be considered balanced schemes.

Table 5.
Statistical results of multi-objective flood control optimization scheduling of cascade reservoirs.
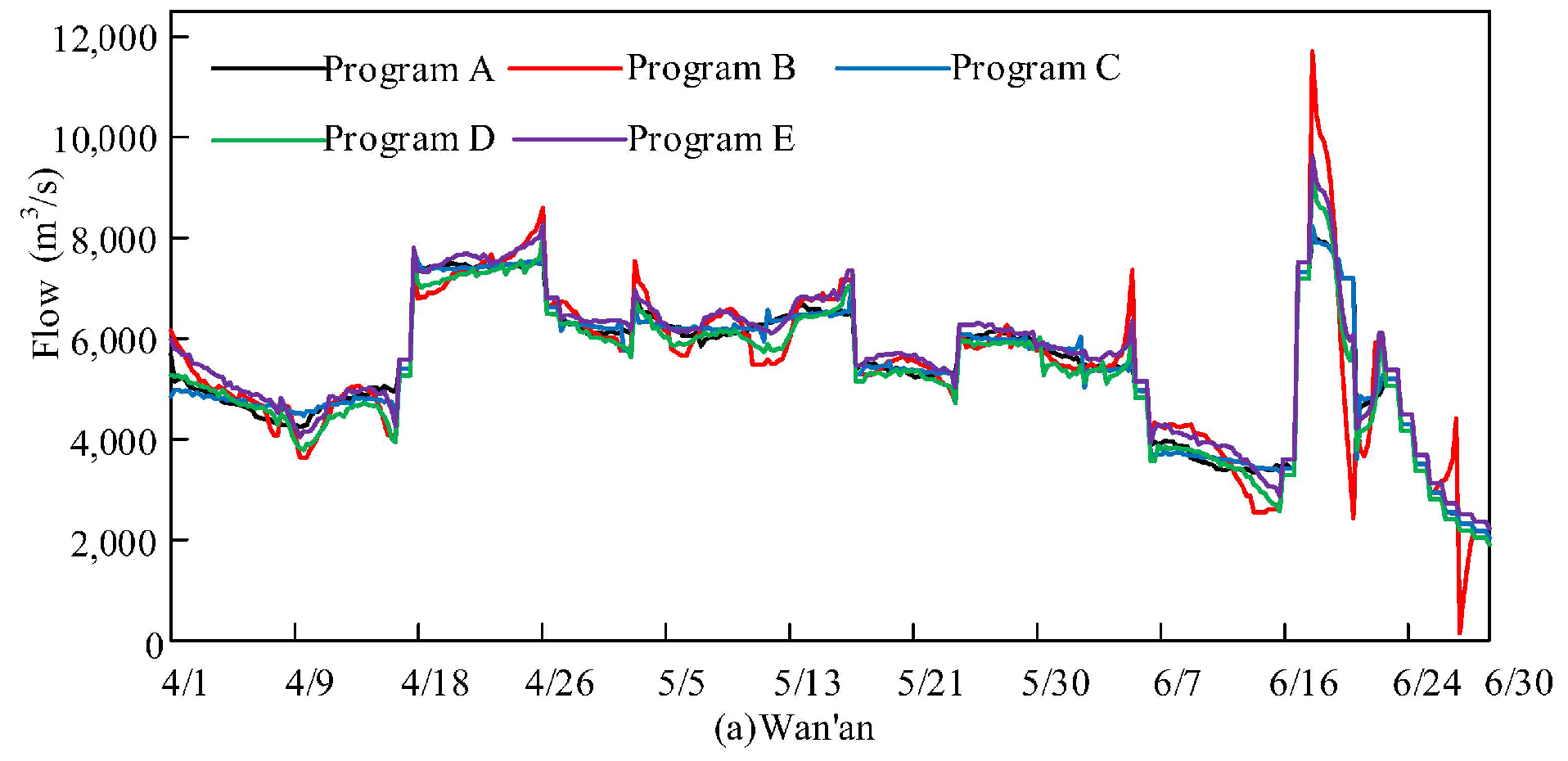
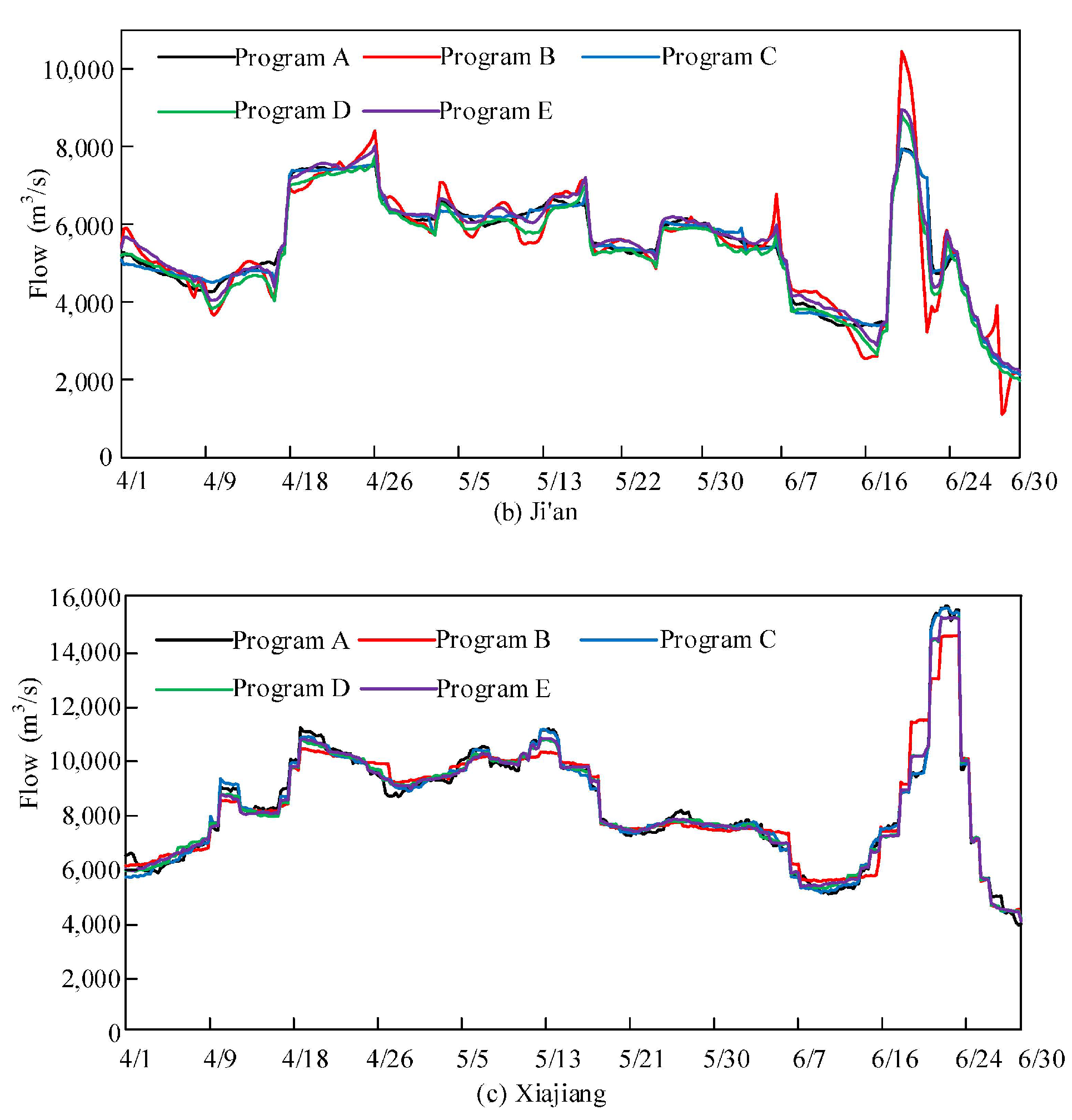
According to the experimental results in Table 5, it can be concluded that: (1) When the multi-objective weights are focused on the upstream Wan’an Reservoir or downstream Xiajiang Reservoir, the peak discharge of the reservoir that is the focus of attention is the smallest; (2) When adopting an equilibrium scheme, the peak flow of each reservoir and hydrological station performs well, with little difference from the optimal solution; (3) When the multi-objective weights focus on the upstream Wan’an Reservoir, the upstream peak flow is controlled, and the downstream peak flow is also smaller; (4) when the multi-objective weights focus on the downstream Xiajiang Reservoir, the downstream peak flow is controlled. However, because of the neglect of upstream flood control, the upstream Wan’an Reservoir has a larger peak flow, and the weight setting is unreasonable. Figure 7 shows the flow process of multi-objective flood control optimization scheduling results for cascade reservoirs under different weight schemes; the flow processes of each reservoir remain consistent with the above conclusions.
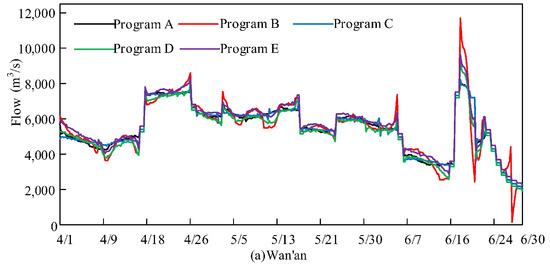
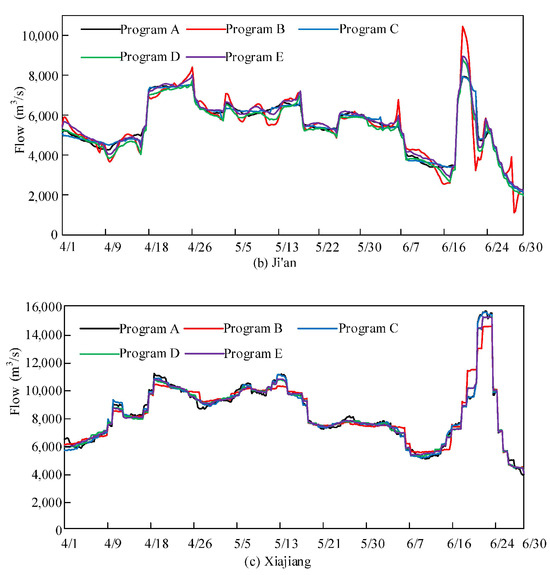
Figure 7.
Flow process of multi-objective flood control optimization scheduling results for cascade reservoirs under different weight programs.
In summary, when performing multi-objective joint flood control optimization scheduling of cascade reservoirs, for the control points from upstream to downstream in space, either an equilibrium scheme or a scheme focusing on upstream flood control should be adopted. Thus, the overall flood control effect from upstream to downstream is better.
7. Discussion
Research on solving the optimization scheduling problem of cascade reservoirs has gone through many years and has already formed a relatively mature system. At present, engineering practice and theoretical research using mathematical programming and intelligent optimization methods have achieved fruitful results. Mathematical programming methods are based on theoretical foundations. When dealing with nonlinear, strongly coupled, and multiple complex constraint problems, the non-analytical nature of actual engineering problems increases the difficulty of further research on related technologies, particularly the large computational burden caused by high-dimensional problems, which poses a dilemma for traditional mathematical programming methods in dealing with nonlinear problems [38]. Although intelligent optimization algorithms cannot guarantee optimal convergence and have poor convergence stability, they can adapt to nonlinear and multi-complex constraint problems based on random search strategies, especially for problems where mathematical expressions are not analytical and can also be applied.
With the development of computer technology, the convergence performance of intelligent algorithms can be further enhanced. In addition, in practical engineering, whether algorithms can solve the optimal problem is not the most concerning issue, because there are many uncertainties in the real world [39]. Therefore, an algorithm that adapts to practical engineering problems should provide better results as soon as possible to support dispatching personnel in making quick decisions and adjustments [40]. This study proposes an algorithm improvement strategy in response to this idea, which strengthens the optimization ability of the algorithm through conservative strategies for elite populations and adaptive differential evolution strategies for general populations. In particular, the conservative strategy of elite populations may not only be effective for differential evolution algorithms. In future research, the research team will attempt to combine it with different types of algorithms to analyze its application effects.
8. Conclusions
The main research conclusions of this article are as follows:
- (1)
- To address the premature convergence of the greedy differential mutation in the differential evolution algorithm, an elite population conservative strategy and a general population adaptive differential mutation strategy were proposed. This strengthened individual diversity in population evolution, leading to the development of ECDE.
- (2)
- Numerical experiments with 10 test functions showed that the ECDE stably converged to the optimum for seven functions and performed the best among SHADE, SaDE, DE, GA, and PSO in terms of convergence accuracy and stability.
- (3)
- In the engineering case study of the single-objective flood-control scheduling of cascade reservoirs, only ECDE, SHADE, and GA found feasible solutions, with ECDE performing optimally in terms of the mean, standard deviation, and range of results.
- (4)
- Using ECDE for the multi-objective flood control optimization of cascade reservoirs revealed that in multi-objective optimization, weight settings should follow upstream priority or equilibrium programs; downstream priority programs lead to poor upstream flood control performance.
Author Contributions
Z.H. and X.X. designed and conducted the experiments; Z.H. wrote the draft of the paper; T.W. and B.W. proposed the main structure of this study; L.C. and C.W. provided useful advice and made some corrections; J.F. and B.X. prepared the figures for this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by Open Research Fund Project of Jiangxi Academy of Water Resources, China (2022SKSH01), National Natural Science Foundation of China (52209024, 42271044, 52394234, 52169001), Natural Science Foundation of Jiangxi Province, China (20243BCE51170, 20224BAB214077, 20242BAB25311), the Major Science and Technology Project of the Ministry of Water Resources, P.R.C. (SKS-2022117, SKS-2022057, SKS-2022010), and the Open Research Fund supported by CRSRI (CKWV20231164/KY).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Mohanavelu, A.; Soundharajan, B.S.; Kisi, O. Modeling Multi-Objective Pareto-Optimal Reservoir Operation Policies Using State-of-the-Art Modeling Techniques. Water Resour. Manag. 2022, 36, 3107–3128. [Google Scholar] [CrossRef]
- He, Z.; Wang, C.; Wang, Y.; Wei, B.; Zhou, J.; Zhang, H.; Qin, H. Dynamic Programming with Successive Approximation and Relaxation Strategy for Long-Term Joint Power Generation Scheduling of Large-Scale Hydropower Station Group. Energy 2021, 222, 119960. [Google Scholar] [CrossRef]
- Wang, W.; Jia, B.; Simonovic, S.P.; Wu, S.; Fan, Z.; Ren, L. Comparison of Representative Heuristic Algorithms for Multi-Objective Reservoir Optimal Operation. Water Resour. Manag. 2021, 35, 2741–2762. [Google Scholar] [CrossRef]
- Moeini, R.; Soltani-nezhad, M.; Daei, M. Constrained Gravitational Search Algorithm for Large Scale Reservoir Operation Optimization Problem. Eng. Appl. Artif. Intell. 2017, 62, 222–233. [Google Scholar] [CrossRef]
- Foued, B.A.; Sameh, M. Application of Goal Programming in a Multi-Objective Reservoir Operation Model in Tunisia. Eur. J. Oper. Res. 2001, 133, 352–361. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Madadi, M.R.; Akbarifard, H.; Qaderi, K. Comprehensive Assessment of 20 State-of-the-Art Multi-Objective Meta-Heuristic Algorithms for Multi-Reservoir System Operation. J. Hydrol. 2022, 613, 128469. [Google Scholar] [CrossRef]
- Hu, M.; Huang, G.H.; Sun, W.; Li, Y.; Ding, X.; An, C.; Zhang, X.; Li, T. Multi-Objective Ecological Reservoir Operation Based on Water Quality Response Models and Improved Genetic Algorithm: A Case Study in Three Gorges Reservoir, China. Eng. Appl. Artif. Intell. 2014, 36, 332–346. [Google Scholar] [CrossRef]
- Kong, Y.; Mei, Y.; Wang, X.; Ben, Y. Solution Selection from a Pareto Optimal Set of Multi-Objective Reservoir Operation via Clustering Operation Processes and Objective Values. Water 2021, 13, 1046. [Google Scholar] [CrossRef]
- Xueshan, A.; Jie, D.; Baiyin, Y.; Jiajun, G.; Senlin, C.; Zhengyu, M. Research on Multi-Objective Decision Making of Hydropower Station Group Based on CRITIC-TOPSIS Method. Smart Innov. Syst. Technol. 2023, 260, 95–107. [Google Scholar] [CrossRef]
- Needham, J.T.; Watkins Jr, D.W.; Lund, J.R.; Nanda, S.K. Linear Programming for Flood Control in the Iowa and Des Moines Rivers. J. Water Resour. Plan. Manag. 2000, 126, 118–127. [Google Scholar] [CrossRef]
- Chen, J.; Qi, X.; Qiu, G.; Chen, L. Improved Progressive Optimality Algorithm and Its Application to Determination of Optimal Release Trajectory of Long-Term Power Generation Operation of Cascade Reservoirs. Adv. Water Resour. 2022, 166, 104253. [Google Scholar] [CrossRef]
- Fayaed, S.S.; Fiyadh, S.S.; Khai, W.J.; Ahmed, A.N.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Koting, S.; Mohd, N.S.; Binti Jaafar, W.Z.; et al. Improving Dam and Reservoir Operation Rules Using Stochastic Dynamic Programming and Artificial Neural Network Integration Model. Sustainability 2019, 11, 5367. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Cheng, C.; Wu, X. Peak Operation of Hydropower System with Parallel Technique and Progressive Optimality Algorithm. Int. J. Electr. Power Energy Syst. 2018, 94, 267–275. [Google Scholar] [CrossRef]
- Bai, T.; Wu, L.; Chang, J.X.; Huang, Q. Multi-Objective Optimal Operation Model of Cascade Reservoirs and Its Application on Water and Sediment Regulation. Water Resour. Manag. 2015, 29, 2751–2770. [Google Scholar] [CrossRef]
- Marcelino, C.G.; Leite, G.M.C.; Delgado, C.A.D.M.; de Oliveira, L.B.; Wanner, E.F.; Jiménez-Fernández, S.; Salcedo-Sanz, S. An Efficient Multi-Objective Evolutionary Approach for Solving the Operation of Multi-Reservoir System Scheduling in Hydro-Power Plants. Expert. Syst. Appl. 2021, 185, 115638. [Google Scholar] [CrossRef]
- Chen, H.T.; Wang, W.C.; Chen, X.N.; Qiu, L. Multi-Objective Reservoir Operation Using Particle Swarm Optimization with Adaptive Random Inertia Weights. Water Sci. Eng. 2020, 13, 136–144. [Google Scholar] [CrossRef]
- Mansouri, M.; Safavi, H.R.; Rezaei, F. An Improved MOPSO Algorithm for Multi-Objective Optimization of Reservoir Operation under Climate Change. Environ. Monit. Assess. 2022, 194, 261. [Google Scholar] [CrossRef]
- Kumar, V.; Sharma, K.V.; Yadav, S.M.; Deshmukh, A. Self-Adaptive Metaheuristic Optimization Technique for Multi-Objective Reservoir Operation. Aqua Water Infrastruct. Ecosyst. Soc. 2023, 72, 1582–1606. [Google Scholar] [CrossRef]
- Dash, S.S.; Sahoo, B.; Raghuwanshi, N.S. An Adaptive Multi-Objective Reservoir Operation Scheme for Improved Supply-Demand Management. J. Hydrol. 2022, 615, 128718. [Google Scholar] [CrossRef]
- Yu, X.; Xu, Y.P.; Gu, H.; Guo, Y. Multi-Objective Robust Optimization of Reservoir Operation for Real-Time Flood Control under Forecasting Uncertainty. J. Hydrol. 2023, 620, 129421. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, J.Z.; Wang, G.Q.; Zhang, Y.C. Multi-Objective Optimization of Reservoir Flood Dispatch Based on Multi-Objective Differential Evolution Algorithm. Shuili Xuebao/J. Hydraul. Eng. 2009, 40, 513–519. [Google Scholar]
- He, Z.; Zhou, J.; Qin, H.; Jia, B.; Lu, C. Long-Term Joint Scheduling of Hydropower Station Group in the Upper Reaches of the Yangtze River Using Partition Parameter Adaptation Differential Evolution. Eng. Appl. Artif. Intell. 2019, 81, 1–13. [Google Scholar] [CrossRef]
- Bilal; Pant, M.; Rani, D. Large Scale Reservoir Operation through Integrated Meta-Heuristic Approach. Memet. Comput. 2021, 13, 359–382. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Kheyrandish, A.; Jamei, M.; Gharabaghi, B. Optimizing Operating Rules for Multi-Reservoir Hydropower Generation Systems: An Adaptive Hybrid Differential Evolution Algorithm. Renew. Energy 2021, 167, 774–790. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Differential Evolution With Composite Trial Vector Generation Strategies and Control Parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-History Based Parameter Adaptation for Differential Evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Zha, G.; Zhou, J.Z.; Yang, X.; Fang, W.; Dai, L.; Wang, Q.N.; Ding, X.L. Modeling and Solving of Joint Flood Control Operation of Large-Scale Reservoirs: A Case Study in the Middle and Upper Yangtze River in China. Water 2021, 13, 41. [Google Scholar] [CrossRef]
- Okkan, U.; Kirdemir, U. Locally Tuned Hybridized Particle Swarm Optimization for the Calibration of the Nonlinear Muskingum Flood Routing Model. J. Water Clim. Change 2020, 11, 343–358. [Google Scholar] [CrossRef]
- Akbari, R.; Hessami-Kermani, M.R. A New Method for Dividing Flood Period in the Variable-Parameter Muskingum Models. Hydrol. Res. 2022, 53, 241–257. [Google Scholar] [CrossRef]
- Niazkar, M.; Zakwan, M. Chapter 24—Parameter Estimation of a New Four-Parameter Muskingum Flood Routing Model. In Computers in Earth and Environmental Sciences; Pourghasemi, H.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 337–349. ISBN 978-0-323-89861-4. [Google Scholar]
- Gong, W.; Fialho, Á.; Cai, Z.; Li, H. Adaptive Strategy Selection in Differential Evolution for Numerical Optimization: An Empirical Study. Inf. Sci. 2011, 181, 5364–5386. [Google Scholar] [CrossRef]
- Qin, A.K.; Suganthan, P.N. Self-Adaptive Differential Evolution Algorithm for Numerical Optimization. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; IEEE CEC 2005. Proceedings. Volume 2. [Google Scholar]
- Wang, Y.; Liu, Z.-Z.; Li, J.; Li, H.-X.; Wang, J. On the Selection of Solutions for Mutation in Differential Evolution. Front. Comput. Sci. 2018, 12, 297–315. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J. Step-by-Step Improvement of JADE and SHADE-Based Algorithms: Success or Failure? Swarm Evol. Comput. 2018, 43, 88–108. [Google Scholar] [CrossRef]
- Li, S.; He, Z.; Huang, W.; Wei, B.; Yan, F.; Fu, J.; Xiong, B. Study on the Constraint Handling Method for High-Dimensional Optimization of Cascade Reservoirs. J. Clean. Prod. 2024, 449, 141784. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.; Song, S.; Li, Y.; Hu, H.; Feng, J.; Xu, S.; Yang, K. Multi-Objective Operation-Decision-Making-Risk Propagation Analysis for Cascade Reservoirs Affected by Future Streamflow Process Variations. J. Hydrol. 2023, 620, 129518. [Google Scholar] [CrossRef]
- He, Z.; Zhou, J.; Qin, H.; Jia, B.; Feng, K. A Fast Water Level Optimal Control Method Based on Two Stage Analysis for Long Term Power Generation Scheduling of Hydropower Station. Energy 2020, 210, 118531. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).