A Dam Safety State Prediction and Analysis Method Based on EMD-SSA-LSTM
Abstract
1. Introduction
2. The Selection of Factors Affecting the Service State of the Dam Is Diverse
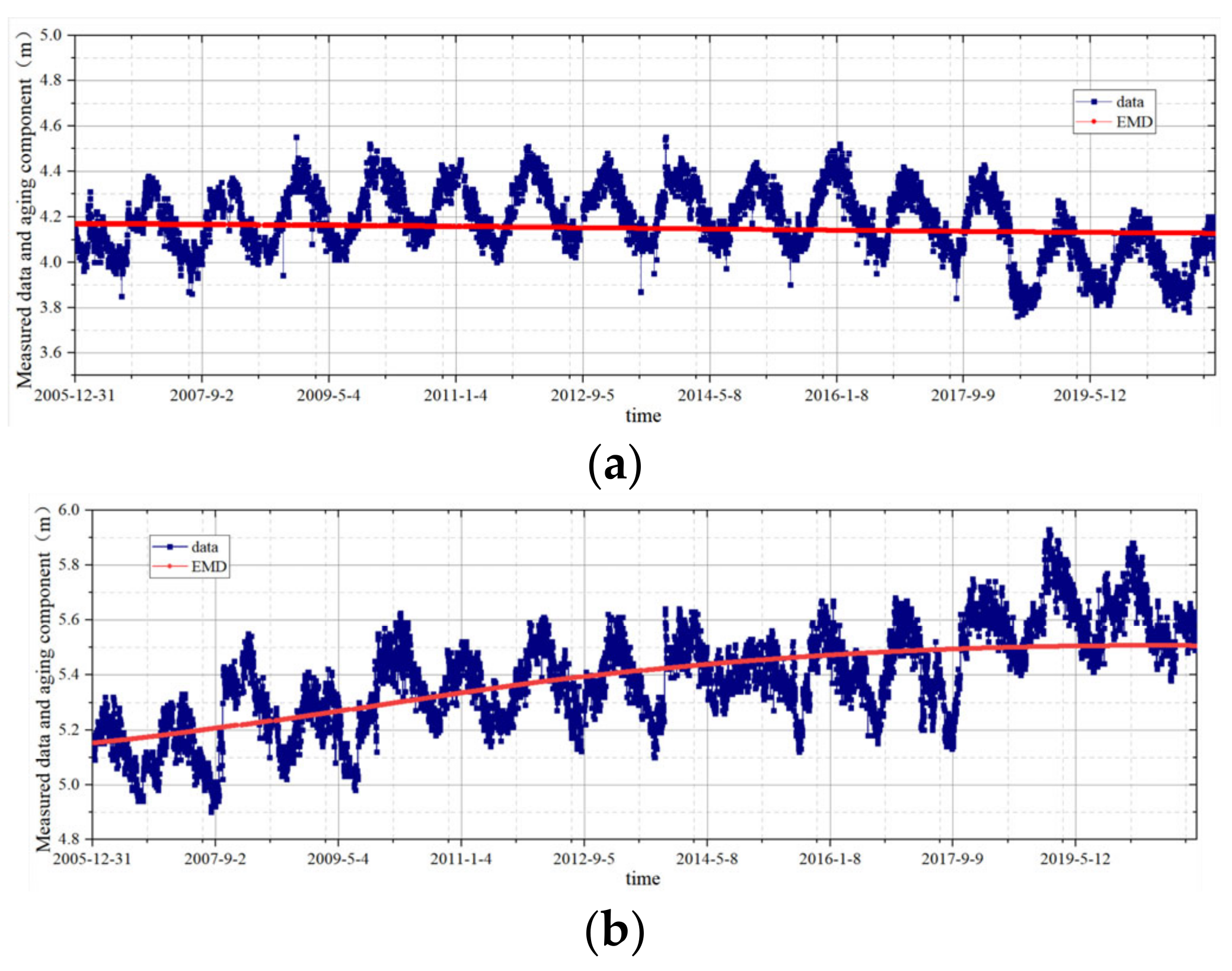
2.1. Empirical Mode Decomposition of Aging Factors
- (1)
- The number of zero crossings and extrema is the same throughout the entire data set, or the two differ by at most one.
- (2)
- The sum of the mean of the upper and lower envelopes composed of local maxima and local minima at any point is zero.
2.2. Multivariate Time Series Analysis and Modeling
3. Prediction Model Construction
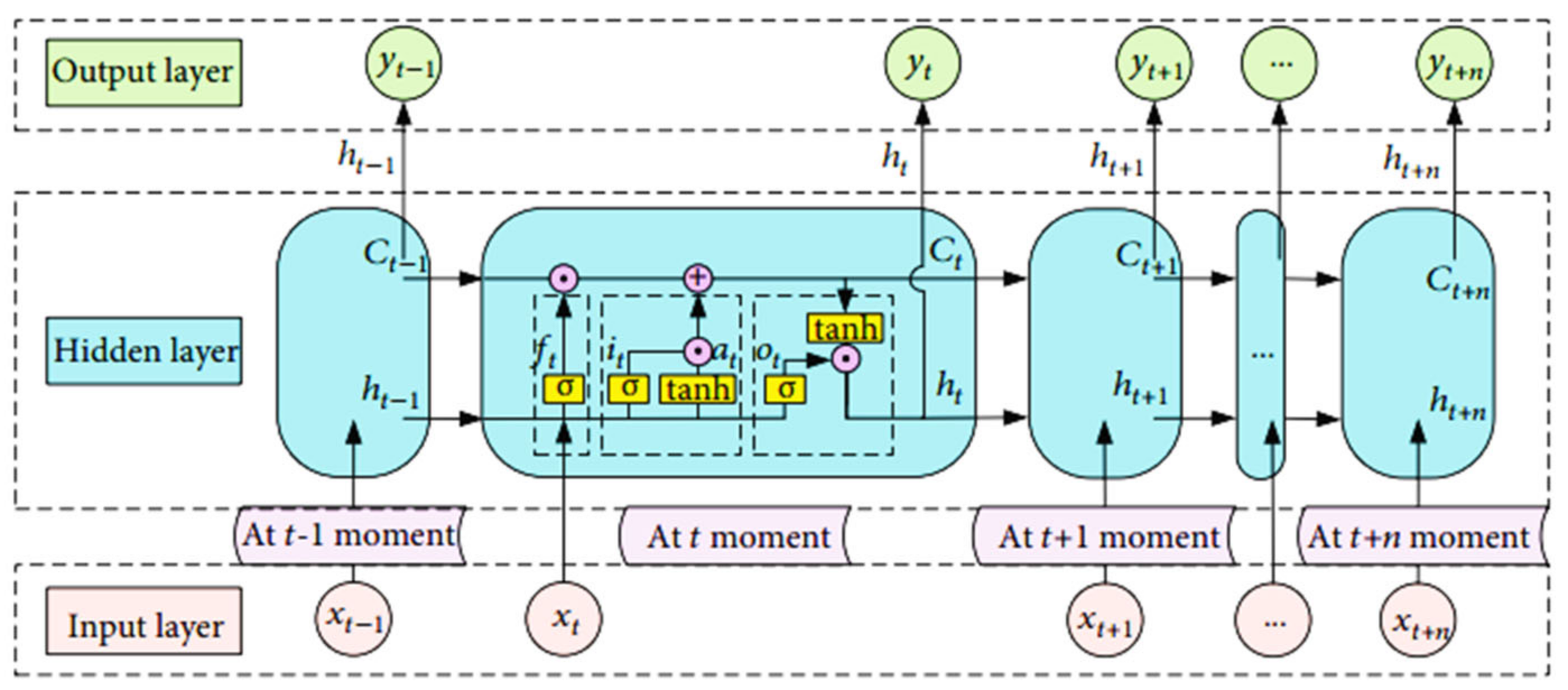
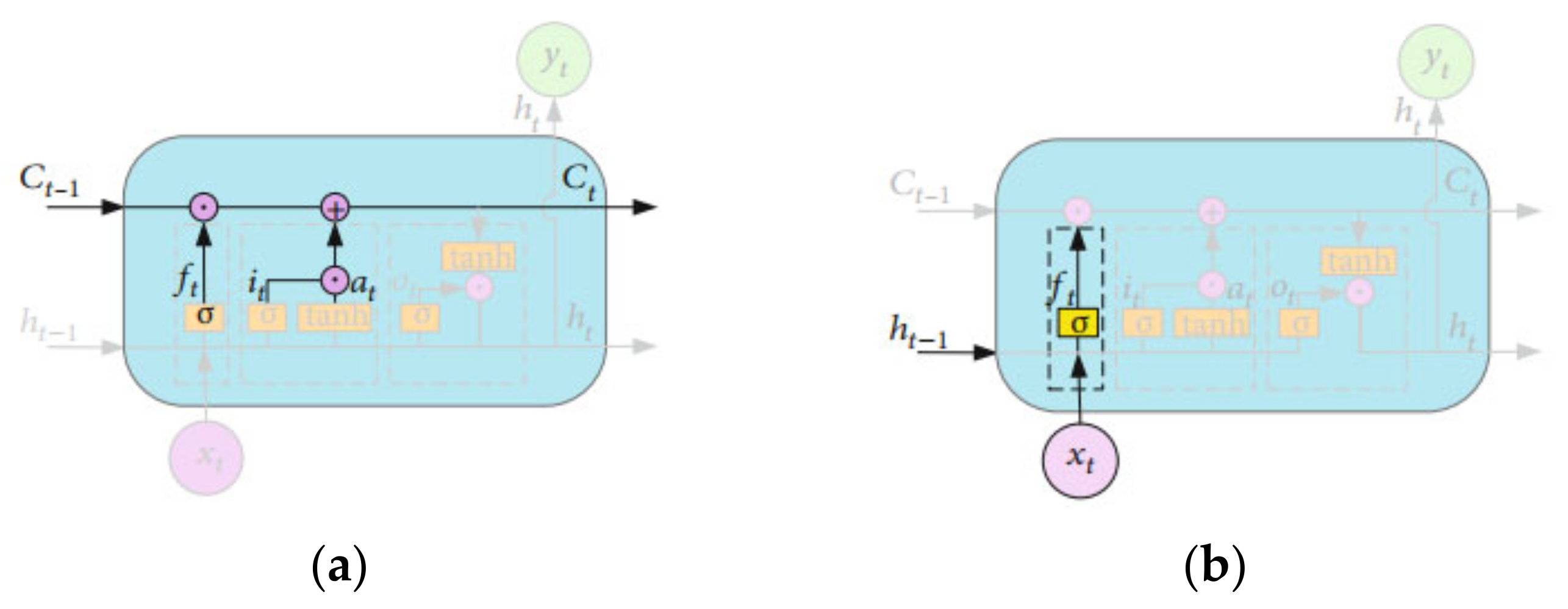
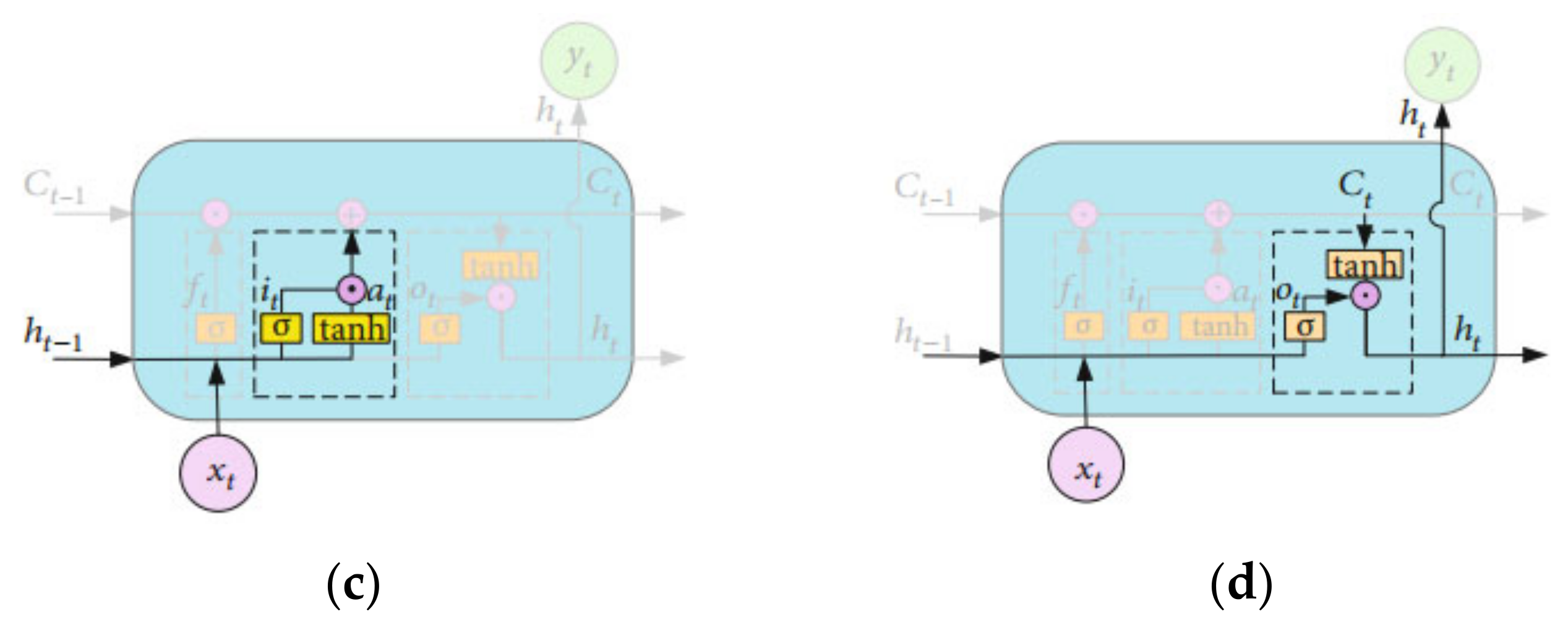
3.1. Long Short-Term Memory Network
- (1)
- Initially, using the external state from the previous time step and the current input , calculate the forget gate , input gate , and output gate ; then, compute the candidate value .
- (2)
- Combine and to determine whether to update the memory cell .
- (3)
- Combine to output the updated internal state information from the gate mechanism to the external state .
3.2. Sparrow Search Algorithm
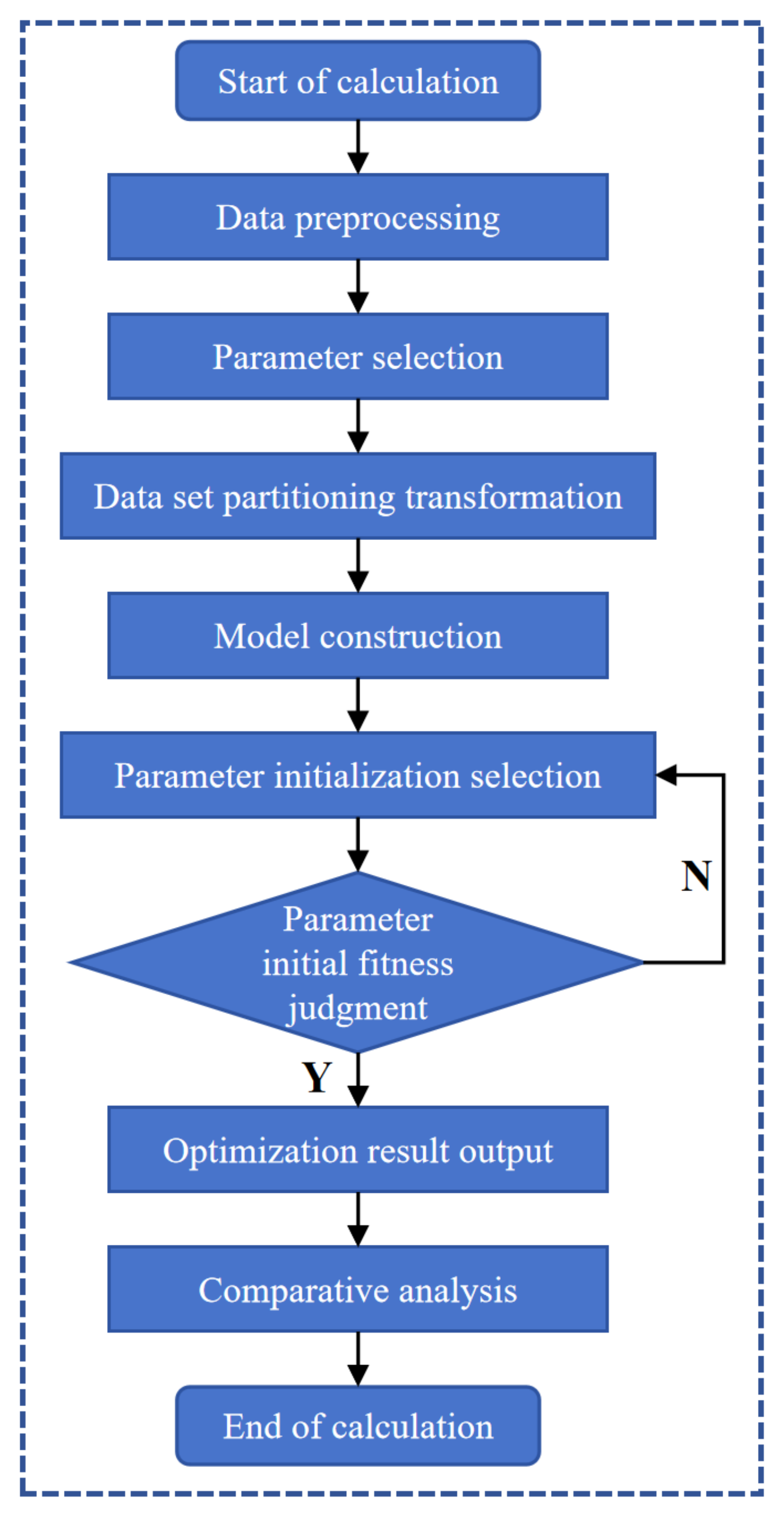
3.3. EMD-SSA-LSTM Prediction Model Calculation Process
- (1)
- Data preprocessing: For the collected seepage flow monitoring data of the dam, the preprocessing method in Section 2.1 is used to handle outliers without compromising the integrity and trend of the original data.
- (2)
- Parameter selection: Taking dam seepage pressure as an example, along with the collected environmental factors, 15 influencing factors, including water pressure, temperature, and aging, are selected for factor parameter configuration. The mathematical model is shown in Equation (7).
- (3)
- Data set partitioning and transformation: The preprocessed data are transformed into supervised learning data using the series_to_supervised function to construct a 3-to-1 supervised learning data type, predicting the current day’s data using the data from the previous three days. A total of 16 years of monitoring data from 2004 to 2020 was collected, with the first 90% used as training data and the last 10% (approximately 2 years) used as prediction data, with normalization applied to the data using the MinMaxScaler function.
- (4)
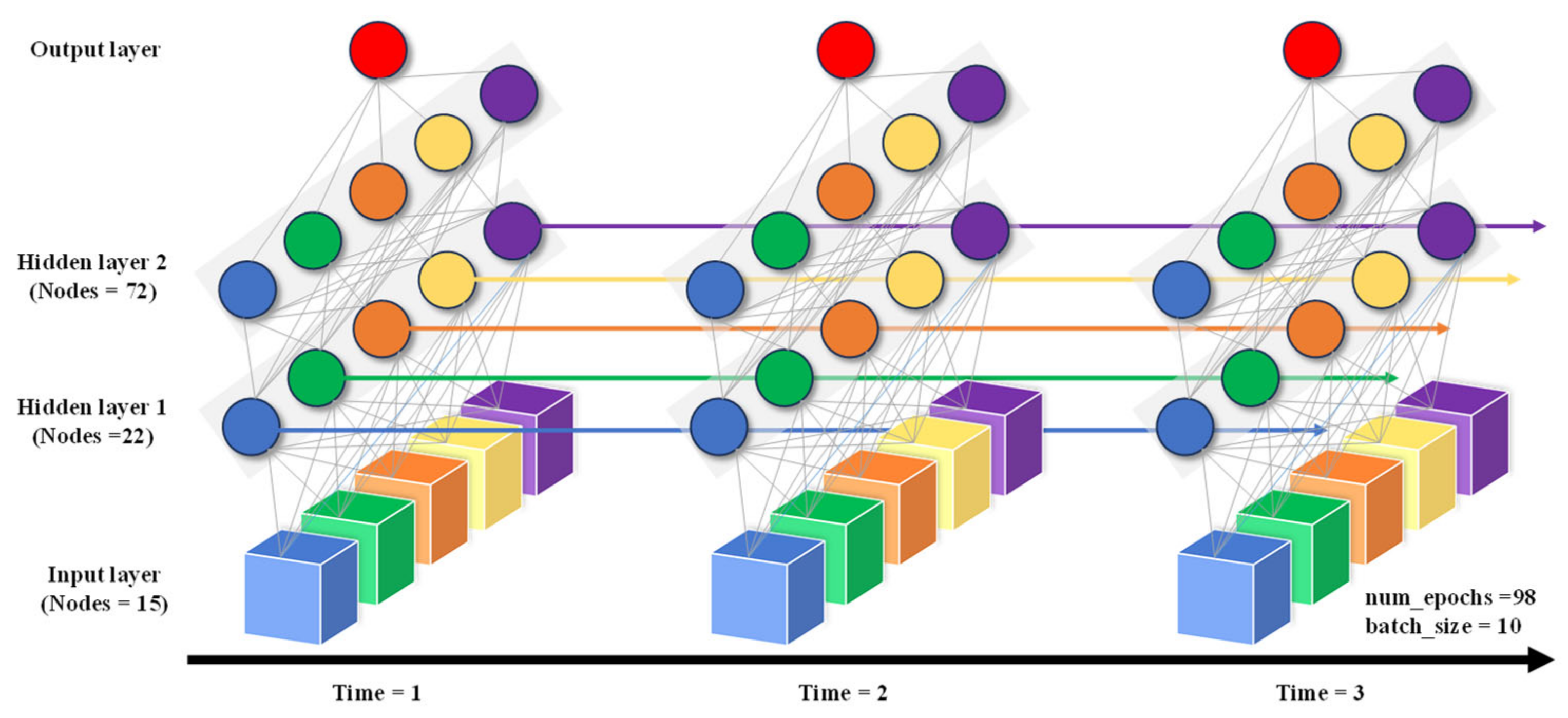
- Model construction: For the prediction of dam seepage data, an LSTM neural network is built based on Tensorflow. To improve computational efficiency, GPU support is utilized, and a double-layer LSTM neural network is constructed.
- (5)
- Model initialization: The iteration count, the number of nodes in two hidden layers, and the training sample size in the LSTM neural network model are selected as optimization objectives. The SSA algorithm is initialized with the iteration count, population size, producer ratio, and initial parameter threshold, followed by the initialization calculation. See as Table 1.
- (6)
- Fitness calculation: The validation set mean squared error is used as the fitness function to find a set of hyperparameters that minimize the network’s error. Equations (8)–(10) are employed to update the positions of the sparrows in SSA, obtaining new fitness values for the sparrow population and saving the optimal individual and global optimal positions in the population.
- (7)
- Output optimization results: The particle values calculated by SSA optimization are used as the iteration count, the number of nodes in two hidden layers, and the training sample size for the LSTM neural network model.
- (8)
- Calculation and comparative analysis: For the predicted data, metrics such as Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), Mean Absolute Error (MAE), and R-squared (R2) are used to evaluate the model accuracy. A comparative analysis is conducted with the prediction effects of GPU, Recurrent Neural Network (RNN), Backpropagation Neural Network (BPNN), and the commonly used multiple linear regression.
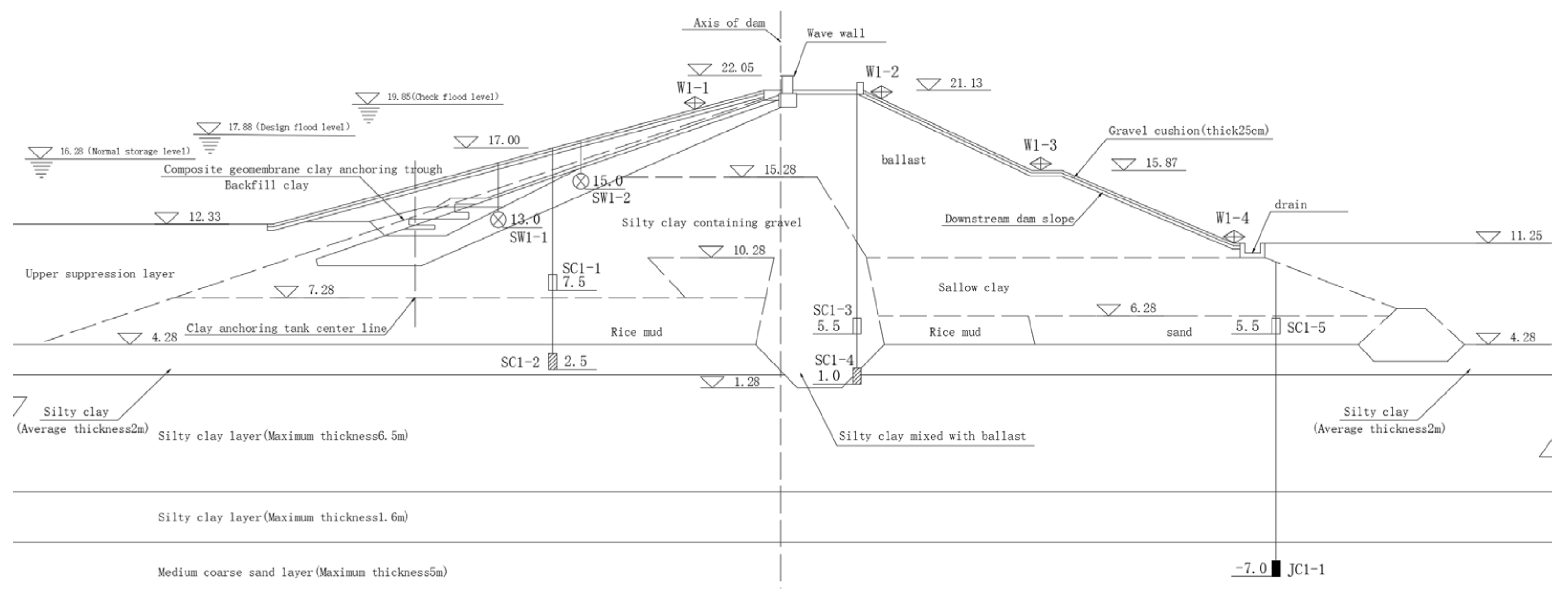
4. Study Area Introduction
5. Results and Discussion
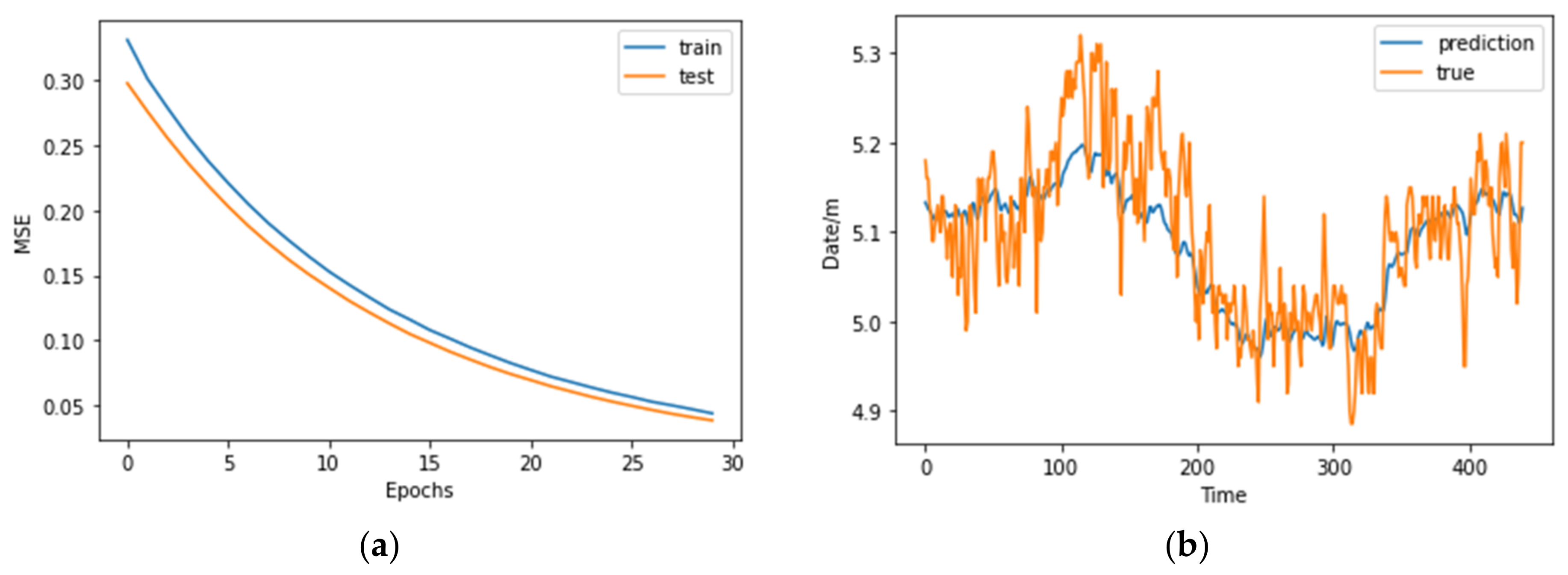
5.1. EMD-SSA-LSTM Prediction Model Calculation Process
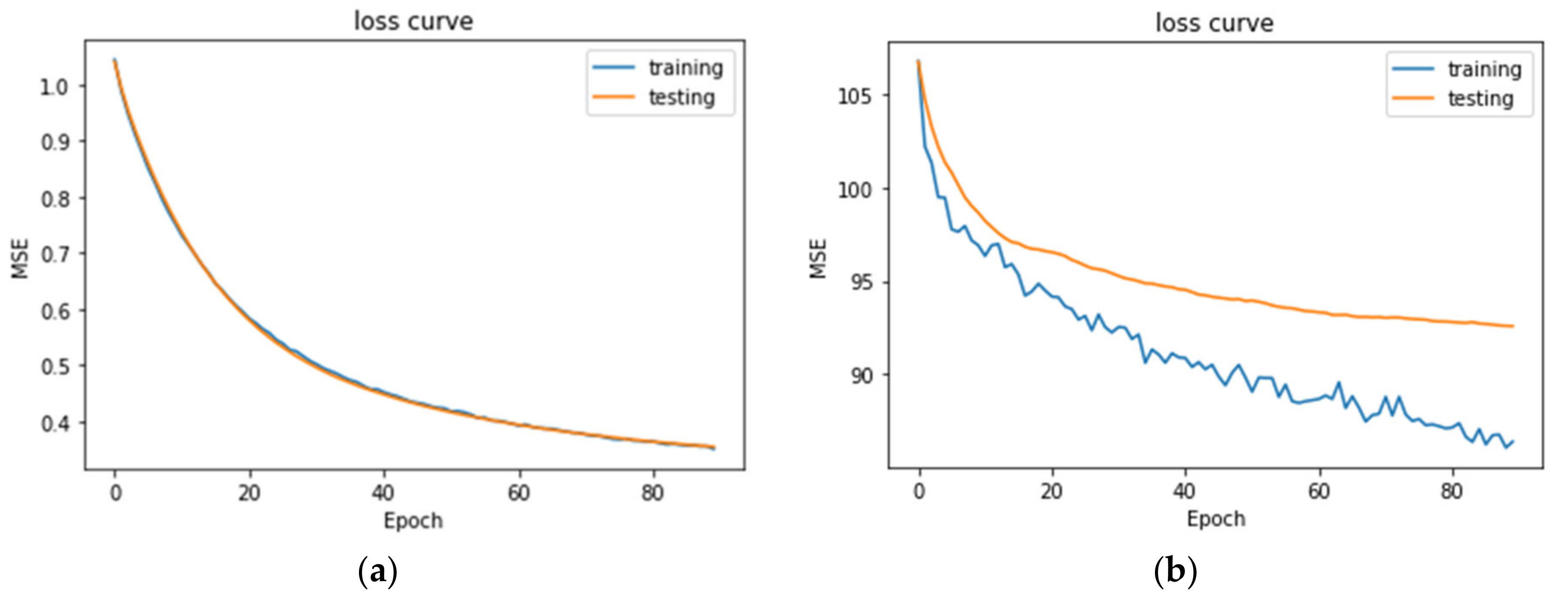
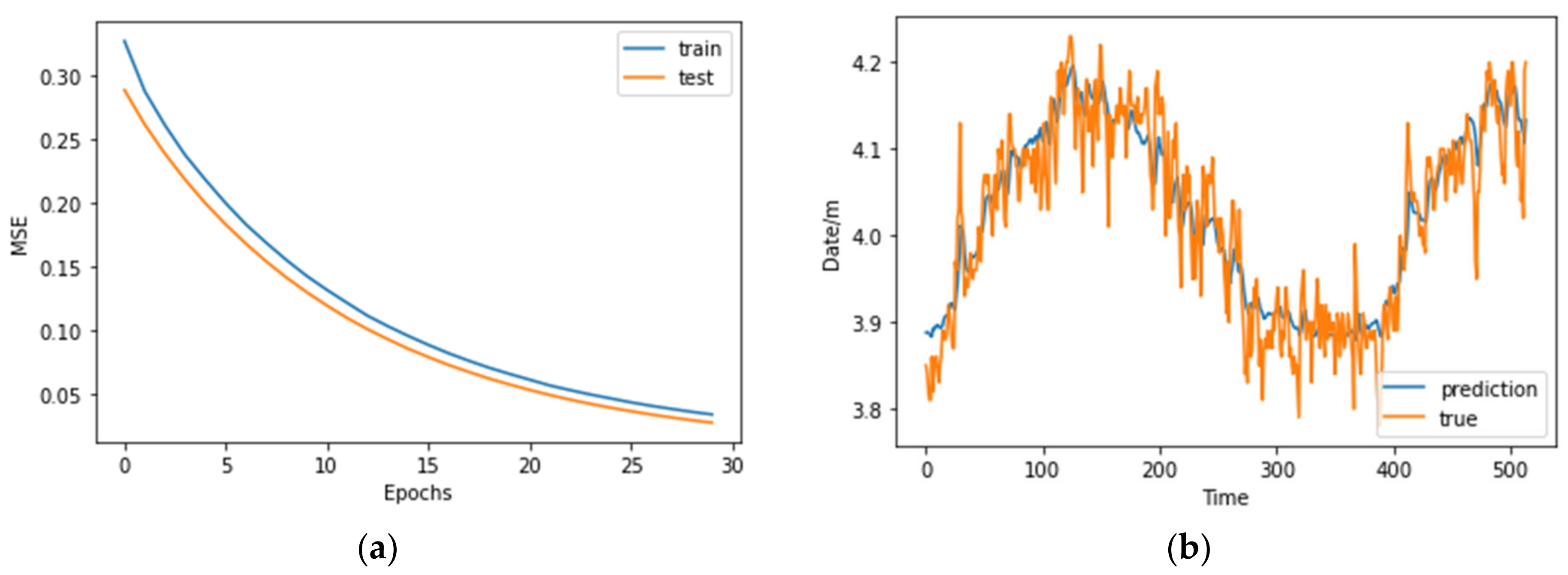
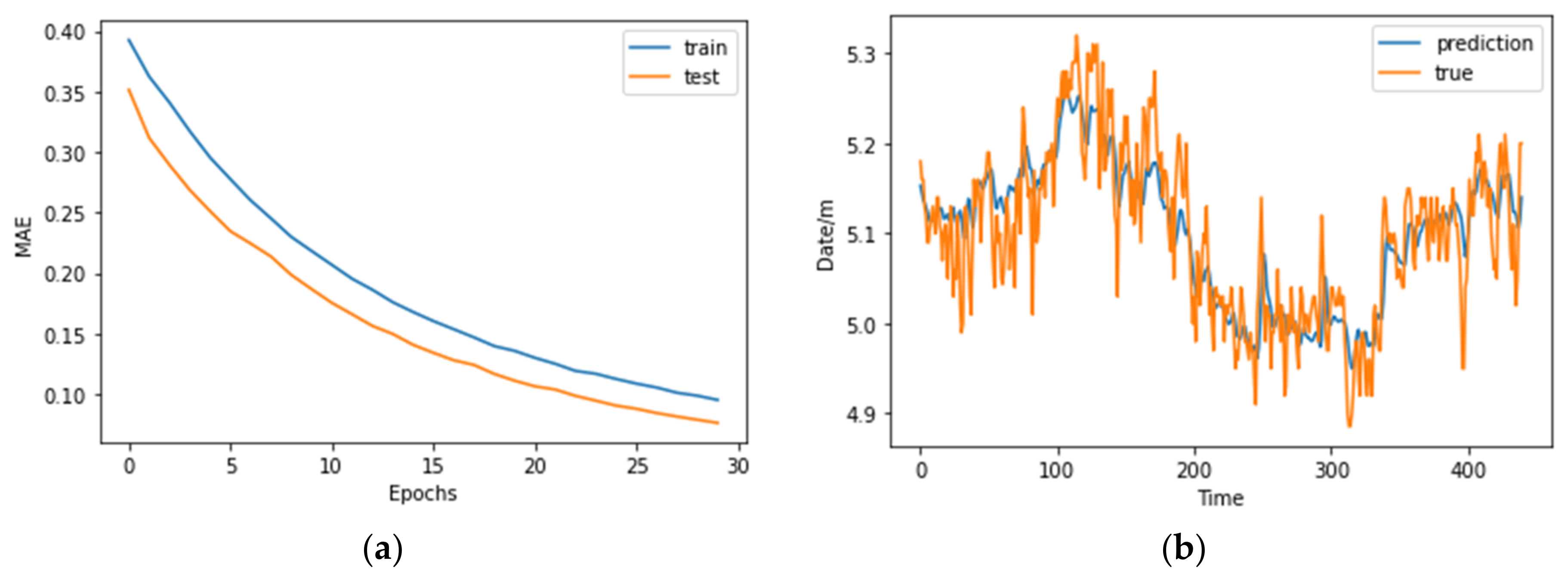
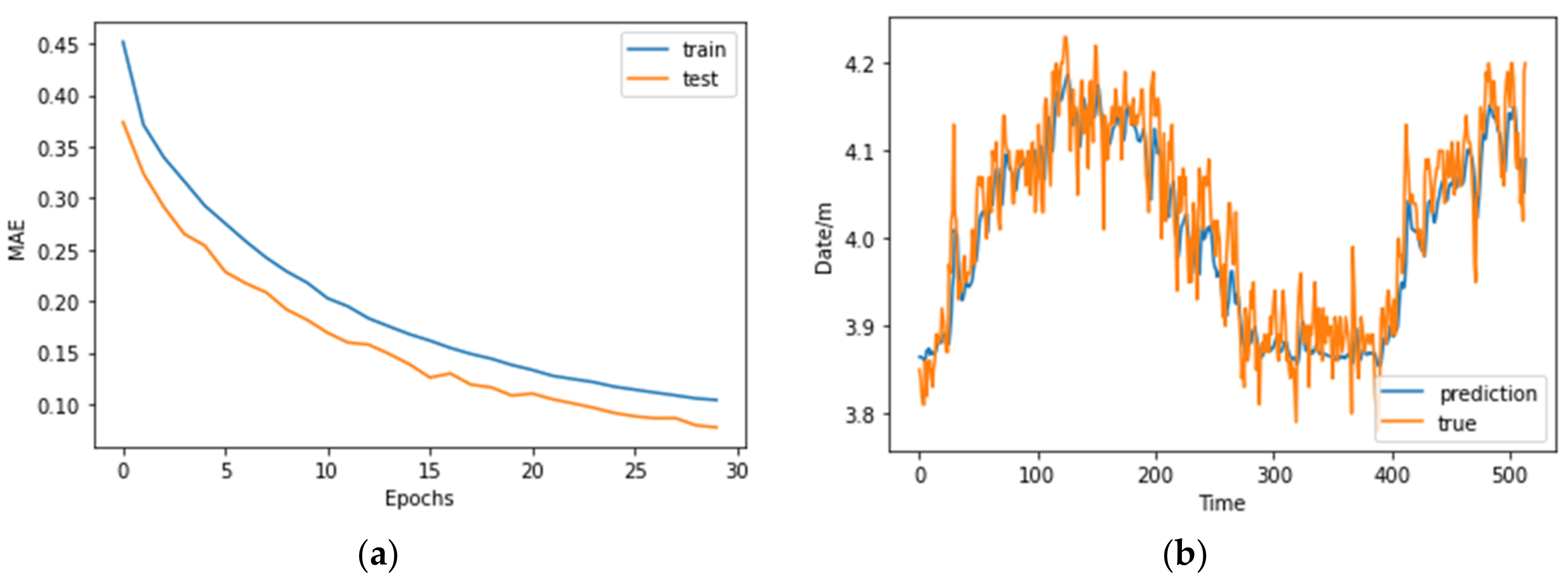
5.2. Parameter Optimization of Multivariate Time Prediction Model
- Optimizer
- 2.
- Loss Function
- 3.
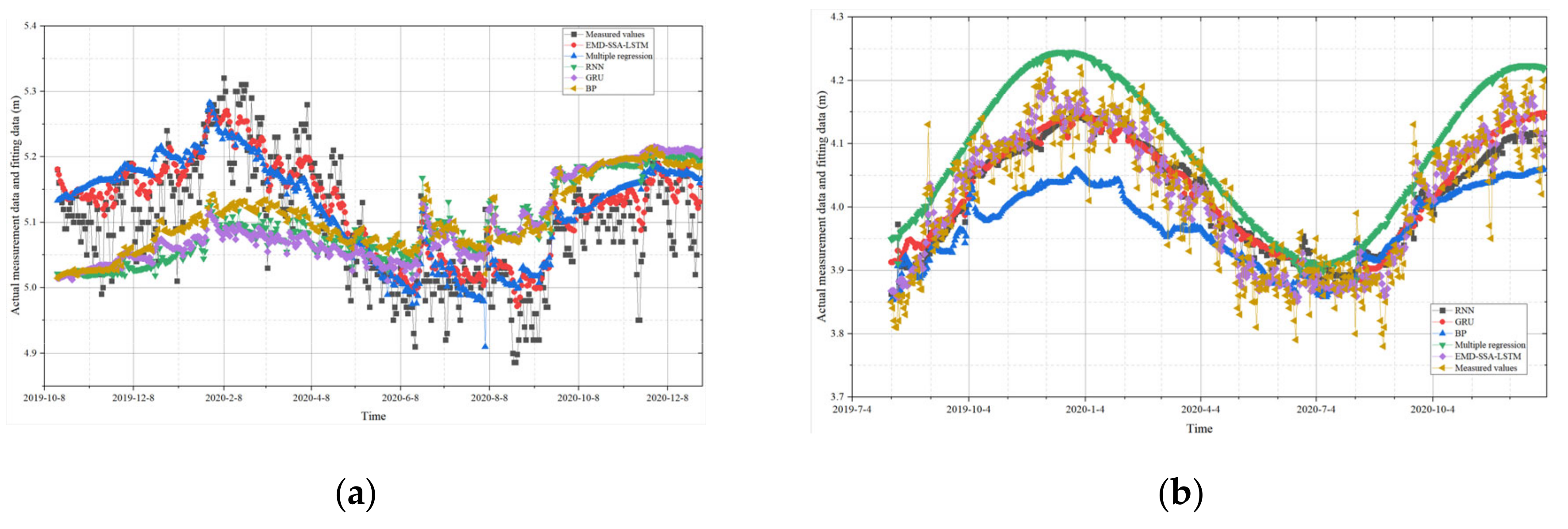
- Comparative analysis of prediction accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Prakash, G.; Dugalam, R.; Barbosh, M.; Sadhu, A. Recent Advancement of Concrete Dam Health Monitoring Technology: A Systematic Literature Review. Structures 2022, 44, 766–784. [Google Scholar] [CrossRef]
- Ma, C.; Xu, X.; Yang, J.; Cheng, L. Safety Monitoring and Management of Reservoir and Dams. Water 2023, 15, 1078. [Google Scholar] [CrossRef]
- Garsole, P.A.; Bokil, S.; Kumar, V.; Pandey, A.; Topare, N.S. A Review of Artificial Intelligence Methods for Predicting Gravity Dam Seepage, Challenges and Way-Out. AQUA Water Infrastruct. Ecosyst. Soc. 2023, 72, 1228–1248. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.A.; Angel, M.; Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch. Comput. Methods Eng. 2017, 24, 1–21. [Google Scholar] [CrossRef]
- Zhu, Y.; Niu, X.; Gu, C.; Yang, D.; Sun, Q.; Fernández-Rodríguez, E. Using the DEMATEL-VIKOR Method in Dam Failure Path Identification. Int. J. Environ. Res. Public Health 2020, 17, 1480. [Google Scholar] [CrossRef] [PubMed]
- Sivasuriyan, A.; Vijayan, D.S.; Munusami, R.; Devarajan, P. Health Assessment of Dams under Various Environmental Conditions Using Structural Health Monitoring Techniques: A State-of-Art Review. Environ. Sci. Pollut. Res. 2021, 29, 86180–86191. [Google Scholar] [CrossRef] [PubMed]
- Adamo, N.; Al-Ansari, N.; Sissakian, V.; Laue, J.; Knutsson, S. Dam Safety: Use of Instrumentation in Dams. J. Earth Sci. Geotech. Eng. 2020, 11, 145–202. [Google Scholar] [CrossRef]
- Li, B.; Yang, J.; Hu, D. Dam Monitoring Data Analysis Methods: A Literature Review. Struct. Control Health Monit. 2019, 27, e2501. [Google Scholar] [CrossRef]
- Chen, S.; Gu, C.; Lin, C.; Zhang, K.; Zhu, Y. Multi-Kernel Optimized Relevance Vector Machine for Probabilistic Prediction of Concrete Dam Displacement. Eng. Comput. 2020, 37, 1943–1959. [Google Scholar] [CrossRef]
- Yang, X.; Xiang, Y.; Shen, G.; Sun, M. A Combination Model for Displacement Interval Prediction of Concrete Dams Based on Residual Estimation. Sustainability 2022, 14, 16025. [Google Scholar] [CrossRef]
- Zhang, K.; Gu, C.; Zhu, Y.; Chen, S.; Dai, B.; Li, Y.; Shu, X. A Novel Seepage Behavior Prediction and Lag Process Identification Method for Concrete Dams Using HGWO-XGBoost Model. IEEE Access 2021, 9, 23311–23325. [Google Scholar] [CrossRef]
- Yang, D.; Gu, C.; Zhu, Y.; Dai, B.; Zhang, K.; Zhang, Z.; Li, B. A Concrete Dam Deformation Prediction Method Based on LSTM with Attention Mechanism. IEEE Access 2020, 8, 185177–185186. [Google Scholar] [CrossRef]
- Gu, C.; Fu, X.; Shao, C.; Shi, Z.; Su, H. Application of Spatiotemporal Hybrid Model of Deformation in Safety Monitoring of High Arch Dams: A Case Study. Int. J. Environ. Res. Public Health 2020, 17, 319. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Xie, M.; Zhang, K.; Li, Z. A Dam Deformation Residual Correction Method for High Arch Dams Using Phase Space Reconstruction and an Optimized Long Short-Term Memory Network. Mathematics 2023, 11, 2010. [Google Scholar] [CrossRef]
- Zhang, F.; Lu, X.; Li, Y.; Gao, Z.; Zhang, H.; Huang, H. A Self-Matching Model for Online Anomaly Recognition of Safety Monitoring Data in Dams. Struct. Health Monit. 2022, 22, 746–773. [Google Scholar] [CrossRef]
- Mohammadi, M.; Al-Fuqaha, A.; Sorour, S.; Guizani, M. Deep Learning for IoT Big Data and Streaming Analytics: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 2923–2960. [Google Scholar] [CrossRef]
- Li, M.; Shen, Y.; Ren, Q.; Li, H. A New Distributed Time Series Evolution Prediction Model for Dam Deformation Based on Constituent Elements. Adv. Eng. Inform. 2019, 39, 41–52. [Google Scholar] [CrossRef]
- Ribeiro, L.S.; Wilhelm, V.E.; de Jairo Marlon Corrêa, F.; Santos, A. A Comparative Analysis of Long-Term Concrete Deformation Models of a Buttress Dam. Eng. Struct. 2019, 193, 301–307. [Google Scholar] [CrossRef]
- Chen, B.; Hu, T.; Huang, Z.; Fang, C. A Spatio-Temporal Clustering and Diagnosis Method for Concrete Arch Dams Using Deformation Monitoring Data. Struct. Health Monit. 2018, 18, 1355–1371. [Google Scholar] [CrossRef]
- Mata, J. Interpretation of Concrete Dam Behaviour with Artificial Neural Network and Multiple Linear Regression Models. Eng. Struct. 2011, 33, 903–910. [Google Scholar] [CrossRef]
- Sharma, M.J.; Yu, S.J. Stepwise Regression Data Envelopment Analysis for Variable Reduction. Appl. Math. Comput. 2015, 253, 126–134. [Google Scholar] [CrossRef]
- Yu, H.; Wu, Z.; Bao, T.; Zhang, L. Multivariate Analysis in Dam Monitoring Data with PCA. Sci. China Technol. Sci. 2010, 53, 1088–1097. [Google Scholar] [CrossRef]
- Hu, W.L.; Deng, N.W.; Liu, Q.S. Optimization Study of Stepwise Regression and Partial Least Squares Regression Models for Dam Security Monitoring. Appl. Mech. Mater. 2014, 578–579, 1101–1107. [Google Scholar] [CrossRef]
- Tatin, M.; Briffaut, M.; Dufour, F.; Simon, A.; Fabre, J.-P. Statistical Modelling of Thermal Displacements for Concrete Dams: Influence of Water Temperature Profile and Dam Thickness Profile. Eng. Struct. 2018, 165, 63–75. [Google Scholar] [CrossRef]
- Sevieri, G.; De Falco, A. Dynamic Structural Health Monitoring for Concrete Gravity Dams Based on the Bayesian Inference. J. Civ. Struct. Health Monit. 2020, 10, 235–250. [Google Scholar] [CrossRef]
- Wang, S.; Xu, C.; Liu, Y.; Wu, B. A Spatial Association-Coupled Double Objective Support Vector Machine Prediction Model for Diagnosing the Deformation Behaviour of High Arch Dams. Struct. Health Monit. 2021, 21, 945–964. [Google Scholar] [CrossRef]
- Li, Z.; Yin, C.; Chen, R.; Wu, Z.; Chen, J.; Lu, X. A novel deformation monitoring model for high arch dams using impulse response-based equivalent temperature and machine learning-aided separate modeling. Expert Syst. Appl. 2024, 238, 122328. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Goulet, J. Real-Time Anomaly Detection with Bayesian Dynamic Linear Models. Struct. Control Health Monit. 2019, 26, e2404. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, D.; Liu, Y. Deformation Prediction System of Concrete Dam Based on IVM-SCSO-RF. Water 2022, 14, 3739. [Google Scholar] [CrossRef]
- Lei, W.; Wang, J. Dynamic Stacking Ensemble Monitoring Model of Dam Displacement Based on the Feature Selection with PCA-RF. J. Civ. Struct. Health Monit. 2022, 12, 557578. [Google Scholar] [CrossRef]
- Su, H.; Wen, Z.; Chen, Z.; Tian, S. Dam Safety Prediction Model Considering Chaotic Characteristics in Prototype Monitoring Data Series. Struct. Health Monit. 2016, 15, 639–649. [Google Scholar] [CrossRef]
- Yavaşoğlu, H.H.; Kalkan, Y.; Tiryakioğlu, İ.; Yigit, C.O.; Özbey, V.; Alkan, M.N.; Bilgi, S.; Alkan, R.M. Monitoring the Deformation and Strain Analysis on the Ataturk Dam, Turkey. Geomat. Nat. Hazards Risk 2017, 9, 94–107. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Z.; Gu, C.; Li, Y.; Zhang, K.; Xie, M. A Coupled Model for Dam Foundation Seepage Behavior Monitoring and Forecasting Based on Variational Mode Decomposition and Improved Temporal Convolutional Network. Struct. Control. Health Monit. 2023, 2023, 3879096. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Mahdavi, G.; Nuss, L.K.; Lall, U. The Role of Artificial Intelligence and Digital Technologies in Dam Engineering: Narrative Review and Outlook. Eng. Appl. Artif. Intell. 2023, 126, 106813. [Google Scholar] [CrossRef]
- Chen, W.; Wang, X.; Tong, D.; Cai, Z.; Zhu, Y.; Liu, C. Dynamic Early-Warning Model of Dam Deformation Based on Deep Learning and Fusion of Spatiotemporal Features. Knowl. Based Syst. 2021, 233, 107537. [Google Scholar] [CrossRef]
- El Bilali, A.; Moukhliss, M.; Taleb, A.; Nafii, A.; Alabjah, B.; Brouziyne, Y.; Mazigh, N.; Teznine, K.; Mhamed, M. Predicting Daily Pore Water Pressure in Embankment Dam: Empowering Machine Learning-Based Modeling. Environ. Sci. Pollut. Res. 2022, 29, 47382–47398. [Google Scholar] [CrossRef]
- Johari, A.; Talebi, A.; Heydari, A. Prediction of Discharge Flow Rate beneath Sheet Piles Using Gene Expression Programming Based on Scaled Boundary Finite Element Modelling Database. Sci. Iran. 2020, 28, 645–655. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, S.; Ou, B.; Liu, Z.; Hu, M. Prediction of Dam Deformation Using SSA-LSTM Model Based on Empirical Mode Decomposition Method and Wavelet Threshold Noise Reduction. Water 2022, 14, 3380. [Google Scholar] [CrossRef]
- Wei, B.; Chen, L.; Li, H.; Yuan, D.; Wang, G. Optimized Prediction Model for Concrete Dam Displacement Based on Signal Residual Amendment. Appl. Math. Model. 2020, 78, 20–36. [Google Scholar] [CrossRef]
- Yuan, D.; Wei, B.; Xie, B.; Zhong, Z. Modified Dam Deformation Monitoring Model Considering Periodic Component Contained in Residual Sequence. Struct. Control Health Monit. 2020, 27, e2633. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Mo, W. A Time Varying Filter Approach for Empirical Mode Decomposition. Signal Process. 2017, 138, 146–158. [Google Scholar] [CrossRef]
- Chen, S.; Cao, S.; Sun, Y.; Lin, Y.; Gao, J. Seismic Time-Frequency Analysis via Time-Varying Filtering Based Empirical Mode Decomposition Method. J. Appl. Geophys. 2022, 204, 104731. [Google Scholar] [CrossRef]
- Stallone, A.; Cicone, A.; Materassi, M. New Insights and Best Practices for the Successful Use of Empirical Mode Decomposition, Iterative Filtering and Derived Algorithms. Sci. Rep. 2020, 10, 15161. [Google Scholar] [CrossRef] [PubMed]
- Stefenon, S.F.; Ribeiro, M.H.D.M.; Nied, A.; Yow, K.C.; Mariani, V.C.; dos Santos Coelho, L.; Seman, L.O. Time Series Forecasting Using Ensemble Learning Methods for Emergency Prevention in Hydroelectric Power Plants with Dam. Electr. Power Syst. Res. 2022, 202, 107584. [Google Scholar] [CrossRef]
- Xu, S.; Li, W.; Zhu, Y.; Xu, A. A Novel Hybrid Model for Six Main Pollutant Concentrations Forecasting Based on Improved LSTM Neural Networks. Sci. Rep. 2022, 1, 144342. [Google Scholar] [CrossRef]
- Reddybattula, K.D.; Nelapudi, L.S.; Moses, M.; Devanaboyina, V.R.; Ali, M.A.; Jamjareegulgarn, P.; Panda, S.K. Ionospheric TEC Forecasting over an Indian Low Latitude Location Using Long Short-Term Memory (LSTM) Deep Learning Network. Universe 2022, 8, 562. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Wen, S.; Wei, H.; Yang, Y.; Guo, Z.; Zeng, Z.; Huang, T.; Chen, Y. Memristive LSTM Network for Sentiment Analysis. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1794–1804. [Google Scholar] [CrossRef]
- Vankadara, R.K.; Mosses, M.; Siddiqui, M.I.H.; Ansari, K.; Panda, S.K. Ionospheric Total Electron Content Forecasting at a Low-Latitude Indian Location Using a Bi-Long Short-Term Memory Deep Learning Approach. IEEE Trans. Plasma Sci. 2023, 51, 3373–3383. [Google Scholar] [CrossRef]
- Liu, R.; Mo, Y. Performance of a Novel Enhanced Sparrow Search Algorithm for Engineering Design Process: Coverage Optimization in Wireless Sensor Network. Processes 2022, 10, 1691. [Google Scholar] [CrossRef]



| Name of Parameter | Value | |
|---|---|---|
| Iterations | 10 | |
| Sparrow population | 20 | |
| Optimization dimension | 4 | |
| Finder alert threshold | 0.8 | |
| Finder ratio | 20% | |
| Scout ratio | 20% | |
| Data range | Iterations | [10–100] |
| Number of nodes in the first hidden layer | [1–100] | |
| Number of nodes in the second hidden layer | [1–100] | |
| Number of samples selected for training | [10–100] | |
| Hole Number | Dam Axis Distance (m) | Station Number |
|---|---|---|
| Under the geomembrane | −18.50 | SW3-1 |
| U-3 | +33.00 | JC4-2 |
| U-4 | +100.00 | JC1-2, SC2-6 |
| Optimizer Type | MAPE | RMSE | MAE | MSE | R2 |
|---|---|---|---|---|---|
| Adagrad | 0.0087 | 0.0569 | 0.0448 | 0.0032 | 0.6380 |
| Adadelta | 0.0233 | 0.1405 | 0.1195 | 0.0197 | −1.2067 |
| Adam | 0.0393 | 0.2228 | 0.2018 | 0.0496 | −4.5486 |
| Adamax | 0.0100 | 0.0650 | 0.0510 | 0.0042 | 0.5270 |
| Ftrl | 0.0542 | 0.2935 | 0.2779 | 0.0862 | −8.6334 |
| Nadam | 0.0182 | 0.1082 | 0.0936 | 0.0117 | −0.3097 |
| RMSprop | 0.0182 | 0.1124 | 0.0938 | 0.0126 | −0.4125 |
| SGD | 0.0094 | 0.0599 | 0.0482 | 0.0035 | 0.5976 |
| Optimizer Type | MAPE | RMSE | MAE | MSE | R2 |
|---|---|---|---|---|---|
| MSE | 0.0087 | 0.0569 | 0.0448 | 0.0032 | 0.6380 |
| MAE | 0.0083 | 0.0528 | 0.0426 | 0.0027 | 0.6884 |
| MAPE | 0.1244 | 0.6545 | 0.6360 | 0.4284 | −46.9011 |
| MSLE | 0.0094 | 0.0611 | 0.0484 | 0.0037 | 0.5815 |
| squared_hinge | 1.0873 | 5.5581 | 5.5437 | 30.8931 | −3452.79 |
| categorical_hinge | 0.5152 | 2.6577 | 2.6308 | 7.0637 | −788.71 |
| LogCosh | 0.0116 | 0.0731 | 0.0597 | 0.4024 | 0.0053 |
| Evaluation Index | EMD-SSA-LSTM | RNN | GRU | BP Neural Network | Multiple Linear Regression |
|---|---|---|---|---|---|
| MSE | 0.0026 | 0.0107 | 0.0106 | 0.0086 | 0.0038 |
| RMSE | 0.0519 | 0.1035 | 0.1030 | 0.1052 | 0.0616 |
| MAE | 0.0407 | 0.0884 | 0.0893 | 0.0854 | 0.0485 |
| R2 | 0.6759 | −0.2892 | −0.2775 | −0.0356 | 0.6068 |
| Evaluation Index | EMD-SSA-LSTM | RNN | GRU | BP Neural Network | Multiple Linear Regression |
|---|---|---|---|---|---|
| MSE | 0.0016 | 0.0027 | 0.0026 | 0.0066 | 0.0071 |
| RMSE | 0.0401 | 0.0516 | 0.0513 | 0.1352 | 0.0842 |
| MAE | 0.0314 | 0.0410 | 0.0405 | 0.1129 | 0.0711 |
| R2 | 0.8674 | 0.7803 | 0.7833 | 0.4504 | 0.8067 |
| Evaluation Index | EMD-SSA-LSTM | RNN | GRU | BP Neural Network | Multiple Linear Regression |
|---|---|---|---|---|---|
| MSE | 0.0156 | 0.0070 | 0.0070 | 0.0366 | 0.0113 |
| RMSE | 0.0395 | 0.0838 | 0.0836 | 0.2584 | 0.1061 |
| MAE | 0.0340 | 0.0626 | 0.0629 | 0.2120 | 0.0819 |
| R2 | 0.9199 | 0.6404 | 0.6417 | −0.8765 | 0.7878 |
| Evaluation Index | EMD-SSA-LSTM | RNN | GRU | BP Neural Network | Multiple Linear Regression |
|---|---|---|---|---|---|
| MSE | 0.0026 | 0.0085 | 0.0083 | 0.0117 | 0.0038 |
| RMSE | 0.0512 | 0.0924 | 0.0911 | 0.1267 | 0.0616 |
| MAE | 0.0386 | 0.0796 | 0.0776 | 0.1040 | 0.0486 |
| R2 | 0.7710 | 0.2562 | 0.2768 | −0.0179 | 0.7333 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Xiang, Y.; Wang, Y.; Shen, G. A Dam Safety State Prediction and Analysis Method Based on EMD-SSA-LSTM. Water 2024, 16, 395. https://doi.org/10.3390/w16030395
Yang X, Xiang Y, Wang Y, Shen G. A Dam Safety State Prediction and Analysis Method Based on EMD-SSA-LSTM. Water. 2024; 16(3):395. https://doi.org/10.3390/w16030395
Chicago/Turabian StyleYang, Xin, Yan Xiang, Yakun Wang, and Guangze Shen. 2024. "A Dam Safety State Prediction and Analysis Method Based on EMD-SSA-LSTM" Water 16, no. 3: 395. https://doi.org/10.3390/w16030395
APA StyleYang, X., Xiang, Y., Wang, Y., & Shen, G. (2024). A Dam Safety State Prediction and Analysis Method Based on EMD-SSA-LSTM. Water, 16(3), 395. https://doi.org/10.3390/w16030395







