An Integrated Current–Wave–Sediment Model for Coastal and Estuary Simulation
Abstract
1. Introduction
2. Governing Equations and Numerical Methods
2.1. Current Flow Equations
2.2. Wave Equations
2.3. Sediment Transport Equations
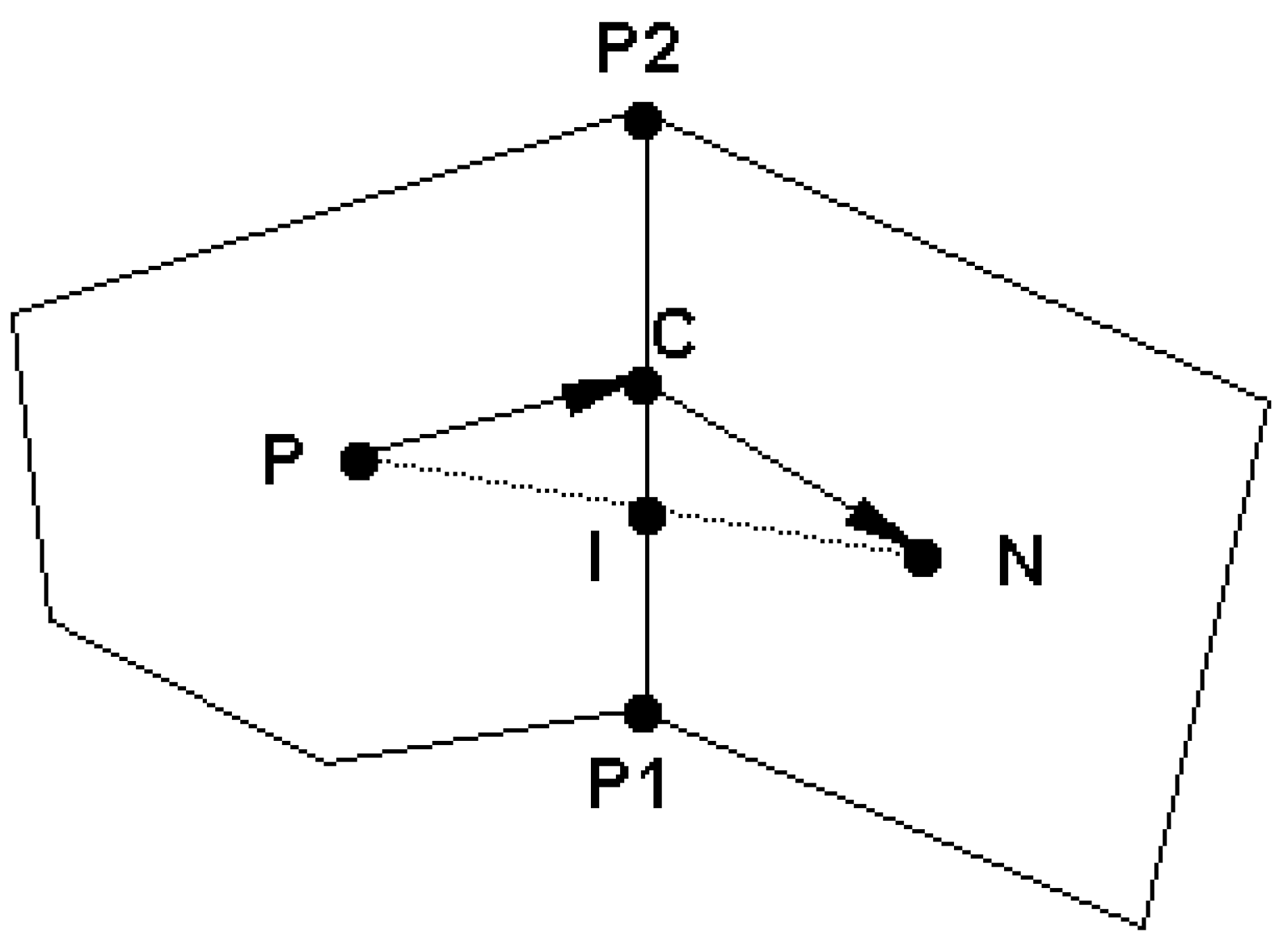
2.3.1. Basic Physical Processes and Definitions
2.3.2. Governing Equations
2.4. Numerical Methods
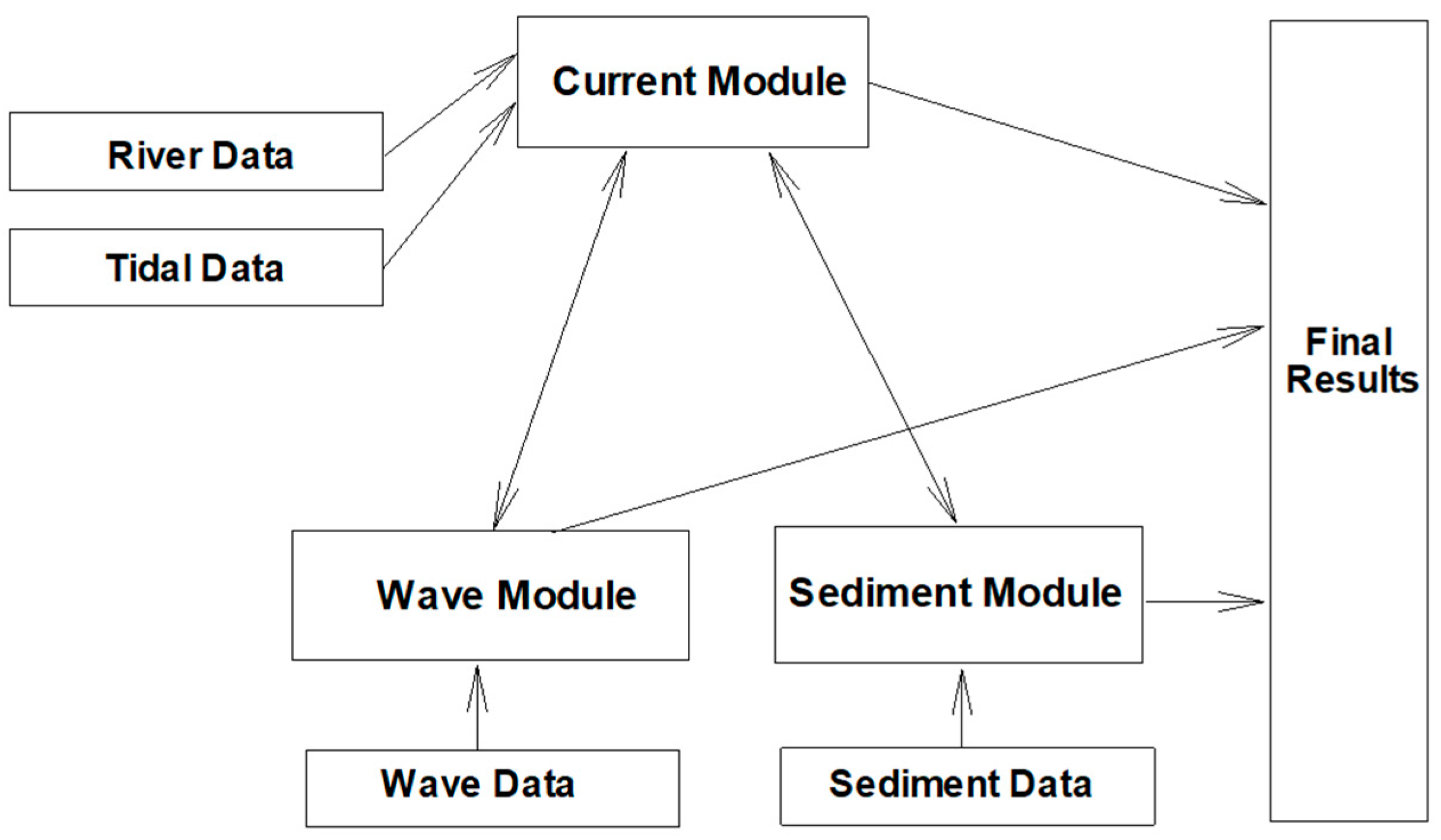
2.5. Model Integeration
3. Model Verification and Validation
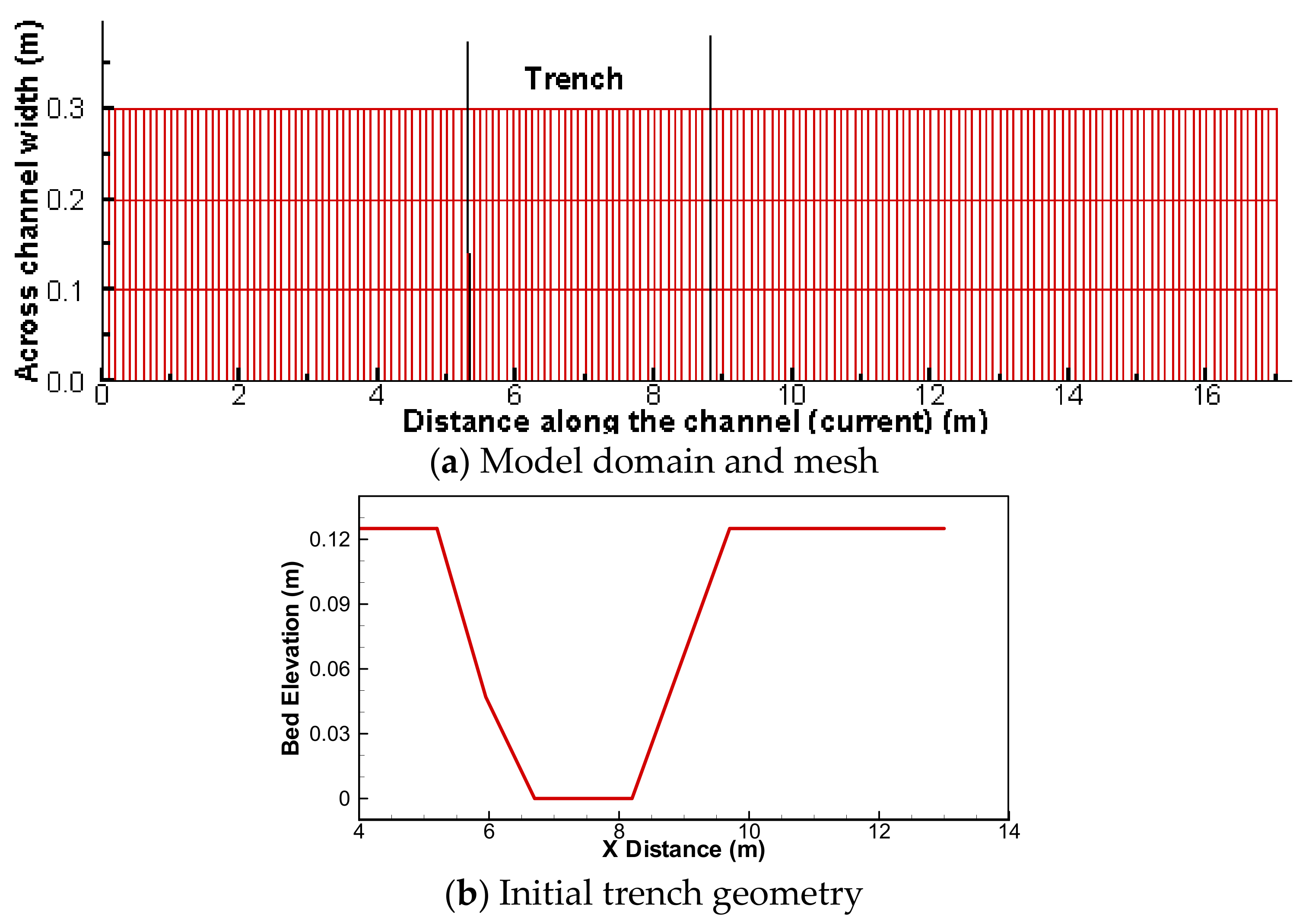
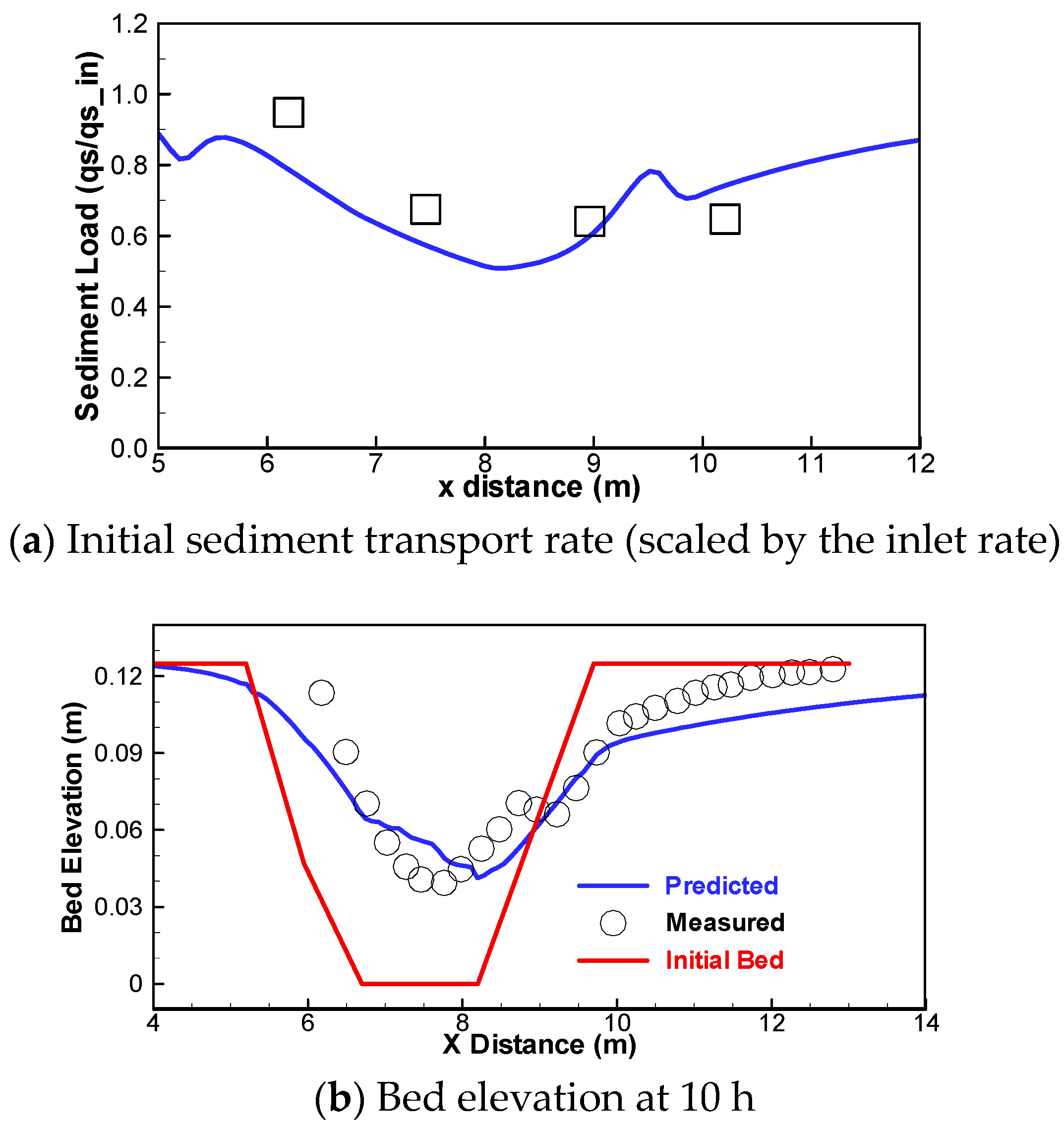
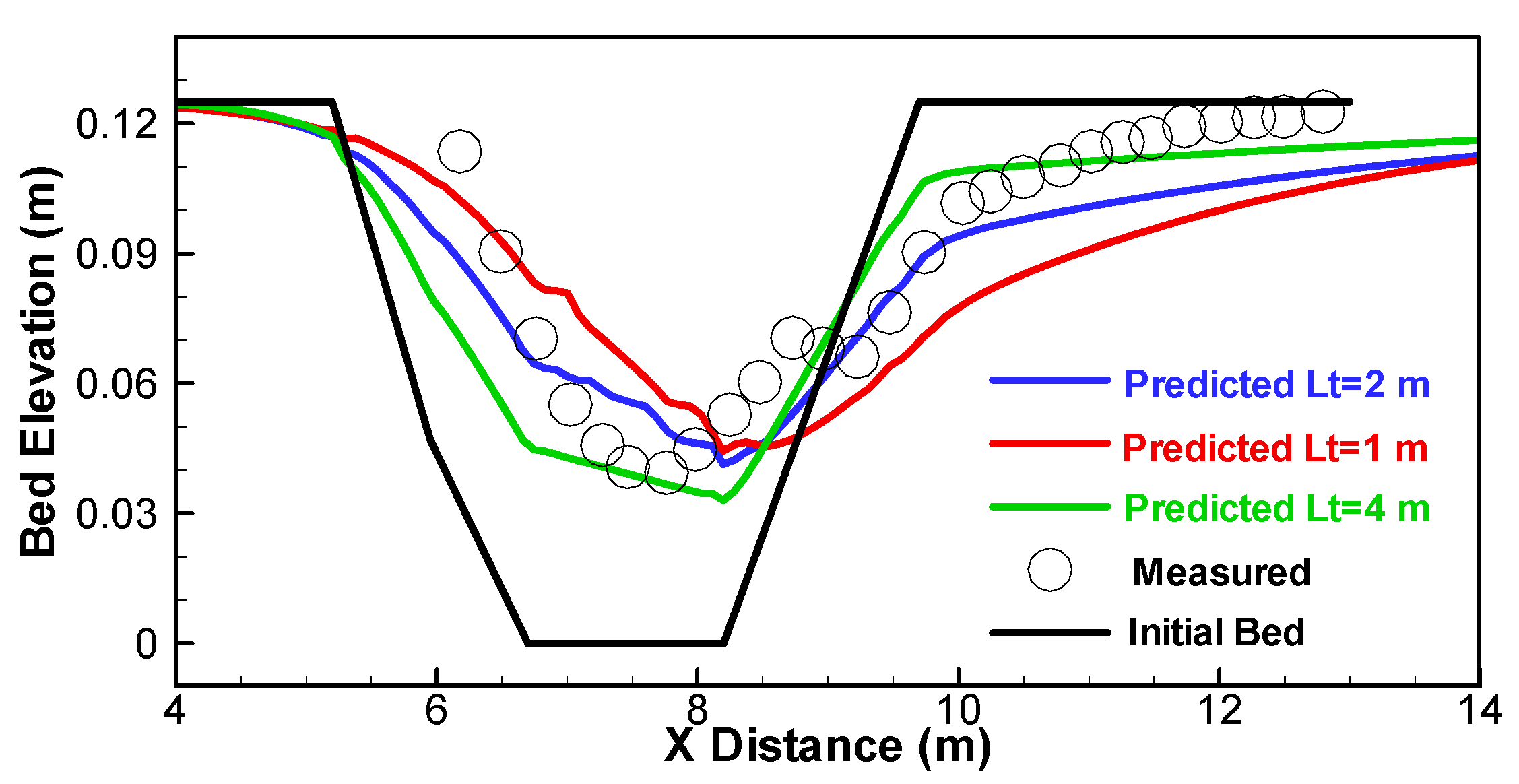
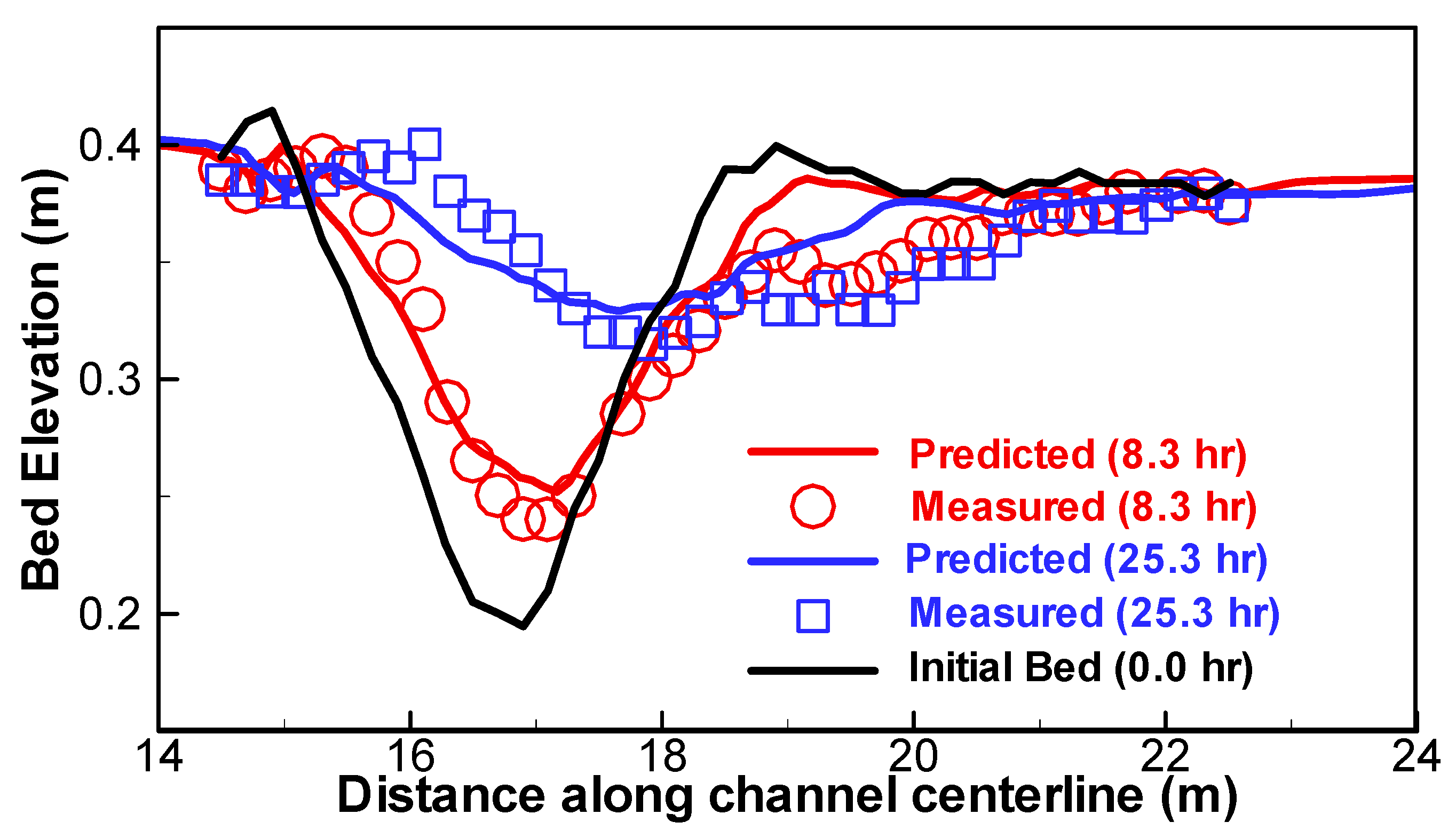
3.1. Sediment Transport in a Trench with Wave Traveling along the Current
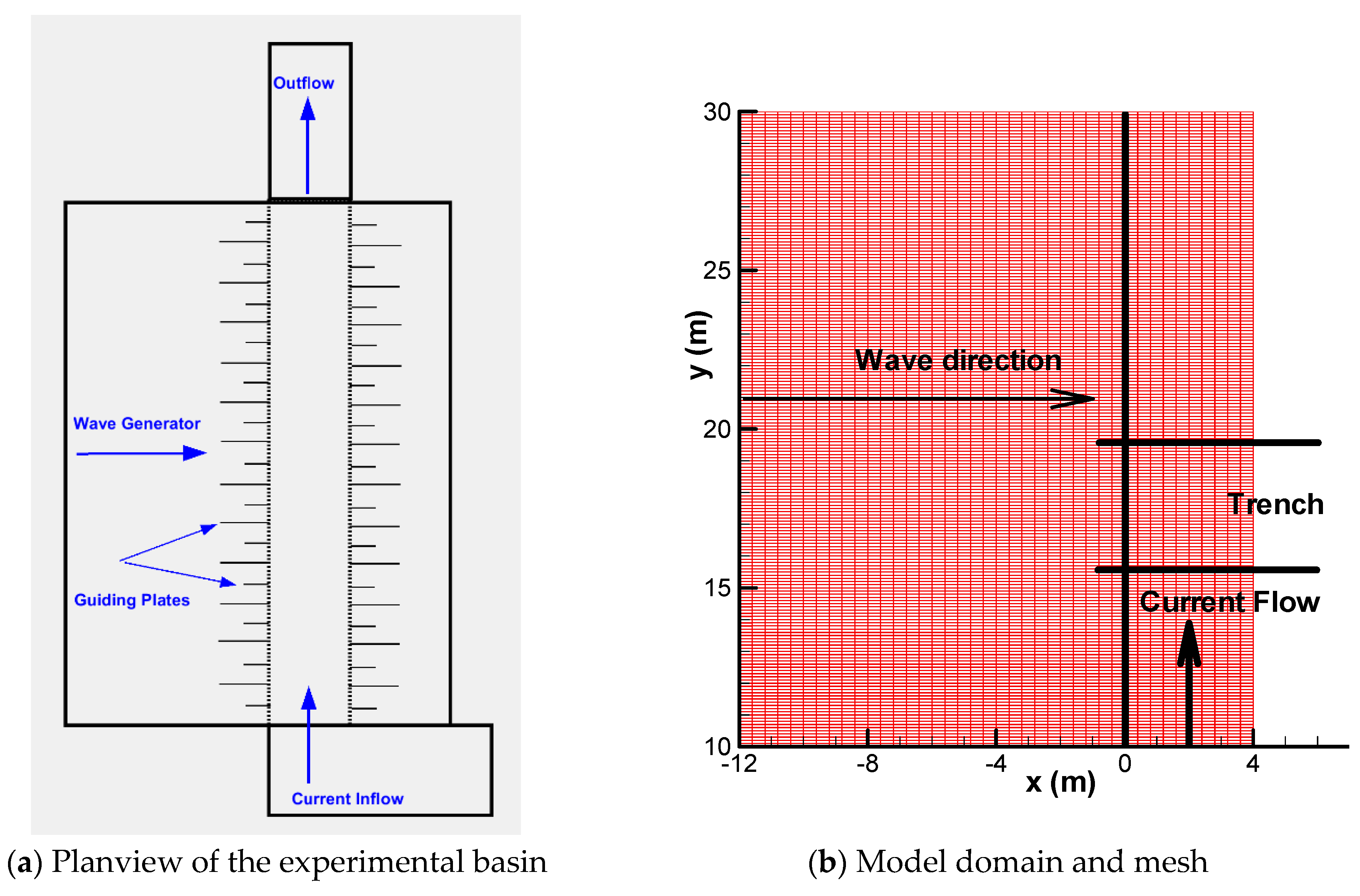
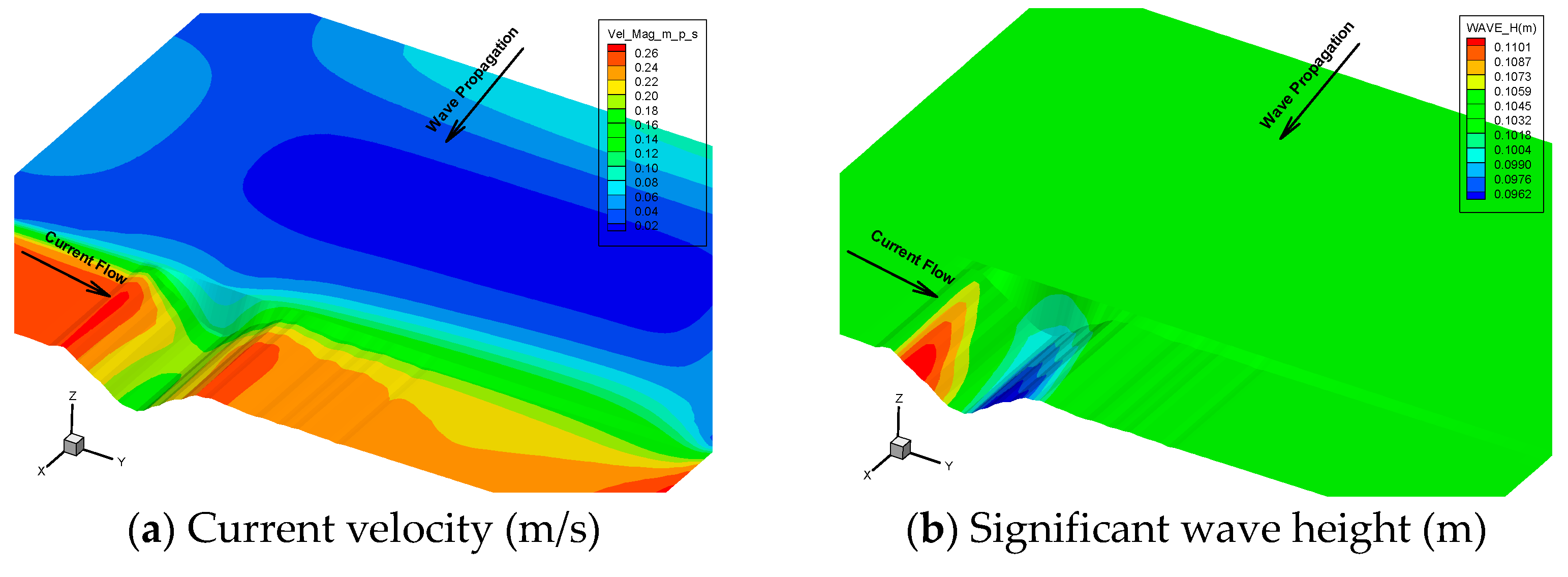
3.2. Sediment Transport in a Trench with Wave Propogating Normal to the Current
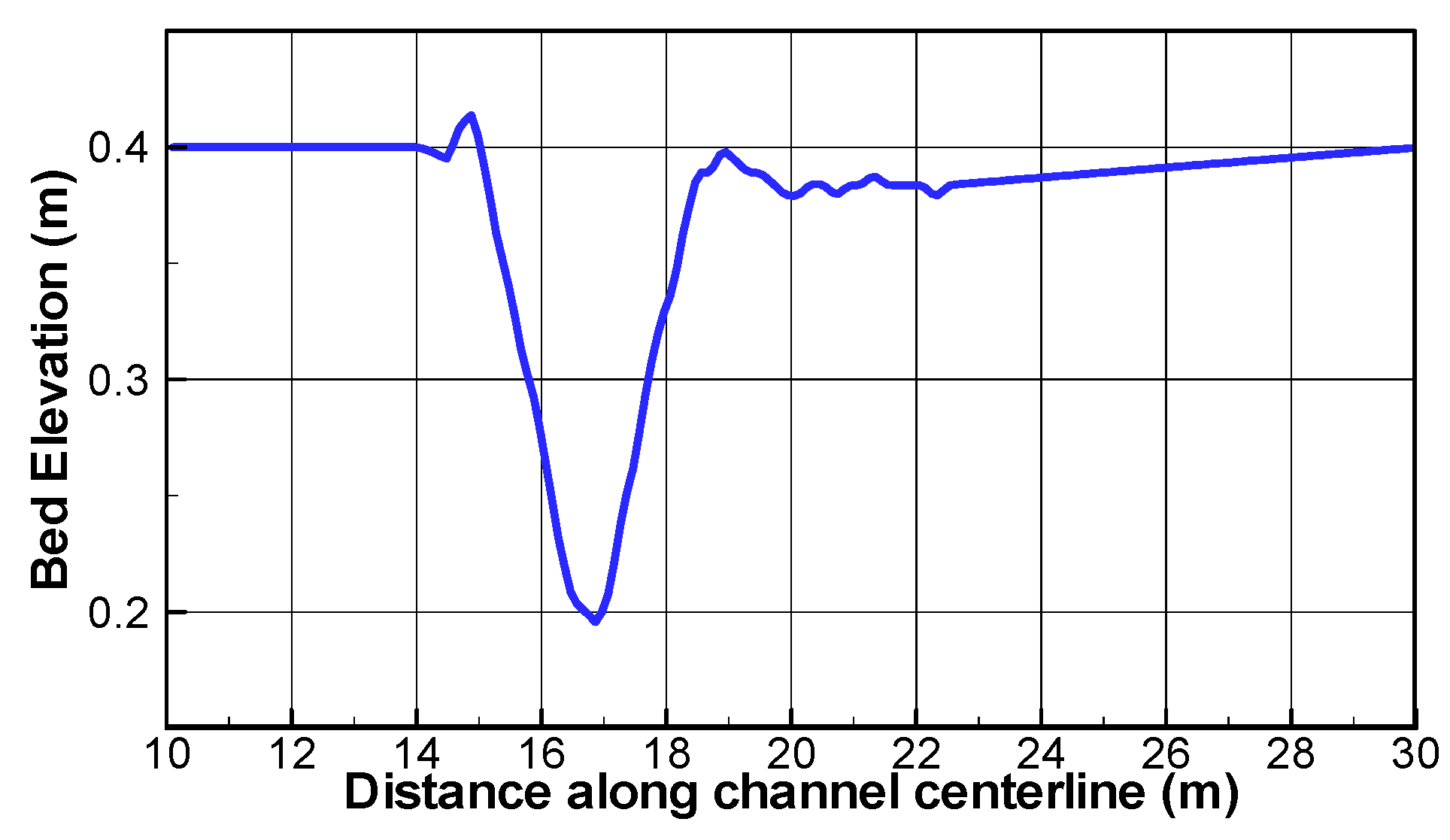
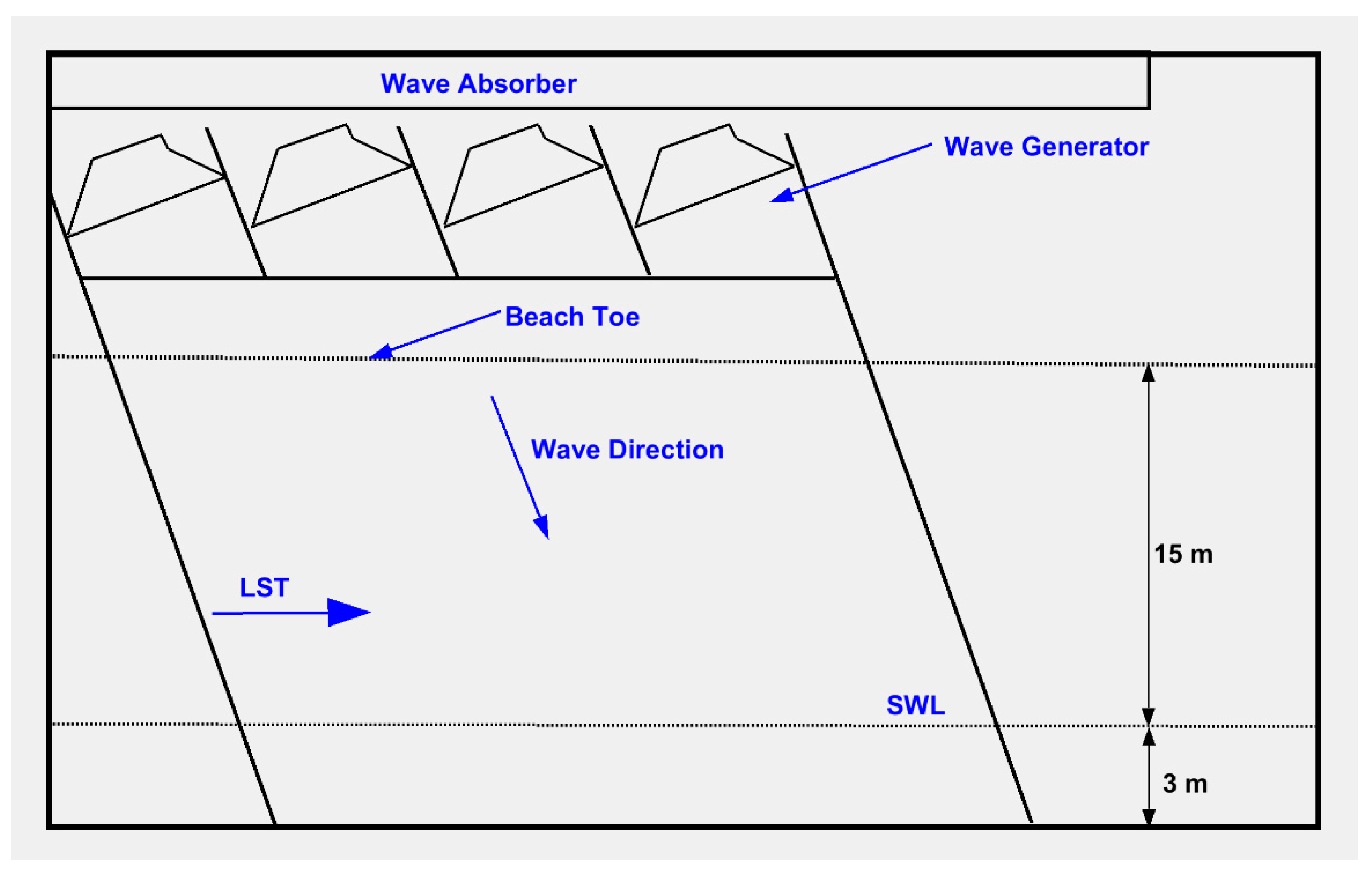
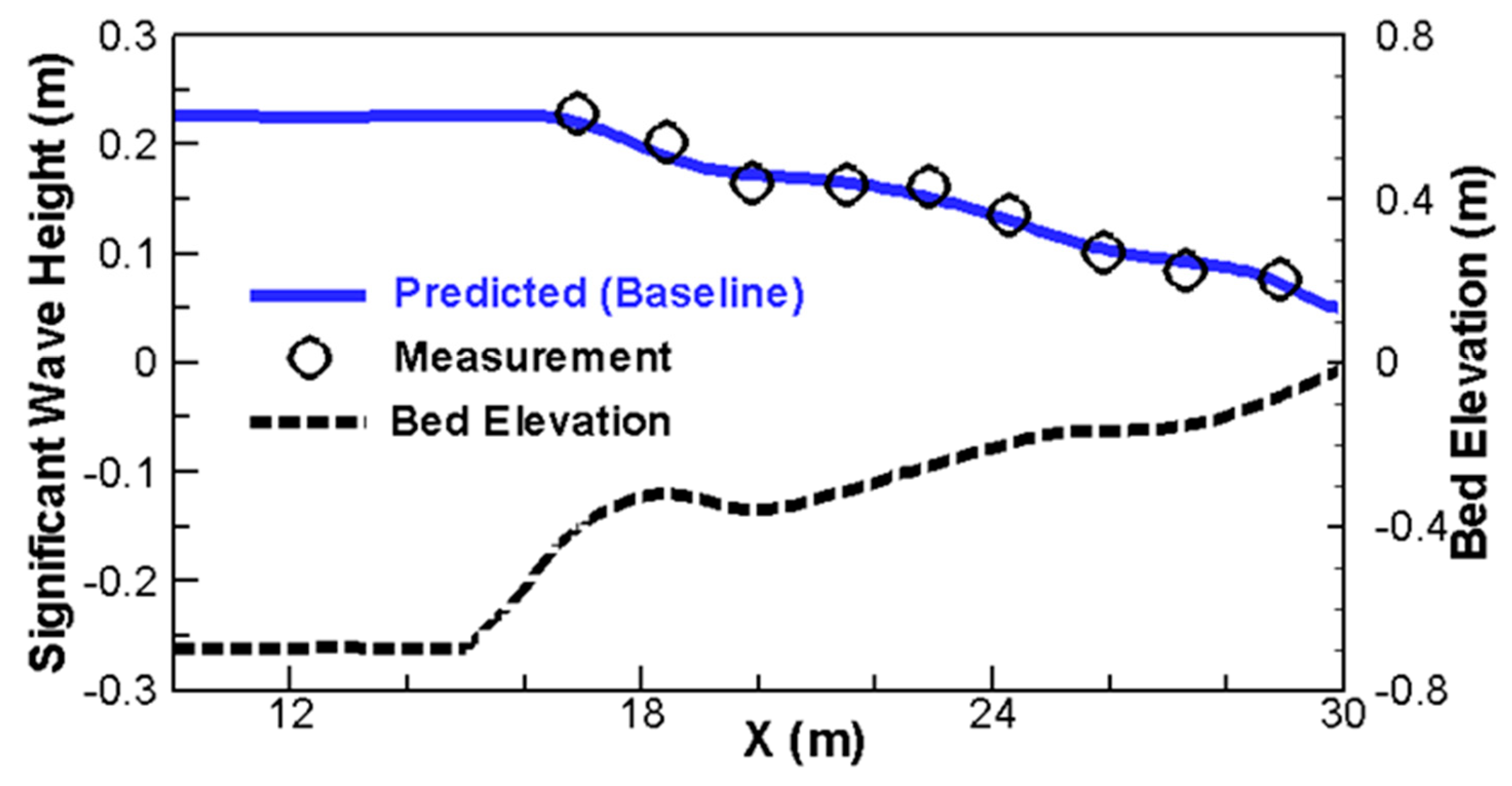
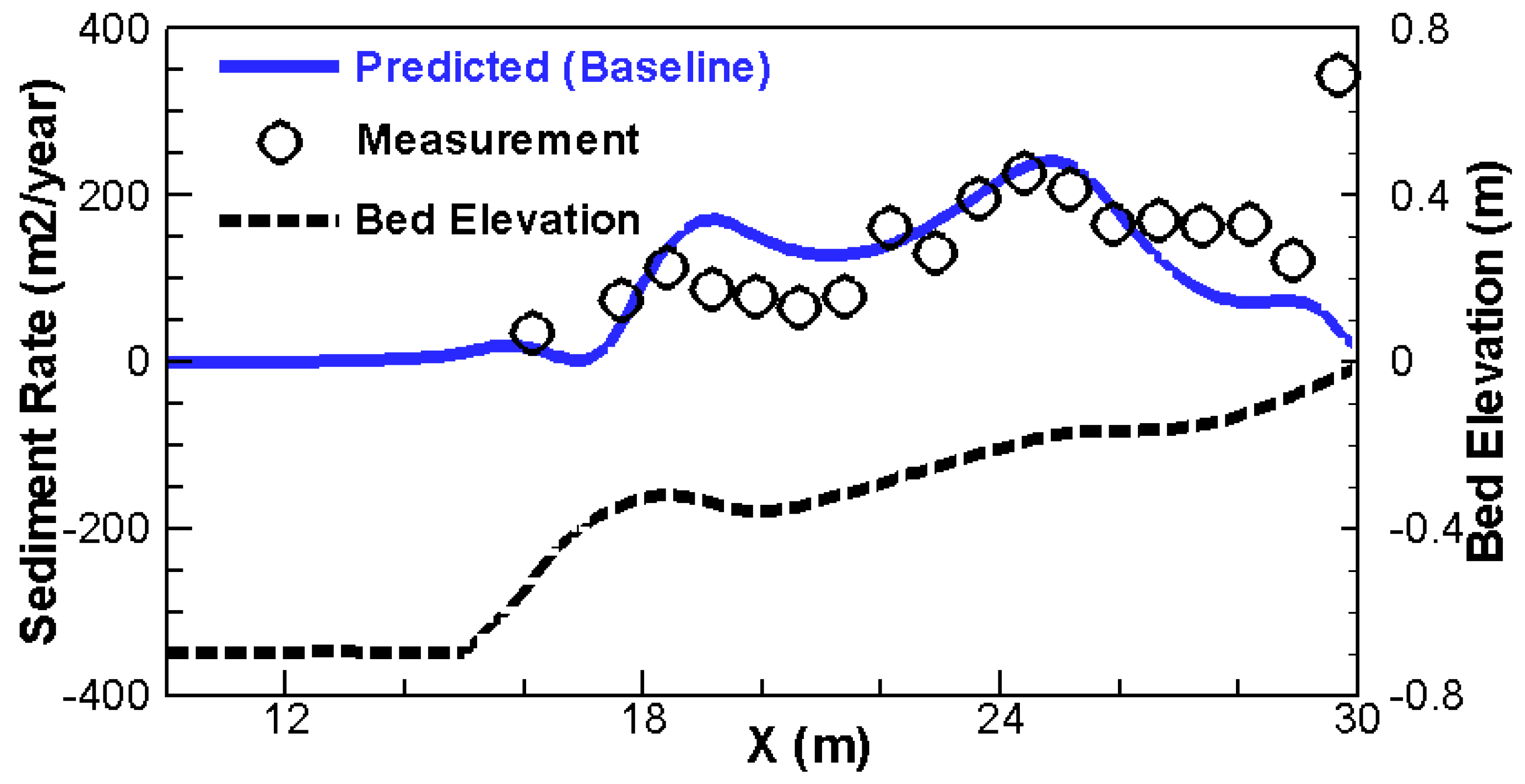
3.3. Sediment Transport in a Beach Surf Zone
4. Concluding Remarks
Funding
Data Availability Statement
Conflicts of Interest
References
- Amoudry, L.O.; Souza, A.J. Deterministic coastal morphological and sediment transport modeling: A review and discussion. Rev. Geophys. 2011, 49, RG2002. [Google Scholar] [CrossRef]
- Deng, J.; Woodroffe, C.D.; Roger, K.; Harff, J. Morphogenetic modelling of coastal and estuarine evolution. Earth Sci. Rev. 2017, 171, 254–271. [Google Scholar] [CrossRef]
- Sanchez, A.; Wu, W.; Beck, T.M. A depth-averaged 2-D model of flow and sediment transport in coastal water. Ocean Dyn. 2016, 66, 1475–1495. [Google Scholar] [CrossRef]
- Lu, Y.; Li, S.; Zuo, L.; Liu, H.; Roelvink, J.A. Advances in sediment transport under combined action of waves and currents. Int. J. Sediment. Res. 2015, 30, 351–360. [Google Scholar] [CrossRef]
- Klingbeil, K.; Lemarié, F.; Debreu, L.; Burchard, H. The numerics of hydrostatic structured-grid coastal ocean models: State of the art and future perspectives. Ocean Model. 2018, 125, 80–105. [Google Scholar] [CrossRef]
- Kim, H.S.; Lai, Y.G. Estuary and Coastal Modeling: Literature Review and Model Design; Technical Report No. ENV-2019-034; Technical Service Center, Bureau of Reclamation: Denver, CO, USA, 2019. [Google Scholar]
- Sanchez, A. An Implicit Finite-Volume Depth-Integrated Model for Coastal Hydrodynamic and Multiple-Sized Sediment Transport. Ph.D. Thesis, National Center for Computational Hydroscience and Engineering, The University of Mississippi, Oxford, MS, USA, 2013. [Google Scholar]
- Sorensen, O.R.; Kofoed-Hansen, H.; Rugbjerg, M.; Sorensen, L.S. A third-generation spectral wave model using an unstructured finite volume technique. In Proceedings of the Coastal Engineering Conference, Lisbon, Portugal, 19–24 September 2004; American Society of Civil Engineers: Reston, VA, USA, 2004; Volume 29, p. 894. [Google Scholar]
- Bellotti, G.; Franco, L.; Cecioni, C. Regional Downscaling of Copernicus ERA5 Wave Data for Coastal Engineering 561 Activities and Operational Coastal Services. Water 2021, 13, 859. [Google Scholar] [CrossRef]
- Lin, L.; Demirbilek, Z.; Mase, H.; Zheng, J.; Yamada, F. CMS-Wave: A Nearshore Spectral Wave Processes Model for Coastal Inlets and Navigation Projects; Technical Report ERDC/CHL TR-08-13; U.S. Army Engineer Research and Development Center, Coastal and Hydraulics Laboratory: Vicksburg, MS, USA, 2008. [Google Scholar]
- Ding, Y.; Zhang, Y.; Jia, Y. CCHE2D-Coast: Model Description and Graphical User Interface; NCCHE Technical Report; The University of Mississippi: Oxford, MS, USA, 2016; 88p. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- SWAN Team. SWAN Scientific and Technical Documentation Cycle III version 41.20AB; Technical and scientific documentation; Delft University of Technology: Delft, The Netherlands, 2019. [Google Scholar]
- Genseberger, M.; Donners, J. Hybrid SWAN for Fast and Efficient Practical Wave Modelling—Part 2. In Computational Science—ICCS 2020, Proceedings of the 20th International Conference, Amsterdam, The Netherlands, 3–5 June 2020; Krzhizhanovskaya, V.V., Zavodszky, G., Lees, M.H., Dongarra, J.J., Sloot, P.M.A., Brissos, S., Teixeira, J., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12139, p. 12139. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.T.M.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries, and Coastal Seas; Aqua Publications: Blokzil, The Netherlands, 1993; Available online: http://www.aquapublications.nl (accessed on 15 October 2020).
- van Ledden, M. Sand-Mud Segregation in Estuaries and Tidal Basins. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2003. [Google Scholar]
- Warner, J.C.; Perlin, N.; Skyllingstad, E.D. Using the model coupling toolkit to couple earth system models. Environ. Model. Softw. 2008, 23, 1240–1249. [Google Scholar] [CrossRef]
- Luo, J.; Li, M.; Sun, Z.; O’Connor, B.A. Numerical modelling of hydrodynamics and sand transport in the tide-dominated coastal-to-estuarine region. Mar. Geol. 2013, 342, 14–27. [Google Scholar] [CrossRef]
- Dietrich, J.; Zijlema, M.; Westerink, J.; Holthuijsen, L.; Dawson, C.; Luettich, R., Jr.; Jensen, R.; Smith, J.; Stelling, G.; Stone, G. Modeling hurricane waves and storm surge using integrally-coupled, scalable computations. Coast. Eng. 2011, 58, 45–65. [Google Scholar] [CrossRef]
- Qi, J.; Jing, Y.; Chen, C.; Zhang, J. Numerical Simulation of Tidal Current and Sediment Movement in the Sea Area near Weifang Port. Water 2023, 15, 2516. [Google Scholar] [CrossRef]
- Christakos, K.; Björkqvist, J.V.; Tuomi, L.; Furevik, B.R.; Breivik, Ø. Modelling wave growth in narrow fetch geome-557 tries: The white-capping and wind input formulations. Ocean Model. 2021, 157, 101730. [Google Scholar] [CrossRef]
- Buttolph, A.M.; Reed, C.W.; Kraus, N.C.; Ono, N.; Larson, M.; Camenen, B.; Hanson, H.; Wamsley, T.; Zundel, A.K. Two-Dimensional Depth-Averaged Circulation Model CMS-M2D: Version 3.0, Report 2: Sediment Transport and Morphology Change; Technical Report, ERDC/CHL TR-06-9; Coastal and Hydraulics Laboratory, ERDC, US Army Corps of Engineers: Vicksburg, MS, USA, 2006. [Google Scholar]
- Mase, H. Multidirectional random wave transformation model based on energy balance equation. J. Coast. Eng. 2001, 43, 317–337. [Google Scholar] [CrossRef]
- Favaretto, C.; Martinelli, L.; Vigneron, E.M.P.; Ruol, P. Wave Hindcast in Enclosed Basins: Comparison among SWAN, STWAVE and CMS-Wave Models. Water 2022, 14, 1087. [Google Scholar] [CrossRef]
- Nassar, K.; Masria, A.; Mahmod, W.E.; Negm, A.; Fath, H. Hydro-morphological modeling to characterize the adequacy of jetties and subsidiary alternatives in sedimentary stock rationalization within tidal inlets of marine lagoons. Appl. Ocean Res. 2019, 84, 92–110. [Google Scholar] [CrossRef]
- Mera, M.; Chrisnatilova, D. Numerical Simulation to Determine the Effectiveness of Groynes and Breakwaters as Protective Structures for Gandoriah Beach, Pariaman City. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1041, 012001. [Google Scholar] [CrossRef]
- Lin, L.; Demirbilek, Z.; Thomas, R.C.; Rosati, J. Verification and Validation of the Coastal Modeling System; Report 2: 572 CMS-Wave; U.S. Army Engineer Research and Development Center, Coastal and Hydraulics Laboratory: Vicksburg, MS, USA, 2011. [Google Scholar]
- Ding, Y.; Wang, S.S.Y. Development and Application of a Coastal and Estuarine Morphological Process Modeling System. J. Coast. Res. 2010, 10052, 127–140. [Google Scholar] [CrossRef]
- Ding, Y.; Kuiry, S.; Elgohry, M.; Jia, Y.; Altinakar, M.S.; Yeh, K.-C. Impact assessment of sea-level rise and hazardous storms on coasts and estuaries using integrated processes model. Ocean Eng. 2013, 71, 74–95. [Google Scholar] [CrossRef]
- Ding, Y.; Yeh, K.-C.; Wei, S.-T. Integrated coastal process modeling and impact assessment of floating and sedimentation in coasts and estuaries. Coast. Eng. Proc. 2017, 1, 18. [Google Scholar] [CrossRef]
- Hsieh, T.-C.; Ding, Y.; Yeh, K.-C.; Jhong, R.K. Investigation of Morphological Changes in the Tamsui River Estuary Using an Integrated Coastal and Estuarine Processes Model. Water 2020, 12, 1084. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, S.S.Y. CCHE2D: Two-Dimensional Hydrodynamics and Sediment Transport Model for Unsteady Open Channel Flows over Loose Bed; Technical Report No. NCCHE-TR-2001-1; National Center for Computational Hydroscience and Engineering, The University of Mississippi: Oxford, MS, USA, 2001. [Google Scholar]
- Lai, Y.G. Two-Dimensional Depth-Averaged Flow Modeling with an Unstructured Hybrid Mesh. J. Hydraul. Eng. 2010, 136, 12–23. [Google Scholar] [CrossRef]
- Lai, Y.G.; Kim, H.S. A Near-Shore Linear Wave Model with the Mixed Finite Volume and Finite Difference Unstructured Mesh Method. Fluids 2020, 5, 199. [Google Scholar] [CrossRef]
- Eisma, D.; Ji, Z.; Chen, S.; Chen, M.; van der Gaast, S.J. Clay Mineral Composition of Recent Sediments along the China Coast, in the Yellow Sea and the East China Sea; NIOZ-Rapport 1995-4; Nederlands Instituut voor Onderzoek der Zee: Den Burg, The Netherlands, 1995. [Google Scholar]
- Wu, W. Computational River Dynamics; Taylor and Francis: Abingdon, UK, 2008. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Rodi, W. Turbulence Models and Their Application in Hydraulics. A State-of-the-Art Review. IAHR Monograph, 3rd ed.; Balkema: Zutphen, The Netherlands, 1993. [Google Scholar]
- Tolman, H.L. A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- van Rijn, L.C.; Havinga, F.J. Transport of fine sands by currents and waves. II. J. Waterw. Port Coast. Ocean Eng. 1995, 121, 123–133. [Google Scholar] [CrossRef]
- van Rijn, L.C. Unified view of sediment transport by currents and waves, I: Initiation of bed motion, bed roughness, and bed-load transport. J. Hydraul. Eng. ASCE 2007, 133, 649–667. [Google Scholar] [CrossRef]
- Miller, M.C.; McCave, I.N.; Komar, P.D. Threshold of sediment motion under unidirectional current. Sedimentology 1977, 24, 507–527. [Google Scholar] [CrossRef]
- Lai, Y.G. A Two-Dimensional Depth-Averaged Sediment Transport Mobile-Bed Model with Polygonal Meshes. Water 2020, 12, 1032. [Google Scholar] [CrossRef]
- Johnson, H.K.; Zyserman, J.A. Controlling spatial oscillations in bed level update schemes. Coast. Eng. 2002, 46, 109–126. [Google Scholar] [CrossRef]
- Soulsby, R.L. Dynamics of Marine Sands: A Manual for Practical Applications; Thomas Telford Publications: London, UK, 1997. [Google Scholar]
- van Rijn, L.C. Unified view of sediment transport by currents and waves, II: Suspended transport. J. Hydraul. Eng. ASCE 2007, 133, 668–689. [Google Scholar] [CrossRef]
- Gaeuman, D.; Sklar, L.; Lai, Y.G. Flume experiments to constrain bedload adaptation length. J. Hydrol. Eng. 2014, 20, 1–5. [Google Scholar] [CrossRef]
- Bayram, A.; Larson, M.; Miller, H.C.; Kraus, N.C. Cross-shore distribution of longshore sediment transport: Comparison between predictive formulas and field measurements. Coast. Eng. 2001, 44, 79–99. [Google Scholar] [CrossRef]
- Camenen, B.; Larroude, P. Comparison of sediment transport formulae for the coastal environment. Coast. Eng. 2003, 48, 111–132. [Google Scholar] [CrossRef]
- Camenen, B.; Larson, M. A general formula for non-cohesive bed load sediment transport. Estuar. Coast. Shelf Sci. 2005, 63, 249–260. [Google Scholar] [CrossRef]
- Camenen, B.; Larson, M. A Unified Sediment Transport Formulation for Coastal Inlet Application; Technical Report ERDC/CHL CR-07-1; US Army Engineer Research and Development Center: Vicksburg, MS, USA, 2007. [Google Scholar]
- Camenen, B.; Larson, M. A general formula for noncohesive suspended sediment transport. J. Coast. Res. 2008, 24, 615–627. [Google Scholar] [CrossRef]
- Nam, P.T.; Larson, M.; Hanson, H.; Hoan, L.X. A numerical model of nearshore waves, currents, and sediment transport. Coast. Eng. 2009, 56, 1084–1096. [Google Scholar] [CrossRef]
- Hsu, T.W.; Ou, S.H.; Liau, J.M.; Zanke, U.; Roland, A.; Mewis, P. Development and implement of a spectral finite element wave model. In Proceedings of the 5th International Symposium on Wave Measurement and Analysis, Madrid, Spain, 3–7 July 2005. [Google Scholar]
- Hsu, T.W.; Ou, S.H.; Liau, J.M. Hindcasting nearshore wind waves using a FEM code for SWAN. Coast. Eng. 2005, 52, 177–195. [Google Scholar] [CrossRef]
- Collins, N.; Theurich, G.; Deluca, C.; Suarez, M.; Trayanov, A.; Balaji, V.; Li, P.; Yang, W.; Hill, C.; Da Silva, C. Design and implementation of components in the earth system modeling framework. Int. J. High Perform. Comput. Appl. 2005, 19, 341–350. [Google Scholar] [CrossRef]
- Gregersen, J.B.; Gijsbers, P.J.A.; Westen, S.J.P.; Blind, M. OpenMI: The essential concepts and their implications for legacy software. Adv. Geosci. 2005, 4, 37–44. [Google Scholar] [CrossRef]
- Cats, G. Numerical Modeling of Wave-Current Interaction with the Use of a Two-Way Coupled System. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
- Samaras, A.G. Towards integrated modelling of Watershed-Coast System morphodynamics in a changing climate: A critical review and the path forward. Sci. Total Environ. 2023, 882, 163625. [Google Scholar] [CrossRef]
- van Rijn, L.C. Sedimentation of dredged channels by currents and waves. J. Waterw. Port Coast. Ocean Eng. 1986, 112, 541–559. [Google Scholar] [CrossRef]
- Havinga, F.J. Sediment Concentrations and Transport in Case of Irregular Non-Breaking Waves with a Current. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 1992. Rep. H840 Parts E, F, G.. [Google Scholar]
- Hamilton, D.G.; Ebersole, B.A. Establishing uniform longshore currents in a large-scale sediment transport facility. Coast. Eng. 2001, 42, 199–218. [Google Scholar] [CrossRef]
- Wang, P.; Ebersole, B.A.; Smith, E.R.; Johnson, B.D. Temporal and spatial variations of surf-zone currents and suspended sediment concentration. Coast. Eng. 2002, 46, 175–211. [Google Scholar] [CrossRef]
- Gravens, M.B.; Wang, P.; Kraus, N.C.; Hanson, H. Physical model investigation of morphology development at headland structures. In Proceedings of the 30th International Conference on Coastal Engineering, San Diego, CA, USA, 3–8 September 2006; World Scientific Press: San Diego, CA, USA, 2006; pp. 3617–3629. [Google Scholar]
- Gravens, M.B.; Wang, P. Data Report: Laboratory Testing of Longshore Sand Transport by Waves and Currents. In Morphology Change Behind Headland Structures; Geology Faculty Publications: Tampa, FL, USA, 2007; Volume 258, Available online: https://scholarcommons.usf.edu/gly_facpub/258 (accessed on 15 March 2021).


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Y.G. An Integrated Current–Wave–Sediment Model for Coastal and Estuary Simulation. Water 2024, 16, 415. https://doi.org/10.3390/w16030415
Lai YG. An Integrated Current–Wave–Sediment Model for Coastal and Estuary Simulation. Water. 2024; 16(3):415. https://doi.org/10.3390/w16030415
Chicago/Turabian StyleLai, Yong G. 2024. "An Integrated Current–Wave–Sediment Model for Coastal and Estuary Simulation" Water 16, no. 3: 415. https://doi.org/10.3390/w16030415
APA StyleLai, Y. G. (2024). An Integrated Current–Wave–Sediment Model for Coastal and Estuary Simulation. Water, 16(3), 415. https://doi.org/10.3390/w16030415





