Representing Hourly Energy Prices in a Large-Scale Monthly Water System Model
Abstract
:1. Introduction
2. Materials and Methods
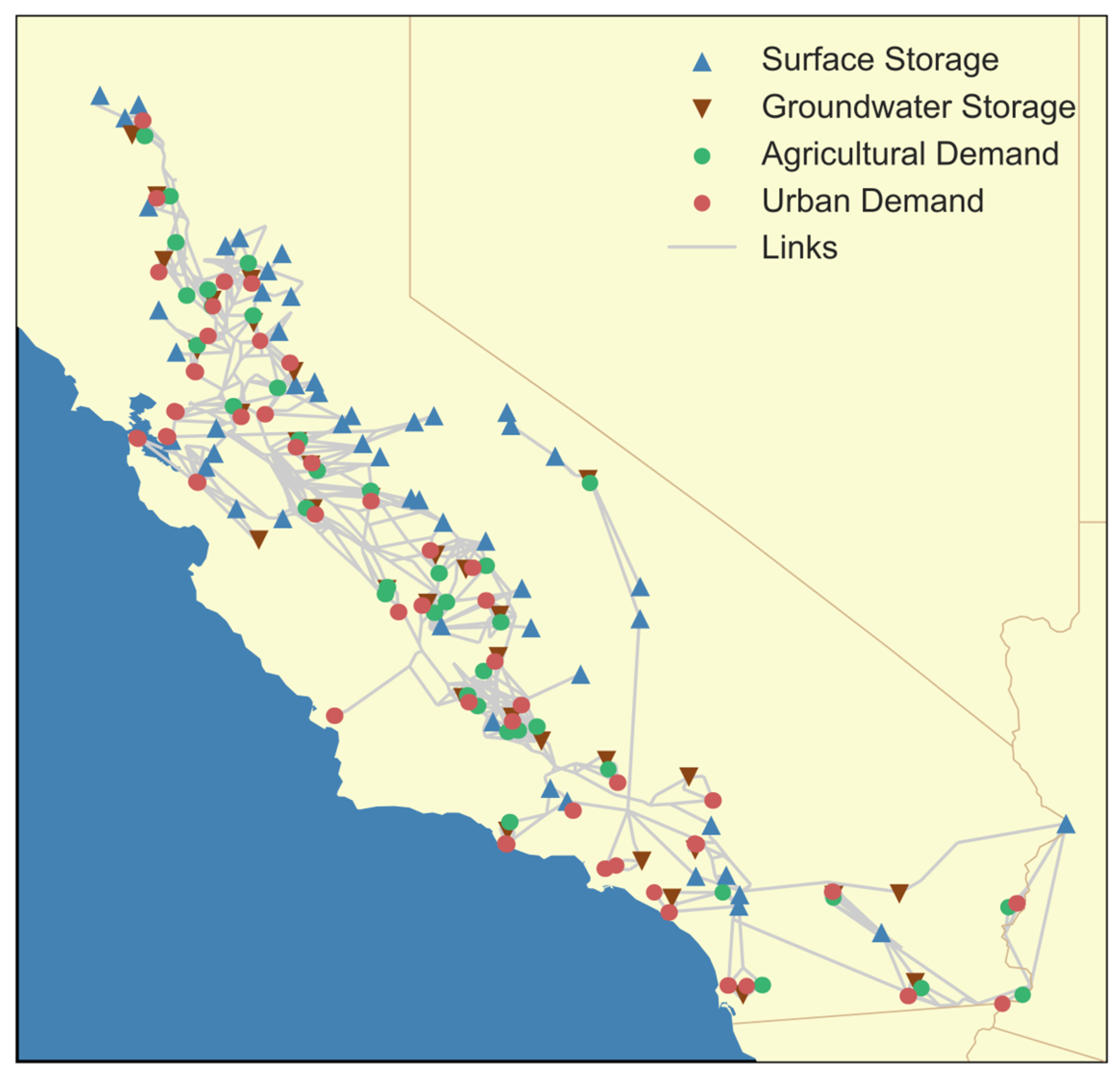
2.1. CALVIN Hydroeconomic Model
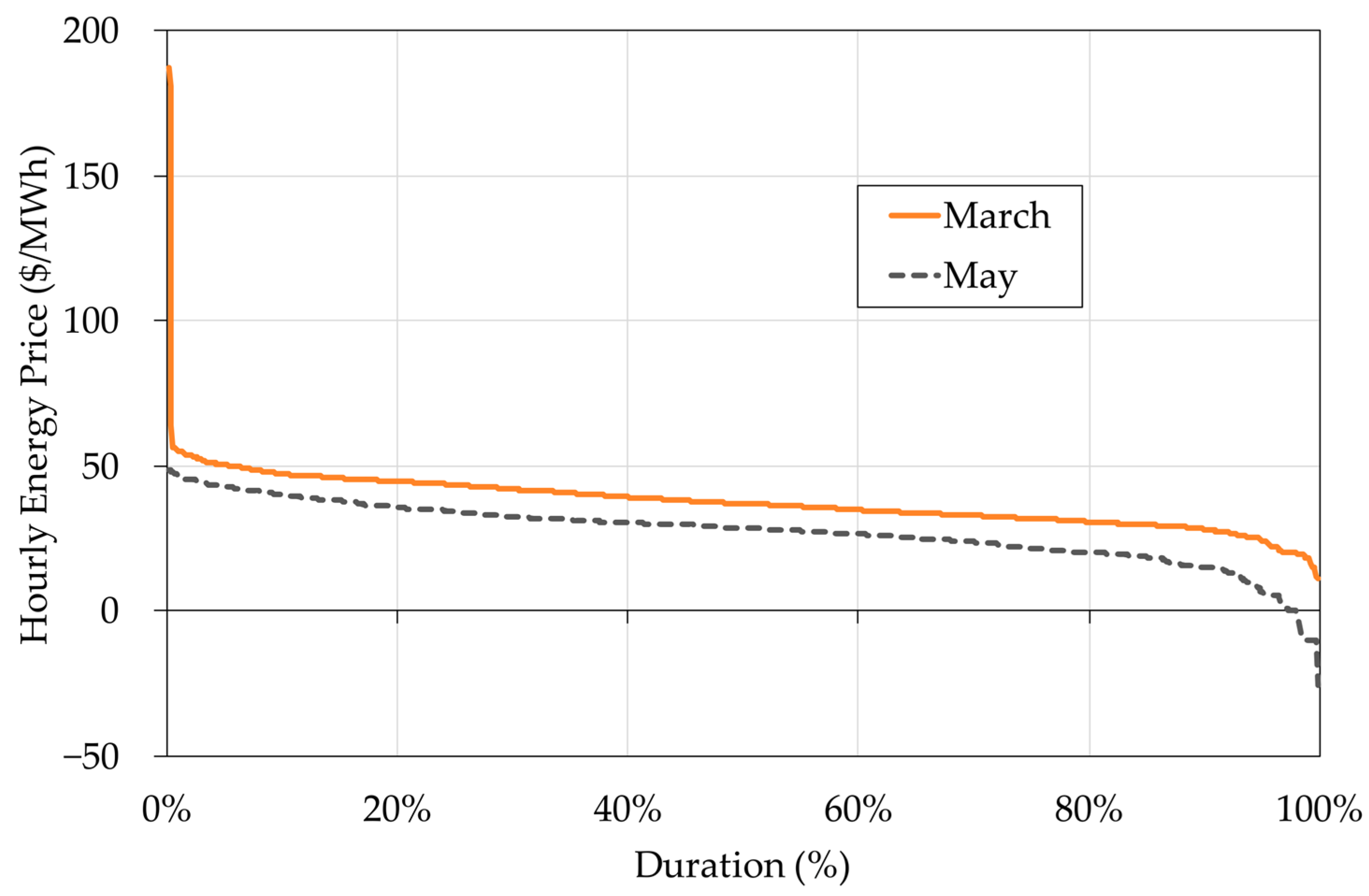
2.2. Representing Hourly Varying Energy Prices in Monthly Models
3. Results
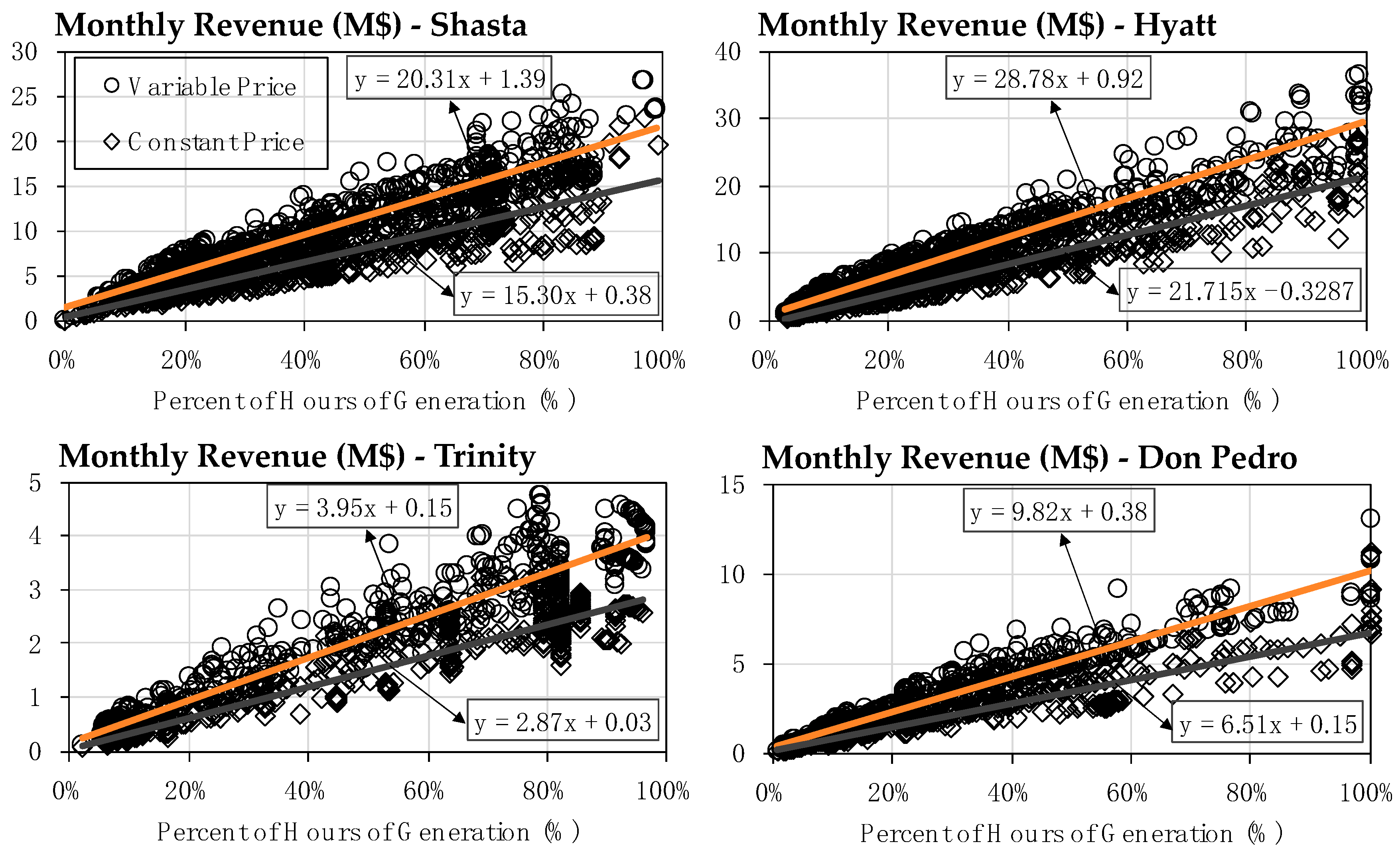
3.1. Power Generation and Revenue
3.2. Water Supply Operations
3.3. Pumping Plant Operations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Loucks, D.P. Water resource systems models: Their role in planning. J. Water Resour. Plan. Manag. 1992, 118, 214–223. [Google Scholar] [CrossRef]
- Yeh, W.W.-G.; Becker, L. Multiobjective analysis of multireservoir operations. Water Resour. Res. 1982, 18, 1326–1336. [Google Scholar] [CrossRef]
- Savic, D.A.; Simonovic, S.P. An interactive approach to selection and use of single multipurpose reservoir models. Water Resour. Res. 1991, 27, 2509–2521. [Google Scholar] [CrossRef]
- Leta, M.K.; Demissie, T.A.; Tränckner, J. Optimal operation of Nashe hydropower reservoir under land use land cover change in Blue Nile River Basin. Water 2022, 14, 1606. [Google Scholar] [CrossRef]
- Yeh, W.W.-G. Reservoir management and operations models: A state-of-the-art review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Wurbs, R.A. Reservoir-system simulation and optimization models. J. Water Resour. Plan. Manag. 1993, 119, 455–472. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Ward, F.A.; Lynch, T.P. Integrated river basin optimization: Modeling economic and hydrologic interdependence. J. Am. Water Resour. Assoc. 1996, 32, 1127–1138. [Google Scholar] [CrossRef]
- Vichete, W.D.; Méllo Júnior, A.V.; Soares, G.A.d.S. A water allocation model for multiple uses based on a proposed hydro-economic method. Water 2023, 15, 1170. [Google Scholar] [CrossRef]
- Davis, M.D. Integrated water resource management and water sharing. J. Water Resour. Plan. Manag. 2007, 133, 427–445. [Google Scholar] [CrossRef]
- Marques, G.F.; Tilmant, A. The economic value of coordination in large-scale multireservoir systems: The Parana River case. Water Resour. Res. 2013, 49, 7546–7557. [Google Scholar] [CrossRef]
- Li, C.; He, L.; Liu, D.; Feng, Z. A Scientometric review for uncertainties in integrated simulation–optimization modeling system. Water 2024, 16, 285. [Google Scholar] [CrossRef]
- Tejada-Guibert, J.A.; Stedinger, J.R.; Staschus, K. Optimization of value of CVP’s hydropower production. J. Water Resour. Plan. Manag. 1990, 116, 52–70. [Google Scholar] [CrossRef]
- Madani, K.; Lund, J.R. Modeling California’s high-elevation hydropower systems in energy units. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Olivares, M.A.; Lund, J.R. Representing energy price variability in long-and medium-term hydropower optimization. J. Water Resour. Plan. Manag. 2012, 138, 606–613. [Google Scholar] [CrossRef]
- Ring, B.J. Dispatch Based Pricing in Decentralised Power Systems. Ph.D. Dissertation, University of Canterbury, Christchurch, New Zealand, 1995. [Google Scholar]
- Madrigal Martinez, M. Optimization Models and Techniques for Implementation and Pricing of Electricity Markets. Ph.D. Dissertation, University of Waterloo, Waterloo, ON, Canada, 2001. [Google Scholar]
- Pritchard, G.; Philbot, A.; Neame, P. Hydroelectric reservoir optimization in a pool market. Math. Program. 2004, 103, 445–461. [Google Scholar] [CrossRef]
- Wu, Y.; Su, C.; Liu, S.; Guo, H.; Sun, Y.; Jiang, Y.; Shao, Q. Optimal decomposition for the monthly contracted electricity of cascade hydropower plants considering the bidding space in the day-ahead spot market. Water 2022, 14, 2347. [Google Scholar] [CrossRef]
- Liu, S.; Luo, J.; Chen, H.; Wang, Y.; Li, X.; Zhang, J.; Wang, J. Third-monthly hydropower scheduling of cascaded reservoirs using successive quadratic programming in trust corridor. Water 2023, 15, 716. [Google Scholar] [CrossRef]
- Li, J.; Saw, M.M.M.; Chen, S.; Yu, H. Short-term optimal operation of Baluchaung II hydropower plant in Myanmar. Water 2020, 12, 504. [Google Scholar] [CrossRef]
- Dogan, M.S. Integrated Water Operations in California: Hydropower, Overdraft, and Climate Change. Master’s Thesis, University of California, Davis, CA, USA, 2015. [Google Scholar]
- Draper, A.J.; Jenkins, M.W.; Kirby, K.W.; Lund, J.R.; Howitt, R.E. Economic-engineering optimization for California water management. J. Water Resour. Plan. Manag. 2003, 129, 155–164. [Google Scholar] [CrossRef]
- Dogan, M.S.; Fefer, M.A.; Herman, J.D.; Hart, Q.J.; Merz, J.R.; Medellin-Azuara, J.; Lund, J.R. An open-source Python implementation of California’s hydro-economic optimization model. Environ. Model. Softw. 2018, 108, 8–13. [Google Scholar] [CrossRef]
- Arnold, W. The Economic Value of Carryover Storage in California’s Water Supply System with Limited Hydrologic Foresight. Master’s Thesis, University of California, Davis, CA, USA, 2021. [Google Scholar]
- Locational Marginal Energy Price Data. Available online: http://www.caiso.com (accessed on 6 December 2023).
- Chronological reconstructed Sacramento and San Joaquin Valley Water Year Hydrologic Classification Indices. Available online: https://cdec.water.ca.gov/reportapp/javareports?name=WSIHIST (accessed on 22 January 2024).





| Hydropower Facility | Power Plant Capacity (MW) | Reservoir Storage Capacity (106 m3) | Turbine Release Capacity (m3/s) |
|---|---|---|---|
| Shasta a | 629 | 5612 | 561 |
| Spring Creek a | 180 | 296 | 143 |
| Carr | 154 | 296 | 97 |
| Trinity a | 140 | 3019 | 132 |
| Keswick | 117 | 29 | 494 |
| Hyatt a | 644 | 4367 | 523 |
| Colgate a | 325 | 1147 | 107 |
| Folsom a | 199 | 1205 | 245 |
| New Narrows | 49 | 86 | 121 |
| Thermalito Fore/Afterbay | 115 | 70 | 503 |
| New Melones a | 300 | 2953 | 270 |
| Don Pedro a | 203 | 2504 | 260 |
| Holm a | 157 | 372 | 23 |
| Kirkwood a | 122 | 444 | 21 |
| New Exchequer | 95 | 1263 | 89 |
| Gianelli a | 424 | 2518 | 376 |
| Moccasin a | 104 | 1 | 19 |
| O’Neill a | 25 | 70 | 42 |
| Pine Flat | 190 | 1233 | 231 |
| Castaic | 1247 | 401 | 123 |
| Devil Canyon | 280 | 90 | 46 |
| Warne | 78 | 7 | 47 |
| San Francisquito 1 and 2 | 123 | - | 22 |
| Gorges | 112 | - | 23 |
| Mojave | 32 | - | 56 |
| Others | 92 | - | 359 |
| Pumping Facility | Pumping Plant Capacity (MW) | Flow Capacity (m3/s) |
|---|---|---|
| Badger Hill | 6 | 270 |
| Banks a | 212 | 245 |
| Buena Vista | 90 | 146 |
| Contra Costa 1 | 3 | 9 |
| Dos Amigos | 99 | 340 |
| Del Valle a | 0 | 3 |
| Eagle | 72 | 52 |
| Edmonston | 622 | 127 |
| Gianelli a,b | 151 | 317 |
| Iron | 72 | 52 |
| Julian Hinds | 72 | 52 |
| Los Vaqueros | 23 | 6 |
| Las Perillas | 2 | 270 |
| Mallard Slough | 5 | 1 |
| Old River | 36 | 7 |
| O’Neill a,b | 19 | 121 |
| Oso a | 37 | 90 |
| Pearlblossom | 95 | 83 |
| South Bay a | 4 | 9 |
| Tracy | 92 | 133 |
| Walnut Creek | 61 | 14 |
| Wheeler Ridge | 107 | 127 |
| Chrisman | 233 | 127 |
| Facility | Turbine Release (m3/s) | Generation (GWh/Year) | Revenue (USD M/Year) | Revenue | |||
|---|---|---|---|---|---|---|---|
| Constant Price | Variable Price | Constant Price | Variable Price | Constant Price | Variable Price | Change (%) | |
| Shasta a | 217 | 216 | 2286 | 2285 | 75.5 | 110.6 | 46.5 |
| Spring Creek a | 32 | 31 | 381 | 381 | 13.5 | 19.4 | 43.4 |
| Carr | 25 | 25 | 354 | 354 | 12.2 | 12.4 | 1.5 |
| Trinity a | 48 | 48 | 408 | 409 | 13.0 | 19.0 | 46.7 |
| Keswick | 244 | 243 | 465 | 464 | 15.5 | 15.4 | −0.8 |
| Hyatt a | 154 | 152 | 2190 | 2183 | 76.7 | 111.6 | 45.5 |
| Colgate a | 47 | 46 | 1356 | 1361 | 45.8 | 64.0 | 39.9 |
| Folsom a | 100 | 99 | 655 | 653 | 22.1 | 32.0 | 44.6 |
| New Narrows | 60 | 60 | 277 | 277 | 9.5 | 9.4 | −1.0 |
| Thermalito | 137 | 136 | 293 | 290 | 10.3 | 10.2 | −0.9 |
| New Melones a | 40 | 40 | 495 | 496 | 15.9 | 25.2 | 58.5 |
| Don Pedro a | 56 | 55 | 611 | 610 | 18.6 | 29.5 | 58.2 |
| Holm a | 17 | 13 | 869 | 673 | 30.6 | 27.8 | −9.2 |
| Kirkwood a | 13 | 13 | 364 | 355 | 12.6 | 15.8 | 25.1 |
| New Exchequer | 36 | 36 | 275 | 277 | 8.5 | 8.6 | 1.0 |
| Gianelli a | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Moccasin a | 13 | 13 | 167 | 167 | 5.8 | 7.4 | 27.4 |
| O’Neill a | 37 | 10 | 33 | 9 | 1.2 | 0.4 | −68.0 |
| Pine Flat | 60 | 60 | 445 | 444 | 13.2 | 13.2 | −0.1 |
| Castaic | 35 | 35 | 872 | 872 | 33.2 | 33.2 | 0.0 |
| Devil’s Canyon | 37 | 37 | 1051 | 1051 | 37.2 | 37.2 | 0.0 |
| Warne | 36 | 36 | 522 | 522 | 19.2 | 19.2 | 0.0 |
| San Francisquito 1 and 2 | 14 | 14 | 629 | 629 | 23.1 | 23.1 | 0.1 |
| Gorges | 7 | 7 | 366 | 366 | 12.5 | 12.5 | 0.0 |
| Mojave | 37 | 37 | 90 | 90 | 3.2 | 3.2 | 0.0 |
| Others | 244 | 242 | 642 | 642 | 20.5 | 20.5 | −0.3 |
| Statewide | 1745 | 1704 | 16,094 | 15,857 | 550 | 681 | 24 |
| Year Type | Average Generation (TWh/Year) | Average Revenue (USD M/Year) | Revenue Change (%) | ||
|---|---|---|---|---|---|
| Constant Price | Variable Price | Constant Price | Variable Price | ||
| Wet | 16.3 | 15.7 | 548 | 701 | 28 |
| Above Normal | 12.8 | 12.4 | 436 | 569 | 31 |
| Below Normal | 10.9 | 10.9 | 367 | 501 | 36 |
| Dry | 9.4 | 9.5 | 313 | 435 | 39 |
| Critical | 7.3 | 7.2 | 242 | 338 | 40 |
| Central Valley Average | 12.0 | 11.8 | 403 | 535 | 33 |
| Facility | Discharge Rate (m3/s) | Energy Use (GWh/Year) | Energy Cost (USD M/Year) | Energy Cost Change (%) | |||
|---|---|---|---|---|---|---|---|
| Constant Price | Variable Price | Constant Price | Variable Price | Constant Price | Variable Price | ||
| Banks a | 148.71 | 152.69 | 1130 | 1160 | 39 | 36 | −10 |
| Del Valle a | 0.06 | 0.06 | 0.10 | 0.10 | 0.0044 | 0.0018 | −59 |
| Gianelli a,b | 31.83 | 31.81 | 198 | 198 | 9 | 5 | −41 |
| O’Neill a,b | 24.49 | 20.54 | 37 | 31 | 2 | 1 | −40 |
| Oso a | 31.37 | 31.37 | 225 | 225 | 8 | 5 | −41 |
| South Bay a | 0.06 | 0.06 | 1.28 | 1.28 | 0.0555 | 0.0242 | −56 |
| Others | 845.95 | 841.90 | 10,983 | 10,959 | 384 | 383 | 0 |
| Statewide | 1928 | 1920 | 12,574 | 12,574 | 442 | 430 | −3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dogan, M.S.; White, E.; Yao, Y.; Lund, J.R. Representing Hourly Energy Prices in a Large-Scale Monthly Water System Model. Water 2024, 16, 562. https://doi.org/10.3390/w16040562
Dogan MS, White E, Yao Y, Lund JR. Representing Hourly Energy Prices in a Large-Scale Monthly Water System Model. Water. 2024; 16(4):562. https://doi.org/10.3390/w16040562
Chicago/Turabian StyleDogan, Mustafa Sahin, Ellie White, Yiqing Yao, and Jay R. Lund. 2024. "Representing Hourly Energy Prices in a Large-Scale Monthly Water System Model" Water 16, no. 4: 562. https://doi.org/10.3390/w16040562
APA StyleDogan, M. S., White, E., Yao, Y., & Lund, J. R. (2024). Representing Hourly Energy Prices in a Large-Scale Monthly Water System Model. Water, 16(4), 562. https://doi.org/10.3390/w16040562







