Towards an Understanding of Hydraulic Sensitivity: Graph Theory Contributions to Water Distribution Analysis
Abstract
1. Introduction
2. Literature Review
2.1. Graph Theory Integration in Water Distribution Systems
2.2. Application and Impact in WDS
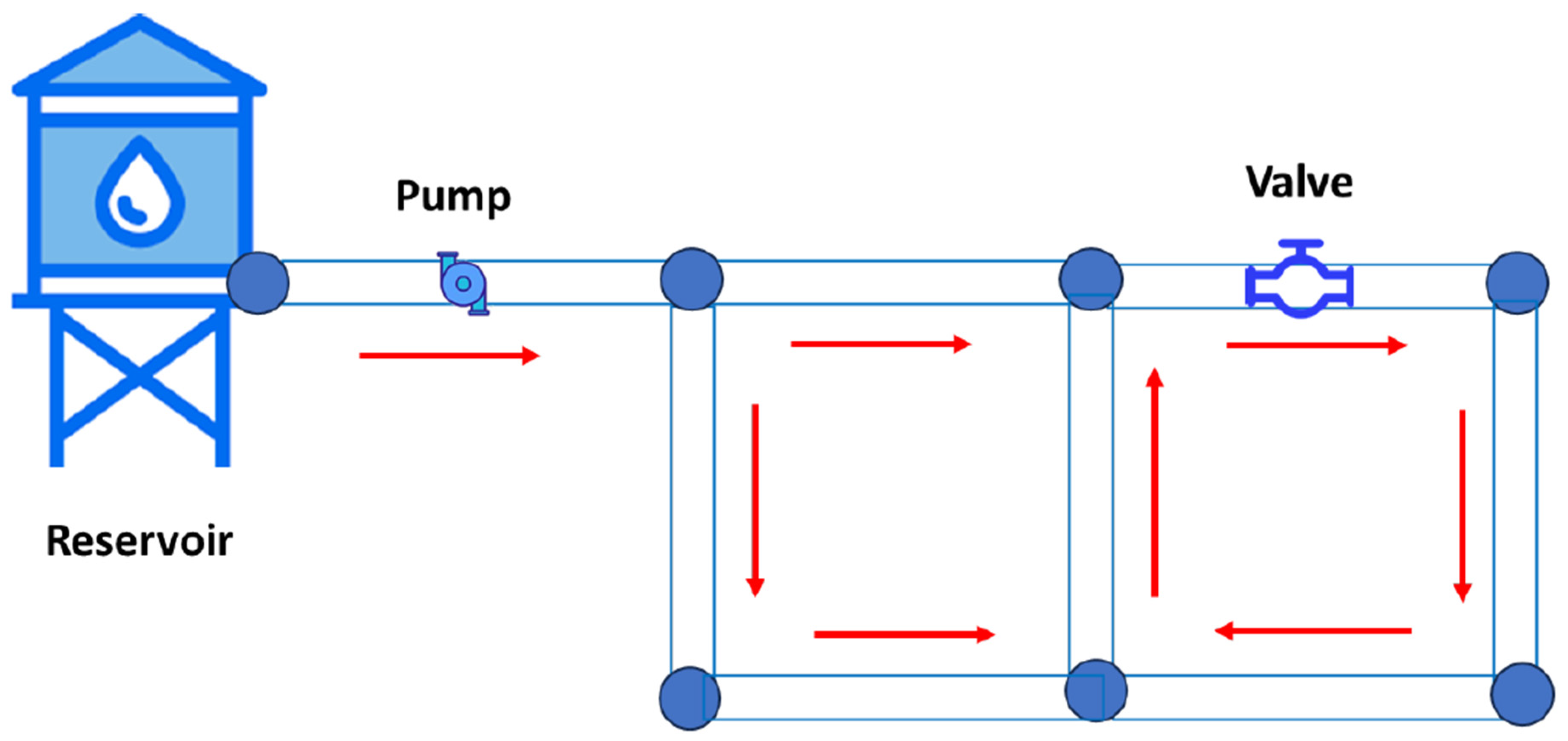
3. Graph Theory Fundamentals and Hydraulic Metrics in WDS Analysis
3.1. Graph Properties
3.2. Hydraulic Measures
- 1.
- Elevation (m)—The node’s height, which influences the gravitational pressure in the system.
- 2.
- Demand (m3/h)—The water requirement at that node is essential for ensuring adequate supply.
- 3.
- Pressure (m)—The fluid force exerted at the node is critical for water delivery and system integrity.
- 1.
- Length (m)—The distance between two nodes, affecting headloss and velocity.
- 2.
- Diameter (mm)—The width of the pipe, which dictates the flow rate and velocity.
- 3.
- Flow (m3/h)—The volume of water moving through the pipe per unit of time.
- 4.
- Velocity (m3/h)—The velocity of the water flow is crucial for preventing sedimentation and ensuring effective scouring.
- 5.
- Headloss (m/s)—The loss of pressure due to friction within the length of the pipe.
- 6.
- Volume (m3)—The pipe’s water capacity can be influenced by the pipe’s cross-sectional area.
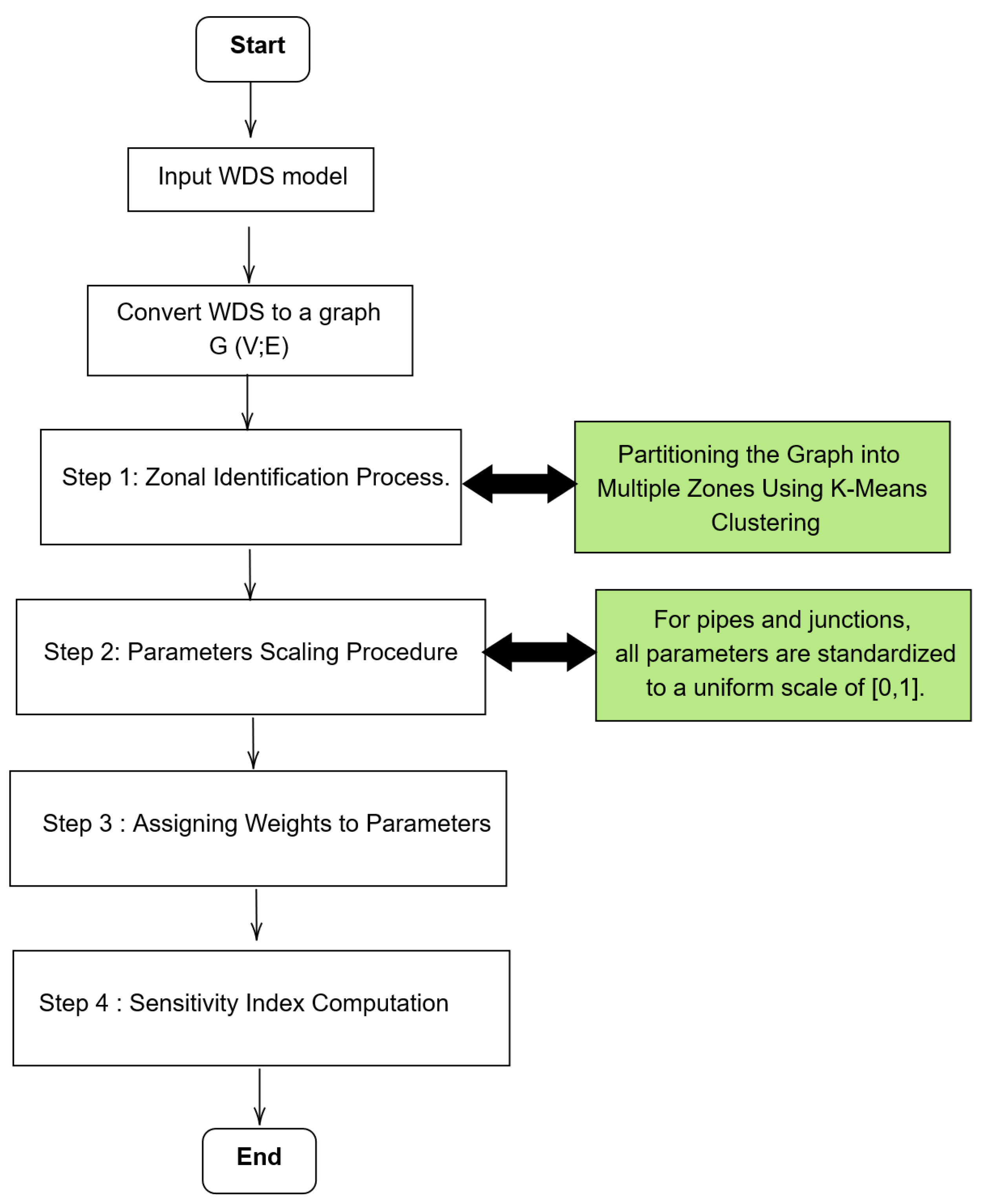
4. Methodology
4.1. General Overview
4.2. Zonal Identification Process
4.3. Parameters Scaling Procedure
4.4. Assigning Weights to Parameters
4.5. Sensitivity Index Computation
4.6. Theoretical Examination
- 1.
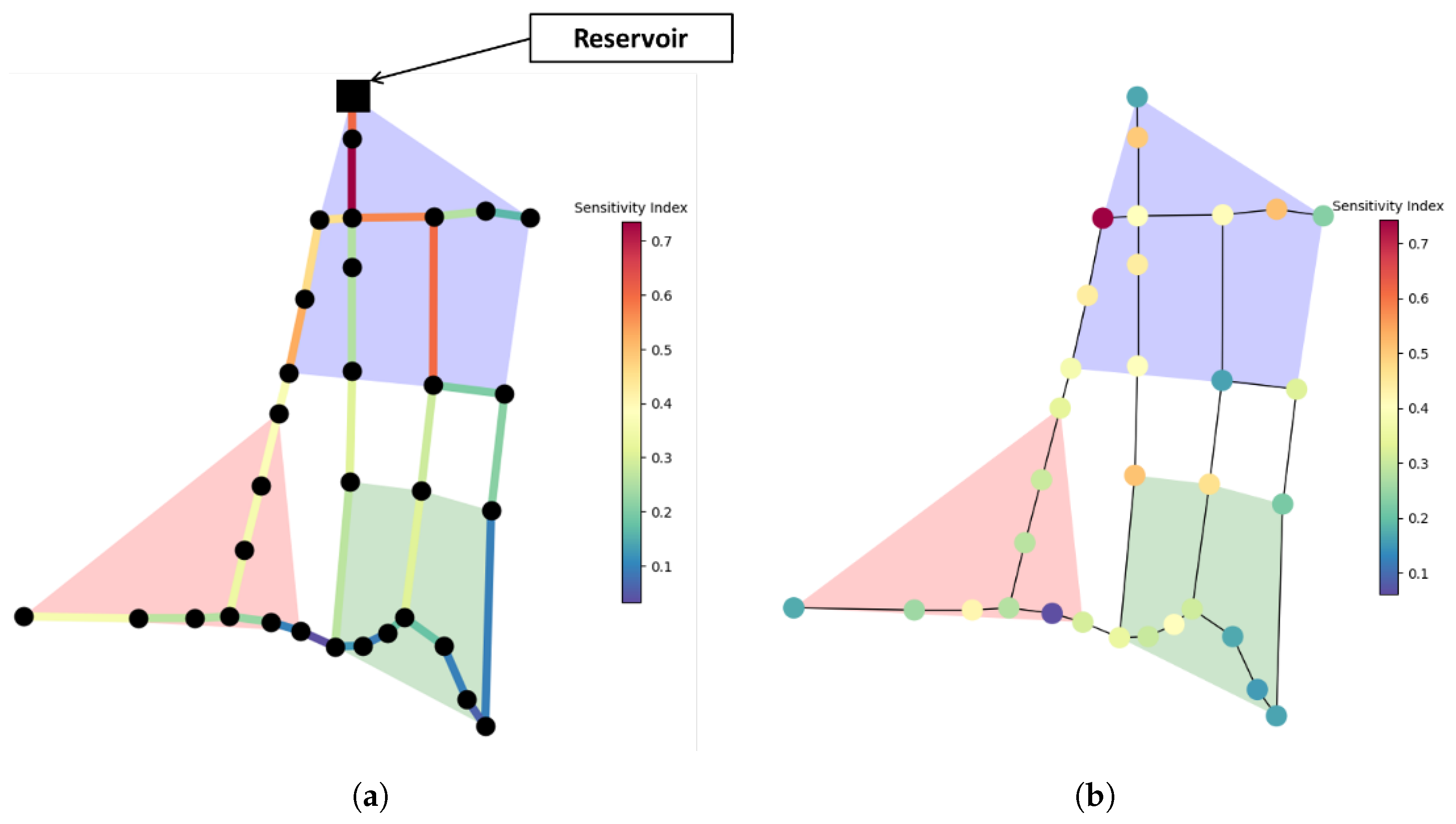
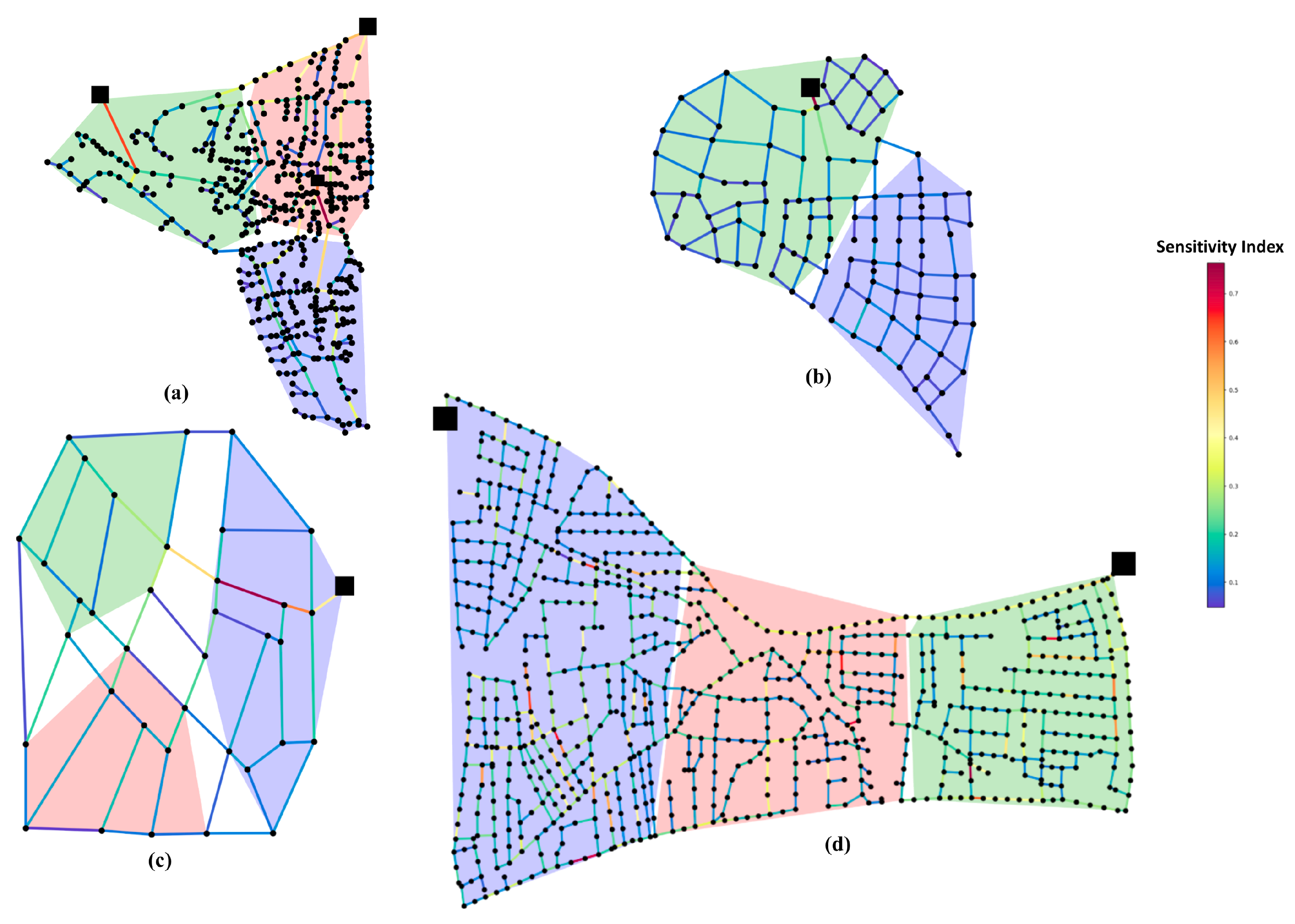
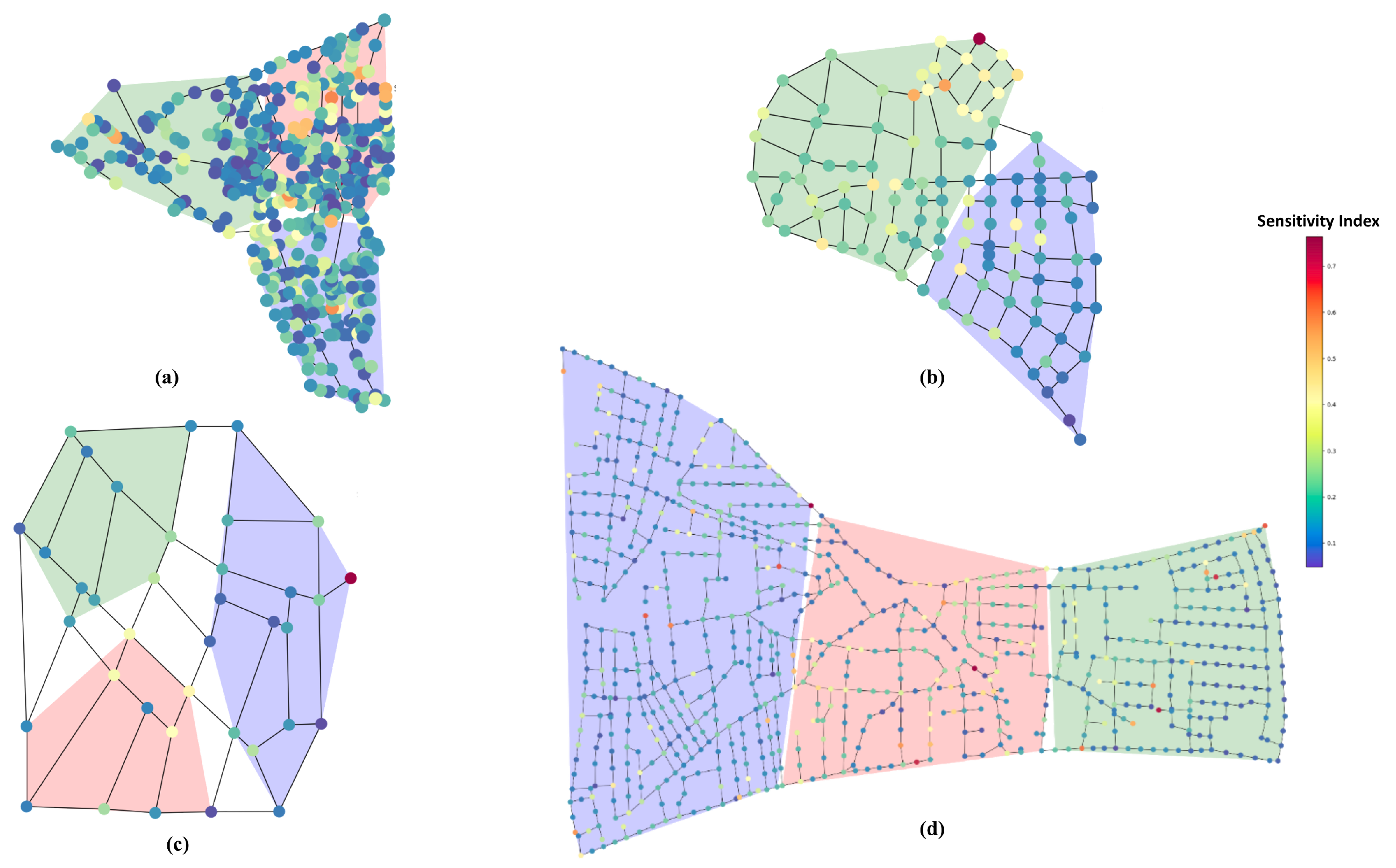
- Zonal Identification Process: At the outset of our analysis, we initiated the process with the Elbow method—a strategic approach to identifying the most suitable number of clusters for our dataset. As shown in Figure 4a, the number 3 emerges as the optimal number of clusters, as indicated by the ’elbow’ in the figure. After determining this, we apply the k-means clustering algorithm, which enables us to effectively partition the dataset into three coherent and distinct zones (green zone, red zone, and blue zone) (see Figure 4b).
- 2.
- Parameters Scaling Procedure: Upon identifying all of the distinct zones within the network, we advance to the pivotal normalization step. This process is essential as it uniformly scales all parameter values to a standard range between 0 and 1.For this illustrative example, let us calculate the normalization value for the first pipe in the network. To achieve this, we will utilize min–max normalization for each parameter.If we denote L, D, F, V, H, Vol, and EB as the actual values for the length, diameter, flow, velocity, headloss, volume, and edge betweenness of the first pipe, and Lmin Lmin, Lmax Lmax, and so on as the minimum and maximum values for these parameters, based on Equation (6), the normalized values for all parameters would be calculated as:Normalized length ;Normalized diameter ;Normalized flow ;Normalized velocity ;Normalized headloss ;Normalized volume ;Normalized edge betweenness .This normalization allows us to compare and analyze these parameters on an equal footing, as they are all rescaled to a uniform range, facilitating further steps such as weighting or sensitivity analysis.
- 3.
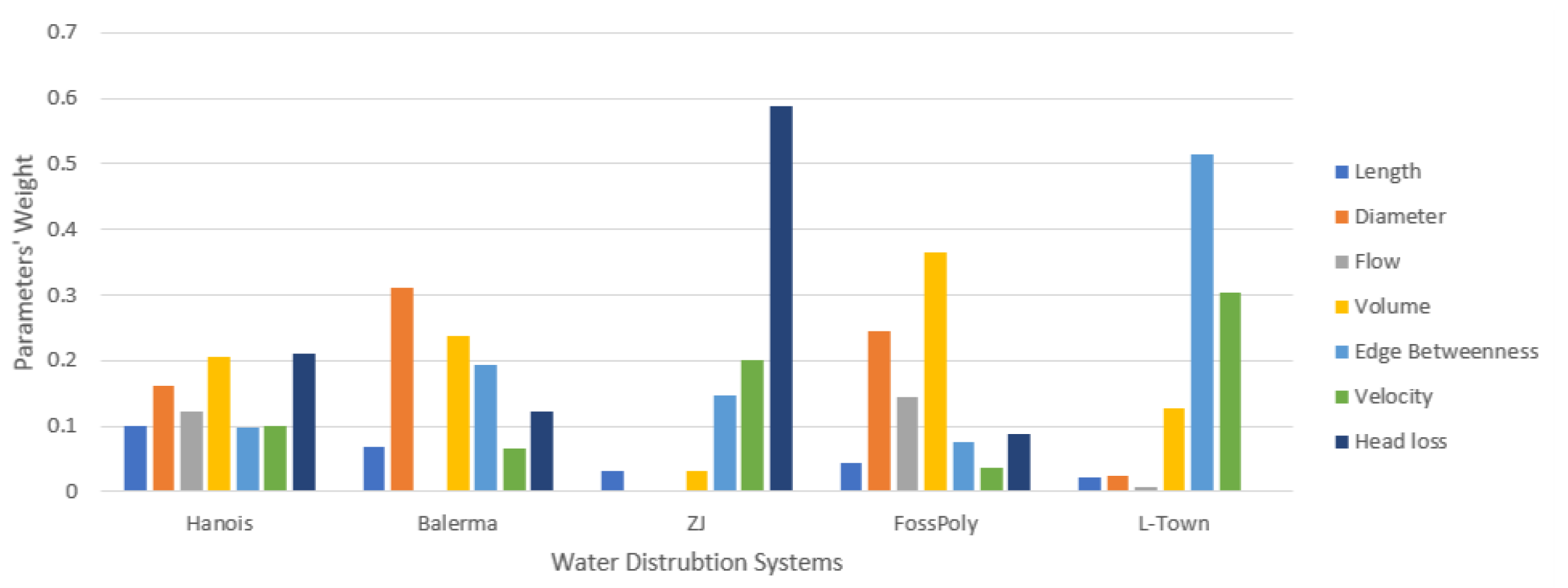
- Assigning Weights to Parameters: Upon establishing the seven critical parameters of the network—length, diameter, flow, velocity, headloss, volume, and edge betweenness—we embark on the task of allocating a distinctive weight to each. This allocation process utilizes the respective entropy values of these parameters as a foundation.To compute the entropy, we first calculate the probability distribution of each unique value within a parameter. For example, for the length parameter, we tally the frequency of each unique length measurement and normalize these frequencies to form a probability distribution:After that we calculate the entropy:where H(X) is the Shannon entropy for the length values, is the probability of each unique length, and N is the number of unique lengths.So, the entropy of each parameter is:Entropy length = 3.284;Entropy diameter = 3.141;Entropy flow = 3.232;Entropy velocity = 3.033;Entropy headloss = 3.295;Entropy volume = 3.287;Entropy edge betweenness = 3.022.After calculating the entropies for each parameter, the next step is to convert these entropy values into weights that can be used in our analysis. Transforming entropies into weights involves normalizing the entropy values to account for the number of unique values each parameter can take. This is performed using the concept of reduced entropy.The formula for reduced entropy () is given by:where E is the entropy of a particular parameter, and N is the count of unique values that the parameter can take.Based on reduced entropy, we calculate the weight of each parameter using this formula:where m is the total number of parameters. The resulting weights are exemplified as:Weight length = 0.101;Weight diameter = 0.161;Weight flow = 0.123;Weight velocity = 0.206;Weight headloss = 0.097;Weight volume = 0.1;Weight edge betweenness = 0.211.
- 4.
- Sensitivity Index Computation: The Sensitivity Index Computation is the culmination of our methodological process where each parameter’s relative importance, as determined by the previously calculated weights, is utilized to quantify the network’s vulnerability to leaks. So, the Sensitivity Index for the first pipe is:Upon performing this calculation, the resultant Sensitivity Index for the first pipe is determined to be 0.59. This quantifies the combined effect of all weighted parameters for that specific pipe, providing a singular, comprehensive metric of its sensitivity.
5. Case Studies
5.1. Dataset
5.2. Results: Sensitivity Index
5.2.1. Pipes’ Sensitivity Index Results
- 1.
- Length: It holds moderate importance in most networks but is least important in L-Town, where the pipe lengths are very close.
- 2.
- Diameter: This parameter is crucial in Balerma due to the variance of pipe diameter, whereas its importance varies in other networks.
- 3.
- Flow: In FossPoly 1 and Hanoi, the flow’s importance is markedly high, suggesting that it is a crucial parameter for the networks’ operation.
- 4.
- Volume: The high importance of volume in FossPoly 1 suggests an emphasis on storage capacity within the network.
- 5.
- Edge Betweenness: The prominence of edge betweenness in L-Town could indicate a focus on network connectivity or the diversity of paths because L-Town is a larger graph.
- 6.
- Velocity: In ZJ, velocity is notably essential, pointing to a prioritization of water delivery speed or system dynamics.
- 7.
- Head Loss: The high importance of head loss in ZJ reflects the network’s susceptibility to pressure drops or its emphasis on energy efficiency.
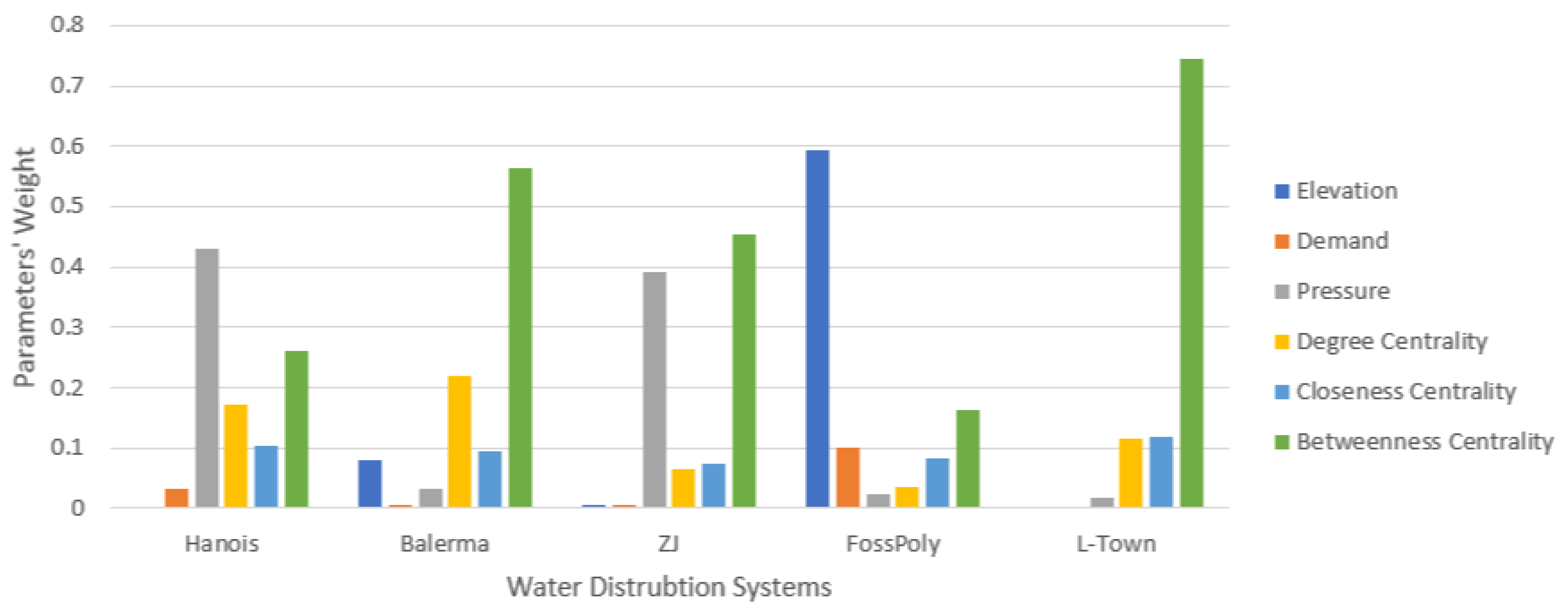
5.2.2. Junctions’ Sensitivity Index Results
- 1.
- Elevation: This parameter seems moderately to highly important in Balerma and FossPoly 1 but less significant in Hanoi, ZJ, and L-Town due to the same values of elevation of the junctions within networks.
- 2.
- Demand: Demand holds varying weights across the networks, being most significant in FossPoly 1 and least in L-Town.
- 3.
- Pressure: Pressure is essential in ZJ and Hanoi, indicating that the networks’ performance is sensitive to pressure variations.
- 4.
- Degree Centrality: Degree centrality has a substantial weight in Balerma, suggesting that the number of immediate connections to a node is a significant factor in this network.
- 5.
- Closeness Centrality: FossPoly 1 WDS presents a higher weight for closeness centrality, implying that the efficiency of water distribution to any given node is a priority for this network.
- 6.
- Betweenness Centrality: Betweenness centrality has an essential weight in all networks, indicating that controlling the flow through nodes that act as bridges within networks is a critical aspect of its design and functionality.
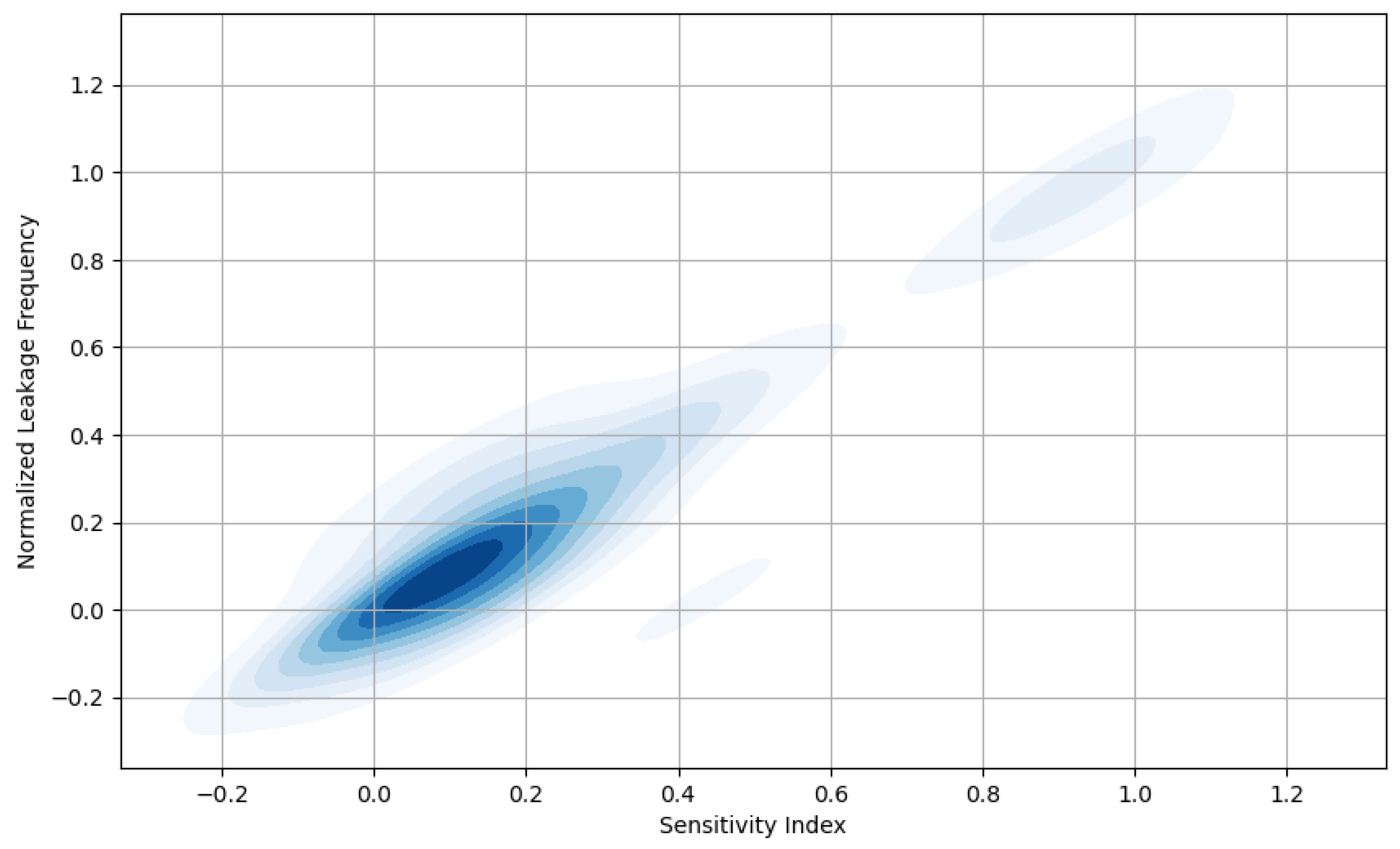
5.3. Validation of Sensitivity Index Using Historical Data from L-Town WDS
6. Practical Implications of Findings
- Targeted Maintenance and Repair: Sensitivity analysis identifies the most vulnerable points in the network where leaks are likely to appear. This enables maintenance and repairs to be targeted, giving priority to zones requiring more immediate attention, thus reducing downtime and maintenance costs [57,58].
- Optimal Sensor Placement: Sensitivity analysis identifies the most critical points in the water distribution network. By understanding where the network is most vulnerable, utilities can strategically place sensors (pressure, acoustic, …) where they are most needed to effectively detect leaks [59].
- Energy and Cost Savings: Detecting and repairing leaks quickly saves both energy and money. Less water loss means less water to treat and distribute, which reduces the water distribution system’s energy footprint and operating costs [62].
- Environmental Benefits: Reducing leakage and improving the efficiency of water systems can reduce their impact on the environment. This includes reducing water wastage, energy consumption, and greenhouse gas emissions associated with water treatment and distribution [63].
7. Summary and Conclusions
- Pipe Characteristics and System Performance:Analysis of pipe networks reveals the nuanced impact of hydraulic parameters on system performance. Pipe length is typically of moderate importance, with uniformity in some systems negating its influence. Larger diameters are pivotal for accommodating high flow volumes at lower velocities, Ismaeel and Zayed, in their paper [65], indicate that the main indicator contributing to the performance of pipes is the diameter of pipe, underscoring his critical role in the overall effectiveness and reliability of the pipe network. In this study, we note that larger diameters often correlate with higher edge betweenness centrality, reflecting their crucial role in network flow. Similarly, pipes characterized by high flow are integral to the network, indicated by their high edge betweenness, and are thus focal points for leak detection efforts to preserve network integrity. Additionally, pipes with substantial volume capacities are essential during peak demand, while excessive velocities may signal critical throughput but risk infrastructure damage and inefficiency. Furthermore, the pronounced head loss could highlight pipes that are long or of a smaller diameter, potentially reducing their edge betweenness if more efficient alternatives are available.
- Node Analysis for Leak Detection:In the context of leak detection, node analysis reveals potential correlations between hydraulic measures and graph theory metrics. A junction’s elevation can affect the hydraulic pressure due to gravitational forces. High-demand nodes are often characterized by greater centrality, requiring connections to multiple pipes for sufficient water supply. Such nodes may also exhibit elevated betweenness centrality, indicating their importance in the distribution network. Conversely, closeness centrality might decrease if a node is strategically positioned near others to meet its high demand efficiently. Nodes experiencing higher pressure are likely to be pivotal in directing flow, reflecting increased degree and betweenness centrality while also demonstrating higher closeness centrality due to their strategic location for effective distribution. These interdependencies between a node’s physical characteristics and network centrality underscore the complex dynamics that shape a water distribution system’s topology. To utilize these insights for leak detection, precise network modeling and comprehensive analysis are essential to determine the exact relationships within a specific system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cook, C.; Bakker, K. Water security: Debating an emerging paradigm. Glob. Environ. Chang. 2012, 22, 94–102. [Google Scholar] [CrossRef]
- Irfeey, A.M.M.; Alotaibi, B.A.; Najim, M.M.M.; Shah, A.A. Water Valuation in Urban Settings for Sustainable Water Management. Water 2023, 15, 3105. [Google Scholar] [CrossRef]
- Rehman, R.; Aslam, M.S.; Jasińska, E.; Javed, M.F.; Goňo, M. Guidelines for the Technical Sustainability Evaluation of the Urban Drinking Water Systems Based on Analytic Hierarchy Process. Resources 2023, 12, 8. [Google Scholar] [CrossRef]
- Al Qahtani, T.; Yaakob, M.S.; Yidris, N.; Sulaiman, S.; Ahmad, K.A. A review on water leakage detection method in the water distribution network. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 68, 152–163. [Google Scholar] [CrossRef]
- Gupta, A.; Kulat, K. A selective literature review on leak management techniques for water distribution system. Water Resour. Manag. 2018, 32, 3247–3269. [Google Scholar] [CrossRef]
- Liemberger, R.; Wyatt, A. Quantifying the global non-revenue water problem. Water Supply 2019, 19, 831–837. [Google Scholar] [CrossRef]
- Kingdom, B.; Liemberger, R.M.P. The Challenge of Reducing Non-Revenue Water (NRW) in Developing Countries-How the Private Sector Can Help: A Look at Performance-Based Service Contracting; World Bank Group: Washington, DC, USA, 2006; Volume 14. [Google Scholar]
- D’Ercole, M.; Righetti, M.; Ugarelli, R.M.; Berardi, L.; Bertola, P. An Integrated Modeling Approach to Optimize the Management of a Water Distribution System: Improving the Sustainability while Dealing with Water Loss, Energy Consumption and Environmental Impacts. Procedia Eng. 2016, 162, 433–440. [Google Scholar] [CrossRef]
- Kofinas, D.; Ulanczyk, R.; Laspidou, C.S. Simulation of a Water Distribution Network with Key Performance Indicators for Spatio-Temporal Analysis and Operation of Highly Stressed Water Infrastructure. Water 2020, 12, 1149. [Google Scholar] [CrossRef]
- Gautam, J.; Chakrabarti, A.; Agarwal, S.; Singh, A.; Gupta, S.; Singh, J. Monitoring and forecasting water consumption and detecting leakage using an IoT system. Water Supply 2020, 20, 1103–1113. [Google Scholar] [CrossRef]
- Torrent, S.G.; Pérez, R. Modelling daily water consumption through potential curves. Disaggregating apparent and real losses. Urban Water J. 2020, 17, 292–302. [Google Scholar] [CrossRef]
- Romero-Ben, L.; Alves, D.; Blesa, J.; Cembrano, G.; Puig, V.; Duviella, E. Leak detection and localization in water distribution networks: Review and perspective. Annu. Rev. Control 2023, 55, 392–419. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Applying Network Theory to Quantify the Redundancy and Structural Robustness of Water Distribution Systems. J. Water Resour. Plan. Manag. 2012, 138, 153–161. [Google Scholar] [CrossRef]
- Venkatraman, Y.; Narayanaa Y, K.; Balas, V.E.; Rad, D. Graph Theory Applications to Comprehend Epidemics Spread of a Disease. Broad Res. Artif. Intell. Neurosci. 2021, 12, 161–177. [Google Scholar] [CrossRef]
- Khan, A.; Uddin, S.; Srinivasan, U. Chronic disease prediction using administrative data and graph theory: The case of type 2 diabetes. Expert Syst. Appl. 2019, 136, 230–241. [Google Scholar] [CrossRef]
- Guze, S. Graph theory approach to the vulnerability of transportation networks. Algorithms 2019, 12, 270. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, Q.; Zhong, T.; Chen, D.; Zhang, N. Variational Graph Neural Networks for Road Traffic Prediction in Intelligent Transportation Systems. IEEE Trans. Ind. Inform. 2021, 17, 2802–2812. [Google Scholar] [CrossRef]
- Vicente, S.; Fuertes-Miquel, O.E.; Coronado-Hernández, D.M.M.; Iglesias-Rey, P.L. Hydraulic modeling during filling and emptying processes in pressurized pipelines: A literature review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- Sun, C.; Parellada, B.; Puig, V.; Cembrano, G. Leak Localization in Water Distribution Networks Using Pressure and Data-Driven Classifier Approach. Water 2020, 12, 54. [Google Scholar] [CrossRef]
- Ostapkowicz, P.; Bratek, A. Detection of Multiple Leaks in Liquid Transmission Pipelines Using Static Flow Model. In Intelligent and Safe Computer Systems in Control and Diagnostics; Kowalczuk, Z., Ed.; Springer: Cham, Switzerland, 2023; pp. 242–253. [Google Scholar] [CrossRef]
- Ulusoy, A.J.; Stoianov, I.; Chazerain, A. Hydraulically informed graph theoretic measure of link criticality for the resilience analysis of water distribution networks. Appl. Netw. Sci. 2018, 3, 31. [Google Scholar] [CrossRef]
- Dunn, S.; Wilkinson, S.M. Identifying Critical Components in Infrastructure Networks Using Network Topology. J. Infrastruct. Syst. 2013, 19, 157–165. [Google Scholar] [CrossRef]
- Agathokleous, A.; Christodoulou, C.; Christodoulou, S.E. Topological robustness and vulnerability assessment of water distribution networks. Water Resour. Manag. 2017, 31, 4007–4021. [Google Scholar] [CrossRef]
- Di Nardo, A.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G.F. Applications of Graph Spectral Techniques to Water Distribution Network Management. Water 2018, 10, 45. [Google Scholar] [CrossRef]
- Giudicianni, C.; Di Nardo, A.; Greco, R.; Scala, A. A community-structure-based method for estimating the fractal dimension, and its application to water networks for the assessment of vulnerability to disasters. Water Resour. Manag. 2021, 35, 1197–1210. [Google Scholar] [CrossRef]
- Dastgir, A.; Hesarkazzazi, S.; Oberascher, M.; Hajibabaei, M.; Sitzenfrei, R. Graph method for critical pipe analysis of branched and looped drainage networks. Water Sci. Technol. 2023, 87, 157–173. [Google Scholar] [CrossRef] [PubMed]
- Cavallaro, L.; Bagdasar, O.; De Meo, P.; Fiumara, G.; Liotta, A. Graph and Network Theory for the Analysis of Criminal Networks. In Data Science and Internet of Things: Research and Applications at the Intersection of DS and IoT; Fortino, G., Liotta, A., Gravina, R., Longheu, A., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 139–156. [Google Scholar] [CrossRef]
- Ficara, A.; Curreri, F.; Cavallaro, L.; De Meo, P.; Fiumara, G.; Bagdasar, O.; Liotta, A. Social network analysis: The use of graph distances to compare artificial and criminal networks. J. Smart Environ. Green Comput. 2021, 1, 14. [Google Scholar] [CrossRef]
- Adraoui, M.; Retbi, A.; Idrissi, M.K.; Bennani, S. Maximal cliques based method for detecting and evaluating learning communities in social networks. Future Gener. Comput. Syst. 2022, 126, 1–14. [Google Scholar] [CrossRef]
- Akachar, E.; Ouhbi, B.; Frikh, B. ACSIMCD: A 2-phase framework for detecting meaningful communities in dynamic social networks. Future Gener. Comput. Syst. 2021, 125, 399–420. [Google Scholar] [CrossRef]
- Ruiz-Frau, A.; Ospina-Alvarez, A.; Villasante, S.; Pita, P.; Maya-Jariego, I.; de Juan, S. Using graph theory and social media data to assess cultural ecosystem services in coastal areas: Method development and application. Ecosyst. Serv. 2020, 45, 101176. [Google Scholar] [CrossRef]
- Şahin, E.; Yüce, H. Prediction of Water Leakage in Pipeline Networks Using Graph Convolutional Network Method. Appl. Sci. 2023, 13, 7427. [Google Scholar] [CrossRef]
- Barros, D.; Almeida, I.; Zanfei, A.; Meirelles, G.; Luvizotto, E.; Brentan, B. An Investigation on the Effect of Leakages on the Water Quality Parameters in Distribution Networks. Water 2023, 15, 324. [Google Scholar] [CrossRef]
- Kim, K.; Koo, J.; Iseley, D.T.; Park, H.; Kim, T.; Hyung, J. Novel Method for Segment Identification in Water Distribution Network through Node-Based Adjacency Matrix. J. Pipeline Syst. Eng. Pract. 2023, 14, 04023030. [Google Scholar] [CrossRef]
- Tzatchkov, V.G.; Alcocer-Yamanaka, V.H.; Ortíz, V.B. Graph Theory Based Algorithms for Water Distribution Network Sectorization Projects. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–15. [Google Scholar] [CrossRef]
- Tzatchkov, V.G.; Alcocer-Yamanaka, V.H. Graph theory based single and multiple source water distribution network partitioning. Tecnol. y Cienc. Agua 2019, 10, 197–221. [Google Scholar] [CrossRef]
- Shekofteh, M.; Jalili Ghazizadeh, M.; Yazdi, J. A methodology for leak detection in water distribution networks using graph theory and artificial neural network. Urban Water J. 2020, 17, 525–533. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di Nardo, A.; Oliva, G.; Scala, A. The faster the better: On the shortest paths role for near real-time decision making of water utilities. Reliab. Eng. Syst. Saf. 2021, 212, 107589. [Google Scholar] [CrossRef]
- Dzuwa, C.; Nkhonjera, G.; Musonda, I.; Onososen, A. Identifying Risky Zones in Water Distribution Networks Using Node Burst Indices. In Proceedings of the International Conference on Computing in Civil and Building Engineering, Cape Town, South Africa, 26–28 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 273–285. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Giudicianni, C.; Di Nardo, A.; Di Natale, M.; Greco, R.; Santonastaso, G.F.; Scala, A. Topological Taxonomy of Water Distribution Networks. Water 2018, 10, 444. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Chen, J.; Feng, X.; Xiao, S. An iterative method for leakage zone identification in water distribution networks based on machine learning. Struct. Health Monit. 2021, 20, 1938–1956. [Google Scholar] [CrossRef]
- Eesa, A.S.; Arabo, W.K. A Normalization Methods for Backpropagation: A Comparative Study. Sci. J. Univ. Zakho 2017, 5, 319–323. [Google Scholar] [CrossRef]
- Raju, V.N.G.; Lakshmi, K.P.; Jain, V.M.; Kalidindi, A.; Padma, V. Study the Influence of Normalization/Transformation process on the Accuracy of Supervised Classification. In Proceedings of the 2020 Third International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20–22 August 2020; pp. 729–735. [Google Scholar] [CrossRef]
- Jayalakshmi, T.; Santhakumaran, A. Statistical normalization and back propagation for classification. Int. J. Comput. Theory Eng. 2011, 3, 1793–8201. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Yurong, Q.; Jeon, G. Weight assignment using entropy. Int. J. Multimed. Ubiquitous Eng. 2016, 11, 353–362. [Google Scholar] [CrossRef]
- Jin, Y.; Yumei, W.; Ping, L. Approximate entropy-based leak detection using artificial neural network in water distribution pipelines. In Proceedings of the 2010 11th International Conference on Control Automation Robotics & Vision, Singapore, 7–10 December 2010; pp. 1029–1034. [Google Scholar] [CrossRef]
- Cui, H.; Sivakumar, B.; Singh, V.P. Entropy Applications in Environmental and Water Engineering. Entropy 2018, 20, 598. [Google Scholar] [CrossRef]
- Fujiwara, O.; Khang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Reca, J.; Martínez, J. Genetic algorithms for the design of looped irrigation water distribution networks. Water Resour. Res. 2006, 42, W05416. [Google Scholar] [CrossRef]
- Zheng, F.; Simpson, A.R.; Zecchin, A.C. A combined NLP-differential evolution algorithm approach for the optimization of looped water distribution systems. Water Resour. Res. 2011, 47, W08531. [Google Scholar] [CrossRef]
- Bragalli, C.; D’Ambrosio, C.; Lee, J.; Lodi, A.; Toth, P. On the optimal design of water distribution networks: A practical MINLP approach. Optim. Eng. 2012, 13, 219–246. [Google Scholar] [CrossRef]
- Vrachimis, S.; Eliades, D.; Taormina, R.; Ostfeld, A.; Kapelan, Z.; Liu, S.; Kyriakou, M.; Pavlou, P.; Qiu, M.; Polycarpou, M. Dataset of BattLeDIM: Battle of the leakage detection and isolation methods. In Proceedings of the 2nd Int CCWI/WDSA Joint Conference, Valencia, Spain, 18–22 July 2022; Queen’s Univ.: Kingston, ON, Canada, 2020. [Google Scholar] [CrossRef]
- Jung, D.; Yoo, D.G.; Kang, D.; Kim, J.H. Linear Model for Estimating Water Distribution System Reliability. J. Water Resour. Plan. Manag. 2016, 142, 04016022. [Google Scholar] [CrossRef]
- Righetti, M.; Bort, C.M.G.; Bottazzi, M.; Menapace, A.; Zanfei, A. Optimal Selection and Monitoring of Nodes Aimed at Supporting Leakages Identification in WDS. Water 2019, 11, 629. [Google Scholar] [CrossRef]
- Nault, J.; Papa, F. Lifecycle Assessment of a Water Distribution System Pump. J. Water Resour. Plan. Manag. 2015, 141, A4015004. [Google Scholar] [CrossRef]
- Naserizade, S.S.; Nikoo, M.R.; Montaseri, H. A risk-based multi-objective model for optimal placement of sensors in water distribution system. J. Hydrol. 2018, 557, 147–159. [Google Scholar] [CrossRef]
- Fu, G.; Kapelan, Z.; Reed, P. Reducing the Complexity of Multiobjective Water Distribution System Optimization through Global Sensitivity Analysis. J. Water Resour. Plan. Manag. 2012, 138, 196–207. [Google Scholar] [CrossRef]
- Racoviceanu, A.I.; Karney, B.W. Life-Cycle Perspective on Residential Water Conservation Strategies. J. Infrastruct. Syst. 2010, 16, 40–49. [Google Scholar] [CrossRef]
- Wang, M.; Barkdoll, B.D. A sensitivity analysis method for water distribution system tank siting for energy savings. Urban Water J. 2017, 14, 713–719. [Google Scholar] [CrossRef]
- Herstein, L.M.; Filion, Y.R.; Hall, K.R. Evaluating Environmental Impact in Water Distribution System Design. J. Infrastruct. Syst. 2009, 15, 241–250. [Google Scholar] [CrossRef]
- Hutton, C.J.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.; Savić, D.A. Dealing with Uncertainty in Water Distribution System Models: A Framework for Real-Time Modeling and Data Assimilation. J. Water Resour. Plan. Manag. 2014, 140, 169–183. [Google Scholar] [CrossRef]
- Ismaeel, M.; Zayed, T. Integrated Performance Assessment Model for Water Networks. J. Infrastruct. Syst. 2018, 24, 04018005. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adraoui, M.; Diop, E.B.; Ebnou Abdem, S.A.; Azmi, R.; Chenal, J. Towards an Understanding of Hydraulic Sensitivity: Graph Theory Contributions to Water Distribution Analysis. Water 2024, 16, 646. https://doi.org/10.3390/w16050646
Adraoui M, Diop EB, Ebnou Abdem SA, Azmi R, Chenal J. Towards an Understanding of Hydraulic Sensitivity: Graph Theory Contributions to Water Distribution Analysis. Water. 2024; 16(5):646. https://doi.org/10.3390/w16050646
Chicago/Turabian StyleAdraoui, Meriem, El Bachir Diop, Seyid Abdellahi Ebnou Abdem, Rida Azmi, and Jérôme Chenal. 2024. "Towards an Understanding of Hydraulic Sensitivity: Graph Theory Contributions to Water Distribution Analysis" Water 16, no. 5: 646. https://doi.org/10.3390/w16050646
APA StyleAdraoui, M., Diop, E. B., Ebnou Abdem, S. A., Azmi, R., & Chenal, J. (2024). Towards an Understanding of Hydraulic Sensitivity: Graph Theory Contributions to Water Distribution Analysis. Water, 16(5), 646. https://doi.org/10.3390/w16050646







