A Framework for Quantifying Reach-Scale Hydraulic Roughness in Mountain Headwater Streams
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Dye Trace Method
2.3. Determining Hydraulic Parameters from Field Measurements
2.4. Hydraulic Geometry Relation
3. Results
3.1. Reach-Average Hydraulic Roughness
3.2. Flow Discharge and Its Relation to Velocity
3.3. Relation between Flow Velocity and Hydraulic Roughness
4. Discussion
4.1. Comparison of Point Velocity and Reach-Average Velocity
4.2. Use of Dye Tracer
4.3. Quantifying Hydraulic Roughness
4.4. Limitations of the Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nitsche, M.; Rickenmann, D.; Kirchner, J.W.; Turowski, J.; Badoux, A. Macroroughness and variations in reach-averaged flow resistance in steep mountain streams. Water Resour. Res. 2012, 48, W12518. [Google Scholar] [CrossRef]
- Rickenmann, D. Methods for the Quantitative Assessment of Channel Processes in Torrents (Steep Streams); CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Holland, F.; Bragg, R. Fluid Flow for Chemical Engineers; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Richardson, M.E. Refinement of Tracer Dilution Methods for Discharge Measurements in Steep Mountain Streams. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2015. [Google Scholar]
- Aberle, J.; Smart, G. The influence of roughness structure on flow resistance on steep slopes. J. Hydraul. Res. 2003, 41, 259–269. [Google Scholar] [CrossRef]
- Waldon, M.G. Estimation of average stream velocity. J. Hydraul. Eng. 2004, 130, 1119–1122. [Google Scholar] [CrossRef]
- Wilson, J.; Cobb, E.; Kilpatrick, F. Fluorometric Procedures for Dye Tracing; Department of the Interior, US Geological Survey: Denver, CO, USA, 1986; Volume 31.
- Moore, R. Slug injection using salt in solution. Streamline Watershed Manag. Bull. 2005, 8, 1–6. [Google Scholar]
- Kilpatrick, F.A.; Wilson, J.F. Measurement of Time of Travel in Streams by Dye Tracing; US Government Printing Office: Washington, DC, USA, 1989; Volume 3. [Google Scholar]
- Thome, C.R.; Zevenbergen, L.W. Estimating mean velocity in mountain rivers. J. Hydraul. Eng. 1985, 111, 612–624. [Google Scholar] [CrossRef]
- de Lange, S.I.; Naqshband, S.; Hoitink, A. Quantifying hydraulic roughness from field data: Can dune morphology tell the whole story? Water Resour. Res. 2021, 57, e2021WR030329. [Google Scholar] [CrossRef]
- Bathurst, J. Flow resistance estimation in mountain rivers. J. Hydraul. Eng. 1985, 111, 625–643. [Google Scholar] [CrossRef]
- Zimmermann, A. Flow resistance in steep streams: An experimental study. Water Resour. Res. 2010, 46, W09536. [Google Scholar] [CrossRef]
- Warmink, J.J.; Booij, M.J.; Van der Klis, H.; Hulscher, S.J. Quantification of uncertainty in design water levels due to uncertain bed form roughness in the Dutch river Waal. Hydrol. Process. 2013, 27, 1646–1663. [Google Scholar] [CrossRef]
- Ferguson, R. Flow resistance equations for gravel- and boulder-bed streams. Water Resour. Res. 2007, 43, W05427. [Google Scholar] [CrossRef]
- Rickenmann, D.; Recking, A. Evaluation of flow resistance in gravel-bed rivers through a large field data set. Water Resour. Res. 2011, 47, W07538. [Google Scholar] [CrossRef]
- Lee, A.J.; Ferguson, R.I. Velocity and flow resistance in step-pool streams. Geomorphology 2002, 46, 59–71. [Google Scholar] [CrossRef]
- National Institute of Forest Science. Current Status of Nationwide Forest Watershed Test Sites; National Institute of Forest Science: Seoul, Republic of Korea, 2022; pp. 60–101. [Google Scholar]
- Yochum, S.E. Flow Resistance Prediction in High-Gradient Streams; Colorado State University: Fort Collins, CO, USA, 2010. [Google Scholar]
- David, G.; Wohl, E.; Yochum, S. Relationship of Bed and Bank Resistance to Total Flow Resistance in a High Gradient Stream, Fraser Experimental Forest, Colorado, USA; AGU Fall Meeting Abstracts: San Francisco, CA, USA, 2010. [Google Scholar]
- Buffington, J.M.; Montgomery, D.R. Effects of hydraulic roughness on surface textures of gravel-bed rivers. Water Resour. Res. 1999, 35, 3507–3521. [Google Scholar] [CrossRef]
- Schneider, J.M.; Rickenmann, D.; Turowski, J.M.; Kirchner, J.W. Self-adjustment of stream bed roughness and flow velocity in a steep mountain channel. Water Resour. Res. 2015, 51, 7838–7859. [Google Scholar] [CrossRef]
- Moran, G.W. Locally-Weighted-Regression Scatter-Plot Smoothing (LOWESS): A Graphical Exploratory Data Analysis Technique. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, September 1984. [Google Scholar]
- Wolman, M.G. A method of sampling coarse river-bed material. EOS Trans. Am. Geophys. Union 1954, 35, 951–956. [Google Scholar]
- Rice, S.; Church, M. Sampling surficial fluvial gravels; the precision of size distribution percentile sediments. J. Sediment. Res. 1996, 66, 654–665. [Google Scholar] [CrossRef]
- Rickenmann, D. Bedload Transport Capacity of Slurry Flows at Steep Slopes; Swiss Federal Institute of Technology Zürich: Zürich, Switzerland, 1990. [Google Scholar]
- Comiti, F.; Mao, L.; Wilcox, A.; Wohl, E.E.; Lenzi, M.A. Field-derived relationships for flow velocity and resistance in high-gradient streams. J. Hydrol. 2007, 340, 48–62. [Google Scholar] [CrossRef]
- Sappa, G.; Ferranti, F.; Pecchia, G. Validation of salt dilution method for discharge measurements in the upper valley of aniene river (central italy). In Proceedings of the 13th International Conference on Environment, Ecosystem and Development, Athens, Greece, 29 June–2 July 2015. [Google Scholar]
- Stewardson, M. Hydraulic geometry of stream reaches. J. Hydrol. 2005, 306, 97–111. [Google Scholar] [CrossRef]
- Yang, H.; Lee, S.-J.; Im, S. Hydraulic Relation of Discharge and Velocity in Small, Steep Mountain Streams Using the Salt-dilution Method. J. Korean Soc. For. Sci. 2018, 107, 158–165. [Google Scholar]
- Tazioli, A. Experimental methods for river discharge measurements: Comparison among tracers and current meter. Hydrol. Sci. J. 2011, 56, 1314–1324. [Google Scholar] [CrossRef]
- Bencala, K.E.; Rathbun, R.E.; Jackman, A.P.; Kennedy, V.C.; Zellweger, G.W.; Avanzino, R.J. Rhodamine WT dye losses in a mountain stream environment. J. Am. Water Resour. Assoc. 1983, 19, 943–950. [Google Scholar] [CrossRef]
- McDermott, M.; Rife, J. Mitigating shallows in LIDAR scan matching using spherical voxels. IEEE Robot. Autom. Lett. 2022, 7, 12363–12370. [Google Scholar] [CrossRef]
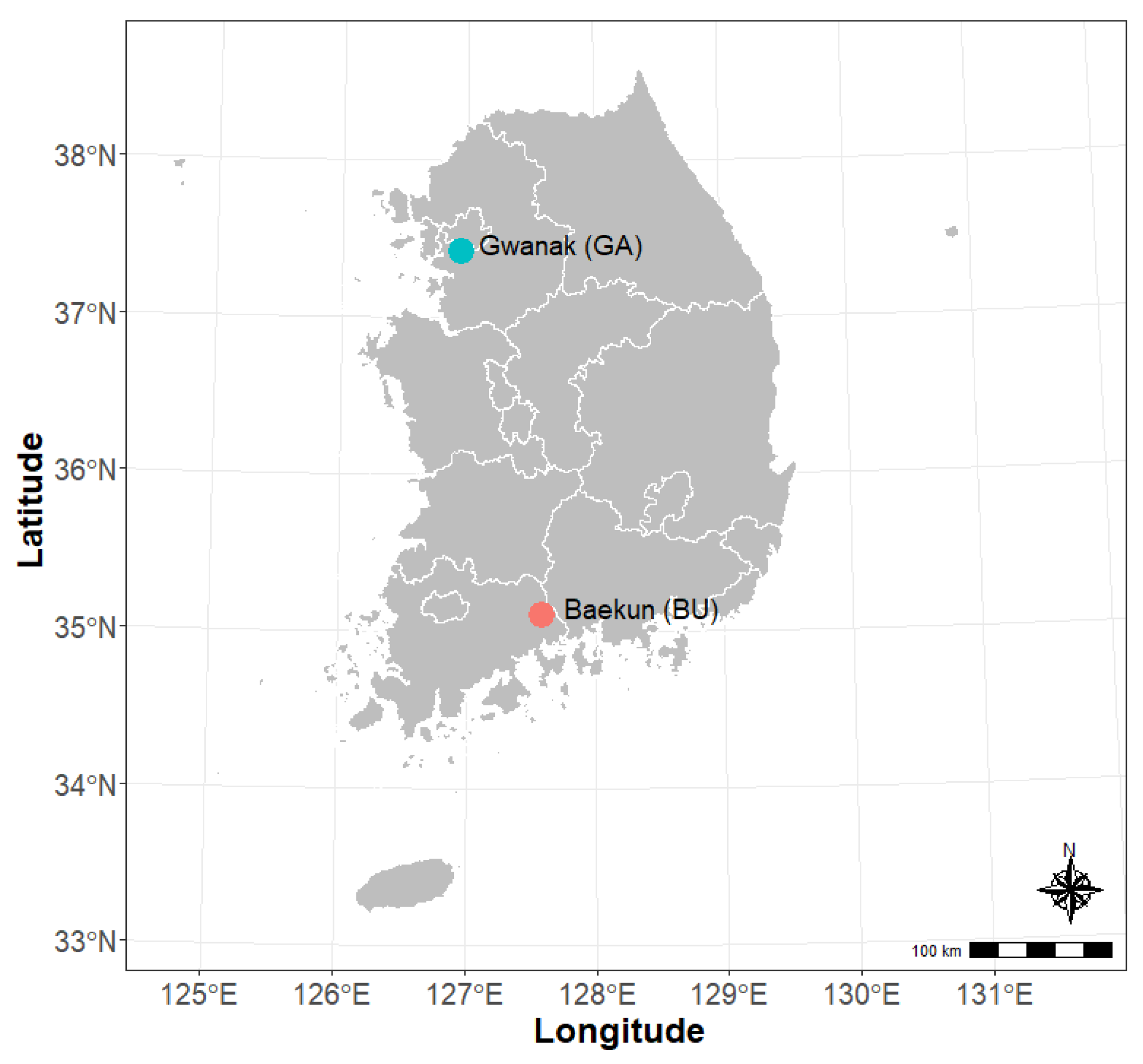


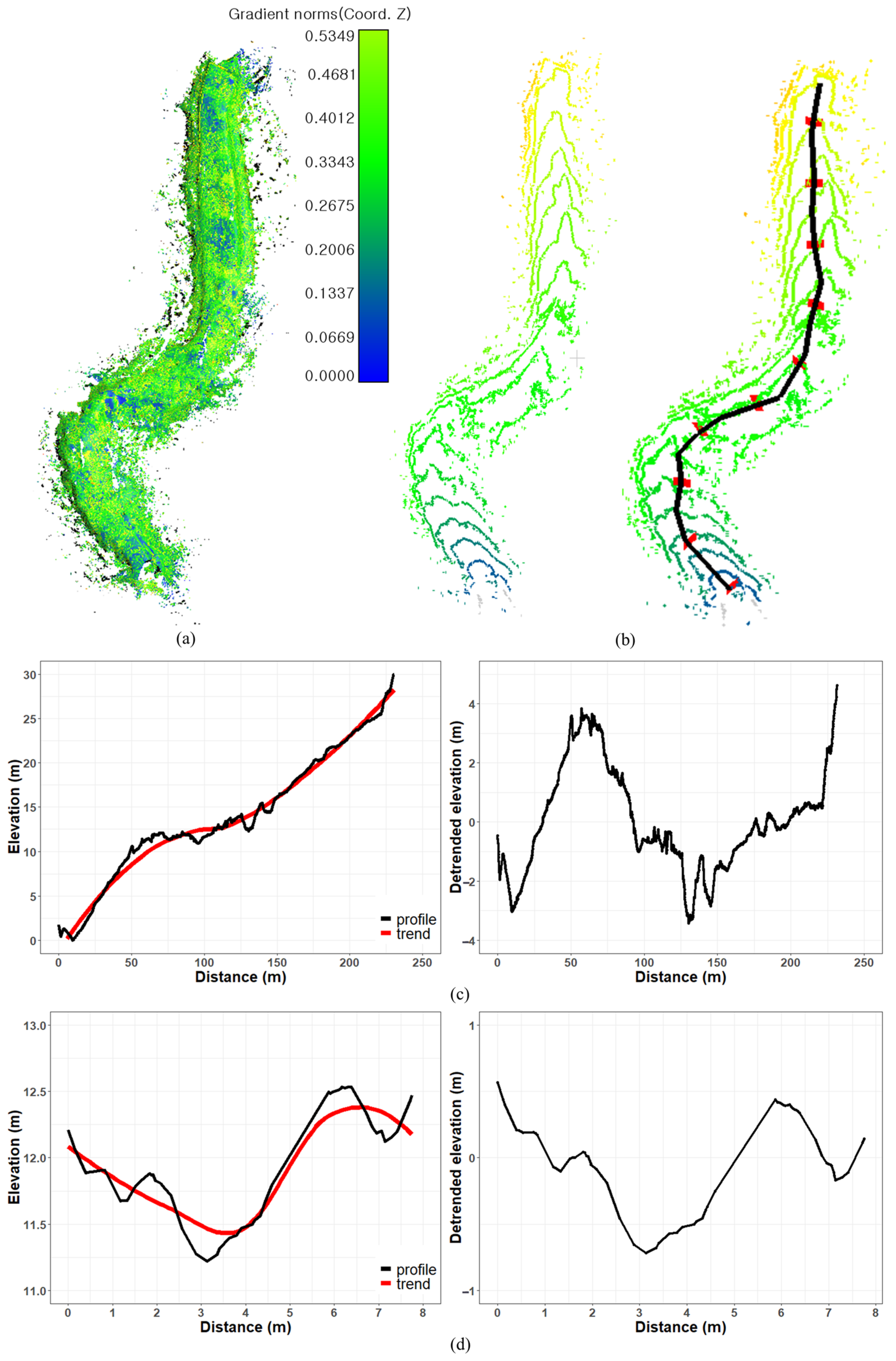

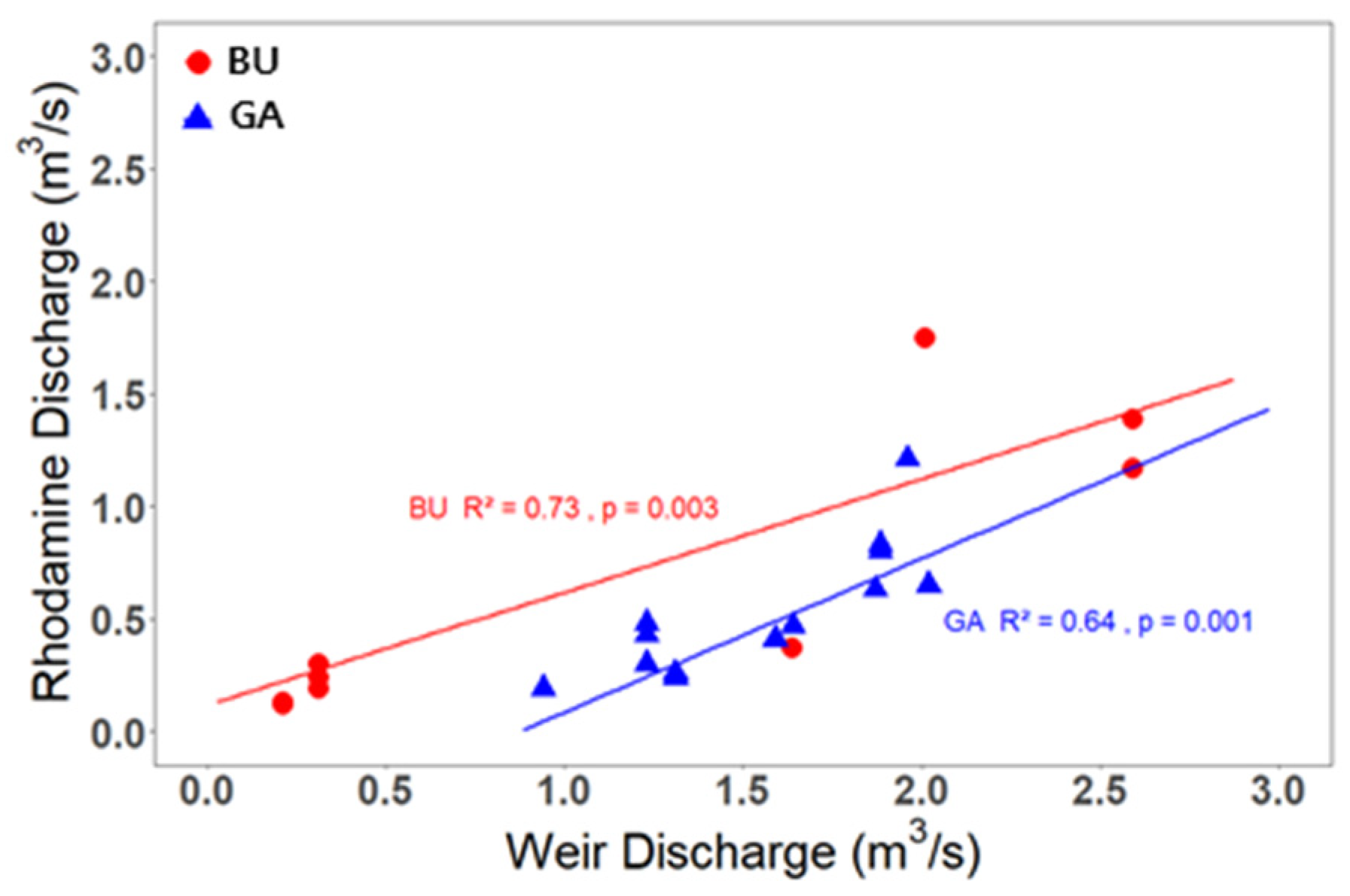
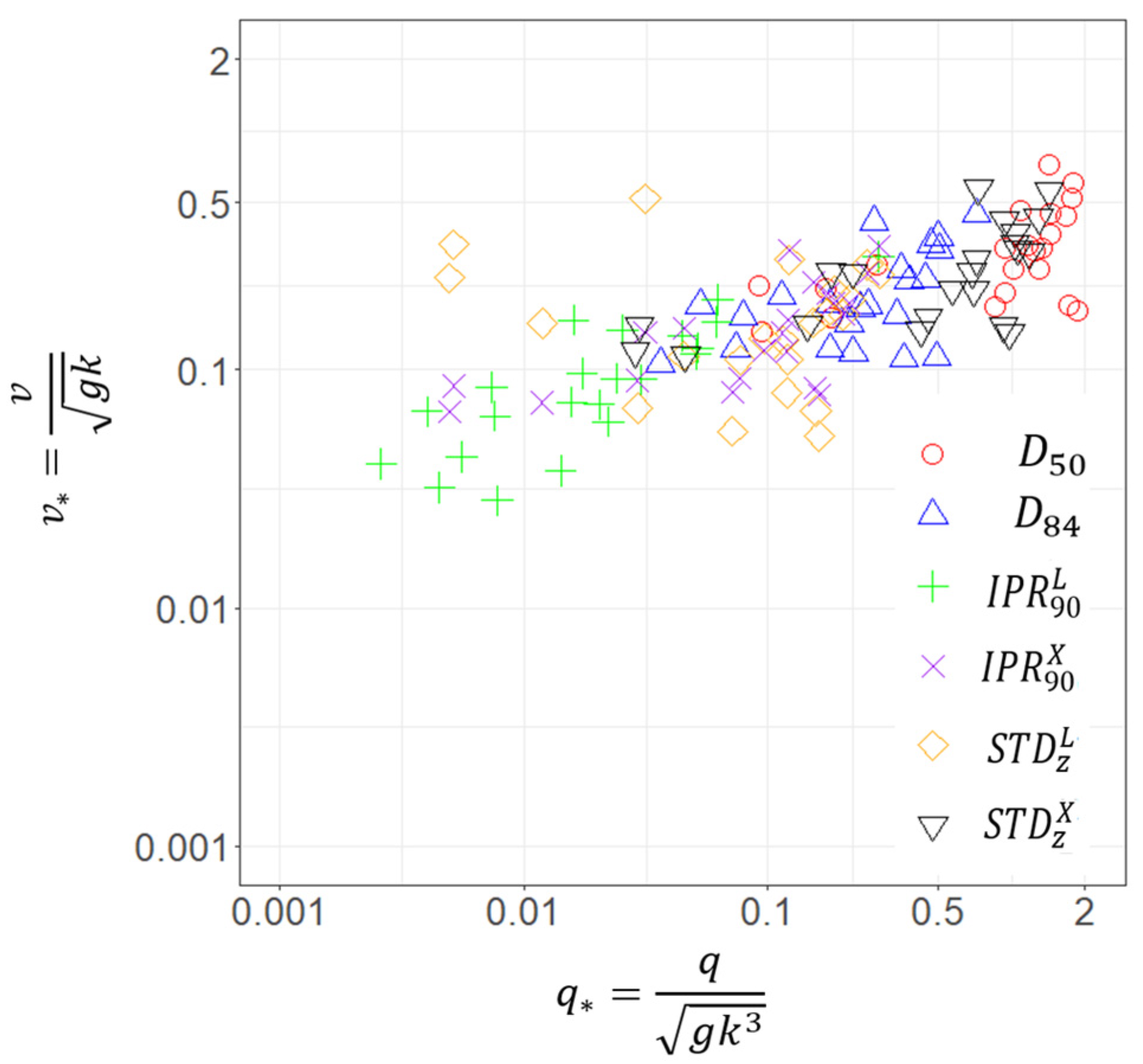
| Location | Coordinates (°) | Average Slope (%) | Morphology | Basin Area (ha) |
|---|---|---|---|---|
| Gwanak | 37°26′–28′ N 126°55′–58′ E | 6 | Cascade | 266.7 |
| Baekun | 35°01′–20′ N 127°30′–34′ E | 11 | Cascade | 284.7 |
| Site | (m/s) | (m3/s) | (m) | Slope (m/m) | (m) | (m) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| GA1 | 0.57 | 2.02 | 102.2 | 0.04 | 0.17 | 0.48 | 3.59 | 1.12 | 0.77 | 0.23 |
| GA2 | 0.96 | 1.87 | 84.4 | 0.05 | 0.18 | 0.54 | 3.59 | 1.12 | 0.92 | 0.28 |
| GA3 | 0.43 | 1.76 | 82.6 | 0.03 | 0.18 | 0.54 | 3.49 | 1.06 | 0.92 | 0.28 |
| GA4 | 0.23 | 0.94 | 113.2 | 0.07 | 0.16 | 0.39 | 5.29 | 1.78. | 0.84 | 0.26 |
| GA5 | 0.46 | 1.59 | 113.2 | 0.07 | 0.16 | 0.39 | 5.29 | 1.78 | 0.84 | 0.26 |
| GA6 | 0.66 | 1.96 | 164.8 | 0.05 | 0.16 | 0.39 | 6.20 | 1.79 | 0.82 | 0.25 |
| GA7 | 0.42 | 1.64 | 42.2 | 0.07 | 0.18 | 0.54 | 2.15 | 0.62 | 0.60 | 0.19 |
| GA8 | 0.43 | 1.23 | 32 | 0.04 | 0.18 | 0.54 | 1.24 | 0.42 | 0.53 | 0.17 |
| GA9 | 0.34 | 1.23 | 51.8 | 0.06 | 0.17 | 0.48 | 2.32 | 0.65 | 0.82 | 0.25 |
| GA10 | 0.28 | 1.23 | 30.4 | 0.02 | 0.18 | 0.54 | 2.19 | 0.67 | 0.95 | 0.29 |
| GA11 | 0.33 | 1.76 | 176.9 | 0.04 | 0.16 | 0.39 | 6.04 | 1.74 | 0.78 | 0.24 |
| GA12 | 0.24 | 1.31 | 90.5 | 0.02 | 0.17 | 0.48 | 4.16 | 1.30 | 0.84 | 0.26 |
| GA13 | 0.22 | 1.31 | 163.9 | 0.04 | 0.16 | 0.39 | 6.22 | 1.79 | 0.82 | 0.25 |
| BU1 | 0.63 | 2.01 | 51.2 | 0.20 | 0.20 | 0.40 | 1.63 | 0.54 | 0.63 | 0.21 |
| BU2 | 0.48 | 1.76 | 60.4 | 0.15 | 0.21 | 0.40 | 1.70 | 0.60 | 0.65 | 0.22 |
| BU3 | 0.22 | 0.21 | 72.1 | 0.10 | 0.18 | 0.33 | 3.07 | 1.05 | 0.61 | 0.21 |
| BU4 | 0.24 | 0.21 | 34.6 | 0.05 | 0.28 | 0.53 | 0.70 | 0.24 | 1.11 | 0.45 |
| BU5 | 0.37 | 0.31 | 72.1 | 0.10 | 0.18 | 0.33 | 3.07 | 1.05 | 0.61 | 0.21 |
| BU6 | 0.34 | 0.31 | 37.5 | 0.15 | 0.25 | 0.42 | 0.61 | 0.20 | 2.67 | 0.83 |
| BU7 | 0.43 | 0.31 | 30.6 | 0.15 | 0.38 | 0.55 | 0.49 | 0.17 | 2.60 | 0.81 |
| BU8 | 0.81 | 2.59 | 72.1 | 0.10 | 0.18 | 0.33 | 3.07 | 1.05 | 0.61 | 0.21 |
| BU9 | 0.73 | 2.59 | 37.5 | 0.15 | 0.25 | 0.42 | 0.61 | 0.20 | 2.67 | 0.83 |
| Roughness Variable | Hydraulic Geometry Relation | Measured–Estimated Velocity | |
|---|---|---|---|
| RMSE (m/s) | |||
| 0.68 | 0.07 | ||
| 0.66 | 0.22 | ||
| 0.42 | 0.07 | ||
| 0.42 | 0.53 | ||
| 0.31 | 0.91 | ||
| 0.28 | 0.16 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.-H.; Lee, J.; Kim, T.; Choi, H.T.; Im, S. A Framework for Quantifying Reach-Scale Hydraulic Roughness in Mountain Headwater Streams. Water 2024, 16, 647. https://doi.org/10.3390/w16050647
Kim T-H, Lee J, Kim T, Choi HT, Im S. A Framework for Quantifying Reach-Scale Hydraulic Roughness in Mountain Headwater Streams. Water. 2024; 16(5):647. https://doi.org/10.3390/w16050647
Chicago/Turabian StyleKim, Tae-Hyun, Jeman Lee, Taehyun Kim, Hyung Tae Choi, and Sangjun Im. 2024. "A Framework for Quantifying Reach-Scale Hydraulic Roughness in Mountain Headwater Streams" Water 16, no. 5: 647. https://doi.org/10.3390/w16050647
APA StyleKim, T.-H., Lee, J., Kim, T., Choi, H. T., & Im, S. (2024). A Framework for Quantifying Reach-Scale Hydraulic Roughness in Mountain Headwater Streams. Water, 16(5), 647. https://doi.org/10.3390/w16050647









