Next Article in Journal
Rainfall–Mining Coupling Effects on Slope Failure Mechanism and Evolution Process: A Case Study of Open-Pit to Underground Mining
Previous Article in Journal
Research Trends and Future Prospects of Constructed Wetland Treatment Technology in China
Previous Article in Special Issue
Groundwater Hydraulics in Increased Spring Discharge following Earthquakes: Some Applications and Considerations
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 16
Issue 5
10.3390/w16050739
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Cross-Correlation among Seismic Events, Rainfalls, and Carbon Dioxide Anomalies in Spring Water: Insights from Geochemical Monitoring in Northern Tuscany, Italy

by
Lisa Pierotti
1,
Cristiano Fidani
2,3,*,
Gianluca Facca
1 and
Fabrizio Gherardi
1
1
Istituto di Geoscienze e Georisorse CNR, 56124 Pisa, Italy
2
Istituto Nazionale di Geofisica e Vulcanologia, 00143 Roma, Italy
3
Central Italy Electromagnetic Network, 63020 Fermo, Italy
*
Author to whom correspondence should be addressed.
Water 2024, 16(5), 739; https://doi.org/10.3390/w16050739
Submission received: 27 November 2023 / Revised: 22 February 2024 / Accepted: 24 February 2024 / Published: 29 February 2024
(This article belongs to the Special Issue How Earthquakes Affect Groundwater)
Browse Figures
Versions Notes

Abstract

:
Variations in the CO2 dissolved in water springs have long been observed near the epicenters of moderate and strong earthquakes. In a recent work focused on data collected during the 2017–2021 period from a monitoring site in the Northern Apennines, Italy, we noticed a significant correlation between CO2 anomalies and moderate-to-weak seismic activity. Here, we extended this analysis by focusing on data collected from the same site during a different period (2010–2013) and by integrating the CENSUS method with an artificial neural network (ANN) in the already-tested protocol. As in our previous work, a fit of the computed residual CO2 distributions allowed us to evidence statistically relevant CO2 anomalies. Thus, we extended a test of the linear dependence of these anomalies to seismic events over a longer period by means of binary correlations. This new analysis also included strong seismic events. Depending on the method applied, we observed different time lags. Specifically, using the CENSUS methodology, we detected a CO2 anomaly one day ahead of the earthquake and another anomaly eleven days ahead. However, no anomaly was observed with the ANN methodology. We also investigated possible correlations between CO2 concentrations and rain events and between rain events and earthquakes, highlighting the occurrence of a CO2 anomaly one day after a rain event of at least 10 mm and no linear dependence of seismic and rain events. Similar to our previous work, we achieved a probability gain of around 4, which is the probably of earthquake increases after CO2 anomaly observations.

1. Introduction

The first observations of high concentrations of CO2 in soil gas in correspondence with faults and major fractures were made in the Caucasus [1], and one of the earliest examples of the long-time monitoring of escaping gas during the occurrence of earthquakes was carried out in southern Dagestan [2]. The possible link between earthquake occurrence and gas release at the surface had been considered in relation to strong seismic events [3,4]. Water springs with elevated levels of dissolved CO2 have been observed worldwide around seismic zones [5], and the presence of high concentrations of CO2 of predominantly mantellic and/or metamorphic origins has been considered a major factor controlling pore pressure in fractures. Moreover, carbon dioxide degassing has been a recurrent, observed phenomenon in many active tectonic regions [6,7]. Several observations of CO2 and H2 emanations nearby faults can prove to be a powerful means of identifying the state of the activity of those same faults [8]. Therefore, models based on the dilatancy phenomenon have been proposed to relate CO2 and other gaseous emissions to earthquakes [9]. A close interplay between local magmatism and fluid release at the surface has been hypothesized also in Iceland [10], and the link there was explained by advancing a ‘‘dual-mechanism model’’. This model considers the reciprocal influence among fluids ascending from below the brittle crust and plate motion building strain [11]. During earthquakes, deep-seated fluids migrate upward through faults, resulting in micro-earthquakes.
CO2 excesses have also been observed in extensional domains [12]. The coincidence of CO2 emissions in highly seismic regions has been confirmed on occasion of major events [13,14], in many aftershock evolutions [15,16,17,18,19,20], as well as with small seismic events [21]. The release of deep-seated CO2 may occur by diffuse venting/soil degassing or concentrated flow through lakes, vents, and hot and cold springs [22]. The amount of gaseous carbon escaping into the atmosphere is under quantification at a global scale [23]. The flux of endogenous CO2 can affect aquifer dynamics at a regional scale and can be traced by variations in the total concentration of dissolved inorganic carbon and its isotope signature [24,25,26,27].
From a different perspective, high-pressure fluids can induce the movements of faults [28]. Specifically, the rise of fluids along fault planes can contribute to weakening processes in rocks [29]. Techniques resolving changes in Vp and Vp/Vs during strong seismic activity have recently suggested that a large volume of fluids pushed up, mobilizing groundwater [30], both in Central [31] and Northern Italy [32]. These have a potential impact on water precursory phenomena [33,34]. Simulation experiments have also been performed in underground laboratories, which confirmed the influence of fluids in the seismogenic process [35]. The occurrence of fluid-triggered seismicity has also been proven [36]. Finally, a relationship between earthquake dilatancy and resistivity has been proposed [37]. Moreover, pressure-impressed electric currents due to gas passage through fractured asperities have been observed in laboratory experiments [38]. These experiments were used to speculate a causal mechanism of the seismo-EM phenomena observed in recent earthquakes [39].
Since the early 1990s, the potential relationship between CO2 degassing and earthquakes has been inferred by manual techniques in Italy [40]. The processing of continuous CO2 time series began in the early 2000s with the operation of automatic monitoring stations [41,42,43]. This study aims to statistically assess the possible influence of low-magnitude earthquakes on the release of CO2 at Gallicano, Northern Tuscany, where one of the automatic stations of the Geochemical Network of Tuscany (GNT) is currently monitoring selected geochemical parameters in the water issued by the local thermo-mineral spring. Following a satellite data processing procedure [44], we applied a new statistical interpretative approach to investigate CO2 time series recorded by the Gallicano station during the period of 2010–2013. This procedure relies on the selection of relevant gas anomalies and on the identification of anomalies statistically correlated to small earthquakes, as has already been successfully carried out for the CO2 time series collected during the period of 2017–2021 [45]. Compared to this previous study, in this paper we have considered the incorporation of artificial neural network (ANN) techniques in the identification of possible geochemical anomalies. Moreover, for the period of 2010–2013, we have analyzed not only weak main shocks, as had been performed in our past study [45], but also a second set of main shocks that comprises strong (M5+) events with major aftershocks. The earthquakes examined in this paper have been also characterized in terms of the ratio between the epicentral distance from the spring and the linear length of the seismic source. Finally, what is new in comparison with our previous work [45] is our verification of rain magnitude’s influence on dissolved CO2 variations, using two levels of rainfall in the procedure. We carried out this study with the multiple purpose of (i) validating the results of the 2017–2021 period [45], (ii) comparing the performance of different statistical approaches, and (iii) assessing in more detail any possible correlation between rainfall and seismic events. This ultimately helps in building confidence in assessing and quantifying mutual correlations among low-to-moderate seismic events, geochemical anomalies, and rain events by the integration of advanced statistical methods in the “conventional” analysis of hydrogeochemical data. The proposed statistical methods also allow for estimating the conditional probabilities of earthquake occurrence around the Gallicano site, which represents a significant step forward in terms of forecasting improvement.

2. Seismicity

The Gallicano spring (Figure 1) is located in a sector of northwestern Apennines (Garfagnana Valley) where a NW–SE trending cluster of seismic activity is observed.
The area is characterized by an elevated seismic risk [48,49]. Several earthquakes with a magnitude (MW) larger than 5.5 occurred in this area. Strong historical events are indicated by red circles in Figure 1. On the 14 August 1846, an earthquake with an estimated MW of 6.0 occurred around 60 km south of the Gallicano spring, near the Orciano Pisano village (Colline Pisane earthquake). Two historical earthquakes took place in the Mugello Valley, to the NE of Firenze (13 June 1542: estimated magnitude of 6.0; 29 June 1919: estimated magnitude of 6.2). On the 5 June 1501, an earthquake with an estimated magnitude of 5.9 occurred near the Maranello village, in the Modena province, on the northwestern slopes of the Apennines. Lastly, the Lunigiana and Garfagnana Valleys experienced a catastrophic event of an estimated magnitude of 6.5 on the 7 September 1920 [46].
We retrieved information on regional earthquakes in the period of 2010–2013 from the ISIDe catalog http://iside.rm.ingv.it (accessed on 23 February 2024), and we used the International Catalog of Earthquakes to estimate the moment magnitude of the strongest earthquakes https://earthquake.usgs.gov/earthquakes/search (accessed on 23 February 2024). Our database considered 4046 seismic events with a magnitude greater than or equal to 0.7 that occurred within a radius of 50 km from the Gallicano site. They are reported by small squares whose dimensions are proportional to their magnitudes on the geographical area on the left of Figure 2. The seismic events were declustered following the Reasemberg algorithm [50], using the publicly available routine of Z-map [51]; they are reported on the geographical area in Figure 2, in the middle. Figure 2, on the top right, describes the maximum curvature solution of the Gutenberg–Richter law, where gray events represent the non-cumulative distribution. The resulting magnitude of completeness is 1.5, and, in this region, b-value = 0.90 ± 0.05 and a-value = 3.909 ± 0.002 represent the coefficients of the red line. Figure 2, on the bottom right, highlights the depth distribution of the seismic events within the limit of 50 km chosen for this study.
We identified two groups of declustered earthquakes consisting of the largest earthquakes of the day. A first set of shocks was obtained by collecting events occurring around the Gallicano spring (≤50 km) with a magnitude greater than or equal to 0.7, to which aftershocks were added again (46 events in total). A second set of main shocks (Ml ≥ 1.5), which also includes two main events (MW = 5.9 and MW = 5.8), occurred in the Modena province, outside the Tuscany region (forty events in total). The identification of the first set of events represents a major advancement of our previous study [45] and allows for a deeper understanding of the possible influence of aftershocks on dissolved CO2. Moreover, the selection criterion for both sets was their distance from Gallicano being limited by their energy by three Dobrovolsky radii [52], as in [45]. The set of seismic events is reported in Table 1 with colors to highlight differences between the two groups. MW was reported in column 7 for the major events so as to directly calculate the fault linear length from [53], as follows:
M W = 4.24 + 1.67 l o g ( L f )  
where Lf is the fault length, considered to be adapted to the normal and inverse fault mechanisms commonly observed in Italy [54]. An Ml above 4 was also used with (1) when the MW was not retrieved, as the difference between MW and Ml can be ignored [54] for these magnitudes, while an approximate equation was used for the MW of the smaller events [55]:
M W = 2 3 M l + 1.15
where the fault area A = Lf2 is related to [53].
M w = 4 + l o g A  
The distance from the epicenters to the Gallicano spring was reported in column 8, and the linear length of the seismic sources was reported in column 9 of Table 1.

3. Hydrogeological and Hydrogeochemical Setting

The Gallicano spring emerges, with an average outflow of 1.5 L/s, on the Apuan side of the Serchio basin, in the bed of the “Turrite di Gallicano” river (right tributary of the Serchio river), in correspondence with a NW–SE-trending synthetic quaternary fault of the Serchio graben [49]. Regarding the low thermality of the waters (T~24 °C), De Stefani [56] reports the following: “……they are less saline and less hot waters due to the greater quantity of superficial and river waters that mix in them”. Chemical analyses available in the literature [57,58] indicate, for the Gallicano spring, a Cl-SO4-Ca chemical composition and a salinity between 3 and 4 g/L. Near the spring, in the bed of the “Turrite di Gallicano” river, gaseous emissions have been reported for a long time [56], with an abundant presence of helium (7940 ppb dissolved in water and 2360 ppb directly from the gaseous vents), attributed to the presence of a fault crossing [57].
Within a seismic prevention/prediction program, financially supported by the Regional Government of Tuscany, Italy, for studying possible geochemical precursors to seismic activity [59], the Gallicano spring was selected as a suitable site for the installation of a continuous automatic monitoring station of selected chemical–physical parameters of the water (for the selection criteria, see [41]). The automatic station was installed on the 15 April 2003, and it is still operative, with two considerable periods of inactivity (1 December 2008–30 June 2010 and 21 October 2013–12 December 2016). In addition to continuous monitoring, since 2003, the spring has been sampled every month for chemical and isotopic analyses [41].
To describe the deep hydrogeological structures which, in the Serchio river basin, constitute the locus of the deep hydrothermal circulation feeding also the Gallicano spring and to understand the mode of this circulation, the hydrostructural model of the northern Apennines in Figure 3A (modified after [60]) and the circulation model in Figure 3B were considered. In this model, the geological formations have been grouped into three hydrogeological units based on their permeability characteristics. The following hydrostructural elements are distinguished, from top to bottom: impermeable cover (IC), carbonate aquifer system (CAS), and impermeable substratum (IS).
The impermeable cover (IC) consists of shales and sandstones of Tuscan nappe and by the clayey complex of the Liguride formations and Pliocene—Quaternary clay. It should be highlighted that the IC, thus defined with respect to the underlying CAS, hosts modest aquifer levels, which do not modify its hydrogeological role but are, in any case, sites of superficial circulation which feed springs characterized by near-ambient temperatures, very low salinity (<200 mg/L), and predominant Ca-HCO3 facies (type-A water in Figure 4). The IC allows for connections between the underlying CAS and the outside, especially in correspondence with the cataclastic bands associated with NW–SE-trending antithetic quaternary faults; the latter can act as recharge zones as well as ascent paths for hydrothermal fluids.
The CAS is composed of Mesozoic evaporitic and carbonate rocks belonging to non-metamorphic (subset Ss1) and metamorphic (subset sS2) Tuscan units, intercalated by low-permeability layers, which cause aquicludes and aquitards (at). If the low-permeability limit outcrops along their entire perimeter, the hydrostructures of the CAS give rise to perched aquifers feeding depression, contact, and overflow springs, characterized by near-ambient water temperatures, low or high salinity (up to 1.6 g/L), and chemical composition varying from HCO3-Ca to SO4-Ca (type-B water in Figure 4). If the low-permeability limit deepens, the hydrostructures of the CAS feed hydrothermal circuits. It is noteworthy that the considerable depth of the low-permeability limit on the north-eastern side of the Serchio graben ensures the high piezometric loads and hydraulic gradients associated with these hydrostructures, allowing the large development of hydrothermal circuits in the Serchio Valley. In the eastern sector of the Serchio Valley (Apennines), the CAS is sandwiched between the impermeable cover (IC) and the low-permeability substratum (IS) and feeds thermo-artesian springs with AN ascent pattern through cataclastic belts associated with the NW–SE fault systems of the eastern side of the Serchio graben. The abundant presence of the IC ensures considerable protection to deep-circulating water, limiting possible mixing with the cold and hyposaline waters of more superficial circulation mechanisms. On the Apuan side, the CAS outcrops abundantly, while the IC is downthrown by the NW–SE normal faults that border the western side of the Serchio graben system. Therefore, the IC acts as a hydraulic barrier for water from the deep circulation system that rises to the surface, by overflow, driven by the synthetic neotectonic faults of the Serchio graben. Due to the lack of an impermeable cover, cold and dilute waters of superficial circulation mechanisms recharged by local rainwater are locally allowed to mix with deep waters. For this reason, the thermo-artesian springs of Pieve Fosciana (T = 36 °C) and Bagni di Lucca (T = 54 °C), which emerge on the eastern side of the basin, have higher temperatures than the thermo-mineral springs that emerge on the western side, such as the Gallicano spring. The ternary diagrams of Figure 4 allow one to identify the chemical facies of a thermo-mineral spring based on reciprocal relationships between the main anions and cations (Pieve Fosciana: Cl-Na facies; Bagni di Lucca: SO4-Ca facies; Gallicano and Barga: Cl-Na-Ca facies) acquired by interaction with the anhydrite and/or halite layers of a deep Triassic carbonate–evaporite reservoir [41,43].
The impermeable substratum, IS, is the low-permeability limit of the CAS and is represented by the Paleozoic basement. It mainly consists of quartzites, conglomerates, sandstones, and phyllites.

Continuous Geochemical Monitoring during the 2010–2013 Period

By elaborating the time series collected during the period of 2010–2013, we achieved an accurate definition of the geochemical background of the natural system. Table 2 and Figure 5 show the descriptive statistic and the continuous geochemical signals, respectively, of water temperature (°C—box A), electrical conductivity (µS/cm—box B), pH (box C), redox potential (mV—box D), and the concentration of dissolved CO2 (%—box E) acquired by the automatic station in the period of 2010–2013. The box F of Figure 5 shows the rainfall (mm) trend recorded at the Gallicano pluviometric station https://www.sir.toscana.it/pluviometria-pub (accessed on 23 February 2024).
The signals of temperature (Figure 5A) and electrical conductivity (Figure 5B) are consistent over time, with the highest values recorded in the months of October, before the autumn rains. The effects of rainfall on these signals appear with seasonal decreases but also with an abrupt fall (up to 1 °C) after intense rainfall events. This agrees with the circulation model (Figure 2B), according to which rainfall directly feeds the cold hyposaline superficial circulation which, in turn, due to the lack of CI, dilutes the deep component before it rises to the surface. This mixing also involves an increase in pH (Figure 5C), which shows an anti-correlated trend to the two previous signals. The redox potential (Figure 5D) has an average value of 387 mV, indicative of predominantly oxidized conditions in the aquifer. The discontinuous trend of this parameter is not real but is due to the long stabilization times needed for the electrode after each monthly cleaning operation.
Regarding the %CO2 signal, four “macroscopic” CO2 anomalies can be recognized in Figure 5E. A slight increase in dissolved CO2 was observed at the beginning of April 2012, followed by a sharp decrease in the middle of the month. Months later, sharp drops in concentration were observed in October 2012 and a significant peak towards the end of November. All three variations almost reached a 1% CO2 concentration. Finally, from the end of May 2013, a sharp rise in dissolved CO2 was observed, which increased by approximately 1.5%. Three of the four macroscopic anomalies preceded the most significant seismic events around the Gallicano spring. The variation in April 2012 anticipated the strong events in Modena on the 20 and 29 May 2012 (MW = 5.9 and 5.8); the variation in November 2012 anticipated the event that occurred in Pieve Fosciana (MW = 4.9); and the variation in May 2013 anticipated the events that occurred under the Apuan Alps chain (MW = 5.1, 4.4, and 4.5). The three abrupt variations anticipated all seismic events with a magnitude M > 4, reported in Figure 5E using red circles, taking place within one or two months from the variations.
The significant variations in dissolved CO2 observed in May 2013, approximately one month before the Apuan Alps’ seismic event (MW = 5.1), can be interpreted using the described hydrogeological model. A possible decrease in permeability during the preparatory phase of an earthquake has been suggested [41]. In fact, the phases of crustal deformation that precede earthquakes can induce permeability variations in the deeper layers of the CAS and contribute to a greater release of gases towards the surface, including CO2. Therefore, water from the deep circulation system may reach the surface with a higher concentration of CO2 before a seismic event. Moreover, minor variations in dissolved CO2 concentrations are generally observed during extended rainfall, as observed in our research for the months of October 2010, 2011, and 2012, in which they were all negative and 0.2–0.5% in amplitude. This depends on the fact that hydrothermal circuits, richer in dissolved CO2, are diluted by cold-water circuits, with less concentration of dissolved CO2, fed by rainfall infiltrated trough carbonate outcrops and main disjunctive lines (Figure 3B). However, the other negative and positive variations in CO2 concentrations in Figure 5E lack of a visual association with seismic or rain events. Finally, there are no settlements near the spring nor are there any known anthropogenic influences on the concentration of CO2. Thus, several sudden minor variations remain unexplained at this level of the analysis.

4. Statistical Methods

A first attempt to assess the statistical correlation between mild-to-moderate seismic events and small-amplitude CO2 anomalies in Gallicano was recently carried out based on data collected during the period of April 2017–March 2021. The CO2 anomalies, highlighted by fitting the residual component of the signals with Pearson type-VII functions, were tested in our previous work for their linear dependence to seismic events by binary correlations [45]. In that framework, correlations were used also to estimate the conditional probabilities of seismic events, allowing for a sort of “earthquake forecasting experiment” based on continuous geochemical signals. Continuing with the same approach, here, we focus on the possible binary correlation between geochemical anomalies and mild-to-moderate seismic events that occurred around Gallicano in the period of 2010–2013.

4.1. Processing of CO2 Time Series to Highlight Anomalies

Similar to [45], we fitted the CO2 residual signal using a Pearson type-VII function by defining a threshold over which CO2 fluctuations had a 99% probability of being anomalies. We followed and compared two distinct approaches. Firstly, we decomposed the time series according to the Census I method [61], and then we trained an ANN [62] to reproduce a synthetic signal of the CO2. The residual signal was obtained by a comparison of real (i.e., CO2 time series acquired by the station) and synthetic data (i.e., CO2 time series built by the ANN).
Before applying these two procedures, the raw data were filtered with appropriate moving median-smoothing methods [63,64] to filter out the outliers (Table 2). The CO2 residual signal obtained from the comparison between the CO2 measured signal and a CO2 synthetic signal was analyzed to detect anomalous variations. Two kinds of synthetic signals were generated using CENSUS and ANN. The CO2 residuals were compared with several distribution functions to obtain the best fit. Then, the anomalies were defined by the cumulative probability function as having a 95–99% probability of not belonging to the distribution.

4.1.1. Decomposition of CO2 Time Series by Census I Method

We decomposed the CO2 time series with the Census I method [61], as implemented in the statistical software STATISTICA 12.0 [65]. This procedure allowed us to detrend the CO2 signal for external influences based on a reference analysis spanning 3 months. More details on the procedure can be found in [41]. Data series of CO2 irregular components and residuals are plotted in Figure 6 together with selected earthquakes for comparison.

4.1.2. Creation of Synthetic CO2 Time Series by ANN

The ANN has already been used to detect CO2 anomalies in another spring of GNT [42]. In the current study, an ANN was used in parallel with Census I to compare their respective performances. The ANN method relies on a progressive learning process that emulates the training process of the human brain [66]. For this study, we used the multi-layer perceptrons’ network (MLP) method [67], as implemented in the STATISTICA 12 software, also suitable for non-Gaussian data distributions [68].
CO2 anomalies were identified on the residual signal after a comparison of the measured signal and the synthetic signal processed by ANN analysis. To reproduce the synthetic CO2 signal, we trained the ANN with the signals recorded by the station for water temperature, electrical conductivity, and redox potential. We provided air temperature and rainfall data downloaded from http://www.sir.toscana.it/ (accessed on 23 February 2024) as the input, using the measured CO2 signal as the optimization target. We used 70% of the total dataset for training, 15% for validation (15%), and the remaining 15% for the test sets. One hundred synthetic models were retrieved by ANN, and the best reconstruction of the CO2 signal was determined based on the best correlation between the synthetic and the original signals. Figure 6B shows that the best reconstruction by ANN failed to describe the CO2 recordings in the last 4 months of the time series. Accordingly, we excluded this observation period from further investigations.

4.2. Meteorological Data

Operative since 2000, the automatic meteorological station of Gallicano (179 m asl) is located in the municipality of Gallicano, E-NE of the spring, at a distance of about 800 m. This station collects cumulative rain data every 5 min. In this work, we used meteorological data from the web archive of the Gallicano pluviometric station https://www.sir.toscana.it/pluviometria-pub (accessed on 23 February 2024). The data from June 2010 to October 2013 agree with the estimated value of about 1800 mm/yr for the previous 20 years. The Gallicano station was flooded after the exceptional rain event of the 21 October 2013 (318.8 mm of rain recorded in a single day; Figure 5F).
Previous studies ([41]) have demonstrated that local precipitations may dilute the CO2 concentration of the deep-water component feeding the Gallicano spring. Because of this mixing relationship, we tentatively identified a couple of rain time series in correspondence with daily rain amounts of 10 and 20 mm, under the hypothesis that these thresholds could pinpoint the onset of meteoric-dominated conditions.

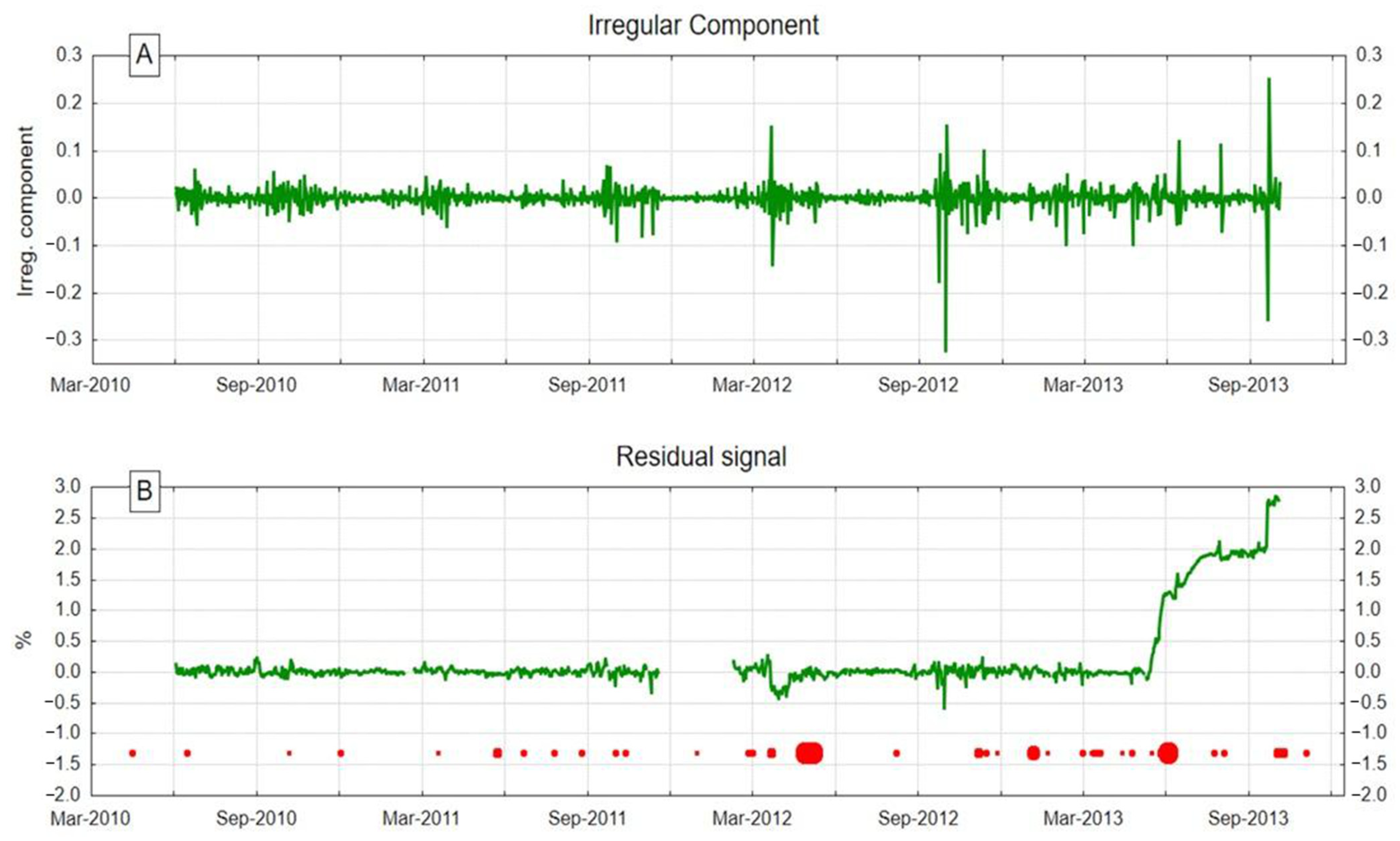
5. Results

The identification of CO2 anomalies was not simple due to the complex variability in the observable phenomena and their dependence on several environmental parameters, such as mixing with deep and shallow water, and, therefore, on meteorological parameters. The main starting approach was to attempt to apply some methods to subtract from the signal the possible seasonal and external dependence. The irregular component obtained from Census I and the residuals obtained from ANN were two attempts to reduce the CO2 input dataset. Then, the next step was to statistically determine what were the possible anomalies in these residuals’ time series. Moreover, the final step was to correlate them with the seismic events selected around the Gallicano spring.

5.1. CO2 Anomalies

Both time series distributions were modeled by several functions, and the best fits were obtained, in both cases, using the Pearson type-VII function [69], which means that such distributions exhibited peaked and symmetric distributions which were preliminary modeled using Gaussian and Lorentzian functions. However, these widely recognized functions failed to accurately depict the tails of the data. The Pearson type-VII function [69], which is essentially a Lorentzian function raised to a power, proved more adept at realistically handling tails than both Gaussian and Lorentzian functions, thanks to its adjustable power parameter. The outcome was an improved confidence level in the fitting, also with a straightforward cumulative integral. The parametric distribution function was as follows:
P ( x ) = A Γ [ m ] Γ ⌈ m − 1 2 ⌉ π ( 2 m − 1 ) 1 + ( x − μ ) 2 σ 2 ( 2 m − 1 ) − m
where A is a multiplicative factor, Γ is the function gamma of Euler, μ the average, and σ2 its variance. The best fit for the distribution by Census I was obtained using the parameters m = 1.51, μ = 3.5 × 10−4, σ2 = 5.76 × 10−3, and A = 13.699. The distribution was described in 56 intervals minus four parameters so as to have 52 degrees of freedom. χ2 was 6.9, which ensured an approximation with a goodness > 99%. The best fit for the distribution by ANN, excluding the last 140 samples (days) in which the time series was not well described, was obtained using the parameters m = 1.99, μ = 2.0 × 10−4, σ2 = 4.55 × 10−3, and A = 28.611. The distribution was described in 51 intervals minus four parameters to have 47 degrees of freedom. χ2 was 9.4, which ensured an approximation with a goodness > 99%.
The anomalies were identified by setting thresholds that correspond to well-defined probabilities of occurrence. The cumulative probability corresponding to a threshold value was calculated to evaluate the probability of each test input overcoming such a value. The cumulative of the probability distribution (4) was summed through Gauss’s hypergeometric function [70]:
P r ( x ) = 1 2 + ( x − μ ) σ [ π ( 2 m − 1 ) ] 1 / 2 Γ [ m ] Γ [ m − 1 / 2 ] F 1 2 m ; 1 2 ; 3 2 ; − ( x − μ ) 2 σ 2 ( 2 m − 1 )
The probability for the CO2 residual time series’ fluctuations to be considered anomalies was chosen to equal 99%. Thus, Equation (5) produced a ∆x = 0.07409 for the Census I residuals and a ∆x = 0.2278 for the ANN residuals. The symmetry of the distribution required positive and negative thresholds around the averages μ, which were defined as x+ = 0.07444 and x− = −0.07374 and x+ = 0.2280 and x− = −0.2276 for Census I and ANN cases, which produced 23 and 21 CO2 anomalies, respectively. The residual time series were transformed into binary series with a time step of one day, where “1” appeared when the datum went beyond these thresholds and “0” when it appeared somewhere else. The probability of an anomalous measurement was defined by its frequency:
P = N ( 1 ) N t o t
with Ntot being the number of days, equal to 1208 for the measurement retrieved by Census I and 1068 for that retrieved by ANN. Thus, probabilities of 0.019 and 0.020 occurred for the two sets of anomalies, respectively.

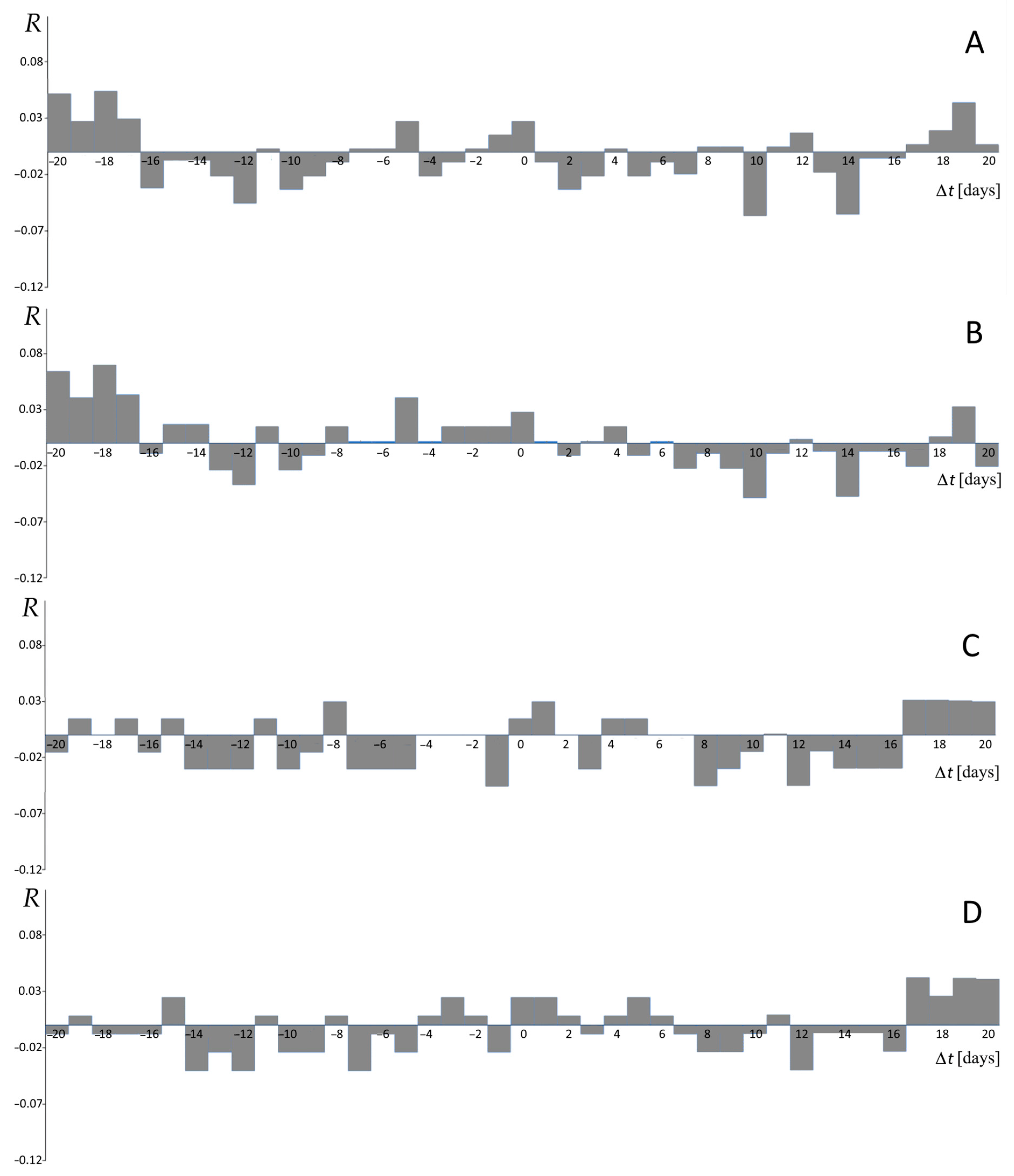
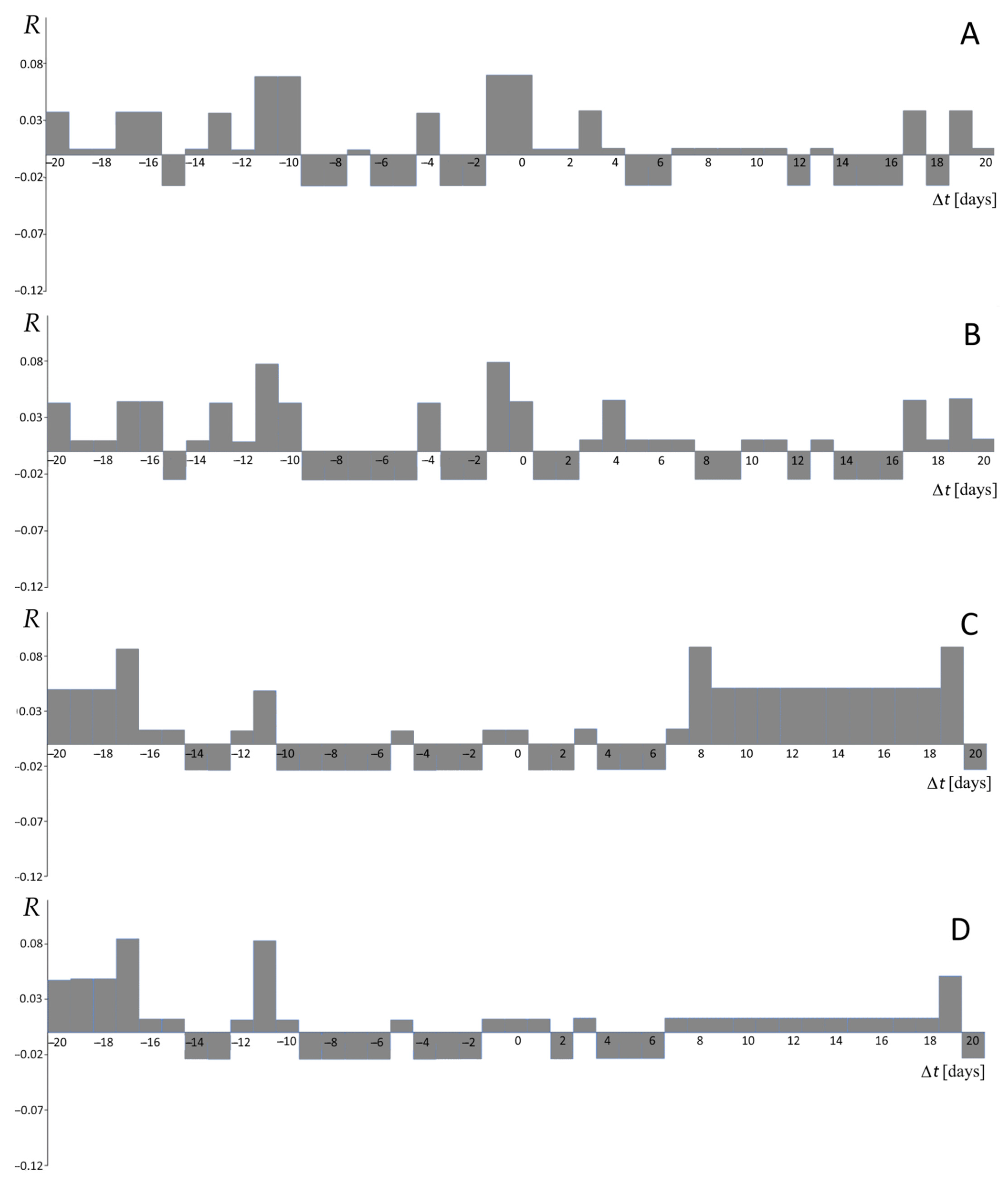
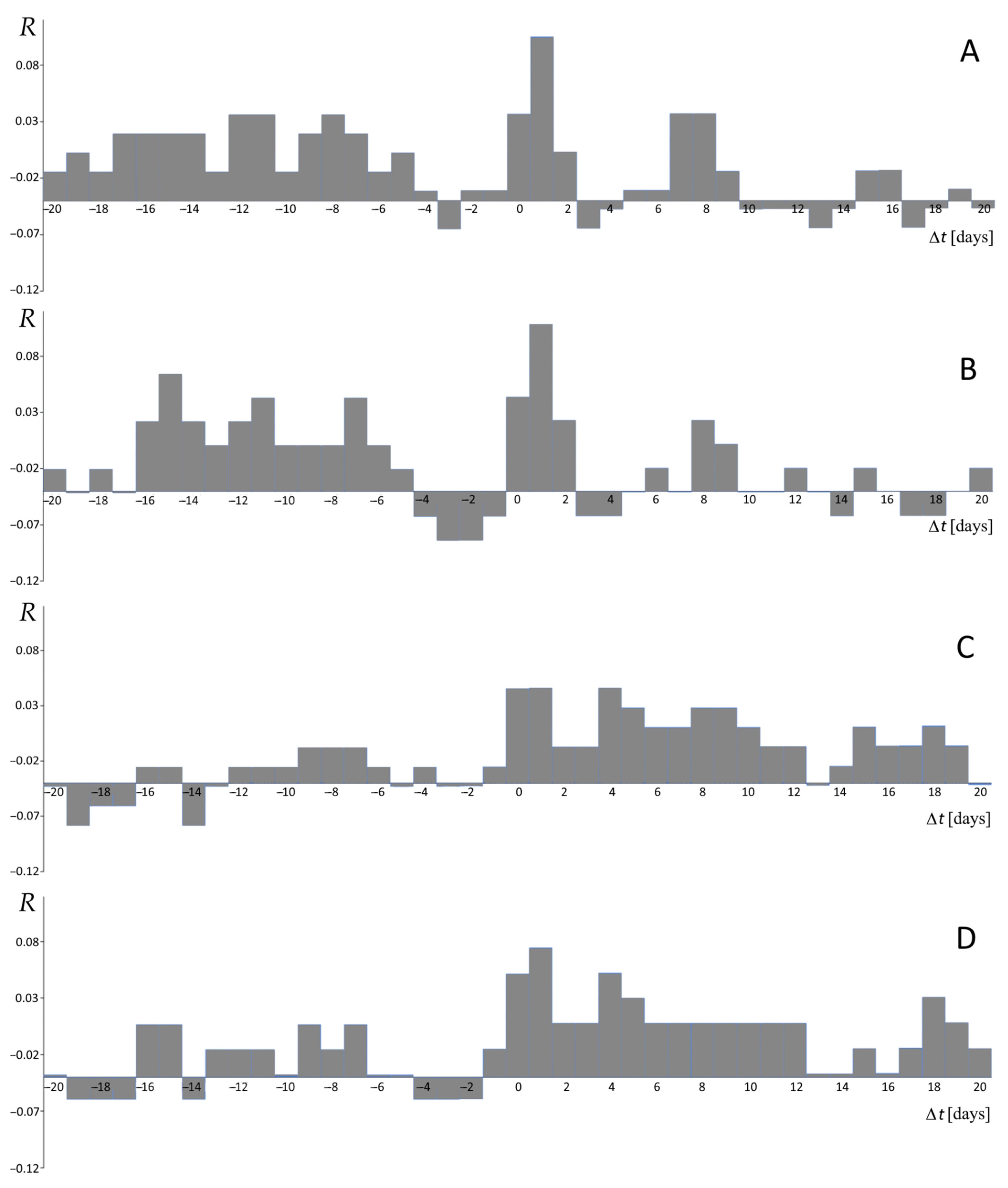
5.2. Correlations

Binary time series of seismic and rainfall events were defined during the same period as the identified anomalies. The respective symbol “1” appeared when earthquakes were selected and when rainfalls went beyond the thresholds of 10 mm and 20 mm, and “0” was used in other cases. Then, Pearson correlation coefficients R were calculated, which assumed values between −1 and 1, with a negative R meaning an anti-correlation, R = 0 no correlation, and a positive R denoting a correlation. A total of six time series was considered in this study, comparing them two-by-two, for a total of twelve correlation coefficient histograms: both Census I and ANN CO2 anomalies with the first set of earthquakes and, after, with the second ones, as defined in Section 2; following this, both Census I and ANN CO2 anomalies were compared with rainfall amounts of 10 mm and 20 mm; and, finally, both series of earthquakes were compared with rainfall amounts of 10 mm and 20 mm. Formally defining CO2 anomalous events with (EC), earthquake events with (EQ), and rainfall events with (ER), the Pearson correlation coefficients are as follows:
R ( E i   ; E j ) = Σ E i × E j N t o t − P E i P E j P E i 1 − P E i P E j 1 − P E j
where E = {EQ, EC, ER}, i and j run over the number of considered days, and ∑ Ei × Ej runs over each couple of different events, summing their coincidences. Both P(Ei) and P(Ej) were defined by (6). When, as in this case, a correlation is calculated between binary series, it is called a Matthews correlation [71], and Equation (7) holds [72]. R-histograms were obtained by introducing a time shift ∆t, which lasted from 1 to 20 days earlier and later than the anomalous event, thus
R ( E i ; E j ( Δ t ) ) = Σ E i × E j ( Δ t ) N t o t − P E i P E j P E i 1 − P E i P E j 1 − P E j
∆t in (8) indicates that the time of the event Ej is given by i × t + ∆t, where i × t is the time step of the event Ei. P(Ej) = N(Ej = 1)/Ntot does not depend on ∆t. A conditional probability of the event Ei, given the observation of Ej, can be demonstrated to be related to the R coefficient [73]. Thus, when ∆t < 0, the event Ej precedes the event Ei, and the conditional probability becomes a forecasting probability written as
P ( E i ∣ E j ( Δ t ) ) = P E i + R ( E i ; E j ( Δ t ) ) P E i 1 − P E i 1 P E j − 1
Equation (9) retrieves the probability of Ei following the observation of the Ej anomaly by ∆t. The ratio P(Ei|Ej(∆t))/P(Ei) defines the event Ei’s probability increase that is observed after the Ej anomaly measurement; this is, for definition, the probability gain Gij(∆t).
The 12 cross-correlation histograms were plotted with a time step ∆t of ±1 to a ∆t of ±20 days. The correlations between rainfalls and earthquakes are reported in Figure 7. The four combinations of two couples of time series show no significant correlation between the rainfalls and the considered seismic phenomena, as the p-value associated with each peak is greater than 0.05. The plot of Figure 8 reports four new correlation histograms between seismic and CO2 events, where a significant peak is observed having time differences of 0, −1, −10, and −11 days in Figure 8A, and −1 and −11 days in Figure 8B. Being ∆t the time difference TCO2 − TEQ, the CO2 anomalies anticipated the earthquakes by one day and by eleven days. The cross-correlation peaks are around 0.08. We evaluated the significance of the 0.08 correlation peak by the p-value, resulting in p < 0.05, which tells us that the alternative hypothesis cannot be discarded. Based on Equation (9), such peaks are equivalent to increased probabilities that a seismic event may occur the same day, one day, 10 days, and 11 days after a CO2 anomaly, i.e., P(EQ|EC). Compared with the frequency of the earthquakes, in our case, P(EQ) = 0.0323, with the conditional probability P(EQ|EC) = 4.14 P(EQ) being a probability gain of G ≈ 4.
The histograms in Figure 9 describe the four correlations of combined time series between rainfalls and CO2 anomalies. Here, another correlation peak at ∆t = TCO2 − TRain = +1 days descends when CO2 anomalies are identified by Census I, indicating CO2 anomalies following rainfalls by one day, with a high significance (p-value < 0.01). More weakly and even less defined in time are the peaks occurred when CO2 anomalies are identified by ANN. In these cases, less significant (p-values even < 0.05) correlation peaks are observed for events on the same day, +1 day, and +4 days from rainfall, indicating that rainfalls tend to anticipate CO2 anomalies by up to 4 days. This last, less clear result is probably due to the way in which CO2 anomalies are recovered by ANN, a method which takes into account rain time series themselves, therefore already partially subtracting rainfall contributions.

6. Discussion and Conclusions

A first statistical processing of water-dissolved CO2 data acquired continuously at the thermo-mineral spring of Gallicano, Italy, disclosed their positive correlation with earthquakes, where significant dissolved gas variations anticipated small seismic events by two days [45]. The extended procedure to obtain CO2 vs. rainfalls and earthquakes vs. rainfalls time series showed only a slight correlation between the CO2 anomalies and precipitation (in particular, rainfall occurred 1 day before the CO2 anomalies), while it highlighted the complete absence of correlation between seismic and meteoric events. The evidence of a lack of any relationship between earthquakes and rainfall is reinforced by the results shown in Figure 7. It reports no significant correlation peaks at different time lags from −20 to 20 days for all the combinations of seismic main shocks or strongest shocks with 10 mm or 20 mm rainfall events.
Moreover, the results about the significance of the peaks in Figure 8 still underline the trend of observing significant dissolved CO2 variation events before small earthquakes around the Gallicano site. However, some differences in the result of −2 days observed for the years from 2017 to 2021 exist with the time lags being −1 and −11 days in these cases, considering both main shocks and strongest shocks. Such differences were probably due to the different geological settings of the seismic events, which occurred at different hypocenters with respect to the hypocenters of the previously considered period. Specifically, time lags of −10 and −11 days can be linked to seismic events of magnitudes generally higher than the events’ magnitude in the previously considered period. Noteworthy is the fact than an increase in the correlation coefficient was also observed for the time lags of −10 and −11 days in Figure 4 (middle) for the 2017–2021 period, which resulted not significant in our previous analysis [45]. It was also observed, for the extreme magnitudes in this study, that an M5.1 event was anticipated by an anomaly observed 20 days before, and, in our previous study, an M3.5 event was anticipated by an anomaly observed 3 days before. The ratio between the epicenter of an earthquake and the spring’s distance and the linear length of the seismic source apparently decreases with increased earthquake magnitudes (Table 1), a phenomenon which agrees with the evidence that CO2 anomalies related to closer seismic sources and/or larger seismic events can be detected earlier, at the point of monitoring. A time lag of 0 days was also observed only when strongest shocks were considered, meaning that the aftershocks were, in this case, contributing to such a peak. Correlation peaks were not observed when ANN was used to select dissolved CO2 concentration anomalies, which should mean that this method was unable to select significant dissolved gas variations possibly related to earthquakes.
Finally, the results of Figure 9 strongly confirm the observation of dissolved CO2 concentration anomalies one day after rainfall events. The weak correlation peak (+1 day) observed in our previous study became very significant when dissolved CO2 concentration anomalies were selected by Census I for the period of 2010–2013, independently from whether the rainfall consisted of 10 or 20 mm cumulative rain events. Significant results, even if a little less so, were observed when selecting CO2 anomalies by ANN, this time only for 20 mm cumulative rain events, which further underlined the poor effectiveness of this method. CO2 variations subsequent to rainfall events agree with the groundwater circulation model developed by [41] for the Gallicano spring. According to this model, rainfall directly feeds a shallow circulation of water that is cold and poor in CO2, which mixes with hydrothermal circuits, richer in CO2, developed in a deep evaporitic-carbonatic reservoir. The mixing between the two components occurs before the outflow of water to the surface (Figure 3B).
In conclusion, we proposed a cross-correlation analysis between seismic events and rainfalls, seismic events and CO2 anomalies, and rainfalls and CO2 anomalies, highlighted in the thermo-mineral waters of Gallicano spring, a site in which automatic and continuous monitoring has been carried out since 2003. We focused our analysis on the time series collected during the period of June 2010–October 2013.
We processed CO2 time series with both the Census and ANN methods to reconstruct two synthetic trends. Then, we fit residual distributions using Pearson type-VII functions to evidence anomalous fluctuations in dissolved CO2 contents. These anomalies were defined based on a threshold according to which the values had a 99% probability of not happening by chance. By cross-correlating the binary series of CO2 anomalies and earthquakes with a low-to-moderate magnitude, positive correlations were highlighted for CO2 anomalies that occurred 1 and 11 days before the earthquakes, unlike our previous analysis, of the period of 2017–2021, which provided an anticipation of the anomalies with respect to the earthquakes 2 days earlier. Nevertheless, the probability gain resulted again to be around 4. We also expanded the same statistical approach to double the amount of cumulative precipitation and to an earthquake set also containing aftershocks. We estimated negligible correlations among any seismic and rain event sets compared to the CO2 vs. earthquakes case, confirming the results from our previous study. Instead, a strong correlation appeared between rainfall and CO2, occurring mainly one day after intense rainfalls, which reinforces the slight evidence which emerged in our previous work. The time lag of 1 day between CO2 anomalies and earthquake observations in this work is similar to the time lag of 2 days obtained when studying the 2017–2021 period [45]. Moreover, a new time lag of 10–11 days was observed here with another significant correlation, which fits two different earthquake sets around Gallicano, which could be related to the generally higher magnitude of the earthquakes considered in this research. For what concerns the correlation between CO2 anomalies and rainfalls, which were weakly observed in our past study [45], here, they were confirmed with a strong significance.
Figure 3B reports how mixing thought between hydrothermal circuits, richer in dissolved CO2, and cold-water circuits, with less concentration of dissolved CO2, is conceived. Since the deep-water contribution is richer in CO2 (we obtain this information via chemical analyses), an increase in CO2 may arise from deeper levels of the reservoir, as a result of changes in permeability associated with the preparatory phases of earthquakes. Moreover, diffused water from significant rainfalls can quickly intercept the rising spring water in the more superficial layers, so as to produce the observed negative anomalies. Overall, this study suggests that statistical methods are an efficient tool for supporting the “standard” analysis of hydrogeochemical data in the search of correlations between seismicity and variations in observational data. Furthermore, it also emphasizes that the availability of continuous time series is an essential prerequisite to advance the mere observation of “anomalous” data towards the identification of reliable precursors of seismic events.

Author Contributions

Conceptualization, L.P., C.F. and F.G.; methodology, L.P. and C.F.; software, C.F.; validation, L.P., C.F., F.G. and G.F.; resources, L.P. and G.F.; data curation, L.P. and G.F.; writing—original draft preparation, C.F.; writing—review and editing, L.P., C.F. and F.G.; supervision, F.G.; project administration, L.P., G.F. and F.G.; funding acquisition, L.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by Seismic Prevention Service of the Tuscany Region grant number [Decreto Dirigenziale Regione Toscana n.1666—22/03/2002].

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors after request.

Acknowledgments

The authors are grateful to the Seismic Sector of the Tuscany region, Italy, which has financed this research. We acknowledge many people at INGV for many constructive discussions and their insightful comments on a previous draft, which allowed us to improve the manuscript. We are also indebted to three anonymous reviewers and the Editor for their careful reading and constructive comments.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Netreba, A.V.; Fridman, A.I.; Plotnikov, I.A.; Khurin, M.I. On the large-scale 504 mapping of closed ore-bearing areas in the north Caucasus with the uses of gas surveying as a geochemical method. Geokhimia 1971, 8, 1016–1021. (In Russian) [Google Scholar]
  2. Kravtsov, A.I.; Voitov, G.I. Evaluation of the role of faults in the gas exchange between the lithosphere and the atmosphere illustrated in southern Daghestan. Proc. High. Educ. Inst. Geol. Explor. 1976, 19, 18–26. (In Russian) [Google Scholar]
  3. Gold, T. Terrestrial sources of carbon and earthquake outgassing. J. Petroleum Geol. 1979, 1, 3–19. [Google Scholar] [CrossRef]
  4. Gold, T.; Soter, S. Natural Explosive Noises. Science 1981, 212, 1297–1298. [Google Scholar] [CrossRef]
  5. Irwin, W.P.; Barnes, I. Tectonic relations of carbon dioxide discharges and earthquake. J. Geophys. Res. 1980, 85, 3115–3121. [Google Scholar] [CrossRef]
  6. Barnes, I.; Irwin, P.W.; White, D.E. Global Distribution of Carbon Dioxide Discharges, and Major Zones of Seismicity; Barnes, I., Irwin, P.W., White, D.E., Eds.; Water Resources Investigation WRI 78-39; U.S. Geological Survey: Washington, DC, USA, 1978; pp. 1–17. [CrossRef]
  7. Gold, T.; Soter, S. Fluid ascent through the solid lithosphere and its relation to earthquakes. Pure Appl. Geophys. 1984, 122, 492–530. [Google Scholar] [CrossRef]
  8. Sugisaki, R.; Ido, M.; Takeda, H.; Isobe, Y.; Hayashi, Y.; Nakamura, N.; Satake, H.; Mizutani, Y. Origin of hydrogen and carbon dioxide in fault gases and its relation to fault activity. J. Geol. 1983, 91, 239–258. [Google Scholar] [CrossRef]
  9. King, C.Y. Gas geochemistry applied to earthquake prediction: An overview. J. Geophys. Res. 1986, 91, 12269–12281. [Google Scholar] [CrossRef]
  10. Stefànsson, R. Advances in Earthquake Prediction, Research and Risk Mitigation. In Springer and Praxis Book; Springer: Berlin/Heidelberg, Germany, 2011; p. 274. [Google Scholar]
  11. Stefànsson, R.; Halldòrsson, P. Strain release and strain build-up in the South Iceland seismic zone. Tectonophysics 1988, 159, 267–276. [Google Scholar] [CrossRef]
  12. Tamburello, G.; Pondrelli, S.; Chiodini, G.; Rouwet, D. Global-scale control of extensional tectonics on CO2 Earth degassing. Nat. Commun. 2018, 9, 4608. [Google Scholar] [CrossRef]
  13. Kingsley, S.P.; Biagi, P.E.; Piccolo, R.; Capozzi, V.; Ermini, A.; Khatkevichs, Y.M.; Gordeevs, E.I. Hydrogeochemical precursors of strong earthquakes: A realistic possibility in Kamchatka. Phys. Chem. Earth C 2001, 26, 769–774. [Google Scholar] [CrossRef]
  14. Bräuer, K.; Kämpf, H.; Strauch, G.; Weise, S.M. Isotopic evidence (3He/4He, 13C-CO2) of fluid-triggered intraplate seismicity. J. Geophys. Res. 2003, 108, 2070. [Google Scholar] [CrossRef]
  15. Ventura, G.; Cinti, F.R.; Di Luccio, F.; Pino, N.A. Mantle wedge dynamics versus crustal seismicity in the Apennines (Italy). Geochem. Geophys. Geosys. 2007, 8, Q02013. [Google Scholar] [CrossRef]
  16. Massin, F.; Farrell, J.; Smith, R.B. Repeating Earthquakes in the Yellowstone Volcanic Field: Implications for Rupture Dynamics, Ground Deformation, and Migration in Earthquake Swarms. J. Volcanol. Geotherm. Res. 2013, 257, 159–173. [Google Scholar] [CrossRef]
  17. Miller, S.A. Advances in Geophysics; Dmowska, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 54, pp. 1–46. [Google Scholar]
  18. Fischer, T.; Matyska, C.; Heinicke, J. Earthquake-enhanced permeability–evidence from carbon dioxide release following the ML 3.5 earthquake in West Bohemia. Earth Planet. Sci. Lett. 2017, 460, 60–67. [Google Scholar] [CrossRef]
  19. Yoshida, K.; Hasegawa, A. Hypocenter Migration and Seismicity Pattern Change in the Yamagata-Fukushima Border, NE Japan, Caused by Fluid Movement and Pore Pressure Variation. J. Geophys. Res. Solid Earth 2018, 123, 5000–5017. [Google Scholar] [CrossRef]
  20. Chiodini, G.; Cardellini, C.; Di Luccio, F.; Selva, J.; Frondini, F.; Caliro, S.; Rosiello, A.; Beddini, G.; Ventura, G. Correlation between tectonic CO2 Earth degassing and seismicity is revealed by a 10-year record in the Apennines, Italy. Sci. Adv. 2020, 6, eabc2938. [Google Scholar] [CrossRef] [PubMed]
  21. Heinicke, J.; Koch, U.; Martinelli, G. CO2 and Radon measurements in the Vogtland area (Germany)—A contribute to earthquake prediction research. Geophys. Res. Lett. 1995, 22, 771–774. [Google Scholar] [CrossRef]
  22. Heinicke, J.; Braun, T.; Burgassi, P.; Italiano, F.; Martinelli, G. Gas flow anomalies in seismogenic zones in the Upper Tiber Valley, Central Italy. Geophys. J. Int. 2006, 167, 794–806. [Google Scholar] [CrossRef]
  23. Hunt, J.A.; Zafu, A.; Mather, T.A.; Pyle, D.M.; Barry, P.H. Spatially variable CO2 degassing in the main Ethiopian rift: Implications for magma storage, volatile transport, and rift-related emissions. Geochem. Geophys. Geosyst. 2017, 18, 3714–3737. [Google Scholar] [CrossRef]
  24. Rose, T.P.; Davisson, M.L. Radiocarbon in hydrologic systems containing dissolved magmatic carbon dioxide. Science 1996, 273, 1367–1370. [Google Scholar] [CrossRef]
  25. Sorey, M.L.; Evans, W.C.; Kennedy, B.M.; Farrar, C.D.; Hainsworth, L.J.; Hausback, B. Carbon dioxide and helium emissions from a reservoir of magmatic gas beneath Mammoth Mountain, California. J. Geophys. Res. Solid Earth 1998, 103, 15303–15323. [Google Scholar] [CrossRef]
  26. Chiodini, G.; Frondini, F.; Kerrick, D.M.; Rogie, J.; Parello, F.; Peruzzi, L.; Zanzari, A.R. Quantification of deep CO2 fluxes from Central Italy. Examples of carbon balance for regional aquifers and of soil diffuse degassing. Chem. Geol. 1999, 159, 205–222. [Google Scholar] [CrossRef]
  27. Caliro, S.; Chiodini, G.; Avino, R.; Cardellini, C.; Frondini, F. Volcanic degassing at Somma–Vesuvio (Italy) inferred by chemical and isotopic signatures of groundwater. Appl. Geochem. 2005, 20, 1060–1076. [Google Scholar] [CrossRef]
  28. Cox, S.F. Faulting processes at high fluid pressures: An example of fault valve behavior from the Wattle Gully Fault, Victoria, Australia. J. Geophys. Res. Solid Earth 1995, 100, 12841–12859. [Google Scholar] [CrossRef]
  29. Collettini, C.; Cardellini, C.; Chiodini, G.; De Paola, N.; Holdsworth, R.E.; Smith, S.A.F. Fault weakening due to CO2 degassing in the Northern Apennines: Short-and long-term processes. Geol. Soc. Lond. Spec. Publ. 2008, 299, 175–194. [Google Scholar] [CrossRef]
  30. Chiarabba, C.; De Gori, P.; Valoroso, L.; Petitta, M.; Carminati, E. Large extensional earthquakes push-up terrific amount of fluids. Sci. Rep. 2022, 12, 14597. [Google Scholar] [CrossRef]
  31. Gabrielli, S.; Gabrielli, S.; Akinci, A.; Ventura, G.; Napolitano, F.; Del Pezzo, E.; De Siena, L. Fast Changes in Seismic Attenuation of the Upper Crust due to Fracturing and Fluid Migration: The 2016–2017 Central Italy Seismic Sequence. Front. Earth Sci. 2022, 10, 909698. [Google Scholar] [CrossRef]
  32. Fonzetti, R.; Valoroso, L.; De Gori, P.; Chiarabba, C. Fault and Fluid Interaction during the 2012 Emilia (Northern Italy) Seismic Sequence. Seismol. Res. Lett. 2023, 94, 671–684. [Google Scholar] [CrossRef]
  33. Manga, M.; Wang, C.Y. Earthquake Hydrology. In Treatise on Geophysics, 2nd ed.; Elsevier: Oxford, UK, 2015; Volume 4, pp. 305–328. [Google Scholar]
  34. Martinelli, G.; Facca, G.; Genzano, N.; Gherardi, F.; Lisi, M.; Pierotti, L.; Tramutoli, V. Earthquake-related signals in Central Italy detected by hydrogeochemical and satellite techniques. Front. Earth Sci. 2020, 8, 584716. [Google Scholar] [CrossRef]
  35. Gischig, V.S.; Giardini, D.; Amann, F.; Hertrich, M.; Krietsch, H.; Loew, S.; Maurer, H.; Villiger, L.; Wiemer, S.; Bethmann, F.; et al. Hydraulic stimulation and fluid circulation experiments in underground laboratories: Stepping up the scale towards engineered geothermal systems. Geomech. Energy Environ. 2020, 24, 100175. [Google Scholar] [CrossRef]
  36. Guglielmi, Y.; Cappa, F.; Henry, P.; Elsworth, E. Seismicity triggered by fluid injection–induced aseismic slip. Science 2015, 348, 1224–1226. [Google Scholar] [CrossRef]
  37. Wang, W.; Shan, J.; Ni, Z.; Cai, J. Relationship between earthquake dilatancy and electric precursor phenomena. Nat. Hazards 2015, 79, 249–262. [Google Scholar] [CrossRef]
  38. Enomoto, Y. Coupled interaction of earthquake nucleation with deep Earth gases: A possible mechanism for seismo-electromagnetic phenomena. Geophys. J. Int. 2012, 191, 1210–1214. [Google Scholar] [CrossRef]
  39. Enomoto, Y.; Yamabe, T.; Okumura, N. Causal mechanisms of seismo-EM phenomena during the 1965–1967 Matsushiro earthquake swarm. Sci. Rep. 2017, 7, 44774. [Google Scholar] [CrossRef] [PubMed]
  40. Martinelli, G.; Tamburello, G. Geological and geophysical factors constraining the occurrence of earthquake precursors in geofluids: A review and reinterpretation. Front. Earth Sci. 2020, 8, 596050. [Google Scholar] [CrossRef]
  41. Pierotti, L.; Botti, F.; D’Intinosante, V.; Facca, G.; Gherardi, F. Anomalous CO2 content in the Gallicano thermo-mineral spring (Serchio Valley, Italy) before the 21 June 2013, Alpi Apuane earthquake (M = 5.2). Phys. Chem. Earth Parts A/B/C 2015, 85, 131–140. [Google Scholar] [CrossRef]
  42. Pierotti, L.; Gherardi, F.; Facca, G.; Piccardi, L.; Moratti, G. Detecting CO2 anomalies in a spring on Mt. Amiata volcano (Italy). Phys. Chem. Earth Parts A/B/C 2017, 98, 161–172. [Google Scholar] [CrossRef]
  43. Gherardi, F.; Pierotti, L. The suitability of the Pieve Fosciana hydrothermal system (Italy) as a detection site for geochemical seismic precursors. Appl. Geochem. 2018, 92, 166–179. [Google Scholar] [CrossRef]
  44. Fidani, C. West Pacific Earthquake Forecasting Using NOAA Electron Bursts with Independent L-Shells and Ground-Based Magnetic Correlations. Front. Earth Sci. 2021, 9, 673105. [Google Scholar] [CrossRef]
  45. Fidani, C.; Gherardi, F.; Facca, G.; Pierotti, L. Correlation between small earthquakes and anomalies in spring waters: A statistical experiment on the probability of seismic occurrence. Front. Earth Sci. 2023, 11, 1128949. [Google Scholar] [CrossRef]
  46. Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P.; Antonucci, A. Catalogo Parametrico dei Terremoti Italiani (CPTI15), Versione 4.0; Istituto Nazionale di Geofisica e Vulcanologia: Italy, 2022. [Google Scholar]
  47. DISS Working Group. Database of Individual Seismogenic Sources (DISS), Version 3.3.0: A Compilation of Potential Sources for Earthquakes Larger than M 5.5 in Italy and Surrounding Areas; Istituto Nazionale di Geofisica e Vulcanologia: Italy, 2021. [Google Scholar] [CrossRef]
  48. Stucchi, M.; Meletti, C.; Montaldo, V.; Crowley, H.; Calvi, G.M.; Boschi, E. Seismic Hazard Assessment (2003–2009) for the 686 Italian Building Code. Bull. Seismol. Soc. Am. 2011, 101, 1885–1911. [Google Scholar] [CrossRef]
  49. Molli, G.; Manighetti, I.; Bennett, R.; Malavieille, J.; Serpelloni, E.; Storti, F.; Giampietro, T.; Bigot, A.; Pinelli, G.; Giacomelli, S.; et al. Active fault systems in the Inner Northwest Apennines, Italy: A reappraisal one century after the 1920 Mw~6.5 Fivizzano earthquake. Geosciences 2021, 11, 139. [Google Scholar] [CrossRef]
  50. Reasenberg, P. Second-Order Moment of Central California Seismicity, 1969–1982. J. Geophys. Res. 1985, 90, 5479–5495. [Google Scholar] [CrossRef]
  51. Wiemer, S. A Software Package to Analyze Seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
  52. Dobrovolsky, I.P.; Zubkov, S.I.; Miachkin, V.I. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
  53. Leonard, M. Earthquake Fault Scaling: Self-Consistent Relating of Rupture Length, Width, Average Displacement, and Moment Release. Bull. Seismol. Soc. Am. 2010, 100, 1971–1988. [Google Scholar] [CrossRef]
  54. Trippetta, F.; Petricca, P.; Billi, A.; Collettini, C.; Cuffaro, M.; Lombardi, A.M.; Scrocca, D.; Ventura, G.; Morgante, A.; Doglioni, C. From mapped faults to fault-length earthquake magnitude (FLEM): A test on Italy with methodological implications. Solid Earth 2019, 10, 1555–1579. [Google Scholar] [CrossRef]
  55. Munafò, I.; Malagnini, L.; Chiaraluce, L. On the Relationship between Mw and ML for Small Earthquakes. Bull. Seismol. Soc. Am. 2016, 106, 2402–2408. [Google Scholar] [CrossRef]
  56. De Stefani, C. Le acque termali di Torrite in Garfagnana. Boll. Soc. Geol. It. 1904, XXIII, 117–148. (In Italian) [Google Scholar]
  57. Bencini, A.; Duchi, V.; Martini, M. Geochemistry of thermal springs of Tuscany, (Italy). Chem. Geol. 1977, 19, 229–252. [Google Scholar] [CrossRef]
  58. Fanelli, M.; Bellucci, L.; Nachira, F. Manifestazioni idrotermaliit aliane. CNR–PFE. In Geothermal Energy Subproject RF 13; Appendix; 1982. CNR Edition. (In Italian) [Google Scholar]
  59. Cioni, R.; Guidi, M.; Pierotti, L.; Scozzari, A. An automatic monitoring network installed in Tuscany (Italy) for studying possible geochemical precursory phenomena. Nat. Hazards Earth Syst. Sci. 2007, 7, 405–416. [Google Scholar] [CrossRef]
  60. Baldacci, F.; Raggi, G. Lineamenti geologici e idrogeologici della regione dell’Appennino Ligure Toscano a nord dell’Arno. Contributo alle conoscenze delle risorse geotermiche del territorio italiano, CNR–PFE. In Geothermal Energy Subproject RF 13; 1982; pp. 68–85. CNR Edition. (In Italian) [Google Scholar]
  61. Makridakis, S.; Wheelwright, S.C.; Hyndman, R.J. Forecasting Methods and Applications, 3rd ed.; John Wiley and Sons: New York, NY, USA, 1998; p. 642. [Google Scholar]
  62. Muller, B.; Reinhardt, J. Neural Networks: An Introduction; Springer: Berlin/Heidelberg, Germany, 1990; p. 280. [Google Scholar]
  63. Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
  64. Velleman, P.F.; Hoaglin, D.C. Applications, Basics, and Computing of Exploratory Data Analysis; Duxbury Press: Boston, MA, USA, 1981. [Google Scholar]
  65. Statsoft Inc. STATISTICA (Data Analysis Software System) Version 12 for Windows: Statistics; STATSOFT Inc.: Tulsa, OK, USA, 2013. [Google Scholar]
  66. Muller, B.; Reinhardt, J.; Strickland, M.T. Physics of Neural Networks, Neural Networks: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
  67. Rumelhart, D.E.; McClelland, J.L.; PDP Research Group. Parallel Distributed Processing-Explorations in the Microstructure of Cognition, Volume 1: Foundations; MIT Press: Cambridge, MA, USA, 1986; p. 547. [Google Scholar]
  68. Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinformatics 2008, 10, 3–22. [Google Scholar] [CrossRef]
  69. Pearson, K. Mathematical contributions to the theory of evolution, XIX: Second supplement to a memoir on skew variation. Philos. Trans. R. Soc. A 1916, 216, 429–457. [Google Scholar] [CrossRef]
  70. Johnson, N.L.; Samuel Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1995; Volume 2. [Google Scholar]
  71. Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phagelysozyme. Biochim. Biophys. Acta (BBA)-Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
  72. Fidani, C. Probability, Causality and False Alarms Using Correlations between Strong Earthquakes and NOAA High Energy Electron Bursts. Ann. Geophys. 2020, 63, 543. [Google Scholar] [CrossRef]
  73. Fidani, C. Improving Earthquake Forecasting by Correlations between Strong Earthquakes and NOAA Electron Bursts. Terr. Atmos. Ocean. Sci. 2018, 29, 117–130. [Google Scholar] [CrossRef]
Water 16 00739 g001
Figure 1. Location of the monitoring site at Gallicano (green pentagon). White dots = epicenters of the seismic events considered in this study; yellow star = epicenter of the main seismic event in Tuscany of 2010–2013; red dots = MW ≥ 6 earthquake after Rovida et al. [46] catalog (CPTI15 v.4.0); red lines = normal faults; green lines = inverse faults; yellow transparent boxes = seismogenic sources (after DISS Working group, 2021, version 3.3 [47]); and orange triangles = gaseous emissions points extracted from the Googas online catalog http://hdl.handle.net/2122/3060 (accessed on 23 February 2024).
Figure 1. Location of the monitoring site at Gallicano (green pentagon). White dots = epicenters of the seismic events considered in this study; yellow star = epicenter of the main seismic event in Tuscany of 2010–2013; red dots = MW ≥ 6 earthquake after Rovida et al. [46] catalog (CPTI15 v.4.0); red lines = normal faults; green lines = inverse faults; yellow transparent boxes = seismogenic sources (after DISS Working group, 2021, version 3.3 [47]); and orange triangles = gaseous emissions points extracted from the Googas online catalog http://hdl.handle.net/2122/3060 (accessed on 23 February 2024).
Water 16 00739 g001
Water 16 00739 g002
Figure 2. The distribution of the earthquakes from the dataset used in this analysis is on the left. Brown line: Tyrrhenian coastline; blue line: main local faults; green pentagon: Gallicano monitoring site; and yellow star: location of the most energetic seismic event occurred in the period of interest. the Declustered earthquakes are distributed on the map in the middle. The frequency–magnitude distribution and the earthquakes’ depth distribution are on the right.
Figure 2. The distribution of the earthquakes from the dataset used in this analysis is on the left. Brown line: Tyrrhenian coastline; blue line: main local faults; green pentagon: Gallicano monitoring site; and yellow star: location of the most energetic seismic event occurred in the period of interest. the Declustered earthquakes are distributed on the map in the middle. The frequency–magnitude distribution and the earthquakes’ depth distribution are on the right.
Water 16 00739 g002
Water 16 00739 g003
Figure 3. (A) Hydrostructural model of the Northern Apennines (modified after [60]). (B). Circulation model of the Gallicano hydrothermal system (al = alluvium; IC = impermeable cover; CAS = carbonate aquifer system; cr = non-metamorphic carbonate rocks; er = evaporites; mcr = permeable metamorphic carbonate rocks; and IS = impermeable substratum). Not to scale.
Figure 3. (A) Hydrostructural model of the Northern Apennines (modified after [60]). (B). Circulation model of the Gallicano hydrothermal system (al = alluvium; IC = impermeable cover; CAS = carbonate aquifer system; cr = non-metamorphic carbonate rocks; er = evaporites; mcr = permeable metamorphic carbonate rocks; and IS = impermeable substratum). Not to scale.
Water 16 00739 g003
Water 16 00739 g004
Figure 4. Triangular diagrams for the Serchio basin springs. Anions (A) and cations (B) relative to the total concentrations are computed on a meq/L basis. Green pentagon: Gallicano spring; red dots: Pieve Fosciana spring; white square: Barga spring; grey dots: Bagni di Lucca spring; yellow square: type-A water; and blue diamond: type-B water.
Figure 4. Triangular diagrams for the Serchio basin springs. Anions (A) and cations (B) relative to the total concentrations are computed on a meq/L basis. Green pentagon: Gallicano spring; red dots: Pieve Fosciana spring; white square: Barga spring; grey dots: Bagni di Lucca spring; yellow square: type-A water; and blue diamond: type-B water.
Water 16 00739 g004
Water 16 00739 g005
Figure 5. Geochemical parameters measured continuously in the Gallicano station (blue lines) compared with seismic events: (A) temperature (°C); (B) electrical conductivity (µS/cm); (C), pH; (D) redox potential (mV); (E) CO2 (vol.% of the headspace of the measurement cell). Red lines: temporal trend of the mobile average of each parameter (average on a 30-day window). (F) Rainfall (mm) recorded at the Gallicano pluviometric station data from https://www.sir.toscana.it/pluviometria-pub (accessed on 23 February 2024).
Figure 5. Geochemical parameters measured continuously in the Gallicano station (blue lines) compared with seismic events: (A) temperature (°C); (B) electrical conductivity (µS/cm); (C), pH; (D) redox potential (mV); (E) CO2 (vol.% of the headspace of the measurement cell). Red lines: temporal trend of the mobile average of each parameter (average on a 30-day window). (F) Rainfall (mm) recorded at the Gallicano pluviometric station data from https://www.sir.toscana.it/pluviometria-pub (accessed on 23 February 2024).
Water 16 00739 g005
Water 16 00739 g006
Figure 6. (A): Irregular component of CO2 time series. (B): Residual signal obtained by the difference between the CO2 measured signal and the CO2 simulated signal via ANN. The red dots mark the selected seismic events in Section 3. The dots’ dimensions progressively increase with the local magnitude (Ml).
Figure 6. (A): Irregular component of CO2 time series. (B): Residual signal obtained by the difference between the CO2 measured signal and the CO2 simulated signal via ANN. The red dots mark the selected seismic events in Section 3. The dots’ dimensions progressively increase with the local magnitude (Ml).
Water 16 00739 g006
Water 16 00739 g007
Figure 7. The four correlation histograms with ∆t from −20 to 20 days, obtained between (A): first group of earthquakes and rainfalls > 10 mm; (B): main shocks and rainfalls > 10 mm; (C): first group of earthquakes and rainfalls > 20 mm; and (D): main shocks and rainfalls > 20 mm. No significant correlation peaks appear.
Figure 7. The four correlation histograms with ∆t from −20 to 20 days, obtained between (A): first group of earthquakes and rainfalls > 10 mm; (B): main shocks and rainfalls > 10 mm; (C): first group of earthquakes and rainfalls > 20 mm; and (D): main shocks and rainfalls > 20 mm. No significant correlation peaks appear.
Water 16 00739 g007
Water 16 00739 g008
Figure 8. The four correlation histograms with ∆t from −20 to 20 days, obtained between (A): CO2 Census I and first group of earthquakes; (B): CO2 Census I and main shocks; (C): CO2 ANN and first group of earthquakes; and (D): CO2 ANN and main shocks. Significant correlation peaks (p-value < 0.05) appear in (A,B) at ∆t = −1 and −11 days, which means that the CO2 anomalies anticipate the earthquakes.
Figure 8. The four correlation histograms with ∆t from −20 to 20 days, obtained between (A): CO2 Census I and first group of earthquakes; (B): CO2 Census I and main shocks; (C): CO2 ANN and first group of earthquakes; and (D): CO2 ANN and main shocks. Significant correlation peaks (p-value < 0.05) appear in (A,B) at ∆t = −1 and −11 days, which means that the CO2 anomalies anticipate the earthquakes.
Water 16 00739 g008
Water 16 00739 g009
Figure 9. The four correlation histograms with ∆t from −20 to 20 days, obtained between (A): CO2 Census I and rainfalls > 10 mm; (B): CO2 Census I and rainfalls > 20 mm; (C): CO2 ANN and rainfalls > 10 mm; and (D): CO2 ANN and rainfalls > 20 mm. Significant correlation peaks (p-value < 0.05) appear more markedly in (A,B) at ∆t = +1 and less markedly in (C,D), which means that more intense rainfalls are followed by CO2 anomalies.
Figure 9. The four correlation histograms with ∆t from −20 to 20 days, obtained between (A): CO2 Census I and rainfalls > 10 mm; (B): CO2 Census I and rainfalls > 20 mm; (C): CO2 ANN and rainfalls > 10 mm; and (D): CO2 ANN and rainfalls > 20 mm. Significant correlation peaks (p-value < 0.05) appear more markedly in (A,B) at ∆t = +1 and less markedly in (C,D), which means that more intense rainfalls are followed by CO2 anomalies.
Water 16 00739 g009
Table 1. The entire set of seismic events used in this study is differentiated with a red color for the first group and with a green color for the second one. MW is reported in column 7 when it is available from international databases or retrieved with Equation (2). Column 8 reports the distance between the epicenter and Gallicano. Column 9 reports the linear lengths of the seismic sources retrieved with Equation (1), when the MW is available from international databases (*), or retrieved with Equation (3).
Table 1. The entire set of seismic events used in this study is differentiated with a red color for the first group and with a green color for the second one. MW is reported in column 7 when it is available from international databases or retrieved with Equation (2). Column 8 reports the distance between the epicenter and Gallicano. Column 9 reports the linear lengths of the seismic sources retrieved with Equation (1), when the MW is available from international databases (*), or retrieved with Equation (3).
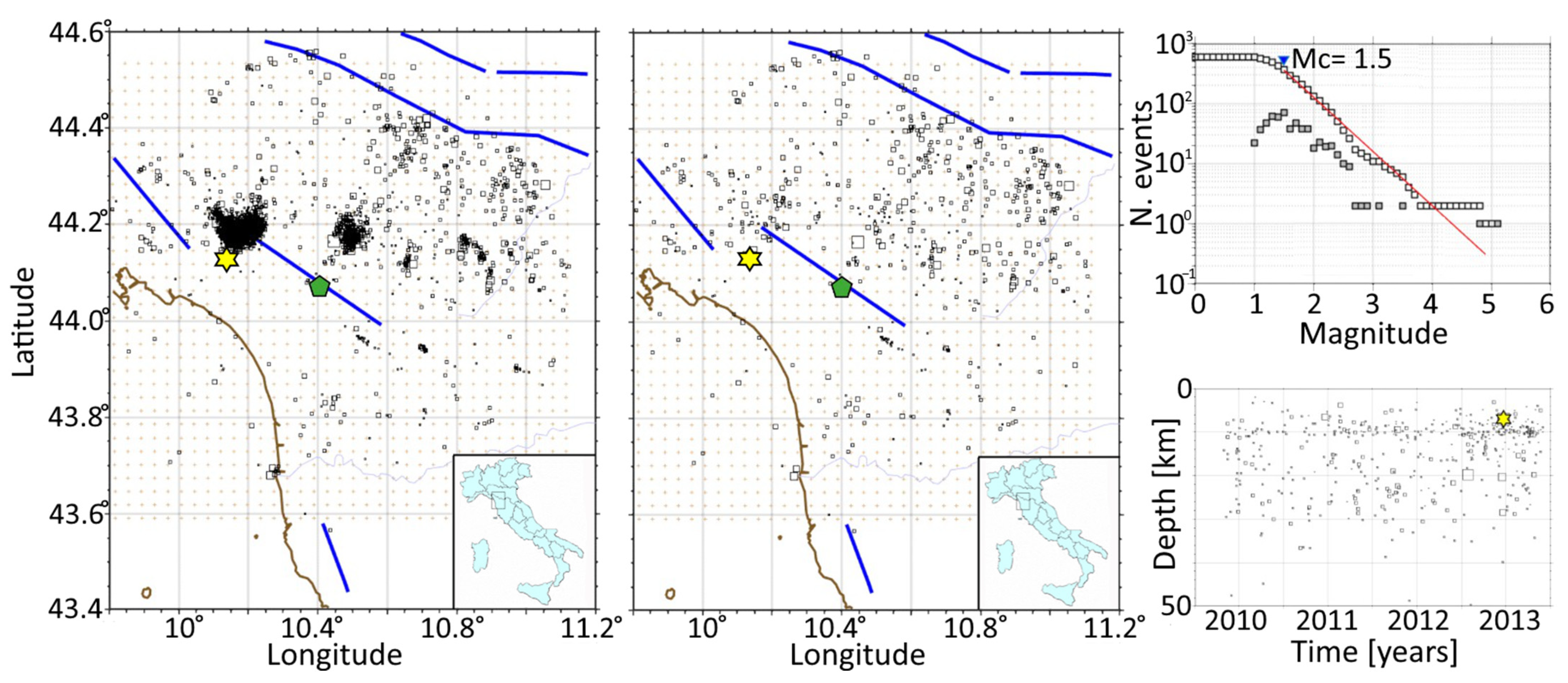
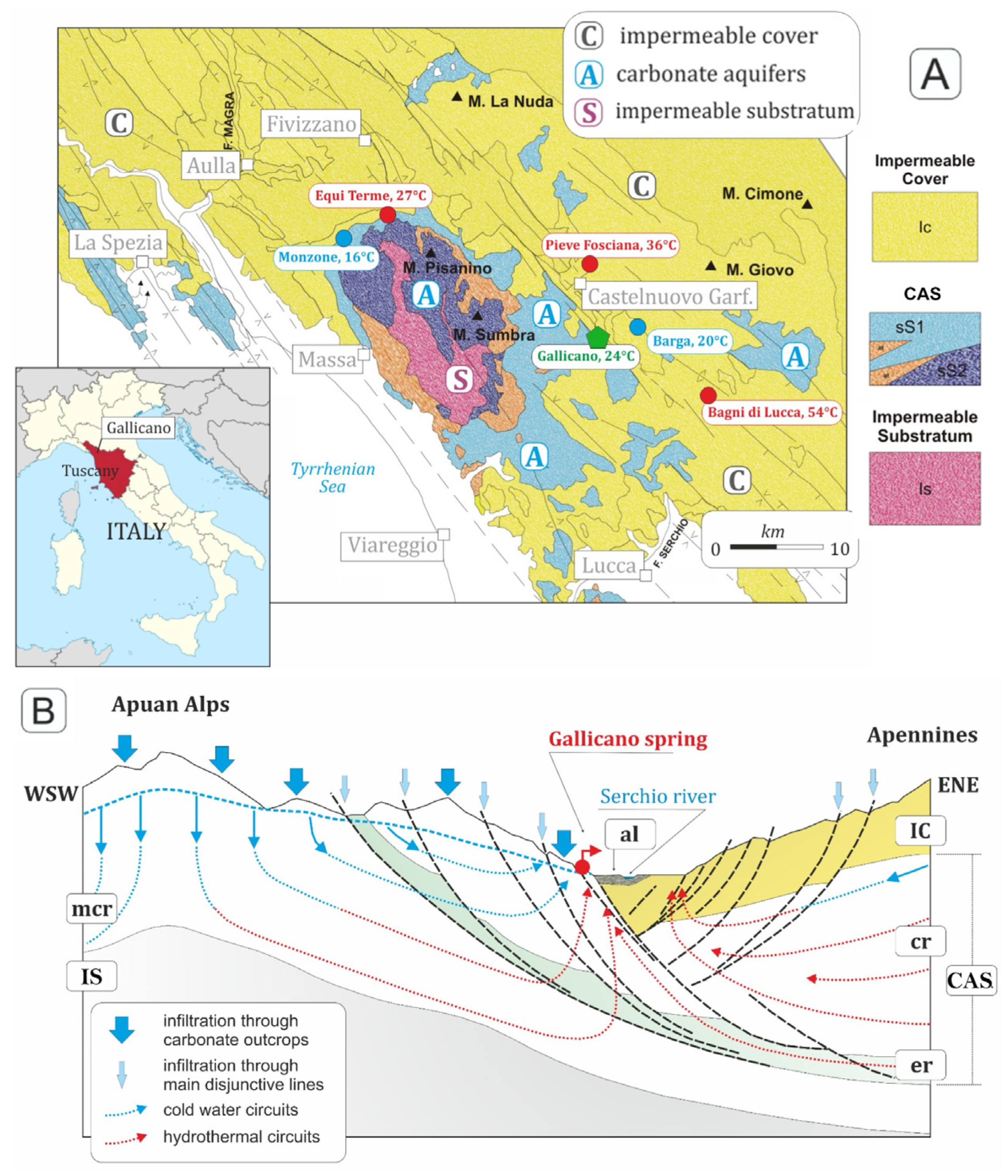
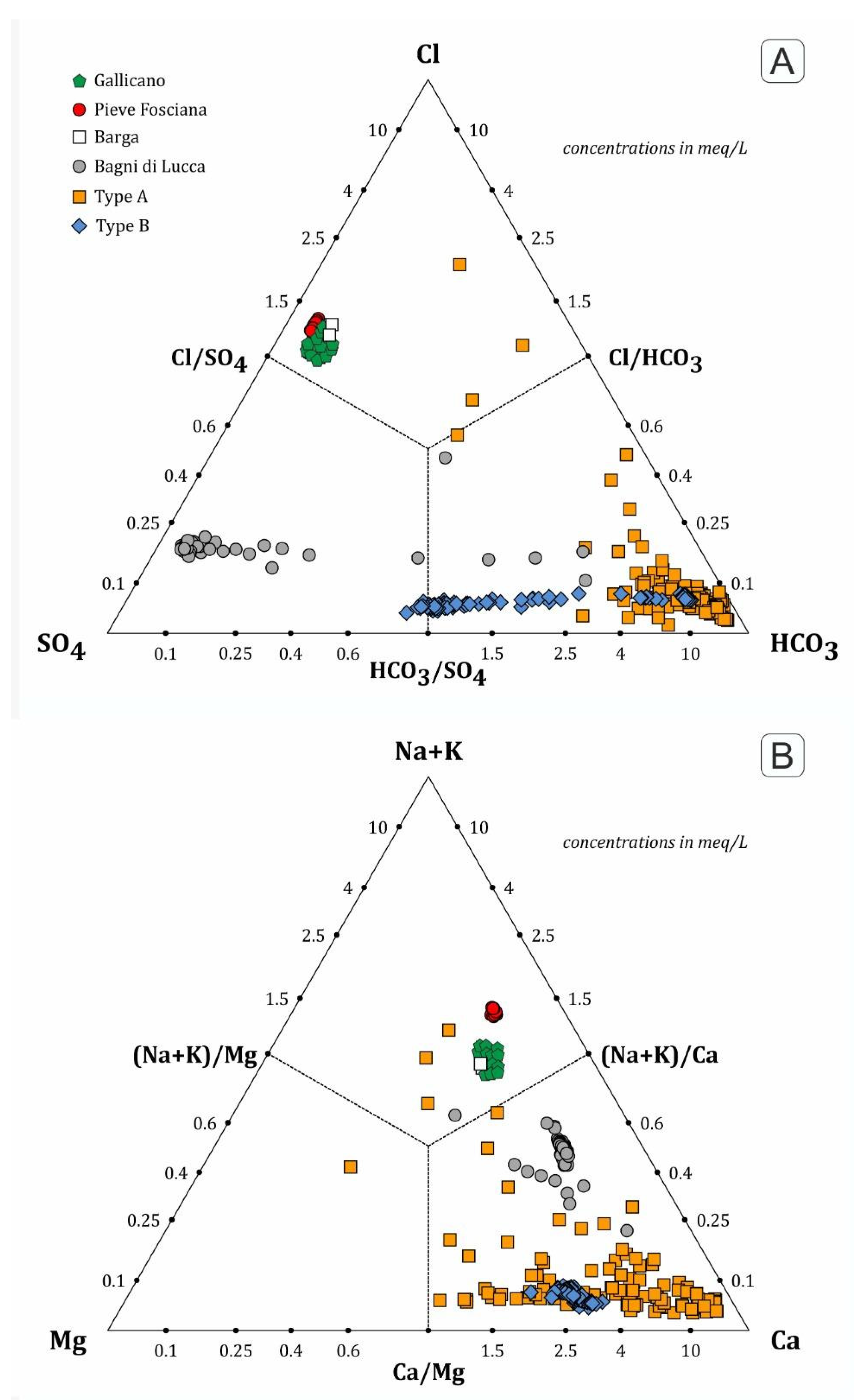
N.Date and Time
[YYYY-MM-DD hh:mm:ss]		Latitude
[°]		Longitude
[°]		Depth
[km]		Magnitude Ml (INGV)Magnitude MW (2) (* USGS)Distance from Gallicano [km]Lf
[km]		D/Lf
12010-07-14 09:10:4210.363043.88507.42.42.720.30.2581.2
22010-11-03 15:28:4810.581044.111010.31.92.4130.1776.47
32010-12-29 02:15:3510.510043.98405.32.12.510.30.251.5
42011-04-15 01:39:1510.433044.129010.71.52.17.80.1265
52011-05-22 12:26:4810.461044.03904.90.71.63.20.0745.71
62011-06-19 14:35:3410.815044.15206.53.63.532.20.6351.11
72011-07-12 04:11:3910.432044.01101.30.81.75.50.0778.57
82011-07-17 21:50:5710.567044.239017.02.42.722.50.2590
92011-08-20 20:02:4810.893044.07503.92.93.136.70.3799.19
102011-09-19 06:24:1610.763044.27209.82.62.935.40.29122.07
112011-10-26 16:26:2810.776044.143012.42.42.729.20.25116.8
122011-11-06 01:33:5910.682044.148017.52.32.732.20.23140
132012-01-22 05:31:1510.474044.111010.11.92.46.60.1738.82
142012-03-19 19:33:0310.123044.24205.02.72.932.50.32101.56
152012-03-24 19:18:0410.273044.316019.02.8331.50.3492.65
162012-04-12 23:01:4810.573044.313022.33.13.230.50.4370.93
172012-04-13 22:13:5610.896044.08309.53.33.337.10.574.2
182012-05-18 20:10:5210.175244.17579.12.42.724.50.2598
192012-05-20 02:03:5311.228044.88906.365.9 *113.711.299.55
202012-05-29 07:00:0311.086044.85108.15.85.8 *103.48.5712.06
212012-08-28 01:56:1410.660544.095816.22.42.718.70.2574.8
222012-11-26 19:18:5510.674244.117821.63.23.320.50.4644.56
232012-12-04 16:38:2711.009044.13638.82.93.146.80.37126.49
242012-12-16 11:24:2710.443744.12587.01.62.27.50.1357.69
252013-01-25 14:48:1810.445844.164319.84.84.9 *11.62.484.68
262013-02-09 02:19:1010.368544.07856.11.72.35.60.1537.33
272013-02-20 11:09:5910.530044.156813.53.03.113.40.433.5
282013-03-29 12:59:2110.418744.12228.41.72.37.20.1548
292013-04-01 23:35:1110.476344.195314.82.02.515.50.1886.11
302013-04-05 03:23:4210.506544.166215.02.32.713.20.2357.39
312013-04-08 11:38:5710.516044.157813.52.62.912.90.2944.48
322013-05-02 17:10:1410.453744.08376.81.52.13.10.1225.83
332013-05-13 18:35:4710.446243.84038.32.52.824.30.2790
342013-06-03 15:33:1210.441844.119310.01.82.36.70.1641.87
352013-06-14 18:22:2311.054344.281220.33.73.655.40.6881.47
362013-06-15 19:41:1610.146244.148210.43.43.6 *25.20.3181.29
372013-06-19 10:51:0710.713844.419328.53.53.5 *45.80.36127.22
382013-06-21 10:33:5710.135744.13087.05.15.1*25.13.267.7
392013-06-23 13:24:0110.200844.16839.24.44.4 *22.31.2417.98
402013-06-29 05:21:3410.169844.15135.93.53.523.50.5840.52
412013-06-30 02:57:4210.186744.15956.14.54.5 *22.81.4315.94
422013-07-09 09:12:5710.177744.16256.23.13.223.70.4355.12
432013-07-12 18:07:2210.106744.201710.03.53.530.60.5852.76
442013-08-10 13:11:0910.239344.19625.82.72.921.90.3268.44
452013-08-14 15:35:5010.190344.17589.33.53.5 *23.50.3665.28
462013-08-21 05:32:1310.580744.248515.42.8324.10.3470.88
472013-10-03 19:07:1510.327044.215010.12.22.619.50.2192.86
482013-10-19 12:29:3510.263843.680710.53.53.543.70.5875.34
492013-10-25 09:17:0010.501244.258219.83.13.222.80.4353.02
502013-11-19 21:05:4810.700343.94535.02.22.625.20.21120
Table 2. Descriptive statistic for the parameters monitored continuously at the Gallicano station.
Table 2. Descriptive statistic for the parameters monitored continuously at the Gallicano station.
MeanMedianMinimumMaximumStd. Dev
Temperature (°C)22.522.620.423.70.76
Electrical Conductivity (µS/cm)5444557140076088461
pH6.976.976.897.070.03
ORP (mV)38739317146138.8
CO2 (%)2.372.191.465.060.60
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Pierotti, L.; Fidani, C.; Facca, G.; Gherardi, F. Cross-Correlation among Seismic Events, Rainfalls, and Carbon Dioxide Anomalies in Spring Water: Insights from Geochemical Monitoring in Northern Tuscany, Italy. Water 2024, 16, 739. https://doi.org/10.3390/w16050739

AMA Style

Pierotti L, Fidani C, Facca G, Gherardi F. Cross-Correlation among Seismic Events, Rainfalls, and Carbon Dioxide Anomalies in Spring Water: Insights from Geochemical Monitoring in Northern Tuscany, Italy. Water. 2024; 16(5):739. https://doi.org/10.3390/w16050739

Chicago/Turabian Style

Pierotti, Lisa, Cristiano Fidani, Gianluca Facca, and Fabrizio Gherardi. 2024. "Cross-Correlation among Seismic Events, Rainfalls, and Carbon Dioxide Anomalies in Spring Water: Insights from Geochemical Monitoring in Northern Tuscany, Italy" Water 16, no. 5: 739. https://doi.org/10.3390/w16050739

APA Style

Pierotti, L., Fidani, C., Facca, G., & Gherardi, F. (2024). Cross-Correlation among Seismic Events, Rainfalls, and Carbon Dioxide Anomalies in Spring Water: Insights from Geochemical Monitoring in Northern Tuscany, Italy. Water, 16(5), 739. https://doi.org/10.3390/w16050739

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop