Comparing Remote Sensing and Geostatistical Techniques in Filling Gaps in Rain Gauge Records and Generating Multi-Return Period Isohyetal Maps in Arid Regions—Case Study: Kingdom of Saudi Arabia
Abstract
:1. Introduction
- Selecting an appropriate technique to fill the data gaps in the rain gauge records for the study area.
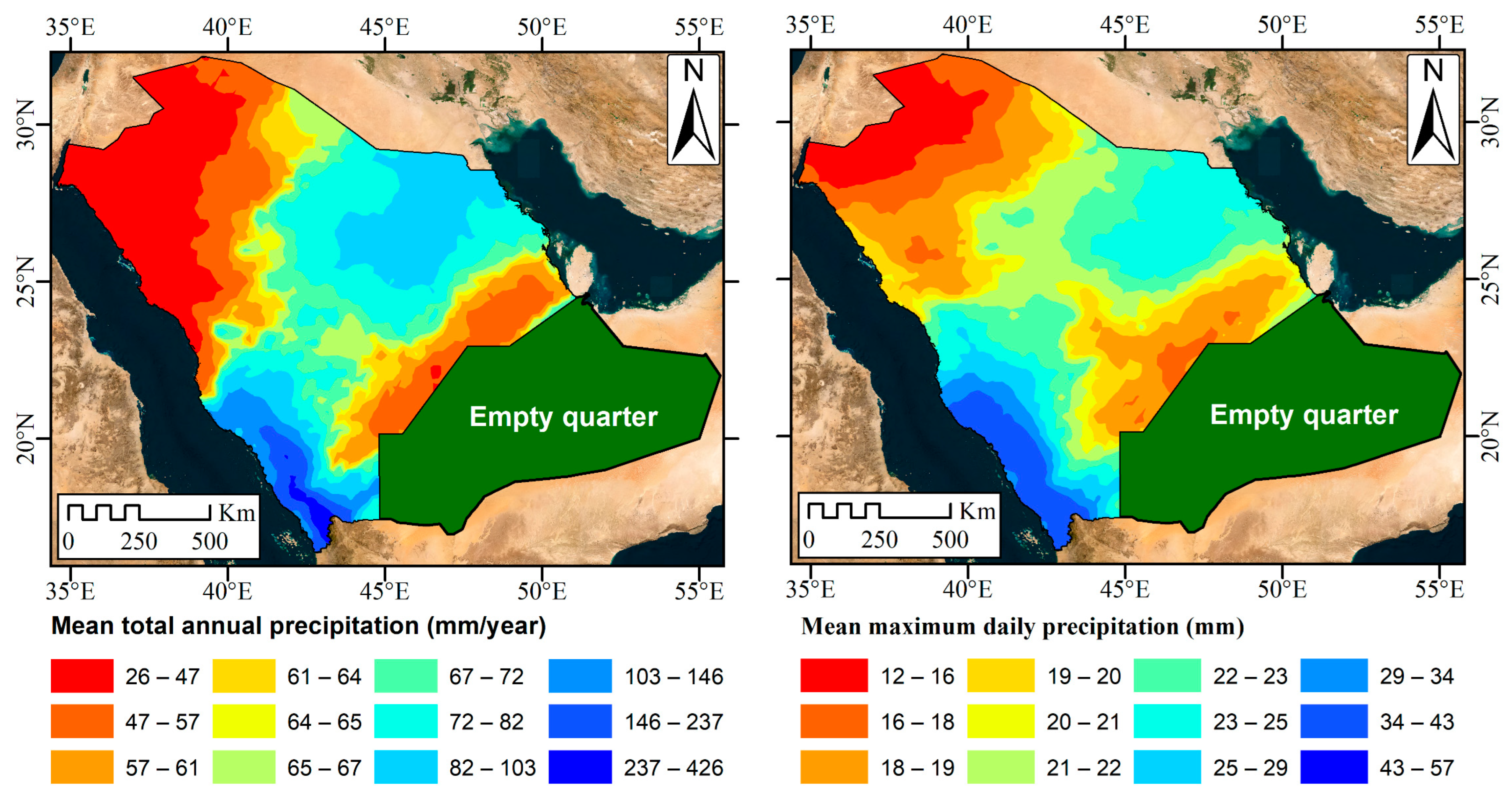
- Providing gap-free spatial distribution of gridded total annual and maximum daily precipitation to overcome the deficiency in rain gauge coverage.
- Performing frequency analysis for the maximum daily gridded data to generate storm isohyetal maps with different return periods across the Kingdom of Saudi Arabia (KSA).
| Satellite Precipitation Datasets (SPDs) | Start Date | Coverage | Resolution | |
|---|---|---|---|---|
| [CHIRPS] Climate Hazards group Infra-Red Precipitation combined with terrestrial Stations observations [24]. | January 1981 | 50°-N | 50°-S | 0.05°/(Daily) |
| [PERSIANN] Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks [25]. | March 2000 | 60°-N | 60°-S | 0.25°/(Hourly) |
| [PERSIANN-CCS] PERSIANN-Cloud Classification System [25]. | January 2003 | 60°-N | 60°-S | 0.04°/(Hourly) |
| [PERSIANN-CDR] PERSIANN—Climate Data Record [25]. | January 1983 | 60°-N | 60°-S | 0.25°/(Daily) |
| [PDIR-Now] PERSIANN—Dynamic Infrared Rain Rate near real-time [25]. | March 2000 | 60°-N | 60°-S | 0.04°/(Hourly) |
| [TRMM *] The Tropical Rainfall Measuring Mission [26]. | January 1998 | 50°-N | 50°-S | 0.25/(3-h) |
| [CMORPH] Climate Prediction Center morphing method [27]. | January 1998 | 60°-N | 60°-S | 0.07/(30-min) |
| [GPM-IMERG] Global Precipitation Measurement mission Integrated Multi-satellitE Retrievals [28]. | June 2000 | 90°-N | 90°-S | 0.1/(30-min) |
| [GPCP] Global Precipitation Climatology Center [29]. | January 2000 | 90°-N | 90°-S | 0.5/(Daily) |
| [CPC] Climate Prediction Center [30]. | January 1979 | 89.5°-N | 89.5°-S | 0.5/(Daily) |
- The performance of SPDs is highly dependent on rainfall variability. Many datasets underestimate precipitation during wet seasons and overestimate it during dry ones.
- The majority of SPDs showed a better correlation with coarse temporal resolution (more than one-day resolution) compared to daily and sub-daily records, but displayed improved accuracy when using finer-resolution data.
- In high-altitude areas, SPDs demonstrated lower performance compared to lower altitudes.
- The performance of SPDs varies from one area to another and within the same area from one season to another.
- (A)
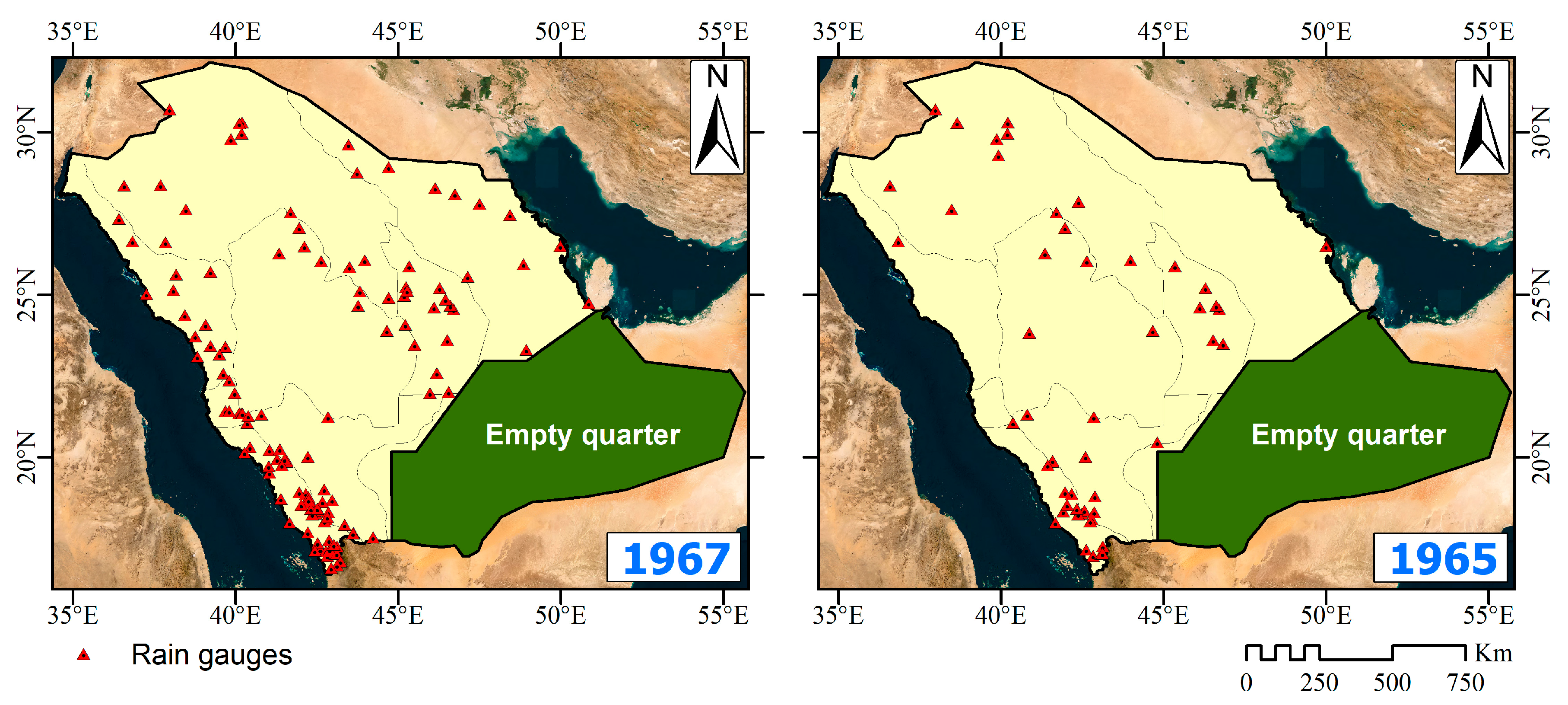
- Sparse Rain Gauge Coverage: Traditional rain gauge networks in arid regions often suffer from inadequate spatial distribution, resulting in limited data coverage and gaps.
- (B)
- Data Gaps: Furthermore, existing rain gauge data may contain gaps due to various factors, further complicating data analysis and interpretation.
- Geostatistical Interpolation: Leveraging geostatistical interpolation techniques, we aim to extrapolate rainfall estimates for ungauged locations, thereby enhancing the overall understanding of rainfall distribution patterns.
- Utilizing Satellite Precipitation Data: Additionally, we explore the utilization of satellite precipitation data as a supplementary source. While not as precise as conventional rain gauges, satellite data offers broader spatial coverage and has the potential to fill data gaps, thereby complementing traditional approaches.
2. Materials and Methods
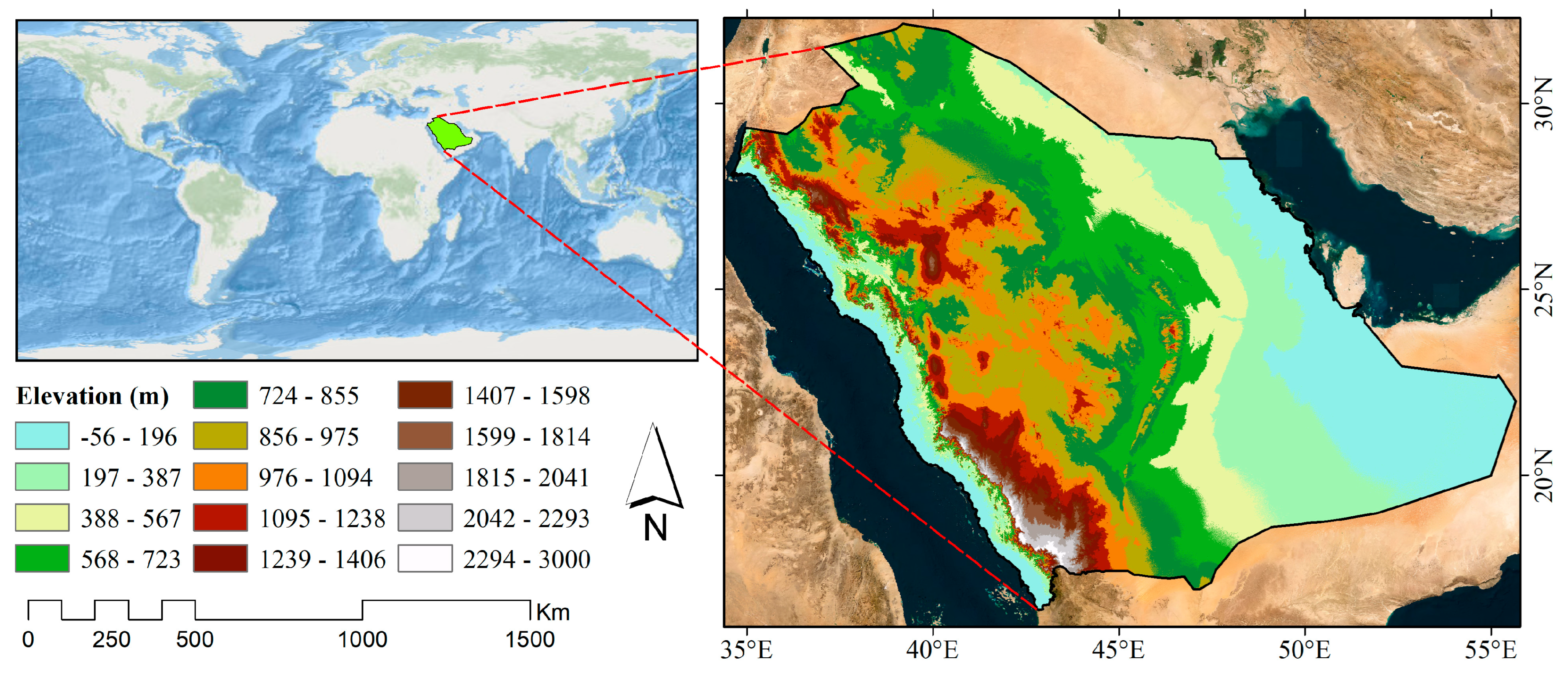
2.1. Study Area
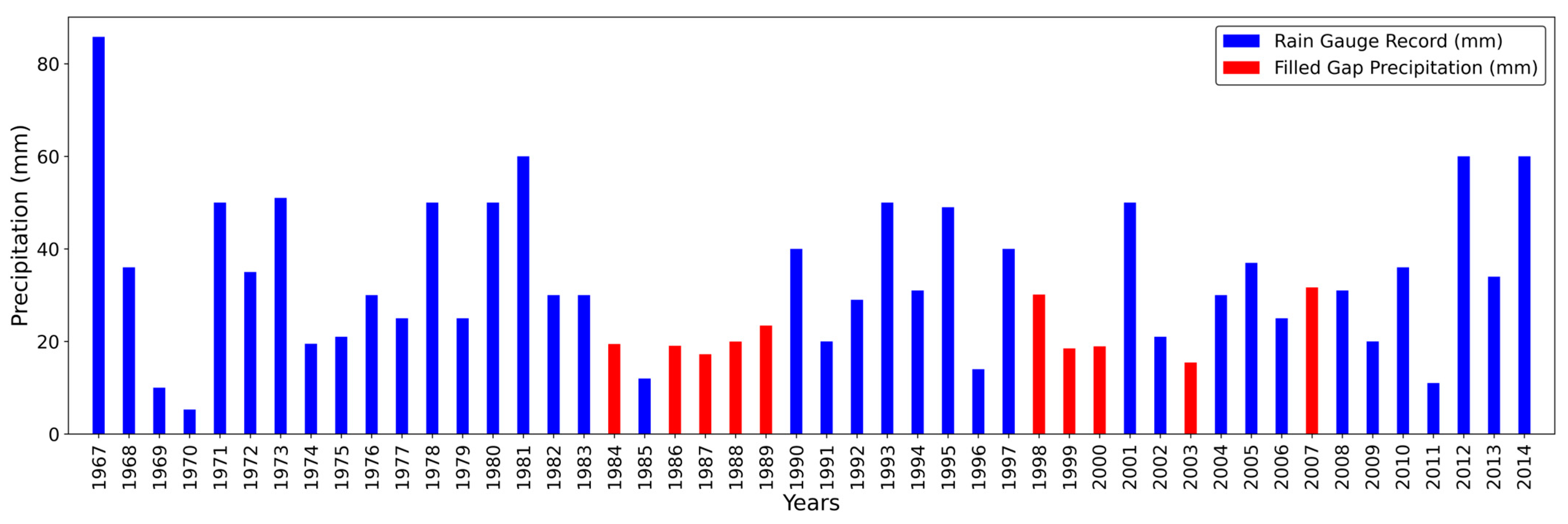
2.2. Rain Gauges
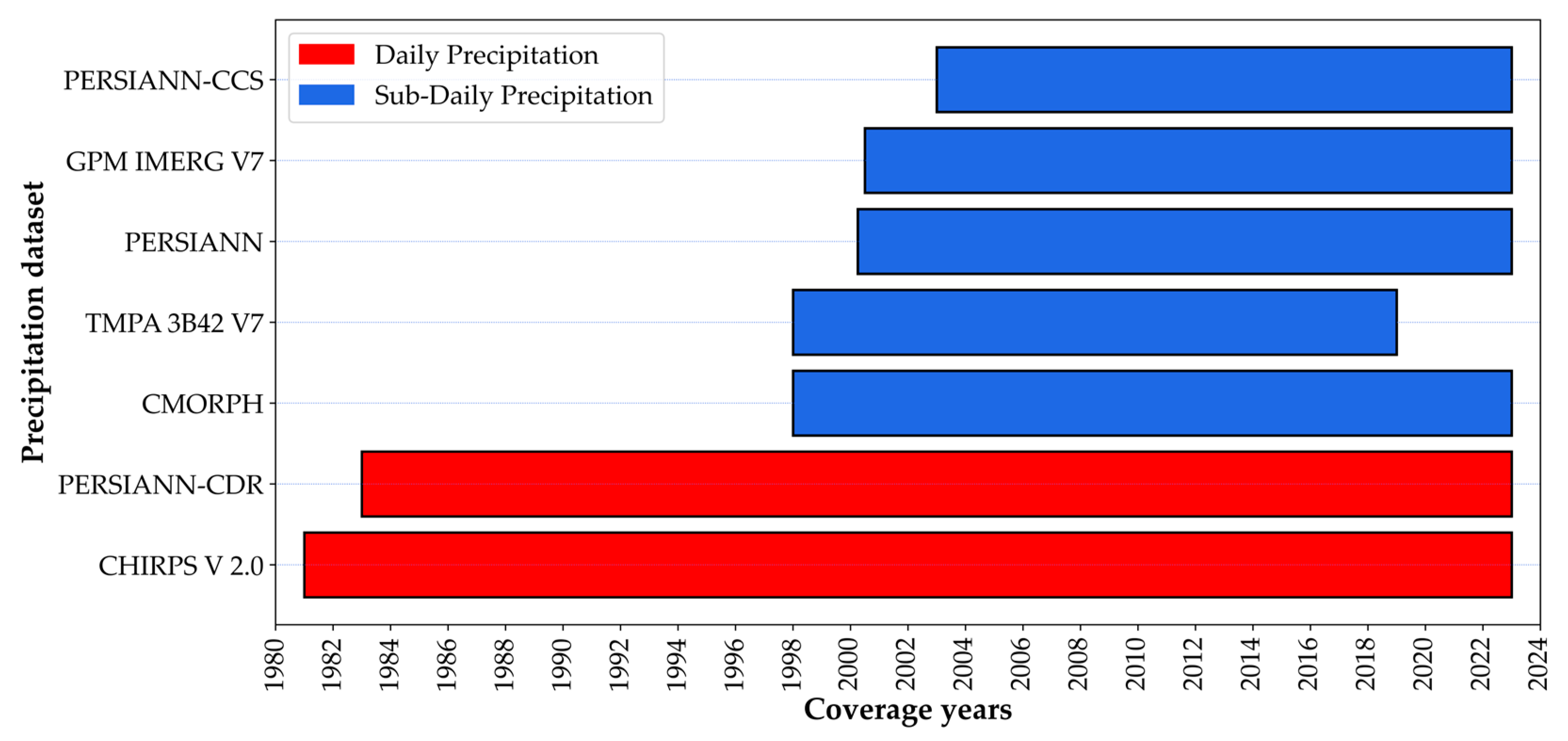
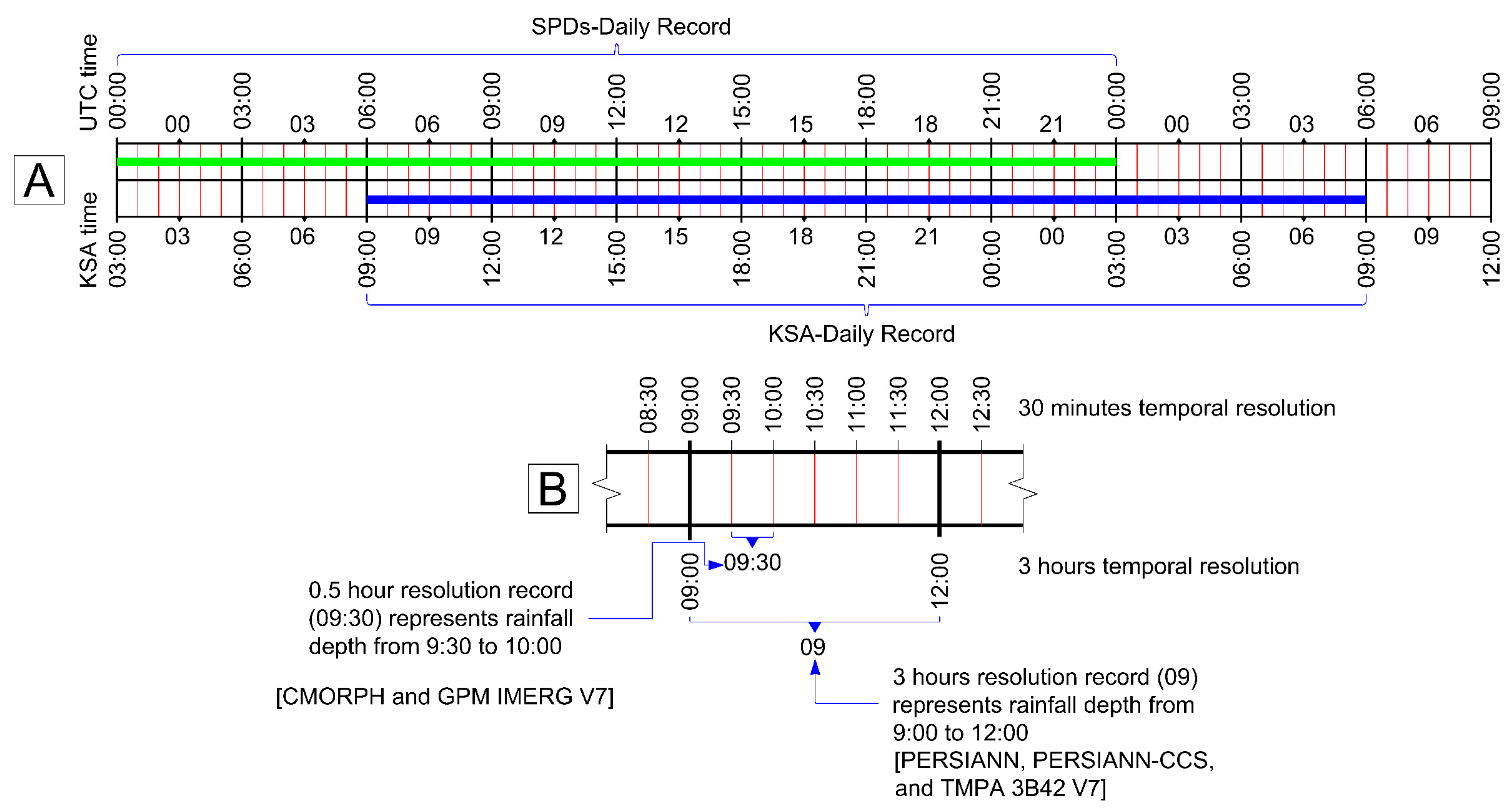
2.3. Satellite Data
- PERSIANN dataset which is available in hourly, 3-hourly, 6-hourly, daily, monthly, and annual temporal resolution from March 2000 to the near present with spatial distribution.
- PERSIANN-CDR dataset which is available in daily, monthly, and annual temporal resolution from January 1983 to the near present with spatial distribution.
- PERSIANN-CCS dataset which is available in hourly, 3-hourly, 6-hourly, daily, monthly, and annual temporal resolution from January 2003 to the present with spatial distribution.
2.4. Interpolation of Ground Station Data
- are the measured values at locations , respectively.

- : Semivariance at distance h
- The range is the distance between two measured values that, when exceeded, the semivariogram is flattened and the two points are no longer correlated.
- The nugget is the value of variance in a very short distance.
- The sill is the maximum variance located at a distance .
- The partial sill is the difference between the sill and the nugget values.
| Model | Equation | ||
|---|---|---|---|
| Circular | (2) | ||
| Spherical | (3) | ||
| Exponential | (4) | ||
| Gaussian | (5) | ||
| K-Bessel | (6) | ||
| J-Bessel | (7) | ||
| Stable | (8) | ||
- : the estimate of the variable of interest at the location.
- the measured value of the variable of interest at the location.
- the weight of .
3. Results and Discussion
- and are the predicted values and average value of the variable respectively.
- n/; is the number of records.
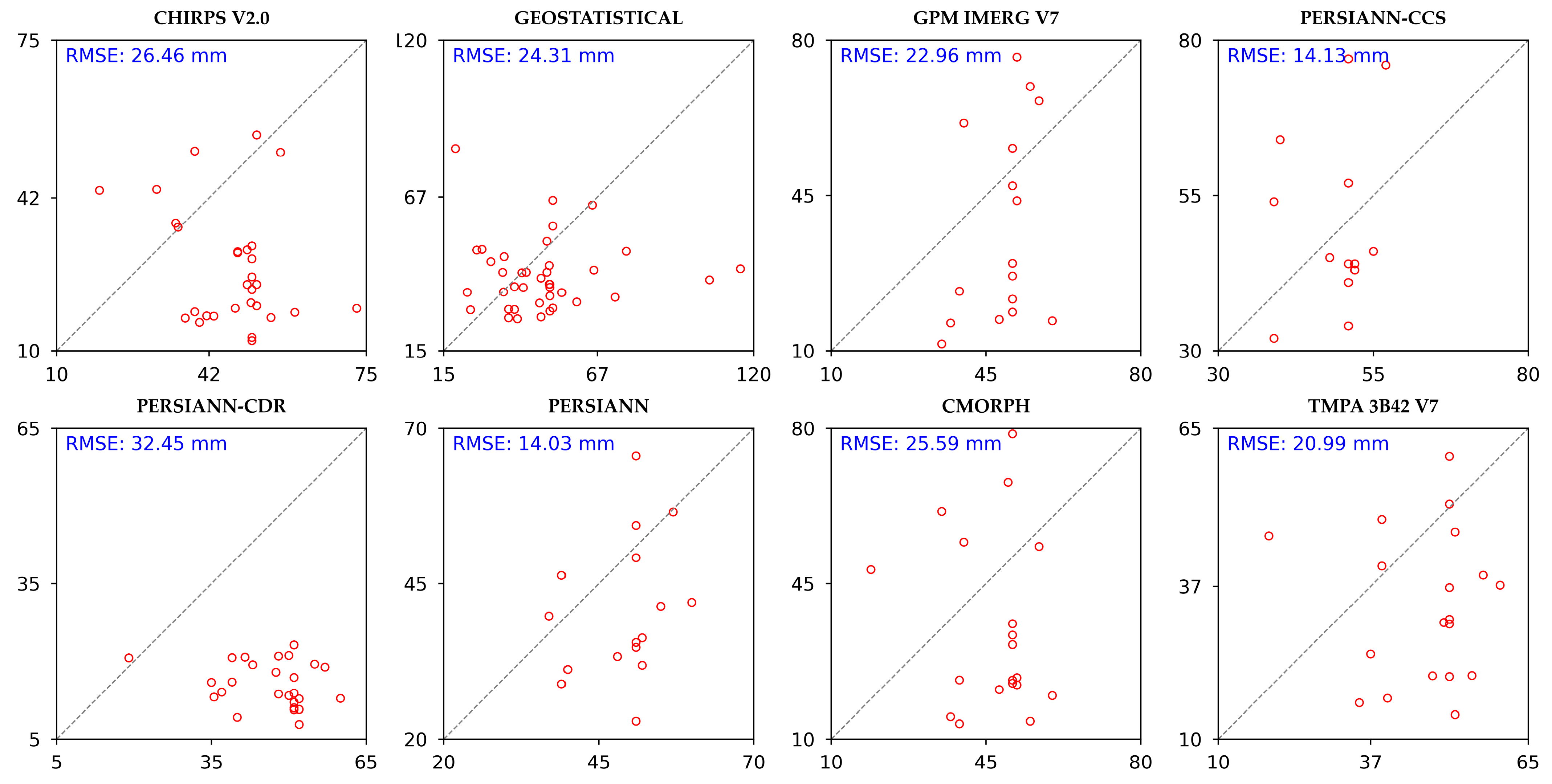

- is the number of observations, and equals 48 in the case of gap-filled data series.
- is the number of observations in the class interval i.
- is the expected number of observations in the class interval (i) according to the tested PDF.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Study Type Location | Datasets | Gauges Study Accuracy | Study Period | Main Findings |
|---|---|---|---|---|
| Combined study Tapajos River basin—Amazon | TRMM 3B42 | 118 RG.&23 FG. Daily and Monthly | 1998–2006 for rain 2000–2003 for Flow | The TRMM estimates closely align with those obtained from the rain gauge record when averaged over the entire basin. The generated modeled hydrographs demonstrated acceptable accuracy, as evidenced by the comparison with 23 flow gauges within the basin [105]. |
| Statistical study Iran | TRMM 3B42 | Grid-1 Daily, Seasonal, Annual | 1998–2006 | The TRMM 3B42 data showed a weak correlation with daily records but displayed improved accuracy when assessing annual data. However, it tended to underestimate the average annual precipitation [106]. |
| Combined study Gilgel Abay basin-Ethiopia | CMORPH, TMPA 3B42RT, TMPA 3B42, PERSIANN | 4 RG.&1 FG. Daily and Monthly | 2006–2007 | Datasets utilizing microwave data (such as CMORPH and TMPA 3B42RT) consistently exhibit superior streamflow modeling, displaying a bias on the order of 53%. In contrast, the PERSIANN dataset, which relies on infrared data, demonstrates lower performance with a bias of 83%. Among these datasets, TMPA 3B42, which integrates both satellite and ground gauge data, exhibits the lowest performance, showing a bias of 8% [107]. |
| Statistical study China | PERSIANN-CDR | Grid-2 daily | 1983–2006 | PERSIANN-CDR effectively captured the spatial and temporal daily extreme rainfall characteristics, especially in the humid Manson region of eastern China. However, its performance notably diminished in arid and mountainous terrains, such as the Tibetan Plateau in the west and the Taklamakan Desert in the northwest [108]. |
| Statistical study 9 watersheds all over the world | 10 Datasets | 1052 RG. Daily, Monthly, Annual | 2000–2013 | The performance of satellite precipitation datasets is highly dependent on rainfall variability. Many datasets underestimate precipitation during wet seasons and overestimate it during dry ones [109]. |
| Statistical study Iraq | TRMM-3B42 | 4 RG. Monthly | 2000–2010 | A high correlation was observed between TMPA3B42 and ground stations at the monthly temporal scale. There was an overestimation of TRMM rainfall estimates recorded in most of the rainy months [110]. |
| Statistical study Iran | TMPA-3B42V7, PERSIANN, CMORPH | Grid-3 Daily and Monthly | 2003–2008 | TRMM TMPA 3B42 v7 demonstrates superior performance compared to the other two datasets across all the examined regions in Iran [111]. |
| Hydrological Gandak Himalayan River-China | TMPA 3B42 V7 | 5 FG.-Daily | 2000–2010 | The TRMM 3B42 dataset proves effective in hydrological modeling for rainfall intensities categorized as moderate to heavy (ranging from 7.5 to 124.4 mm/day). However, its performance is limited for both light rainfall (less than 7.5 mm/day) and extremely heavy rainfall (greater than 124.4 mm/day) intensities [112]. |
| Statistical study East India | IMERG V6, TRMM-TMPA-3B42 V7,GSMap V6 | Grid-4 Daily | June 2014 to September 2014 | Low correlation coefficients were reported between daily data and all datasets. IMERG and GSMap demonstrated superior performance compared to the TMPA dataset in detecting light rain events. Significant uncertainty is associated with all satellite-based precipitation products in regions characterized by orographic-dominated precipitation [113]. |
| Statistical study China | CHIRPS | Grid-5 Daily | 1981–2014 | CHIRPS exhibited superior performance during high-intensity rainfall events when contrasted with low-intensity rainfall in arid regions. Its accuracy is notably influenced by the movement of the monsoon. Additionally, CHIRPS datasets demonstrated better performance in the basins of southern China in comparison to those in northwestern and northern China [114]. |
| Statistical study KSA | GPM-IMERG (early, late, final) runs | 189 RG. Daily | October 2015 to April 2016 | The IMERG early run demonstrated satisfactory accuracy in the central, eastern, and certain western regions of KSA. However, notable fluctuations in accuracy were observed in other areas. Conversely, the final run exhibited improved accuracy in the southern and western regions but revealed higher errors in the northern and central parts [115]. |
| Statistical study China | TMPA-3B42V7, CMORPH-CRT, GPM-IMERG-V05B, GPM-IMERG-V04A | 542 RG. Daily, Seasonal, Annual | March 2014 to February 2017 | All datasets underestimated the depth of rainfall over the mountainous Tibetan Plateau and Xinjiang province, except IMERG V04A. IMERG V05B showed an improvement in rectifying the underestimation observed in IMERG V04A. IMERG demonstrated superior capabilities in detecting rainfall events compared to the other datasets. There is potential for enhancement in all datasets, especially in arid regions and high-altitude areas [116]. |
| Statistical study China | GPM IMERG (03, 04, 05) | Grid-6 Hourly and Daily | June 2014 to May 2015 | The final runs of IMERG V04 and V05 showed significant improvements compared to V03, except in the mountainous regions of the Tibetan Plateau and Xinjiang province [117]. |
| Statistical study KSA | PERSIANN-CDR, PERSIANN, TMPA-3B42, CMORPH | 29 RG. Daily and Monthly | 2003–2011 | All satellites exhibited superior performance during wet seasons compared to dry ones. Gauge-adjusted datasets (PERSIANN-CDR and TRMM 3B42) demonstrated a higher accuracy in detecting rainfall occurrences compared to the other unadjusted datasets [36]. |
| Combined study Meki and Ketar Basins-Ethiopia | CFSR, CHIRPS, PERSIANN-CDR, TMPA 3B42 V7 | 9 RG.&2 FG. Daily and Monthly | 1985–2004 | The CHIRPS dataset outperformed the other datasets in the statistical assessment of rainfall depth, as well as in the daily and monthly simulation of streamflow. Conversely, the reanalysis product CFSR exhibited the poorest performance, characterized by the highest mean error and relative biased ratio [118]. |
| Statistical study Egypt | GSMap, GPM-IMERG, CHIRPS | 29 RG. Daily | March 2014 to May 2018 | No consistent performance was observed among the tested datasets. CHIRPS exhibited the highest accuracy in predicting rainfall amounts [119] |
| Statistical study China | TMPA-3B42, GPM-IMERG | 830 RG. Daily | 2000–2017 | Both datasets captured the spatial pattern of extreme events, with an underestimation of extreme rainfall rates. The IMERG dataset demonstrated slightly better accuracy compared to the TMPA. The performance was notably superior in humid areas, while it showed a reduction in accuracy in arid and mountainous regions [120]. |
| Statistical study Upper Ganga River-India | TMPA 3B43 V7 | Grid-5 Monthly | 1998–2013 | TMPA underestimated precipitation amounts exceeding 400 mm and overestimated precipitation within the range of 100 to 370 mm. The correlation coefficients were higher during the post-monsoon and winter seasons compared to the pre-monsoon and monsoon seasons, with values of 0.65 and 0.57, respectively [121]. |
| Statistical study Mexico | CMORPH-CRT | 14 RG. 30 min and Daily | 2000–2018 | CMORPH-CRT exhibits a low to moderate correlation with rain gauge records, often associated with an overestimation of rainfall depth. Furthermore, CMORPH-CRT tends to overstate the frequency of precipitation events [122]. |
| Statistical study Zambezi Basin-South Africa | CMORPH | 66 RG. Daily, Weekly, Seasonal | 1998–2013 | The CMORPH dataset detects rainfall occurrences with 60% accuracy. It demonstrates higher precision during wet seasons in contrast to dry periods. Moreover, the predictive accuracy at a weekly temporal scale surpasses that of the daily scale [123]. |
| Statistical study Fincha & Neshe Basins-Blue Nile-Ethiopia | CHIRPS | 6 RG. Monthly, Seasonal, Annual | 1991–2015 | CHIRPS tends to overestimate precipitation in high-altitude regions while underestimating it in lower-altitude areas. Despite its coarse temporal resolution, which exceeds daily intervals, CHIRPS demonstrates satisfactory performance in satellite-based estimates of rainfall [124]. |
| Combined study Eastern Nile Basin-East Africa | TMPA-3B42V7 and CHIRPS | 35 RG.&3 FG Daily and Monthly | 1998–2007 | Although both datasets exhibit similar performance in terms of false alarm ratio (FAR), the TMPA 3B42 V7 demonstrates a higher probability of detection (POD) compared to CHIRPS. Both datasets yield satisfactory accuracy when simulating monthly discharge at the Blue Nile flow stations using the Hydro-Beam distributed hydrological model [125]. |
| Hyd. study Volta River basin-West Africa | 17 Datasets | 11 FG.-Daily | 2003–2012 | There is not a single precipitation dataset that can be considered the most effective for all hydrological processes. However, when it comes to evaluating daily streamflow, TAMSAT, CHIRPS, and PERSIANN-CDR exhibited the highest performance [126]. |
| Statistical study Bali Island | GSMap, IMERG, CHIRPS | 27 RG. Daily, Pentadal, Monthly, Seasonal | 2015–2017 | The datasets offer imprecise representations of the occurrence rates of light and heavy rainfall, defined as depths less than 1 mm per day and greater than 50 mm per day, respectively. Conversely, they tend to overestimate the frequency of moderate rainfall events, which range from 5 to 10 mm per day. Among the three datasets, IMERG demonstrated superior performance [127]. |
| Statistical study Shuaishui River Basin-China | GPM IMERG V6,TMPA 3B42V7 | 13 RG. Hourly, Daily, Monthly | 2009–2017 | The accuracy in estimating monthly precipitation was superior in both datasets compared to other temporal resolutions. The GPM dataset outperformed the TRMM dataset in estimating daily rainfall precipitation. However, neither dataset was able to satisfactorily estimate hourly rainfall [128]. |
| Statistical study Brazilian Amazonia | CHIRPS | 45 RG. Monthly and Annual | 1981–2017 | The CHIRPS datasets yield underestimated values for precipitation depth during the rainiest months. As a result, it was determined that CHIRPS is insufficient for accurately depicting rainfall trends in the study area [129]. |
| Statistical study Nigeria | 16 satellite precipitation estimates | 11 RG. Monthly | 2000–2012 | The precipitation estimates from IMERG-Final-V6 and Multi-Source Weighted-Ensemble Precipitation (MSWEP) v.2.2 demonstrated superior performance compared to other methods, thus making them the recommended choices for future hydrological studies [130]. |
| Combined study Ganjiang River Basin-China | TMPA 3B42, PERSIANN, CMORPH, CHIRPS | 36 RG.&9 FG Daily and Monthly | 1998–2014 for rain 2000–2014 for flow | CMORPH demonstrates the highest accuracy in capturing daily precipitation, while TMPA 3B42 exhibits the best performance in providing monthly precipitation data. Both datasets outperform PERSIANN and CHIRPS in capturing extreme precipitation events. Additionally, TMPA 3B42 yields the most accurate hydrologic model, as evidenced by the H17 streamflow results [131]. |
| Combined study West Rapti River basin-Nepal | PERSIANN-CCS, CHIRPS, IMERG | 18 RG.&3 FG. Daily and Monthly | 1981–2015 | All satellite data exhibited a noteworthy false alarm ratio. Among the satellite datasets, IMERG data outperformed the others in accurately estimating rainfall depth and simulating stream discharge. On the contrary, PERSIANN-CCS demonstrated a notable tendency to underestimate rainfall depth [132]. |
| Statistical study South Korea | CMORPH | 48 RG. Hourly, Daily, Monthly, Annual | 1998–2015 | CMORPH tends to underestimate precipitation in South Korea, with the extent of underestimation differing across various regions. Coastal areas show lower accuracy compared to inland regions. Estimates for precipitation during wet seasons are generally more reliable than those for dry seasons. Accuracy at annual-to-daily resolution levels is satisfactory, but adjustments may be necessary at the hourly resolution [133]. |
| Statistical study Thailand | TMPA 3B42V7, CMORPH | 91 RG. Daily, Monthly, Annual | 1998–2012 | TRMM and CMORPH exhibited limited capability in capturing the features of extreme events. Overall, TRMM demonstrated superior performance compared to CMORPH in depicting precipitation patterns for the north, northeast, east, and south regions of Thailand. Both datasets showed similar performance in central Thailand [134]. |
| Combined study Beijiang, Huai, and Liao River basins-China | CHIRPS, PERSIANN-CDR, TMPA 3B42 V7 | GRID-7 &3 FG. Daily, Monthly, Annual | 2002–2015 | The monthly precipitation estimates outperformed the daily estimates across all three datasets. TRMM 3B42 V7 demonstrated the highest accuracy, followed by CHIRPS. When simulating streamflow, these datasets exhibited superior performance in regions with higher humidity compared to arid areas. Specifically, TMPA 3B42 V7 exhibited the best performance in humid regions, while PERSIANN-CDR performed best in arid regions [135]. |
| Statistical study Tibetan plateau-China | TMPA-3B42V7, CMORPH, IMERGV05 | 87 RG. Monthly and Annual | 2001–2016 | At the monthly scale, all datasets exhibited stronger correlations compared to the annual scale. GPM demonstrated superior performance compared to TRMM and CMORPH. However, all three datasets displayed a tendency to underestimate annual precipitation [136]. |
| Statistical study Punjab province-Pakistan | PERSIANN-CCS, PERSIANN-CDR SM2RAIN-ASCAT CHIRPS-2.0 | 26 RG. Daily, Monthly, Seasonal, Annual | 2010–2018 | All datasets exhibited superior performance in the northern region of Punjab Province in comparison to other areas. The alignment of all datasets with monthly gauge records surpassed that with daily records. CHIRPS-2.0 and SM2RAIN-ASCAT demonstrated higher performance across all seasons when compared to PERSIANN-CCS and PERSIANN-CDR [137]. |
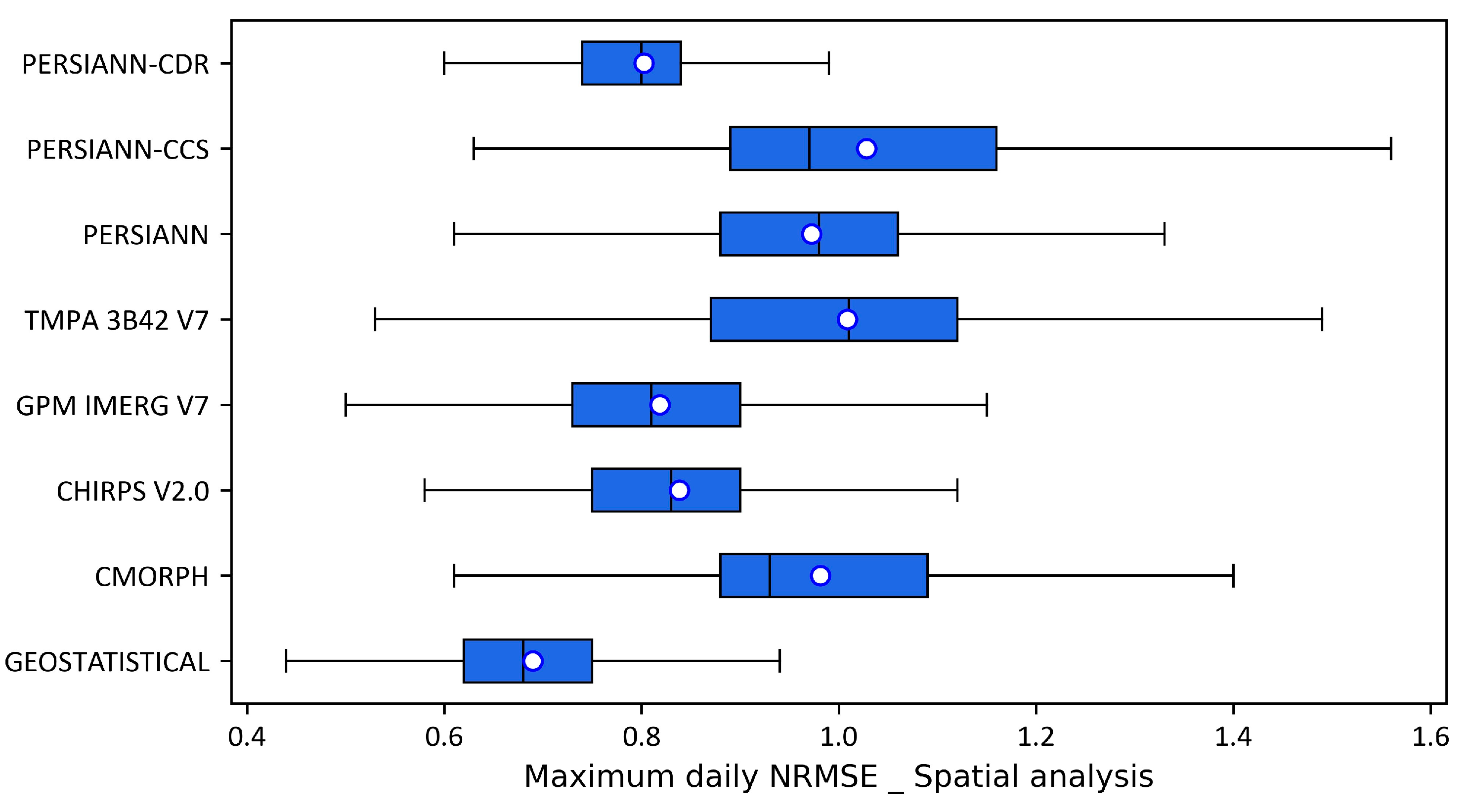
| Statistical study KSA | CMORPH, PERSIANN-CDR, CHIRPS V2.0, TMPA 3B42 V7, GPM IMERG V6 | 324 RG. Daily, Monthly, Annual, Maximum daily | 1981–2014 | The daily resolution exhibits the lowest correlation, which sees a slight improvement in total annual and maximum daily evaluations. The highest correlation is found within the monthly temporal resolution records. The maximum probability of detection is achieved by GPM IMERG V6 and PERSIANN-CDR, albeit with a high false alarm ratio. In high-altitude areas, all datasets demonstrate a lower performance when compared to intermediate altitudes ranging from 500 to 750 m [78]. |
- GRID-1: Synoptic gauge data of the Islamic Republic of Iran Meteorological Organization (IRIMO)- Version 0902 .
- GRID-2: East Asia (EA) ground-based gridded daily precipitation dataset .
- GRID-3: Iran Water Resources Management Co. (IWRM) daily rainfall grid 2003 to 2008.
- GRID-4: India Meteorological Department (IMD) gridded monthly precipitation [138].
- GRID-5: Gridded daily precipitation based on 2480 rain gauges across China.
- GRID-6: 30,000 gauges utilized to generate hourly gridded data over Mainland China—China Meteorological Data Service Center.
- GRID-7: China Meteorological Data Service Center daily precipitation grid (http://data.cma.cn/) .
| Location | Interpolation Techniques | Study Period | Gauges Used | Error Assessment Criteria | Main Findings |
|---|---|---|---|---|---|
| Oahu-Hawaii | OK-KED-LR-IDW-TP | 2005–2008 | 21 | RMSE | The OK interpolation technique demonstrated better performance compared to all other tested methods, while TP exhibited the highest error [44]. |
| Gojam-Ethiopia. | UK-SK-OK-GPI-LPI-RBF-IDW | 2000–2008 | 7 | RMSE-ME | The OK interpolation technique outperformed all other methods tested, with GPI showing the highest error [45]. |
| Northeast of Iran | OK-OCK-LR-KED-SKLM-IDW | 1973–2008 | 32 | RMSE-ME | Geostatistical interpolation techniques outperformed deterministic ones. OCK and KED displayed the slimmest prediction error from April to October, while OK showed the best performance during the remaining months [46]. |
| Aconcagua River basin- Chile | KED-OIM-TP | 10 years | 9 | RMSE-ME | OIM exhibited better performance than TP and KED. Despite KED and TP having the same RMSE, KED displayed better mean error performance than TP [139]. |
| Hamadan Province-Iran | OK-OCK-RBF-GPI-LPI-IDW | 1982–2012 | 35 | CC-MARE | OCK, with an exponential variogram technique, exhibited the best performance in predicting precipitation spatial distribution [47]. |
| Zayandeh-Rud River basin-Iran. | OK-UK-TS-RS-NN-IDW | 1970–2014 | 18 | MAE-RMSE | OK with Gaussian semi-variogram was selected as the appropriate technique for precipitation spatial analysis [48]. |
| Libya | EBK-RBF-IDW-GPI-KIB | 1970–2010 | 63 | MAPE | RBF and IDW demonstrated similar accuracy, outperforming all other tested methods [140]. |
| Chongqing Province (China) | OK-KIB-DIB-RBF-IDW-EBK | 1991–2019 | 34 | MSE-MAE-MAPE-SMAPE-NSE | KIB achieved the highest accuracy, while IDW demonstrated the lowest accuracy across all assessment indices [49]. |
| Pakistan | SK-OK-UK-GPI-LPI-EBK-EBKRP-RBF-IDW | 1961–2020 | 82 | RMSSE-ASE-MSTE-RMSE-ME | EBKRP outperformed all other techniques, with GPI showing the lowest performance [50]. |
| Rio Grande do Sul, Brazil | OCK-OK-UK_IDW | 1960–2017 | 18 | MSE-RMSE-MD | Rainfall maps generated by Kriging techniques were smoother than those produced by IDW, and OCK showed the best performance among other Kriging techniques [141]. |
| New Zealand | COK-OK-KED-IDW | 1951–2012 | 294 | RMSE-MAE | Generally, geostatistical methods outperformed IDW, with COK exhibiting the best performance among all geostatistical techniques [142]. |
| Emilia-Romagna region-Italy | TP-IDW-TPS-OK-OCK | 2008–2018 | ERA5-GRID | NSE-KGE-B-CC | The OK method showcased the best performance among the four methods across three time scales (annual, monthly, and annual maximum daily precipitation) [143]. |
| South America | OK-OCK-IDW | 1983–2017 | 359 | RMSE-SRMSE | OCK, utilizing a spherical semi-variogram, emerged as the optimal precipitation interpolator [144]. |
| Cumbria, Northwest England | OK-OCK-NNI | Annual Average | 82 | RMSE | CK outperformed NNI and OK, achieving an overall improvement of approximately 40% [145]. |
- Geostatistical techniques: Ordinary Kriging (OK), Universal Kriging (UK), Simple Kriging (SK), Cokriging (OCK), Kriging with External Drift (KED), Empirical Bayesian Kriging (EBK), Kernel Interpolation with Barrier (KIB), Diffusion Interpolation with Barrier (DIB), Empirical Bayesian Kriging Regression Prediction (EBKRP), and Simple Kriging with Varying Local Mean (SKLM).
- Deterministic techniques: Radial Basis Function (RBF), Global Polynomial Interpolation (GPI), Local Polynomial Interpolation (LPI), Linear Regression (LR), Inverse Distance Weighting (IDW), Thiessen Polygon (TP), Natural Neighbor Interpolation (NNI), Optimal Interpolation Method (OIM), Natural Neighbor (NN), Regularized Spline (RS), Tension Spline (TS), and Thin Plate Spline (TPS).
- The accuracy and performance assessment criteria: Root Mean Squared Error (RMSE), Standardized Root Mean Squared Error (SRMSE), Mean Error (ME), Mean Squared Error (MSE), Mean Absolute Error (MAE), Root Mean Square Standardized Error (RMSSE), Average Standard Error (ASE), Mean Standardized Error (MSTE), Mean Absolute Relative Error (MARE), Modified Willmott’s Concordance Index (MD), Mean Absolute Percentage Error (MAPE), Nash-Sutcliffe Efficiency (NSE), Kling-Gupta Efficiency (KGE), Bias (B), and Correlation Coefficient (CC).
Appendix B
Appendix B.1. Deterministic Interpolation Techniques
- : the predicted unknown value at point .
- : the weight value of the sampled point .
- : the value of the sampled point .
- : the distance between the sampled point and the predicted point .
- : the power of decreasing weight with distance.

Appendix B.2. Geostatistical Interpolation Techniques
- : the estimate of the variable of interest at the location.
- the measured value of the variable of interest at the location.
- the weight of .
- the stationary mean of the random variable .
- : the semi variance between points.
- the global variance of the study area.
- : the predicted value using simple Kriging at location .
- : the measured value at location .
- : the Kriging weight of the measured value at location where .
- : the number of measured data locations.
- Lagrange multiplier
- : the trend component of the random variable
- : the residual component of the random variable
- : coefficient, ).
- : the number of functions used in the trend modeling.
- : function of location coordinates function ( function).
- : the primary variable values atnearby locations.
- : the secondary variable values atnearby locations.
- : the Cokriging weights for the primary variable.
- : the Cokriging weights for the secondary variable.
References
- Naylor, K.A.; Gaya, S.; Ward, F.; Selim, L.; Rees, N.; Burdziej, J.; Barkhof, M. Water Security for All. In Proceedings of the UN 2023 Water Conference, New York, NY, USA, 4–6 October 2021; Volume 56. [Google Scholar]
- Khan, M.Y.A.; ElKashouty, M.; Subyani, A.M.; Tian, F.; Gusti, W. GIS and RS intelligence in delineating the groundwater potential zones in Arid Regions: A case study of southern Aseer, southwestern Saudi Arabia. Appl. Water Sci. 2022, 12, 3. [Google Scholar] [CrossRef]
- Wang, R.; Chen, J.; Chen, X.; Wang, Y. Variability of precipitation extremes and dryness/wetness over the southeast coastal region of China, 1960–2014. Int. J. Climatol. 2017, 37, 4656–4669. [Google Scholar] [CrossRef]
- Gaur, M.K.; Squires, V.R. Geographic Extent and Characteristics of the World’s Arid Zones and Their Peoples. In Climate Variability Impacts on Land Use and Livelihoods in Drylands; Gaur, M.K., Squires, V.R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–20. ISBN 978-3-319-56681-8. [Google Scholar]
- Mallick, J.; Talukdar, S.; Alsubih, M.; Salam, R.; Ahmed, M.; Kahla, N.B.; Shamimuzzaman, M. Analysing the trend of rainfall in Asir region of Saudi Arabia using the family of Mann-Kendall tests, innovative trend analysis, and detrended fluctuation analysis. Theor. Appl. Climatol. 2021, 143, 823–841. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Wah Win, K.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM multi-satellite precipitation products in streamflow simulations in a data sparse mountainous watershed in Myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Ahmed, K.; Wang, X.J. Selection of climate models for projection of spatiotemporal changes in temperature of Iraq with uncertainties. Atmos. Res. 2018, 213, 509–522. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Wang, X. Uncertainty in estimated trends using gridded rainfall data: A case study of Bangladesh. Water 2019, 11, 349. [Google Scholar] [CrossRef]
- Abdul Razzaq, Z.T. The feasibility of using TRMM satellite data for missing terrestrial stations in Iraq for mapping the rainfall contour lines. Civ. Eng. Beyond Limits 2020, 3, 15–19. [Google Scholar] [CrossRef]
- WMO. Volume I: Hydrology—From Measurement to Hydrological Information; WMO: Geneva, Switzerland, 2008; Volume I, ISBN 9789263101686. [Google Scholar]
- de Moraes Cordeiro, A.L.; Blanco, C.J.C. Assessment of satellite products for filling rainfall data gaps in the Amazon region. Nat. Resour. Model. 2021, 34, e12298. [Google Scholar] [CrossRef]
- Al-Areeq, A.M.; Al-Zahrani, M.A.; Sharif, H.O. Assessment of the performance of satellite rainfall products over Makkah watershed using a physically based hydrologic model. Appl. Water Sci. 2022, 12, 246. [Google Scholar] [CrossRef]
- Hobouchian, M.P.; Salio, P.; García Skabar, Y.; Vila, D.; Garreaud, R. Assessment of satellite precipitation estimates over the slopes of the subtropical Andes. Atmos. Res. 2017, 190, 43–54. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Petersen, W.A.; Christian, H.J.; Rutledge, S.A. TRMM observations of the global relationship between ice water content and lightning. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Dewan, A.; Hu, K.; Kamruzzaman, M.; Uddin, M.R. Evaluating the spatiotemporal pattern of concentration, aggressiveness and seasonality of precipitation over Bangladesh with time–series Tropical Rainfall Measuring Mission data. In Extreme Hydroclimatic Events and Multivariate Hazards in a Changing Environment; Elsevier: Amsterdam, The Netherlands, 2019; pp. 191–219. ISBN 9780128148990. [Google Scholar]
- Nashwan, M.S.; Shahid, S.; Dewan, A.; Ismail, T.; Alias, N. Performance of five high resolution satellite-based precipitation products in arid region of Egypt: An evaluation. Atmos. Res. 2019, 236, 104809. [Google Scholar] [CrossRef]
- Longman, R.J.; Newman, A.J.; Giambelluca, T.W.; Lucas, M. Characterizing the uncertainty and assessing the value of gap-filled daily rainfall data in hawaii. J. Appl. Meteorol. Climatol. 2020, 59, 1261–1276. [Google Scholar] [CrossRef]
- Abu Romman, Z.; Al-Bakri, J.; Al Kuisi, M. Comparison of methods for filling in gaps in monthly rainfall series in arid regions. Int. J. Climatol. 2021, 41, 6674–6689. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Gualda, J.E.; García-Marín, A.P. Assessing machine learning models for gap filling daily rainfall series in a semiarid region of spain. Atmosphere 2021, 12, 1158. [Google Scholar] [CrossRef]
- Fagandini, C.; Todaro, V.; Tanda, M.G.; Pereira, J.L.; Azevedo, L.; Zanini, A. Missing Rainfall Daily Data: A Comparison among Gap-Filling Approaches. Math. Geosci. 2023, 56, 191–217. [Google Scholar] [CrossRef]
- Himanshu, S.K.; Pandey, A.; Patil, A. Hydrologic Evaluation of the TMPA-3B42V7 Precipitation Data Set over an Agricultural Watershed Using the SWAT Model. J. Hydrol. Eng. 2018, 23, 05018003. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Nguyen, P.; Shearer, E.-J.; Tran, H.; Ombadi, M.; Hayatbini, N.; Palacios, T.; Huynh, P.; Braithwaite, D.; Updegraff, G.; Hsu, K.-L.; et al. The CHRS Data Portal for Distributing PERSIANN Family Global Satellite Precipitation Data. In Proceedings of the AGU Fall Meeting Abstracts, Washington, DC, USA, 10–14 December 2018; Volume 2018, p. H51S-1571. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Adler, R.F. TRMM (TMPA) Precipitation L3 1 Day 0.25 Degree x 0.25 Degree V7. Available online: https://disc.gsfc.nasa.gov/datasets/TRMM_3B42_Daily_7/summary (accessed on 19 October 2023).
- Pingping, X.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. NOAA Climate Data Record (CDR) of CPC Morphing Technique (CMORPH) High Resolution Global Precipitation Estimates, Version 1; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2018.
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J. GPM IMERG Final Precipitation L3 1 Day 0.1 Degree x 0.1 Degree V07. Available online: https://disc.gsfc.nasa.gov/datasets/GPM_3IMERGDF_07/summary?keywords=imergv7 (accessed on 20 October 2023).
- Huffman, G.J.; Behrangi, A.; Bolvin, D.T.; Nelkin, E.J. GPCP Version 3.2 Daily Precipitation Data Set; Huffman, G.J., Behrangi, A., Bolvin, D.T., Nelkin, E.J., Eds.; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2021.
- Xie, P.; Chen, M.; Shi, W. CPC unified gauge-based analysis of global daily precipitation. In Proceedings of the Preprints, 24th Conference on Hydrology, Atlanta, GA, USA, 17–21 January 2010; Volume 2. [Google Scholar]
- Beikahmadi, N.; Francipane, A.; Noto, L.V. Smart Data Blending Framework to Enhance Precipitation Estimation through Interconnected Atmospheric, Satellite, and Surface Variables. Hydrology 2023, 10, 128. [Google Scholar] [CrossRef]
- Schaefer, J.T. The Critical Success Index as an Indicator of Warning Skill. Weather Forecast. 1990, 5, 570–575. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall spatial estimations: A review from spatial interpolation to multi-source data merging. Water 2019, 11, 579. [Google Scholar] [CrossRef]
- Wehling, P.; LaBudde, R.A.; Brunelle, S.L.; Nelson, M.T. Probability of Detection (POD) as a Statistical Model for the Validation of Qualitative Methods. J. AOAC Int. 2019, 94, 335–347. [Google Scholar] [CrossRef]
- Setti, S.; Yumnam, K.; Rathinasamy, M.; Agarwal, A. Assessment of satellite precipitation products at different time scales over a cyclone prone coastal river basin in India. J. Water Clim. Chang. 2022, 14, 38–65. [Google Scholar] [CrossRef]
- Sultana, R.; Nasrollahi, N. Evaluation of remote sensing precipitation estimates over Saudi Arabia. J. Arid Environ. 2018, 151, 90–103. [Google Scholar] [CrossRef]
- Alharbi, R.S.; Dao, V.; Jimenez Arellano, C.; Nguyen, P. Comprehensive Evaluation of Near-Real-Time Satellite-Based Precipitation: PDIR-Now over Saudi Arabia. Remote Sens. 2024, 16, 703. [Google Scholar] [CrossRef]
- Verma, P.A.; Shankar, H.; Saran, S. Comparison of Geostatistical and Deterministic Interpolation to Derive Climatic Surfaces for Mountain Ecosystem. In Remote Sensing of Northwest Himalayan Ecosystems; Navalgund, R.R., Kumar, A.S., Nandy, S., Eds.; Springer: Singapore, 2019; pp. 537–547. ISBN 978-981-13-2128-3. [Google Scholar]
- Zhou, F.; Guo, H.C.; Ho, Y.S.; Wu, C.Z. Scientometric analysis of geostatistics using multivariate methods. Scientometrics 2007, 73, 265–279. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Wagner, P.D.; Fiener, P.; Wilken, F.; Kumar, S.; Schneider, K. Comparison and evaluation of spatial interpolation schemes for daily rainfall in data scarce regions. J. Hydrol. 2012, 464–465, 388–400. [Google Scholar] [CrossRef]
- Tobler, W.R. Smooth Pycnophylactic Interpolation for Geographical Regions. J. Am. Stat. Assoc. 1979, 74, 519–530. [Google Scholar] [CrossRef] [PubMed]
- Mair, A.; Fares, A. Comparison of Rainfall Interpolation Methods in a Mountainous Region of a Tropical Island. J. Hydrol. Eng. 2011, 16, 371–383. [Google Scholar] [CrossRef]
- Getahun, Y.S. Spatial-Temporal Analysis of Climate Elements, Vegetation Characteristics, and Sea Surface Temperature Anomaly—A Case Study in Gojam, Ethiopia. Master’s Thesis, Universidade NOVA de Lisboa, Lisbon, Portugal, 2012. [Google Scholar]
- Delbari, M.; Afrasiab, P.; Jahani, S. Spatial interpolation of monthly and annual rainfall in northeast of Iran. Meteorol. Atmos. Phys. 2013, 122, 103–113. [Google Scholar] [CrossRef]
- Sadeghi, S.H.; Nouri, H.; Faramarzi, M. Assessing the spatial distribution of rainfall and the effect of altitude in Iran (Hamadan Province). Air Soil Water Res. 2017, 10, 1178622116686066. [Google Scholar] [CrossRef]
- Amini, M.A.; Torkan, G.; Eslamian, S.; Zareian, M.J.; Adamowski, J.F. Analysis of deterministic and geostatistical interpolation techniques for mapping meteorological variables at large watershed scales. Acta Geophys. 2019, 67, 191–203. [Google Scholar] [CrossRef]
- Yang, R.; Xing, B. A comparison of the performance of different interpolation methods in replicating rainfall magnitudes under different climatic conditions in chongqing province (China). Atmosphere 2021, 12, 1318. [Google Scholar] [CrossRef]
- Ali, G.; Sajjad, M.; Kanwal, S.; Xiao, T.; Khalid, S.; Shoaib, F.; Gul, H.N. Spatial–temporal characterization of rainfall in Pakistan during the past half-century (1961–2020). Sci. Rep. 2021, 11, 6935. [Google Scholar] [CrossRef]
- Sluiter, R.; Sluiter, D.R. Interpolation Methods for Climate Data: Literature Review; KNMI: De Bilt, The Netherlands, 2009. [Google Scholar]
- Johnston, K.; Ver Hoef, J.M.; Krivoruchko, K.; Lucas, N. Using ArcGIS Geostatistical Analyst; ESRI: Redlands, CA, USA, 2001; ISBN 1589480066. [Google Scholar]
- González-Álvarez, Á.; Viloria-Marimón, O.M.; Coronado-Hernández, Ó.E.; Vélez-Pereira, A.M.; Tesfagiorgis, K.; Coronado-Hernández, J.R. Isohyetal maps of daily maximum rainfall for different return periods for the Colombian Caribbean Region. Water 2019, 11, 358. [Google Scholar] [CrossRef]
- Bedient, P.B.; Huber, W.C.; Vieux, B.E. Hydrology and Floodplain Analysis: International Edition, 5th ed.; Law Express Questions & Answers; Pearson Education: New Jersey, NJ, USA, 2013; ISBN 9780273774280. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology, 1st ed.; McGraw-Hill: New York, NY, USA, 1988; ISBN 0-07-010810-2. [Google Scholar]
- Khaled Hamed, A.R.R. Flood Frequency Analysis, 1st ed.; Chen, W.F., Ed.; CRC Press: Boca Raton, FL, USA, 2000; ISBN 0-412-55280-9. [Google Scholar]
- Elsherif, S.M.; El-Zawahry, A.; Soliman, A.H. Spatio-Temporal Rainfall Variability Analysis, Case Study: KSA. Int. J. Eng. Trends Technol. 2021, 69, 136–143. [Google Scholar] [CrossRef]
- Huynh Ngoc Phien, A.A.; Sunchindah, A. Rainfall distribution in northeastern Thailand/Sur la distribution de pluie dans le nord-est de Thailande. Hydrol. Sci. Bull. 1980, 25, 167–182. [Google Scholar] [CrossRef]
- Abdulali, B.A.A.; Abu Bakar, M.A.; Ibrahim, K.; Mohd Ariff, N. Extreme Value Distributions: An Overview of Estimation and Simulation. J. Probab. Stat. 2022, 2022, 5449751. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S.; Shin, H.; Heo, J.-H. Appropriate model selection methods for nonstationary generalized extreme value models. J. Hydrol. 2017, 547, 557–574. [Google Scholar] [CrossRef]
- Kim, H.; Kim, T.; Shin, J.-Y.; Heo, J.-H. Improvement of Extreme Value Modeling for Extreme Rainfall Using Large-Scale Climate Modes and Considering Model Uncertainty. Water 2022, 14, 478. [Google Scholar] [CrossRef]
- Agilan, V.; Umamahesh, N. V What are the best covariates for developing non-stationary rainfall Intensity-Duration-Frequency relationship? Adv. Water Resour. 2017, 101, 11–22. [Google Scholar] [CrossRef]
- Vasiliades, L.; Galiatsatou, P.; Loukas, A. Nonstationary Frequency Analysis of Annual Maximum Rainfall Using Climate Covariates. Water Resour. Manag. 2015, 29, 339–358. [Google Scholar] [CrossRef]
- Chen, P.-C.; Wang, Y.-H.; You, G.J.-Y.; Wei, C.-C. Comparison of methods for non-stationary hydrologic frequency analysis: Case study using annual maximum daily precipitation in Taiwan. J. Hydrol. 2017, 545, 197–211. [Google Scholar] [CrossRef]
- WMO. Guide to Hydrological Practice, Volume I—Hydrology—From Measurement to Hydrological Information; World Meteorological Organization: Geneva, Switzerland, 2020; ISBN 978-92-63-10168-6. [Google Scholar]
- Hasanean, H.; Almazroui, M. Rainfall: Features and variations over Saudi Arabia, a review. Climate 2015, 3, 578–626. [Google Scholar] [CrossRef]
- Chowdhury, S.; Al-Zahrani, M. Characterizing water resources and trends of sector wise water consumptions in Saudi Arabia. J. King Saud Univ.—Eng. Sci. 2015, 27,, 68–82. [Google Scholar] [CrossRef]
- OBG. The Report: Saudi Arabia; Oxford Business Group: London, UK, 2019. [Google Scholar]
- Al-Ahmadi, K.; Al-Ahmadi, S. Rainfall-altitude relationship in Saudi Arabia. Adv. Meteorol. 2013, 2013, 363029. [Google Scholar] [CrossRef]
- Clark, A.; Amdt, R. Lakes of the Rub’ al-Khali. Saudi Aramco World 1989, 40, 28–33. [Google Scholar]
- Ghazanfar, S.A.; Fisher, M. Vegetation of the Arabian Peninsula; Ghazanfar, S.A., Fisher, M., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1998; ISBN 978-90-481-5020-5. [Google Scholar]
- Almazroui, M. Calibration of TRMM rainfall climatology over Saudi Arabia during 1998–2009. Atmos. Res. 2011, 99, 400–414. [Google Scholar] [CrossRef]
- Helmi, A.M.; Elgamal, M.; Farouk, M.I.; Abdelhamed, M.S.; Essawy, B.T. Evaluation of Geospatial Interpolation Techniques for Enhancing Spatiotemporal Rainfall Distribution and Filling Data Gaps in Asir Region, Saudi Arabia. Sustainability 2023, 15, 14028. [Google Scholar] [CrossRef]
- Al-Zahrani, M.; Husain, T. An algorithm for designing a precipitation network in the south-western region of Saudi Arabia. J. Hydrol. 1998, 205, 205–216. [Google Scholar] [CrossRef]
- Sulafa Hag-Elsafi; El-Tayib, M. Spatial and statistical analysis of rainfall in the Kingdom of Saudi Arabia from 1979 to 2008. Weather 2016, 71, 262–266. [CrossRef]
- Abdullah, M.A.; Almazroui, M. Climatological study of the southwestern region of Saudi Arabia. I. Rainfall analysis. Clim. Res. 1998, 9, 213–223. [Google Scholar]
- Subyani, A.M. Geostatistical study of annual and seasonal mean rainfall patterns in southwest Saudi Arabia/Distribution géostatistique de la pluie moyenne annuelle et saisonnière dans le Sud-Ouest de l’Arabie Saoudite. Hydrol. Sci. J. 2004, 49, 803–817. [Google Scholar] [CrossRef]
- Helmi, A.M.; Abdelhamed, M.S. Evaluation of CMORPH, PERSIANN-CDR, CHIRPS V2.0, TMPA 3B42 V7, and GPM IMERG V6 Satellite Precipitation Datasets in Arabian Arid Regions. Water 2023, 15, 92. [Google Scholar] [CrossRef]
- KSA-MWA. Hydrological Publications No. 98 Vol. 4 Years (1963–1980); Kingdom of Saudi Arabia, Ministry of Agriculture and Water, Hydrology Division, Department of Water Resources and Development: Riyadh, Saudi Arabia, 1980.
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M. Climatologically aided interpolation (CAI) of terrestrial air temperature. Int. J. Climatol. 1995, 15, 221–229. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Paredes-Trejo, F.; Barbosa, H.A.; Kumar, T.V.L.; Thakur, M.K.; de Oliveira Buriti, C. Assessment of the CHIRPS-Based Satellite Precipitation Estimates. In Inland Waters; Devlin, A., Pan, J., Shah, M.M., Eds.; IntechOpen: Rijeka, Croatia, 2020. [Google Scholar]
- Hsu, K.; Ashouri, H.; Braithwaite, D.; Sorooshian, S. Climate Algorithm Theoretical Basis Document (C-ATBD)—Precipitation—PERSIANN-CDR; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2014.
- Sorooshian, S.; Hsu, K.; Braithwaite, D.; Ashouri, H. NOAA Climate Data Record (CDR) of Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks (PERSIANN-CDR), Version 1 Revision 1; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2014.
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN family of global satellite precipitation data: A review and evaluation of products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef]
- Wang, K.; Kong, L.; Yang, Z.; Singh, P.; Guo, F.; Xu, Y.; Tang, X.; Hao, J. GPM Annual and Daily Precipitation Data for Real-Time Short-Term Nowcasting: A Pilot Study for a Way Forward in Data Assimilation. Water 2021, 13, 1422. [Google Scholar] [CrossRef]
- Xu, F.; Guo, B.; Ye, B.; Ye, Q.; Chen, H.; Ju, X.; Guo, J.; Wang, Z. Systematical Evaluation of GPM IMERG and TRMM 3B42V7 Precipitation Products in the Huang-Huai-Hai Plain, China. Remote Sens. 2019, 11, 697. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The global precipitation measurement (GPM) mission for science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.; Sorooshian, S.; Tan, J.; Xie, P. NASA GPM Integrated Multi-Satellite Retrievals for GPM (IMERG) Algorithm Theoretical Basis Document (ATBD) Version 06; NASA: Greenbelt, MD, USA, 2020.
- Biernacik, P.; Kazimierski, W.; Włodarczyk-Sielicka, M. Comparative Analysis of Selected Geostatistical Methods for Bottom Surface Modeling. Sensors 2023, 23, 3941. [Google Scholar] [CrossRef]
- Chile, J.-P.; Delfiner, P. Geostatistics—Modeling Spatial Uncertainty, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; ISBN 978-0-470-18315-1. [Google Scholar]
- Rojimol, J. Development of Optimal Geostatistical Model for Geotechnical Applications; Indian Institute of Technology Hyderabad: Hyderabad, India, 2013. [Google Scholar]
- Rouhani, S.; Mohan Srivastava, R.; Desbarats, A.J.; Cromer, M.V.; Ivan Johnson, A. Geostatistics for Environmental and Geotechnical Applications; ASTM: West Conshohocken, PA, USA, 1996; ISBN 978-0-8031-5337-0. [Google Scholar]
- Mazzella, A.; Antonio, M. The Importance of the Model Choice for Experimental Semivariogram Modeling and Its Consequence in Evaluation Process. J. Eng. 2013, 2013, 960105. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Department of Commerce—United States of America: Dover, NY, USA, 1975.
- Noel, A.C. Cressie Statistics for Spatial Data (Revised Edition); John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993; ISBN 0-471-00255-0. [Google Scholar]
- Gooverts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997; ISBN 0-19-511538-4. [Google Scholar]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B 1974, 36, 111–147. [Google Scholar] [CrossRef]
- Geisser, S. The Predictive Sample Reuse Method with Applications. J. Am. Stat. Assoc. 1975, 70, 320–328. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- Javanmard, S.; Yatagai, A.; Nodzu, M.I.; BodaghJamali, J.; Kawamoto, H. Comparing high-resolution gridded precipitation data with satellite rainfall estimates of TRMM_3B42 over Iran. Adv. Geosci. 2010, 25, 119–125. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation of satellite rainfall products through hydrologic simulation in a fully distributed hydrologic model. Water Resour. Res. 2011, 47, 1–11. [Google Scholar] [CrossRef]
- Miao, C.; Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Duan, Q. Evaluation of the PERSIANN-CDR daily rainfall estimates in capturing the behavior of extreme precipitation events over China. J. Hydrometeorol. 2015, 16, 1387–1396. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.H.; Delrieu, G.; Hong, Y.; Hsu, Y.C.; et al. Multiregional satellite precipitation products evaluation over complex terrain. J. Hydrometeorol. 2016, 17, 1817–1836. [Google Scholar] [CrossRef]
- Abdulrida, M.A.; Al-Jumaily, K.J. Comparisons of Monthly Rainfall Data with Satellite Estimates of TRMM 3B42 over Iraq. Int. J. Sci. Res. Publ. 2016, 6, 494–501. [Google Scholar]
- Moazami, S.; Golian, S.; Hong, Y.; Sheng, C.; Kavianpour, M.R. Comprehensive evaluation of four high-resolution satellite precipitation products under diverse climate conditions in Iran. Hydrol. Sci. J. 2016, 61, 420–440. [Google Scholar] [CrossRef]
- Kumar, B.; Lakshmi, V. Accessing the capability of TRMM 3B42 V7 to simulate streamflow during extreme rain events: Case study for a Himalayan River Basin. J. Earth Syst. Sci. 2018, 127, 27. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef]
- Bai, L.; Shi, C.; Li, L.; Yang, Y.; Wu, J. Accuracy of CHIRPS Satellite-Rainfall Products over Mainland China. Remote Sens. 2018, 10, 362. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Al-Zahrani, M.A.; Sharif, H.O. Assessment of global precipitation measurement satellite products over Saudi Arabia. J. Hydrol. 2018, 559, 1–12. [Google Scholar] [CrossRef]
- Wei, G.; Lü, H.; Crow, W.T.; Zhu, Y.; Wang, J.; Su, J. Comprehensive Evaluation of GPM-IMERG, CMORPH, and TMPA Precipitation Products with Gauged Rainfall over Mainland China. Adv. Meteorol. 2018, 2018, 3024190. [Google Scholar] [CrossRef]
- Wang, C.; Tang, G.; Han, Z.; Guo, X.; Hong, Y. Global intercomparison and regional evaluation of GPM IMERG Version-03, Version-04 and its latest Version-05 precipitation products: Similarity, difference and improvements. J. Hydrol. 2018, 564, 342–356. [Google Scholar] [CrossRef]
- Musie, M.; Sen, S.; Srivastava, P. Comparison and evaluation of gridded precipitation datasets for streamflow simulation in data scarce watersheds of Ethiopia. J. Hydrol. 2019, 579, 124168. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Wang, X. Assessment of satellite-based precipitation measurement products over the hot desert climate of Egypt. Remote Sens. 2019, 11, 555. [Google Scholar] [CrossRef]
- Fang, J.; Yang, W.; Luan, Y.; Du, J.; Lin, A.; Zhao, L. Evaluation of the TRMM 3B42 and GPM IMERG products for extreme precipitation analysis over China. Atmos. Res. 2019, 223, 24–38. [Google Scholar] [CrossRef]
- Shukla, A.K.; Ojha, C.S.P.; Singh, R.P.; Pal, L.; Fu, D. Evaluation of TRMM precipitation dataset over Himalayan Catchment: The upper Ganga Basin, India. Water 2019, 11, 613. [Google Scholar] [CrossRef]
- Bruster-Flores, J.L.; Ortiz-Gómez, R.; Ferriño-Fierro, A.L.; Guerra-Cobián, V.H.; Burgos-Flores, D.; Lizárraga-Mendiola, L.G. Evaluation of precipitation estimates CMORPH-CRT on regions of Mexico with different climates. Water 2019, 11, 1722. [Google Scholar] [CrossRef]
- Gumindoga, W.; Rientjes, T.H.M.; Haile, A.T.; Makurira, H.; Reggiani, P. Performance evaluation of CMORPH satellite precipitation product in the Zambezi Basin. Int. J. Remote Sens. 2019, 40, 7730–7749. [Google Scholar] [CrossRef]
- Geleta, C.D.; Deressa, T.A. Evaluation of Climate Hazards Group InfraRed Precipitation Station (CHIRPS) satellite-based rainfall estimates over Finchaa and Neshe Watersheds, Ethiopia. Eng. Reports 2021, 3, e12338. [Google Scholar] [CrossRef]
- Abdelmoneim, H.; Soliman, M.R.; Moghazy, H.M. Evaluation of TRMM 3B42V7 and CHIRPS Satellite Precipitation Products as an Input for Hydrological Model over Eastern Nile Basin. Earth Syst. Environ. 2020, 4, 685–698. [Google Scholar] [CrossRef]
- Dembélé, M.; Schaefli, B.; van de Giesen, N.; Mariéthoz, G. Suitability of 17 gridded rainfall and temperature datasets for large-scale hydrological modelling in West Africa. Hydrol. Earth Syst. Sci. 2020, 24, 5379–5406. [Google Scholar] [CrossRef]
- Liu, C.Y.; Aryastana, P.; Liu, G.R.; Huang, W.R. Assessment of satellite precipitation product estimates over Bali Island. Atmos. Res. 2020, 244, 105032. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Tan, M.L.; Li, X.; Wang, G.; He, R. Nine-year systematic evaluation of the GPM and TRMM precipitation products in the shuaishui river basin in east-central China. Remote Sens. 2020, 12, 1042. [Google Scholar] [CrossRef]
- Cavalcante, R.B.L.; da Silva Ferreira, D.B.; Pontes, P.R.M.; Tedeschi, R.G.; da Costa, C.P.W.; de Souza, E.B. Evaluation of extreme rainfall indices from CHIRPS precipitation estimates over the Brazilian Amazonia. Atmos. Res. 2020, 238, 104879. [Google Scholar] [CrossRef]
- Nwachukwu, P.N.; Satge, F.; Yacoubi, S.E.; Pinel, S.; Bonnet, M.P. From trmm to GPM: How reliable are satellite-based precipitation data across Nigeria? Remote Sens. 2020, 12, 3964. [Google Scholar] [CrossRef]
- Wang, Q.; Xia, J.; She, D.; Zhang, X.; Liu, J.; Zhang, Y. Assessment of four latest long-term satellite-based precipitation products in capturing the extreme precipitation and streamflow across a humid region of southern China. Atmos. Res. 2021, 257, 105554. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Aryal, A.; Kawaike, K.; Yamanoi, K.; Nakagawa, H.; Bhatta, B.; Karki, S.; Thapa, B.R. Evaluation of precipitation elasticity using precipitation data from ground and satellite-based estimates and watershed modeling in Western Nepal. J. Hydrol. Reg. Stud. 2021, 33, 100768. [Google Scholar] [CrossRef]
- Kim, J.; Han, H. Evaluation of the CMORPH high-resolution precipitation product for hydrological applications over South Korea. Atmos. Res. 2021, 258, 105650. [Google Scholar] [CrossRef]
- Yang, W.T.; Fu, S.M.; Sun, J.H.; Zheng, F.; Wei, J.; Ma, Z. Comparative Evaluation of the Performances of TRMM-3B42 and Climate Prediction Centre Morphing Technique (CMORPH) Precipitation Estimates over Thailand. J. Meteorol. Soc. Japan 2021, 99, 1525–1546. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, C.; Yeh, P.J.F.; Li, J.; Hu, B.X.; Feng, P.; Jun, C. Evaluation and comparison of precipitation estimates and hydrologic utility of CHIRPS, TRMM 3B42 V7 and PERSIANN-CDR products in various climate regimes. Atmos. Res. 2022, 265, 105881. [Google Scholar] [CrossRef]
- Yu, S.; Lu, F.; Zhou, Y.; Wang, X.; Wang, K.; Song, X.; Zhang, M. Evaluation of Three High-Resolution Remote Sensing Precipitation Products on the Tibetan Plateau. Water 2022, 14, 2169. [Google Scholar] [CrossRef]
- Anjum, M.N.; Irfan, M.; Waseem, M.; Leta, M.K.; Niazi, U.M.; Rahman, S.U.; Ghanim, A.; Mukhtar, M.A.; Nadeem, M.U. Assessment of PERSIANN-CCS, PERSIANN-CDR, SM2RAIN-ASCAT, and CHIRPS-2.0 Rainfall Products over a Semi-Arid Subtropical Climatic Region. Water 2022, 14, 147. [Google Scholar] [CrossRef]
- Pai, D.S.; Rajeevan, M.; Sreejith, O.P.; Mukhopadhyay, B.; Satbha, N.S. Development of a new high spatial resolution (0.25° × 0.25°) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. MAUSAM 2014, 65, 1–18. [Google Scholar] [CrossRef]
- Jacquin, A. Interpolation of daily precipitation in mountain catchments with limited data availability. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 27 April–2 May 2014; p. 13973. [Google Scholar]
- Bentaher, L. Evaluation of Geostatistical Interpolation Methods for Rainfall data Estimation in Libya. Albahit J. Appl. Sci. 2020, 1, 54–59. [Google Scholar]
- Ananias, D.R.S.; Liska, G.R.; Beijo, L.A.; Liska, G.J.R.; de Menezes, F.S. The assessment of annual rainfall field by applying different interpolation methods in the state of Rio Grande do Sul, Brazil. SN Appl. Sci. 2021, 3, 687. [Google Scholar] [CrossRef]
- Caloiero, T.; Pellicone, G.; Modica, G.; Guagliardi, I. Comparative Analysis of Different Spatial Interpolation Methods Applied to Monthly Rainfall as Support for Landscape Management. Appl. Sci. 2021, 11, 9566. [Google Scholar] [CrossRef]
- Liu, Y.; Zhuo, L.; Pregnolato, M.; Han, D. An assessment of statistical interpolation methods suited for gridded rainfall datasets. Int. J. Climatol. 2022, 42, 2754–2772. [Google Scholar] [CrossRef]
- Cerón, W.L.; Andreoli, R.V.; Kayano, M.T.; Canchala, T.; Carvajal-Escobar, Y.; Souza, R.A.F. Comparison of spatial interpolation methods for annual and seasonal rainfall in two hotspots of biodiversity in South America. An. Acad. Bras. Cienc. 2021, 93, e20190674. [Google Scholar] [CrossRef] [PubMed]
- Page, T.; Beven, K.J.; Hankin, B.; Chappell, N.A. Interpolation of rainfall observations during extreme rainfall events in complex mountainous terrain. Hydrol. Process. 2022, 36, e14758. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989; ISBN 978-0195050134. [Google Scholar]
- Huang, F.; Liu, D.; Tan, X.; Wang, J.; Chen, Y.; He, B. Explorations of the implementation of a parallel IDW interpolation algorithm in a Linux cluster-based parallel GIS. Comput. Geosci. 2011, 37, 426–434. [Google Scholar] [CrossRef]
- Guan, X.; Wu, H. Parallel optimization of IDW interpolation algorithm on multicore platform. In Proceedings of the Geoinformatics 2008 and Joint Conference on GIS and Built Environment: Advanced Spatial Data Models and Analyses, Guangzhou, China, 28–29 June 2008. [Google Scholar]
- Gradka, R.; Kwinta, A. A short review of interpolation methods used for terrain modeling. Geomat. Landmanag. Landsc. 2018, 4, 29–47. [Google Scholar] [CrossRef]
- Alcaras, E.; Amoroso, P.P.; Parente, C. The Influence of Interpolated Point Location and Density on 3D Bathymetric Models Generated by Kriging Methods: An Application on the Giglio Island Seabed (Italy). Geosciences 2022, 12, 62. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. South. African Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide, 2nd ed.; Oxford University Press: New York, NY, USA, 1997; ISBN 0195100158. [Google Scholar]
- Whittle, P. Prediction and Regulation by Linear Least-Square Methods; NED-New; University of Minnesota Press: Minneapolis, MN, USA, 1983; ISBN 9780816611485. [Google Scholar]
- Journel, A.G.; Rossi, M.E. When do we need a trend model in kriging? Math. Geol. 1989, 21, 715–739. [Google Scholar] [CrossRef]
- Edward, H.; Isaaks, R.M.S. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments. Hydrol. Process. 2017, 31, 2143–2161. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C. Mining Geostatistics; Academic Press: London, UK; New York, NY, USA, 1978; ISBN 0123910501. [Google Scholar]
- Cressie, N. Fitting variogram models by weighted least squares. J. Int. Assoc. Math. Geol. 1985, 17, 563–586. [Google Scholar] [CrossRef]
- Gribov, A.; Krivoruchko, K. Empirical Bayesian kriging implementation and usage. Sci. Total Environ. 2020, 722, 137290. [Google Scholar] [CrossRef] [PubMed]
- Krivoruchko, K. Empirical Bayesian Kriging—Implemented in ArcGIS Geostatistical Analyst. 2012. Available online: https://www.esri.com/news/arcuser/1012/files/ebk.pdf (accessed on 26 September 2023).
- Krivoruchko, K.; Gribov, A. Evaluation of empirical Bayesian kriging. Spat. Stat. 2019, 32, 100368. [Google Scholar] [CrossRef]








| Semivariogram Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| Circular | Spherical | Exponential | Gaussian | K-Bessel | J-Bessel | Stable | ||
| Geostatistical model | Ordinary Kriging | OK-CI | OK-SP | OK-EX | OK-GA | OK-KB | OK-JB | OK-ST |
| Simple Kriging | SK-CI | SK-SP | SK-EX | SK-GA | SK-KB | SK-JB | SK-ST | |
| Universal Kriging | UK-CI | UK-SP | UK-EX | UK-GA | UK-KB | UK-JB | UK-ST | |
| Ordinary Cokriging | OCK-CI | OCK-SP | OCK-EX | OCK-GA | OCK-KB | OCK-JB | OCK-ST | |
| Simple Cokriging | SCK-CI | SCK-SP | SCK-EX | SCK-GA | SCK-KB | SCK-JB | SCK-ST | |
| Universal Cokriging | UCK-CI | UCK-SP | UCK-EX | UCK-GA | UCK-KB | UCK-JB | UCK-ST | |
| Empirical Bayesian Kriging | EBK | |||||||
| Year | Max. Daily | Tot. Annual | Year | Max. Daily | Tot. Annual |
|---|---|---|---|---|---|
| 1967 | UCK-JB | UK-JB | 1991 | OK-JB | OCK-KB |
| 1968 | UCK-CI | SCK-SP | 1992 | OK-JB | OCK-JB |
| 1969 | OCK-ST | SCK-ST | 1993 | SCK-KB | UCK-JB |
| 1970 | UK-JB | OK-GA | 1994 | OK-JB | OCK-SP |
| 1971 | SCK-ST | OCK-CI | 1995 | OK-JB | OCK-CI |
| 1972 | OK-JB | OCK-CI | 1996 | OCK-KB | OCK-EX |
| 1973 | OK-JB | OCK-JB | 1997 | SCK-ST | UCK-ST |
| 1974 | SCK-JB | OK-JB | 1998 | OK-GA | UCK-GA |
| 1975 | UCK-JB | OCK-SP | 1999 | OCK-CI | UCK-JB |
| 1976 | OCK-EX | OCK-JB | 2000 | OK-EX | OK-JB |
| 1977 | UK-JB | OCK-JB | 2001 | OCK-ST | OCK-KB |
| 1978 | UK-JB | OCK-JB | 2002 | OCK-GA | OCK-CI |
| 1979 | OCK-ST | OCK-GA | 2003 | SCK-GA | UK-JB |
| 1980 | OCK-JB | OK-JB | 2004 | OCK-JB | OK-CI |
| 1981 | OCK-ST | OCK-CI | 2005 | OCK-JB | UK-JB |
| 1982 | UCK-JB | OK-JB | 2006 | OCK-KB | OCK-EX |
| 1983 | OK-JB | UCK-CI | 2007 | UK-ST | OK-GA |
| 1984 | OCK-JB | OCK-JB | 2008 | OCK-JB | SCK-KB |
| 1985 | OCK-KB | OK-GA | 2009 | UK-JB | OCK-JB |
| 1986 | OCK-EX | OCK-CI | 2010 | OCK-ST | SCK-EX |
| 1987 | OCK-JB | OK-JB | 2011 | SK-CI | OK-JB |
| 1988 | OCK-CI | UK-JB | 2012 | UCK-KB | OCK-SP |
| 1989 | SCK-EX | UCK-EX | 2013 | OCK-KB | OCK-JB |
| 1990 | OCK-JB | UCK-KB | 2014 | OCK-EX | UCK-CI |
| Family | Distribution | Equation | Parameters (p) | |
|---|---|---|---|---|
| Gamma | Exponential | (13) | ||
| Gamma | (14) | |||
| Pearson Type (III) | (15) | |||
| Normal | Two Parameters Log-Normal | (16) | ||
| Three Parameters Log-Normal | (17) | |||
| Extreme Value | Generalize Extreme Value (GEV) | (18) | ||
| Extreme Value Type I (EV1) | (19) | |||
| Weibull | (20) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Helmi, A.M.; Farouk, M.I.; Hassan, R.; Mumtaz, M.A.; Chaouachi, L.; Elgamal, M.H. Comparing Remote Sensing and Geostatistical Techniques in Filling Gaps in Rain Gauge Records and Generating Multi-Return Period Isohyetal Maps in Arid Regions—Case Study: Kingdom of Saudi Arabia. Water 2024, 16, 925. https://doi.org/10.3390/w16070925
Helmi AM, Farouk MI, Hassan R, Mumtaz MA, Chaouachi L, Elgamal MH. Comparing Remote Sensing and Geostatistical Techniques in Filling Gaps in Rain Gauge Records and Generating Multi-Return Period Isohyetal Maps in Arid Regions—Case Study: Kingdom of Saudi Arabia. Water. 2024; 16(7):925. https://doi.org/10.3390/w16070925
Chicago/Turabian StyleHelmi, Ahmed M., Mohamed I. Farouk, Raouf Hassan, Mohd Aamir Mumtaz, Lotfi Chaouachi, and Mohamed H. Elgamal. 2024. "Comparing Remote Sensing and Geostatistical Techniques in Filling Gaps in Rain Gauge Records and Generating Multi-Return Period Isohyetal Maps in Arid Regions—Case Study: Kingdom of Saudi Arabia" Water 16, no. 7: 925. https://doi.org/10.3390/w16070925
APA StyleHelmi, A. M., Farouk, M. I., Hassan, R., Mumtaz, M. A., Chaouachi, L., & Elgamal, M. H. (2024). Comparing Remote Sensing and Geostatistical Techniques in Filling Gaps in Rain Gauge Records and Generating Multi-Return Period Isohyetal Maps in Arid Regions—Case Study: Kingdom of Saudi Arabia. Water, 16(7), 925. https://doi.org/10.3390/w16070925








