Analyzing Water Leakages in Parallel Pipe Systems with Rapid Regulating Valve Maneuvers
Abstract
1. Introduction
- A Geographical Information System (GIS) that describes water infrastructure;
- Sensors to measure hydraulic variables in the system;
- Supervisory Control and Data Acquisition (SCADA) systems collect data from sensors placed in situ and transmit it to a central station through a communication system;
- Smart Metering for network control and customer service;
- A computerized maintenance management system;
- A hydraulic model designed to simulate water leakages in water distribution systems.
2. Mathematical Model
2.1. Assumptions
- Friction losses are calculated based on the absolute roughness, internal pipe diameter, and Reynolds number, a common practice in the current literature [28];
- Minor losses are computed using a dimensionless coefficient;
- A resistance coefficient is used for evaluating valve losses in a hydraulic grade line.
2.2. Governing Equations
- a.
- Mass oscillation equation
- b.
- Continuity equation
- c.
- Friction factor equation
2.3. Numerical Resolution
3. Practical Application and Data
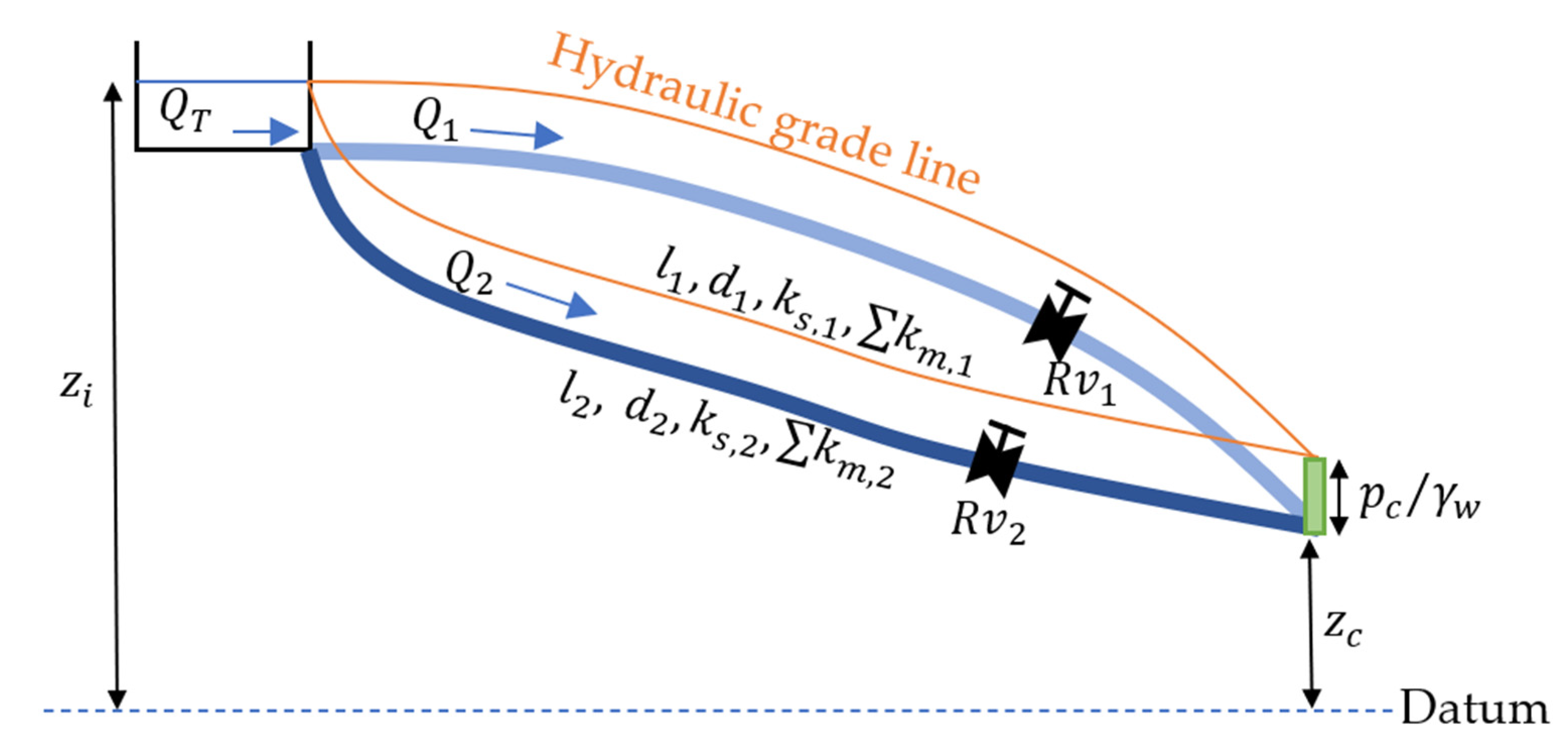
3.1. Application to the Case of Two Parallel Pipes
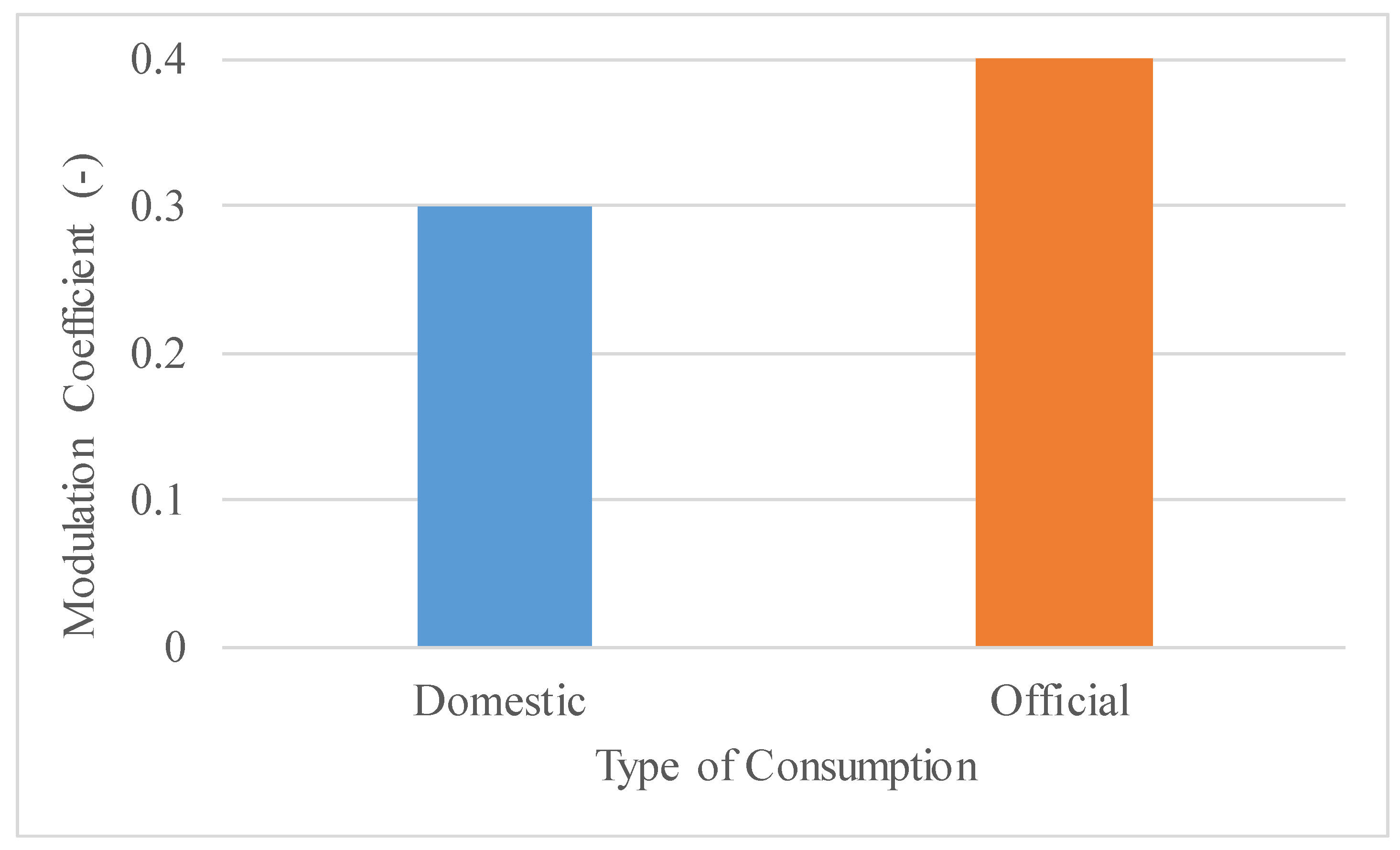
3.2. Data
4. Results
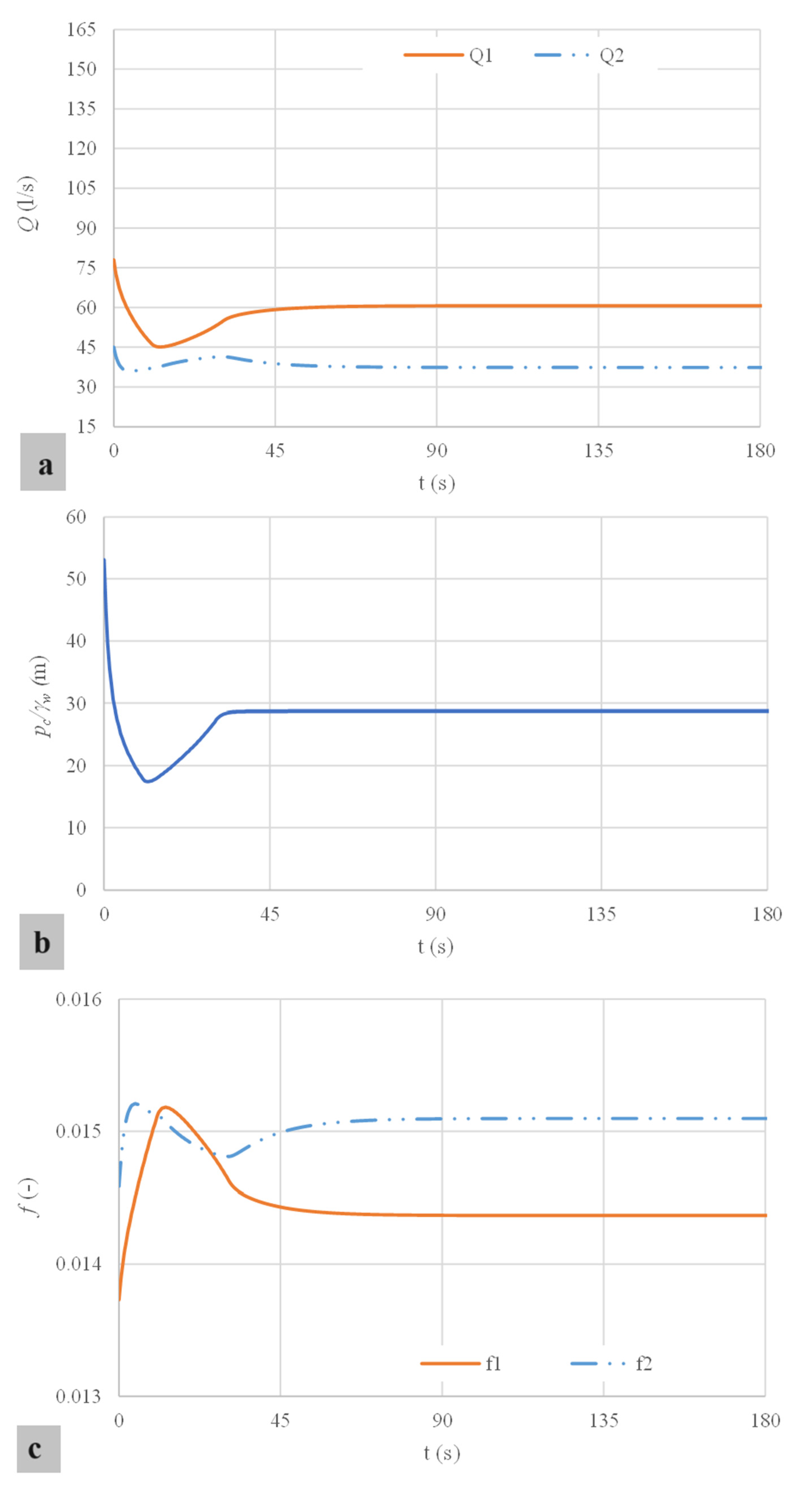
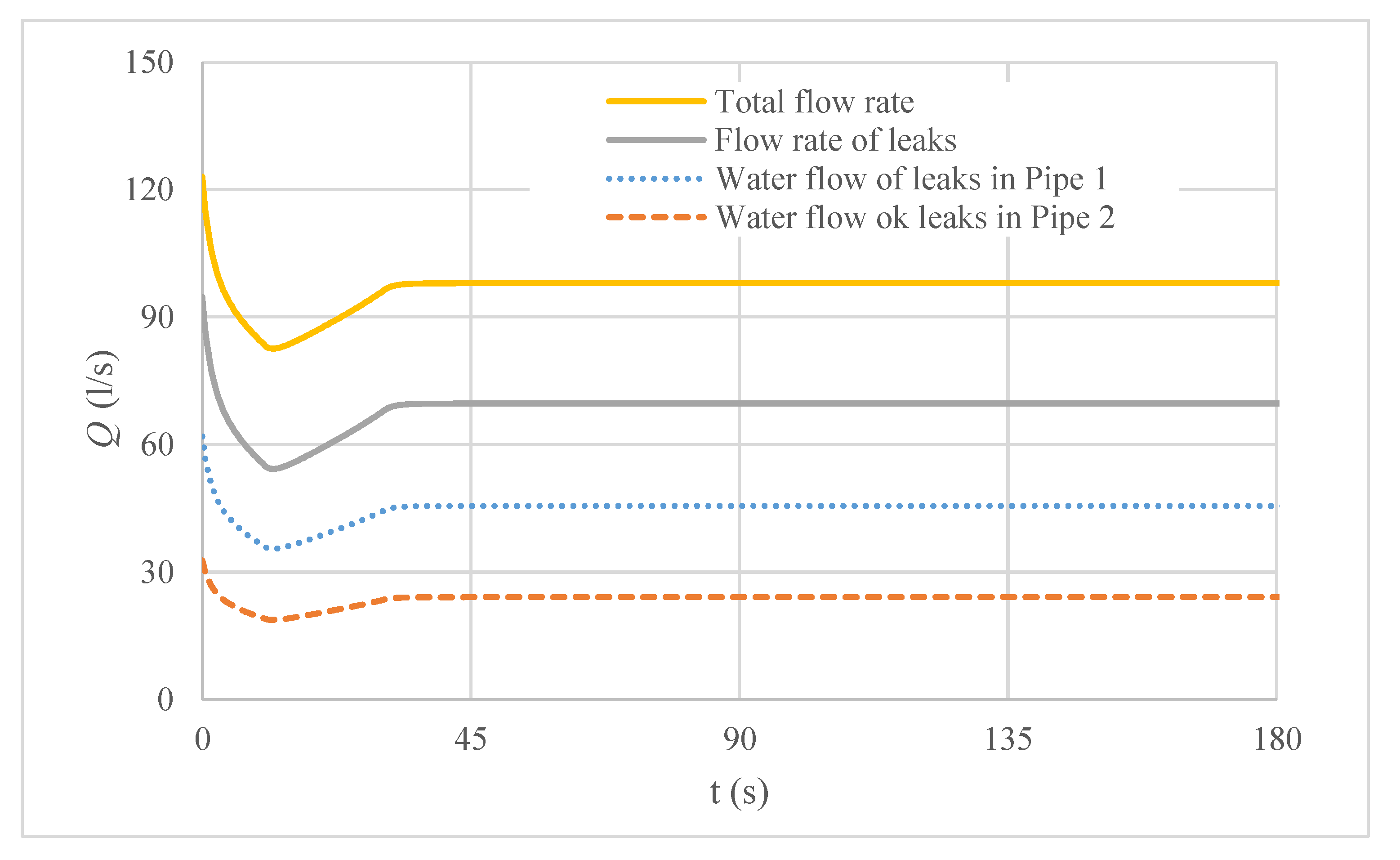
5. Discussion
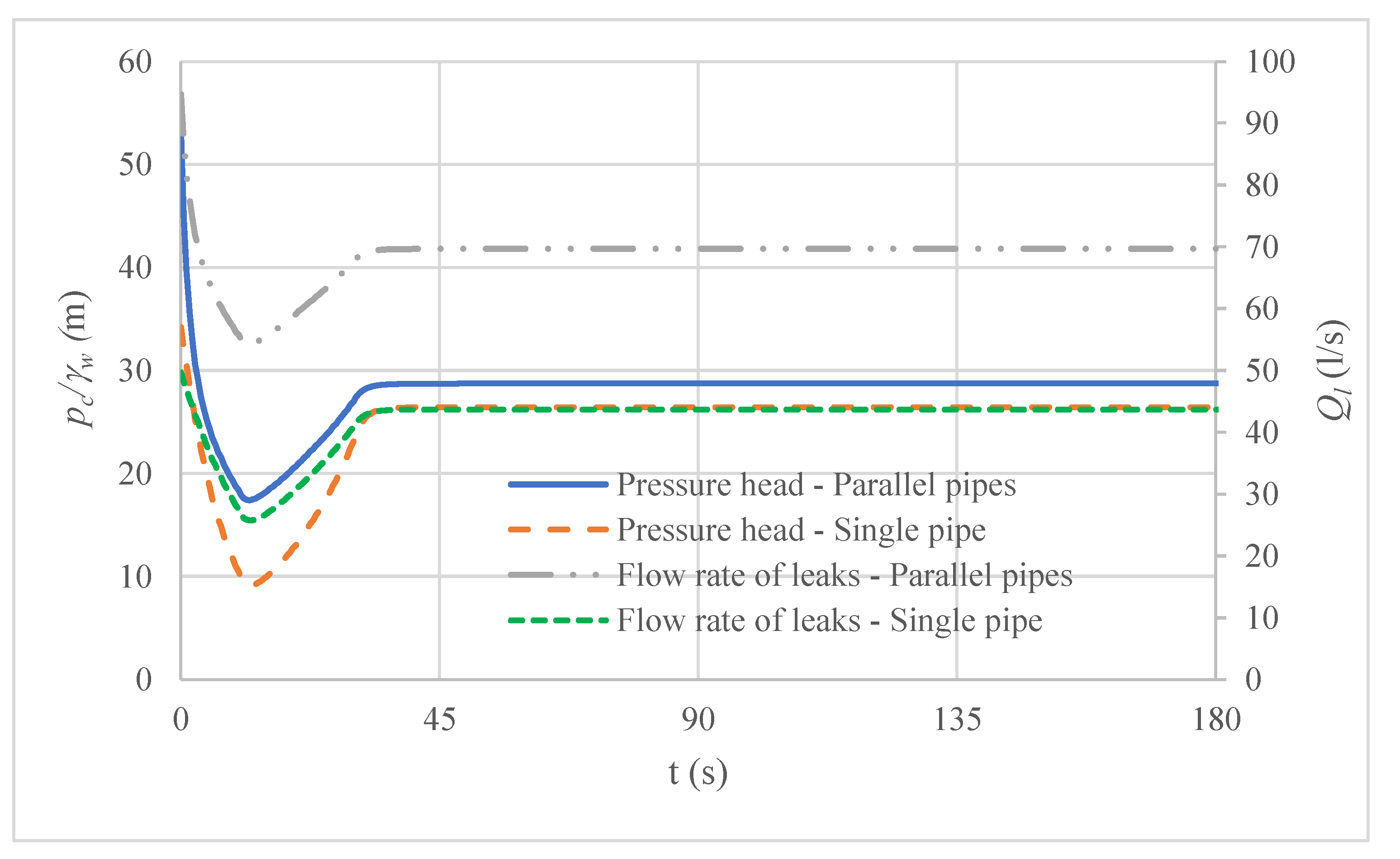
- The practical application is composed of two parallel pipes, and its results can be used for engineers and designers to compute the total leakage volume when two regulating valves are operated following different maneuvers. The mathematical model shows that each problem of parallel pipe requires equations to be solved. In this case (), the variables to compute are , , , , and . Due to the regulating valves acting, the pressure head patterns are changing even for constant consumption (domestic and official), ranging from 53.06 m to 28.75 m. The two parallel pipes’ water flow and friction factor patterns are different and should be separately computed.
- When more parallel pipes are added to reinforce a line, the amount of water volume of leakages is increased since, during the operational time, water installations have more orifices along their length, provoking more water losses. It is then of the utmost importance to reduce the number of parallel pipes during the design stage to save energy production in the injected water flow.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| : | coefficient modulation |
| : | internal pipe diameter (m) |
| : | friction factor (-) |
| : | emitter coefficient (m3/s/m0.5) |
| : | absolute roughness (m) |
| : | gravitational acceleration (m/s2) |
| : | a specified pipe (-) |
| : | pipe length (m) |
| : | number of parallel pipes (-) |
| : | time (s) |
| : | pressure in the common node (Pa) |
| : | resistance coefficient of a regulating valve (ms2/m6) |
| : | Reynolds number (-) |
| : | water flow rate (m3/s) |
| : | commercial consumption (m3/s) |
| : | domestic consumption (m3/s) |
| : | industrial consumption (m3/s) |
| : | official consumption (m3/s) |
| : | physical leakages (m3/s) |
| : | illegal use (m3/s) |
| : | flow by metering error (m3/s) |
| : | water velocity in a pipe (m/s) |
| : | pipe elevation in the first node (m) |
| : | pipe elevation in the common node (m) |
| : | kinematic viscosity (m/s2) |
| : | exponent coefficient of leakages (-) |
| minor losses coefficient (-) | |
| : | water unit weight (N/m3) |
References
- Lambert, A.; Hirner, W. Losses from Water Supply Systems: A Standard Terminology and Recommended Performance Measures; IWA: London, UK, 2000. [Google Scholar]
- Lambert, A.O.; Brown, T.G.; Takizawa, M.; Weimer, D. A review of performance indicators for real losses from water supply systems. J. Water Supply Res. Technol. AQUA 1999, 48, 227–237. [Google Scholar] [CrossRef]
- IBNET. IBNET Indicator Heat Map. February 2021. Available online: https://database.ib-net.org/Reports/Indicators/HeatMap (accessed on 1 February 2024).
- United Nations. Sustainable Development Goals. Available online: https://sdgs.un.org/goals (accessed on 1 February 2024).
- Bibri, S.E.; Krogstie, J. Smart sustainable cities of the future: An extensive interdisciplinary literature review. Sustain. Cities Soc. 2017, 31, 183–212. [Google Scholar] [CrossRef]
- Ishiwatari, Y.; Mishima, I.; Utsuno, N.; Fujita, M. Diagnosis of the ageing of water pipe systems by water quality and structure of iron corrosion in supplied water. Water Sci. Technol. Water Supply 2013, 13, 178–183. [Google Scholar] [CrossRef]
- Li, R.; Huang, H.; Xin, K.; Tao, T. A review of methods for burst/leakage detection and location in water distribution systems. Water Sci. Technol. Water Supply 2015, 15, 429–441. [Google Scholar] [CrossRef]
- Cimorelli, L.; D’Aniello, A.; Cozzolino, L.; Pianese, D. Leakage reduction in WDNs through optimal setting of PATs with a derivative-free optimizer. J. Hydroinform. 2020, 22, 713–724. [Google Scholar] [CrossRef]
- Ramos, H.M.; Kuriqi, A.; Besharat, M.; Creaco, E.; Tasca, E.; Coronado-Hernández, O.E.; Pienika, R.; Iglesias-Rey, P. SmartWater Grids and Digital Twin for the Management of System Efficiency in Water Distribution Networks. Water 2023, 15, 1129. [Google Scholar] [CrossRef]
- Alzamora, F.M.; Carot, M.H.; Carles, J.; Campos, A. Development and Use of a Digital Twin for the Water Supply and Distribution Network of Valencia (Spain). In Proceedings of the 17th International Computing & Control for the Water Industry Conference, Exeter, UK, 1–4 September 2019. [Google Scholar]
- Jiang, Z.; Guo, Y.; Wang, Z. Digital Twin to Improve the virtual-real Integration of Industrial Iot. J. Ind. Inf. Integr. 2021, 22, 100196. [Google Scholar] [CrossRef]
- Liu, M.; Fang, S.; Dong, H.; Xu, C. Review of Digital Twin about Concepts, Technologies, and Industrial Applications. J. Manuf. Syst. 2021, 58, 346–361. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management. Sustain. Cities Soc. 2021, 64, 102562. [Google Scholar] [CrossRef]
- Lu, Q.; Parlikad, A.K.; Woodall, P.; Don Ranasinghe, G.; Xie, X.; Liang, Z.; Konstantinou, E.; Heaton, J.; Schooling, J. Developing a Digital Twin at Building and City Levels: Case Study of West Cambridge Campus. J. Manag. Eng. 2020, 36, 05020004. [Google Scholar] [CrossRef]
- Asadi, S.; Nazari-Heris, M.; Rezaei Nasab, S.; Torabi, H.; Sharifironizi, M. An Updated Review on Net-Zero Energy and Water Buildings: Design and Operation. In Food-Energy-Water Nexus Resilience and Sustainable Development: Decision-Making Methods, Planning, and Trade-Off Analysis; Springer: Cham, Switzerland, 2020; pp. 267–290. [Google Scholar]
- Ávila, C.; Sánchez-Romero, F.-J.; López-Jiménez, P.A.; Pérez- Sánchez, M. Improve Leakage Management to Reach Sustainable Water Supply Networks through by Green Energy Systems. Optimized Case Study. Sustain. Cities Soc. 2022, 83, 103994. [Google Scholar] [CrossRef]
- Jowitt, P.W.; Xu, C. Optimal valve control in water-distribution networks. J. Water Resour. Plan. Manag. 1990, 116, 455–472. [Google Scholar] [CrossRef]
- Giustolisi, O.; Savic, D.; Kapelan, Z. Pressure-driven demand and leakage simulation for water distribution networks. J. Hydraul. Eng. 2008, 134, 626–635. [Google Scholar] [CrossRef]
- Al-Washali, T.; Sharma, S.; Kennedy, M. Methods of assessment of water losses in water supply systems: A review. Water Resour. Manag. 2016, 30, 4985–5001. [Google Scholar] [CrossRef]
- Samir, N.; Kansoh, R.; Elbarki, W.; Fleifle, A. Pressure control for minimizing leakage in water distribution systems. Alex. Eng. J. 2017, 56, 601–612. [Google Scholar] [CrossRef]
- Schwaller, J.; Van Zyl, J.V. Modeling the pressure-leakage response of water distribution systems based on individual leak behavior. J. Hydraul. Eng. 2015, 141, 04014089. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Pérez-Sánchez, M.; Arrieta-Pastrana, A.; Fuertes-Miquel, V.S.; Coronado-Hernández, J.R.; Quiñones-Bolaños, E.; Ramos, H.M. Dynamic effects of a regulating valve in the assessment of water leakages in single pipelines. Water Resour. Manag. 2024. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, O.E.; Mora-Meliá, D.; Iglesias-Rey, P.L. Hydraulic modeling during filling and emptying processes in pressurized pipelines: A literature review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Martínez-Solano, F.J. Rigid water column for simulating the emptying process in a pipeline using pressurized air. J. Hydraul. Eng. 2018, 144, 06018004. [Google Scholar] [CrossRef]
- Prest, E.I.; Schaap, P.G.; Besmer, M.D.; Hammes, F. Dynamic Hydraulics in a Drinking Water Distribution System Influence Suspended Particles and Turbidity, but Not Microbiology. Water 2021, 13, 109. [Google Scholar] [CrossRef]
- Tsagkari, E.; Connelly, S.; Liu, Z.; McBride, A.; Sloan, W.T. The role of shear dynamics in biofilm formation. npj Biofilms Microbiomes 2022, 8, 33. [Google Scholar] [CrossRef] [PubMed]
- Eshkabilov, S.L. Practical MATLAB Modeling with Simulink: Programming and Simulating Ordinary and Partial Differential Equations; Apress: Berkeley, CA, USA, 2020. [Google Scholar]
- Altowayti, W.A.H.; Othman, N.; Tajarudin, H.A.; Al-Dhaqm, A.; Asharuddin, S.M.; Al-Gheethi, A.; Alshalif, A.F.; Salem, A.A.; Din, M.F.M.; Fitriani, N.; et al. Evaluating the Pressure and Loss Behavior in Water Pipes Using Smart Mathematical Modelling. Water 2021, 13, 3500. [Google Scholar] [CrossRef]
- Abreu, J.; Cabrera, E.; Izquierdo, J.; García-Serra, J. Flow Modeling in Pressurized Systmes Revisited. J. Hydraul. Eng. 1999, 125, 1154–1169. [Google Scholar] [CrossRef]

| Variables | Total Variables | |
|---|---|---|
| 1 (single pipeline) | , and | 3 |
| 2 | , , and | 5 |
| 3 | , , , and | 7 |
| … | … | … |
| , , ,…, , and |
| Description | Formula | Equation No. |
|---|---|---|
| Mass oscillation equation applied to the first parallel pipe | (6) | |
| Mass oscillation equation applied to the second parallel pipe | (7) | |
| Continuity equation | (8) | |
| Swamee–Jain equation applied to the first parallel pipe | (9) | |
| Swamee–Jain equation applied to the second parallel pipe | (10) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuertes-Miquel, V.S.; Arrieta-Pastrana, A.; Coronado-Hernández, O.E. Analyzing Water Leakages in Parallel Pipe Systems with Rapid Regulating Valve Maneuvers. Water 2024, 16, 926. https://doi.org/10.3390/w16070926
Fuertes-Miquel VS, Arrieta-Pastrana A, Coronado-Hernández OE. Analyzing Water Leakages in Parallel Pipe Systems with Rapid Regulating Valve Maneuvers. Water. 2024; 16(7):926. https://doi.org/10.3390/w16070926
Chicago/Turabian StyleFuertes-Miquel, Vicente S., Alfonso Arrieta-Pastrana, and Oscar E. Coronado-Hernández. 2024. "Analyzing Water Leakages in Parallel Pipe Systems with Rapid Regulating Valve Maneuvers" Water 16, no. 7: 926. https://doi.org/10.3390/w16070926
APA StyleFuertes-Miquel, V. S., Arrieta-Pastrana, A., & Coronado-Hernández, O. E. (2024). Analyzing Water Leakages in Parallel Pipe Systems with Rapid Regulating Valve Maneuvers. Water, 16(7), 926. https://doi.org/10.3390/w16070926









