A Soil Refractive Index (SRI) Model Characterizing the Functional Relationship Between Soil Moisture Content and Permittivity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Basic Theory
2.2. Laboratory Experiments
3. Results
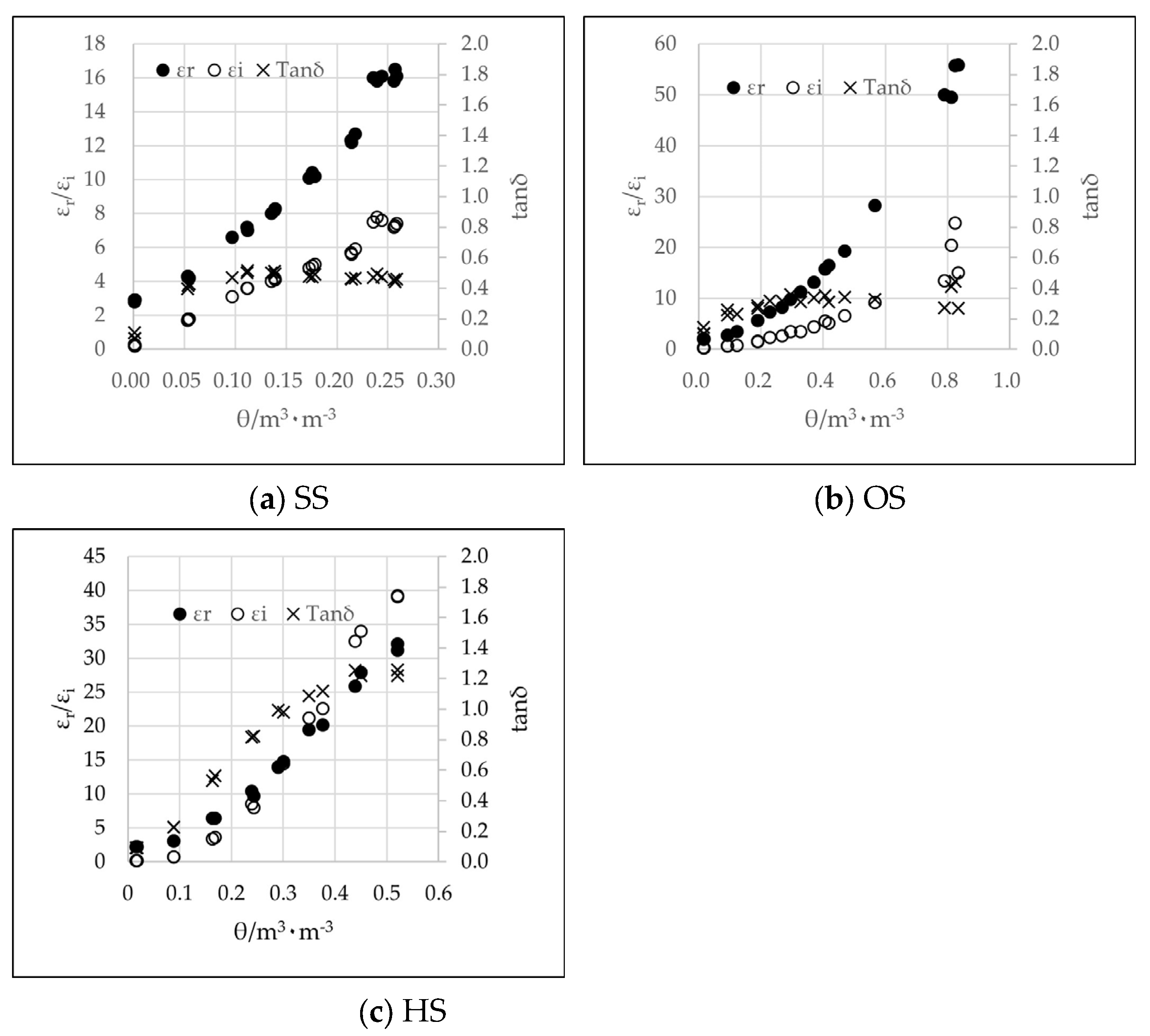
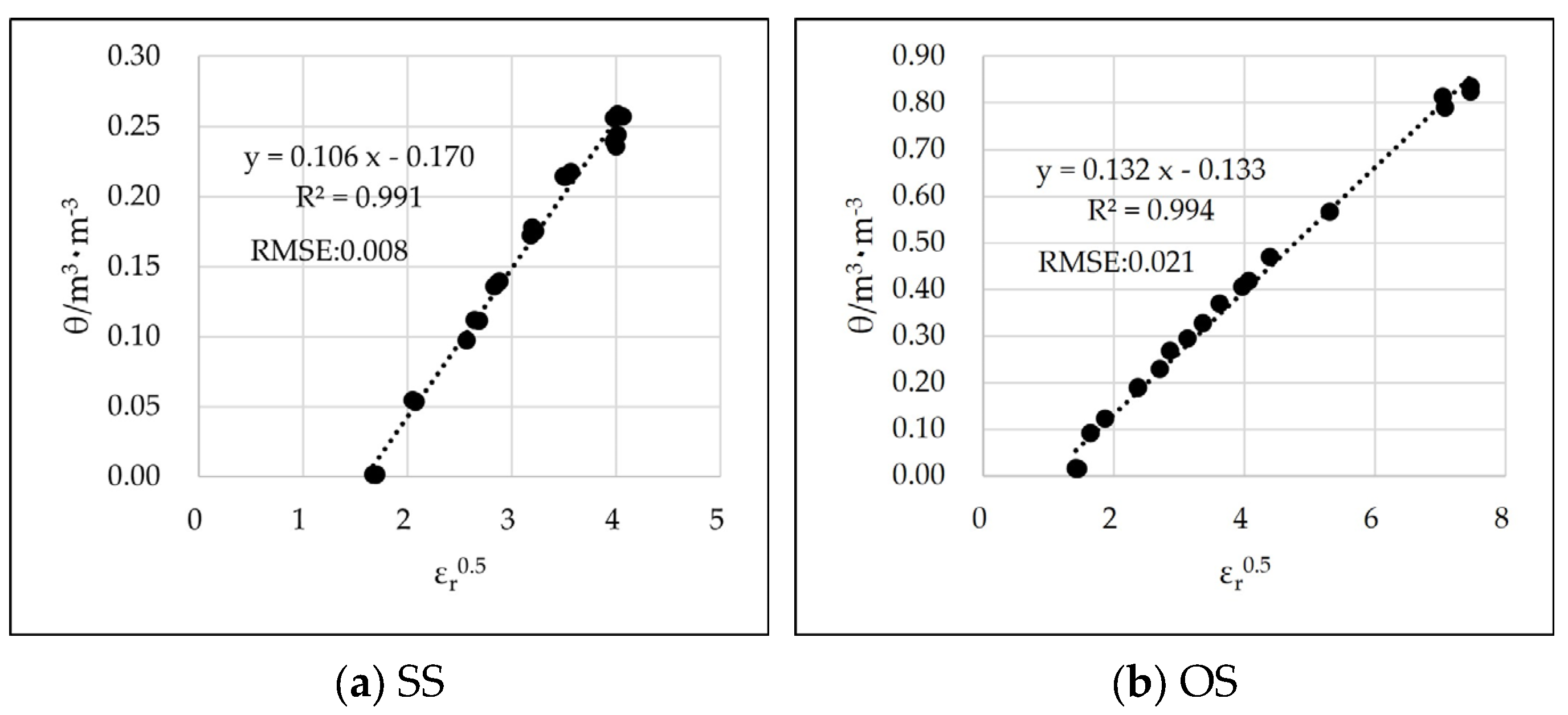
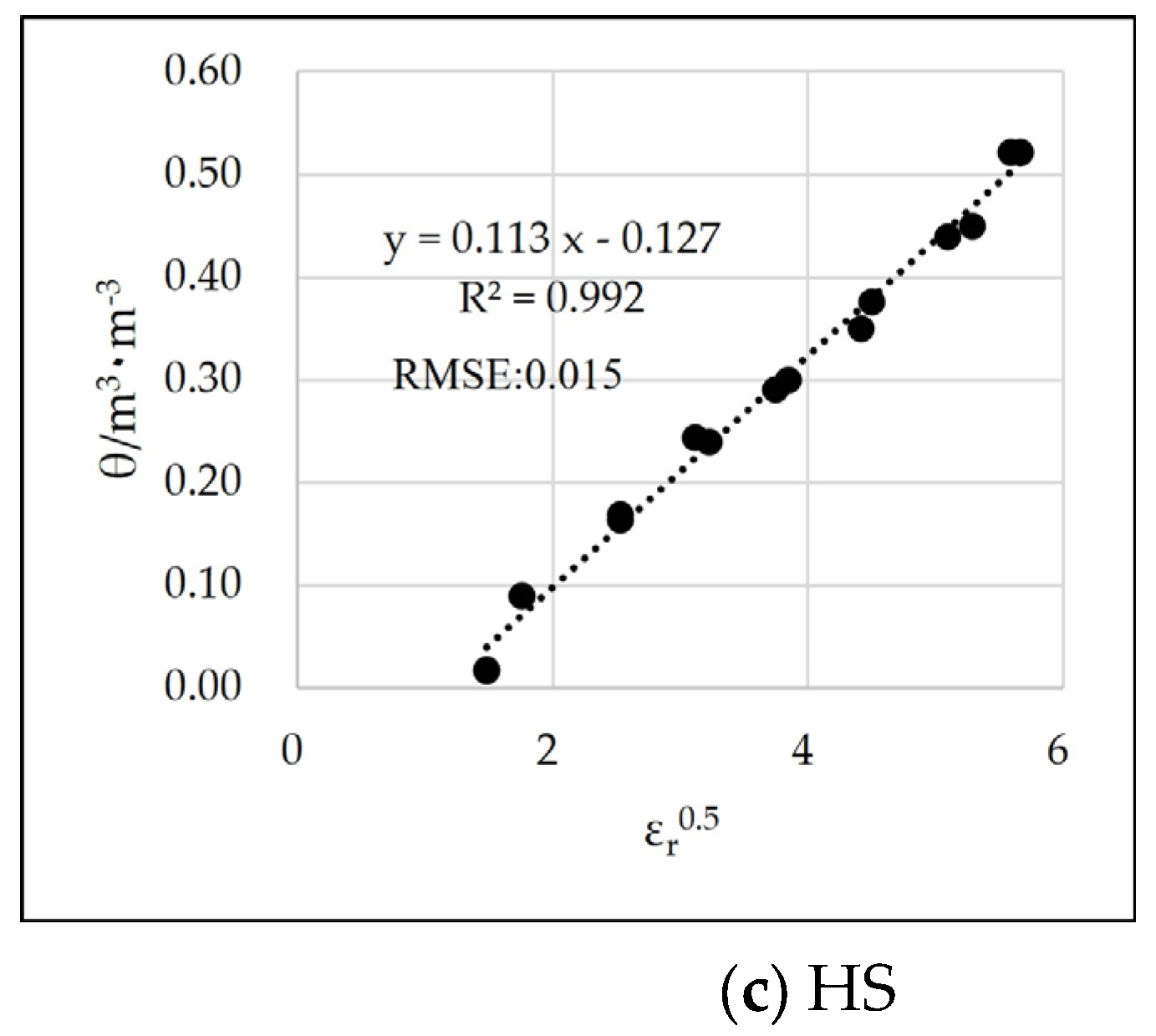
3.1. Experimental Results
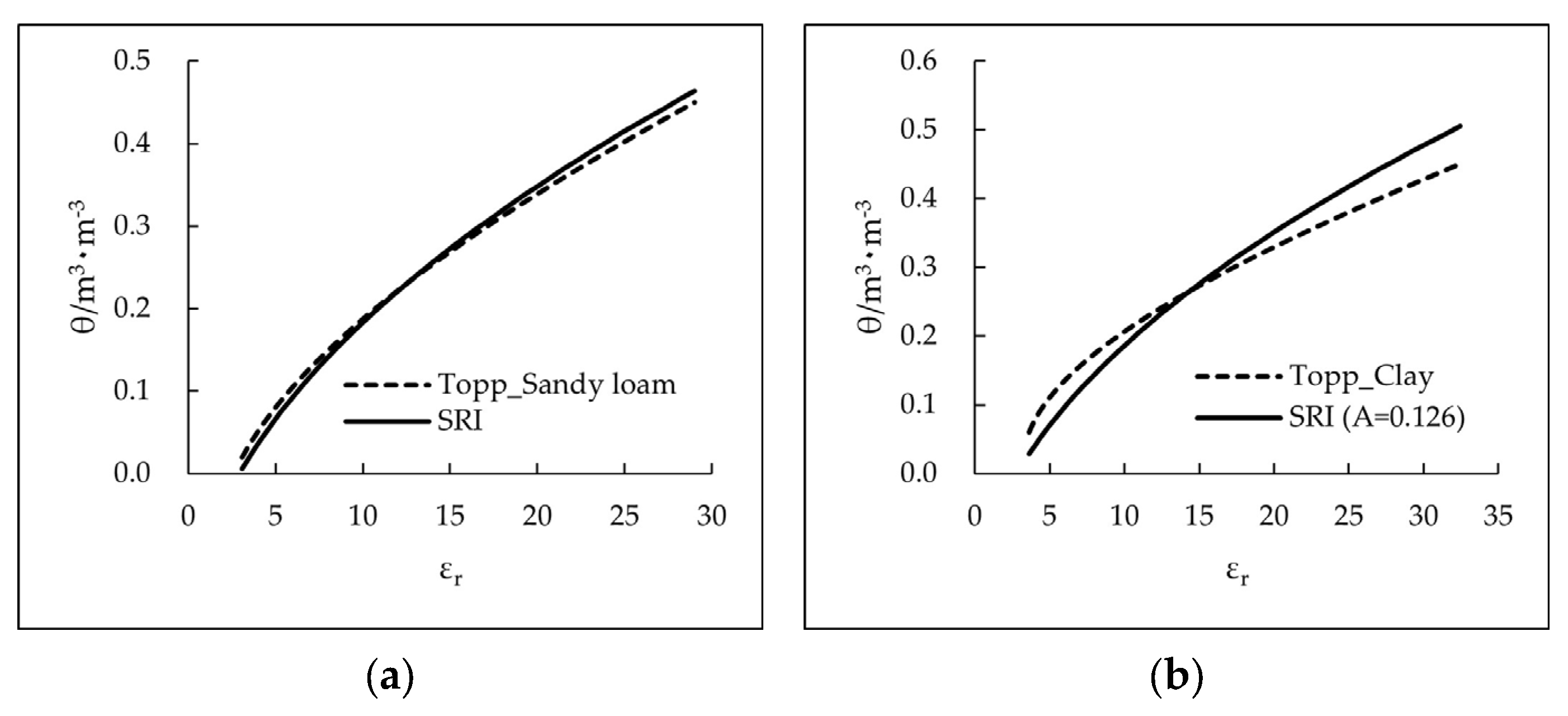
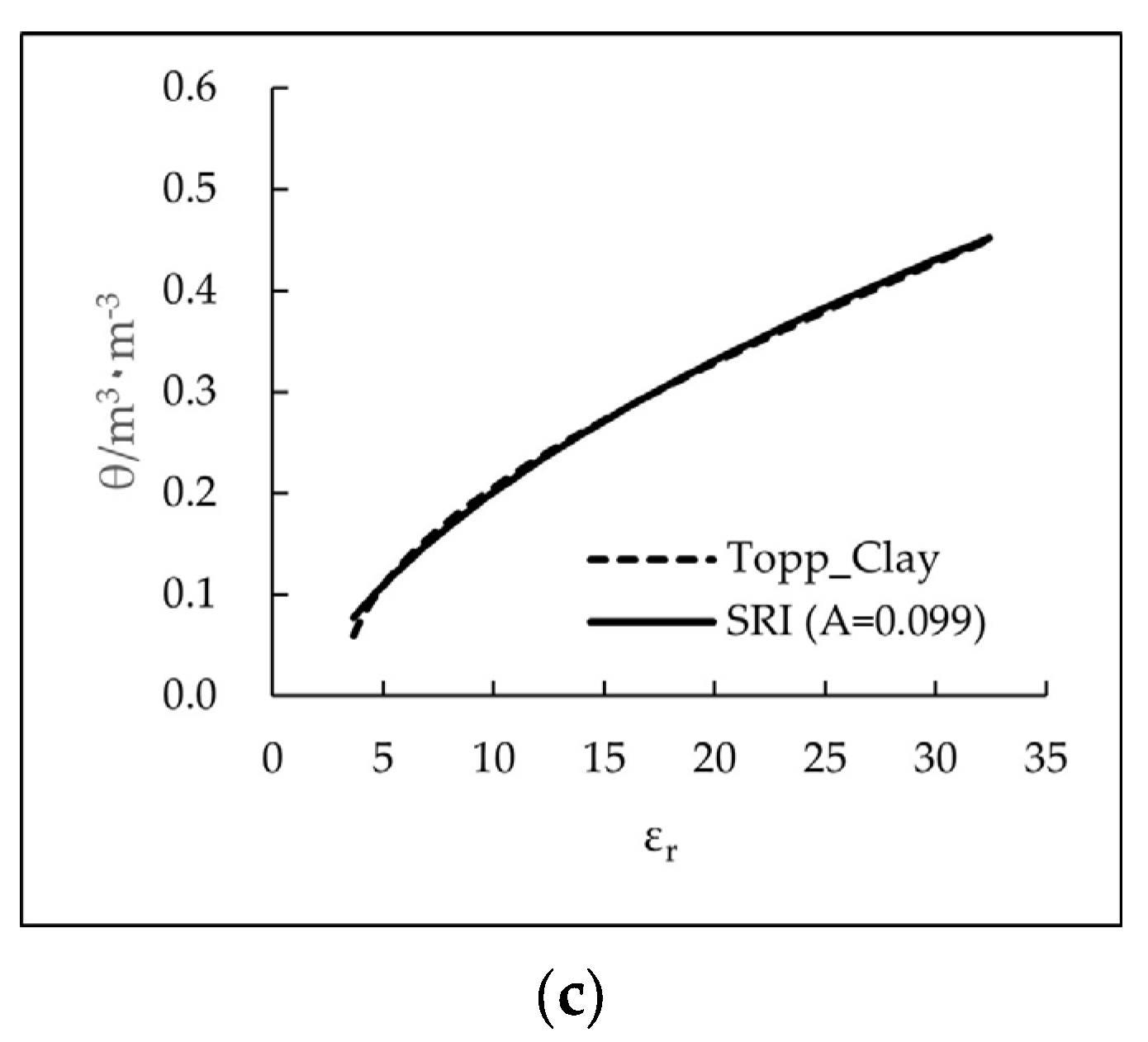
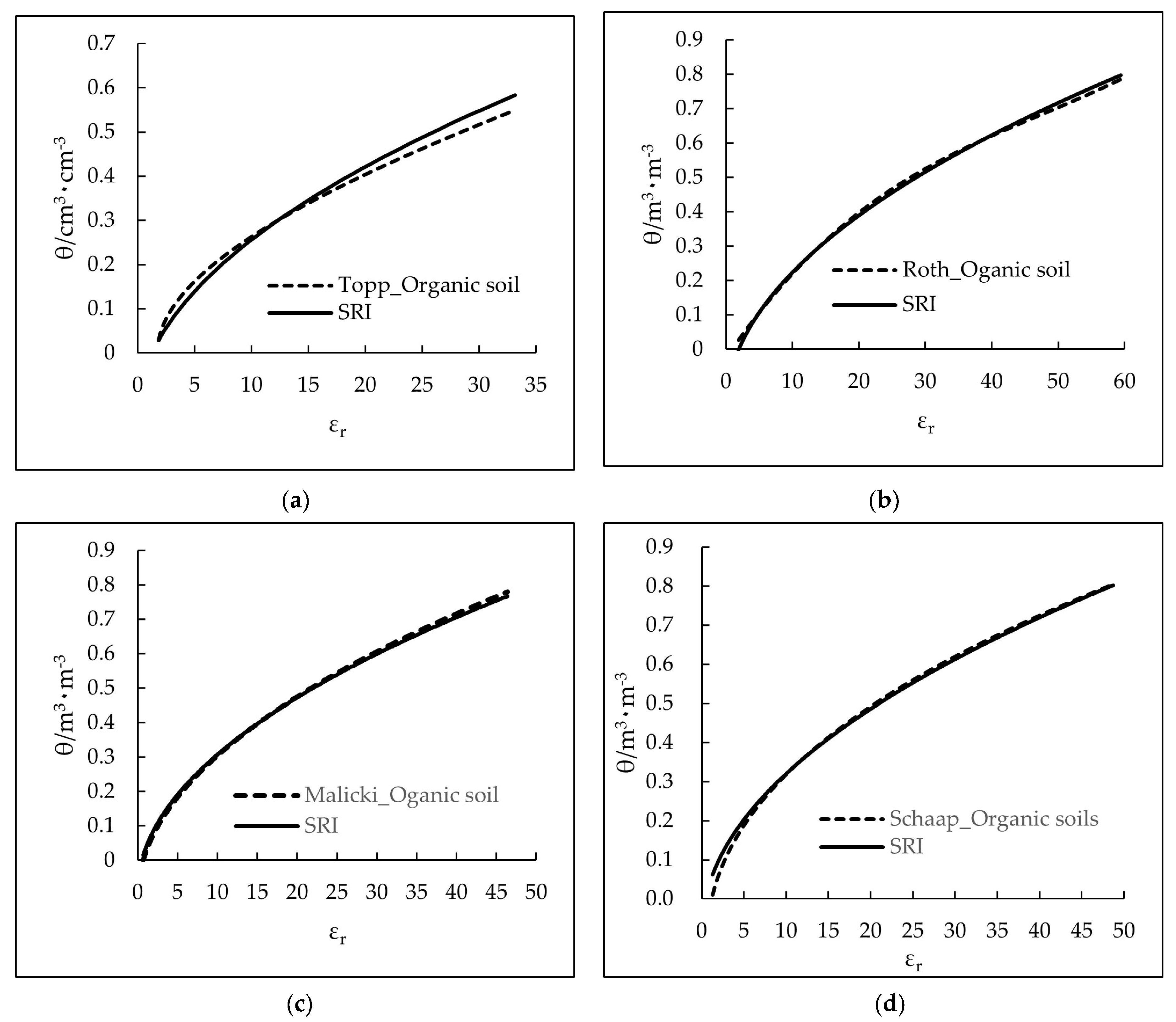
3.2. Verification with Existing Equations
| Source | Original Equation Form | Soil Type | ρ/φ | SRI | RMSE |
|---|---|---|---|---|---|
| Topp et al [11] | Mineral soils | 1.25/ND | 0.019 | ||
| Roth et al. [12] | Mineral soils | 1.429/0.443 | 0.025 | ||
| Malicki et al. [31] | Mineral soils | 1.340/0.481 | 0.015 | ||
| Topp et al. [11] | Organic soils | 0.422/ND | 0.020 | ||
| Roth et al. [12] | Organic soils | 0.397/0.672 | 0.009 | ||
| Malicki et al. [31] | Organic soils | 0.240/0.824 | 0.008 | ||
| Schaap et al. [33] | Organic soils | 0.124/0.905 | 0.012 |
3.3. Influence of Soil Porosity
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huisman, J.A.; Hubbard, S.S.; Redman, J.D.; Annan, A.P. Measuring Soil Water Content with Ground Penetrating Radar: A Review. Vadose Zone J. 2003, 2, 476–491. [Google Scholar] [CrossRef]
- Du, E.; Zhao, L.; Zou, D.; Li, R.; Wang, Z.; Wu, X.; Hu, G.; Zhao, Y.; Liu, G.; Sun, Z. Soil Moisture Calibration Equations for Active Layer GPR Detection—A Case Study Specially for the Qinghai–Tibet Plateau Permafrost Regions. Remote Sens. 2020, 12, 605. [Google Scholar] [CrossRef]
- Ardekani, M.R.M. Off- and on-Ground GPR Techniques for Field-Scale Soil Moisture Mapping. Geoderma 2013, 200–201, 55–66. [Google Scholar] [CrossRef]
- Shamir, O.; Goldshleger, N.; Basson, U.; Reshef, M. Laboratory Measurements of Subsurface Spatial Moisture Content by Ground-Penetrating Radar (GPR) Diffraction and Reflection Imaging of Agricultural Soils. Remote Sens. 2018, 10, 1667. [Google Scholar] [CrossRef]
- Dalton, F.N. Development of Time-Domain Reflectometry for Measuring Soil Water Content and Bulk Soil Electrical Conductivity. In SSSA Special Publications; Clarke Topp, G., Daniel Reynolds, W., Green, R.E., Eds.; Soil Science Society of America: Madison, WI, USA, 2012; pp. 143–167. ISBN 978-0-89118-925-1. [Google Scholar]
- Noborio, K. Measurement of Soil Water Content and Electrical Conductivity by Time Domain Reflectometry: A Review. Comput. Electron. Agric. 2001, 31, 213–237. [Google Scholar] [CrossRef]
- Qin, A.; Ning, D.; Liu, Z.; Duan, A. Analysis of the Accuracy of an FDR Sensor in Soil Moisture Measurement under Laboratory and Field Conditions. J. Sens. 2021, 2021, 6665829. [Google Scholar] [CrossRef]
- Kelleners, T.J.; Soppe, R.W.O.; Robinson, D.A.; Schaap, M.G.; Ayars, J.E.; Skaggs, T.H. Calibration of Capacitance Probe Sensors Using Electric Circuit Theory. Soil. Sci. Soc. Amer J. 2004, 68, 430–439. [Google Scholar] [CrossRef]
- Robinson, D.A.; Gardner, C.M.K.; Evans, J.; Cooper, J.D.; Hodnett, M.G.; Bell, J.P. The Dielectric Calibration of Capacitance Probes for Soil Hydrology Using an Oscillation Frequency Response Model. Hydrol. Earth Syst. Sci. 1998, 2, 111–120. [Google Scholar] [CrossRef]
- Li, Z.-L.; Leng, P.; Zhou, C.; Chen, K.-S.; Zhou, F.-C.; Shang, G.-F. Soil Moisture Retrieval from Remote Sensing Measurements: Current Knowledge and Directions for the Future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic Determination of Soil Water Content: Measurements in Coaxial Transmission Lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Roth, C.H.; Malicki, M.A.; Plagge, R. Empirical Evaluation of the Relationship between Soil Dielectric Constant and Volumetric Water Content as the Basis for Calibrating Soil Moisture Measurements by TDR. J. Soil Sci. 1992, 43, 1–13. [Google Scholar] [CrossRef]
- Almeida, K.S.S.A.D.; Souza, L.D.S.; Paz, V.P.D.S.; Coelho Filho, M.A.; Hoces, E.H. Models for Moisture Estimation in Different Horizons of Yellow Argisol Using TDR. Semina Ciênc. Agrár. 2017, 38, 1727–1736. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, S.; Shan, W. Development of a Frozen Soil Dielectric Constant Model and Determination of Dielectric Constant Variation during the Soil Freezing Process. Cold Reg. Sci. Technol. 2018, 151, 28–33. [Google Scholar] [CrossRef]
- He, H.; Zou, W.; Jones, S.B.; Robinson, D.A.; Horton, R.; Dyck, M.; Filipović, V.; Noborio, K.; Bristow, K.; Gong, Y.; et al. Critical Review of the Models Used to Determine Soil Water Content Using TDR-Measured Apparent Permittivity. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2023; Volume 182, pp. 169–219. ISBN 978-0-443-19268-5. [Google Scholar]
- Loor, G.P.D. Dielectric Properties of Heterogeneous Mixtures Containing Water. J. Microw. Power 1968, 3, 67–73. [Google Scholar] [CrossRef]
- Loor, G.P.D. Dielectric Properties of Heterogeneous Mixtures with a Polar Constituent. Appl. Sci. Res. Sect. B 1964, 11, 310–320. [Google Scholar] [CrossRef]
- Friedman, S.P. A Saturation Degree-dependent Composite Spheres Model for Describing the Effective Dielectric Constant of Unsaturated Porous Media. Water Resour. Res. 1998, 34, 2949–2961. [Google Scholar] [CrossRef]
- Jones, S.B.; Friedman, S.P. Particle Shape Effects on the Effective Permittivity of Anisotropic or Isotropic Media Consisting of Aligned or Randomly Oriented Ellipsoidal Particles. Water Resour. Res. 2000, 36, 2821–2833. [Google Scholar] [CrossRef]
- Dobson, M.; Ulaby, F.; Hallikainen, M.; El-rayes, M. Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- He, H.; Dyck, M.; Zhao, Y.; Si, B.; Jin, H.; Zhang, T.; Lv, J.; Wang, J. Evaluation of Five Composite Dielectric Mixing Models for Understanding Relationships between Effective Permittivity and Unfrozen Water Content. Cold Reg. Sci. Technol. 2016, 130, 33–42. [Google Scholar] [CrossRef]
- Comas, X.; Slater, L.; Reeve, A. Spatial Variability in Biogenic Gas Accumulations in Peat Soils Is Revealed by Ground Penetrating Radar (GPR). Geophys. Res. Lett. 2005, 32, 2004GL022297. [Google Scholar] [CrossRef]
- Parsekian, A.D.; Slater, L.; Giménez, D. Application of Ground-penetrating Radar to Measure Near-saturation Soil Water Content in Peat Soils. Water Resour. Res. 2012, 48, 2011WR011303. [Google Scholar] [CrossRef]
- Birchak, J.R.; Gardner, C.G.; Hipp, J.E.; Victor, J.M. High Dielectric Constant Microwave Probes for Sensing Soil Moisture. Proc. IEEE 1974, 62, 93–98. [Google Scholar] [CrossRef]
- Whalley, W.R. Considerations on the Use of Time-domain Reflectometry (TDR) for Measuring Soil Water Content. J. Soil Sci. 1993, 44, 1–9. [Google Scholar] [CrossRef]
- Brovelli, A.; Cassiani, G. Effective Permittivity of Porous Media: A Critical Analysis of the Complex Refractive Index Model. Geophys. Prospect. 2008, 56, 715–727. [Google Scholar] [CrossRef]
- Pérez, M.; Mendez, D.; Avellaneda, D.; Fajardo, A.; Páez-Rueda, C.I. Time-Domain Transmission Sensor System for on-Site Dielectric Permittivity Measurements in Soil: A Compact, Low-Cost and Stand-Alone Solution. HardwareX 2023, 13, e00398. [Google Scholar] [CrossRef]
- Blonquist, J.M.; Jones, S.B.; Robinson, D.A. Standardizing Characterization of Electromagnetic Water Content Sensors: Part 2. Evaluation of Seven Sensing Systems. Vadose Zone J. 2005, 4, 1059–1069. [Google Scholar] [CrossRef]
- Campbell, J.E. Dielectric Properties and Influence of Conductivity in Soils at One to Fifty Megahertz. Soil Sci. Soc. Am. J. 1990, 54, 332–341. [Google Scholar] [CrossRef]
- Lane, J.A.; Saxton, J.A. Dielectric Dispersion in Pure Polar Liquids at Very High Radio Frequencies—III. The Effect of Electrolytes in Solution. Proc. R. Soc. Lond. A 1952, 214, 531–545. [Google Scholar] [CrossRef]
- Malicki, M.A.; Plagge, R.; Roth, C.H. Improving the Calibration of Dielectric TDR Soil Moisture Determination Taking into Account the Solid Soil. Eur. J Soil Sci. 1996, 47, 357–366. [Google Scholar] [CrossRef]
- Dirksen, C.; Dasberg, S. Improved Calibration of Time Domain Reflectometry Soil Water Content Measurements. Soil Sci. Soc. Am. J. 1993, 57, 660–667. [Google Scholar] [CrossRef]
- Schaap, M.G.; De Lange, L.; Heimovaara, T.J. TDR Calibration of Organic Forest Floor Media. Soil Technol. 1997, 11, 205–217. [Google Scholar] [CrossRef]
- Heimovaara, T.J. Frequency Domain Analysis of Time Domain Reflectometry Waveforms: 1. Measurement of the Complex Dielectric Permittivity of Soils. Water Resour. Res. 1994, 30, 189–199. [Google Scholar] [CrossRef]



| Soil | OM (%) | PD (g/cm3) | ρ (g/cm3) | Porosity | Sand (%) | Silt (%) | Clay (%) |
|---|---|---|---|---|---|---|---|
| OS | 76.7 ± 0.9 | 1.670 ± 0.02 | 0.217 ± 0.5 | 0.870 | 34.9 ± 3 | 57.6 ± 2 | 7.5 ± 1 |
| HS | 54.0 ± 1.0 | 1.850 ± 0.01 | 0.519 ± 0.3 | 0.720 | 16.8 ± 2 | 67.5 ± 1 | 15.7 ± 2 |
| SS | 4.3 ± 0.3 | 2.673 ± 0.01 | 1.523 ± 0.1 | 0.430 | 75.4 ± 1 | 18.9 ± 0.6 | 5.7 ± 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, E.; Zhao, L.; Hu, G.; Xing, Z.; Wu, T.; Wu, X.; Li, R.; Zou, D.; Liu, G.; Wang, L.; et al. A Soil Refractive Index (SRI) Model Characterizing the Functional Relationship Between Soil Moisture Content and Permittivity. Water 2025, 17, 399. https://doi.org/10.3390/w17030399
Du E, Zhao L, Hu G, Xing Z, Wu T, Wu X, Li R, Zou D, Liu G, Wang L, et al. A Soil Refractive Index (SRI) Model Characterizing the Functional Relationship Between Soil Moisture Content and Permittivity. Water. 2025; 17(3):399. https://doi.org/10.3390/w17030399
Chicago/Turabian StyleDu, Erji, Lin Zhao, Guojie Hu, Zanpin Xing, Tonghua Wu, Xiaodong Wu, Ren Li, Defu Zou, Guangyue Liu, Lingxiao Wang, and et al. 2025. "A Soil Refractive Index (SRI) Model Characterizing the Functional Relationship Between Soil Moisture Content and Permittivity" Water 17, no. 3: 399. https://doi.org/10.3390/w17030399
APA StyleDu, E., Zhao, L., Hu, G., Xing, Z., Wu, T., Wu, X., Li, R., Zou, D., Liu, G., Wang, L., Li, Z., Zhang, Y., Xiao, Y., & Zhao, Y. (2025). A Soil Refractive Index (SRI) Model Characterizing the Functional Relationship Between Soil Moisture Content and Permittivity. Water, 17(3), 399. https://doi.org/10.3390/w17030399









