Forecasting the River Ice Break-Up Date in the Upper Reaches of the Heilongjiang River Based on Machine Learning
Abstract
:1. Introduction
2. Material and Methods
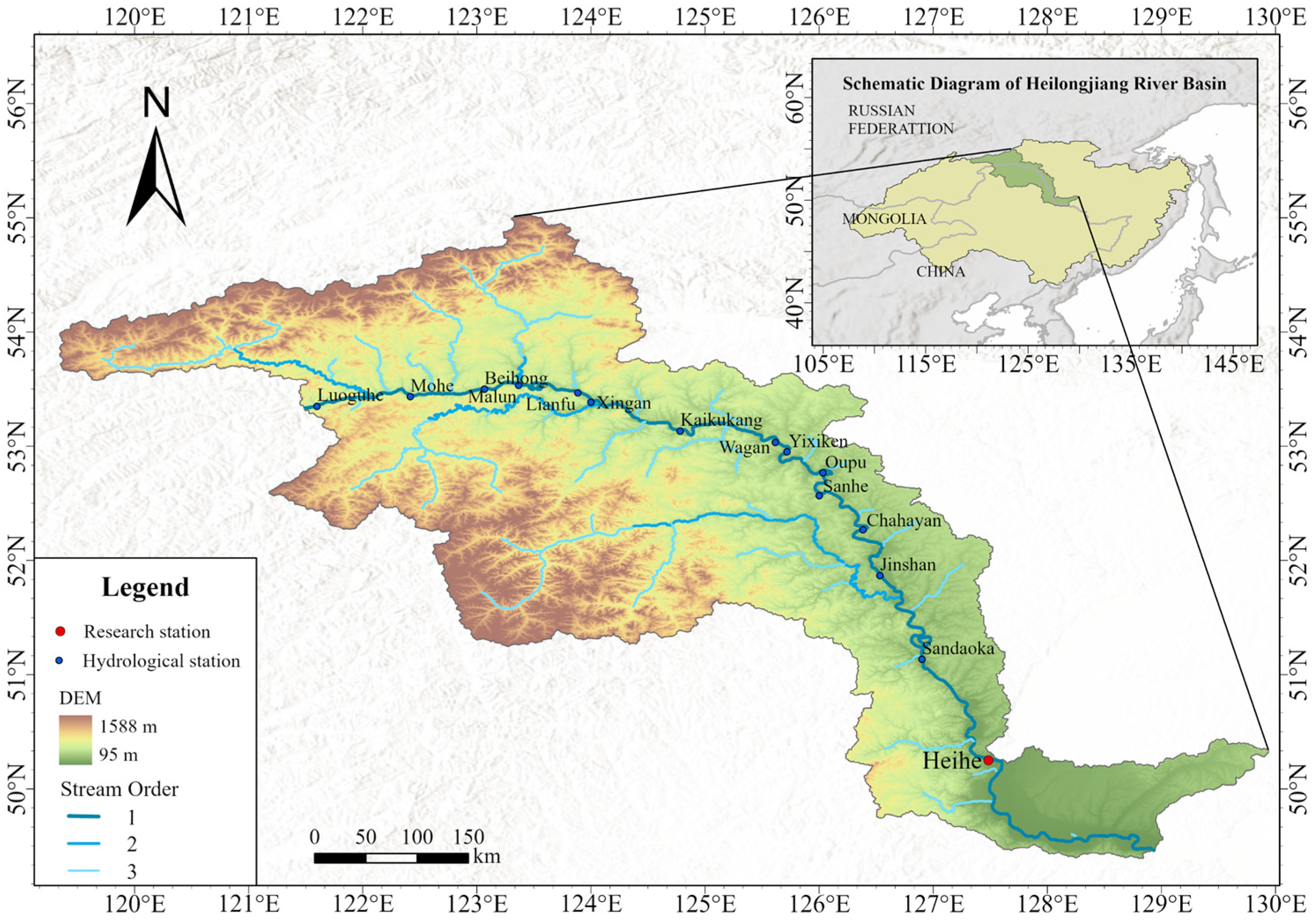
2.1. Overview of the Study Area
2.2. Data Acquisition and Processing
2.3. Calculation of Ice Reserves
2.4. Mann-Kendall Test
2.5. Feature Selection Methods
2.5.1. Pearson Correlation Coefficient
2.5.2. Grey Relational Analysis
2.5.3. Mutual Information
2.5.4. Stepwise Regression
2.6. Machine Learning Algorithms
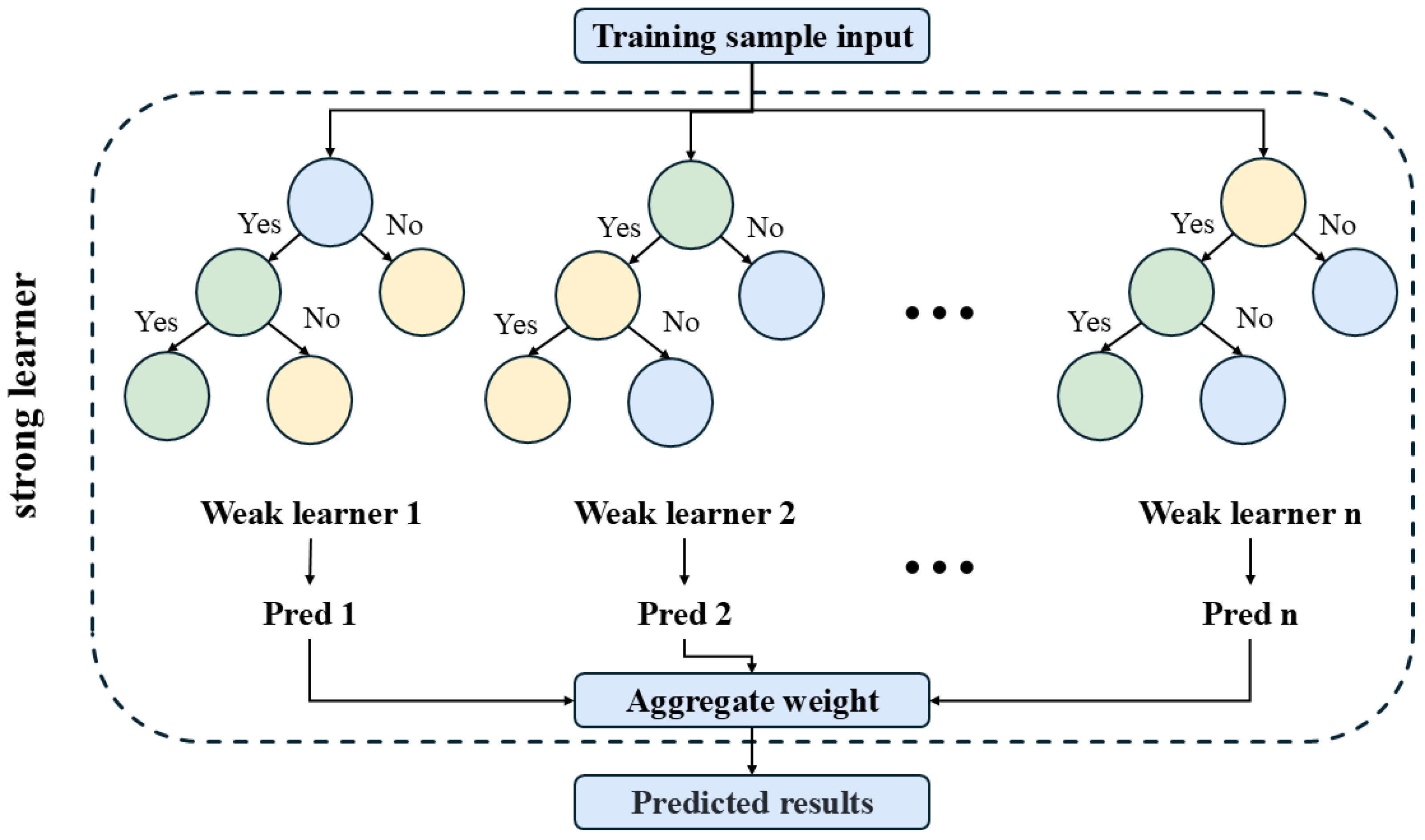
2.6.1. Extreme Gradient Boosting
2.6.2. Back Propagation Neural Network
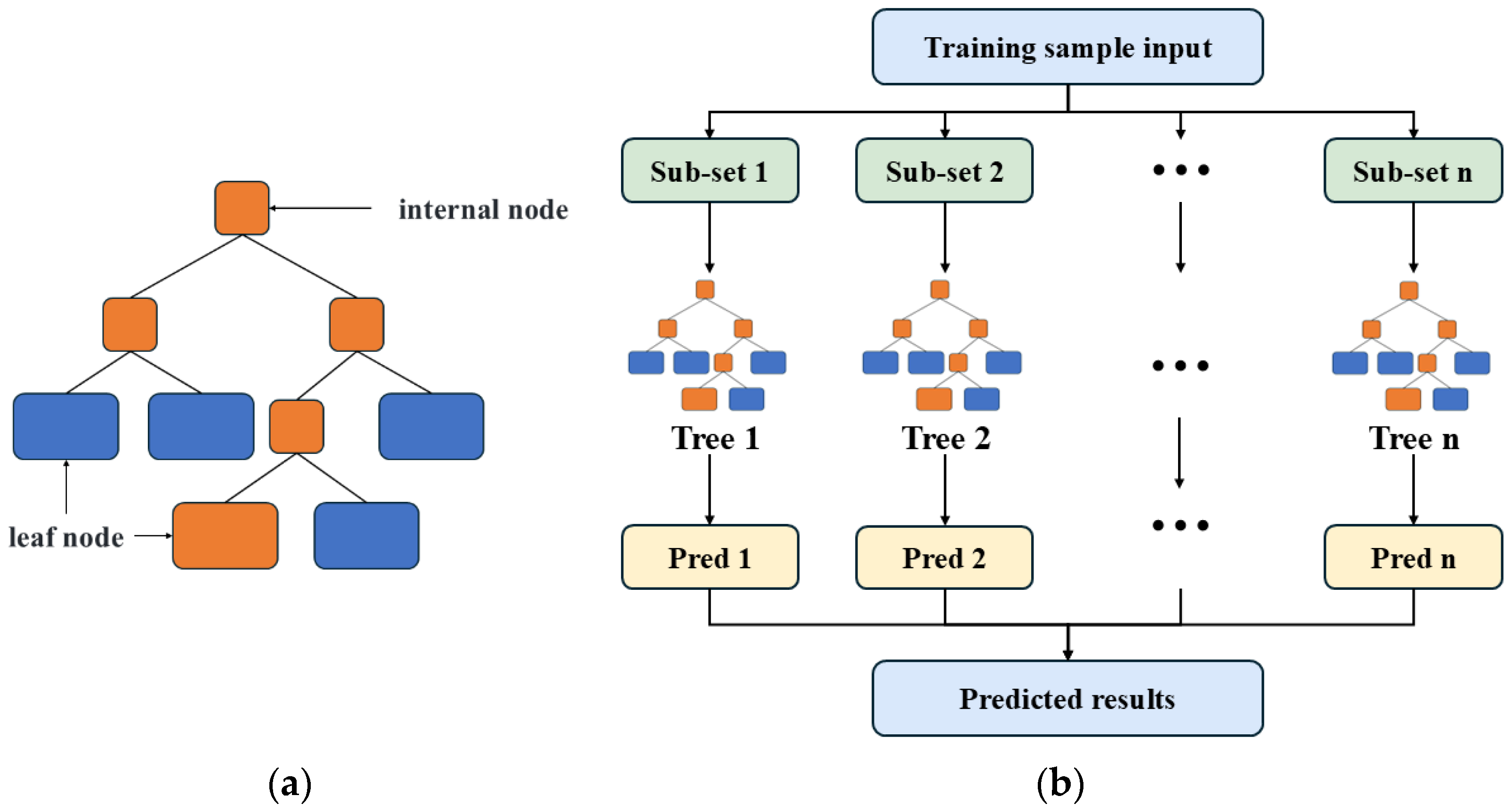
2.6.3. Random Forest
2.6.4. Support Vector Regression
2.7. Settings of Model Parameter
2.8. Evaluation Metrics
2.9. Model Simulations
3. Results and Analysis
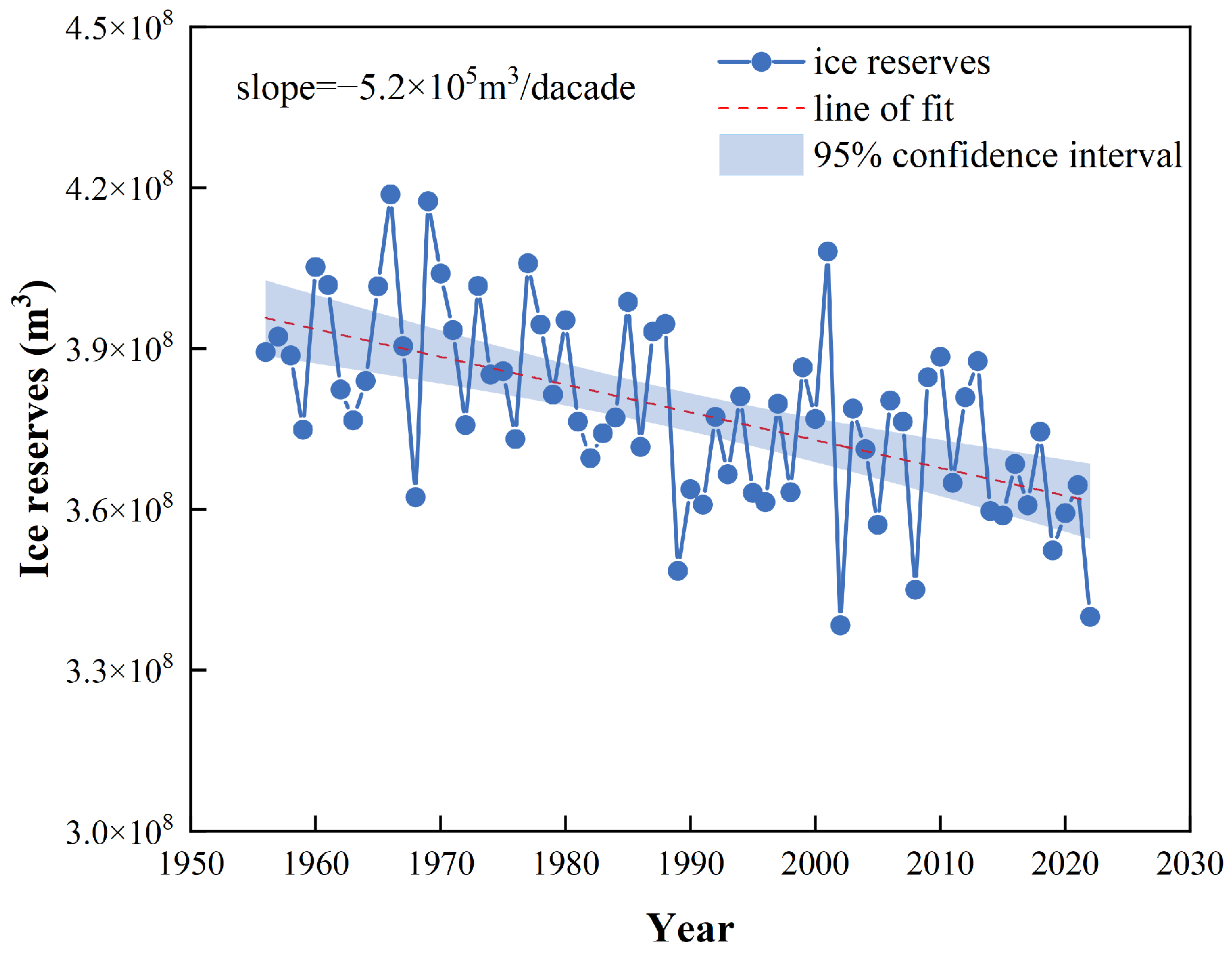
3.1. Ice Conditions Change
3.2. Correlation Analysis
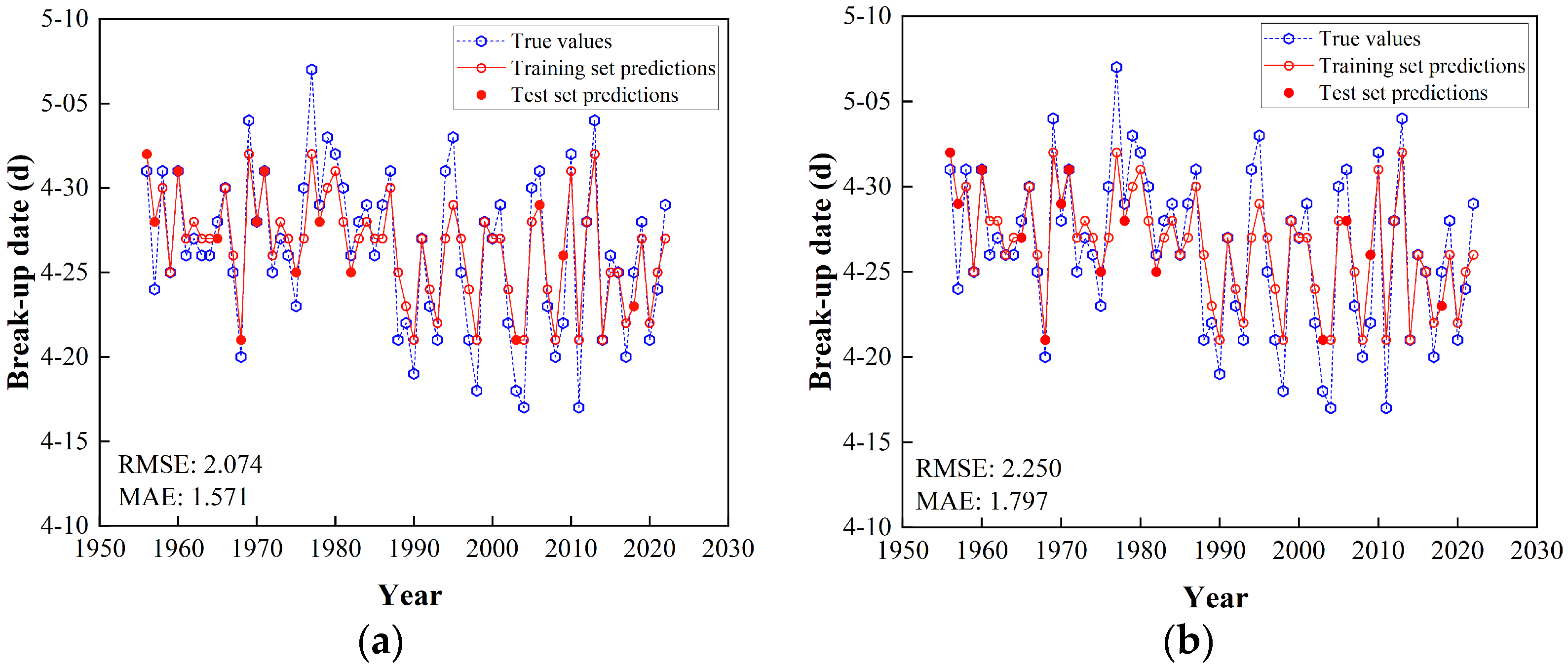
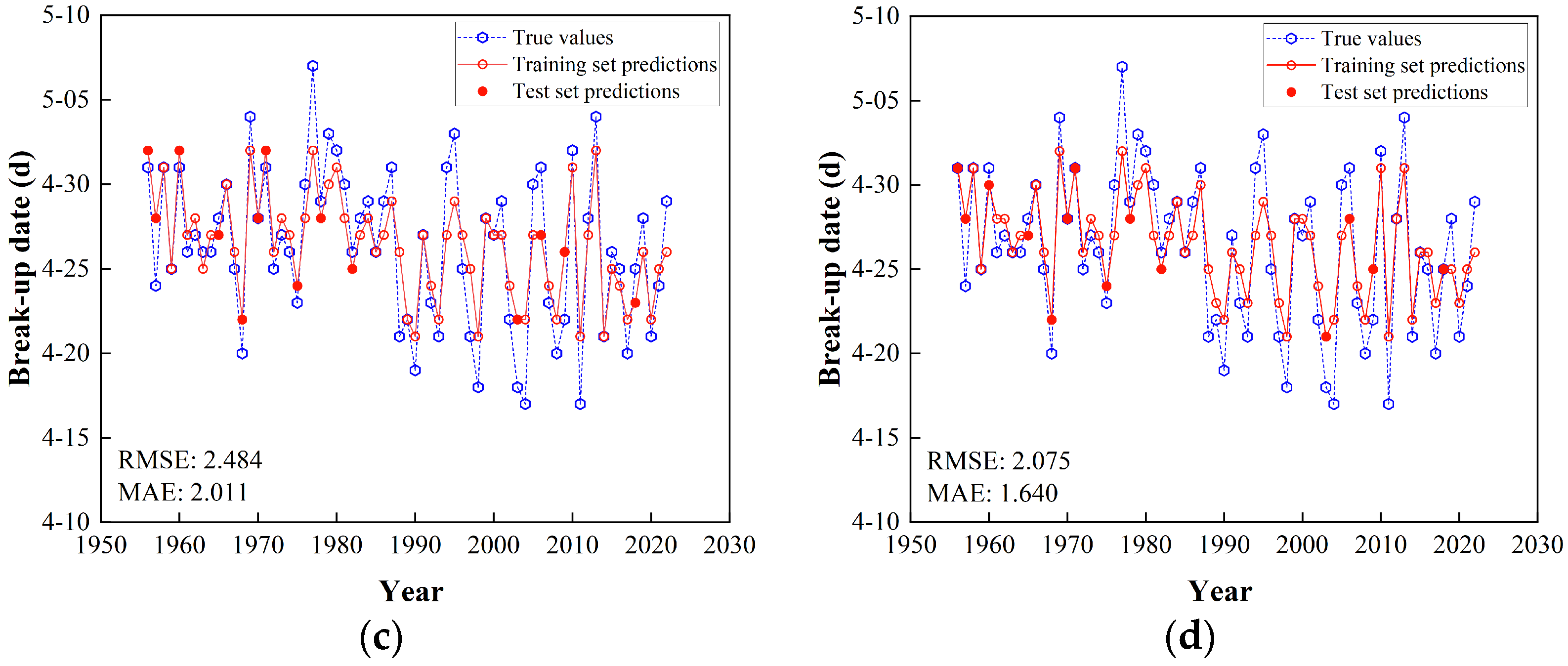
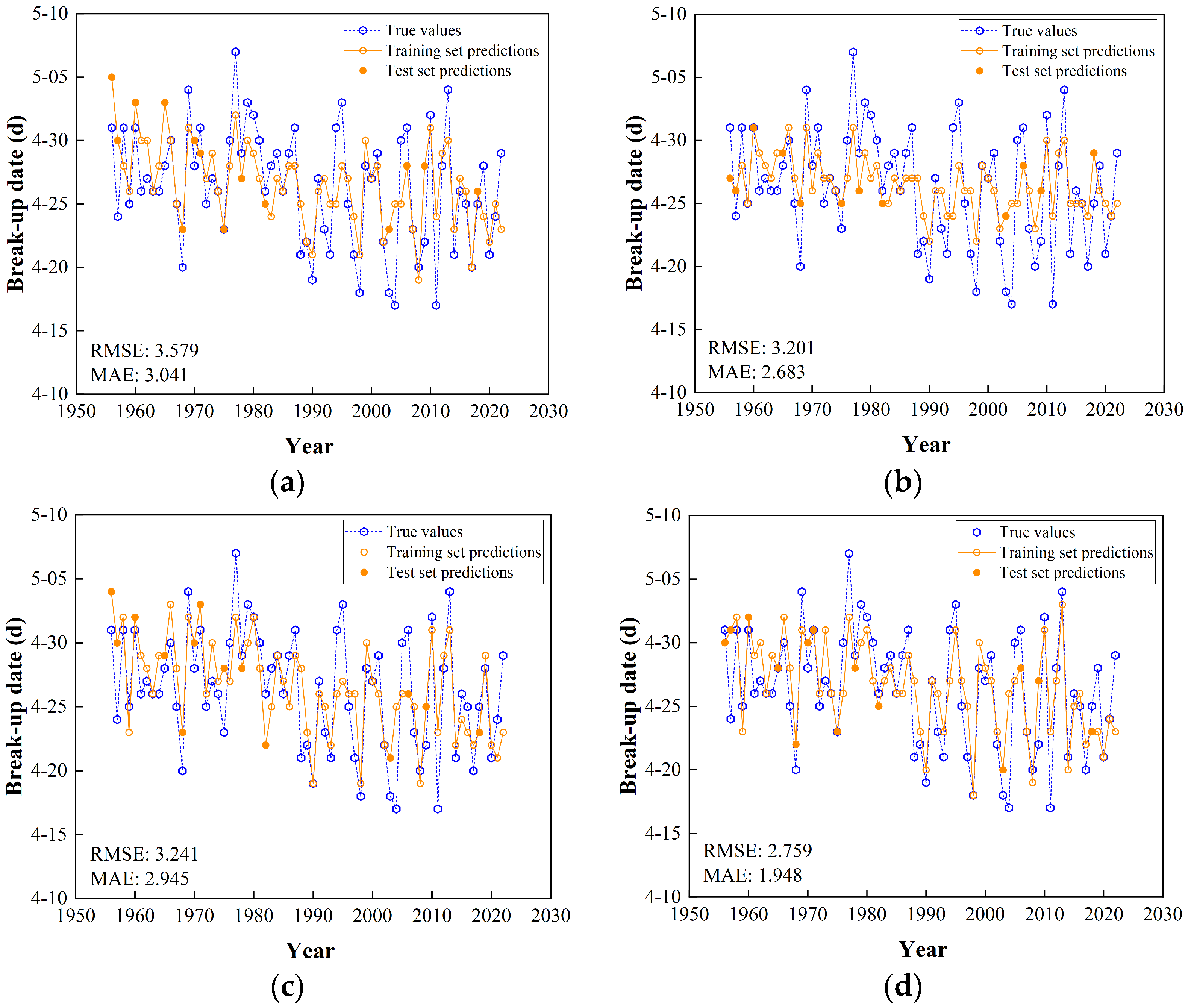
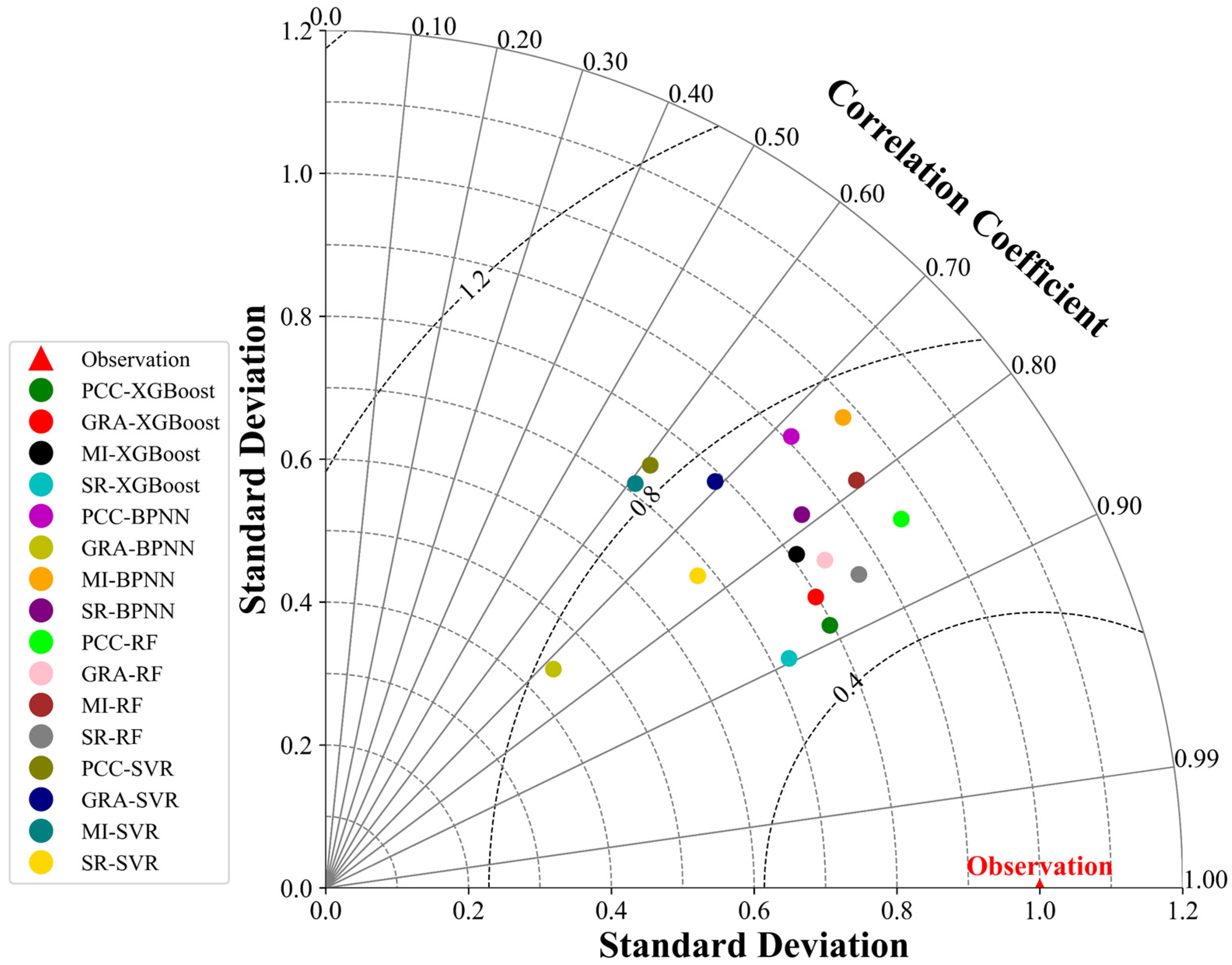
3.3. Results of Predicting River Ice Break-Up Dates
4. Discussion
5. Conclusions
- The river ice break-up date of the Heihe section of the Heilongjiang River shows an early trend, with the river ice break-up date advancing by 0.682 days every 10 years. The ice reserves in the Oupu–Heihe section in the upper reaches of the Heilongjiang River have the most significant impact on the river ice break-up date in the Heihe section. The correlation coefficient, grey relational degree, and mutual information value were 0.480, 0.479, and 0.176, respectively.
- The different feature sets obtained for feature selection using PCC, MI, GRA, and SR reflect the different data characteristics that these methods focus on. Accumulated temperature during the break-up period and average temperature before river ice break-up were considered to have a significant effect on the opening of the river for a wide range of criteria, with abrupt temperature changes being a key factor affecting the timing of the opening of the river.
- The best feature selection method varies depending on the structure of the ML model. By comparing 16 different combinations, PCC-XGBoost resulted in the smallest bias, achieving a prediction accuracy of 85.71%. According to the Standard for Hydrological Information and Hydrological Forecasting, this is classified as a first-class solution and can be used for river opening date prediction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lindenschmidt, K.-E.; Rokaya, P. A stochastic hydraulic modelling approach to determining the probable maximum staging of ice-jam floods. J. Environ. Inform. 2019, 34, 45–54. [Google Scholar] [CrossRef]
- Hicks, F.; Beltaos, S. River Ice. In Cold Region Atmospheric and Hydrologic Studies. The Mackenzie GEWEX Experience; Woo, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 281–305. [Google Scholar] [CrossRef]
- Rokaya, P.; Budhathoki, S.; Lindenschmidt, K.-E. Ice-jam flood research: A scoping review. Nat. Hazards 2018, 94, 1439–1457. [Google Scholar] [CrossRef]
- Cunderlik, J.M.; Ouarda, T.B.M.J. Trends in the timing and magnitude of floods in Canada. J. Hydrol. 2009, 375, 471–480. [Google Scholar] [CrossRef]
- Ghoreishi, M.; Lindenschmidt, K.-E. Unlocking effective ice-jam risk management: Insights from agent-based modeling and comparative analysis of social theories in Fort McMurray, Canada. Environ. Sci. Policy 2024, 157, 103731. [Google Scholar] [CrossRef]
- Pagneux, E.; Gísladóttir, G.; Jónsdóttir, S. Public perception of flood hazard and flood risk in Iceland: A case study in a watershed prone to ice-jam floods. Nat. Hazards 2011, 58, 269–287. [Google Scholar] [CrossRef]
- Das, A.; Lindenschmidt, K.-E. Current status and advancement suggestions of ice-jam flood hazard and risk assessment. Environ. Rev. 2020, 28, 373–379. [Google Scholar] [CrossRef]
- Das, A.; Budhathoki, S.; Lindenschmidt, K.-E. Development of an ice-jam flood forecasting modelling framework for freeze-up/winter breakup. Hydrol. Res. 2023, 54, 648–662. [Google Scholar] [CrossRef]
- Barrette, P.D.; Khan, A.A.; Lindenschmidt, K.-E. A glimpse at twenty-five hydraulic models for river ice. In Proceedings of the 27th IAHR International Symposium on Ice, Gdańsk, Poland, 9–13 June 2024; Available online: https://www.iahr.org/library/infor?pid=30349 (accessed on 20 May 2023).
- Lindenschmidt, K.-E. RIVICE—A Non-Proprietary, Open-Source, One-Dimensional River-Ice Model. Water 2017, 9, 314. [Google Scholar] [CrossRef]
- Fu, H.; Guo, X.; Yang, K.; Wang, T.; Guo, Y. Ice accumulation and thickness distribution before inverted siphon. J. Hydrodyn. 2017, 29, 61–67. [Google Scholar] [CrossRef]
- Carson, R.; Beltaos, S.; Groeneveld, J.; Healy, D.; She, Y.; Malenchak, J.; Morris, M.; Saucet, J.-P.; Kolerski, T.; Shen, H.T. Comparative testing of numerical models of river ice jams. Can. J. Civ. Eng. 2011, 38, 669–678. [Google Scholar] [CrossRef]
- Beltaos, S. Numerical modelling of ice-jam flooding on the Peace-Athabasca delta. Hydrol. Process. 2003, 17, 3685–3702. [Google Scholar] [CrossRef]
- Ladouceur, J.-R.; Morse, B.; Lindenschmidt, K.-E. A comprehensive method to estimate flood levels of rivers subject to ice jams: A case study of the Chaudière River, Québec, Canada. Hydrol. Res. 2023, 54, 995–1016. [Google Scholar] [CrossRef]
- Beltaos, S.; Burrell, B.C. Hydrotechnical advances in Canadian river ice science and engineering during the past 35 years. Can. J. Civ. Eng. 2015, 42, 583–591. [Google Scholar] [CrossRef]
- Lei, Q.; Zhang, D.; Li, J. Discussion on the ice breakup forecasting and analysis method at Jiayin station, Heilongjiang. Heilongjiang Hydr. Sci. Technol. 2010, 39, 16–17. (In Chinese) [Google Scholar]
- Lindenschmidt, K.-E.; Rokaya, P.; Das, A.; Li, Z.; Richard, D. A novel stochastic modelling approach for operational real-time ice-jam flood forecasting. J. Hydrol. 2019, 575, 381–394. [Google Scholar] [CrossRef]
- Smith, J.D.; Lamontagne, J.R.; Jasek, M. Considering uncertainty of historical ice jam flood records in a Bayesian frequency analysis for the Peace-Athabasca Delta. Water Resour. Res. 2024, 60, e2022WR034377. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Y.; Xing, Z.; Wang, X.; Fu, Q. Study on forecasting break-up date of river ice in Heilongjiang Province based on LSTM and CEEMDAN. Water 2023, 15, 496. [Google Scholar] [CrossRef]
- Shevnina, E.V.; Solov’eva, Z.S. Long-term variability and methods of forecasting dates of ice break-up in the mouth area of the Ob and Yenisei rivers. Russ. Meteorol. Hydrol. 2008, 33, 458–465. [Google Scholar] [CrossRef]
- Madaeni, F.; Chokmani, K.; Lhissou, R.; Gauthier, Y.; Tolszczuk-Leclerc, S. Convolutional neural network and long short-term memory models for ice-jam predictions. Cryosphere 2022, 16, 1447–1468. [Google Scholar] [CrossRef]
- Kalke, H.; Loewen, M. Support vector machine learning applied to digital images of river ice conditions. Cold Reg. Sci. Technol. 2018, 155, 225–236. [Google Scholar] [CrossRef]
- Tom, M.; Prabha, R.; Wu, T.; Baltsavias, E.; Leal-Taixé, L.; Schindler, K. Ice monitoring in Swiss lakes from optical satellites and webcams using machine learning. Remote Sens. 2020, 12, 3555. [Google Scholar] [CrossRef]
- Chen, S.; Ji, H. Fuzzy optimization neural network approach for ice forecast in the Inner Mongolia reach of the Yellow River. Hydrol. Sci. J. 2005, 50, 319–330. [Google Scholar] [CrossRef]
- Ge, Q.; Wang, J.; Liu, C.; Wang, X.; Deng, Y.; Li, J. Integrating feature selection with machine learning for accurate reservoir landslide displacement prediction. Water 2024, 16, 2152. [Google Scholar] [CrossRef]
- Paulson, N.H.; Kubal, J.; Ward, L.; Saxena, S.; Lu, W.; Babinec, S.J. Feature engineering for machine learning enabled early prediction of battery lifetime. J. Power Sources 2022, 527, 231127. [Google Scholar] [CrossRef]
- Chicco, D.; Oneto, L.; Tavazzi, E. Eleven quick tips for data cleaning and feature engineering. PLoS Comput. Biol. 2022, 18, e1010718. [Google Scholar] [CrossRef]
- Diebold, F.X.; Göbel, M.; Coulombe, P.G. Assessing and comparing fixed-target forecasts of Arctic sea ice: Glide charts for feature-engineered linear regression and machine learning models. Energy Econ. 2023, 124, 106833. [Google Scholar] [CrossRef]
- Nichol, J.J.; Peterson, M.G.; Peterson, K.J.; Fricke, G.M.; Moses, M.E. Machine learning feature analysis illuminates disparity between E3SM climate models and observed climate change. J. Comput. Appl. Math. 2021, 395, 113451. [Google Scholar] [CrossRef]
- Verdonck, T.; Baesens, B.; Óskarsdóttir, M.; vanden Broucke, S. Special issue on feature engineering editorial. Mach. Learn. 2024, 113, 3917–3928. [Google Scholar] [CrossRef]
- Ji, H.; Zhang, A.; Gao, R.; Zhang, B.; Xu, J. Application of the break-up date prediction model in the Inner Mongolia Reach of the Yellow River. Adv. Sci. Technol. Water Res. 2012, 32, 42–45. [Google Scholar]
- Li, C.; Guo, X.; Wang, Z. Determination on forecast factor of artificial intelligence ice-forecast. Water Resour. Hydropower Eng. 2012, 43, 9–13. (In Chinese) [Google Scholar] [CrossRef]
- Rokaya, P.; Budhathoki, S.; Lindenschmidt, K.-E. Trends in the Timing and magnitude of ice-jam floods in Canada. Sci. Rep. 2018, 8, 5834. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Lindenschmidt, K.-E. Modelling climatic impacts on ice-jam floods: A review of current models, modelling capabilities, challenges, and future prospects. Environ. Rev. 2021, 29, 378–390. [Google Scholar] [CrossRef]
- Salimi, A.; Ghobrial, T.; Bonakdari, H. A comprehensive review of AI-based methods used for forecasting ice jam floods occurrence, severity, timing, and location. Cold Reg. Sci. Technol. 2024, 227, 104305. [Google Scholar] [CrossRef]
- Das, A.; Rokaya, P.; Lindenschmidt, K.-E. The impact of a bias-correction approach (delta change) applied directly to hydrological model output when modelling the severity of ice jam flooding under future climate scenarios. Clim. Change 2022, 172, 19. [Google Scholar] [CrossRef]
- Lubiniecki, T.; Laroque, C.P.; Lindenschmidt, K.-E. Identifying ice-jam flooding events through the application of dendrogeomorphological methods. River Res. Appl. 2024, 40, 191–202. [Google Scholar] [CrossRef]
- Huang, F.; Shen, H.T. Dam removal effect on the lower St. Regis River ice-jam floods. Can. J. Civ. Eng. 2023, 51, 215–227. [Google Scholar] [CrossRef]
- Li, Y.; Han, H.; Sun, Y.; Xiao, X.; Liao, H.; Liu, X.; Wang, E. Risk evaluation of ice flood disaster in the upper Heilongjiang River based on catastrophe theory. Water 2023, 15, 2724. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Z.; Guo, X.; Fu, H.; Liu, W. Prediction of breakup ice jam with Artificial Neural Networks. J. Hydraul. Eng. 2017, 48, 1355–1362. (In Chinese) [Google Scholar] [CrossRef]
- Li, M.; Yang, D.; Hou, J.; Xiao, P.; Xing, X. Distributed hydrological model of Heilongjiang River basin. J. Hydroelectr. Eng. 2021, 40, 65–75. (In Chinese) [Google Scholar]
- Cao, W.; Xiao, D.; Li, G. How to make ice dam forecasting for Heilongjiang River. J. China Hydrol. 2014, 34, 72–76. (In Chinese) [Google Scholar]
- Chang, Y.; Liu, X.; Zhao, X.; Shen, Y. Multi-scale analysis of runoff variability and its influencing factors in the mountainous Hutuo River Basin. J. Water Resour. Eng. 2023, 34, 59–70. (In Chinese) [Google Scholar]
- Massie, D.D.; White, K.D.; Daly, S.F. Application of neural networks to predict ice jam occurrence. Cold Reg. Sci. Technol. 2002, 35, 115–122. [Google Scholar] [CrossRef]
- Rafi, M.N.; Imran, M.; Nadeem, H.A.; Abbas, A.; Pervaiz, M.; Khan, W.; Ullah, S.; Hussain, S.; Saeed, Z. Comparative influence of biochar and doped biochar with Si-NPs on the growth and anti-oxidant potential of Brassica rapa L. under Cd toxicity. Silicon 2022, 14, 11699–11714. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Magnuson, J.J.; Robertson, D.M.; Benson, B.J.; Wynne, R.H.; Livingstone, D.M.; Arai, T.; Assel, R.A.; Barry, R.G.; Card, V.; Kuusisto, E.; et al. Historical trends in lake and river ice cover in the Northern Hemisphere. Science 2000, 289, 1743–1746. [Google Scholar] [CrossRef]
- Prowse, T.D.; Beltaos, S. Climatic control of river-ice hydrology: A review. Hydrol. Process. 2002, 16, 805–822. [Google Scholar] [CrossRef]
- Ji, X.; Zhao, J. Analysis of correlation between sea ice concentration and cloudiness in the central Arctic. Acta Oceanol. Sin. 2015, 37, 92–104. (In Chinese) [Google Scholar] [CrossRef]
- Schweiger, A.J.; Lindsay, R.W.; Vavrus, S.; Francis, J.A. Relationships between Arctic sea ice and clouds during autumn. J. Clim. 2009, 22, 4799–4810. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef]
- Prowse, T.D.; Bonsal, B.R.; Duguay, C.R.; Lacroix, M.P. River-ice break-up/freeze-up: A review of climatic drivers, historical trends and future predictions. Ann. Glaciol. 2007, 46, 443–451. [Google Scholar] [CrossRef]
- Rokaya, P.; Morales-Marín, L.; Bonsal, B.; Wheater, H.; Lindenschmidt, K.-E. Climatic effects on ice phenology and ice-jam flooding of the Athabasca River in western Canada. Hydrol. Sci. J. 2019, 64, 1265–1278. [Google Scholar] [CrossRef]
- Burrell, B.C.; Beltaos, S.; Turcotte, B. Effects of climate change on river-ice processes and ice jams. Int. J. River Basin Manag. 2022, 21, 421–441. [Google Scholar] [CrossRef]
- Yang, X.; Pavelsky, T.M.; Allen, G.H. The past and future of global river ice. Nature 2020, 577, 69–73. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Niazkar, M.; Menapace, A.; Brentan, B.; Piraei, R.; Jimenez, D.; Dhawan, P.; Righetti, M. Applications of XGBoost in water resources engineering: A systematic literature review (Dec 2018–May 2023). Environ. Model. Softw. 2024, 174, 105971. [Google Scholar] [CrossRef]
- Hussain, D.; Khan, A.A. Machine learning techniques for monthly river flow forecasting of Hunza River, Pakistan. Earth Sci. Inform. 2020, 13, 939–949. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, H.; Lin, Y.; Jin, J.; Liu, W.; An, X. Reservoir inflow predicting model based on machine learning algorithm via multi-model fusion: A case study of Jinshuitan river basin. IET Cyber-Syst. Robot. 2021, 3, 265–277. [Google Scholar] [CrossRef]
- Aksoy, H.; Mohammadi, M. Artificial neural network and regression models for flow velocity at sediment incipient deposition. J. Hydrol. 2016, 541, 1420–1429. [Google Scholar] [CrossRef]
- Nielsen, M.A. Neural Networks and Deep Learning; Determination Press: San Francisco, CA, USA, 2015; Available online: http://neuralnetworksanddeeplearning.com/ (accessed on 29 December 2023).
- Hu, H.; Zhang, J.; Li, T. A novel hybrid decompose-ensemble strategy with a VMD-BPNN approach for daily streamflow estimating. Water Resour. Manag. 2021, 35, 5119–5138. [Google Scholar] [CrossRef]
- Dai, W.; Cai, Z. Predicting coastal urban floods using artificial neural network: The case study of Macau, China. Appl. Water Sci. 2021, 11, 161. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]






| Candidate Factors | Code |
|---|---|
| Accumulated temperature during the break-up period (°C) | X1 |
| Date of positive temperature stabilization (d) | X2 |
| Average temperature before river ice break-up (°C) | X3 |
| Ice reserves (m3) | X4 |
| Average wind speed during the break-up period (m/s) | X5 |
| Average snow depth during the break-up period (mm) | X6 |
| Precipitation prior to river freeze-up (mm) | X7 |
| Precipitation during the river freeze-up period (mm) | X8 |
| Precipitation before river ice break-up (mm) | X9 |
| Precipitation during the break-up period (mm) | X10 |
| Average cloud cover during the break-up period (0–1) | X11 |
| Maximum ice thickness (cm) | X12 |
| Dataset | Variable | Minimum | Maximum | Mean |
|---|---|---|---|---|
| Training Set | X1 (°C) | −65.51 | 115.18 | 20.06 |
| X2 (d) | −19 | 17 | 2 | |
| X3 (°C) | −14.51 | −1.68 | −8.69 | |
| X4 (m3) | 2.55 × 108 | 3.21 × 108 | 2.88 × 108 | |
| X5 (m/s) | 2.13 | 3.71 | 2.87 | |
| X6 (mm) | 0 | 88.67 | 6.90 | |
| X7 (mm) | 7.13 | 102.27 | 35.71 | |
| X8 (mm) | 47.50 | 197.50 | 91.80 | |
| X9 (mm) | 1.40 | 38.00 | 13.67 | |
| X10 (mm) | 1.5 | 151.30 | 34.53 | |
| X11 (0–1) | 30.54 | 76.11 | 57.87 | |
| X12 (cm) | 85 | 1.75 | 120 | |
| Test Set | X1 (°C) | −38.64 | 84.12 | 29.39 |
| X2 (d) | −11 | 18 | 3 | |
| X3 (°C) | −14.52 | −3.84 | −10.15 | |
| X4 (m3) | 2.79 × 108 | 3.18 × 108 | 2.98 × 108 | |
| X5 (m/s) | 2.39 | 3.37 | 2.83 | |
| X6 (mm) | 0 | 31.32 | 6.47 | |
| X7 (mm) | 8.95 | 86.47 | 38.57 | |
| X8 (mm) | 44.90 | 137 | 84.88 | |
| X9 (mm) | 2.40 | 26.90 | 14.15 | |
| X10 (mm) | 4.10 | 72.6 | 33.24 | |
| X11 (0–1) | 42.43 | 65.54 | 54.83 | |
| X12 (cm) | 78 | 173 | 119 |
| Model | Parameters | PCC | GRA | MI | SR |
|---|---|---|---|---|---|
| XGBoost | learning_rate | 0.1 | 0.01 | 0.01 | 0.01 |
| max_depth | 11 | 5 | 9 | 9 | |
| n_estimators | 100 | 500 | 300 | 200 | |
| subsample | 0.6 | 0.6 | 1.0 | 0.6 | |
| colsample_bytree | 0.8 | 0.8 | 0.8 | 0.9 | |
| BPNN | hidden_layer_sizes | (50) | (50, 50) | (50) | (50, 50) |
| activation | identity | relu | identity | tanh | |
| solver | lbfgs | lbfgs | lbfgs | adam | |
| alpha | 0.0001 | 0.0001 | 0.0001 | 0.01 | |
| RF | n_estimators | 100 | 200 | 100 | 100 |
| min_samples_split | 4 | 5 | 10 | 5 | |
| min_samples_leaf | 2 | 4 | 2 | 4 | |
| max_depth | 10 | 20 | 10 | 20 | |
| SVR | C | 10 | 10 | 10 | 0.1 |
| kernel | rbf | rbf | rbf | linear | |
| epsilon | 0.2 | 0.2 | 0.2 | 0.1 |
| Study Area | PCC | GRA | MI | SR |
|---|---|---|---|---|
| Heihe section | X1, X2, X3, X4, X6, X8, X11 | X1, X2, X3, X4, X6, X11 | X1, X2, X3, X4 | X1, X3, X5, X7, X9, X11 |
| Model | Methods | Training Set | Test Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | TSS | RMSE | MAE | R2 | NSE | TSS | ||
| XGBoost | PCC | 1.950 | 1.537 | 0.907 | 0.823 | 0.848 | 2.074 | 1.571 | 0.784 | 0.756 | 0.950 |
| GRA | 1.998 | 1.553 | 0.895 | 0.814 | 0.836 | 2.250 | 1.797 | 0.740 | 0.712 | 0.901 | |
| MI | 2.185 | 1.722 | 0.863 | 0.778 | 0.783 | 2.484 | 2.011 | 0.666 | 0.649 | 0.822 | |
| SR | 2.206 | 1.782 | 0.883 | 0.774 | 0.769 | 2.075 | 1.640 | 0.803 | 0.755 | 0.923 | |
| BPNN | PCC | 3.140 | 2.645 | 0.549 | 0.539 | 0.521 | 3.579 | 3.041 | 0.514 | 0.272 | 0.682 |
| GRA | 3.412 | 2.807 | 0.523 | 0.458 | 0.358 | 3.201 | 2.683 | 0.520 | 0.418 | 0.379 | |
| MI | 3.041 | 2.402 | 0.571 | 0.570 | 0.615 | 3.241 | 2.945 | 0.547 | 0.403 | 0.724 | |
| SR | 2.850 | 2.206 | 0.623 | 0.622 | 0.655 | 2.759 | 1.948 | 0.620 | 0.567 | 0.785 | |
| RF | PCC | 1.475 | 1.116 | 0.914 | 0.898 | 0.974 | 2.442 | 2.038 | 0.708 | 0.661 | 0.907 |
| GRA | 1.993 | 1.577 | 0.827 | 0.815 | 0.871 | 2.445 | 2.041 | 0.699 | 0.660 | 0.892 | |
| MI | 2.103 | 1.689 | 0.806 | 0.794 | 0.885 | 2.690 | 2.232 | 0.628 | 0.589 | 0.813 | |
| SR | 2.243 | 1.740 | 0.787 | 0.766 | 0.799 | 2.283 | 1.871 | 0.743 | 0.704 | 0.932 | |
| SVR | PCC | 3.369 | 2.557 | 0.484 | 0.472 | 0.436 | 3.179 | 2.738 | 0.468 | 0.426 | 0.585 |
| GRA | 3.242 | 2.309 | 0.537 | 0.511 | 0.476 | 2.969 | 2.451 | 0.511 | 0.499 | 0.647 | |
| MI | 3.413 | 2.602 | 0.476 | 0.458 | 0.412 | 3.180 | 2.736 | 0.441 | 0.425 | 0.543 | |
| SR | 3.121 | 2.560 | 0.631 | 0.547 | 0.461 | 2.813 | 2.325 | 0.551 | 0.550 | 0.680 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Han, H.; Li, Y.; Wang, E.; Liu, X. Forecasting the River Ice Break-Up Date in the Upper Reaches of the Heilongjiang River Based on Machine Learning. Water 2025, 17, 434. https://doi.org/10.3390/w17030434
Liu Z, Han H, Li Y, Wang E, Liu X. Forecasting the River Ice Break-Up Date in the Upper Reaches of the Heilongjiang River Based on Machine Learning. Water. 2025; 17(3):434. https://doi.org/10.3390/w17030434
Chicago/Turabian StyleLiu, Zhi, Hongwei Han, Yu Li, Enliang Wang, and Xingchao Liu. 2025. "Forecasting the River Ice Break-Up Date in the Upper Reaches of the Heilongjiang River Based on Machine Learning" Water 17, no. 3: 434. https://doi.org/10.3390/w17030434
APA StyleLiu, Z., Han, H., Li, Y., Wang, E., & Liu, X. (2025). Forecasting the River Ice Break-Up Date in the Upper Reaches of the Heilongjiang River Based on Machine Learning. Water, 17(3), 434. https://doi.org/10.3390/w17030434








