The Toppling Deformation and Failure Criteria of a Steep Bedding Rock Slope—The Case of a Bank Slope at the Duonuo Hydropower Station
Abstract
1. Introduction
2. Statistical Analysis of the Characteristics of Large Bedding Toppling Slopes
- (1)
- Slope elevation
- (2)
- Slope heigh
- (3)
- Rock dip β and slope angle α
- (4)
- Lithology
3. Slope Toppling Deformation Process Simulation
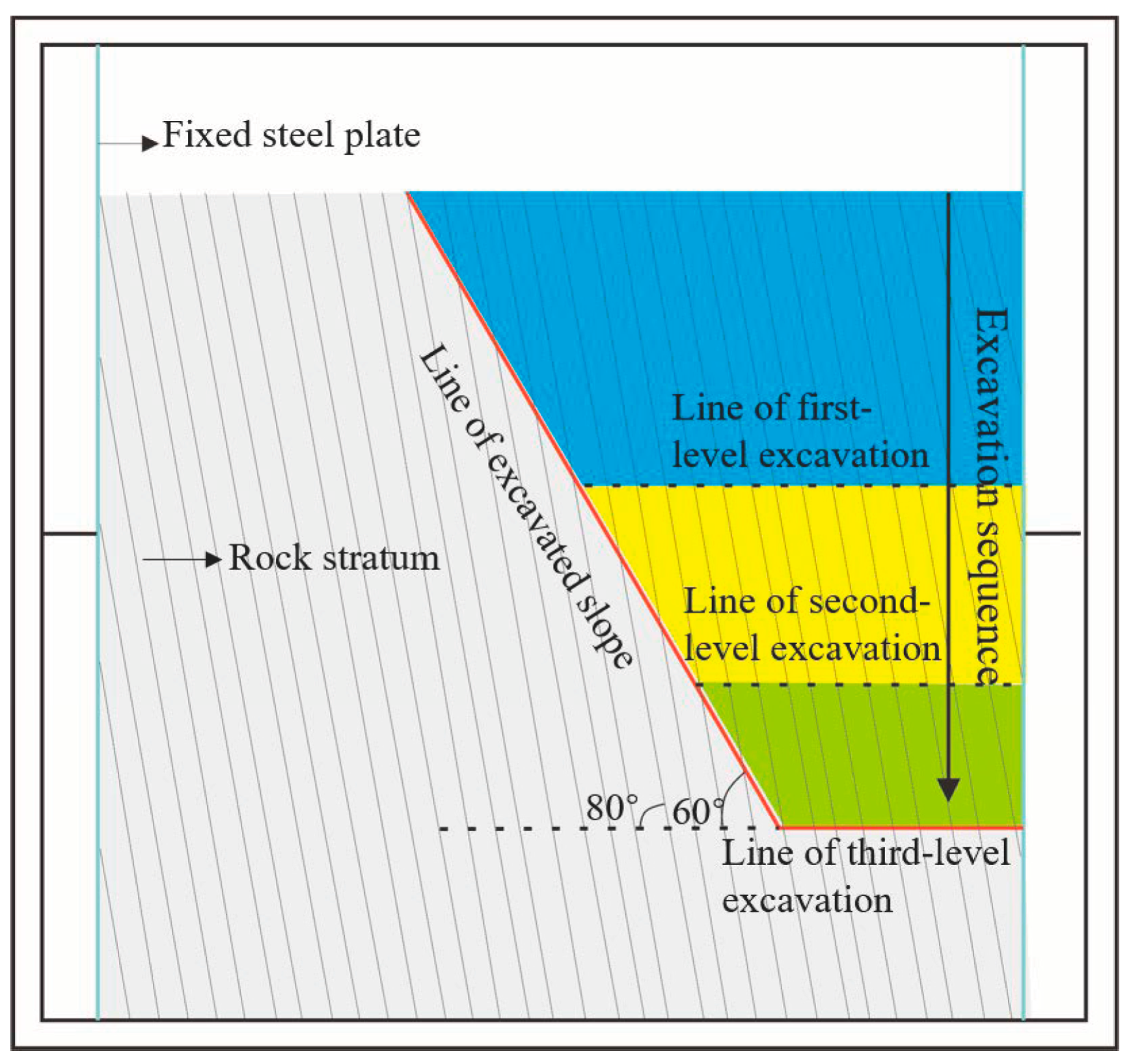
3.1. Experimental Summary
- (1)
- Slope prototype
- (2)
- Test principle
- ➀
- Geometric similarity constant:
- ➁
- Force condition similarity constant: or
- ➂
- Coefficient of friction similarity constant: .
- (3)
- Instrument and equipment
3.2. Model Material and Test Process
- (1)
- Experimental material
- (2)
- Experimental process
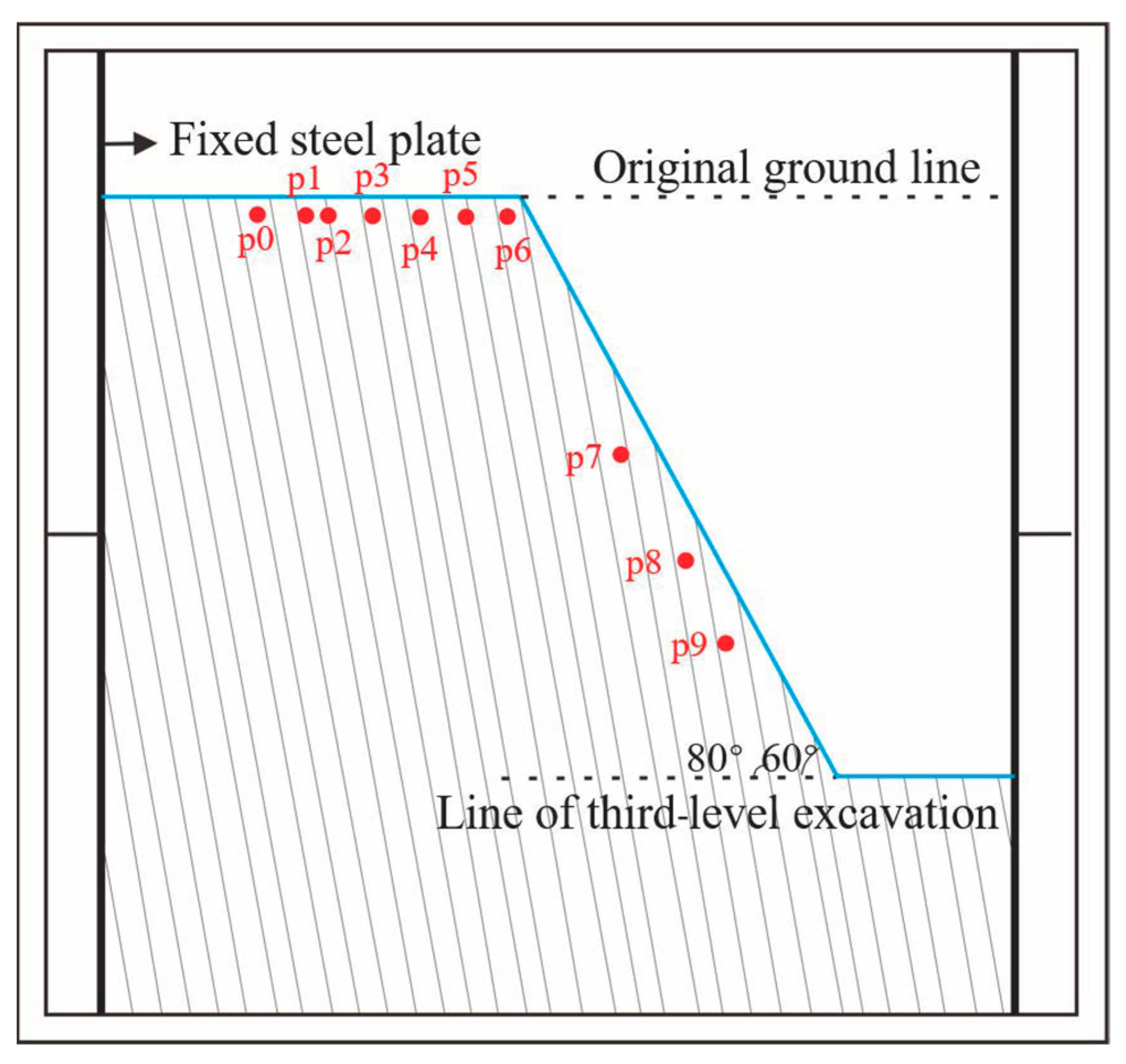
3.3. Experimental Result
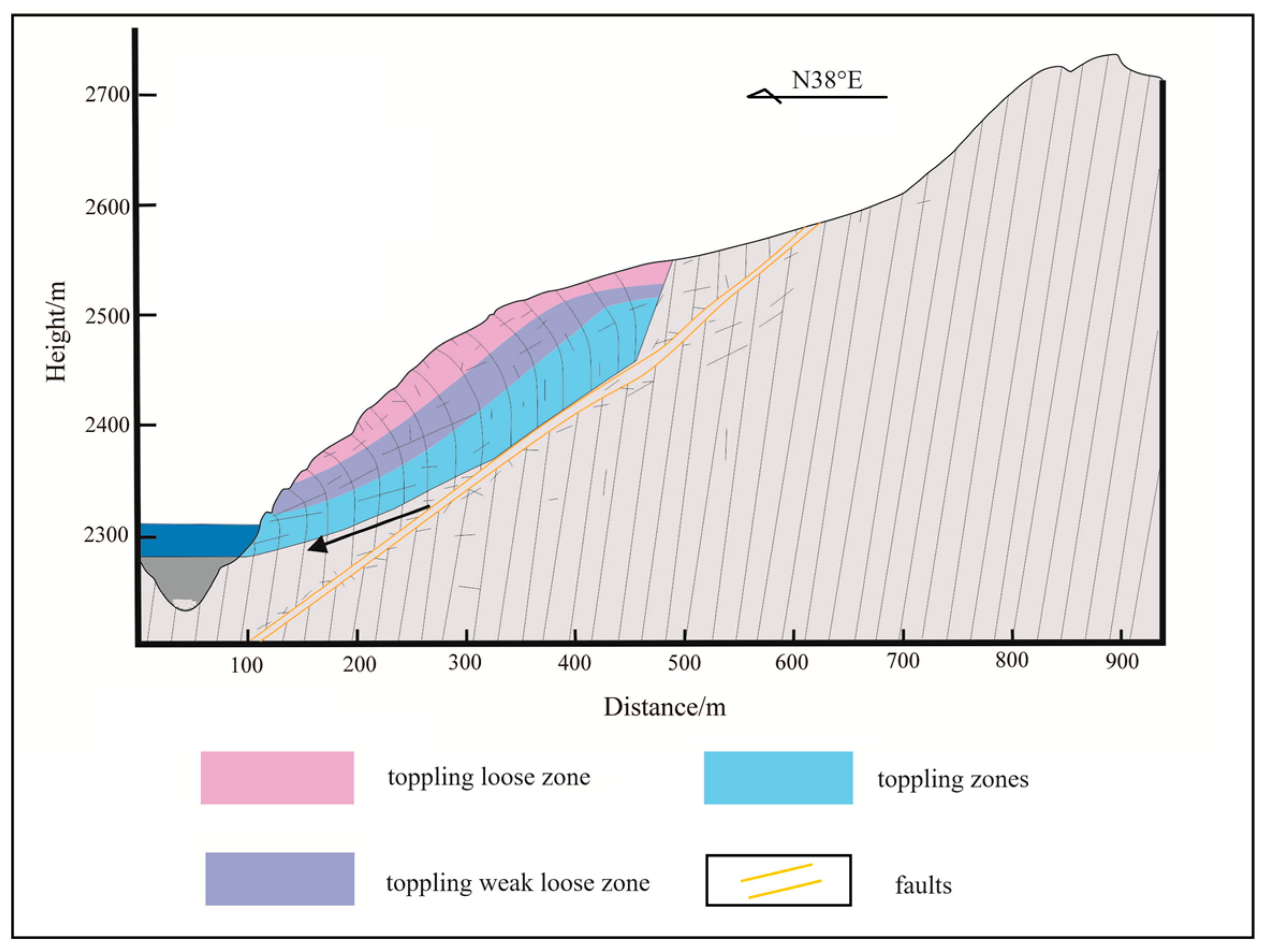
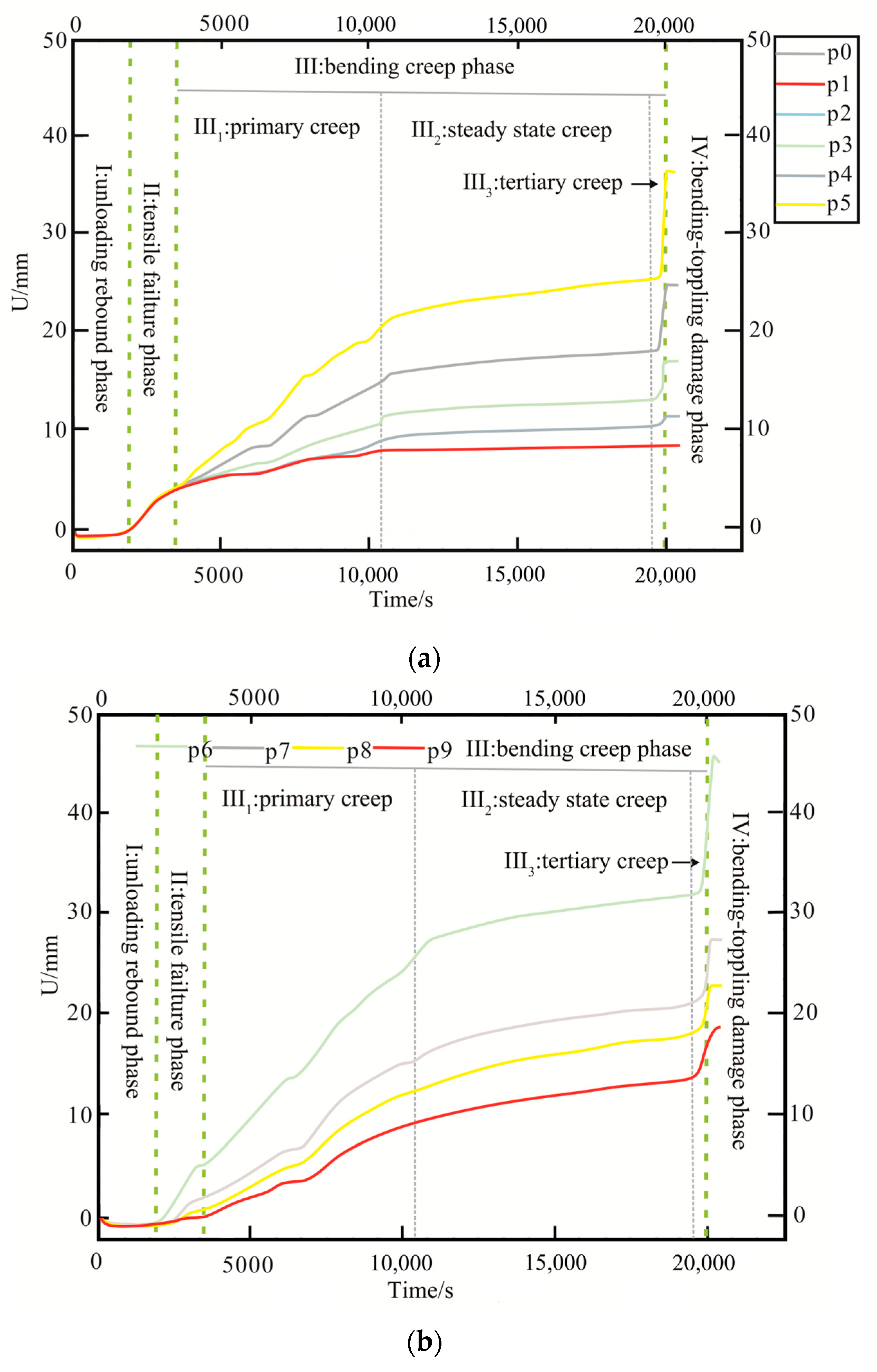
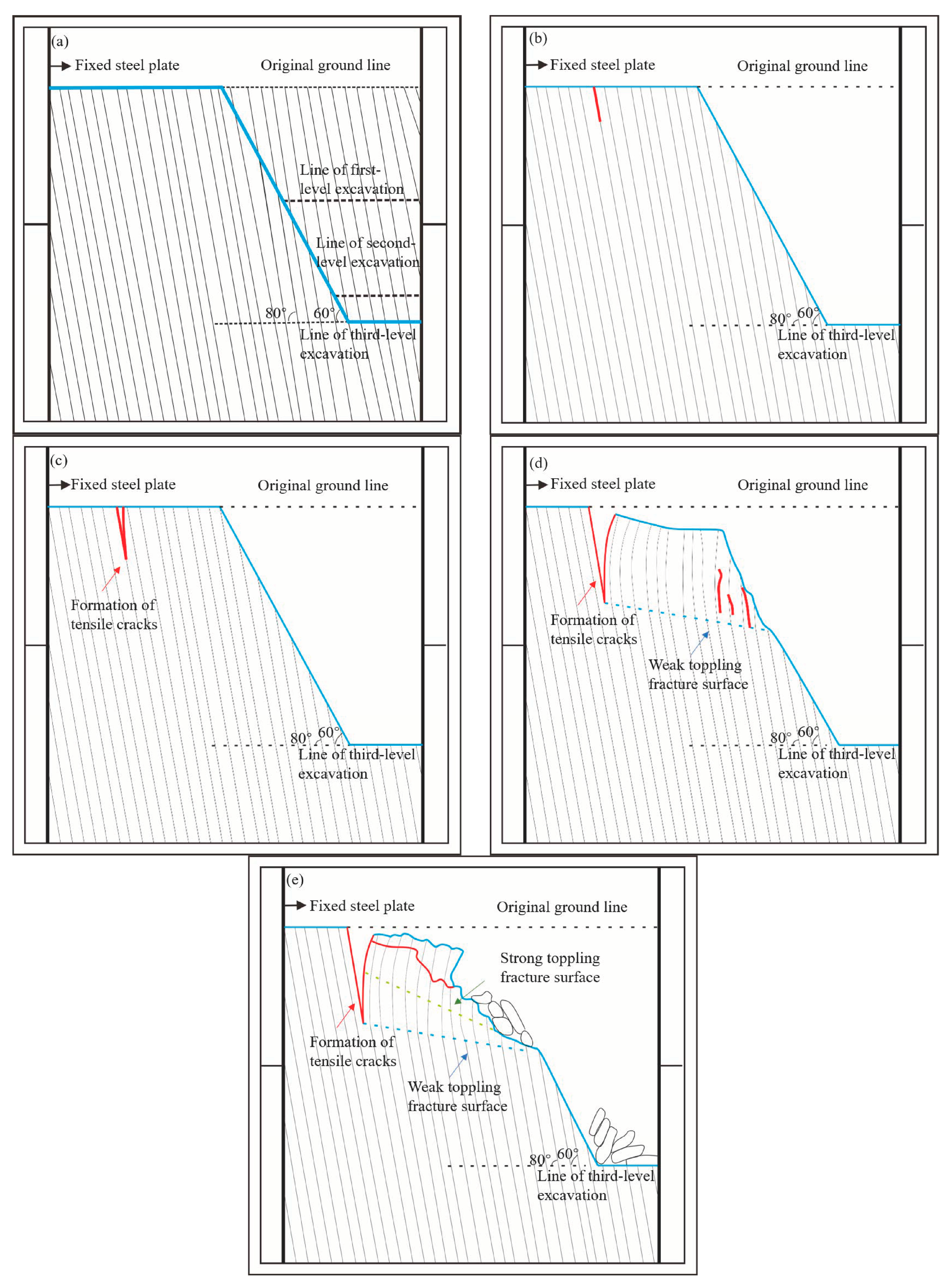
3.4. Geological Evolution Process of Slope Instability
- (1)
- Initial phase
- (2)
- Unloading–rebound phase (I):
- (3)
- Tensile failure phase (II):
- (4)
- Bending creep phase (III):
- (5)
- Bending–toppling damage phase (IV):
4. Bendingoppling Stability Evaluation Method Based on Viscoelastic Mechanics
4.1. Creep Constitutive Model Based on Nonlinear Rheological Mechanism
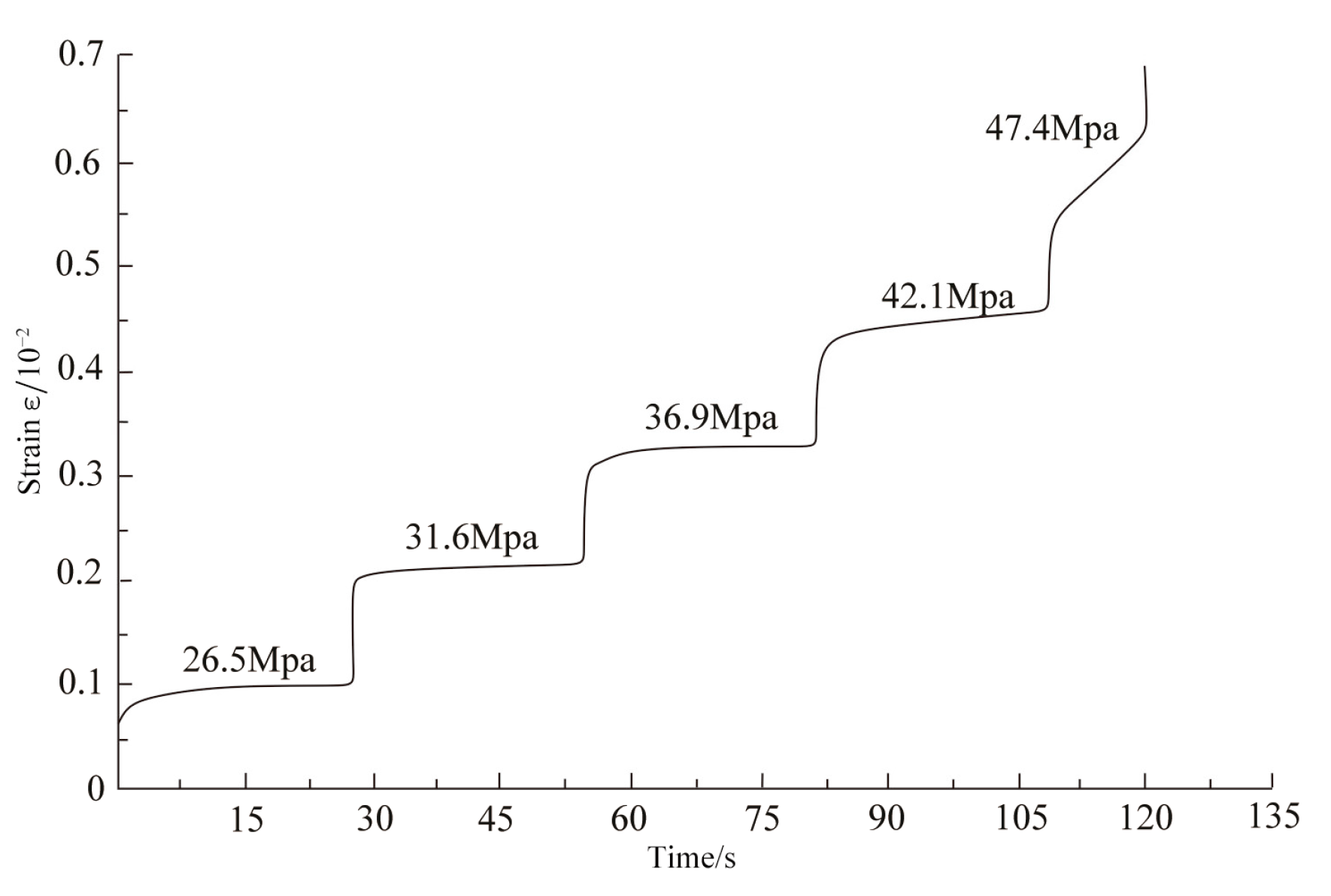
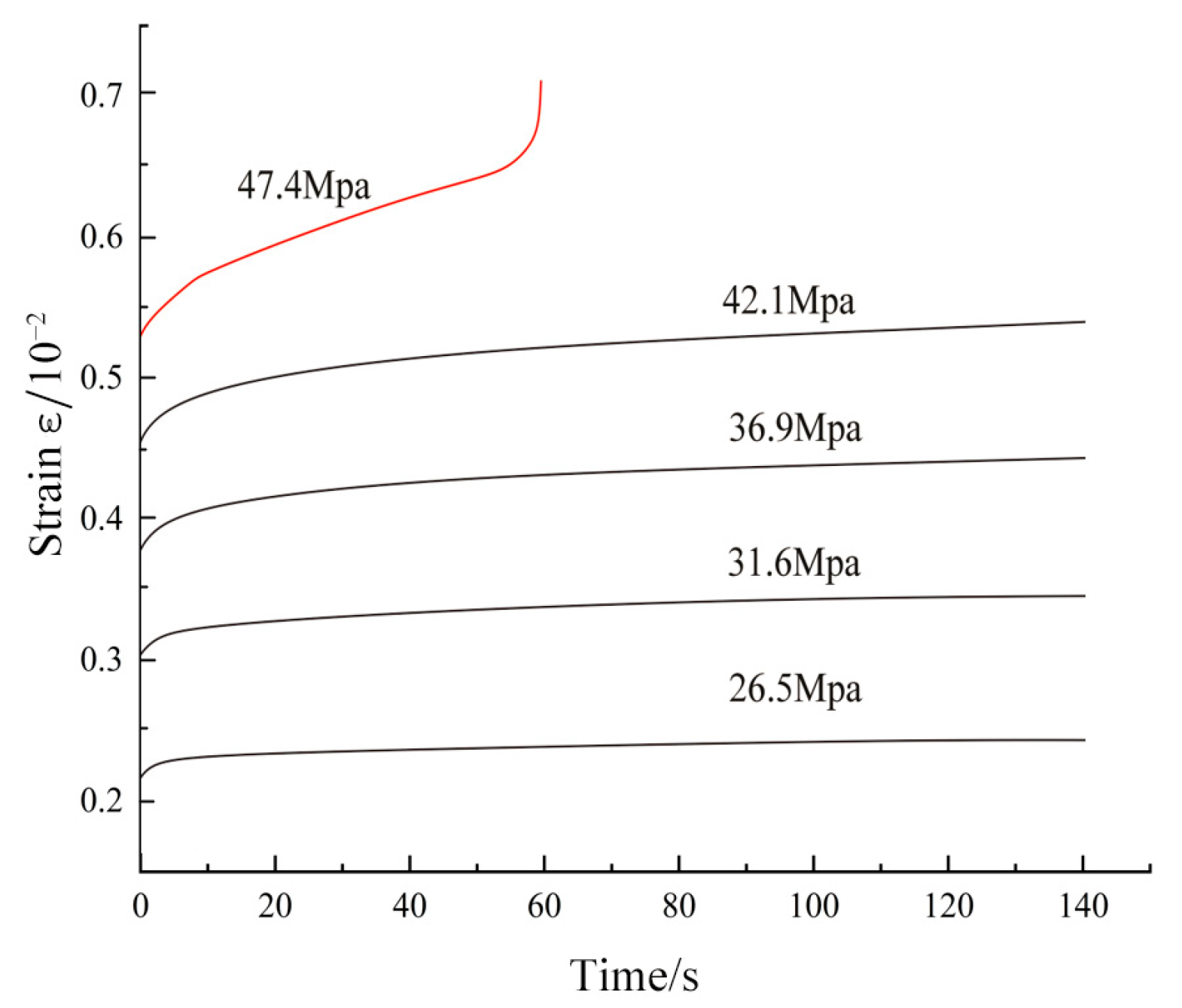
4.1.1. Design of Creep Test Scheme
4.1.2. Analysis of Creep Test Results
4.1.3. Establishment of Slope Creep Constitutive Model
4.1.4. Nonlinear Viscoelastic–Plastic Relaxation Properties
4.2. Aging Deformation Characteristics of Delayed Instability Slope Based on Fractional-Order Bessel Function
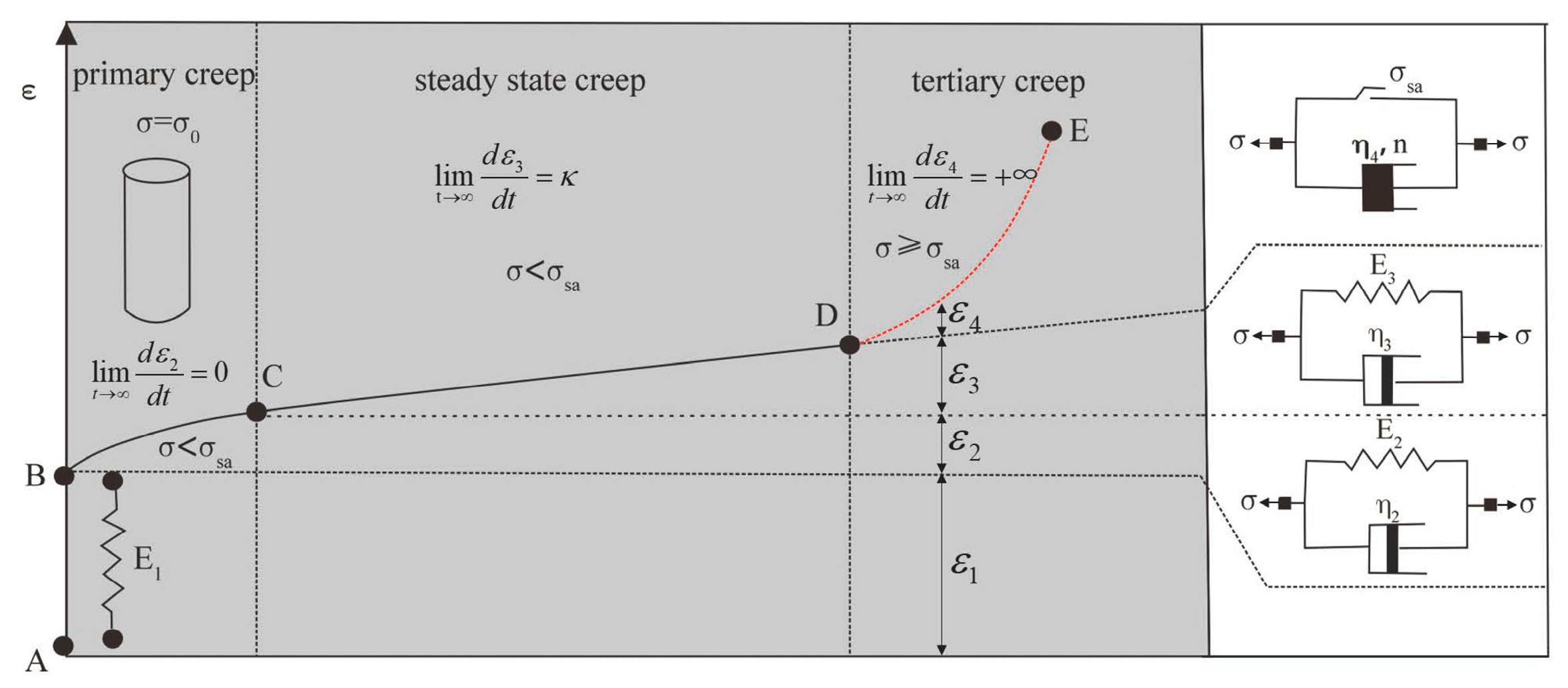
4.3. Establishment of Stability Evaluation Model and Instability Criterion for Tipping–Deformation Slope
- (1)
- Stable slope: Over a long period of time with only rheological phenomenon, no buckling—that is, without losing stability—and its longitudinal load is , that is long-term, stable uniform load. As long as its value is less than self-weight load, the slope will not experience instability.
- (2)
- Transient instability slope: Instability occurs instantaneously, and its longitudinal load is the instantaneous elastic critical load. As long as the initial stress satisfies , instantaneous instability occurs.
- (3)
- Delayed instability slope: In the load range of , the rock slab beam has delayed instability over a limited time. It is important to note that is the ratio of the deflection at the free end of the rock slab at any time to the maximum deflection value (the deflection risk value) when the rock mass fractures as the stability coefficient of the rock slab. Similarly, is the ratio of any time angle at the free end of the rock slab to the maximum angle (angle risk value) at the time of rock mass fracture as the stability coefficient of the rock slab. Then, and can be obtained using Equation (21):
5. Stability Evaluation Method Verification
5.1. Bottom Friction Test Verification
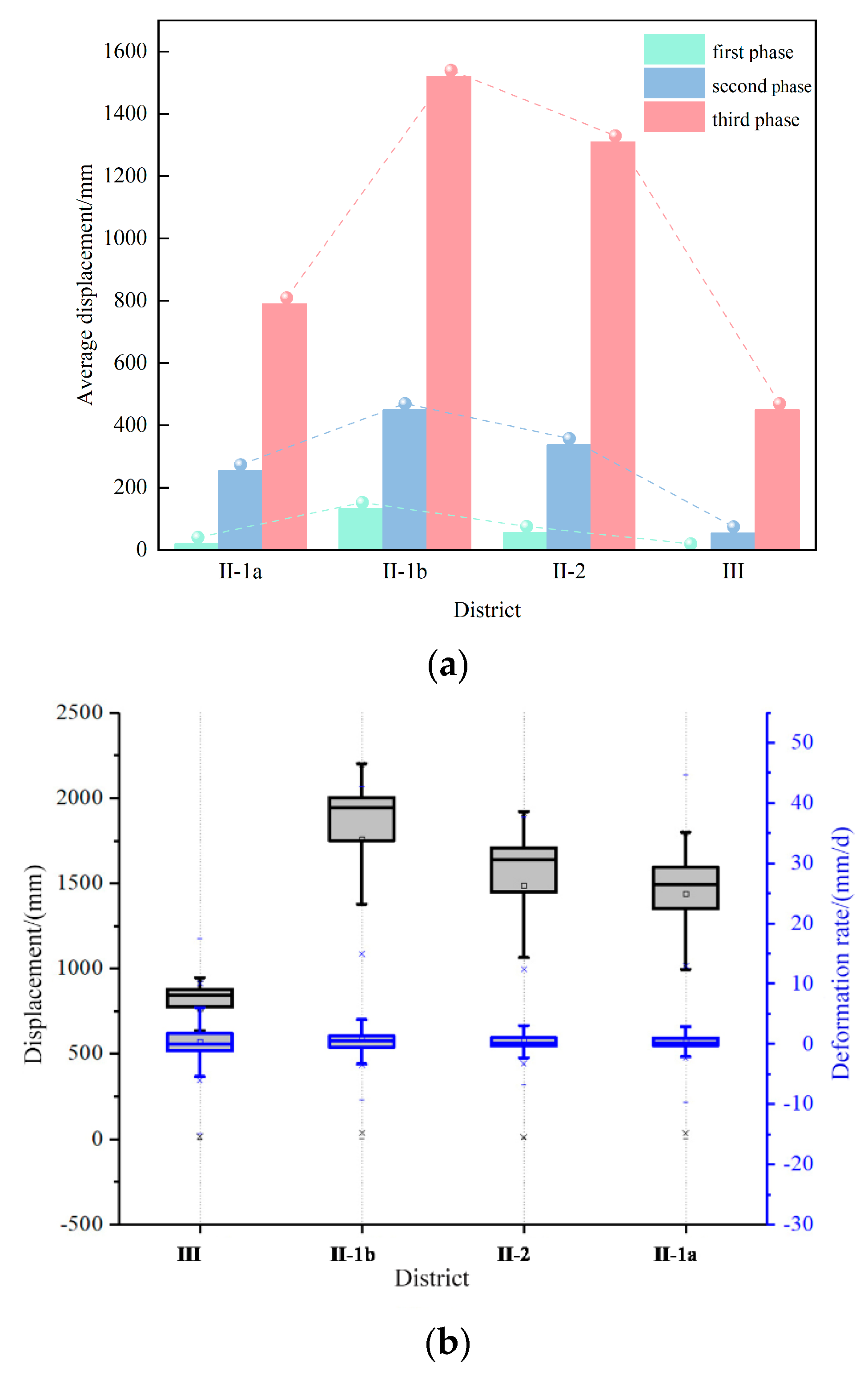
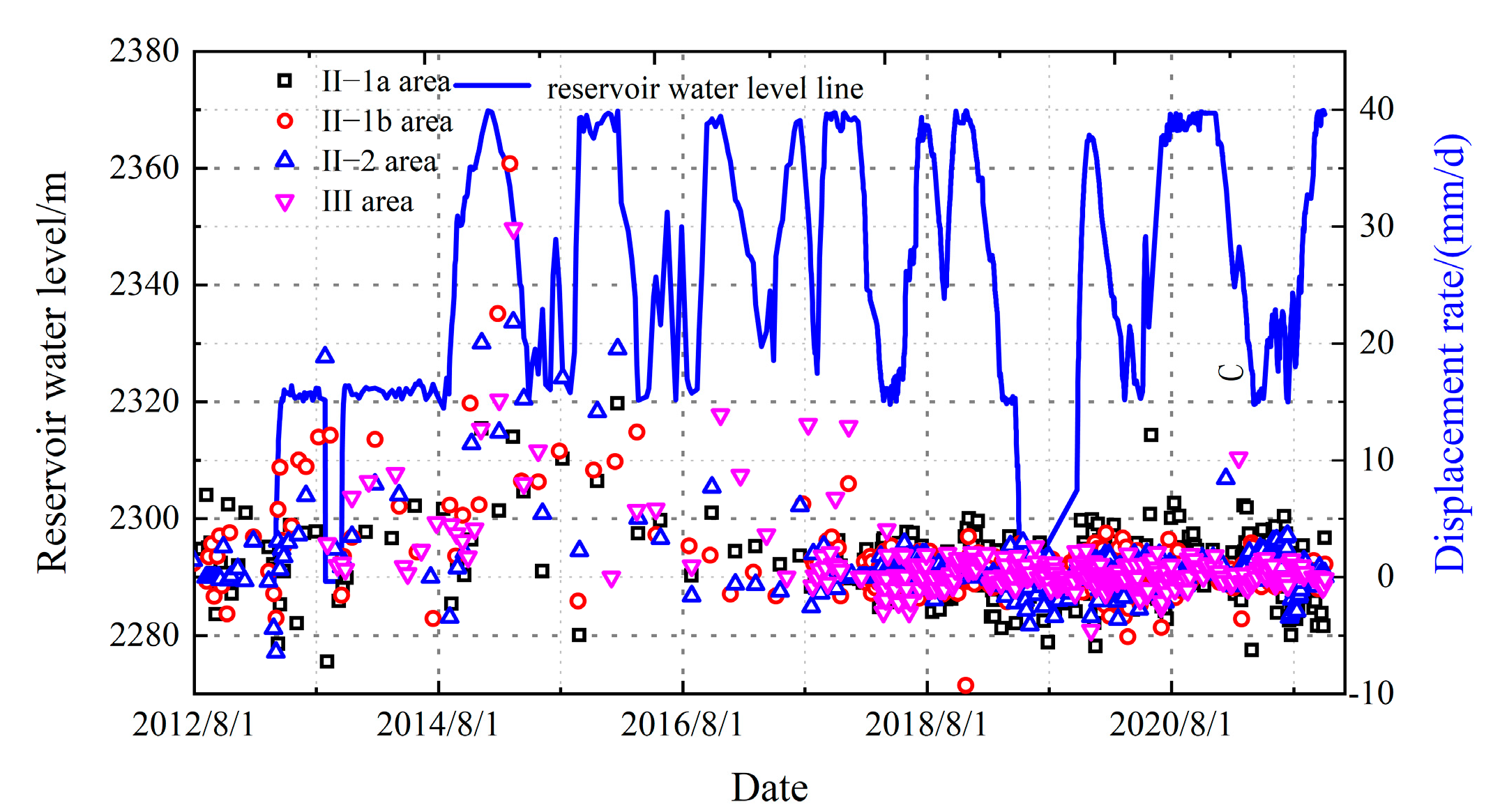
5.2. Verification of Slope of a Hydropower Station
6. Discussion
- (1)
- Under the determined geological prototype conditions, the instability criterion for steep bedding rock slope under the action of self-weight or additional fissure hydrostatic pressure has not yet been established;
- (2)
- The stability of steep bedding rock slopes is a dynamic issue that needs to consider aging effects, and traditional stability methods cannot predict the trend of slope stability changes over time.
- (3)
- Due to the limitations of experimental conditions and sample quantity, this study conducted only indoor uniaxial compression creep tests for rock mass grading loading creep experiments, lacking a certain degree of general applicability. Future research should consider and further explore the creep characteristics of rock masses under complex stress paths in triaxial stress conditions to better reflect the actual stress environment of rock masses in engineering practice.
- (4)
- The stability evaluation model for toppling deformation based on deflection and rotation angle timeliness established in this study may face applicability issues when applied and validated in typical engineering cases due to limitations in tracing the initial deformation time point. Therefore, future work will incorporate geochronological techniques for geotechnical materials and integrate dating data to provide objective and accurate parameters for the evaluation model.
7. Conclusions
- (1)
- Bedding–toppling deformation primarily occurs in areas with significant topographic slope changes, typically developing on mountain slopes at altitudes of 2000–3000 m, with slope angles ranging between 50° and 60°. Furthermore, bedding–toppling deformation predominantly occurs on mountain slopes with interbedded structures, followed by soft rock slopes, and is least developed on hard rock slopes.
- (2)
- Using a bottom friction physical simulation test, combined with the macroscopic deformation characteristics of the model slope, changes in point displacement, and mechanical characteristics, the entire evolution process of slope toppling deformation and failure during valley incision is reconstructed. The toppling deformation process of bedding rock slopes is divided into five stages: the initial phase of the slope, the unloading–rebound stage, the tensile failure phase, the bending creep phase, and the bending–toppling damage phase.
- (3)
- Based on the nonlinear viscoelastic–plastic rheological constitutive model for rock mass, considering time-dependent factors, a quantitative evaluation method for the stability of toppling slopes was developed. The types of rock slope instability were quantitatively classified into three types: stable slope, transient instability slope, and delayed instability slope. Additionally, a stability evaluation model for toppling deformation concerning deflection and angle overtime was established.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goodman, R.E.; Bray, J.W. Toppling of slopes. In Proceedings of the Specialty Conference on Rock Engineering for Foundations and Slopes ASCE/Boulder, Boulder, CO, USA, 15–18 August 1976; pp. 201–234. [Google Scholar]
- Cai, J.C.; Ju, N.P.; Huang, R.Q.; Zheng, D.; Zhao, W.H.; Li, L.Q.; Huang, J. Mechanism of toppling and deformation in hard rock slope: A case of bank slope of Hydropower Station, Qinghai Province, China. J. Mt. Sci. 2019, 16, 924–934. [Google Scholar] [CrossRef]
- Deng, T.X.; Ju, N.P.; Li, L.Q.; Jiang, Y.B.; Lu, X.T. Study on dynamic toppling deformation mechanism of inclined steep-dip bedding slope. Water Resour. Hydropower Eng. 2017, 5, 146–152, (In Chinese with English Abstract). [Google Scholar]
- Huang, R.Q.; Li, Y.S.; Yan, M. The implication and evaluation of toppling failure in engineering geology practice. J. Eng. Geol. 2017, 25, 1165–1181, (In Chinese with English Abstract). [Google Scholar]
- Jiang, L.; Zhang, Q.; Jia, C.J.; Yu, J.; Huang, Q.F. Investigating on deformation characteristics and failure mechanism of bedding rock slope: Field study, long-term monitoring, and reinforcement measures. Environ. Earth Sci. 2024, 83, 45. [Google Scholar] [CrossRef]
- Miao, S.S.; Su, L.J.; Zhang, C.L.; Liu, Z.L.; Wang, B.; Dong, Z.B. Dynamic response characteristics and damage failure process of bedding rock slope in shaking table test. Bull. Eng. Geol. Environ. 2024, 83, 358. [Google Scholar] [CrossRef]
- Tang, H.M.; Zou, Z.X.; Xiong, C.R.; Wu, Y.P.; Hu, X.P.; Wang, L.Q.; Lu, S.; Robert, E.C.; Li, C.D. An evolution model of large consequent bedding rockslides, with particular reference to the Jiweishan rockslide in Southwest China. Eng. Geol. 2015, 186, 17–27. [Google Scholar] [CrossRef]
- Zhang, S.L.; Zhu, Z.H.; Qi, S.C.; Hu, Y.X.; Du, Q.; Zhou, J.W. Deformation process and mechanism analyses for a planar sliding in the Mayanpo massive bedding rock slope at the Xiangjiaba Hydropower Station. Landslides 2018, 15, 2061–2073. [Google Scholar] [CrossRef]
- Zhao, L.H.; Li, D.J.; Tan, H.H.; Cheng, X.; Zuo, S. Characteristics of failure area and failure mechanism of a bedding rockslide in Libo County, Guizhou, China. Landslides 2019, 16, 1367–1374. [Google Scholar] [CrossRef]
- Mu, J.Q.; Li, T.T.; Pei, X.J.; Huang, R.Q.; Lan, F.A.; Zou, X.Q. Evolution mechanism and deformation stability analysis of rock slope block toppling for early warnings. Nat. Hazards 2022, 114, 1171–1195. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, X.; Zheng, Y.; Li, H.; Guo, H. Experimental and numerical study of the mechanism of block–flexure toppling failure in rock slopes. Bull. Eng. Geol. Environ. 2022, 81, 63. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.X.; Liu, T.T. Study on the mechanisms of flexural toppling failure in anti-inclined rock slopes using numerical and limit equilibrium models. Eng Geol. 2018, 237, 116–128. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, R.Q.; Chen, C.X.; Meng, F. Analysis of flexural toppling failure in rock slopes using discrete element method. Front. Earth Sci. 2021, 9, 773088. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Lu, Y.; Li, X.; Li, P. Numerical analysis of evaluation methods and influencing factors for dynamic stability of bedding rock slope. J. Vibroengineering 2017, 19, 1937–1961. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, D.; Song, Q.; Ou, Y. Reliability analysis of slope dynamic stability based on strength reduction FEM. Rock Soil Mech. 2013, 34, 2084–2090, (In Chinese with English Abstract). [Google Scholar]
- Amini, M.; Ardestani, A.; Khosravi, M.H. Stability analysis of slide-toe-toppling failure. Eng. Geol. 2017, 228, 82–96. [Google Scholar] [CrossRef]
- Amini, M.; Majdi, A.; Aydan, Ö. Stability analysis and the stabilisation of flexural toppling failure. Rock Mech. Rock Eng. 2009, 42, 751–782. [Google Scholar] [CrossRef]
- Amini, M.; Majdi, A.; Veshadi, M.A. Stability analysis of rock slopes against block-flexure toppling failure. Rock Mech. Rock Eng. 2012, 45, 519–532. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.X.; Meng, F. Assessing the stability of rock slopes with respect to block-flexure toppling failure using a force-transfer model and genetic algorithm. Rock Mech. Rock Eng. 2020, 53, 3433–3445. [Google Scholar] [CrossRef]
- Zhou, W.J.; Xu, W.Y.; Ning, Y.; Xiao, H.B.; Xie, W.C. Analytical method of stability analyses of toppling rock slopes subjected to flexural toppling failure damage. Eur. J. Environ. Civ. Eng. 2023, 27, 2373–2387. [Google Scholar] [CrossRef]
- Xia, K.Z.; Liu, X.M.; Cheng, C.X. Analysis of mechanism of bedding rock slope instability with catastrophe theory. Rock Soil Mech. 2015, 36, 477–486, (In Chinese with English Abstract). [Google Scholar]
- Jiang, L.; Huang, R.Q. Studies on estimate of sliding-bending rupture of bedded rock slopes. J. Mt. Sci. 2006, 1, 88–94, (In Chinese with English Abstract). [Google Scholar]
- Feng, J.; Zhou, D.P.; Yang, T. Stability analysis of consequent rock slopes using elastic-plastic plate theory. Chin. J. Geotech. Eng. 2010, 32, 1184–1188, (In Chinese with English Abstract). [Google Scholar]
- Liu, X. Introduction to Rock Rheology; Geology Press: Beijing, China, 1994. [Google Scholar]
- Xu, W.Y.; Yang, S.Q.; Chu, W.J. Nonlinear viscoelasto-plastic rheological model (hohai model) of rock and its engineering application. Chin. J. Rock Mech. Eng. 2006, 3, 433–447, (In Chinese with English Abstract). [Google Scholar]
- Li, S.Y.; Chen, Y.; Zhang, L.; Jiao, X.; Cai, R.K.; Liu, Y.K. Stability Evaluation of Typical Rocky High Slope of Baihetan Hydropower Station. Water Resour. Power 2018, 36, 102–105, (In Chinese with English Abstract). [Google Scholar]
- Yan, S.; Du, H.T.; Yu, Q.L.; Yan, H. Static Stability Safety Evaluation of High Bedding Rock Slope. J. Disaster Prev. Mitig. Eng. 2014, 34, 407–414, (In Chinese with English Abstract). [Google Scholar]
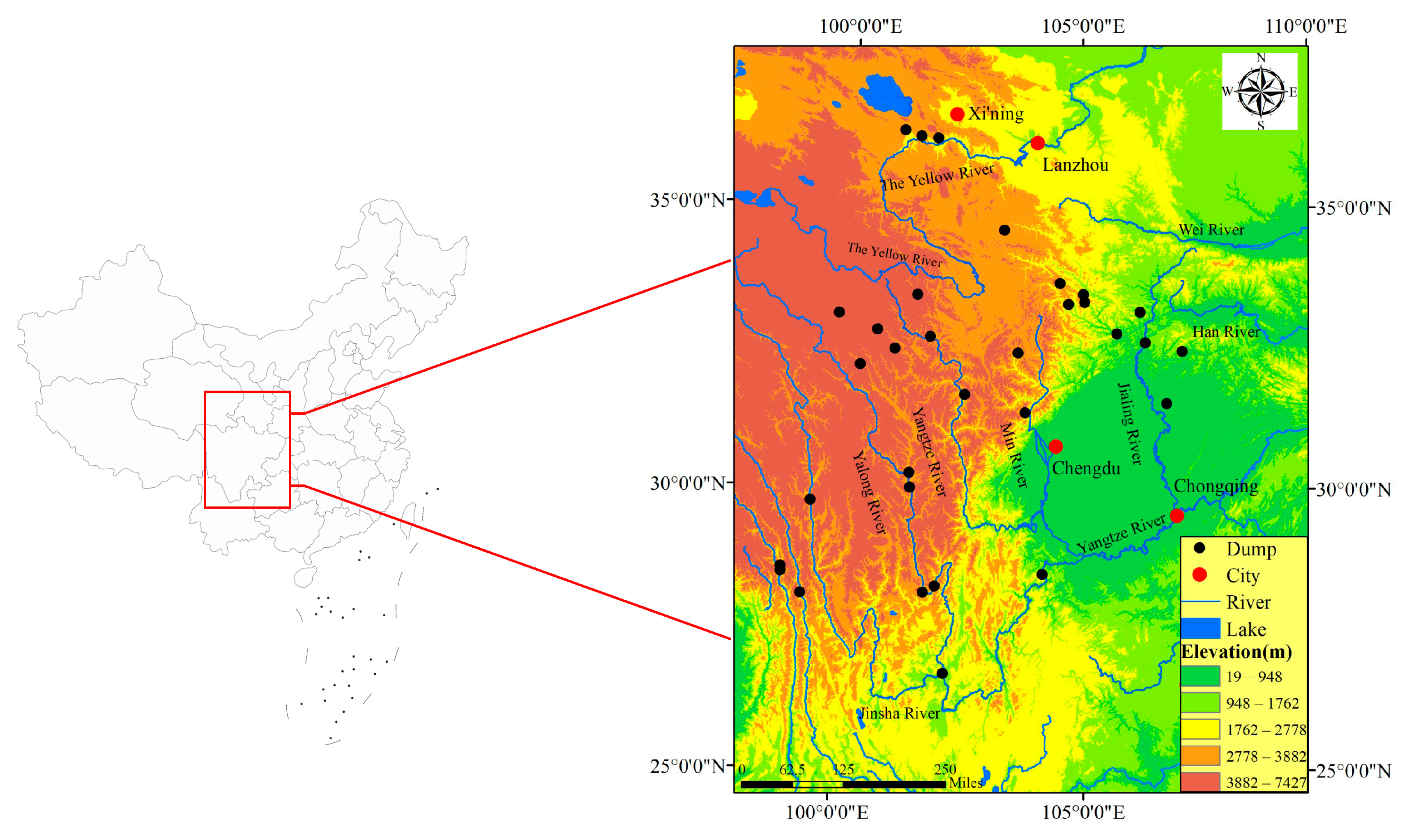

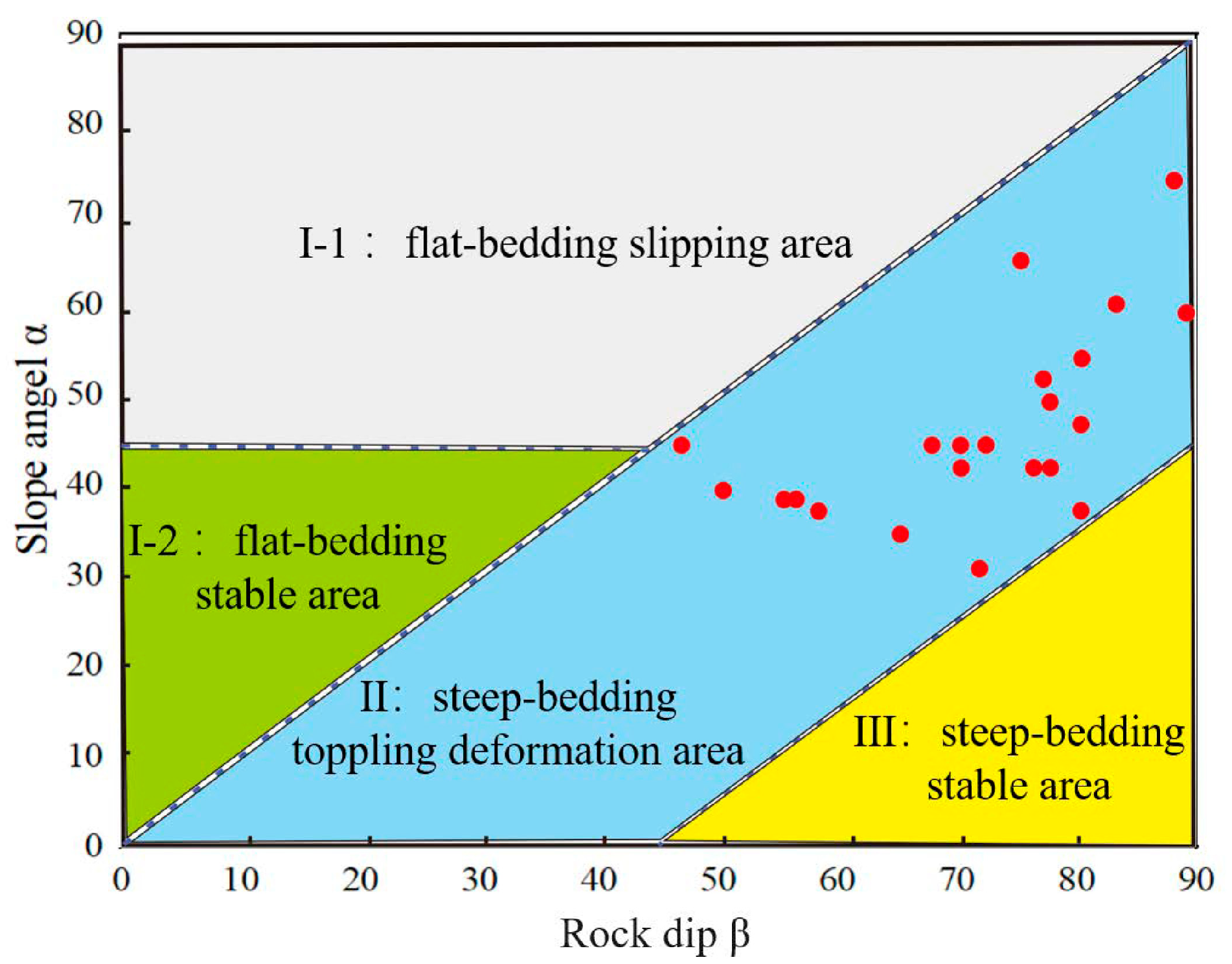



| Number | Elevation (m) | Slope Angle (°) | Lithology | Rock Dip (°) | Number | Elevation (m) | Slope Angle (°) | Lithology | Rock Dip (°) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1930 | 63 | sandstone/slate | 71 | 13 | 2030 | 59 | phyllite | 80 |
| 2 | 3220 | 41 | siltstone | 69 | 14 | 410 | 31 | dolomite | 72 |
| 3 | 2900 | 73 | slate | 86 | 15 | 2600 | 40 | phyllite | 58 |
| 4 | 2120 | 35 | slate | 55 | 16 | 2550 | 44 | sandstone | 70 |
| 5 | 2650 | 60 | granite | 87 | 17 | 998 | 40 | phyllite | 58 |
| 6 | 2850 | 41 | sandstone | 71 | 18 | 1600 | 59 | slate | 70 |
| 7 | 1290 | 35 | limestone | 79 | 19 | 3010 | 40 | schist | 70 |
| 8 | 780 | 41 | phyllite | 72 | 20 | 2300 | 50 | phyllite | 80 |
| 9 | 1120 | 61 | phyllite | 81 | 21 | 2310 | 50 | migmatite | 48 |
| 11 | 2305 | 50 | phyllite | 75 | 22 | 1350 | 40 | dolomite | 50 |
| 11 | 2430 | 51 | sandstone/slate | 75 | 23 | 1310 | 45 | slate | 50 |
| 12 | 2416 | 41 | sandstone | 76 |
| barite:sand:oil = 54:35:11 | ||
| Cohesive force C/Kpa | internal friction φ angle/° | Density ρ /(g/cm3) |
| 5.55 | 38.3 | 2.1 |
| Deviatoric Stress/MPa | |||||
|---|---|---|---|---|---|
| First Level/MPa | Second Level/MPa | Third Level/MPa | Fourth Level/MPa | Fifth Level/MPa | |
| JZ-01 | 26.5 | 31.6 | 36.9 | 42.1 | 47.4 |
| or | instability |
| or | critical state |
| or | stability |
| E1/GPa | E2/GPa | E3/GPa | η2/(GPa·h) | η3/(GPa·h) | η4/(GPa·h) | a |
|---|---|---|---|---|---|---|
| 8.44 | 190.24 | 38.01 | 449.29 | 201.43 | 9844.78 | 0.2 |
| K | L (m) | H (m) | B (m) | tensile strength (Mpa) | the weight of rock q (KN/m) | critical load qmax (KN/m) |
| 0.9 | 25 | 4.5 | 2.2 | 7.24 | 61.7 | 78.2 |
| Sample Number | E1/GPa | E2/GPa | E3/GPa | Long Term Stable load (kN/m) | The Weight of Rock q (kN/m) | |
|---|---|---|---|---|---|---|
| JZ-01 | 9.88 | 237.98 | 40.85 | 16,160 | 65.01 | Due to q being less than , this slope is stable. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Li, X.; Wei, K.; Guo, J.; Heng, X.; Yuan, J.; Ran, W.; Pei, X. The Toppling Deformation and Failure Criteria of a Steep Bedding Rock Slope—The Case of a Bank Slope at the Duonuo Hydropower Station. Water 2025, 17, 594. https://doi.org/10.3390/w17040594
Li T, Li X, Wei K, Guo J, Heng X, Yuan J, Ran W, Pei X. The Toppling Deformation and Failure Criteria of a Steep Bedding Rock Slope—The Case of a Bank Slope at the Duonuo Hydropower Station. Water. 2025; 17(4):594. https://doi.org/10.3390/w17040594
Chicago/Turabian StyleLi, Tiantao, Xuan Li, Kaihong Wei, Jian Guo, Xi Heng, Jing Yuan, Weiling Ran, and Xiangjun Pei. 2025. "The Toppling Deformation and Failure Criteria of a Steep Bedding Rock Slope—The Case of a Bank Slope at the Duonuo Hydropower Station" Water 17, no. 4: 594. https://doi.org/10.3390/w17040594
APA StyleLi, T., Li, X., Wei, K., Guo, J., Heng, X., Yuan, J., Ran, W., & Pei, X. (2025). The Toppling Deformation and Failure Criteria of a Steep Bedding Rock Slope—The Case of a Bank Slope at the Duonuo Hydropower Station. Water, 17(4), 594. https://doi.org/10.3390/w17040594





