Numerical Dissipation Compensation in Liquid Column Separation: An Improved DVCM Approach
Abstract
:1. Introduction
2. Research Methodology
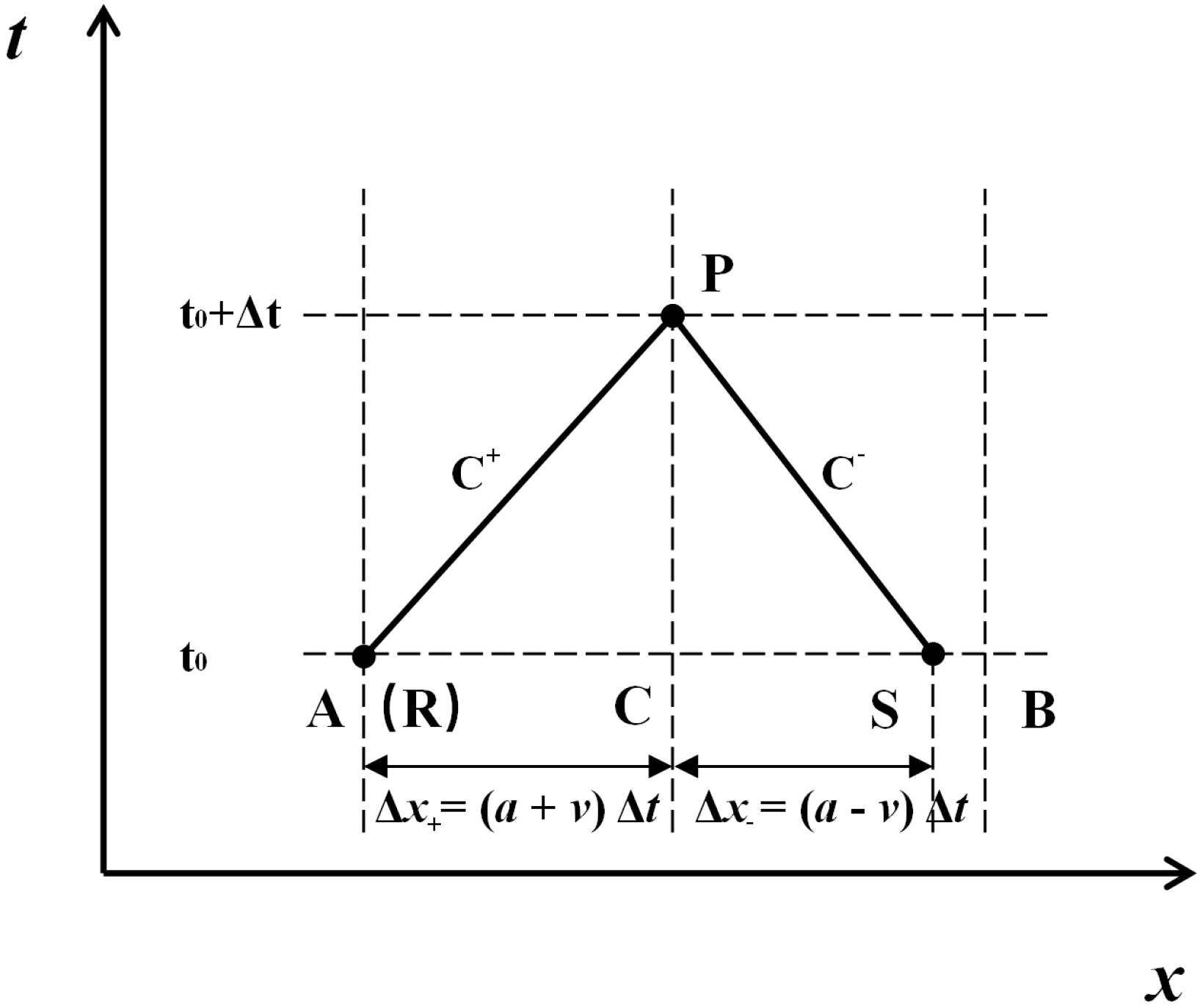
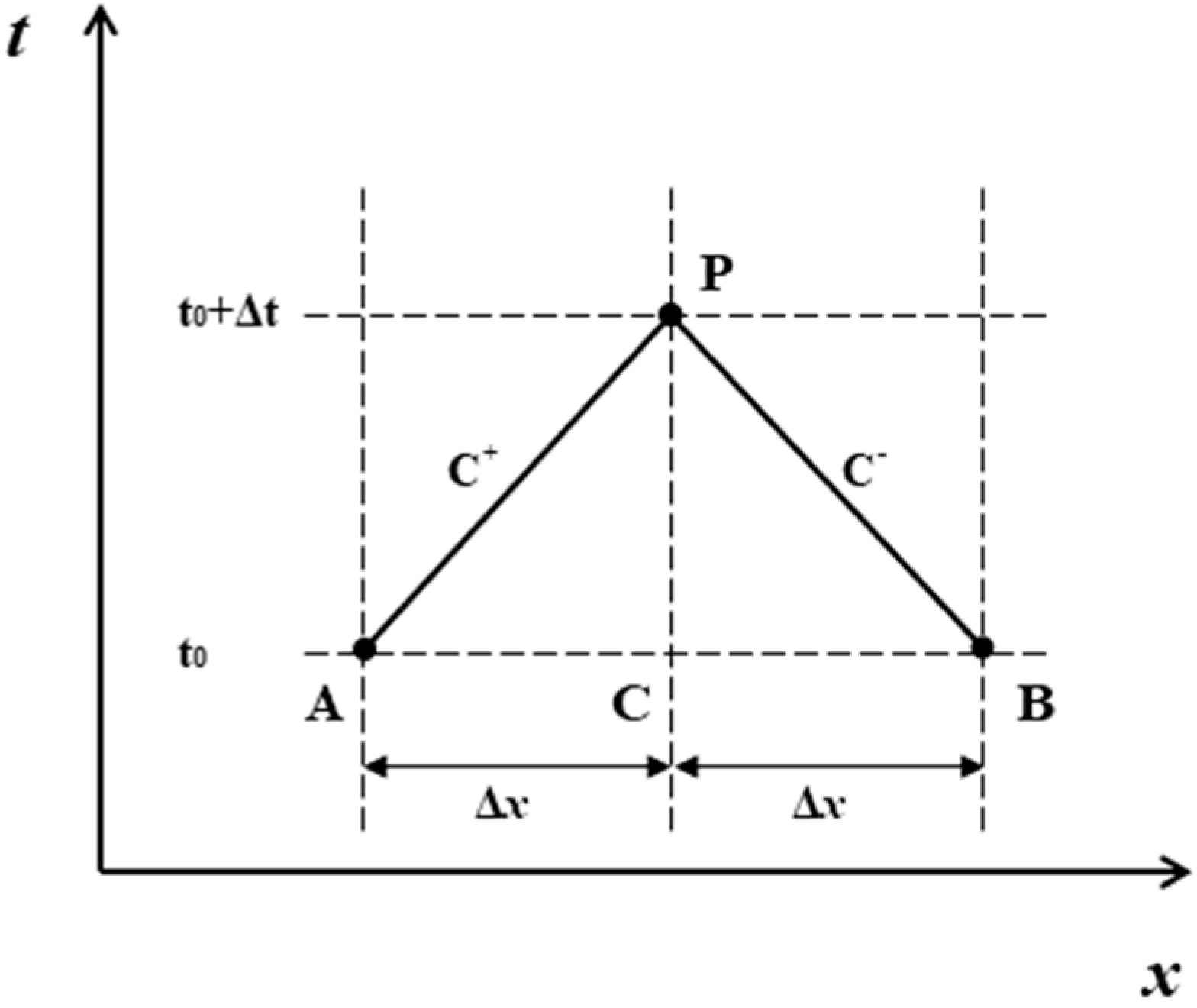
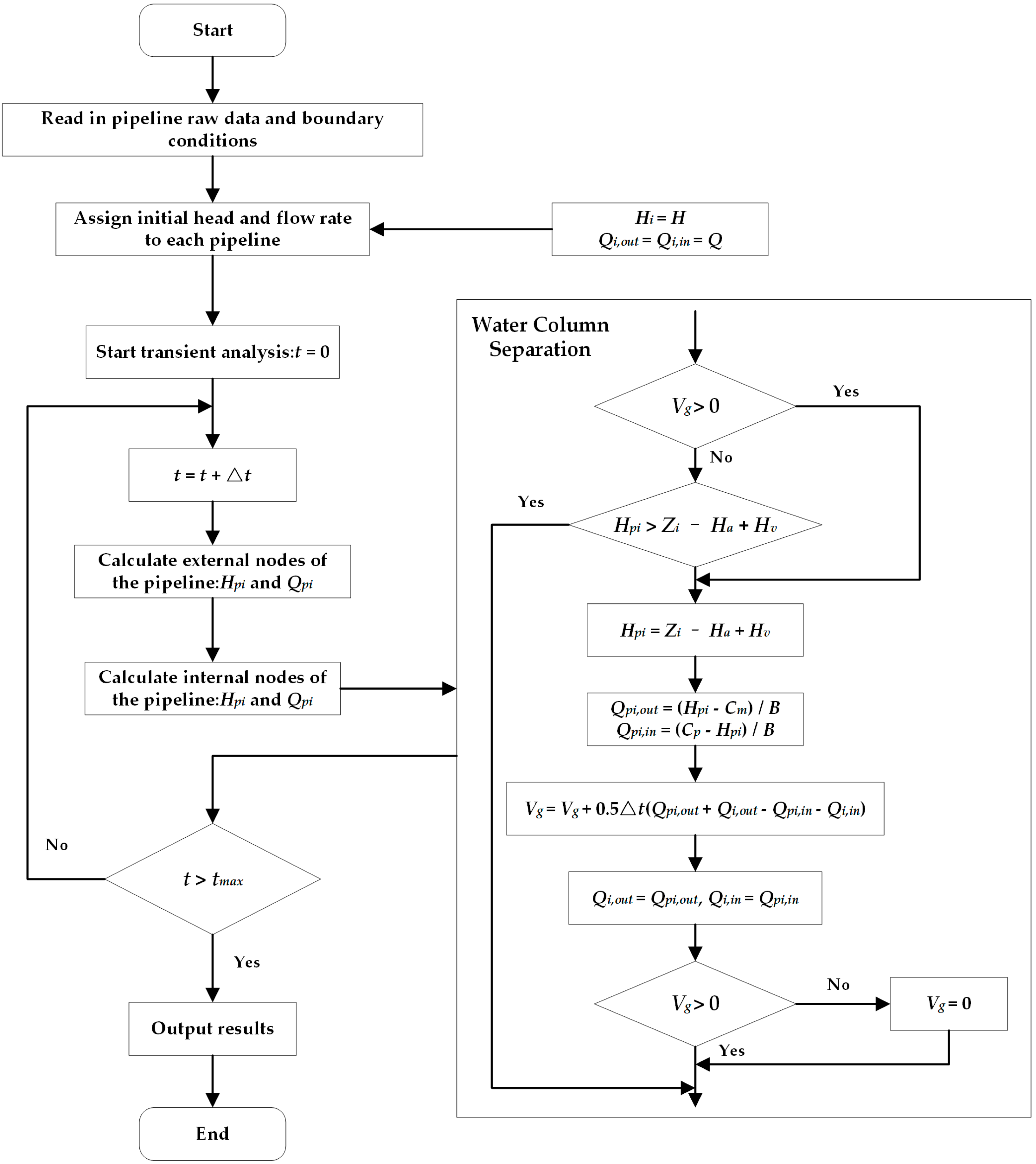
2.1. MOC Algorithm Overview
2.2. DVCM Algorithm Overview
- Determine whether water column separation occurs.
- 2.
- Calculate liquid column separation.
- 3.
- Increase the pressure after reconnection.
2.3. Numerical Dissipation Compensation Methods
2.3.1. Evaluation of Error Model (EAM)
2.3.2. Assessment of the Level of Numerical Dissipation
2.3.3. Parameter Optimization
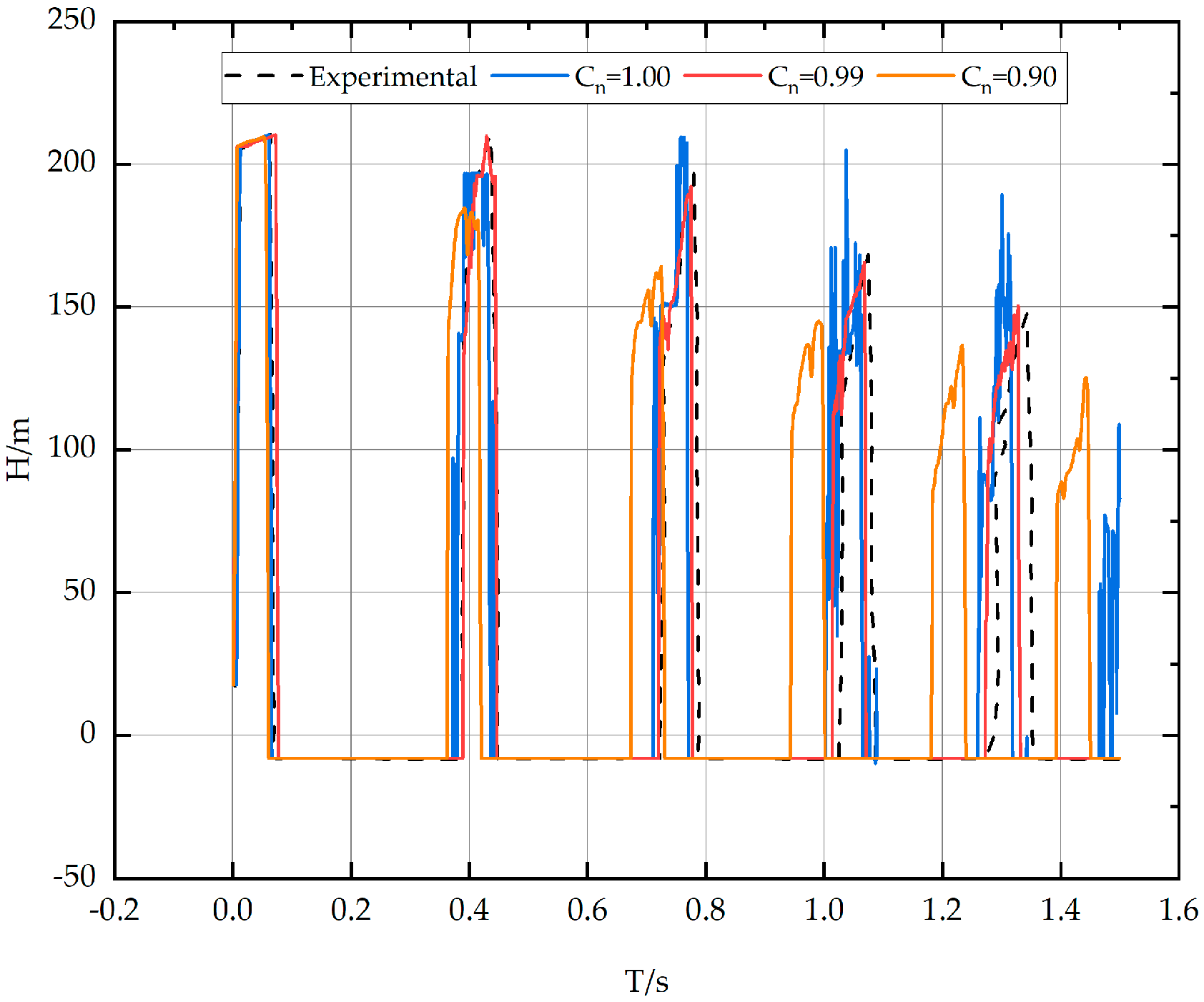
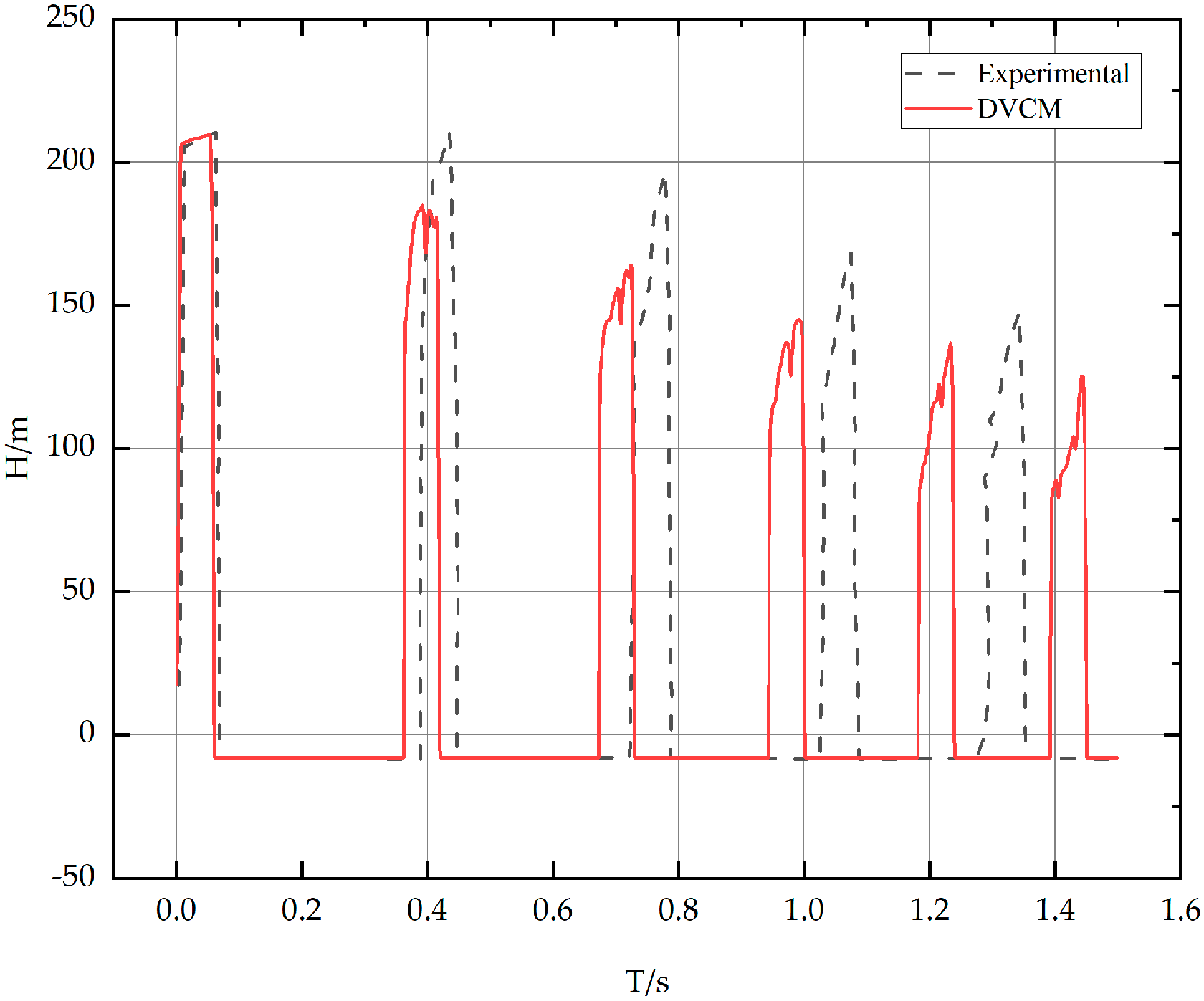
3. Instance Validation
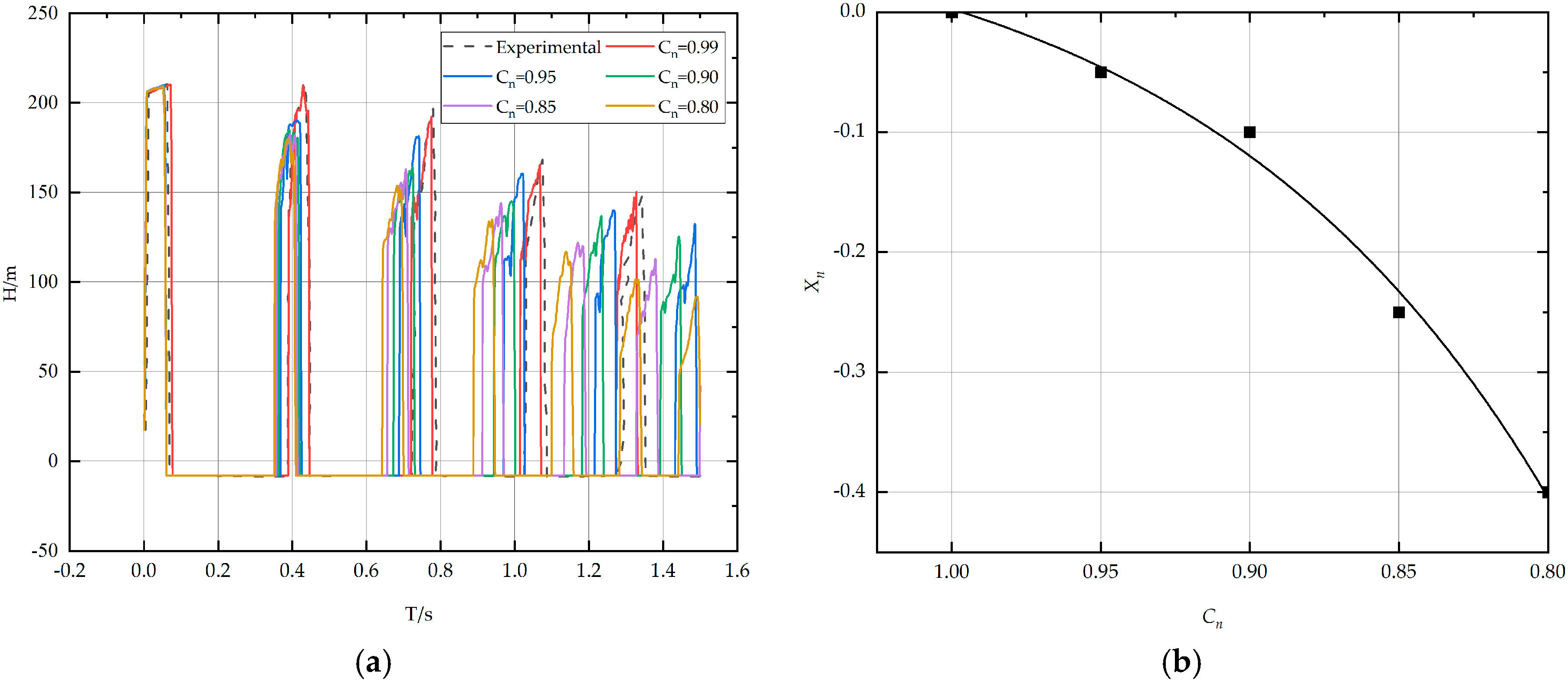
- Analysis of the effect of Cns
- 2.
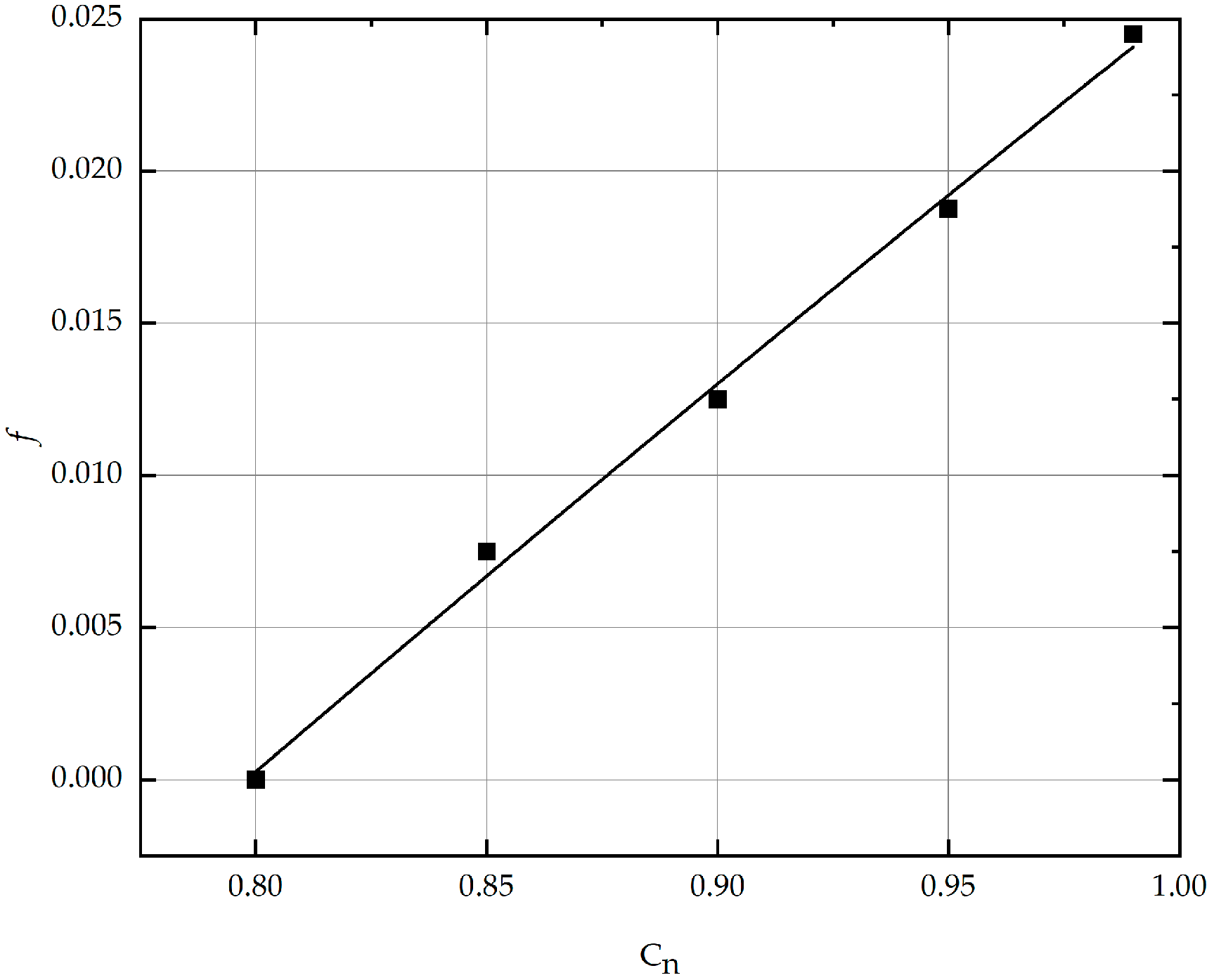
- Impact analysis of the drag coefficient f
- 3.
- Analysis of the relationship between Cn and f parameters
- 4.
- Numerical dissipation compensation
4. Conclusions and Future Work
4.1. Conclusions
- When the characteristic line calculation is used when the Coulomb number Cn deviates from 1; the prediction results of the model will significantly deviate, resulting in lower predicted values of the nodal head rise and liquid–column separation time compared with the actual values. The Courant number in pipeline calculations is an important parameter to ensure the accuracy and reliability of numerical simulations. The model’s energy dissipation significantly impacts the calculation accuracy of the bridging water hammer.
- This paper observes that the total dissipation during numerical calculations can be finely tuned by adjusting the resistance coefficient f of the pipeline without affecting the numerical stability.
- Drawing on Muskingum’s method, reversing the operation to adjust the physical dissipation to compensate for the numerical dissipation can significantly improve the prediction accuracy of the numerical computation of the bridging water strikes in this paper. When the numerical dissipation is balanced with the physical dissipation, the relative errors of the peak head and liquid–column separation time at the DVCM prediction nodes are reduced to under 6%. The strategy of mutual compensation between physical and numerical dissipation not only improves the prediction accuracy of DVCM but also provides new ideas for other numerical simulations to improve computational accuracy and stability.
4.2. Future Work
- Application and optimization in real-world operational environments
- 2.
- Consideration and response to unsteady friction in future simulations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations and Glossary
| DVCM | Discrete vaporous cavity model |
| DGCM | Discrete gaseous cavity model |
| TFM | Two-fluid mathematical model |
| CFL | Courant–Friedrich–Lewy |
| EAM | Evaluation of error model |
| Courant number | |
| Spatial distance | |
| Spatial interpolation on the right side | |
| Spatial interpolation on the left side | |
| Initial calculation time | |
| Minimum calculation time interval | |
| Node water head | |
| Time | |
| Steam volume at node i at time j in the pipeline | |
| Head at node i at the next time step in the pipeline | |
| Flow rate at node i at the next time step in the pipeline | |
| Elevation at node i in the pipeline | |
| Atmospheric pressure head | |
| Vapor pressure head of water | |
| The flow rate into node i at the previous time step | |
| The flow rate into node i at this moment | |
| Flow rate out of node i at the previous time step | |
| Flow rate out of node i at this moment | |
| Characteristic parameters of the method of characteristics | |
| Characteristic parameters of the method of characteristics | |
| Characteristic parameters of the method of characteristics | |
| Maximum calculation time | |
| Friction coefficient | |
| Numerical dissipation error index | |
| Physical dissipation error index | |
| Weight of peak water head | |
| Weight of liquid–column separation duration | |
| The peak water head at node i in the pipeline when the courant number is equal to x | |
| The peak water head at node i in the pipeline when the friction coefficient is equal to x | |
| The duration of liquid–column separation at node i in the pipeline when the courant number is equal to x | |
| The duration of liquid–column separation at node i in the pipeline when the friction coefficient is equal to x | |
| Pipe diameter | |
| Pipeline length | |
| Wave speed | |
| Time interval | |
| Spatial interval |
References
- Zhou, L.; Wang, N.; Zhao, Y. Godunov model for water column separation and water hammer considering dynamic friction. J. Harbin Inst. Technol. 2023, 55, 138–144. [Google Scholar]
- Adamkowski, A.; Lewandowski, M. Investigation of hydraulic transients in a pipeline with column separation. J. Hydraul. Eng. 2012, 138, 935–944. [Google Scholar] [CrossRef]
- Fu, Y.; Xie, C.; Jiang, J. Calculation and study on the secondary pressure surge phenomenon of water hammer under liquid column separation. J. China Three Gorges Univ. (Nat. Sci. Ed.) 2022, 44, 88–94. [Google Scholar]
- Liu, Z.X.; Liu, G.L. Pump Station Water Hammer and Its Protection; Water Resources and Electric Power Press: Beijing, China, 1988; pp. 107–108. [Google Scholar]
- Zhang, Q.; Yan, Y.; Huang, B. Experimental study on transient flow characteristics of leakage in air-containing water conveyance pipelines. J. Hydrodyn. Ser. A 2022, 37, 678–683. [Google Scholar]
- Streeter, V.L. Water hammer analysis. J. Hydraul. Div. 1969, 95, 1959–1972. [Google Scholar] [CrossRef]
- Wiggert, D.C.; Sundquist, M.J. The effect of gaseous cavitation on fluid transients. J. Fluids Eng. 1979, 101, 79–86. [Google Scholar] [CrossRef]
- Wylie, E.B. Simulation of vaporous and gaseous cavitation. J. Fluids Eng. 1984, 106, 307–311. [Google Scholar] [CrossRef]
- Fu, Y.; Jiang, J.; Li, Y.; Ying, R. A Two-Fluid Model-Based Calculation Method for Gas-Liquid Two-Phase Water Hammer. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2018, 46, 126–132. [Google Scholar]
- Hu, L.R. Verification and Application of a Water Hammer Model Based on Discrete Steam/Gas Cavitation Theory. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2023. [Google Scholar]
- Zhou, L.; Lu, Y. SWMM Simulation Capability for Transient Flow in Drainage Pipe. China Water Wastewater 2022, 38, 108–115. [Google Scholar]
- Cai, Y.; Sheng, J. Research on the fast and high-precision characteristic line method analysis of hydraulic pipelines. J. Zhejiang Univ. 1986, 3, 35–46. [Google Scholar]
- Wang, B.Q. Numerical Calculation of Water Hammer Due to Flow Reconnection Based on the Lattice Boltzmann Method. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2017. [Google Scholar]
- Bergant, A.; Simpson, A.R. Estimating unsteady friction in transient cavitating pipe flow. In Proceedings of the 2nd International Conference on Water Pipeline Systems, Edinburgh, UK, 24–26 May 1994. [Google Scholar]
- Niu, L.; Jing, H.; Li, P. Numerical simulation of water hammer considering unsteady friction and cavitation. J. Appl. Mech. 2023. Available online: https://kns.cnki.net/nzkhtml/xmlRead/trialRead.html?dbCode=CAPJ&tableName=CAPJTOTAL&fileName=YYLX20230717002&fileSourceType=1&invoice=d%2bwJ0BWJmTkiULjORYDHPU0khEjm7WoGUZTAGfIO2Agi59NZGH8wZUQgeMQLjF9O46XMRCaqd8GOIE7CCJQ8ftEKcLzzDkBzSBmFZUF1Oq96erTvgXPyfV8VlhxEGJZyUeo6ybGNMROqKwKqixUqr2ycHRUbZ40sDVZXeRgBcO4%3d&appId=KNS_BASIC_PSMC (accessed on 17 February 2025).
- Yang, F.; Jiang, E.; Wang, Y. Sediment transport calculation of multi-sand rivers based on the Muskingum method. People’s Yellow River 2023, 45, 39–42. [Google Scholar]
- Wen, D.D. Theoretical Study and Numerical Simulation of Water Hammer Due to Flow Reconnection and Its Protection. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2015. [Google Scholar]
- Santoro, V.C.; Crimì, A.; Pezzing, A. Developments and limits of discrete vapor cavity models of transient cavitating pipe flow: 1D and 2D flow numerical analysis. J. Hydraul. Eng. 2018, 144, 04018047. [Google Scholar] [CrossRef]
- Jamil, R. Frictional head loss relation between Hazen-Williams and Darcy-Weisbach equations for various water supply pipe materials. Int. J. Water 2019, 13, 333–347. [Google Scholar] [CrossRef]
- Chen, Y.; Du, Y.; Geng, A. Discussion on the Calculation Method of Head Loss Along the Pipeline in Water Supply and Drainage. J. Water Wastewater 2009, 45, 109–111. [Google Scholar]
- Li, Z.; Fan, C.; Shen, H. A New Cavity Model for Water Hammer with Liquid Column Separation. J. Hydraul. Eng. 2024, 44, 37–41+53. [Google Scholar]

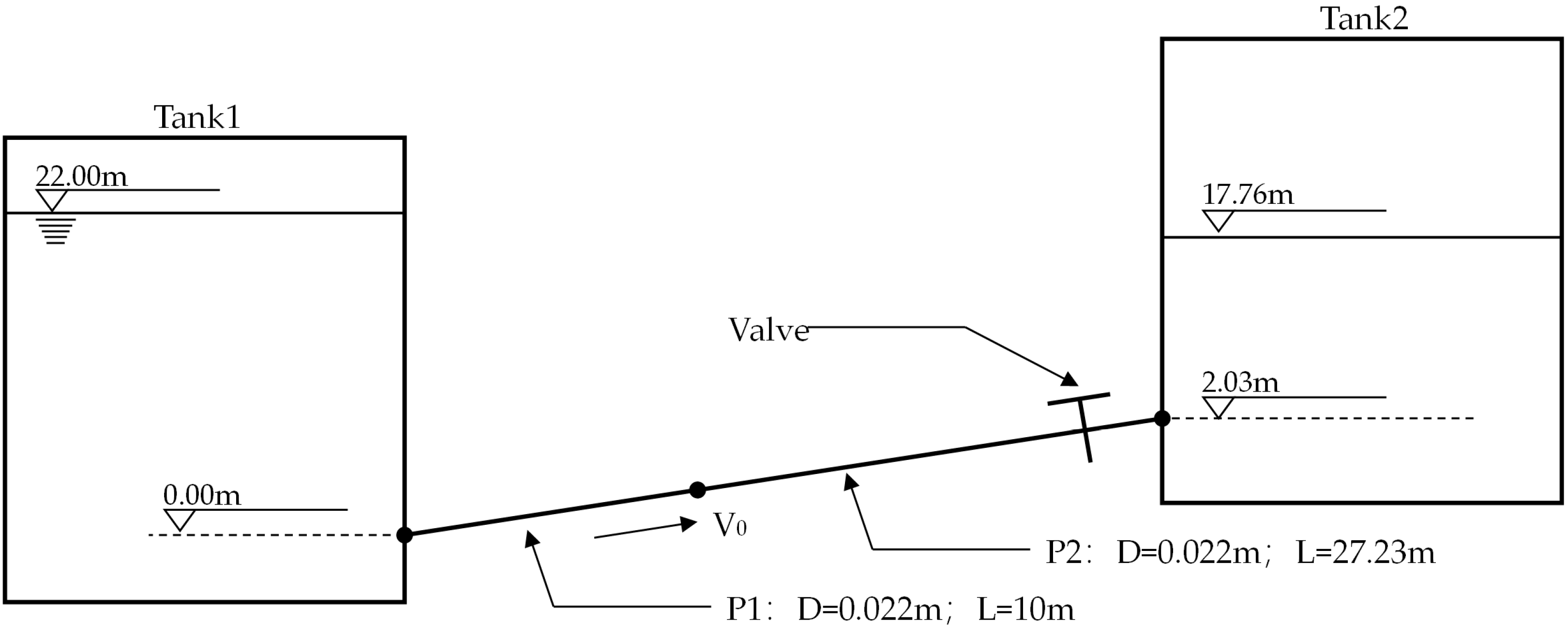


| ID | L/m | D/m | a/(m/s) | dt/s | dx/m | (Cn a·dt/dx) |
|---|---|---|---|---|---|---|
| P1 | 10 | 0.022 | 1319 | 0.001072 | 1.428 | 0.99 |
| P1 | 27.23 | 0.022 | 1319 | 0.001072 | 1.512 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Jiang, J.; Long, Z.; Peng, L.; Jiang, Y.; Cheng, W. Numerical Dissipation Compensation in Liquid Column Separation: An Improved DVCM Approach. Water 2025, 17, 805. https://doi.org/10.3390/w17060805
Chen W, Jiang J, Long Z, Peng L, Jiang Y, Cheng W. Numerical Dissipation Compensation in Liquid Column Separation: An Improved DVCM Approach. Water. 2025; 17(6):805. https://doi.org/10.3390/w17060805
Chicago/Turabian StyleChen, Wenhao, Jianqun Jiang, Zhihong Long, Liyun Peng, Yonghong Jiang, and Weiping Cheng. 2025. "Numerical Dissipation Compensation in Liquid Column Separation: An Improved DVCM Approach" Water 17, no. 6: 805. https://doi.org/10.3390/w17060805
APA StyleChen, W., Jiang, J., Long, Z., Peng, L., Jiang, Y., & Cheng, W. (2025). Numerical Dissipation Compensation in Liquid Column Separation: An Improved DVCM Approach. Water, 17(6), 805. https://doi.org/10.3390/w17060805





