Design of Dewatering Scheme for Deep Foundation Pit with a Multi-Objective Optimization Approach Based on Cost Controlment
Abstract
1. Introduction
2. Overview of Study Site
2.1. Study Area
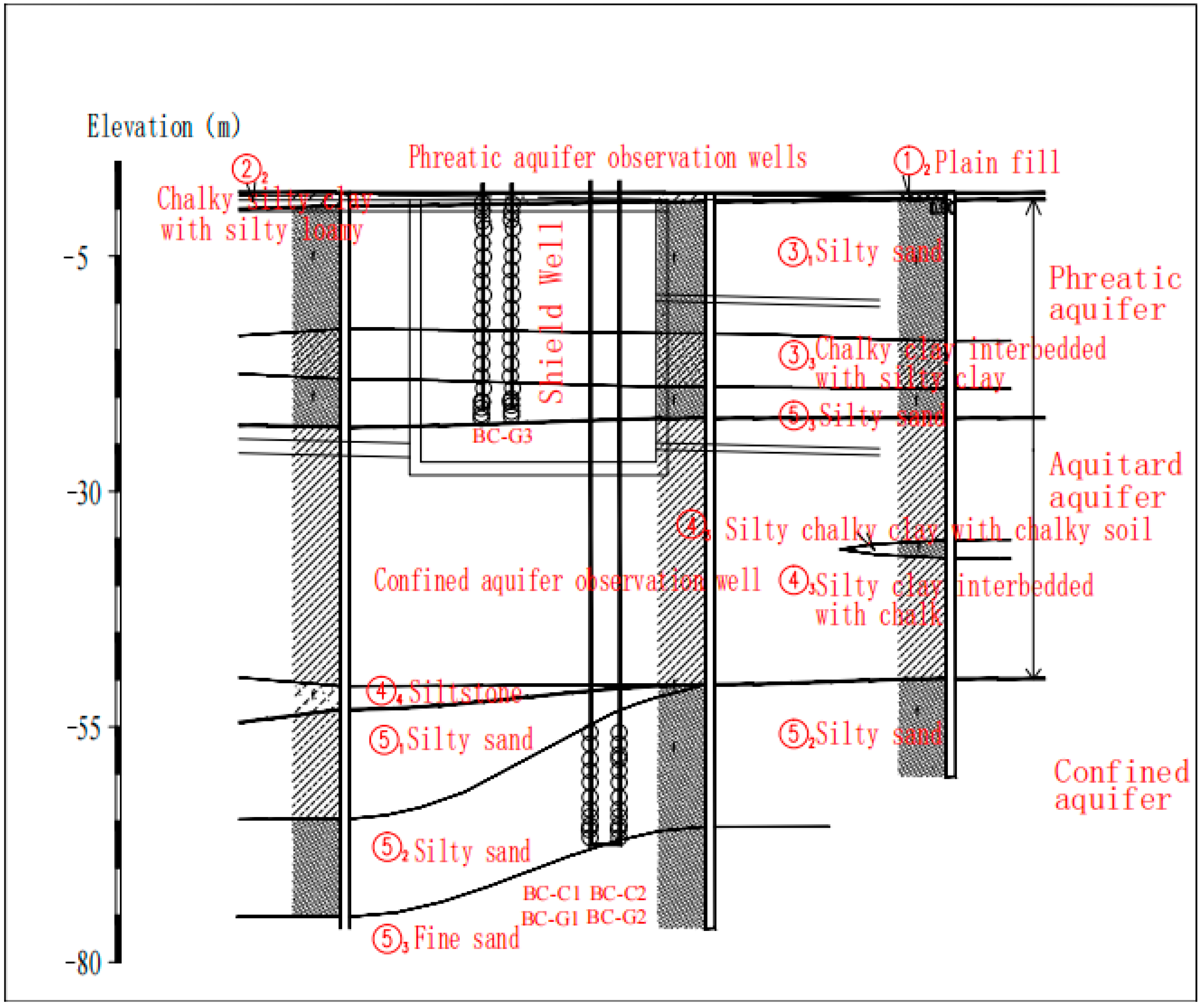
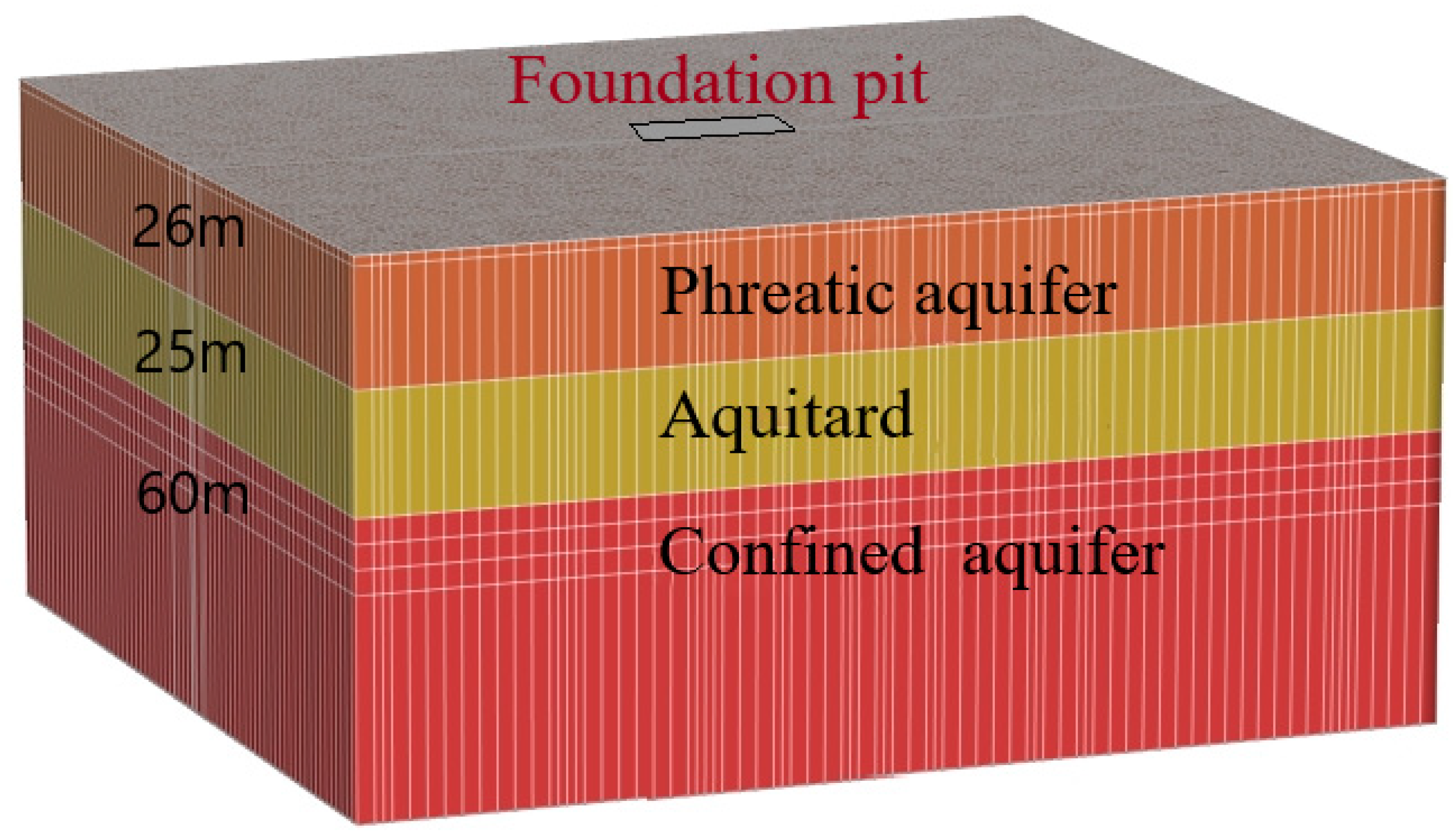
2.2. Engineering Geological and Hydrogeological Conditions
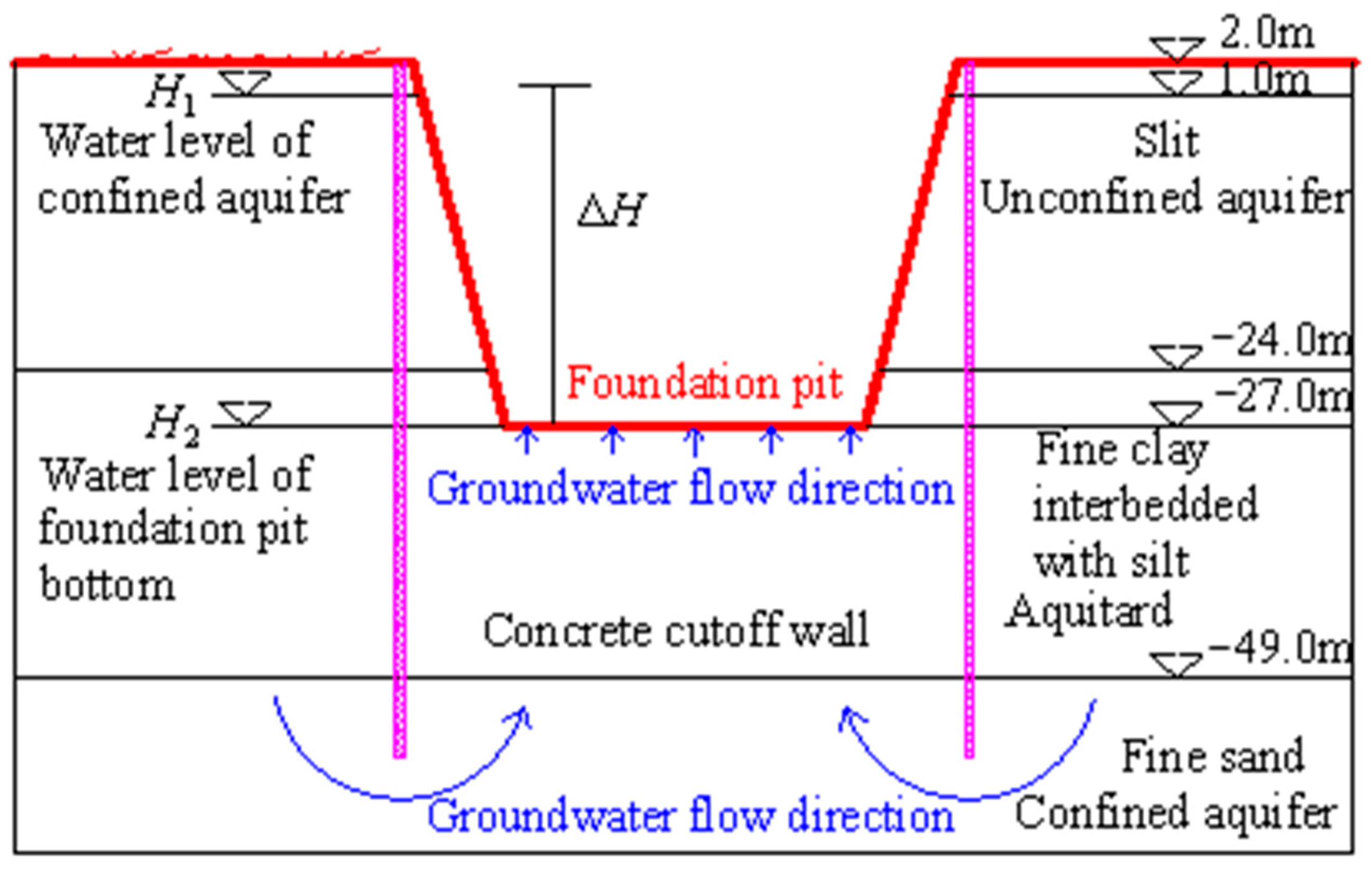
2.3. The Hydrogeological Condition
2.4. Dynamic Characteristics of Groundwater
3. Method
3.1. Mathematical Model
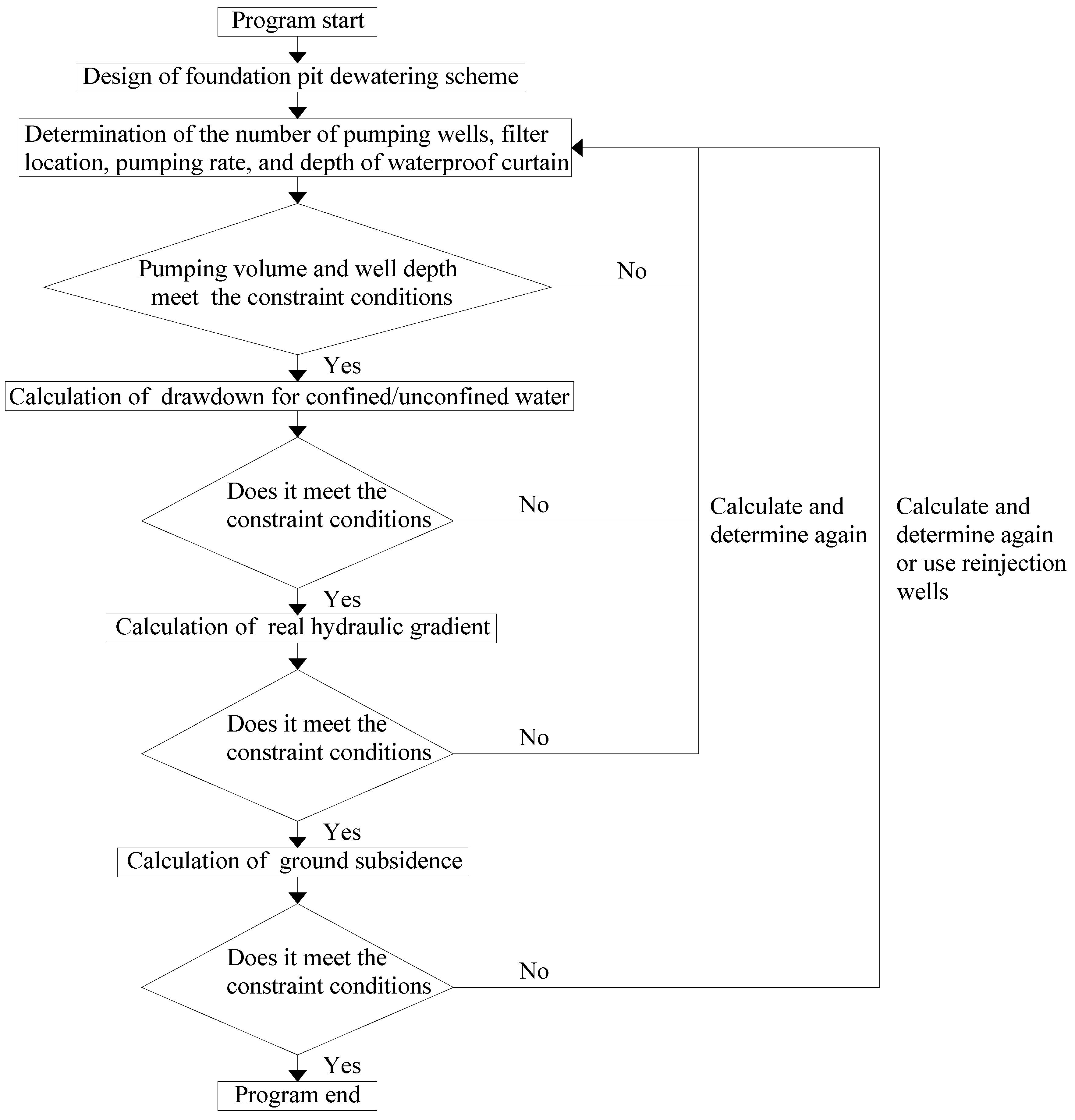
3.2. Optimization Model for Pit Dewatering
3.2.1. Design Variable Selection
3.2.2. Establishment of the Objective Function
3.2.3. Determination of Constraint Conditions
- (1)
- Well pumping flow constraints
- (2)
- Maximum well-depth constraints
- (3)
- Water-level constraints
- (4)
- Subsidence constraints
3.3. The Solution of Pit Settlement Optimization Mathematical Model
4. Results
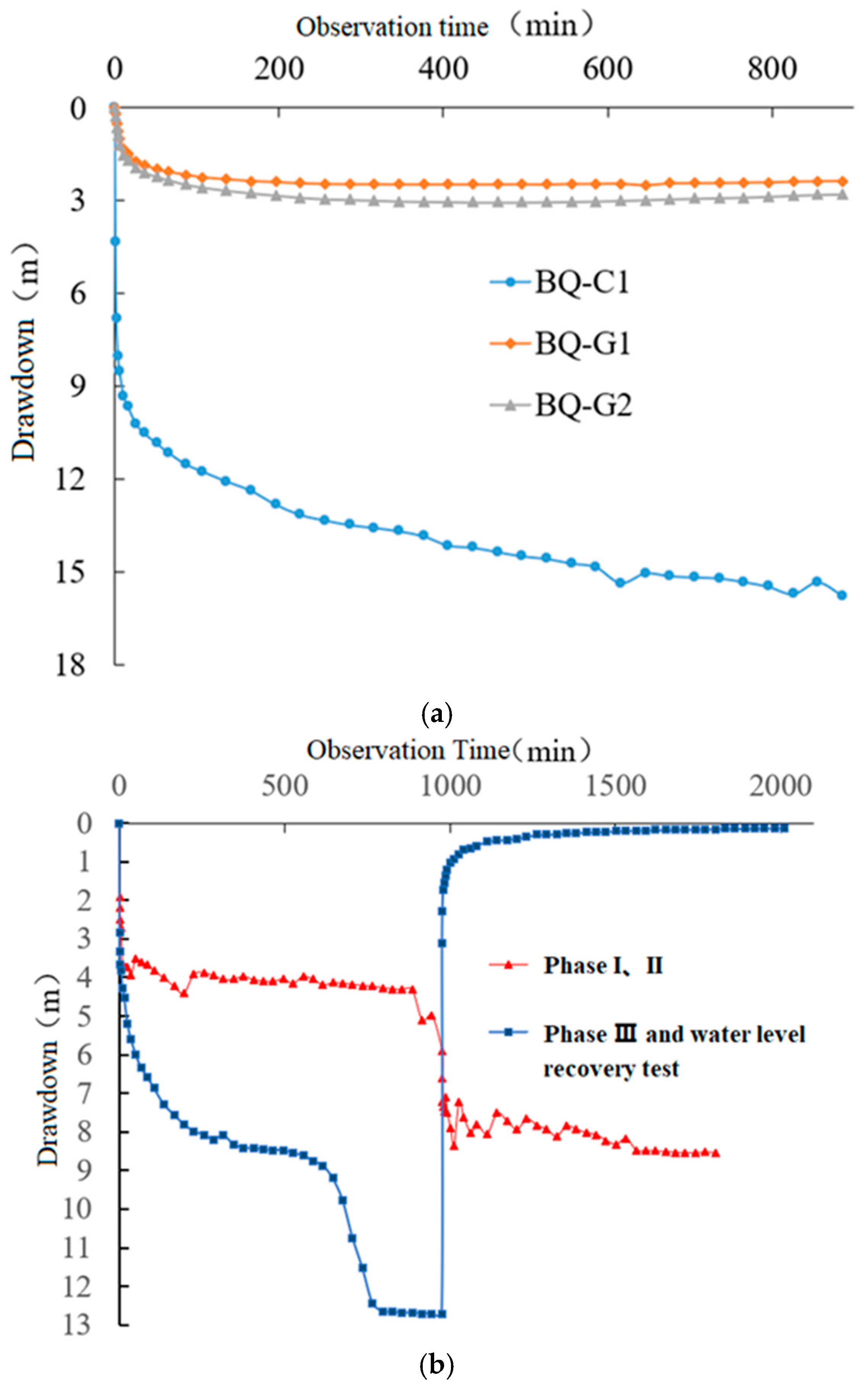
4.1. Calculation Results of Hydrogeological Parameters Based on Pumping Tests
Pumping Test of Phreatic Aquifer
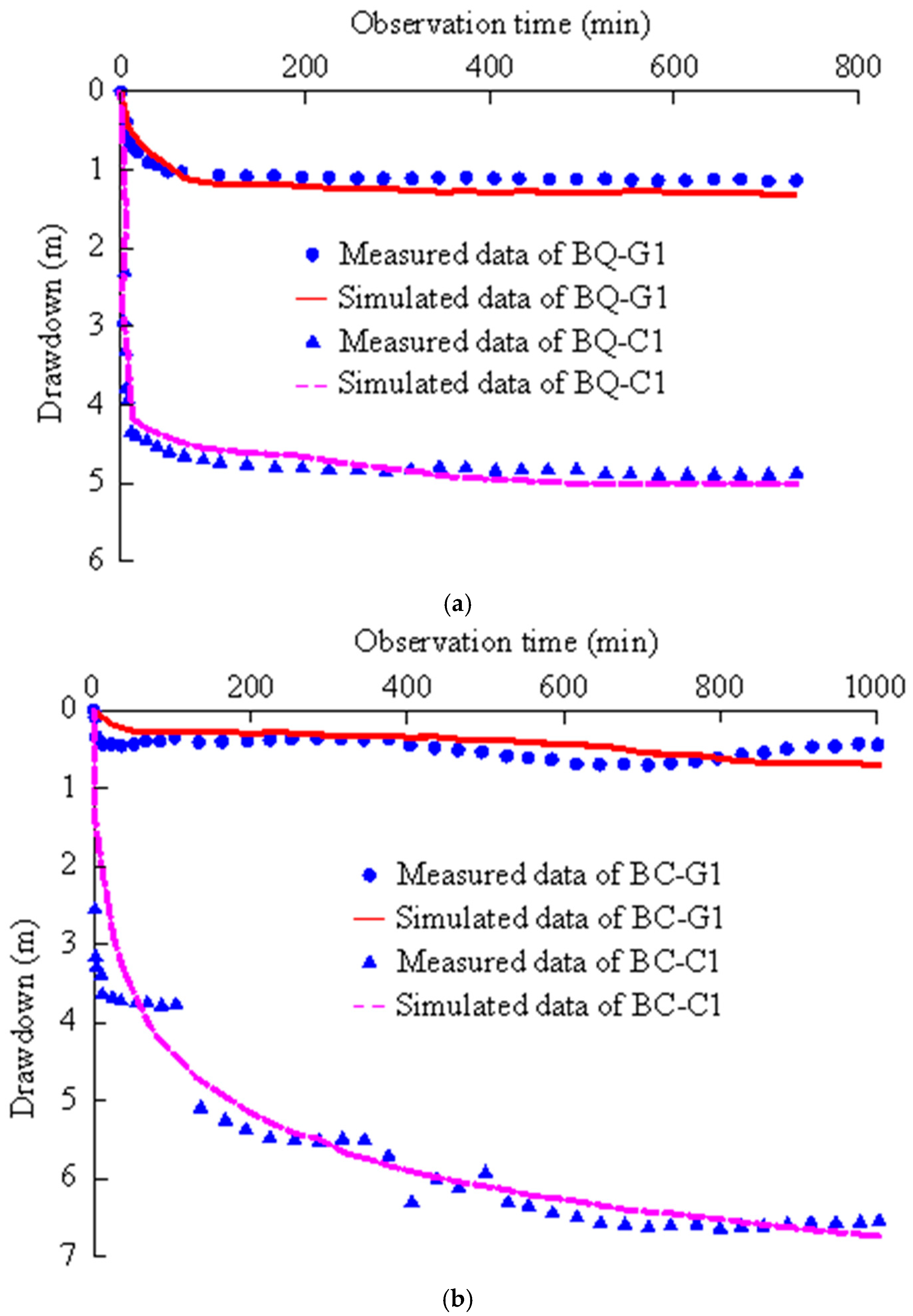
4.2. Identification of Model Parameters Based on Numerical Methods
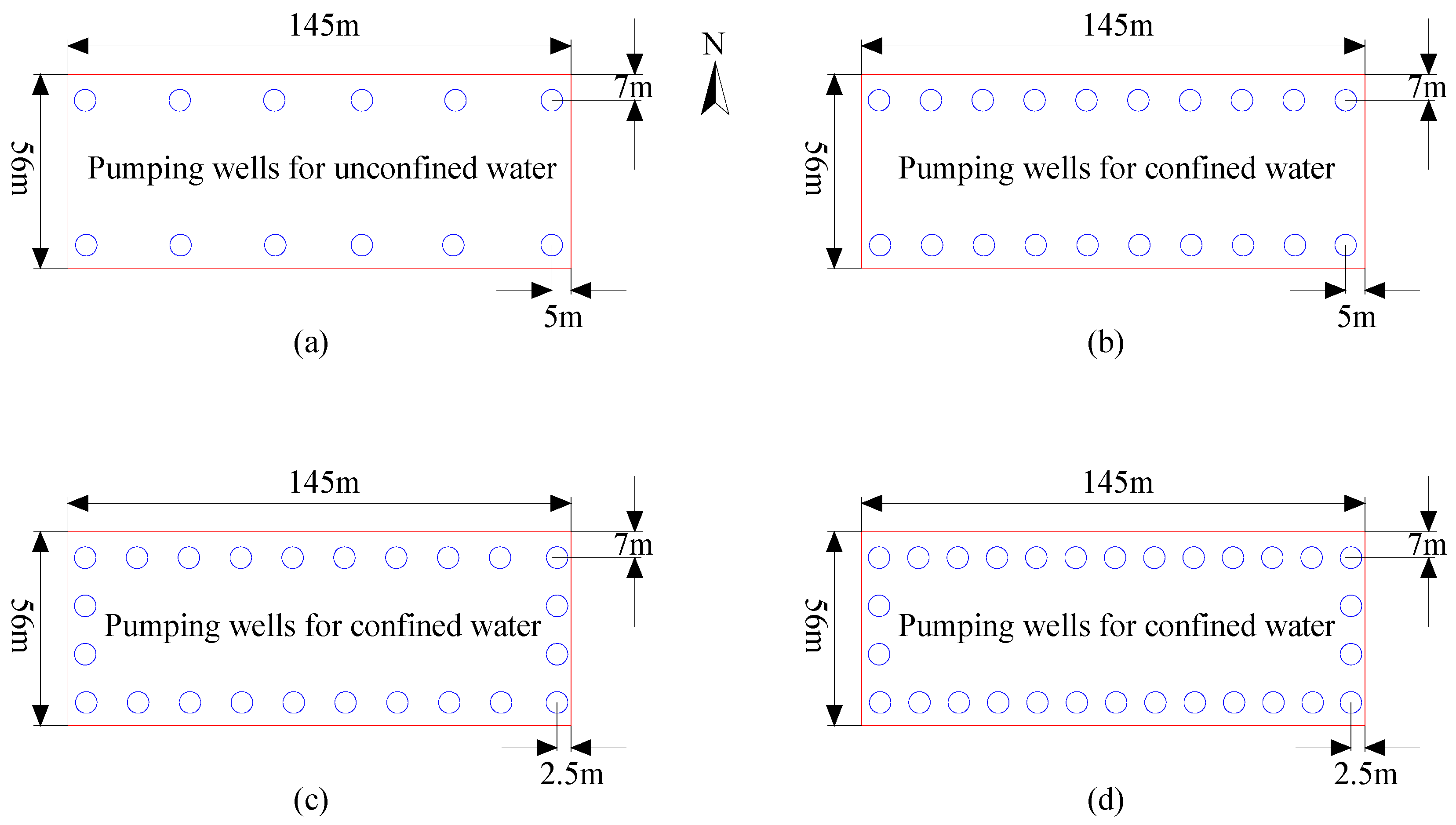
4.3. Optimization Study of Shield Shaft Pit Dewatering Scheme
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, Y.; Zhang, R.; Zhang, D.; Zhou, C. Urban Agglomerations in China: Characteristics and Influencing Factors of Population Agglomeration. Chin. Geogr. Sci. 2023, 33, 719–735. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Y.; Wang, X.; Liu, X.; Zhou, N. Numerical evaluation of a 70-m deep hydropower station foundation pit dewatering. Environ. Earth Sci. 2022, 81, 364. [Google Scholar] [CrossRef]
- Zeng, C.F.; Xue, X.L.; Li, M.K. Use of cross wall to restrict enclosure movement during dewatering inside a metro pit before soil excavation. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2021, 112, 103909. [Google Scholar] [CrossRef]
- Cao, C.; Shi, C.; Liu, L.; Liu, J. Evaluation of the effectiveness of an alternative to control groundwater inflow during a deep excavation into confined aquifers. Environ. Earth Sci. 2020, 79, 502. [Google Scholar] [CrossRef]
- Wang, X.W.; Yang, T.L.; Xu, Y.S.; Shen, S.L. Evaluation of optimized depth of waterproof curtain to mitigate negative impacts during dewatering. J. Hydrol. 2019, 577, 123969. [Google Scholar] [CrossRef]
- Huang, Y.; Bao, Y.; Wang, Y. Analysis of geoenvironmental hazards in urban underground space development in Shanghai. Nat. Hazards 2015, 75, 2067–2079. [Google Scholar] [CrossRef]
- Yu, D.; Lu, J.-P.; Tang, Y.-Q. Optimal Design of Well Spacing in Foundation Pit Multi-well Dewatering Based on Objective Function. J. Shenyang Jianzhu Univ. (Nat. Sci.) 2013, 29, 649–654. [Google Scholar]
- Xu, Y. Optimal Precipitation Analysis of Well Group Based on Objective Function Method and Finite Element Method; Northeastern University: Boston, MA, USA, 2013. [Google Scholar]
- Chen, Z.; Huang, J.; Zhan, H.; Wang, J.; Dou, Z.; Zhang, C.; Chen, C.; Fu, Y. Optimization schemes for deep foundation pit dewatering under complicated hydrogeological conditions using MODFLOW-USG. Eng. Geol. 2022, 303, 106653. [Google Scholar] [CrossRef]
- Liu, L.; Lei, M.; Cao, C.; Shi, C. Dewatering Characteristics and Inflow Prediction of Deep Foundation Pits with Partial Penetrating Curtains in Sand and Gravel Strata. Water 2019, 11, 2182. [Google Scholar] [CrossRef]
- You, Y.; Yan, C.; Xu, B.; Liu, S.; Che, C. Optimization of dewatering schemes for a deep foundation pit near the Yangtze River, China. J. Rock Mech. Geotech. Eng. 2018, 10, 555–566. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Liu, X.; Yang, T.; Wang, H.; Zhu, Y. Areal subsidence under pumping well–curtain interaction in subway foundation pit dewatering: Conceptual model and numerical simulations. Environ. Earth Sci. 2016, 75, 198. [Google Scholar] [CrossRef]
- Zhou, N.; Vermeer, P.A.; Lou, R.; Tang, Y.; Jiang, S. Numerical simulation of deep foundation pit dewatering and optimization of controlling land subsidence. Eng. Geol. 2010, 114, 251–260. [Google Scholar] [CrossRef]
- Alhama, I.; Carrasco, S.N.; Jiménez-Valera, J.A.; Freitas, T.M.; García Guerrero, J.M. A general solution for groundwater flow around deep excavations based on non–dimensionalization techniques. Eng. Geol. 2025, 347, 107938. [Google Scholar] [CrossRef]
- Bear, J. Hydraulics of Groundwater; McGraw-Hill: New York, NY, USA, 2012. [Google Scholar]
- Beale, G.; Read, J. Guidelines for Evaluating Water in Pit Slope Stability; CSIRO Publishing: Clayton, Australia, 2014. [Google Scholar]
- Peng, B.; Feng, R.; Wu, L.; Wei, K.; Wang, P. Settlement Calculation Method for Peat Soil Foundations. Int. J. Geomech. 2023, 23, 04023094. [Google Scholar] [CrossRef]

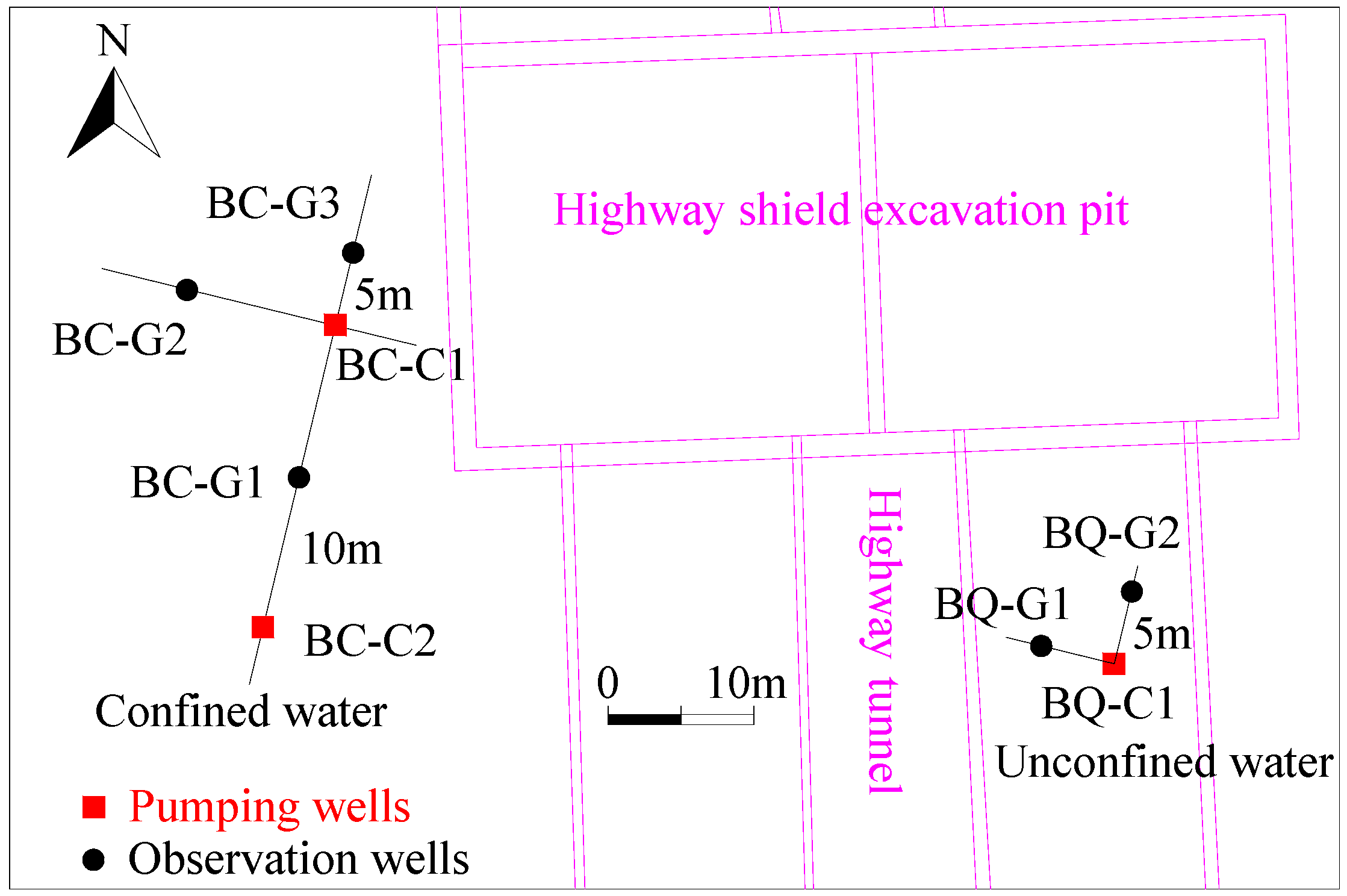

| Observation Well Number | BC-G3 | BC-C1 | BQ-C1 | DZ-G3 -068 | DZ-G3 -035 | DZ-G1 -19 | DZ-T3 -021 | Changjiang River Level |
|---|---|---|---|---|---|---|---|---|
| Observation well type | Phreatic aquifer | Confined aquifer | Phreatic aquifer | Phreatic aquifer | Phreatic aquifer | Confined aquifer | Confined aquifer | River |
| Distance to Yangtze River (m) | 1690 | 1688 | 1985 | 30 | 800 | 2255 | 870 | 0 |
| Range of water level changes (m) | 0.64–0.88 | 0.53–0.75 | 0.45–0.77 | 1.02–1.13 | 0.94–1.02 | 0.07–0.13 | −0.21–−0.61 | 1.77–4.47 |
| Maximum variation (m) | 0.24 | 0.22 | 0.32 | 0.11 | 0.08 | 0.06 | 0.4 | 2.7 |
| Phase | Test Hole Number | Parameters | |||||
|---|---|---|---|---|---|---|---|
| Initial Water Level Depth (m) | Burial Depth of Steady Water Level (m) | Stable Depth of Water Level Fall (m) | Stable Pumping Capacity (m3/d) | Radius of Influence (m) | Permeability Coefficients K (m/d) | ||
| Phase I | BQ-C1 | 2.60 | 7.311 | 4.711 | 274.97 | 81.55 | 1.955 |
| BQ-G1 | 2.475 | 3.584 | 1.109 | 1.938 | |||
| BQ-G2 | 2.42 | 3.65 | 1.23 | 2.011 | |||
| Phase II | BQ-C1 | 2.44 | 11.58 | 9.14 | 504.76 | 162.76 | 2.622 |
| BQ-G1 | 2.35 | 4.405 | 2.055 | 2.046 | |||
| BQ-G2 | 2.30 | 4.605 | 2.305 | 2.133 | |||
| Phase III | BQ-C1 | 1.41 | 16.74 | 15.33 | 747.04 | 284.47 | 3.523 |
| BQ-G1 | 1.31 | 4.85 | 3.54 | 2.238 | |||
| BQ-G2 | 1.27 | 5.04 | 3.77 | 2.300 | |||
| Water Level Change | Phase | Pumping Hole BC-C1 for Confined Aquifer | Observation Hole BC-C2 for Confined Aquifer | Observation Hole BC-G1 for Confined Aquifer | Observation Hole BC-G2 for Confined Aquifer | Observation Hole BC-G3 for Unconfined Aquifer | Observation Holes BRT for Aquitard |
|---|---|---|---|---|---|---|---|
| Initial water level burial depth (m) | I | 1.38 | 1.15 | 1.02 | 1.16 | 0.91 | 1.335 |
| II | 1.50 | 1.25 | 1.11 | 1.25 | 0.84 | 1.320 | |
| III | 1.44 | 1.20 | 1.55 | 1.20 | 0.87 | 1.255 | |
| Stabilization of water table burial depth (m) | I | 5.34 | 1.65 | 1.66 | 1.88 | 0.92 | 1.335 |
| II | 9.74 | 1.74 | 1.81 | 2.07 | 0.90 | 1.335 | |
| III | 11.31 | 1.83 | 1.95 | 2.22 | 0.87 | 1.265 | |
| Stabilization of water level descent depths (m) | I | 3.96 | 0.50 | 0.64 | 0.72 | 0.01 | 0 |
| II | 8.24 | 0.49 | 0.70 | 0.82 | 0.06 | 0.015 | |
| III | 9.87 | 0.63 | 0.40 | 1.02 | 0 | 0.010 |
| Phase | Pumping Test Parameter | |||
|---|---|---|---|---|
| Stabilization of Water Level Descent Depths (m) | Stable Pumping Capacity Q (m3/d) | Hydraulic Conductivity K (m/d) | Radius of Influence R (m) | |
| Phase I | 3.96 | 553.48 | 12.486 | 133.06 |
| Phase II | 8.24 | 731.39 | 7.80 | 220.64 |
| Phase III | 9.87 | 948.80 | 8.77 | 274.95 |
| Serial Number | Number and Type of Well Clusters | Location of Well Clusters | Depth of Curtain (m) | Filter Top and Bottom Elevation (m) | Filter Length (m) | Pumping Flow Rate for a Single Well (m3/d) | Pumping Time (d) | Minimum Water Level Descent Depth Inside the Pit (m) | Observation Points 3 Settlement (mm) | Actual Hydraulic Gradient at the Bottom of the Well | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Phreatic | Confined Water | ||||||||||
| Case1 | 12 phreatic aquifer pumping wells 20 con-fined aquifer pumping wells | (m) (n) | 66 | −13.5~−24 | 10.5 | 296.01 | 6.4 | 26 | 17.2 | 69.36 | 0.67 |
| −51~−60.5 | 9.5 | 544.83 | |||||||||
| Case2 | −13.5~−24 | 10.5 | 296.01 | 22.82 | 9.8 | / | / | ||||
| −53~−62.5 | 9.5 | 544.83 | |||||||||
| Case3 | −13.5~−24 | 10.5 | 296.01 | 26 | 17.32 | 69.36 | 0.66 | ||||
| −49~−58.5 | 9.5 | 544.83 | |||||||||
| Case4 | −13.5~−24 | 10.5 | 296.01 | 26 | 17.15 | 69.63 | 0.67 | ||||
| −49~−60.5 | 11.5 | 544.83 | |||||||||
| Case5 | −13.5~−24 | 10.5 | 296.01 | 24.4 | 10.10 | / | / | ||||
| −49~−62.5 | 13.5 | 544.83 | |||||||||
| Case6 | −13.5~−24 | 10.5 | 296.01 | 7 | 26 | 16.25 | |||||
| −49~−58.5 | 9.5 | 516.16 | |||||||||
| Case7 | −13.5~−24 | 10.5 | 296.01 | 23.6 | 15.22 | ||||||
| −49~−58.5 | 9.5 | 487.48 | |||||||||
| Case8 | −13.5~−24 | 10.5 | 296.01 | 6.4 | 26 | 17.8 | 72.74 | 0.71 | |||
| −49~−59 | 10 | 573.51 | 1 | 13.26 | 17.02 | / | / | ||||
| Case9 | −13.5~−24 | 10.5 | 296.01 | 6.4 | 26 | 19.07 | 75.97 | 0.85 | |||
| −49~−59.5 | 10.5 | 602.18 | 1 | 13.19 | 18.18 | / | / | ||||
| Serial Number | Number and Type of Well Clusters | Location of Well Clusters | Depth of Curtain (m) | Filter Top and Bottom Elevation (m) | Filter Length (m) | Pumping Flow Rate for a Single Well (m3/d) | Pumping Time (d) | Minimum Water Level Descent Depth Inside the Pit (m) | Observation Points 3 Settlement (mm) | Actual Hydraulic Gradient at the Bottom of the Well | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Groundwater Water | Confined Water | ||||||||||
| Case8 | 12 p-a p-wells | (m) | 66 | −13.5~−24 | 10.5 | 296.01 | 6.4 | 26 | 17.2 | 14.32 | 0.71 |
| 20 c-a p-wells | (n) | −49~−58.5 | 9.5 | 544.83 | |||||||
| 9 p-a r-wells | (q) | 1~−3 | 4 | −25 | |||||||
| 9 c-a r-wells | (r) | −49~−54 | 5 | −250 | |||||||
| Case9 | 12 p-a p-wells | (m) | 61 | −13.5~−24 | 10.5 | 296.01 | 6.4 | 26 | 17.08 | 16.44 | 0.73 |
| 24 c-a p-wells | (o) | −49~−60 | 11 | 630.86 | |||||||
| 9 p-a r-wells | (q) | 1~−3 | 4 | −35 | |||||||
| 9 c-a r-wells | (r) | −-49~−54 | 5 | −400 | |||||||
| Case10 | 12 p-a p-wells | (m) | 56 | −13.5~−24 | 10.5 | 296.01 | 6.4 | 26 | 17.11 | 17.16 | 0.75 |
| 30 c-a p-wells | (p) | −49~−61 | 12 | 688.21 | |||||||
| 9 p-a r-wells | (q) | 1~−3 | 4 | −50 | |||||||
| 9 c-a r-wells | (r) | −49~−54 | 5 | −600 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Xie, M.; Chai, C.; Huo, X.; Huang, Y. Design of Dewatering Scheme for Deep Foundation Pit with a Multi-Objective Optimization Approach Based on Cost Controlment. Water 2025, 17, 857. https://doi.org/10.3390/w17060857
Dong Z, Xie M, Chai C, Huo X, Huang Y. Design of Dewatering Scheme for Deep Foundation Pit with a Multi-Objective Optimization Approach Based on Cost Controlment. Water. 2025; 17(6):857. https://doi.org/10.3390/w17060857
Chicago/Turabian StyleDong, Zhigao, Mingze Xie, Chunyang Chai, Xiushi Huo, and Yong Huang. 2025. "Design of Dewatering Scheme for Deep Foundation Pit with a Multi-Objective Optimization Approach Based on Cost Controlment" Water 17, no. 6: 857. https://doi.org/10.3390/w17060857
APA StyleDong, Z., Xie, M., Chai, C., Huo, X., & Huang, Y. (2025). Design of Dewatering Scheme for Deep Foundation Pit with a Multi-Objective Optimization Approach Based on Cost Controlment. Water, 17(6), 857. https://doi.org/10.3390/w17060857






