Next Article in Journal
Use of Mobile Photothermic Installation on Application of Drip Irrigation Technology in Orchards of Mountain and Foothill Areas of Uzbekistan
Next Article in Special Issue
Multiscale Factors Driving Extreme Flooding in China’s Pearl River Basin During the 2022 Dragon Boat Precipitation Season
Previous Article in Journal
Improving Wastewater Quality Using Ultrafiltration Technology for Sustainable Irrigation Reuse
Previous Article in Special Issue
Water Management Instructions as an Element of Improving the State of the Pakoski Reservoir (Central–Western Poland)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 17
Issue 6
10.3390/w17060871
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Intercomparison of Runoff and River Discharge Reanalysis Datasets at the Upper Jinsha River, an Alpine River on the Eastern Edge of the Tibetan Plateau

by
Shuanglong Chen
1,†,
Heng Yang
2,† and
Hui Zheng
3,*
1
Baihetan Hydropower Plant, China Three Gorges Corporation, Liangshan 615421, China
2
Science and Technology Research Institute, China Three Gorges Corporation, Beijing 100038, China
3
Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work and should be considered co-first authors.
Water 2025, 17(6), 871; https://doi.org/10.3390/w17060871
Submission received: 8 February 2025 / Revised: 14 March 2025 / Accepted: 17 March 2025 / Published: 18 March 2025
(This article belongs to the Special Issue Climate Change and Hydrological Processes)
Browse Figures
Versions Notes

Abstract

:
This study assesses the effectiveness and limitations of publicly accessible runoff and river discharge reanalysis datasets through an intercomparison in the Upper Jinsha River, an alpine region with substantial hydropower potential on the eastern edge of the Tibetan Plateau. The examined datasets are the European Centre for Medium-Range Weather Forecast Reanalysis version 5 (ERA5-Land), the Global Flood Awareness System (GloFAS), the Global Reach-Level Flood Reanalysis (GRFR), and the China Natural Runoff Dataset (CNRD). These datasets are created using various meteorological forcing, runoff generation models, river routing models, and calibration methods. To determine the causes of discrepancies, additional simulations were carried out. One simulation, driven by meteorological forcing similar to that of ERA5-Land and GloFAS but utilizing the uncalibrated NoahMP land surface model at a higher spatial resolution, was included to evaluate the effects of meteorological inputs, spatial resolution, and calibration on runoff estimation. Runoff from all datasets was rerouted on a high-resolution river network derived from the 3-arcsecond Multi-Error-Removed Improved-Terrain Hydrography (MERIT-Hydro) dataset, allowing for a comparison between vector- and grid-based river routing models for discharge estimates. The intercomparison is grounded in observations from three gauging stations—Zhimenda, Gangtuo, and Benzilan—at monthly, daily, and hourly scales. The results suggest that model calibration has a more significant influence on runoff and discharge estimates than meteorological data. Calibrated datasets, such as GloFAS and GRFR, perform better than others, despite variations in the forcing data. The runoff characteristics-based calibration method used in GRFR exhibits superior performance at Zhimenda and Benzilan. However, at Gangtuo, GRFR’s performance is unsatisfactory, highlighting the limitation of the machine learning-based method in regions with rugged terrain and limited observations. Vector-based river routing models demonstrate advantages over grid-based models. GloFAS, which uses a grid-based routing model, encounters difficulties in simultaneously producing accurate runoff and discharge estimates. The intercomparison shows that GRFR’s river routing is sub-optimally configured. However, when GRFR’s runoff rerouted, the performance of discharge improves substantially, attaining a Kling–Gupta efficiency of approximately 0.9. These findings offer valuable insights for the further development of reanalysis datasets in this region.

1. Introduction

The rapid growth of global- and continental-scale runoff and discharge reanalysis datasets marks a significant advancement in hydrological research. Datasets such as the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis version 5 (ERA5) [1], ERA5-Land [2], the Global Flood Awareness System (GloFAS) [3,4], and the Global Reach-Level Flood Reanalysis (GRFR) [5,6] provide continuous, spatially comprehensive runoff and river discharge estimates. Additionally, regional datasets like the National Water Model (NWM) of the United States [7], the European Flood Early Warning Systems [8], and the China Natural Runoff Dataset (CNRD) [9,10] provide runoff and discharge estimates tailored to specific regions. These datasets have greatly improved our understanding of river systems [11,12] and their interactions with other components of the Earth system [13]. Furthermore, they have been instrumental in supporting decision-making processes, particularly in the area of water resources utilization and flood protection [7,14].
Reanalysis datasets are generated through a complex chain of methodologies that include meteorological forcing data, land surface models or hydrological models, river routing models, river network delineations, and calibrations. The diversity among these components can significantly influence the estimation of runoff and river discharge. Studies have demonstrated that meteorological forcing data can differ remarkably [15,16]. The use of different meteorological forcing data [17,18], in combination with varying model structure [19], spatial resolutions [20,21,22], parameterizations [23,24], and parameters [25] of land surface models or hydrological models, can lead to disparate estimates of runoff [26,27]. Furthermore, these differences in runoff estimation can be further amplified by the methods employed in river routing [28,29,30].
The diversity in estimation methodologies necessitates careful intercomparison before using reanalysis datasets. In the past decades, a variety of intercomparison studies have been conducted with different objectives. Land surface model comparisons such as the Project for Intercomparison of Land-surface Parameterization Schemes [31] and the Land Surface, Snow and Soil Moisture Model Intercomparison Project [32], conducted with the same meteorological forcing data, greatly help to reveal the weakness of the participant models and the interactions of land surface processes. The Distributed Model Intercomparison Project [33,34] compared distributed models with lumped models. This project revealed the superiority of distributed routing models in reproducing flood peaks and reported the importance of calibration on distributed rainfall-runoff models. Beck et al. [27] compared ten hydrological models at the global scale. Their results further confirm that proper parameter calibration is vital for accurate runoff estimation. The Continental Hydrological Intercomparison Project [35] compared two high-resolution, physics-based models at the continental scale. The intercomparison promotes high-resolution modeling to enhance topographic processing and to improve topographic representation over complex topography. There are also intercomparisons with regional focuses. The Great Lakes Runoff Intercomparison Project [29] and the Nelson Model Intercomparison Project under the Integrated Modelling Program of Canada initiative [30] are two examples. These intercomparison studies aim to select the best-performing estimation methodologies for the region and guide further improvements of operations.
The Upper Jinsha River, the source of the Changjiang River, is notable for its steep gradient and high hydroelectric potential. The river is located on the eastern edge of the Tibetan Plateau. Thirteen hydroelectric facilities have been built or planned along its main stem, collectively possessing an installed capacity of approximately 14.6 gigawatts. The river originates from the Tibetan Plateau. The source area of the river consists of a major part of the Sanjiangyuan National Nature Reserve, the highest and largest nature reserve in China yet. The operations of hydroelectric facilities and natural reserves require accurate estimation of water resources. However, the scarcity of in situ hydrometeorological observations in the region is a notable challenge. In this context, reanalysis datasets of runoff and discharge emerge as an indispensable data source for the area. Simultaneously, the Upper Jinsha River’s intricate topography, high-alpine environmental conditions, and the pressing need for accurate runoff and river discharge estimations render it an exemplary testing ground for these reanalysis datasets.
This study intercompares runoff and river discharge reanalysis data obtained from ERA5-Land, GloFAS, GRFR, and CNRD for the Upper Jinsha River as a pilot analysis. The primary objective is to assess the effectiveness and limitations of the methodologies employed in these reanalyses, providing insights to guide future improvements in runoff and discharge estimation.

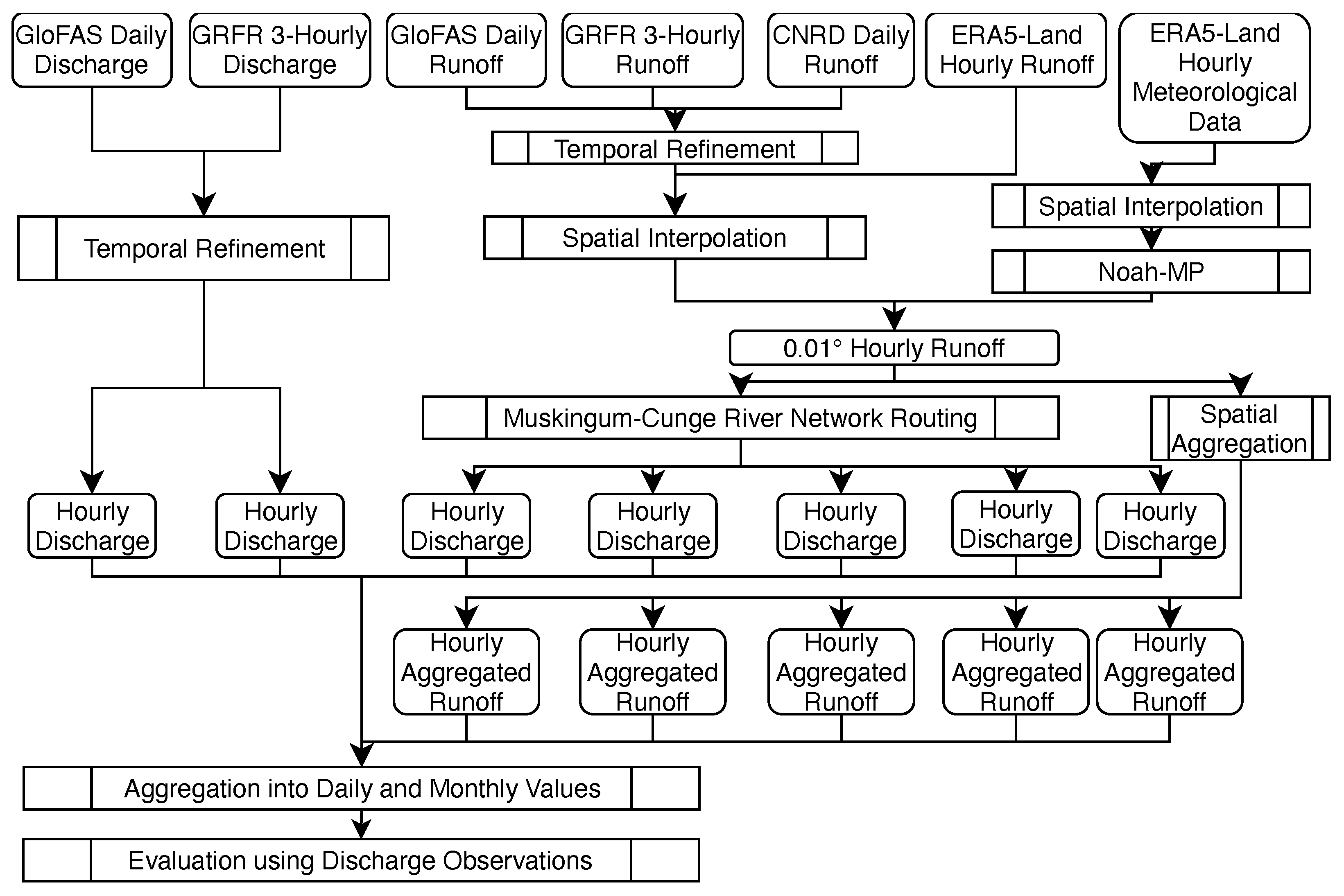
2. Materials and Methods

Figure 1 illustrates the terrain and river network of the upper Jinsha River. The study area encompasses the region upstream of the Benzilan gauging station. The elevation ranges from approximately 6600 m at its highest point to 2000 m at its lowest. The river network was extracted from the Multi-Error-Removed Improved-Terrain Hydrography (MERIT-Hydro) dataset [36,37]. MERIT-Hydro is a globally recognized dataset providing hydrologically conditioned elevation, flow direction, and flow accumulation area data, with a spatial resolution of 3 arcseconds. The river network was extracted using a flow accumulation area threshold of 25 km2, resulting in 5787 river reaches.

2.1. Reanalysis Datasets

Table 1 presents an overview of the datasets employed in this study. ERA5-Land [2] is an enhanced global dataset, an improvement over ERA5 [1]. This dataset features a significant improvement in spatial resolution, increasing from ERA5’s 31 km to 0.1° globally. A variety of land surface variables, including runoff, are simulated using the Carbon Hydrology-Tiled ECMWF Scheme for Surface Exchanges over Land (CHTESSEL) model [38,39], operating at an hourly temporal resolution.
The GloFAS historical reanalysis version 4.0 [3,4] is another dataset produced by the European Centre for Medium-Range Weather Forecasts (ECMWF), with a focus on hydrological variables. GloFAS shares the same spatial resolution of 0.1° as ERA5-Land. It is driven by ERA5 meteorological data, which is highly similar to ERA5-Land. The primary distinctions between GloFAS and ERA5-Land lie in the hydrological model employed, the temporal resolution, and the output variables. GloFAS utilizes the LISFLOOD model [40] at a daily time step. Unlike ERA5-Land, the parameters of LISFLOOD are calibrated against daily river discharge observations using an evolutionary algorithm [41]. LISFLOOD simulates both runoff and river discharge, whereas ERA5-Land provides only runoff estimates.
The GRFR dataset [5] is a comprehensive global dataset providing runoff and river discharge data at a 3-hourly temporal resolution. The runoff is simulated using the Variable Infiltration Capacity (VIC) model [42] at a spatial resolution of 0.05°, which is driven by precipitation data from the Multi-Source Weighted-Ensemble Precipitation (MSWEP) dataset [43] and other meteorological variables from ERA5. The VIC model’s parameters are calibrated [44] at each 0.05° grid cell against a machine learning-derived runoff characteristics dataset produced by Beck et al. [45]. The bias in the VIC-simulated runoff is further corrected using the same runoff characteristics dataset, following the methodology of Lin et al. [6]. The calibrated and bias-corrected runoff data are then utilized to drive the Routing Application for Parallel computatIon of Discharge (RAPID) river routing model [46] for simulating river discharge. The parameters of RAPID are estimated using a statistical relationship that correlates discharge with river width, water depth, channel slope, and celerity [6]. The river network employed in the routing process is also derived from the MERIT Hydro dataset [47].
The China Natural Runoff Dataset (CNRD) [9,10] comprises runoff data at a 0.25° spatial resolution. This dataset is simulated using the VIC model, driven by the China Meteorological Forcing Dataset [48]. The parameters of the VIC model were calibrated against river discharge observations from approximately 200 catchments across China and then extrapolated to ungauged river basins using the multiscale regionalization method [49].
As presented in Table 1, a new dataset was generated in this study for comparative purposes. This dataset was driven by ERA5-Land meteorological data and simulated via a distinct land surface model and river routing model. Given that the new dataset shares a similar meteorological forcing dataset with GloFAS and ERA5-Land, this comparison can effectively isolate the impacts of model selection, spatial resolution, and calibration on runoff and discharge estimations. The model employed in this study emulates the National Water Model (NWM). The Noah with Multi - Parameterization (NoahMP) land surface model [50] was utilized, operating at a spatial resolution of 0.01° from 2008 to 2016. The static parameters for NoahMP are derived from the Weather Research and Forecasting geographic static data (https://www2.mmm.ucar.edu/wrf/users/download/get_sources_wps_geog.html, accessed on 10 November 2024). The initial condition for 2008 is sourced from ERA5-Land. The first year is allocated for model spin-up, with the simulated runoff from 2009 to 2016 used for analysis. NoahMP offers a variety of parameterization schemes for land surface processes, and we adopted the same schemes as those used in the NWM of the United States [7]. The runoff is routed using the variable-parameter Muskingum–Cunge (MC) method on the river network depicted in Figure 1 to estimate river discharge. The routing algorithm mirrors that of the NWM, assuming a trapezoidal channel cross-section. Channel cross-section geometry and roughness parameters are sourced from the default parameter lookup table of the NWM [51] and the Strahler stream order for each river reach within the network. In theory, the MC routing method would outperform the kinematic wave routing method used in GloFAS by also additionally considering diffusive wave dynamics, while the Muskingum routing method used in GRFR would be the least performing among the three. It is important to note that this comparison is theoretical, and actual performance can vary significantly with model implementation and parameter settings.

2.2. River Discharge Observations

We utilized river discharge observations from three gauging stations along the mainstream of the upper Jinsha River: Zhimenda (ZMD), Gangtuo (GT), and Benzilan (BZL), covering the period from 2009 to 2016. Zhimenda serves as the demarcation point between the source region of the Changjiang River and the Upper Jinsha River. All the planned hydroelectric power stations are located on the river segment stretching between Zhimenda and Benzilan. The inclusion of Gangtuo provides additional data coverage along the river’s mainstream. By choosing these stations, the performance of reanalysis datasets in a region of high hydropower potential and complex hydrological processes can be assessed. The selection of this timeframe is justified by the minimal presence of hydroelectric facilities, which ensures that the river discharge data are largely unaffected by human interventions.
The dataset from Zhimenda is compiled at a daily resolution. The dataset comprises 1477 records, with 49% of the days missing between 2009 and 2016. In contrast, Gangtuo and Benzilan provide data at an hourly resolution, aaccumulating 52,246 h and 69,011 h, respectively. The respective missing data rates for these stations are 25% for Gangtuo and 1.6% for Benzilan. Given the nature of our analysis, we have chosen not to impute the missing values, opting instead to focus solely on the complete data records. This choice was made with the aim of maximizing the utilization of available observations in this region where data are scarce. Additionally, by avoiding the use of gap-filling methods, we sought to minimize the potential biases that could be introduced, especially given that the proportion of missing data is substantial.
To our knowledge, the daily river discharge observations at Zhimenda have been used to calibrate GloFAS and GRFR, while the observations at Gangtuo and Benzilan have not been incorporated into the datasets analyzed in this study.

2.3. Evaluation Methods

As shown in Table 1, the datasets vary in spatial and temporal resolution. River discharge estimates are not available in every dataset examined. To address these inconsistencies, we remapped the runoff onto a common 0.01° grid and refined both daily and monthly values to hourly values, as depicted in Figure 2. The spatial remapping was conducted using a first-order conservative method. For temporal refinement, we used the fraction of hourly ERA5-Land runoff to the accumulated runoff within a day or a month to redistribute the daily or monthly values. Subsequently, the runoff from all datasets was routed using the same Muskingum–Cunge (MC) method, as previously described, to estimate river discharge. For GloFAS and GRFR, which provide river discharge estimates, we also refined the 3-hourly or daily values to hourly values using the same refinement method as the runoff.
The river discharge estimates derived from the Muskingum–Cunge method, as well as the temporally refined river discharge data from GRFR and GloFAS, are then compared with the observations at the gauging stations. This evaluation is conducted across three temporal scales—monthly, daily, and hourly—to comprehensively assess the accuracy and consistency of the estimates with the actual observations.
The structure and parameters of the river routing model significantly influence the river discharge estimates. To isolate the impact of river routing on these estimates, we not only compared the model-derived river discharge with observations at gauging stations but also aggregated the runoff above these stations for a more direct comparison. This aggregation helps to isolate the effects of routing by focusing on the input runoff rather than the routing process itself. The aggregated runoff is calculated by summing the runoff within the upstream area of each gauging station. The delineation of the upstream area was based on the flow direction data from the MERIT-Hydro dataset.

2.4. Evaluation Metrics

We employed the Kling–Gupta efficiency (KGE) [52] to assess the performance of the reanalysis datasets. The KGE shares similarities with the commonly used mean squared error (MSE) and Nash–Sutcliffe efficiency (NSE). It incorporates the correlation coefficient, the ratio of the standard deviations, and the ratio of the mean values of both the observed and simulated data. Unlike MSE or NSE, in the KGE, these three components are combined in an independent manner. This enables a straightforward separation of their relative contributions to the overall metric. The KGE is formulated as follows:
KGE = 1 − G 1 2 + G 2 2 + G 3 2 ,
G 1 = r − 1 ,
G 2 = σ s σ o − 1 ,
G 3 = μ s μ o − 1 ,
where r is the correlation coefficient, σ s and σ o are the standard deviations of the simulated and observed data, respectively, and μ s and μ o are the mean values of the simulated and observed data, respectively. The KGE ranges from − ∞ to 1, with a value of 1 indicating a perfect match between the simulated and observed data. A KGE value significantly less than 1 indicates a poor match.
The relative contribution of the three terms in the KGE can be calculated using the following formula [52]:
g i = G i 2 G 1 2 + G 2 2 + G 3 2 , for i = 1 , 2 , 3 ,
where g 1 , g 2 , and g 3 are the relative contributions of correlation coefficient, variability, and bias, respectively. A higher value indicates a greater contribution of the corresponding term to the deviation of the KGE from 1.

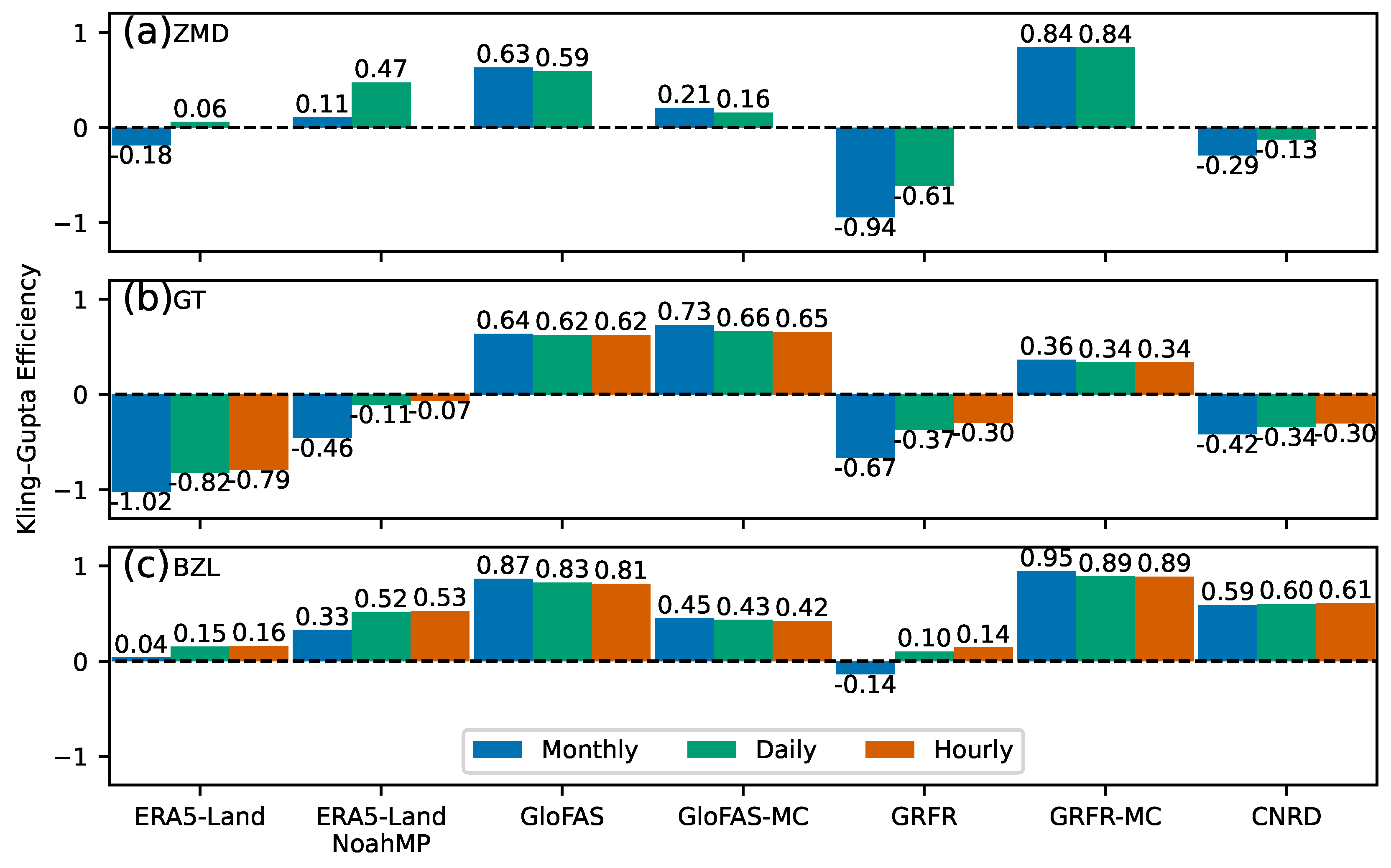
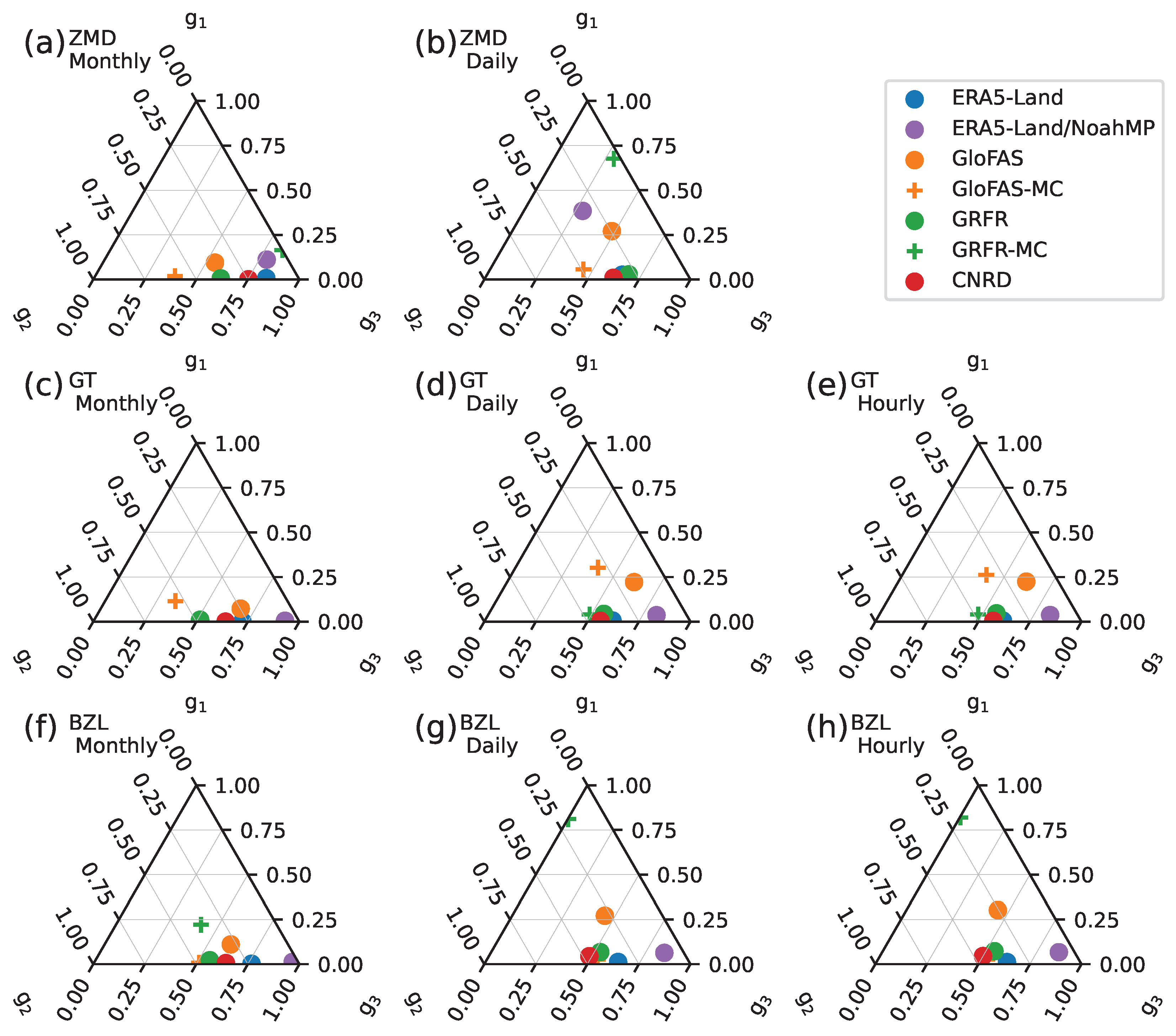
3. Results and Discussion

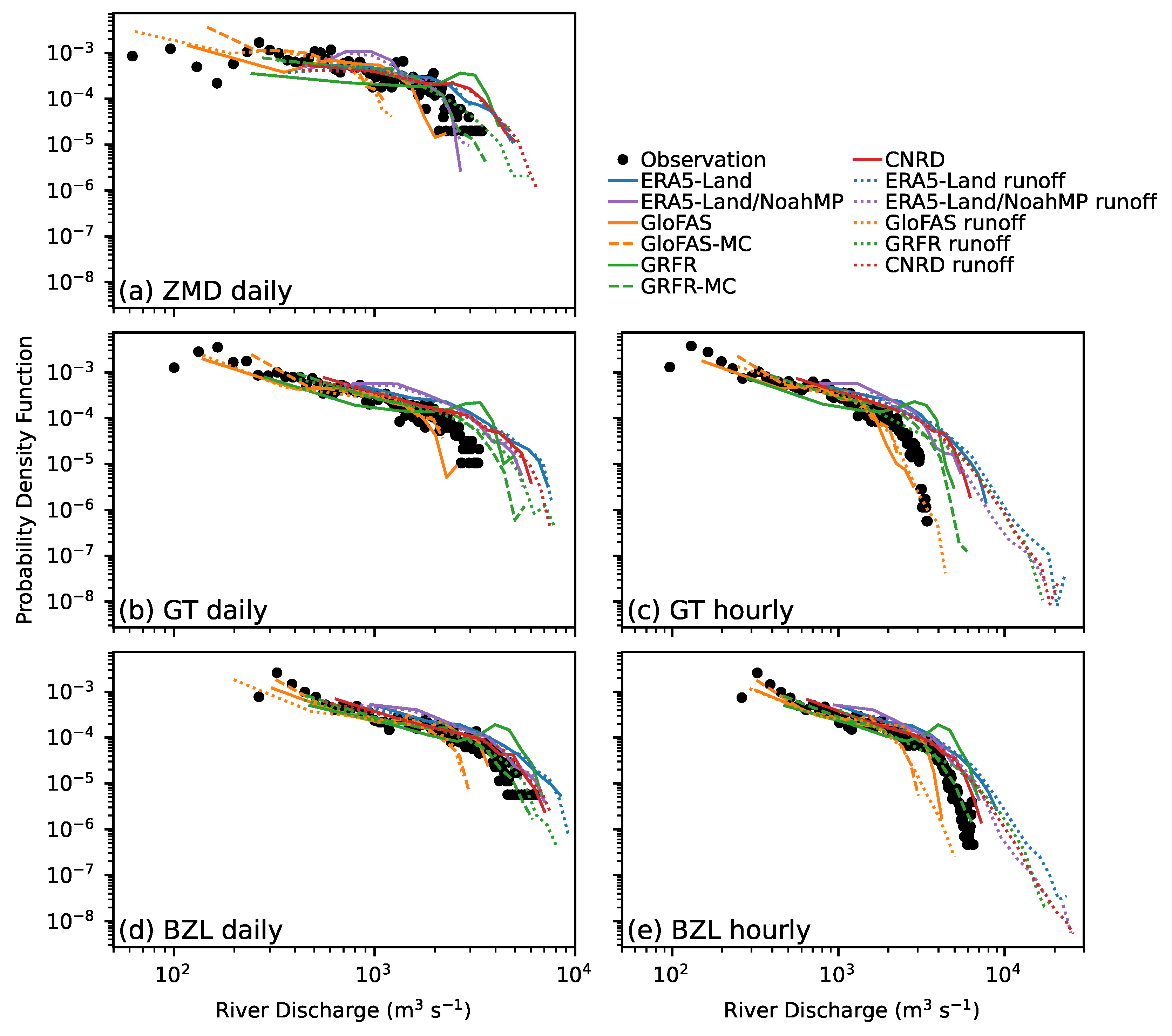
3.1. Runoff

Figure 3 geographically compares the runoff estimates within the Benzilan catchment. The five datasets fall into three categories: ERA5-Land and ERA5-Land/NoahMP; GloFAS and GRFR; and CNRD. The first group utilizes uncalibrated land surface models, the second group employs extensively calibrated hydrological models, and the third group features a hydrological model with parameters that are regionalized rather than individually calibrated. Notably, ERA5-Land, ERA5-Land/NoahMP, and GloFAS exhibit significant differences despite similar meteorological forcing data. On the other hand, GloFAS and GRFR, which are driven by different meteorological forcing data, show close spatial patterns. This comparison indicates that the calibration of land surface models or hydrological models has a profound impact on runoff estimation, more than the meteorological data.
Figure 4 intercompares the monthly variations and annual cycle of the aggregated runoff above Zhimenda, Gangtuo, and Benzilan. Since the river flow travel time is typically smaller than a month [53], it is generally safe to neglect the impact of river routing at the monthly time scale. Both ERA5 and CNRD overestimate the runoff at all examined stations, but the reasons for this overestimation differ. The overestimation in ERA5 is consistent with previous studies, which attribute it to overestimated precipitation in high-altitude regions [54,55,56,57]. In contrast, the overestimation of CNRD is primarily observed in the upstream area of Zhimenda. Given that CMFD, the meteorological data that drive CNRD, has shown closeness to in situ precipitation observations in this region [57], the overestimation of the CNRD runoff is likely due to less constrained hydrological model parameters. CNRD uses parameters calibrated at gauged basins and extrapolates these parameters to ungauged basins using multiscale regionalization functions [9,10]. The scarcity of river discharge gauges on the Tibetan Plateau means that this extrapolation can lead to bias.
The runoff from ERA5-Land/NoahMP exhibits two peaks, particularly in the high-altitude regions above Zhimenda. In contrast, ERA5-Land, which utilizes the same meteorological data, shows an insignificant rise in runoff during spring. The discrepancy between ERA5-Land/NoahMP and ERA5-Land is likely due to differences in the spatial resolution of the land surface model. The higher resolution of ERA5-Land/NoahMP allows for a better capture of the vertical gradient of the land surface temperature. The combination of overestimated precipitation in the ERA5-Land meteorological data and increased snowmelt in low-altitude model grids [21] results in an artificial spring runoff peak not observed in the actual data.
The two calibrated datasets, GloFAS and GRFR, exhibit distinct behaviors. This difference is even evident at Zhimenda, where observations are publicly available through the Global Runoff Data Centre and have been utilized in both datasets. The distinct calibration approaches of the two datasets likely account for this difference. GloFAS is calibrated against river discharge observations [41], while its runoff is not directly calibrated. Since river discharge can be calculated by multiplying the catchment area by runoff, different estimates of the catchment area will lead to different runoff values after the calibration of river discharge. In contrast, GRFR’s runoff is directly calibrated against a machine learning-derived runoff characteristics dataset [44]. The results suggest that the calibration method employed by GRFR is highly effective, yielding the best-performing runoff among the examined datasets.
Figure 5 presents the performance of the aggregated runoff in comparison with discharge observations at the monthly time scale. ERA5-Land consistently underperforms across all stations and time scales, corresponding to the overestimation shown in Figure 4. CNRD also performs poorly in high-altitude areas above Gangtuo due to overestimation, but its performance improves at Benzilan. The performance of CNRD slightly outperforms the high-resolution ERA5-Land/NoahMP. Among the examined datasets, the two calibrated datasets, GloFAS and GRFR, perform the best at almost every station examined, highlighting the importance of calibration for land surface models or hydrological models. Notably, GRFR’s performance is exceptionally good, with a KGE above 0.8 at Zhimenda and Benzilan. GRFR’s high performance underscores the effectiveness of the characteristics-based calibration method. Meanwhile, GRFR shows subpar performance at Gangtuo. This underperformance can be attributed to the underestimation of both the variability and the long-term mean, as detailed in Section 3.2. Since both variability and the long-term mean are the characteristics to which GRFR is calibrated, the poor performance of GRFR at Gangtuo implies that the machine learning-derived runoff characteristics dataset does not accurately represent the runoff characteristics at Gangtuo. This is likely because the terrain at Gangtuo is steep, and the observations from this location were not incorporated into the training dataset.

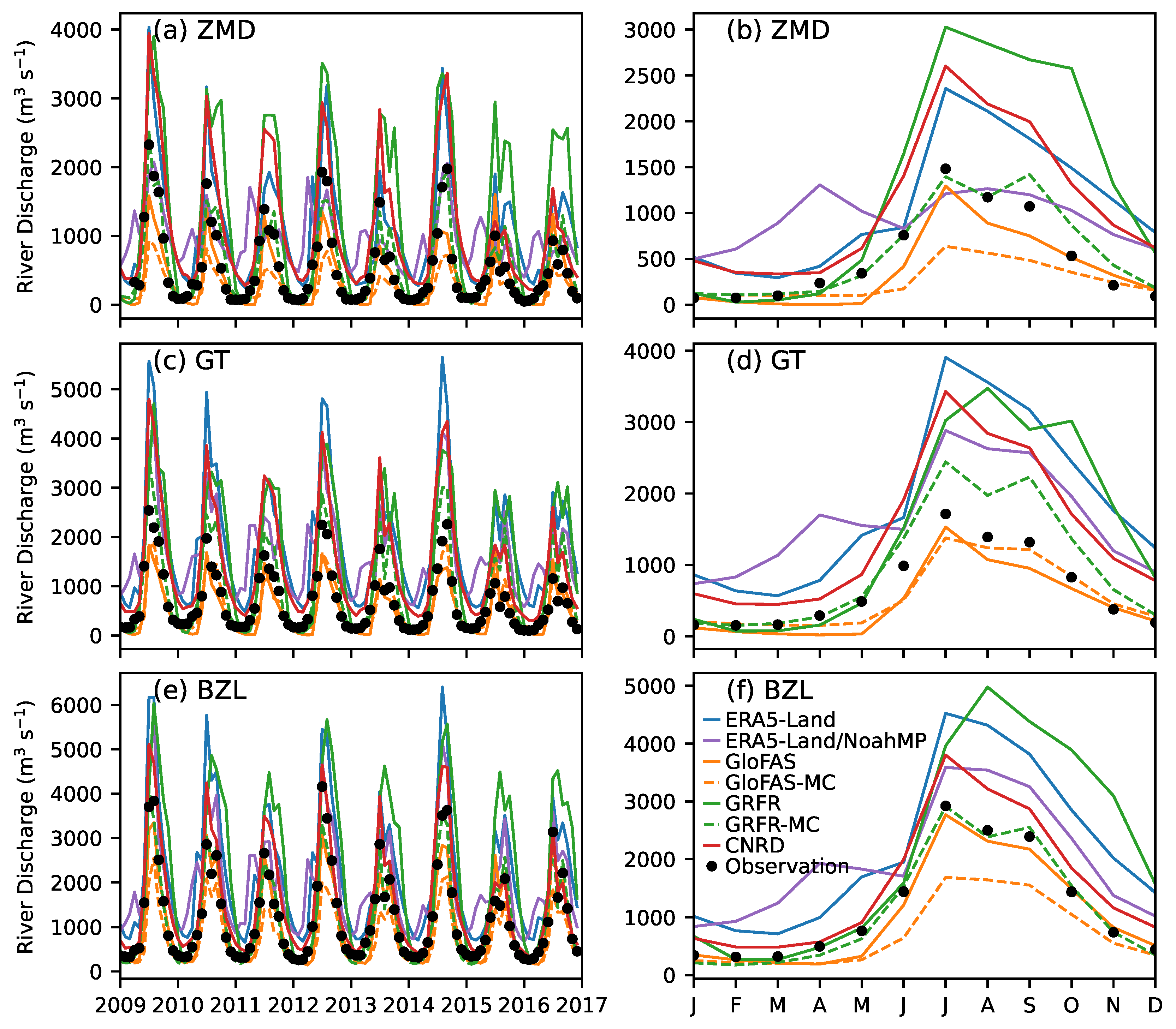
3.2. Streamflow

Figure 6 compares the monthly discharge estimations with observations. The patterns generally follow the runoff pattern shown in Figure 4. The overestimation observed in ERA5-Land and CNRD closely mirrors their runoff overestimation. The artificial spring peak, which is also present in the ERA5-Land/NoahMP discharge, aligns with the runoff pattern.
It is interesting to note that the GloFAS and GRFR discharge behave differently from the runoff. Our rerouted GloFAS runoff (GloFAS-MC in Figure 6) can reproduce the underestimated patterns observed for the runoff (Figure 4), confirming that GloFAS underestimates runoff. However, the underestimation of runoff is no longer presented in the river discharge. GloFAS closely reproduced the observed river discharge (Figure 6). The contradiction between the runoff underestimation and the unbiased discharge estimation suggests that the spatial resolution of GloFAS’s routing grid plays a role. GloFAS is routed on a 1 10 ° grid cell basis, whereas the river basins delineated in this study (as shown in Figure 1) are based on 1 1200 ° grids. The resolution of GloFAS may be too coarse to accurately delineate the river basins. However, this error is mitigated in the discharge due to the calibration, and the impact is transferred to errors in the runoff.
Despite the high skill of GRFR’s runoff demonstrated in Figure 4, the skill of GRFR’s discharge is unexpectedly unsatisfactory. GRFR remarkably overestimates discharge at all gauging stations. The overestimation is also reported in the literature [58,59]. We argue that neither the dynamics nor the parameters of the river routing model should have such significant impacts on monthly discharge, and that the unexpected overestimation in GRFR is likely attributable to some inadequate configurations of the river routing model. Our rerouted discharge (GRFR-MC) using the GRFR runoff and the Muskingum–Cunge routing method can closely reproduce the observed discharge patterns. This confirms that the overestimation in GRFR is not due to the runoff but rather the routing process.
Figure 7 presents the river discharge estimates compared with both daily and hourly observations. The aggregated runoff is also displayed for comparison. The difference between aggregated runoff and river discharge highlights the impact of river routing. The comparison shows that river routing has a marginal impact in low flow conditions and at the monthly time scale. The impact increases with flow rate and on shorter time scales. Significant impacts of river routing are found on the hourly high flow estimations at all gauging stations. This finding suggests the indispensable role of river routing in flood forecasting.
The differences among the examined river discharge estimates are mainly exhibited in high flow conditions. However, these differences do not vary significantly with the time scale of the estimates (i.e., daily or hourly). The GRFR river discharge estimation suspiciously indicates a high probability of discharge at approximately 4000 m 3 s − 1 at all the examined stations, whereas such a high probability is not found in the other estimates including GRFR-MC. This suspicious pattern is another strong indicator of inadequate configurations within GRFR’s routing process. The GloFAS estimate can reproduce the observed discharge probability patterns well. Our rerouted river discharge using the GloFAS runoff and the Muskingum–Cunge method deviates from the observed pattern of discharge probability. The discrepancy arises from the calibration of river discharge, which compensates for imprecise river basin area estimation.
Figure 8 illustrates the skill scores for the estimation of river discharge across monthly, daily, and hourly temporal scales. At the monthly scale, the river discharge estimation’s skill closely mirrors that of the runoff, as depicted in Figure 5. The coincidence hints that the primary determinant of river discharge variability within the study area is the runoff estimation, rather than the river routing process. An exception to this pattern is observed with GloFAS, where the divergence in discharge skill scores from those of runoff is likely due to the coarse and imprecise river routing grid employed, as previously discussed.
Among the examined dataset, GloFAS, GloFAS-MC, and GRFR-MC perform the best at all gauging stations and across all time scales. Proper calibration of the land surface model and the hydrological model is essential for accurate river discharge estimation. As revealed in Figure 9, the primary reasons for the poor performance of the examined datasets, except for GRFR-MC, are errors in reproducing the observed mean and variability of river discharge. GRFR-MC can effectively reproduce the observed mean and variability of river discharge. The KGE of GRFR-MC’s hourly discharge can reach a high score of approximately 0.9 at Benzilan, which again confirms the effectiveness of the characteristics-based calibration method. The relatively lower performance of GRFR at Gangtuo implies that the machine learning-based calibration method employed by GRFR needs to incorporate more local observations to enhance its applicability in specific regions. At all three gauging stations, the deviation of the KGE from 1 for GRFR-MC is mainly attributed to the correlation coefficient, which can be further improved through the calibration of the river routing parameters. The exceptionally high skill of GRFR-MC again confirms the effectiveness of the characteristics-based calibration method.
It is worth noting that the KGE (Figure 8) and the relative contribution within the KGE (Figure 9) are consistent for both hourly and daily estimates. This consistency suggests that calibration at the daily time scale could potentially be applied to the hourly time scale. However, the relative contributions of the correlation coefficient, variability, and bias differ between the monthly, daily, and hourly time scales, as illustrated in Figure 9. At the monthly scale, the datasets under examination mainly exhibit differences in the variability and bias of river discharge estimations. The correlation coefficient plays a relatively minor role, indicating that all the examined datasets are capable of reasonably capturing the timing of the peak discharge, as evidenced by Figure 6. In contrast, at the daily and hourly scales, the correlation coefficient emerges as a crucial factor. This suggests that the examined datasets face challenges in accurately reproducing the observed timing of floods.
The KGE of river discharge is also consistent between daily and monthly estimates for most datasets, with the exception of the high-resolution ERA5-Land/NoahMP estimation (Figure 8). The increase in KGE from the monthly to daily time scale indicates that a more accurate representation of the spatial distribution of runoff and river routing could improve the temporal variations in river discharge estimates, aligning with the concept of the time of concentration [60]. However, these findings are based on a limited number of gauging stations and limited time periods. Further studies are needed to validate these preliminary observations.

4. Conclusions

This study presents a pilot intercomparison of several publicly available large-domain reanalysis datasets of runoff and river discharge in the Upper Jinsha River basin. The datasets under scrutiny include ERA5-Land, GloFAS, GRFR, and CNRD. To enhance the understanding of the effects of calibration, spatial resolution, and meteorological forcing on runoff estimation, a high-resolution runoff simulation has been incorporated into the comparison. The runoff from the examined datasets is rerouted on a high-resolution river network delineated from the 3-arcsecond MERIT-Hydro dataset. This rerouting aids in identifying the impacts of different river routing models and river network delineations on river discharge estimation. The estimated runoff and river discharge are compared with observations at three gauging stations—Zhimenda, Gangtuo, and Benzilan—spanning monthly, daily, and hourly time scales. The principal findings of this study are as follows:
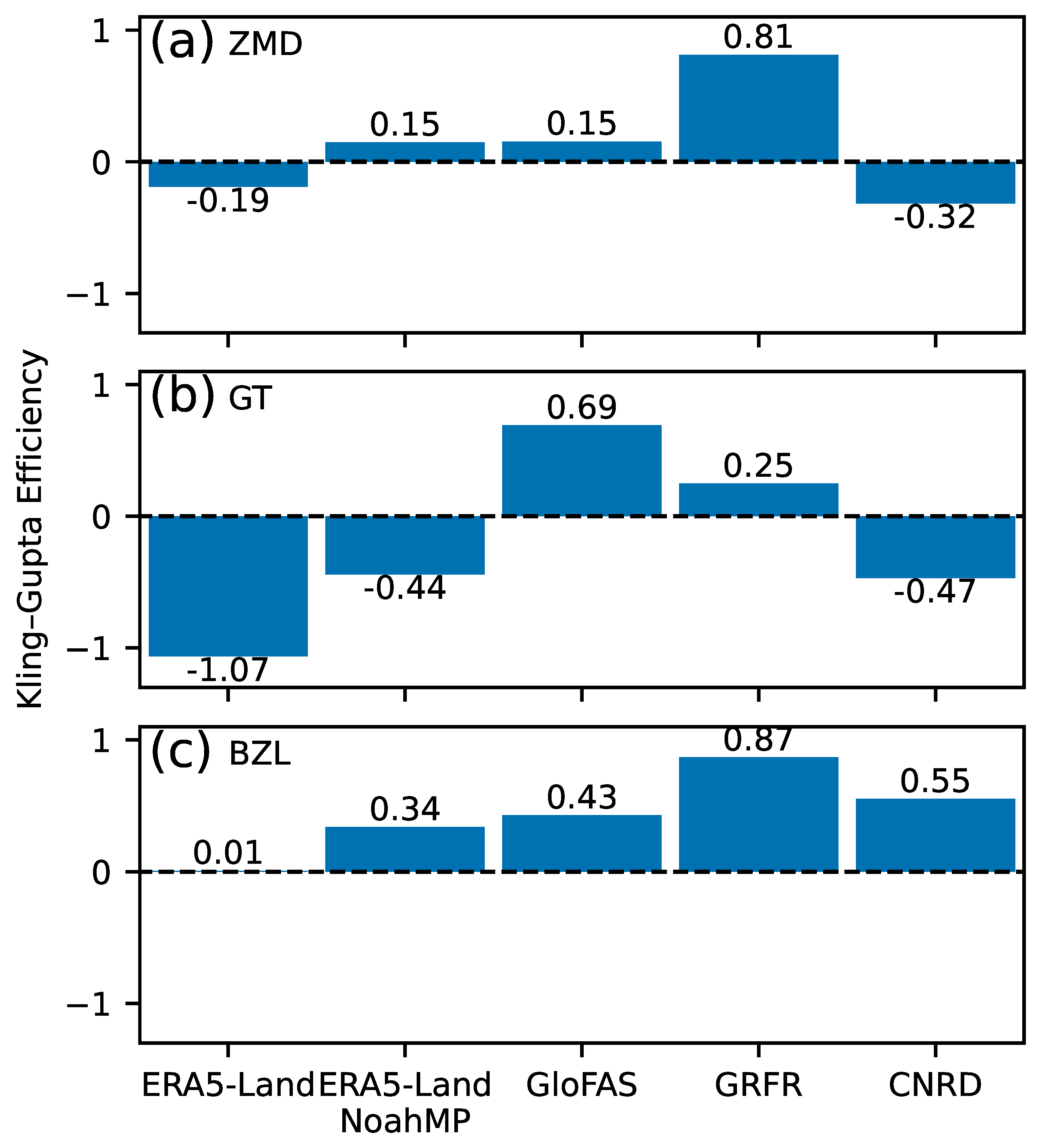
  • Among ERA5-Land, GloFAS, GRFR, and CNRD, GloFAS performs the best in river discharge estimation. The superior performance is attributed to the extensive calibration of model parameters rather than the quality of meteorological forcing. The other datasets, driven by similar meteorological forcing but using uncalibrated models—including ERA5-Land and a high-resolution simulation conducted in this study—did not perform on a par with GloFAS.
  • Despite its high skill in river discharge estimation, GloFAS’s runoff estimation is subpar. This discrepancy is attributable to the coarse resolution of GloFAS’s routing grid. A 0.1° grid cell resolution is insufficient to accurately delineate the catchment area in the study region. Since river discharge is calculated by multiplying runoff by the catchment area, errors in catchment area estimation propagate to runoff estimates during the calibration of river discharge.
  • GRFR demonstrates the best performance in runoff estimation at two out of the three stations examined. The high performance of GRFR runoff is attributed to its runoff characteristics-based calibration method. However, this machine learning-based method is more sensitive to the training dataset used than the traditional method employed by GloFAS. At Gangtuo, the station with steep terrain where observations are not included in the training dataset, GRFR’s performance is subpar.
  • GRFR’s river discharge estimation is unexpectedly poor. GRFR substantially overestimates river discharge, a finding consistent with previous studies. Our study confirms that the overestimation is due to inadequate settings in river routing. By rerouting the discharge using GRFR runoff and the Muskingum–Cunge routing method, we closely reproduce the observed discharge patterns, achieving the best skill among all the examined datasets.
Given the scarcity of in situ observations in the Upper Jinsha River, reanalysis datasets are indispensable for these regions. The findings of this study have implications for both the utilization of existing reanalysis datasets and the future development of new ones. For users of reanalysis datasets, the datasets investigated in this study exhibit notable variances in the estimation of runoff and river discharge. Generally, GloFAS is found to be relatively more reliable for estimating river discharge, while GRFR shows more promise for runoff estimation. For users with prior modeling experience, rerouting the runoff data from GRFR can be beneficial.
For those involved in developing reanalysis datasets, calibrating land surface and hydrological models is a critical step in obtaining accurate runoff and river discharge estimates. The calibration process should be carefully designed to incorporate as many relevant observations as possible within the target region to better capture distinct runoff characteristics, especially for machine learning-based methods. In terms of river routing methods, the vector-based approach demonstrates advantages over the grid-based method. The vector-based method better represents the detailed geometry of the river network and accurately defines the catchment area, both of which are essential for achieving reliable runoff and river discharge estimations.

Author Contributions

Conceptualization, H.Z.; methodology, H.Z.; software, H.Z.; validation, S.C. and H.Y.; formal analysis, S.C. and H.Y.; investigation, S.C. and H.Y.; resources, S.C., H.Y. and H.Z.; data curation, S.C. and H.Y.; writing—original draft preparation, S.C. and H.Y.; writing—review and editing, S.C., H.Y., and H.Z.; visualization, S.C. and H.Y.; supervision, H.Z.; project administration, H.Z.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This study is funded by China Three Gorges Corporation (contract Z5323020043) and the Natural Science Foundation of China (grants 42075165 and 42275178).

Data Availability Statement

The MERIT-Hydro dataset was obtained from https://hydro.iis.u-tokyo.ac.jp/~yamadai/MERIT_Hydro/ (accessed on 10 November 2024). The ERA5-Land dataset was obtained from https://cds.climate.copernicus.eu/datasets/reanalysis-era5-land (accessed on 10 November 2024). The GloFAS v4.0 dataset was obtained from https://ewds.climate.copernicus.eu/datasets/cems-glofas-historical (accessed on 10 November 2024). The GRFR v1.0 dataset was obtained from https://www.reachhydro.org/home/records/grfr (accessed on 10 November 2024). The COMIDs used to extract the river discharge from GRFR are 43037713 for Zhimenda, 43046824 for Gangtuo, and 43066085 for Benzilan, respectively. The CNRD v1.0 dataset was obtained from https://doi.org/10.11888/Atmos.tpdc.272864 (accessed on 10 November 2024). The river discharge observations were obtained from the China Three Gorges Corporation; however, the authors do not have permission to share the data. The delineated river network, the aggregated runoff and simulated river discharge at the gauging stations, along with the scripts for figure generation used throughout this paper, can be found at the GitHub repository https://github.com/hzheng88/paper-2025-upperjsj-streamflow-intercomp (accessed on 3 February 2025).

Acknowledgments

The authors acknowledge the technical support provided by the National Large Scientific Infrastructure “Earth System Numerical Simulation Facility” (https://cstr.cn/31134.02.EL, accessed on 10 November 2024).

Conflicts of Interest

Authors Shuanglong Chen and Heng Yang were employed by the China Three Gorges Corporation. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
  2. Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
  3. Alfieri, L.; Lorini, V.; Hirpa, F.A.; Harrigan, S.; Zsoter, E.; Prudhomme, C.; Salamon, P. A global streamflow reanalysis for 1980–2018. J. Hydrol. X 2020, 6, 100049. [Google Scholar] [CrossRef]
  4. Harrigan, S.; Zsoter, E.; Alfieri, L.; Prudhomme, C.; Salamon, P.; Wetterhall, F.; Barnard, C.; Cloke, H.; Pappenberger, F. GloFAS-ERA5 operational global river discharge reanalysis 1979–present. Earth Syst. Sci. Data 2020, 12, 2043–2060. [Google Scholar] [CrossRef]
  5. Yang, Y.; Pan, M.; Lin, P.; Beck, H.E.; Zeng, Z.; Yamazaki, D.; David, C.H.; Lu, H.; Yang, K.; Hong, Y.; et al. Global reach-level 3-hourly river flood reanalysis (1980–2019). Bull. Am. Meteorol. Soc. 2021, 102, E2086–E2105. [Google Scholar] [CrossRef]
  6. Lin, P.; Pan, M.; Beck, H.E.; Yang, Y.; Yamazaki, D.; Frasson, R.; David, C.H.; Durand, M.; Pavelsky, T.M.; Allen, G.H.; et al. Global reconstruction of naturalized river flows at 2.94 million reaches. Water Resour. Res. 2019, 55, 6499–6516. [Google Scholar] [CrossRef]
  7. Cosgrove, B.; Gochis, D.; Flowers, T.; Dugger, A.; Ogden, F.; Graziano, T.; Clark, E.; Cabell, R.; Casiday, N.; Cui, Z.; et al. NOAA’s National Water Model: Advancing operational hydrology through continental-scale modeling. J. Am. Water Resour. Assoc. 2024, 60, 247–272. [Google Scholar] [CrossRef]
  8. Najafi, H.; Shrestha, P.K.; Rakovec, O.; Apel, H.; Vorogushyn, S.; Kumar, R.; Thober, S.; Merz, B.; Samaniego, L. High-resolution impact-based early warning system for riverine flooding. Nat. Commun. 2024, 15, 3726. [Google Scholar] [CrossRef]
  9. Gou, J.; Miao, C.; Samaniego, L.; Xiao, M.; Wu, J.; Guo, X. CNRD v1.0: A high-quality natural runoff dataset for hydrological and climate studies in china. Bull. Am. Meteorol. Soc. 2021, 102, E929–E947. [Google Scholar] [CrossRef]
  10. Miao, C.; Gou, J.; Fu, B.; Tang, Q.; Duan, Q.; Chen, Z.; Lei, H.; Chen, J.; Guo, J.; Borthwick, A.G.L.; et al. High-quality reconstruction of China’s natural streamflow. Sci. Bull. 2022, 67, 547–556. [Google Scholar] [CrossRef]
  11. Feng, D.; Gleason, C.J.; Lin, P.; Yang, X.; Pan, M.; Ishitsuka, Y. Recent changes to Arctic river discharge. Nat. Commun. 2021, 12, 6917. [Google Scholar] [CrossRef] [PubMed]
  12. Collins, E.L.; David, C.H.; Riggs, R.; Allen, G.H.; Pavelsky, T.M.; Lin, P.; Pan, M.; Yamazaki, D.; Meentemeyer, R.K.; Sanchez, G.M. Global patterns in river water storage dependent on residence time. Nat. Geosci. 2024, 17, 433–439. [Google Scholar] [CrossRef]
  13. Liu, M.; Raymond, P.A.; Lauerwald, R.; Zhang, Q.; Trapp-Müller, G.; Davis, K.L.; Moosdorf, N.; Xiao, C.; Middelburg, J.J.; Bouwman, A.F.; et al. Global riverine land-to-ocean carbon export constrained by observations and multi-model assessment. Nat. Geosci. 2024, 17, 896–904. [Google Scholar] [CrossRef]
  14. Coughlan de Perez, E.; van den Hurk, B.; van Aalst, M.K.; Amuron, I.; Bamanya, D.; Hauser, T.; Jongma, B.; Lopez, A.; Mason, S.; Mendler de Suarez, J.; et al. Action-based flood forecasting for triggering humanitarian action. Hydrol. Earth Syst. Sci. 2016, 20, 3549–3560. [Google Scholar] [CrossRef]
  15. Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
  16. Henn, B.; Newman, A.J.; Livneh, B.; Daly, C.; Lundquist, J.D. An assessment of differences in gridded precipitation datasets in complex terrain. J. Hydrol. 2018, 556, 1205–1219. [Google Scholar] [CrossRef]
  17. Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010, 46, W05521. [Google Scholar] [CrossRef]
  18. Bai, F.; Wei, Z.; Wei, N.; Lu, X.; Yuan, H.; Zhang, S.; Liu, S.; Zhang, Y.; Li, X.; Dai, Y. Global assessment of atmospheric forcing uncertainties in the Common Land Model 2024 simulations. J. Geophys. Res. Atmos. 2024, 129, e2024JD041520. [Google Scholar] [CrossRef]
  19. Butts, M.B.; Payne, J.T.; Kristensen, M.; Madsen, H. An evaluation of the impact of model structure on hydrological modelling uncertainty for streamflow simulation. J. Hydrol. 2004, 298, 242–266. [Google Scholar] [CrossRef]
  20. Haddeland, I.; Matheussen, B.V.; Lettenmaier, D.P. Influence of spatial resolution on simulated streamflow in a macroscale hydrologic model. Water Resour. Res. 2002, 38, 29-1–29-10. [Google Scholar] [CrossRef]
  21. Barnhart, T.B.; Putman, A.L.; Heldmyer, A.J.; Rey, D.M.; Hammond, J.C.; Driscoll, J.M.; Sexstone, G.A. Evaluating distributed snow model resolution and meteorology parameterizations against streamflow observations: Finer is not always better. Water Resour. Res. 2024, 60, e2023WR035982. [Google Scholar] [CrossRef]
  22. Li, L.; Bisht, G.; Leung, L.R. Spatial heterogeneity effects on land surface modeling of water and energy partitioning. Geosci. Model Dev. 2022, 15, 5489–5510. [Google Scholar] [CrossRef]
  23. Zheng, H.; Yang, Z.L.; Lin, P.; Wei, J.; Wu, W.Y.; Li, L.; Zhao, L.; Wang, S. On the sensitivity of the precipitation partitioning into evapotranspiration and runoff in land surface parameterizations. Water Resour. Res. 2019, 55, 95–111. [Google Scholar] [CrossRef]
  24. Zheng, H.; Fei, W.; Yang, Z.L.; Wei, J.; Zhao, L.; Li, L.; Wang, S. An ensemble of 48 physically perturbed model estimates of the 1/8° terrestrial water budget over the conterminous United States, 1980–2015. Earth Syst. Sci. Data 2023, 15, 2755–2780. [Google Scholar] [CrossRef]
  25. Li, J.; Chen, F.; Lu, X.; Gong, W.; Zhang, G.; Gan, Y. Quantifying contributions of uncertainties in physical parameterization schemes and model parameters to overall errors in noah-mp dynamic vegetation modeling. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001914. [Google Scholar] [CrossRef]
  26. Saxe, S.; Farmer, W.; Driscoll, J.; Hogue, T.S. Implications of model selection: A comparison of publicly available, conterminous US-extent hydrologic component estimates. Hydrol. Earth Syst. Sci. 2021, 25, 1529–1568. [Google Scholar] [CrossRef]
  27. Beck, H.E.; van Dijk, A.I.J.M.; de Roo, A.; Dutra, E.; Fink, G.; Orth, R.; Schellekens, J. Global evaluation of runoff from 10 state-of-the-art hydrological models. Hydrol. Earth Syst. Sci. 2017, 21, 2881–2903. [Google Scholar] [CrossRef]
  28. Fry, L.M.; Gronewold, A.D.; Fortin, V.; Buan, S.; Clites, A.H.; Luukkonen, C.; Holtschlag, D.; Diamond, L.; Hunter, T.; Seglenieks, F.; et al. The Great Lakes Runoff Intercomparison Project Phase 1: Lake Michigan (GRIP-M). J. Hydrol. 2014, 519, 3448–3465. [Google Scholar] [CrossRef]
  29. Mai, J.; Shen, H.; Tolson, B.A.; Gaborit, E.; Arsenault, R.; Craig, J.R.; Fortin, V.; Fry, L.M.; Gauch, M.; Klotz, D.; et al. The Great Lakes Runoff Intercomparison Project Phase 4: The Great Lakes (GRIP-GL). Hydrol. Earth Syst. Sci. 2022, 26, 3537–3572. [Google Scholar] [CrossRef]
  30. Ahmed, M.I.; Stadnyk, T.; Pietroniro, A.; Awoye, H.; Bajracharya, A.; Mai, J.; Tolson, B.A.; Shen, H.; Craig, J.R.; Gervais, M.; et al. Learning from hydrological models’ challenges: A case study from the Nelson basin model intercomparison project. J. Hydrol. 2023, 623, 129820. [Google Scholar] [CrossRef]
  31. Henderson-Sellers, A.; Yang, Z.L.; Dickinson, R.E. The Project for Intercomparison of Land-surface Parameterization Schemes. Bull. Am. Meteorol. Soc. 1993, 74, 1335–1349. [Google Scholar] [CrossRef]
  32. van den Hurk, B.; Kim, H.; Krinner, G.; Seneviratne, S.I.; Derksen, C.; Oki, T.; Douville, H.; Colin, J.; Ducharne, A.; Cheruy, F.; et al. LS3MIP (v1.0) contribution to CMIP6: The Land Surface, Snow and Soil moisture Model Intercomparison Project – aims, setup and expected outcome. Geosci. Model Dev. 2016, 9, 2809–2832. [Google Scholar] [CrossRef]
  33. Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.J.; DMIP Participants. Overall Distributed Model Intercomparison Project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
  34. Smith, M.B.; Seo, D.J.; Koren, V.I.; Reed, S.M.; Zhang, Z.; Duan, Q.; Moreda, F.; Cong, S. The Distributed Model Intercomparison Project (DMIP): Motivation and experiment design. J. Hydrol. 2004, 298, 4–26. [Google Scholar] [CrossRef]
  35. Tijerina, D.; Condon, L.; FitzGerald, K.; Dugger, A.; O’Neill, M.M.; Sampson, K.; Gochis, D.; Maxwell, R. Continental hydrologic intercomparison project, phase 1: A large-scale hydrologic model comparison over the continental united states. Water Resour. Res. 2021, 57, e2020WR028931. [Google Scholar] [CrossRef]
  36. Yamazaki, D.; Ikeshima, D.; Sosa, J.; Bates, P.D.; Allen, G.H.; Pavelsky, T.M. MERIT Hydro: A high-resolution global hydrography map based on latest topography dataset. Water Resour. Res. 2019, 55, 5053–5073. [Google Scholar] [CrossRef]
  37. Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
  38. Boussetta, S.; Balsamo, G.; Arduini, G.; Dutra, E.; McNorton, J.; Choulga, M.; Agustí-Panareda, A.; Beljaars, A.; Wedi, N.; Munõz-Sabater, J.; et al. ECLand: The ECMWF land surface modelling system. Atmosphere 2021, 12, 723. [Google Scholar] [CrossRef]
  39. Balsamo, G.; Beljaars, A.; Scipal, K.; Viterbo, P.; van den Hurk, B.; Hirschi, M.; Betts, A.K. A revised hydrology for the ECMWF model: Verification from field site to terrestrial water storage and impact in the Integrated Forecast System. J. Hydrometeorol. 2009, 10, 623–643. [Google Scholar] [CrossRef]
  40. Knijff, J.M.V.D.; Younis, J.; Roo, A.P.J.D. LISFLOOD: A GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci. 2010, 24, 189–212. [Google Scholar] [CrossRef]
  41. Hirpa, F.A.; Salamon, P.; Beck, H.E.; Lorini, V.; Alfieri, L.; Zsoter, E.; Dadson, S.J. Calibration of the Global Flood Awareness System (GloFAS) using daily streamflow data. J. Hydrol. 2018, 566, 595–606. [Google Scholar] [CrossRef] [PubMed]
  42. Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
  43. Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; van Dijk, A.I.J.M.; McVicar, T.R.; Adler, R.F. MSWEP V2 global 3-hourly 0.1° precipitation: Methodology and quantitative assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef]
  44. Yang, Y.; Pan, M.; Beck, H.E.; Fisher, C.K.; Beighley, R.E.; Kao, S.C.; Hong, Y.; Wood, E.F. In quest of calibration density and consistency in hydrologic modeling: Distributed parameter calibration against streamflow characteristics. Water Resour. Res. 2019, 55, 7784–7803. [Google Scholar] [CrossRef]
  45. Beck, H.E.; de Roo, A.; van Dijk, A.I.J.M. Global maps of streamflow characteristics based on observations from several thousand catchments. J. Hydrometeorol. 2015, 16, 1478–1501. [Google Scholar] [CrossRef]
  46. David, C.H.; Maidment, D.R.; Niu, G.Y.; Yang, Z.L.; Habets, F.; Eijkhout, V. River network routing on the NHDPlus dataset. J. Hydrometeorol. 2011, 12, 913–934. [Google Scholar] [CrossRef]
  47. Lin, P.; Pan, M.; Wood, E.F.; Yamazaki, D.; Allen, G.H. A new vector-based global river network dataset accounting for variable drainage density. Sci. Data 2021, 8, 28. [Google Scholar] [CrossRef]
  48. He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef]
  49. Samaniego, L.; Bárdossy, A.; Kumar, R. Streamflow prediction in ungauged catchments using copula-based dissimilarity measures. Water Resour. Res. 2010, 46, W02506. [Google Scholar] [CrossRef]
  50. Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef]
  51. Read, L.K.; Yates, D.N.; McCreight, J.M.; Rafieeinasab, A.; Sampson, K.; Gochis, D.J. Development and evaluation of the channel routing model and parameters within the National Water Model. JAWRA J. Am. Water Resour. Assoc. 2023, 59, 1051–1066. [Google Scholar] [CrossRef]
  52. Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
  53. Allen, G.H.; David, C.H.; Andreadis, K.M.; Hossain, F.; Famiglietti, J.S. Global estimates of river flow wave travel times and implications for low-latency satellite data. Geophys. Res. Lett. 2018, 45, 7551–7560. [Google Scholar] [CrossRef]
  54. Bian, Q.; Xu, Z.; Zhao, L.; Zhang, Y.F.; Zheng, H.; Shi, C.; Zhang, S.; Xie, C.; Yang, Z.L. Evaluation and intercomparison of multiple snow water equivalent products over the Tibetan Plateau. J. Hydrometeorol. 2019, 20, 2043–2055. [Google Scholar] [CrossRef]
  55. Bian, Q.; Xu, Z.; Zheng, H.; Li, K.; Liang, J.; Fei, W.; Shi, C.; Zhang, S.; Yang, Z.L. Multiscale changes in snow over the Tibetan Plateau during 1980–2018 represented by reanalysis data sets and satellite observations. J. Geophys. Res. Atmos. 2020, 125, e2019JD031914. [Google Scholar] [CrossRef]
  56. Sun, H.; Su, F.; Yao, T.; He, Z.; Tang, G.; Huang, J.; Zheng, B.; Meng, F.; Ou, T.; Chen, D. General overestimation of ERA5 precipitation in flow simulations for High Mountain Asia basins. Environ. Res. Commun. 2021, 3, 121003. [Google Scholar] [CrossRef]
  57. Wang, X.; Zhou, J.; Ma, J.; Luo, P.; Fu, X.; Feng, X.; Zhang, X.; Jia, Z.; Wang, X.; Huang, X. Evaluation and comparison of reanalysis data for runoff simulation in the data-scarce watersheds of alpine regions. Remote Sens. 2024, 16, 751. [Google Scholar] [CrossRef]
  58. Tu, T.; Wang, J.; Zhao, G.; Zhao, T.; Dong, X. Scaling from global to regional river flow with global hydrological models: Choice matters. J. Hydrol. 2024, 633, 130960. [Google Scholar] [CrossRef]
  59. Cui, H.; Huang, C. Accuracy evaluation of multiple runoff products: A case study of the middle reaches of the Yellow River. Water 2025, 17, 461. [Google Scholar] [CrossRef]
  60. Beven, K.J. A history of the concept of time of concentration. Hydrol. Earth Syst. Sci. 2020, 24, 2655–2670. [Google Scholar] [CrossRef]
Water 17 00871 g001
Figure 1. Study domain and river network of the source region of the upper Jinsha River. White crosses mark the gauging stations: ZMD, Zhimenda; GT, Gangtuo; BZL, Benzilan.
Figure 1. Study domain and river network of the source region of the upper Jinsha River. White crosses mark the gauging stations: ZMD, Zhimenda; GT, Gangtuo; BZL, Benzilan.
Water 17 00871 g001
Water 17 00871 g002
Figure 2. Workflow of this study.
Figure 2. Workflow of this study.
Water 17 00871 g002
Water 17 00871 g003
Figure 3. Intercomparison of the spatial distribution of multiyear averaged runoff from 2009 to 2016. White crosses denote the gauging stations.
Figure 3. Intercomparison of the spatial distribution of multiyear averaged runoff from 2009 to 2016. White crosses denote the gauging stations.
Water 17 00871 g003
Water 17 00871 g004
Figure 4. Intercomparison of the aggregated runoff at the gauging stations: (a) monthly aggregated runoff at Zhimenda; (b) annual cycle of the aggregated runoff at Zhimenda; (c) monthly aggregated runoff at Gangtuo; (d) annual cycle of the aggregated runoff at Gangtuo; (e) monthly aggregated runoff at Benzilan; and (f) annual cycle of the aggregated runoff at Benzilan.
Figure 4. Intercomparison of the aggregated runoff at the gauging stations: (a) monthly aggregated runoff at Zhimenda; (b) annual cycle of the aggregated runoff at Zhimenda; (c) monthly aggregated runoff at Gangtuo; (d) annual cycle of the aggregated runoff at Gangtuo; (e) monthly aggregated runoff at Benzilan; and (f) annual cycle of the aggregated runoff at Benzilan.
Water 17 00871 g004
Water 17 00871 g005
Figure 5. Kling–Gupta efficiency of the monthly aggregated runoff: (a) the measures at Zhimenda; (b) the measures at Gangtuo; and (c) the measures at Benzilan.
Figure 5. Kling–Gupta efficiency of the monthly aggregated runoff: (a) the measures at Zhimenda; (b) the measures at Gangtuo; and (c) the measures at Benzilan.
Water 17 00871 g005
Water 17 00871 g006
Figure 6. Same as Figure 4, but for river discharge.
Figure 6. Same as Figure 4, but for river discharge.
Water 17 00871 g006
Water 17 00871 g007
Figure 7. Intercomparison of the probability distribution of river discharge and aggregated runoff at the river gauging stations: (a) daily estimates at Zhimenda; (b) daily estimates at Gangtuo; (c) hourly estimates at Gangtuo; (d) daily estimates at Benzilan; and (e) hourly estimates at Benzilan. Dotted lines denote the aggregated runoff. Solid lines denote the river discharge estimates provided by the examined datasets. Dashed lines denote the river discharge estimates using the runoff and the Muskingum–Cunge routing method. Zhimenda is not shown in the hourly estimates due to the lack of hourly observations.
Figure 7. Intercomparison of the probability distribution of river discharge and aggregated runoff at the river gauging stations: (a) daily estimates at Zhimenda; (b) daily estimates at Gangtuo; (c) hourly estimates at Gangtuo; (d) daily estimates at Benzilan; and (e) hourly estimates at Benzilan. Dotted lines denote the aggregated runoff. Solid lines denote the river discharge estimates provided by the examined datasets. Dashed lines denote the river discharge estimates using the runoff and the Muskingum–Cunge routing method. Zhimenda is not shown in the hourly estimates due to the lack of hourly observations.
Water 17 00871 g007
Water 17 00871 g008
Figure 8. Kling–Gupta efficiency of the river discharge estimation: (a) the measures at the Zhimenda station; (b) the measures at the Gangtuo station; and (c) the measures at the Benzilan station.
Figure 8. Kling–Gupta efficiency of the river discharge estimation: (a) the measures at the Zhimenda station; (b) the measures at the Gangtuo station; and (c) the measures at the Benzilan station.
Water 17 00871 g008
Water 17 00871 g009
Figure 9. Ternary plot showing the relative contribution of the correlation coefficient ( g 1 ), variability ( g 2 ), and bias ( g 3 ) to the deviation of the Kling–Gupta efficiency of simulated river discharge from one. The three rows of the plot represent the estimation at Zhimenda, Gangtuo, and Benzilan, respectively. The three columns of the plot represent the results of the monthly, daily, and hourly estimates, respectively.
Figure 9. Ternary plot showing the relative contribution of the correlation coefficient ( g 1 ), variability ( g 2 ), and bias ( g 3 ) to the deviation of the Kling–Gupta efficiency of simulated river discharge from one. The three rows of the plot represent the estimation at Zhimenda, Gangtuo, and Benzilan, respectively. The three columns of the plot represent the results of the monthly, daily, and hourly estimates, respectively.
Water 17 00871 g009
Table 1. The datasets used in this study.
Table 1. The datasets used in this study.
DatasetTime PeriodTemporal ResolutionRunoff ResolutionRiver RoutingReferences
Publically available datasets
ERA5-Land1950–PresentHourly0.10°N/AMuñoz-Sabater et al. [2]
GloFAS v4.01979–PresentDaily0.10°LISFLOODHarrigan et al. [4]
GRFR v1.01980–20193-hourly0.05°RAPIDYang et al. [5]
CNRD v1.01961–2018Monthly0.25°N/AMiao et al. [10]
Datasets produced in this study
ERA5-Land/NoahMP2009–2016Hourly0.01°MCThis study
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chen, S.; Yang, H.; Zheng, H. Intercomparison of Runoff and River Discharge Reanalysis Datasets at the Upper Jinsha River, an Alpine River on the Eastern Edge of the Tibetan Plateau. Water 2025, 17, 871. https://doi.org/10.3390/w17060871

AMA Style

Chen S, Yang H, Zheng H. Intercomparison of Runoff and River Discharge Reanalysis Datasets at the Upper Jinsha River, an Alpine River on the Eastern Edge of the Tibetan Plateau. Water. 2025; 17(6):871. https://doi.org/10.3390/w17060871

Chicago/Turabian Style

Chen, Shuanglong, Heng Yang, and Hui Zheng. 2025. "Intercomparison of Runoff and River Discharge Reanalysis Datasets at the Upper Jinsha River, an Alpine River on the Eastern Edge of the Tibetan Plateau" Water 17, no. 6: 871. https://doi.org/10.3390/w17060871

APA Style

Chen, S., Yang, H., & Zheng, H. (2025). Intercomparison of Runoff and River Discharge Reanalysis Datasets at the Upper Jinsha River, an Alpine River on the Eastern Edge of the Tibetan Plateau. Water, 17(6), 871. https://doi.org/10.3390/w17060871

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop