Study on the Influence of Relative Chord Length and Frequency of Flapping Hydrofoil Device on Hydrodynamic Performance and Bank Slope Scour
Abstract
:1. Introduction
2. Physical Methods
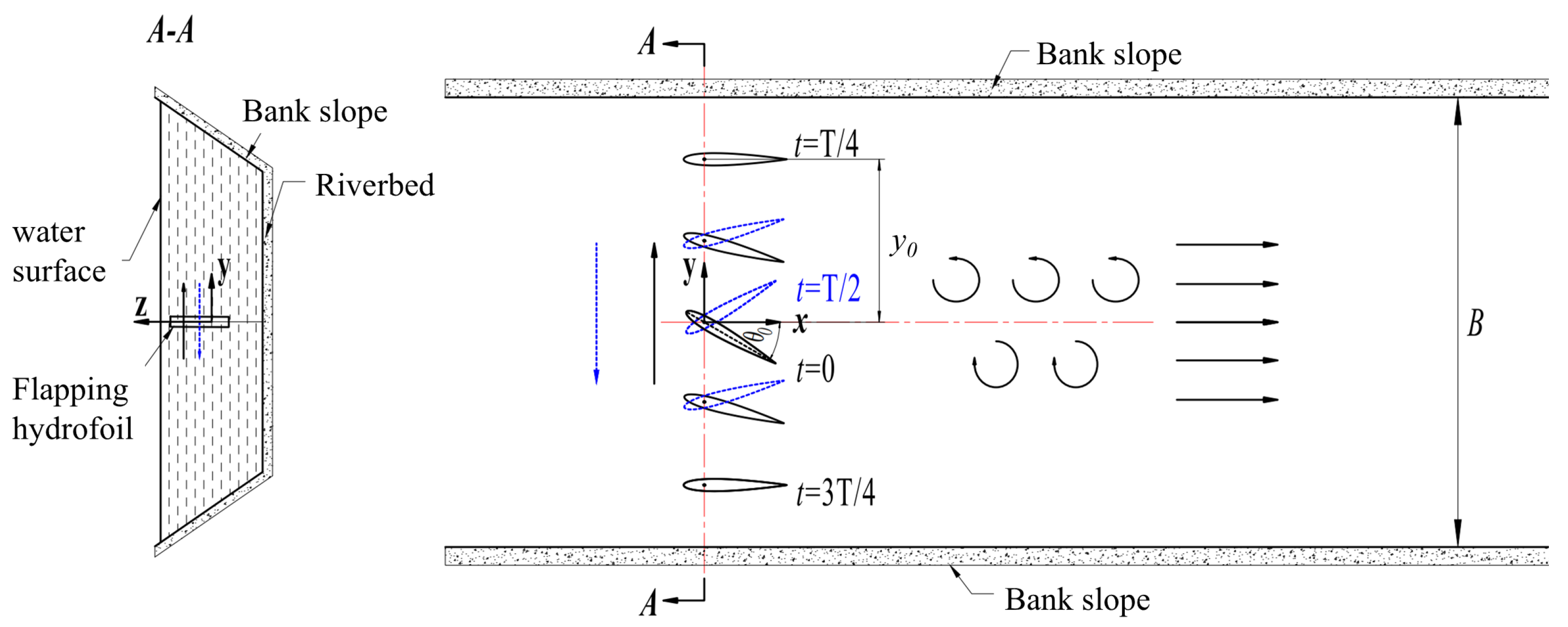
2.1. Modeling and Kinematic Parameters of Flapping Hydrofoils
2.2. Modeling of Bank Slope Scour
3. Numerical Method and Validation
3.1. Control Equations and Turbulence Modeling
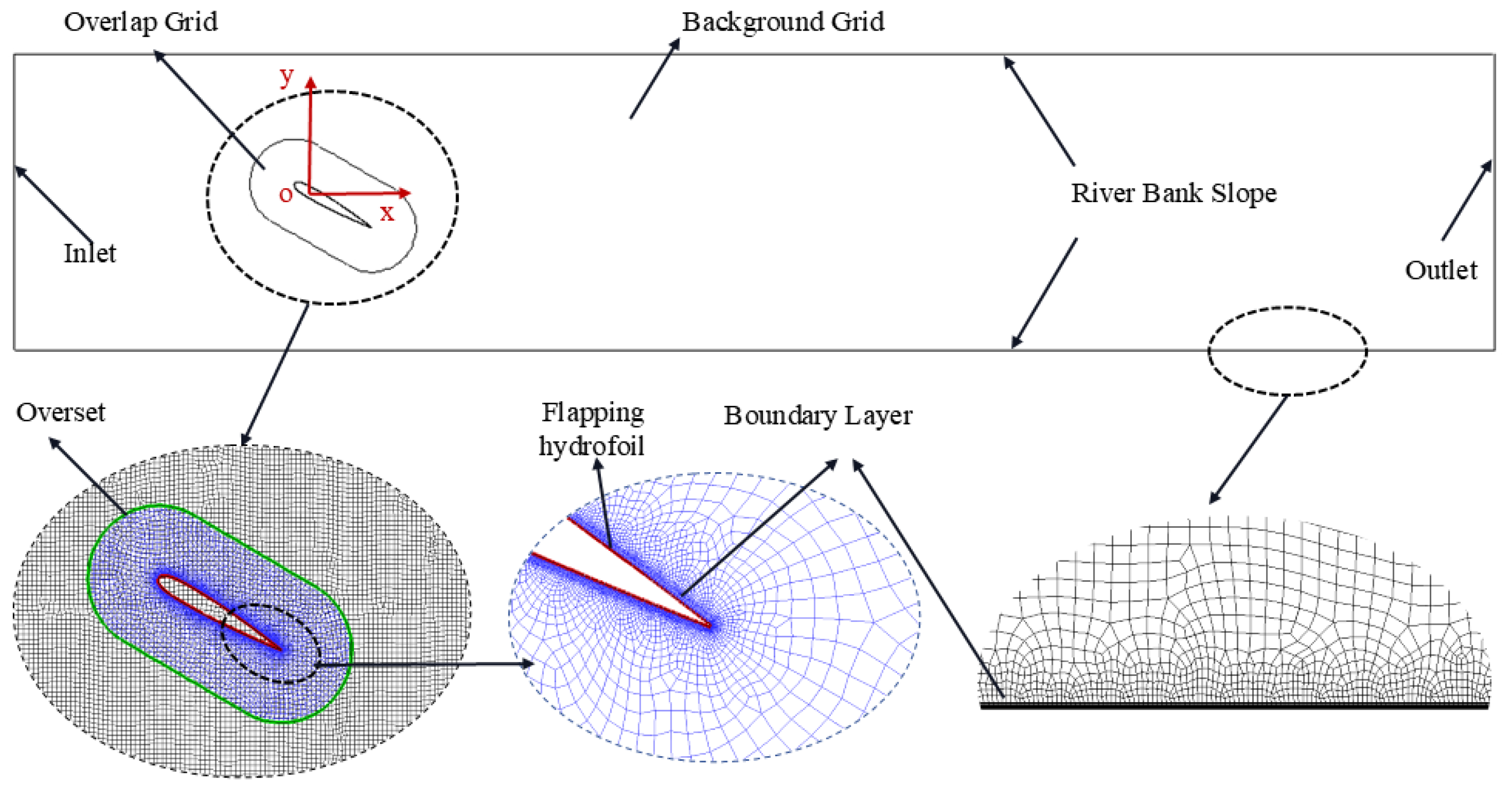
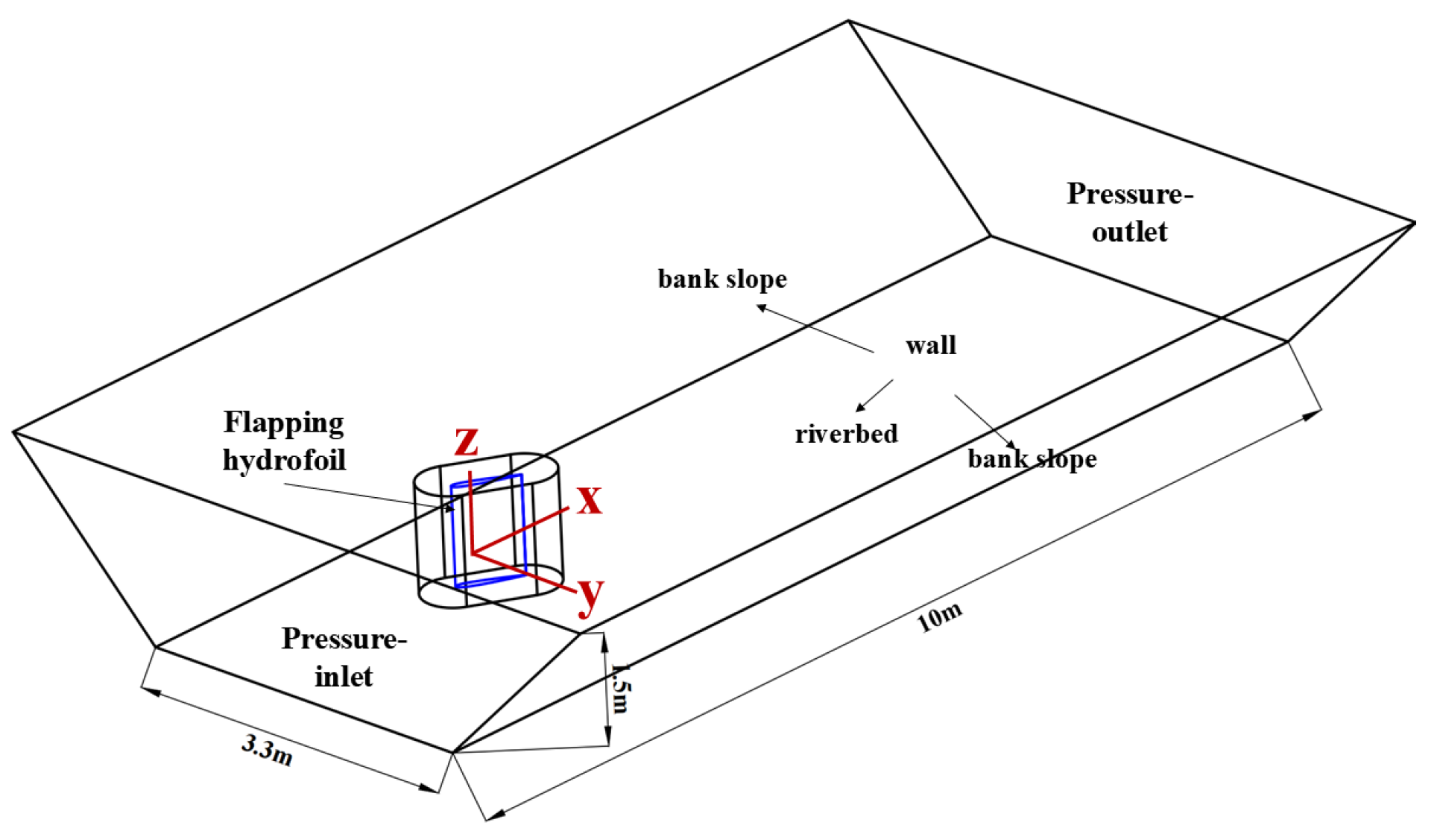
3.2. Computational Domain and Meshing
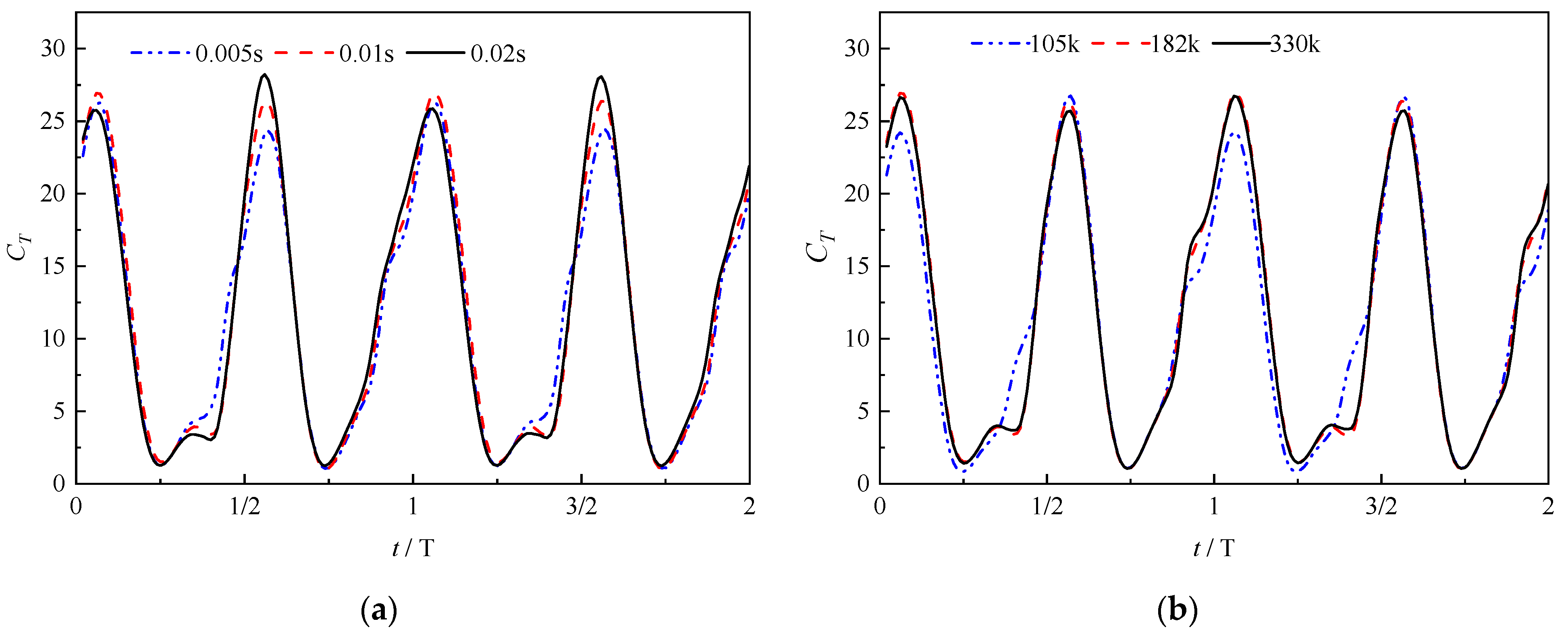
3.3. Numerical Method Validation
4. Determination of Maximum Scour Section
5. Results and Discussion
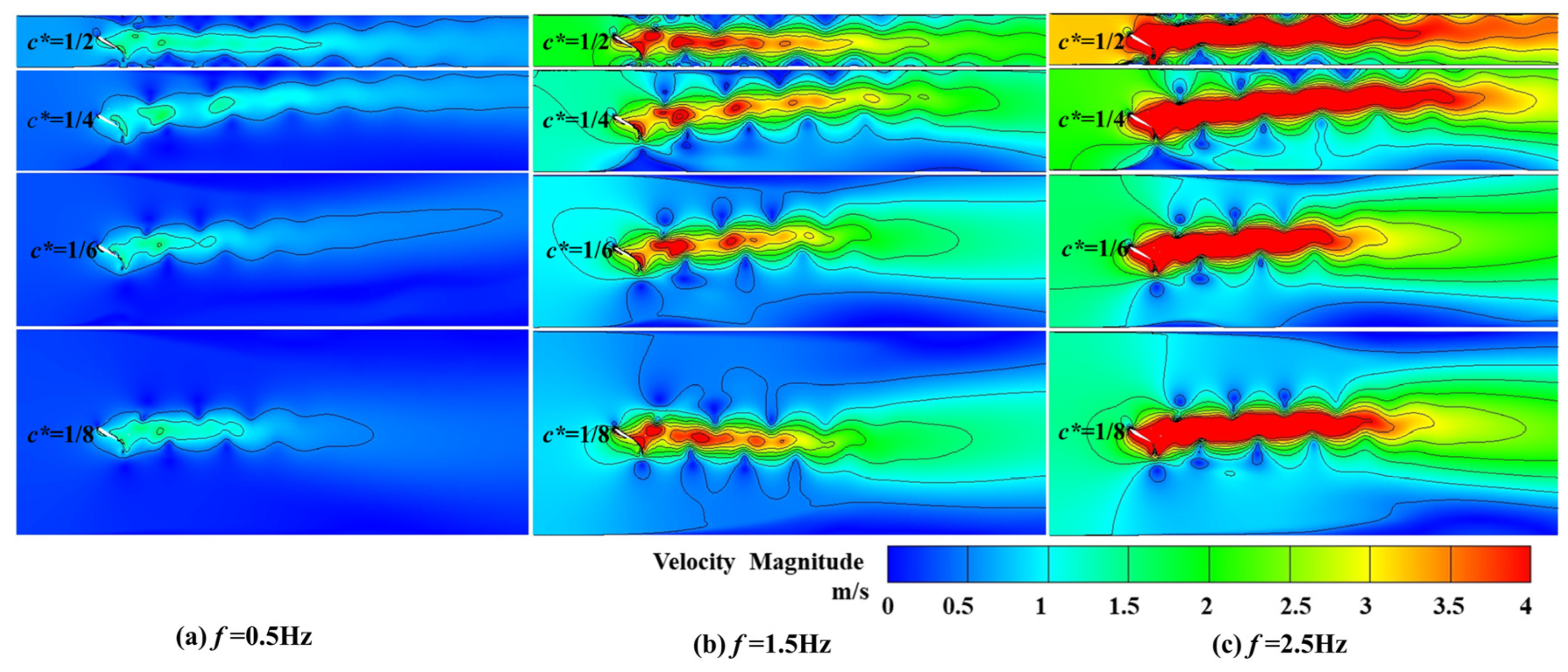
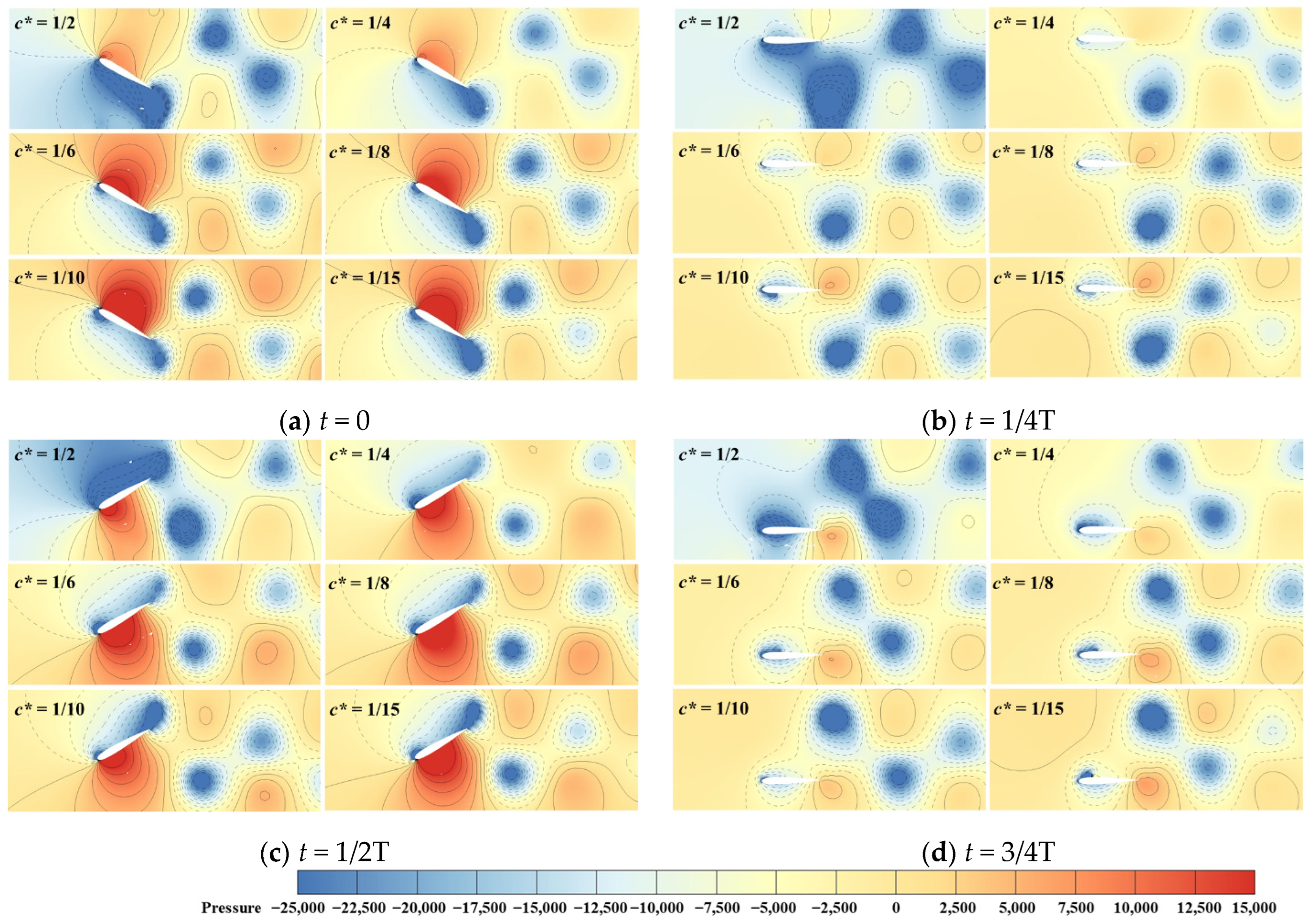
5.1. Effects of Relative Chord Length and Motion Frequency on Bank Slope Scour
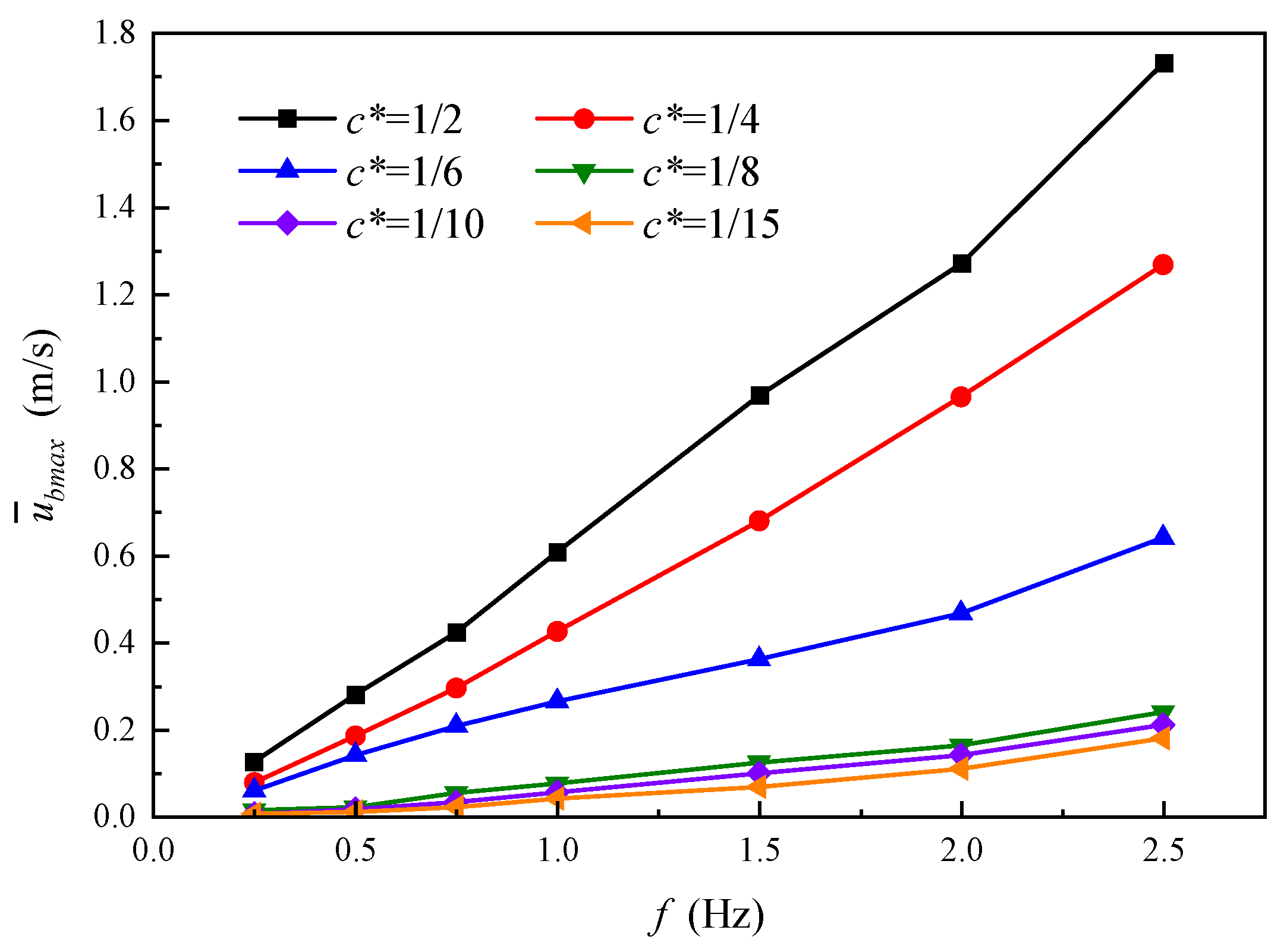
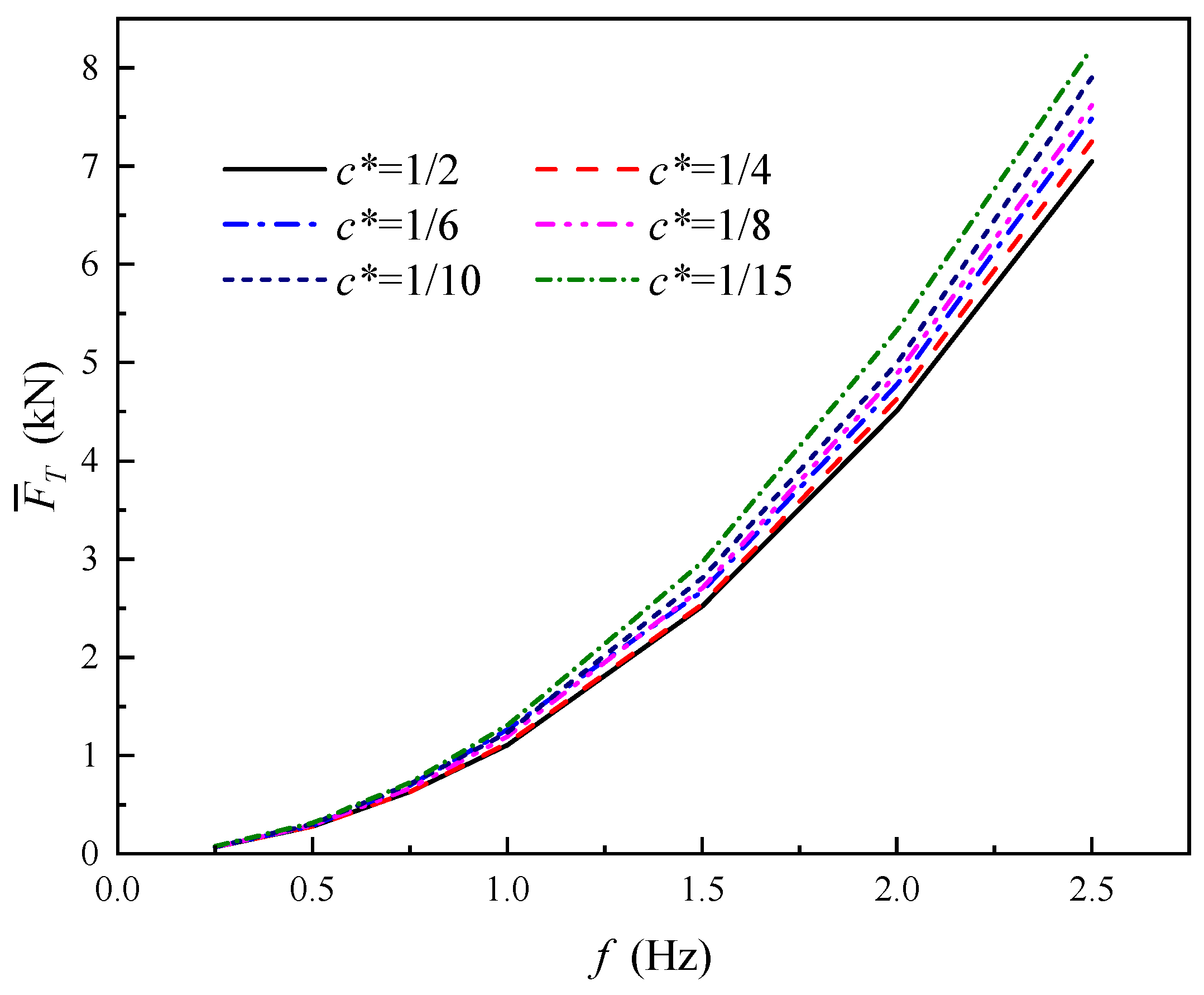
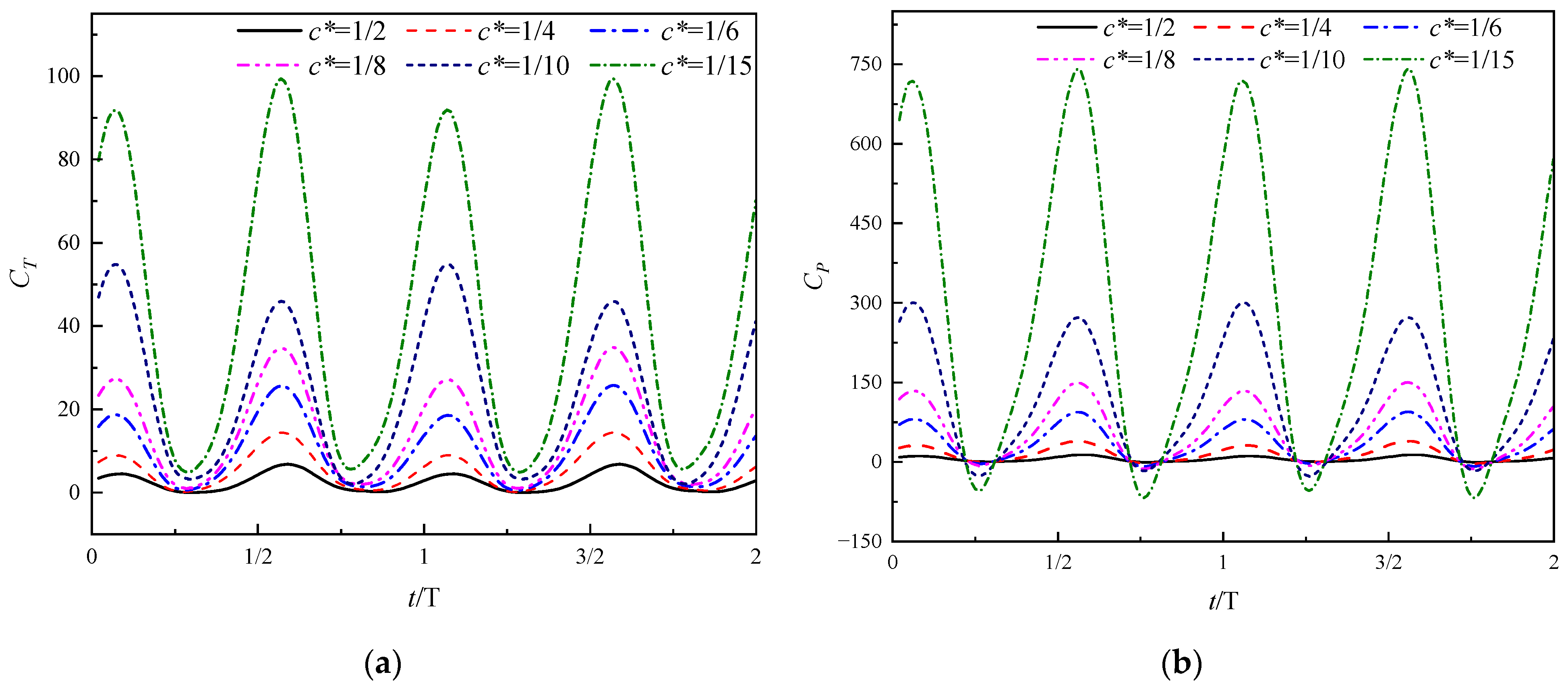
5.2. Effects of Relative Chord Length and Motion Frequency on Pushing-Water Performance
6. Conclusions
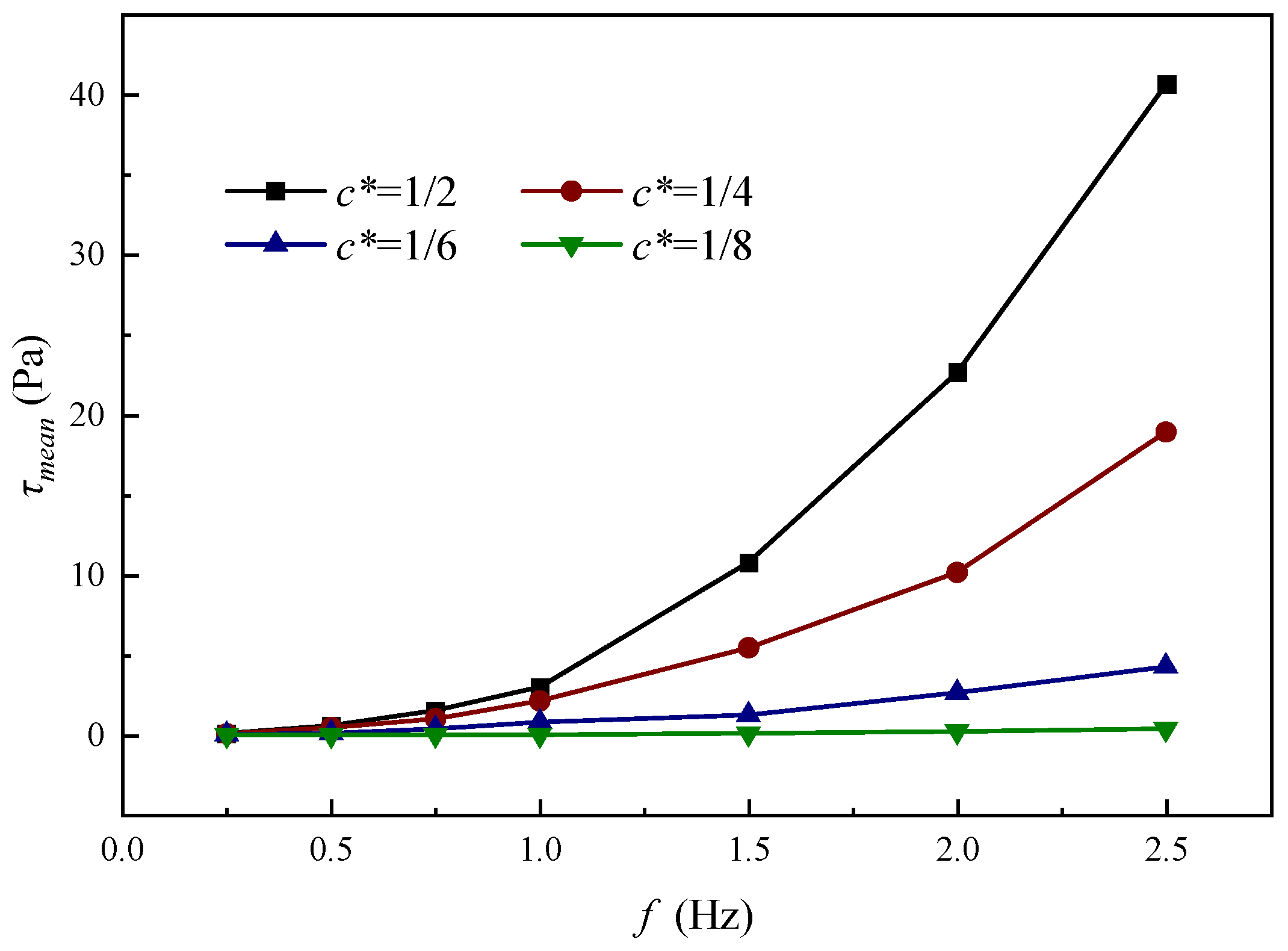
- The near-shore current mean scouring force is proportional to the frequency f and the relative chord length c*, and the effect of frequency f on the flapping hydrofoil’s bank slope scour increases with the relative chord length c*. The pushing-water efficiency of flapping hydrofoil increases significantly with the increase in c*, and tends to level off after increasing gradually with the increase in f. In addition, the effect of c* on the pushing-water efficiency is larger than that of f.
- As the relative chord length c* decreases, the threshold frequency at which bank slopes do not scour gradually increases. When c* is 1/2, 1/4, 1/6, and 1/8, the corresponding bank slope scour-free threshold frequencies are 0.65 Hz, 0.70 Hz, 1.26 Hz, and 3.50 Hz, respectively.
- When c* is certain, reducing f can significantly reduce the near-shore current mean scouring force, but the effect on pushing-water efficiency is small. By reasonably selecting the combination of larger c* and smaller f, the bank slope scours can be effectively reduced while maintaining high pushing-water efficiency. According to the results of this paper, it is recommended to select the combination of c* = 1/2 and f = 0.65 Hz to achieve the optimum effect.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, H.; Yuan, S.; Cao, H. Theory and practice of hydrodynamic reconstruction in plain river networks. Engineering 2023, 24, 202–211. [Google Scholar]
- Zhang, X.; Zheng, X.; Wang, L. Application of Relay Pump Station to Coastal Plain Drainage. J. Chang. River Sci. Res. Inst. 2018, 35, 46–51. [Google Scholar]
- Xie, L.; Wang, F.; He, C. Experimental investigation on hydrodynamic characteristics of a 15-degree slanted axial-flow pump system. J. Hydraul. Eng. 2019, 50, 798–805. [Google Scholar]
- Hua, E.; Tang, S.; Chen, W. Analysis on influence of swinging modes of swing hydrofoil on water propulsion. J. Hydroelectr. Eng. 2022, 41, 93–103. [Google Scholar]
- Hua, E.; Chen, W.; Tang, S.; Xie, R.S.; Guo, X.M.; Xu, G.H. Water Pushing Flow Characteristics of Flapping Hydrofoil Device in Small River. Trans. Chin. Soc. Agric. Mach. 2022, 53, 154–162. [Google Scholar]
- Xu, W.; Xu, G.; Duan, W.; Song, Z.; Lei, J. Experimental and numerical study of a hydrokinetic turbine based on tandem flapping hydrofoils. Energy 2019, 174, 375–385. [Google Scholar]
- Wu, X.; Zhang, X.; Tian, X.; Li, X.; Lu, W. A review on fluid dynamics of flapping foils. Ocean Eng. 2020, 195, 106712. [Google Scholar]
- Von Kármán, T. General aerodynamic theory-perfect fluids. Aerodyn. Theory 1935, 2, 346–349. [Google Scholar]
- Freymuth, P. Propulsive vortical signature of plunging and pitching airfoils. AIAA J. 1988, 26, 881–883. [Google Scholar]
- Chao, L.M.; Pan, G.; Zhang, D.; Yan, G.X. Numerical investigations on the force generation and wake structures of a non-sinusoidal pitching foil. J. Fluids Struct. 2019, 85, 27–39. [Google Scholar]
- Song, B.; Zhou, W. Numerical Simulation Study on Hydrodynamic of Flapping Wing Propulsion Affected by Swing Frequency. Sci. Technol. Eng. 2012, 12, 1821–1824+1840. [Google Scholar]
- Ding, H.; Song, B.; Tian, W. Exploring Propulsion Performance Analysis of Bionic Flapping Hydrofoil. J. Northwestern Polytech. Univ. 2013, 31, 150–156. [Google Scholar]
- Read, D.A.; Hover, F.S.; Triantafyllou, M.S. Forces on oscillating foils for propulsion and maneuvering. J. Fluids Struct. 2003, 17, 163–183. [Google Scholar]
- Zhang, S.; Yan, W.; Zhou, J.; Mei, L.; Yu, D. Influence of tip shapes on hydrodynamic performance of low-aspect-ratio oscillating foils. J. Ship Mech. 2022, 26, 628–644. [Google Scholar]
- Gao, P.; Huang, Q.; Pan, G.; Zhao, J. Experimental study on hydrodynamic characteristics of flexible flapping foil. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2022, 50, 144–148. [Google Scholar] [CrossRef]
- Fan, Z.; Han, J.; Chen, G. Investigation on the influence of aspect ratio on the thrust performance of bionic motion wing under low Reynolds number. Acta Aerodyn. Sin. 2018, 36, 156–162. [Google Scholar]
- Ding, H.; Chen, R.; Zhu, Y.; Shen, H.; Gao, Q. Effect of Frequency–Amplitude Parameter and Aspect Ratio on Propulsion Performance of Underwater Flapping-Foil. Biomimetics 2024, 9, 324. [Google Scholar] [CrossRef]
- Kumar, R.; Shin, H. Thrust prediction of an active flapping foil in waves using CFD. J. Mar. Sci. Eng. 2019, 7, 396. [Google Scholar] [CrossRef]
- Wang, P.; Tian, X.; Lu, W.; Hu, Z.; Luo, Y. Dynamic modeling and simulations of the wave glider. Appl. Math. Model. 2019, 66, 77–96. [Google Scholar]
- Kinsey, T.; Dumas, G. Parametric study of an oscillating airfoil in a power-extraction regime. AIAA J. 2008, 46, 1318–1330. [Google Scholar]
- Li, W.; Bao, Y. Effects of motion parameters on energy harvesting performance of flapping foils. J. Hydroelectr. Eng. 2023, 42, 79–86. [Google Scholar]
- Kinsey, T.; Dumas, G. Computational fluid dynamics analysis of a hydrokinetic turbine based on oscillating hydrofoils. J. Fluids Eng. 2012, 134. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Y.; Zhao, W.; Jiang, E. Review on riverbank soil collapse. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 246, p. 01021. [Google Scholar]
- Dou, G.; Dou, X. Classical Theory of Sediment Movement; Science Press: Beijing, China, 2023. [Google Scholar]
- Ma, Z.P.; Zhang, G.G.; Gao, G.Y.; Tian, G.Z. Discussion on incipient condition of a noncohesive sediment particle on slope under 3D flow. J. Sediment Res. 2014, 3, 36–41. [Google Scholar]
- Wu, Y.; Han, Q.; Ba, Y. Incipient Velocity of Non-Uniform Sediment on Sloping Fluvial Beds. J. Tianjin Univ. 2012, 45, 209–214. [Google Scholar]
- Zhang, F.; Chen, X. Research progress on stability analysis of embankment under effects of river scouring. Adv. Sci. Technol. Water Resour. 2009, 29, 84–88. [Google Scholar]
- Wang, Y.; Kuang, S. Study on bank erosion and its influence on bank collapse. J. China Inst. Water Resour. Hydropower Res. 2005, 4, 251–257+296. [Google Scholar]
- Hu, P.; Cui, X.; Zhou, Z. Principle and Method of River Cross Section Regularization in Watershed Hydrological Model. J. China Hydrol. 2010, 30, 38–41,79. [Google Scholar]
- Lighthill, M.J. Aquatic animal propulsion of high hydromechanical efficiency. J. Fluid Mech. 1970, 44, 265–301. [Google Scholar]
- Hua, E.; Luo, H.; Xie, R.; Chen, W.; Tang, S.; Jin, D. Investigation on the Influence of Flow Passage Structure on the Performance of Bionic Pumps. Processes 2022, 10, 2569. [Google Scholar] [CrossRef]
- Li, Y.; Pan, Z.; Zhang, N. Numerical analysis on the propulsive performance of oscillating wing in ground effect. Appl. Ocean. Res. 2021, 114, 102772. [Google Scholar]
- Cheng, N.S.; Chiew, Y.M. Pickup probability for sediment entrainment. J. Hydraul. Eng. 1998, 124, 232–235. [Google Scholar]
- Hanson, G.J.; Cook, K.R.; Simon, A. Non-vertical jet testing of cohesive streambank materials. In Proceedings of the ASAE Annual Meeting, Chicago, IL, USA, 28 July–31 July 2002. [Google Scholar]
- Karmaker, T.; Dutta, S. Erodibility of fine soil from the composite river bank of Brahmaputra in India. Hydrol. Process. 2011, 25, 104–111. [Google Scholar]
- Du, X.; Zhang, Z. Numerical analysis of influence of four flapping modes on propulsion performance of underwater flapping foils. Eng. Mech. 2018, 35, 249–256. [Google Scholar]
- Shaheed, R.; Mohammadian, A.; Kheirkhah, G.H. A comparison of standard k–ε and realizable k–ε turbulence models in curved and confluent channels. Environ. Fluid Mech. 2019, 19, 543–568. [Google Scholar]

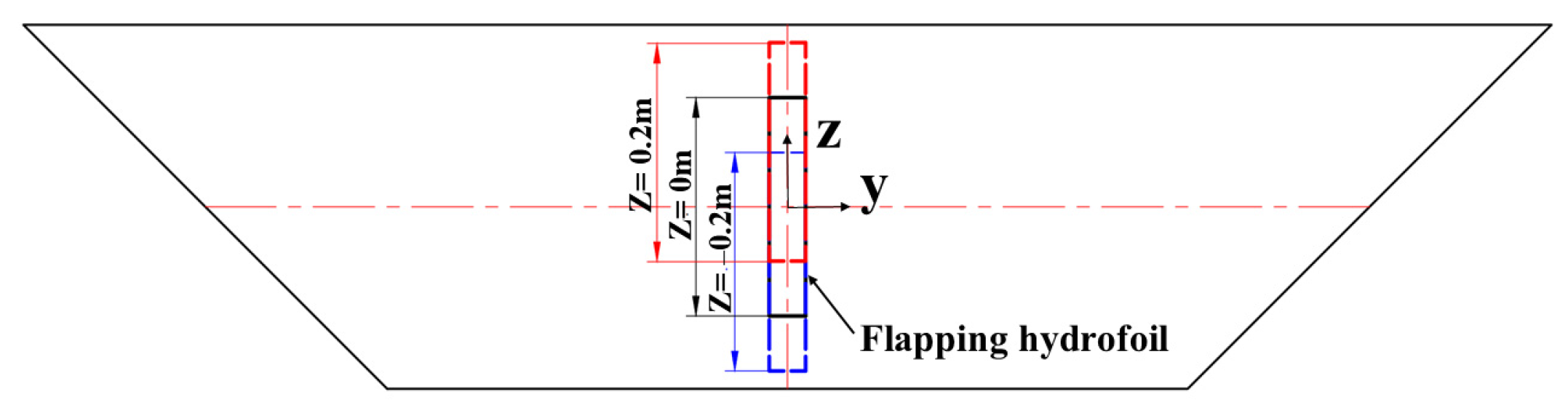
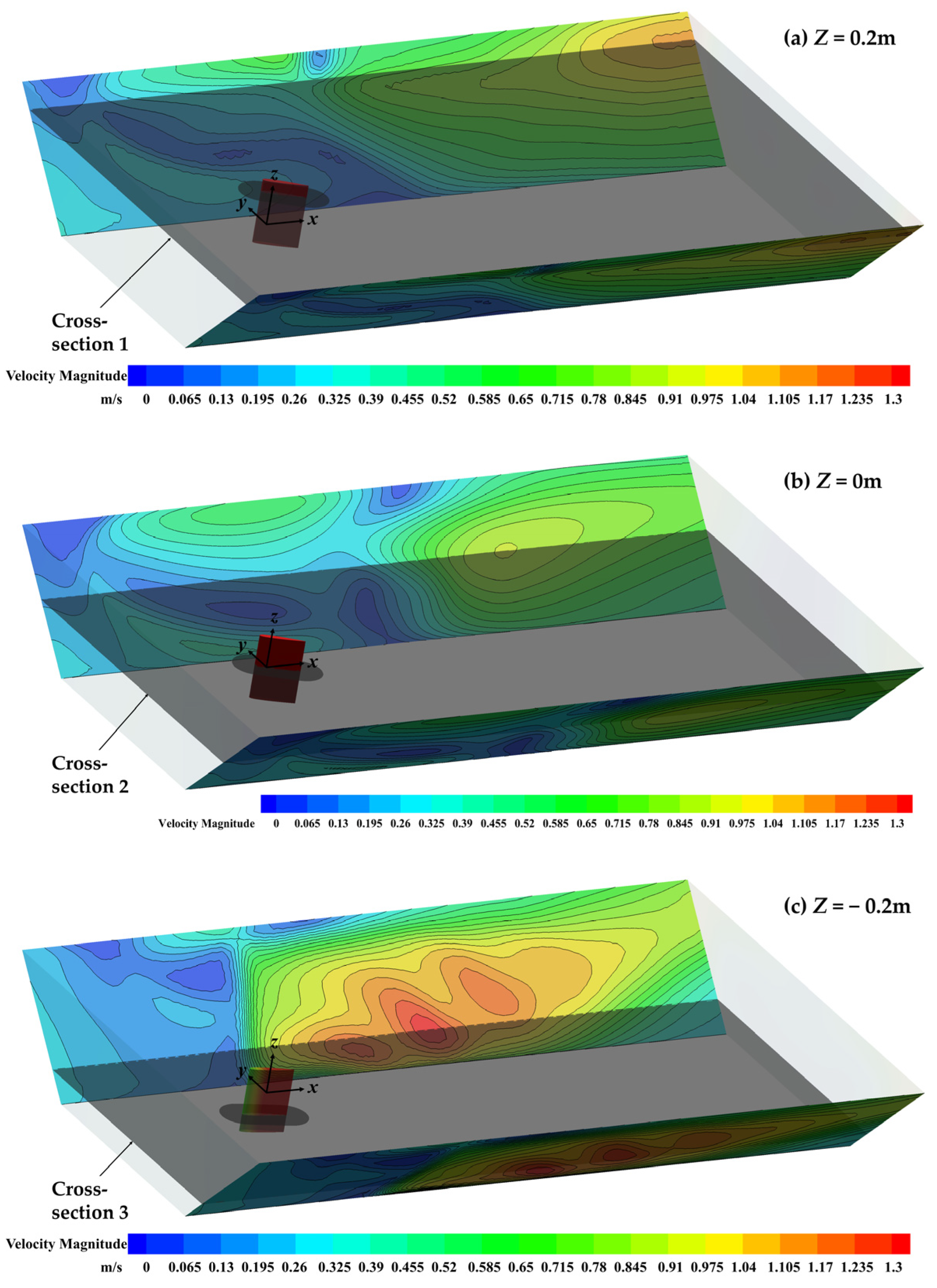

| Installation Heights | Cross-Sections | Maximum Time-Averaged Near-Shore Flow Velocity, m/s | Maximum Scouring Force, Pa |
|---|---|---|---|
| Z = 0.2 m | 1 | 1.04 | 32.46 |
| Z = 0 m | 2 | 0.80 | 19.21 |
| Z = −0.2 m | 3 | 1.28 | 49.17 |
| The Relative Chord Lengths | The τmean—f Relationship | The Threshold Frequencies |
|---|---|---|
| 1/2 | τmean = 1.449 f3 + 3.434 f2 − 1.359 f | 0.65 Hz |
| 1/4 | τmean = 0.881 f3 + 0.582 f2 − 0.574 f | 0.70 Hz |
| 1/6 | τmean = 0.118 f3 + 0.309 f2 − 0.206 f | 1.26 Hz |
| 1/8 | τmean = 0.014 f3 + 0.040 f2 − 0.028 f | 3.50 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, E.; Lu, C.; Xiang, M.; Song, Y.; Wang, T.; Sun, Q. Study on the Influence of Relative Chord Length and Frequency of Flapping Hydrofoil Device on Hydrodynamic Performance and Bank Slope Scour. Water 2025, 17, 1026. https://doi.org/10.3390/w17071026
Hua E, Lu C, Xiang M, Song Y, Wang T, Sun Q. Study on the Influence of Relative Chord Length and Frequency of Flapping Hydrofoil Device on Hydrodynamic Performance and Bank Slope Scour. Water. 2025; 17(7):1026. https://doi.org/10.3390/w17071026
Chicago/Turabian StyleHua, Ertian, Caiju Lu, Mingwang Xiang, Yabo Song, Tao Wang, and Qizong Sun. 2025. "Study on the Influence of Relative Chord Length and Frequency of Flapping Hydrofoil Device on Hydrodynamic Performance and Bank Slope Scour" Water 17, no. 7: 1026. https://doi.org/10.3390/w17071026
APA StyleHua, E., Lu, C., Xiang, M., Song, Y., Wang, T., & Sun, Q. (2025). Study on the Influence of Relative Chord Length and Frequency of Flapping Hydrofoil Device on Hydrodynamic Performance and Bank Slope Scour. Water, 17(7), 1026. https://doi.org/10.3390/w17071026





