Next Article in Journal
Environmental DNA Reveals Ecologically Relevant Temporal and Spatial Variation of Fish Community in Silver Carp- and Bighead Carp-Dominant Drinking Water Reservoirs
Previous Article in Journal
A Critical Review of Nanobubble Flotation for Seawater Treatment Process
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 17
Issue 7
10.3390/w17071056
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Absolute Meteorological Drought Indices Validated Against Irrigation Amounts

by
Jan-Philip M. Witte
1,*,
Gé A. P. H. van den Eertwegh
2 and
Paul J. J. F. Torfs
3
1
Flip Witte Ecohydrologie, 6862DC Oosterbeek, The Netherlands
2
KnowH2O, 6571CB Berg en Dal, The Netherlands
3
Independent Researcher, 6641LD Beuningen, The Netherlands
*
Author to whom correspondence should be addressed.
Water 2025, 17(7), 1056; https://doi.org/10.3390/w17071056
Submission received: 27 February 2025 / Revised: 27 March 2025 / Accepted: 1 April 2025 / Published: 2 April 2025
(This article belongs to the Section Water, Agriculture and Aquaculture)
Browse Figures
Versions Notes

Abstract

:
Dry weather can severely limit water availability, harming agriculture and natural habitats. Several drought indices assess meteorological conditions relative to historical norms, but absolute indices, expressed in millimeters of water depth, are particularly crucial for agriculture. Every millimeter of water that a crop cannot evaporate results in an almost proportional yield loss. Using daily precipitation, potential evapotranspiration, and temperature data, we calculated five absolute drought indices for a sandy area in the Netherlands. We then validated these indices against the annual registered amount of irrigation water from 2001 to 2021, which served as a proxy for the drought experienced by farmers. The cumulative potential precipitation deficit calculated with (a) a temperature sum-dependent start of the growing season or (b) a start in the wet winter season most closely matched irrigation amounts (R2 = 95% and 94%, respectively). The latter index is likely to be applicable in climates where a dry growing season follows a wet season. These indices can be updated daily, providing real-time insight into drought development and can be used in climate projections. To our knowledge, this is the first study to validate meteorological drought indices using irrigation data, which advances the assessment of drought events.

1. Introduction

In 2014, the Royal Netherlands Meteorological Institute (KNMI) announced that summers in the Netherlands could become significantly drier due to climate change [1]. During the extremely dry year of 2018, it became clear that future scenarios could also become reality. This awareness was further reinforced by the very dry years that followed, also affecting other parts of Western Europe: 2019, 2020, and 2022 [2]. Drought damage to crops [3] and nature [4] occurred primarily on the sandy soils of the southern and eastern part of the Netherlands (Figure 1), partly because the supply of surface water in this area is limited. The water availability for plants here depends largely on the weather and partly, where the groundwater table is less than approximately one to two meter below rooting zone [5], on capillary flow from the groundwater table. With the publication in 2024 of new climate scenarios predicting even drier summers [6], adapting water management has become even more critical.
Van Loon [7] describes a cascade of three forms of drought. It begins with meteorological drought, a prolonged period of low precipitation combined with high atmospheric evaporation demand. This meteorological drought propagates into the root zone of plants, where soil moisture decreases to such an extent that plants can no longer take up sufficient water to transpire: soil moisture drought. Finally, the lack of precipitation affects groundwater levels and the discharge of groundwater to streams and other surface waters, leading to hydrological drought. The propagation of dry weather through this cascade occurs with delays: heavy rainfall immediately reduces meteorological drought, but restoring potential evaporation requires replenishing the soil moisture. Only once the soil is at field capacity can groundwater levels and stream discharges recover, which takes the longest.
But it all starts with meteorological drought, being the first and most immediate manifestation of a water deficit in the hydrological cycle. Various indicators are used to quantify this phenomenon, including the following:
  • The Standardized Precipitation Index (SPI) [8], which is a widely used measure of drought that evaluates precipitation over a specific period relative to historical averages. It is dimensionless, with negative values indicating drought and values below −2.0 reflecting extreme drought. Its strength lies in its simplicity and broad applicability across different climates, but it does not consider evapotranspiration, which can be a critical factor in regions with high temperatures.
  • The Standardized Precipitation-Evapotranspiration Index (SPEI) [9] builds on SPI by incorporating potential evapotranspiration. This makes it more suitable for assessing droughts influenced by high evapotranspiration rates.
  • The Rainfall Anomaly Index (RAI) [10] measures deviations in precipitation relative to historical norms, highlighting both drought and excessive rainfall. While straightforward, it lacks the nuance provided by indices like SPEI, which consider evapotranspiration.
  • The Aridity Index (AI) [11] is the ratio of total precipitation to potential evapotranspiration, used for defining arid, semi-arid, and dry sub-humid regions and drought monitoring worldwide. It does not account for short-term climate variability and, like the other indices, it does not provide information about the absolute amount of precipitation deficits.
There are also drought measures that account for soil texture, organic matter content, and groundwater depth, such as the Palmer Drought Severity Index [12], but here we focus on metrics that are solely calculated from weather data.
The KNMI uses SPI and SPEI to monitor meteorological droughts in the Netherlands. These indices, as well as RAI and AI, are particularly useful for international comparison due to their standardized nature. However, their relative characterization of drought, where a statistically extreme event in one location may differ in absolute terms from another, makes them less suitable for assessing the practical impacts of drought on agriculture and ecosystems. For example, the Norwegian coastal city of Bergen can experience an extreme drought for its location, statistically just as extreme as in Madrid; by definition, SPI and SPEI capture this well. However, this advantage also implies a limitation: drought in Bergen, with an average annual precipitation of 2250 mm, is incomparable to a drought in Madrid, where the average annual precipitation is 420 mm. Furthermore, SPI and SPEI are calculated over a fixed time frame, such as 3 months, so these measures do not take into account a possible extension (or shortening) of the growing season due to climate change [13].
For assessing the impact of meteorological drought on agriculture and nature, these relative metrics are therefore not ideal, even in a small country like the Netherlands, as there are already spatiotemporal climatic differences within it [14]. Particularly for agriculture, it is essential to determine whether there is sufficient water in absolute terms, as every millimeter of water that a crop cannot transpire potentially leads to an almost proportional loss in yield via the water-use efficiency of productivity [15].
Given the limitation of relative metrics, this article investigates absolute meteorological drought indices expressed in millimeters of water deficit. These indices offer a more direct link to practical outcomes, such as irrigation requirements, and are therefore better suited for assessing the impacts of drought on agriculture and natural ecosystems, i.e., on soil moisture drought.
This article evaluates the quality of absolute meteorological drought indices by comparing them to irrigation application data. The underlying assumption is that irrigation demand increases as the meteorological drought intensifies, meaning that the irrigation rate serves as an integrated proxy for the drought experienced by farmers. By focusing on absolute metrics, this study aims to bridge the gap between meteorological drought assessment and its practical implications for water management and agricultural productivity.

2. Materials and Methods

2.1. Climate of The Netherlands

The Netherlands is a small EU country (42,000 km2) with a temperate maritime climate, influenced by the North Sea and prevailing westerly winds. The annual evapotranspiration (ET) typically ranges between 500 and 600 mm, while annual precipitation averages 700–900 mm. However, during the growing season, which typically runs from spring to early autumn (April to September), precipitation is often insufficient to compensate for the high ET rates, leading to a precipitation deficit and, finally, drought damage to crops and natural habitats, among other things.

2.2. Irrigation Data

For privacy reasons, data on the amount of irrigation used by each farmer are unavailable. Instead, we used annual irrigation figured for the entire Netherlands (I), calculated by Van der Meer [16] for the years 2001–2021 (Table 1). These figures are based on a sample from the Farm Accountancy Data Network, which includes approximately 1500 agricultural and horticultural businesses nationwide. An evaluation confirmed that the sample meets the necessary criteria for response rate, statistical reliability, and representativeness [17]. Using statistical matching techniques [18,19], Van der Meer [16] estimated the total water usage for the entire sample population (Table 1).
The area irrigated depends on factors such as the number of irrigation devices, access to water and labor, and drought severity. For example, in 2019, over 255,000 hectares were irrigated at least once, with approximately 75% of the water sourced from groundwater and 25% from surface water [20]. Most irrigation water was used for grassland, followed by potatoes and corn [21]. Irrigation typically occurs in amounts of about 25 mm per application [22], with an average cost of 117 euros per hectare per application for labor and energy [21].
Our analysis focuses on meteorological data from the regions with the highest irrigation activity. Although we do not precisely define the exact area where most irrigation occurs, we will refer to it as the ‘irrigation area’, which dominates the figures in Table 1. This area was delineated based on the presence of irrigation reels and sprinklers observed in satellite images from 2018 (Figure 1). It primarily includes the higher sandy soils in the eastern and southern parts of the Netherlands (roughly the area south and east of the orange 1 m above-sea-level contour line in Figure 1) and the polders of lake IJsselmeer.
For the analysis, we required daily values of precipitation, reference ET according to Makkink [23], and average daily temperature for the period 2001–2021. The Makkink equation is used by the KNMI to estimate the amount of water that evaporates from a well-watered grassland, under ideal conditions. We selected 10 meteorological stations with long-term records, shown as red dots in Figure 1, to provide a representative spatial coverage of the irrigation area. For each day, we averaged the data from these 10 stations.
Water 17 01056 g001
Figure 1. Irrigation reels and spray booms detected on satellite images from 2018 (blue dots) [24], and the meteorological stations with complete measurement series for the period 2001–2021 (open and red dots, with the latter characterizing the irrigation area).
Figure 1. Irrigation reels and spray booms detected on satellite images from 2018 (blue dots) [24], and the meteorological stations with complete measurement series for the period 2001–2021 (open and red dots, with the latter characterizing the irrigation area).
Water 17 01056 g001

2.3. Drought Indices

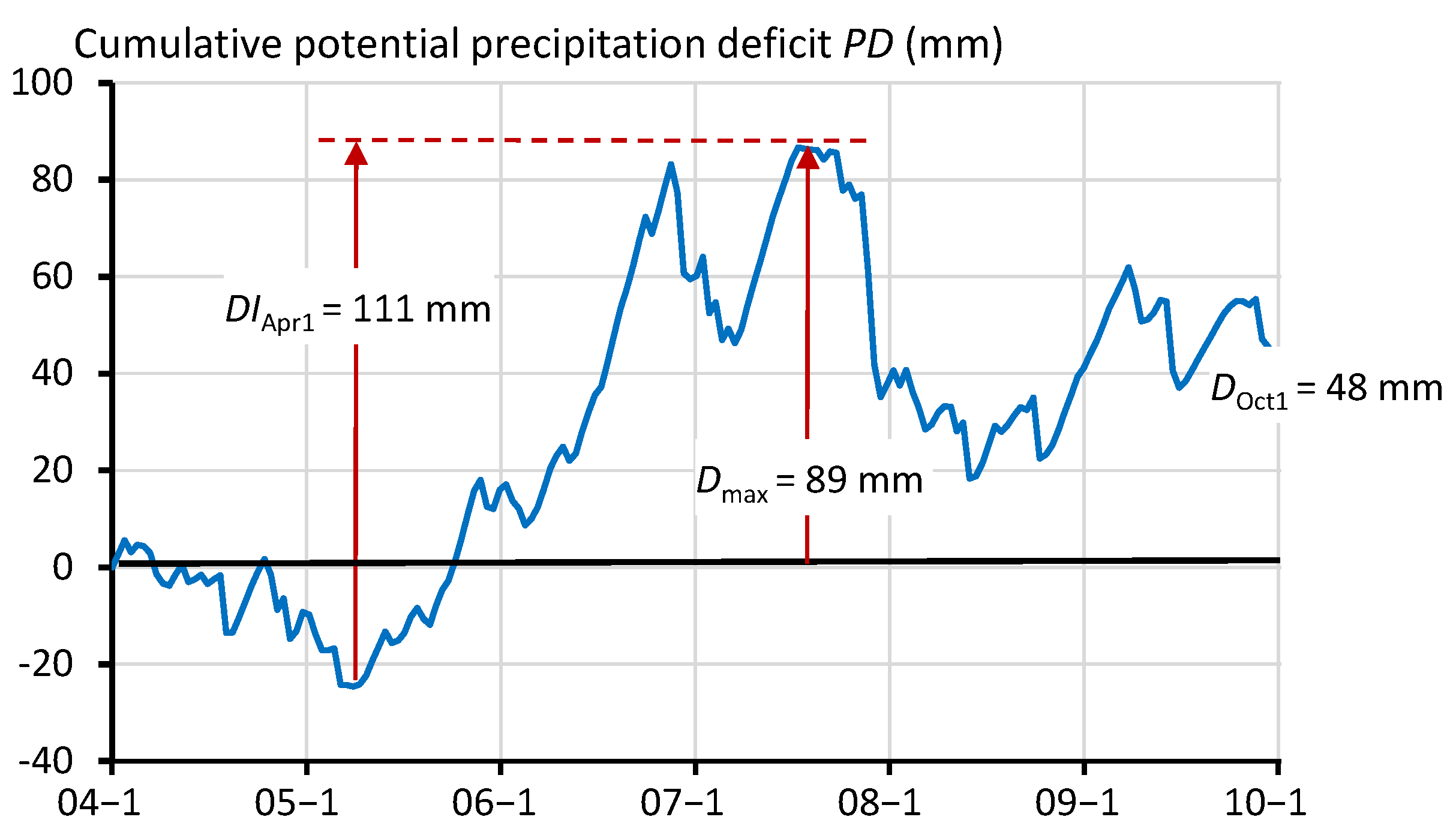
2.3.1. Definition of Cumulative Potential Precipitation Deficit

We based all indices on the cumulative potential precipitation deficit, PD, measured from a date that may differ per index (Table 2). The cumulative potential precipitation deficit, hereinafter also referred to as ‘precipitation deficit’ and ‘deficit’ for brevity, is the difference between the total amount of precipitation and Makkink-ET from that starting date.

2.3.2. Precipitation Deficit at the End of the Growing Season, DOct1

The first drought index analyzed is the cumulative potential precipitation deficit over the growing season, which is defined by the KNMI as the period from April 1 to September 30 [13]. The value of PD on October 1, termed DOct1, represents the deficit at the end of the growing season (Figure 2). Historically, DOct1 has been regarded as a drought indicator and continues to be reported by KNMI in its seasonal deficit graphs on its website (www.knmi.nl, accessed on 15 December 2023), suggesting its utility as a final measure of seasonal drought.

2.3.3. Maximum Value of the Precipitation Deficit, Dmax

The second measure, Dmax, is the maximum value of PD during the growing season, as defined by the KNMI (1 April to 30 September; Figure 2).

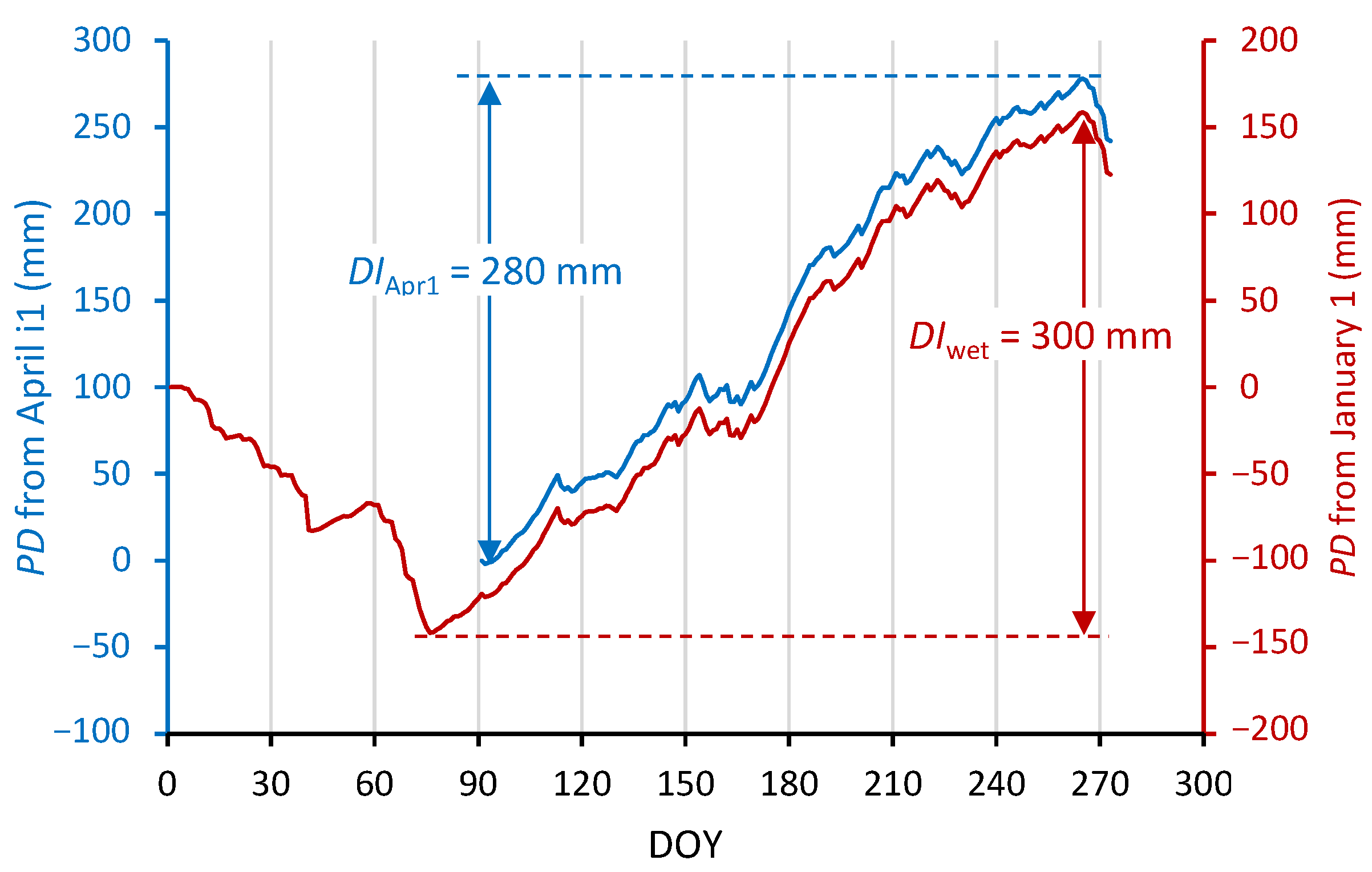
2.3.4. Maximum Increase in the Precipitation Deficit Starting from 1st April, DIApr1

The third drought measure, DIApr1, represents the largest increase in PD between 1 April and 30 September. Unlike previous methods, this calculation includes negative values of PD. Proposed by Van Boheemen [25] in 1980 [25] and later in 1984 adopted by a national commission on drought damage [26] and much later by the KNMI [27], DIApr1 reflects dry spells during the growing season as defined by the KNMI (Figure 2).

2.3.5. Maximum Increase in the Precipitation Deficit with a Starting Date Determined by a Temperature Sum, DIGDD

The fourth index, DIGDD, builds on DIApr1 but introduces a flexible start to the growing season, determined by a temperature sum of 440 °C. In agriculture, the temperature sum, also known as Growing Degree Days, GDD, is widely used to determine optimal planting times, predict crop development stages, and assess harvest timing [28]. We calculated GDD as the cumulative total of daily temperatures (oC) above zero from January 1 onwards. In our new metric, DIGDD, the growing season begins on the day when a GDD of 440 °C is reached. This threshold is the average GDD on April 1 over the years 2001–2021 for all 30 meteorological stations in the Netherlands for which the KNMI has made complete time series available (Figure 1). In this way, we align with the traditional definition of the start of the growing season (1 April for the entire Netherlands) but shift the start date forward or backward depending on whether spring is warmer or colder. Such a flexible definition of spring may be desirable now that the climate is undergoing significant change.

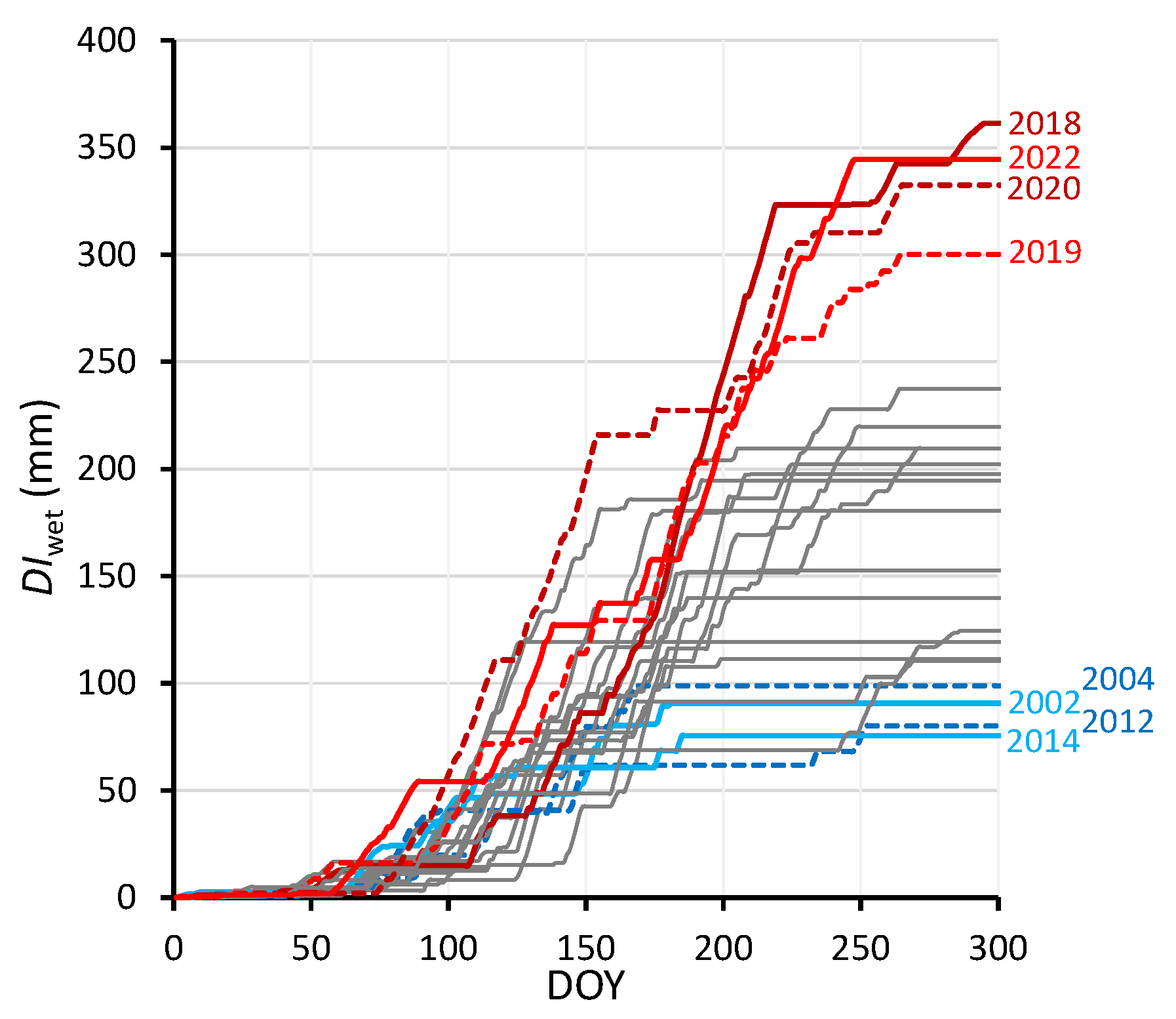
2.3.6. Maximum Increase in the Precipitation Deficit Starting in the Wet Season, DIwet

The fifth index, DIwet, eliminates the predefined growing season start. Instead, for the Netherlands, the deficit is calculated from January 1 onwards, under the assumption that the soil moisture is at field capacity during the wet months. This index aims to simplify the calculation, removing the dependency on start-of-growing-season definitions.
Note that the definition of the start of the growing season does affect the absolute value of PD, but this absolute value has no impact on the increase in that deficit. This is illustrated in Figure 3 for a cumulative potential precipitation deficit in 2019, calculated from both January 1 and April 1. In both cases, the maximum value of the deficit is reached on September 27, amounting to 158.5 and 277.7 mm, respectively. The minimum value of the deficit when measured from 1 January is reached on 18 March, at −141.3 mm, resulting in a DIwet of 300 mm. The minimum value when measured from April 1 is reached on April 2, at −1.8 mm, leading to a DIApr1 of 280 mm.

2.4. Statistical Analysis

We investigated all relationships between absolute drought indices (D) and irrigation amounts (I) using linear, exponential, and quadratic regressions, each calculated with and without an intercept. The linear regression was inadequate, while incorporating an intercept improved results. Quadratic and exponential regressions performed similarly, but we selected the quadratic regression (I = aD2 + bD + c) due to its simplicity and the fact that this function is linear in the coefficients a, b, c. As a measure of the fitted relationship between D and I, we use the explained variance (R2) and, as a measure of the deviation between I and the fitted regressions, the root mean square error (RMSE). Both metrics are functions of the variance of the residuals. The assessment of the regressions will be based on both R2 and RMSE.
Drought indices were compared with each other based on their residual variances. Differences in residual variances were assessed using a permutation test, where drought metrics were shuffled without replacement across years, leaving six randomly selected years unchanged to reduce the influence of outliers. The test was repeated 5000 times, generating a stable probability distribution of residual variances. Differences were considered significant at p < 0.05.
By combining this rigorous statistical method with a diverse set of drought indices, this study evaluates the extent to which meteorological drought metrics align with a practical response to water stress in agriculture.

3. Results

Table 3 presents the five calculated drought indices. Regardless of the indices used, the years 2018, 2019, and 2020 are the driest, followed by 2003 and 2009. The earliest start of the growing season as defined by GDD = 440 °C is March 9 (2007), while the latest start is April 26 (2013).
The five indices are highly correlated, as measured by both Pearson correlation and Spearman rank correlation (Table 4). The correlation of DOct1 with the other four indices is the lowest. The strong interrelation among Dmax, DIApr1, DIGDD, and DIwet is logical, as they are determined by the maximum cumulative precipitation deficit during the growing season and differ only in the lower bound from which the drought index is calculated.
Figure 4 illustrates the relationship between the five drought indices and the applied irrigation amounts during 2001–2021, highlighting the four years with the highest irrigation levels. Statistics describing the quality of these relationships (R2 and RMSE) are indicated in the figure. All regression lines are significant (p < 0.05), indicating that they are suitable for describing these relationships.
Based on the explained variances (Table 4), the three indices DOct1, Dmax, DIApr1 describe the relationship with irrigation amounts I equally well, index DIGDD does this significantly better than all other four indices (Table 5), and index DIwet performs better than DOct1 and DIApr1. It is noteworthy that on the basis of the permutation test, DIGDD and DIwet differ significantly from each other (Table 5), while their explained variances are almost the same (Figure 4: 95% and 94%, respectively) and they are highly correlated (Table 3: R = Rs = 99%). Apparently, the significant difference has little substantive meaning.

4. Discussion

4.1. Discussion of the Results

There is physical logic behind the fact that the relationship between drought severity (D) and irrigation amount (I) is not linear (Figure 4): minor meteorological drought can be well managed by the crop through the soil’s moisture-supplying capacity. Only above a pF of approximately 2.7 do crops begin to suffer from drought [29], and because of the non-linear relationship between moisture content and soil suction, this drought stress increases disproportionately as moisture content decreases further.
Overhead irrigation is common practice in the Netherlands. It began in the 1950s and expanded significantly after Dutch farmers experienced severe drought in 1976 [30,31]. The irrigated area calculated in that year was estimated at 257,625 ha [30] and the amount of irrigation at 259 Mm3 [32], which means that the irrigation capacity was already considerable at that time (compare with the 255,000 ha [20] and 215 Mm3 (Table 1) in the extremely dry year 2019). Although these historical numbers are less reliable than today, they do indicate that irrigation capacity was already significant at the start of our 2001–2021 analysis period. However, irrigation capacity has likely increased further in recent years as farmers have faced recurring droughts. Unfortunately, data on irrigation capacity are lacking, and we do not know the exact irrigation capacity at the beginning of our analysis (2001) or at its end (2021). However, it is reasonable to assume that it has increased whenever farmers encountered severe drought conditions. Since this presumed increase likely coincided with the droughts of 2001–2021, we were unable to isolate the variable ‘year’ as an additional explanatory factor for irrigation levels. Even if irrigation capacity increased during particularly dry periods, it is unlikely that this alone can explain the strong correlation with drought indices. Anticipatory farming practices may help explain why irrigation in 2018 was slightly lower than expected based on regression lines, while it was slightly higher in 2019 and 2020 (Figure 4). In other words, the drought of 2018 may have prompted farmers to invest in irrigation systems.
The results of our analysis depend on the selection of meteorological stations. For this, we used 10 stations located in the area with the highest irrigation activity, covering about half of the Netherlands (Figure 1). However, other selections do not lead to significantly different outcomes: DIGDD and DIwet consistently outperform DIApr1 and Dmax, which in turn perform better than DOct1. For example, if we perform the analysis again using average values from all 30 meteorological stations with complete data series (2001–2021; Figure 1), the statistics are somewhat weaker, but the differences between the indices remain consistent. The explained variances for DOct1, Dmax, DIApr1, DIGDD, and DIwet are then R2 = 72, 87, 85, 95, and 91% (instead of 84, 90, 89, 95, and 94%).

4.2. Discussion of the Indices

Each of the five drought indices is calculated as the difference between the maximum value of the cumulative potential precipitation deficit and a preceding minimum (Table 2). For DOct1 and Dmax, this minimum is predetermined: it is 0 mm on April 1, the start of the growing season according to the KNMI. For the other three indices, the minimum is calculated as the lowest value of PD preceding the maximum. These methods differ only in the start date of the calculation: April 1 for DIApr1, the first day that GDD exceeds 440 °C for DIGDD, and 1 January for DIwet.
Regardless of these differences, for a reliable index in all methods, it is important that the minimum occurs when the soil contains so much water that it can no longer absorb additional precipitation. This is the case when the soil is at field capacity (pF ≈ 2). If there is a period soon after the start date with more precipitation than evaporation, the surplus will contribute to groundwater recharge but will not increase the amount of soil moisture available to plants. This amount only starts to decrease once evaporation exceeds precipitation, marking the onset of drought development.
Only with index DIwet is a moisture condition at field capacity guaranteed at the start date of the calculation, as in the present Dutch climate, a period of at least four months follows September during which precipitation far exceeds evaporation. For index DIGDD, field capacity at the start is certainly not guaranteed, as evidenced by the fact that in 14 of the 20 years studied, DIwet is higher than DIGDD (Table 3).
That a flexible start of the growing season (DIwet and DIGDD) gave the best results in our study is consistent with the findings of Dullaart en Van der Wiel [13], who investigated how different meteorological variables changed between 1965–1993 and 1994–2023 and how these are expected to change as a result of climate change. They concluded that in general, the assumption that the PD is zero at the end of March is not valid, and that this discrepancy has become larger due to climate change.

4.3. Which Drought Index Is to Be Preferred to Characterize Absolute Meteorological Drought?

Based on the relationships with irrigation amounts and taking into account possible applications in climate change scenarios, we prefer a meteorological drought index that is calculated as the maximum increase in the cumulative potential precipitation deficit since (a) a temperature-dependent start of the growing season (DIGDD) or (b) a start in the rainy season (DIwet). Since GDD is only relevant for climates where crop growth needs to commence after a cold winter, we believe that, of the two indices, DIwet is the most suitable for use in climates other than the temperate maritime climate of the Netherlands. In fact, we see no reason why DIwet would not be applicable in all climates with an annual dry season following a distinct wet season, that is, a continuous wet period guaranteeing field capacity. In addition to the temperate maritime climate (Köppen–Geiger climate classification Cfb) of the Netherlands, this condition is usually met in humid subtropical climates (Cfa), semi-arid steppe climates (Bsh), semi-arid or arid climates (BSh/BWk), and monsoon climates (Cw). Within these classes, crops often begin to grow only after a cool winter in climates Cfa, Cfb and Cw, so index DIGDD might be useful there.

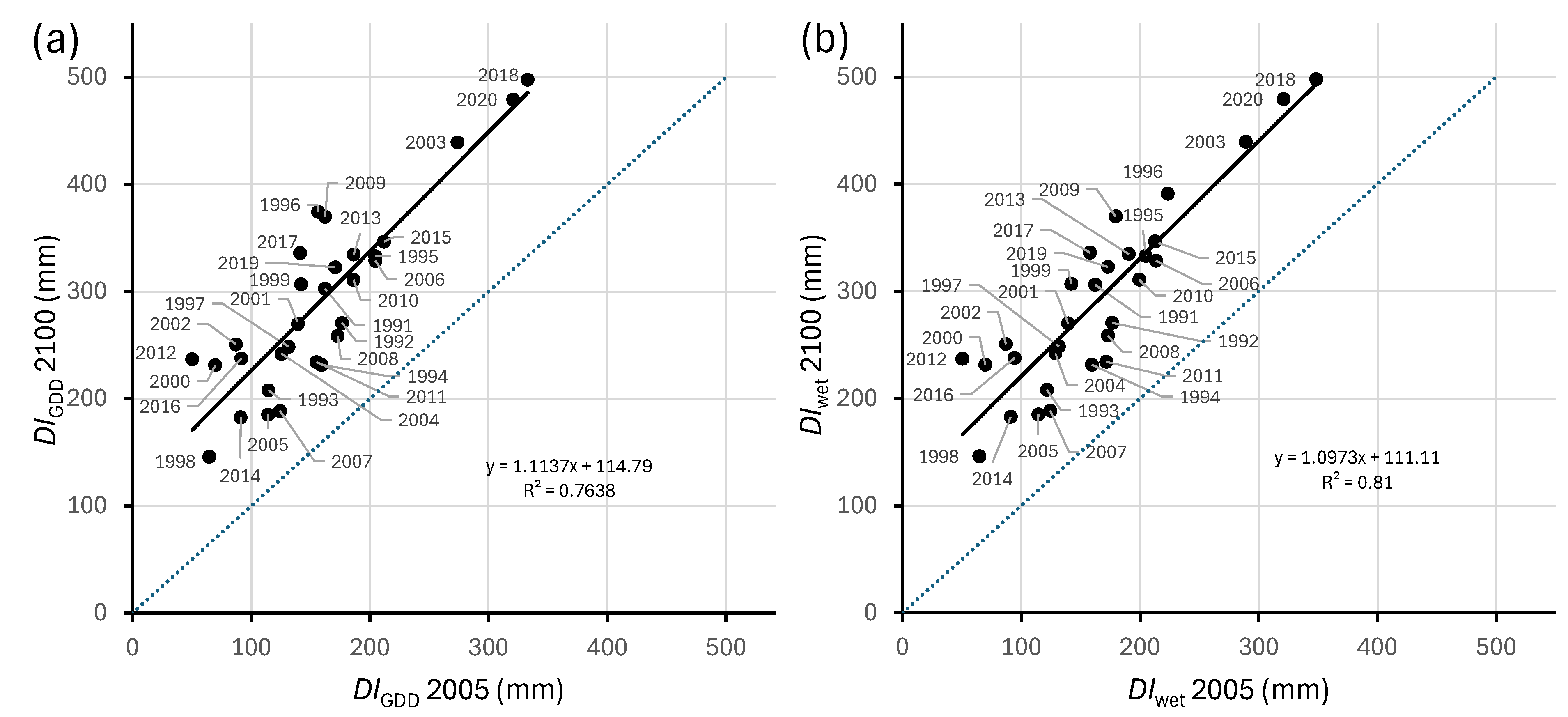
4.4. Example of Two Applications: Daily Drought Monitoring and Climate Change Projection

The maximum increase in PD can be calculated for any day of the year based on weather data from the preceding days, allowing for a daily assessment of meteorological drought conditions. Figure 5 illustrates this for DIwet and the years 2001–2022. The year 2020 was primarily characterized by an extremely dry spring, whereas the drought in the record year 2018 mainly developed after spring (day 150 = 30 May) (Table 2).
To illustrate the applicability in climate scenarios, we calculated the two preferred drought indices (DIGDD and DIwet) for KNMI-weather station De Bilt, located in the center of the Netherlands (Figure 1), under the current climate and the KNMI scenario ‘High emissions, dry’ (Hd), which corresponds to the international climate scenario SSP5-8.5 [33]. For this, we used the time series for the years 1991–2020 (current climate, hereafter referred to as ‘2005’) and the transformed time series of these years projected to 2050, both provided by the KNMI (https://klimaatscenarios-data.knmi.nl/, accessed on 12 February 2024).
Our analysis shows that a temperature sum of 440 °C will be reached 19 to 43 days earlier in De Bilt in 2100, with an average of 28 days. Under the 2100 climate, no growing season will start in April any longer (March 23 is the latest starting date), and in 13 out of 30 years, the start will fall in February, with the earliest date being February 15. The day on which the cumulative potential precipitation deficit reaches its maximum will occur 0 to 122 days later, with an average of 37 days. In 3 out of 30 years, this deficit will occur after September 30 in the 2100 climate, which justifies extending the growing season until December 1. When including this extension, the maximum PD still shifts by 0 to 122 days but now averages 39 days, with the latest date being October 26.
The future climate and the associated extension of the growing season have major consequences for meteorological drought (Figure 6): DIGDD increases by an average of 84% under the dry scenario in De Bilt, and DIwet by 78%. Regardless of the year, drought in 2100 will have increased by approximately 130 mm, the equivalent of five irrigation applications. Moreover, a drought as severe as 2018 will occur once every three to four years in 2100.

4.5. Perspectives for Future Research

Our analysis suggests that DI440 and DIwet are effective absolute indices for assessing meteorological drought events. However, this result is based on a limited dataset (21 years) and a single validation variable: the estimated amount of irrigation used in agriculture. Therefore, it would be valuable to validate these indices against additional ground observations, as has been done in several other studies.
For instance, a recent study used 2405 observed time series of soil moisture from 637 long-term monitoring stations across the conterminous United States to test the ability of various indices, including SPI and SPEI, to accurately characterize soil moisture drought [34]. The optimal time scale for SPI and SPEI increased with depth and averaged 30 days, with a Pearson correlation of 0.573 and 0.596 with soil moisture, respectively (R2 values of 33% and 36%). Another study compared SPI with NDVI for the period 1960–2010 in a typical drought-prone region in North China [35]. Both studies found that soil moisture simulated using a hydrological model better reflected actual drought events than meteorological drought indices. In contrast, a study in Eastern Australia concluded that soil moisture simulated with a physically based model is unlikely to be more useful than SPI due to uncertainties in soil water retention curves [36].
These and other studies show that soil moisture measurements and simulations, as well as NDVI observations, do not always accurately capture drought events. Discrepancies arise due to factors such as crop adaptation to water deficits, water management practices like irrigation and surface water level adjustments, uncertainties in models and measurements, and differences in spatial scales between soil moisture and meteorological data.
A key advantage of using irrigation data in our study is that they provide an integrated measure of annual drought as experienced by farmers. They reflect drought conditions over a large area and implicitly account for soil properties and water supply to the root zone via capillary flow from the groundwater table. In the coming years, new data on water use in Dutch agriculture will become available, allowing us to further assess the robustness of DIGDD and DIwet.

5. Conclusions

  • To the best of our knowledge, this is the first study to compare different meteorological drought indices by validating them against annual irrigation data, which we consider an integrated proxy of the drought experienced by farmers.
  • Of the five indices examined, the cumulative potential precipitation deficit calculated with (a) a temperature sum-dependent start of the growing season or (b) a start in the wet winter season most closely matched irrigation amounts (R2 = 95% and 94%, respectively).
  • Despite almost the same R2, DIGDD significantly outperformed DIwet.
  • The advantage of DIwet is that it does not require defining the start of the growing season and that it has the widest geographical applicability: presumably all climates with an annual dry season following a distinct wet season.
  • DIGDD and DIwet can be recalculated daily, offering an up-to-date view of meteorological drought development throughout the year.

Author Contributions

Conceptualization, J.-P.M.W.; formal analysis, J.-P.M.W. and P.J.J.F.T.; investigation, J.-P.M.W. and G.A.P.H.v.d.E.; writing—original draft preparation, J.-P.M.W.; writing—review and editing, P.J.J.F.T., G.A.P.H.v.d.E., and J.-P.M.W.; visualization, J.-P.M.W. and P.J.J.F.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data is contained within the article.

Acknowledgments

We thank Dion van Deijl and Wilco Terink of KnowH2O for their technical support.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
GDDGrowing Degree days (°C), here defined as the cumulative total of daily temperatures above zero from 1 January onwards
Iannual irrigation amount (Mm3)
PDcumulative potential precipitation deficit (mm)
DOct1PD measured from 1 April at the end of the growing season (mm)
Dmaxmaximum value of PD, measured from 1 April (mm)
DIApr1largest increase in PD, measured from 1 April (mm)
DIGDDlargest increase in PD, measured from GDD (mm)
DIwetlargest increase in PD, measured from a day in the wet season (mm), here 1 January
ETEvapotranspiration (mm/d or mm/yr)

References

  1. Van den Hurk, B.; Siegmund, P.; Tank, A.K. KNMI’14: Climate Change Scenarios for the 21st Century-A Netherlands Perspective; KNMI: The Bilt, The Netherlands, 2014. [Google Scholar]
  2. Aalbers, E.E.; Van Meijgaard, E.; Lenderink, G.; De Vries, H.; Van den Hurk, B.J.J.M. The 2018 west-central European drought projected in a warmer climate: How much drier can it get? Nat. Hazards Earth Syst. Sci. 2023, 23, 1921–1946. [Google Scholar] [CrossRef]
  3. Prins, H.; Jager, J.; Stokkers, R.; van Asseldonk, M. Damage to Dutch Agricultural and Horticultural Crops as a Result of the Drought in 2018. Extent of Crop Yield Losses and Mitigating and Adaptive Measures Taken by Farmers and Growers; Wageningen Economic Research: Wageningen, The Netherlands, 2018. [Google Scholar]
  4. Witte, J.P.M.; Van Deijl, D.; Van den Eertwegh, G.A.P.H. Gevolgen voor de Natuur van de Droge Jaren 2018 en 2019; Resultaten van Een Enquête Onder Deskundigen. Deelrapport van Het Project: Droogte in Zandgebieden van Zuid-, Midden- en Oost-Nederland; FWE & KnowH2O: Oosterbeek, The Netherlands, 2020. [Google Scholar]
  5. Vervoort, R.W.; Van der Zee, S.E.A.T.M. Simulating the effect of capillary flux on the soil water balance in a stochastic ecohydrological framework. Water Resour. Res. 2008, 44, W08425. [Google Scholar] [CrossRef]
  6. Royal Netherlands Meteorological Institute (KNMI). KNMI’23 Klimaatscenario’s voor Nederland; KNMI: De Bilt, The Netherlands, 2023. [Google Scholar]
  7. Van Loon, A.F. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
  8. McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eight Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
  9. Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
  10. Van Rooy, M.P. A rainfall anomally index independent of time and space. Notos 1965, 14, 43–48. [Google Scholar]
  11. Middleton, N.J.; Thomas, D.S.G. (Eds.) World Atlas of Desertification; Edward Arnold: London, UK, 1992. [Google Scholar]
  12. Palmer, W.C. Meteorological drought. Weather Bur. Res. Pap. 1965, 45, 1–58. [Google Scholar]
  13. Dullaart, J.; Van der Wiel, K. Underestimation of meteorological drought intensity due to lengthening of the drought season with climate change. Environ. Res. Clim. 2024, 3, 041004. [Google Scholar] [CrossRef]
  14. Wolters, D.; Homan, C.; Bessembinder, J. Ruimtelijke Klimatologische Verschillen Binnen Nederland; KNMI: De Bilt, The Netherlands, 2011. [Google Scholar]
  15. De Wit, C.T. Transpiration and Crop Yields; Pudoc: Wageningen, The Netherlands, 1958; Volume 64.4, p. 88. [Google Scholar]
  16. Van der Meer, R.W. Watergebruik in de Land- en Tuinbouw, 2021. Berekeningen op Basis van Het Bedrijveninformatienet; Wageningen Economic Research: Wageningen, The Netherlands, 2023. [Google Scholar]
  17. Roskam, J.L.; Van der Meer, R.W.; Van der Veen, H.B. Sample for the Dutch FADN 2017; Wageningen Economic Research: Wageningen, The Netherlands, 2020. [Google Scholar]
  18. De Waal, T. General Approaches for Consistent Estimation Based on Administrative Data and Surveys; Statistics Netherlands: The Hague, The Netherlands, 2015. [Google Scholar]
  19. Vrolijk, H.C.J.; Dol, W.; Kuhlman, T. Integration of Small Area Estimation and Mapping Techniques; Tool for Regional Studies; LEI: The Hague, The Netherlands, 2005. [Google Scholar]
  20. Van der Meer, R.W. Watergebruik in de Land-en Tuinbouw 2019; Wageningen Economic Research: Wageningen, The Netherlands, 2021; Volume 87. [Google Scholar]
  21. Stokkers, R.; Jager, J.; van Asseldonk, M. Beregening in akkerbouw-, Groente- en Voedergewassen in Diverse Regio’ s van Nederland in de Periode 2010–2019; Wageningen Economic Research: Wageningen, The Netherlands, 2022. [Google Scholar]
  22. Van den Eertwegh, G.; Van Bakel, J.; Massop, H.T.L.; Van Dam, J.C.; Bosveld, F.; Veldhuizen, A.A. Efficiëntie van Beregening: Een Deskstudy Naar Kennis en Inzicht Ten Aanzien van Waterverliezen Bij Midden op de Dag Beregenen Vergeleken Met Beregen in de Nachtelijke Uren; KnowH2O: Berg en Dal, The Netherlands, 2020. [Google Scholar]
  23. Makkink, G.F. Testing the Penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
  24. Terink, W.; Van Deijl, D.; Van den Eertwegh, G.; Wonink, S.; Brombacher, J. Een Nieuwe Kaart van Potentieel Beregende Percelen in 2018 voor Toepassing Binnen Het NHI. Combinatie van Bestaande Informatie en Kennis ter Realisatie van een Nieuwe en Gevalideerde Kaart; KnowH2O & eLeaf: Berg en Dal, The Netherlands, 2023. [Google Scholar]
  25. Van Boheemen, P.J.M. Seizoen- en Piekbehoefte aan Kunstmatige Watervoorziening Bij Gras-, Aardappelen en Tuinbouwgewassen; ICW: Wageningen, The Netherlands, 1980. [Google Scholar]
  26. CoGroWa. Landbouwkundige Aspecten van Grondwateronttrekking; Commissie Grondwaterwet Waterleidingbedrijven—Werkgroep Landbouwkundige Aspecten: Utrecht, The Netherlands, 1984. [Google Scholar]
  27. Philip, S.Y.; Kew, S.F.; Van der Wiel, K.; Wanders, N.; Van Oldenborgh, G.J. Regional differentiation in climate change induced drought trends in the Netherlands. Environ. Res. Lett. 2020, 15, 094081. [Google Scholar] [CrossRef]
  28. McMaster, G.S.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef]
  29. Taylor, S.A.; Ashcroft, G.L. Physical Edaphology. The Physics of Irrigated and Nonirrigated Soils; Freeman: San Francisco, CA, USA, 1972. [Google Scholar]
  30. De Wilde, J.G.S.; Linthorst, T.J. Beregening en Bevloeiing in Nederland in 1976; ICW: Wageningen, The Netherlands, 1978. [Google Scholar]
  31. Van Boheemen, P.J.M. Ontwikkeling in de Toepassing van Beregening en Bevloeiing Tot 1983; ICW: Wageningen, The Netherlands, 1985. [Google Scholar]
  32. Pulles, J.W. Beleidsanalyse voor de Waterhuishouding in Nederland—PAWN; Staatsuitgeverij: The Hague, The Netherlands, 1985. [Google Scholar]
  33. Riahi, K.; Van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; O’Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.; Dellink, R.; Fricko, O.; et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Chang. 2017, 42, 153–168. [Google Scholar] [CrossRef]
  34. Hoylman, Z.H.; Holden, Z.; Bocinsky, R.K.; Ketchum, D.; Swanson, A.; Jencso, K. Optimizing drought assessment for soil moisture deficits. Water Resour. Res. 2024, 60, e2023WR036087. [Google Scholar]
  35. Qin, Y.; Yang, D.; Lei, H.; Xu, K.; Xu, X. Comparative analysis of drought based on precipitation and soil moisture indices in Haihe basin of North China during the period of 1960–2010. J. Hydrol. 2015, 526, 55–67. [Google Scholar] [CrossRef]
  36. Halwatura, D.; McIntyre, N.; Lechner, A.M.; Arnold, S. Capability of meteorological drought indices for detecting soil moisture droughts. J. Hydrol. Reg. Stud. 2017, 12, 396–412. [Google Scholar] [CrossRef]
Water 17 01056 g002
Figure 2. Development of the cumulative potential precipitation deficit in 2005 (average over the irrigation area) and three drought indices: the deficit on October 1 (DOct1 = 48 mm), the maximum deficit (Dmax = 89 mm, reached on July 18), and the maximum increase in deficit since April 1 (DIApr1 = 111 mm).
Figure 2. Development of the cumulative potential precipitation deficit in 2005 (average over the irrigation area) and three drought indices: the deficit on October 1 (DOct1 = 48 mm), the maximum deficit (Dmax = 89 mm, reached on July 18), and the maximum increase in deficit since April 1 (DIApr1 = 111 mm).
Water 17 01056 g002
Water 17 01056 g003
Figure 3. Cumulative potential precipitation deficit in 2019 measured from 1 April (blue graph, left y-axis) and 1 January (red graph, right y-axis). The maximum increase in PD is denoted as DIApr1 (for the period from 1 April) and DIwet (for the period from January 1).
Figure 3. Cumulative potential precipitation deficit in 2019 measured from 1 April (blue graph, left y-axis) and 1 January (red graph, right y-axis). The maximum increase in PD is denoted as DIApr1 (for the period from 1 April) and DIwet (for the period from January 1).
Water 17 01056 g003
Water 17 01056 g004
Figure 4. Relationship between five drought indices and irrigation amounts I: (a) DOct1, (b) Dmax, (c) DIApr1, (d) DIGDD, (e) DIwet.
Figure 4. Relationship between five drought indices and irrigation amounts I: (a) DOct1, (b) Dmax, (c) DIApr1, (d) DIGDD, (e) DIwet.
Water 17 01056 g004
Water 17 01056 g005
Figure 5. Trend of DIwet for the years from the 2001–2022 period (irrigation area).
Figure 5. Trend of DIwet for the years from the 2001–2022 period (irrigation area).
Water 17 01056 g005
Water 17 01056 g006
Figure 6. Change in drought index DIGDD (a) and DIwet (b) in 2100 compared to 2005 for meteorological station De Bilt. The 2100 values are based on transformed time series from 1990 to 2020.
Figure 6. Change in drought index DIGDD (a) and DIwet (b) in 2100 compared to 2005 for meteorological station De Bilt. The 2100 values are based on transformed time series from 1990 to 2020.
Water 17 01056 g006
Table 1. Irrigation amounts I (Mm3/yr) in the period 2001–2021 [16].
Table 1. Irrigation amounts I (Mm3/yr) in the period 2001–2021 [16].
YearIYearIYearIYearIYearIYearIYearI
2001432004452007372010802013662016382019215
2002432005362008352011792014402017802020269
20031552006892009532012222015682018264202144
Table 2. Characteristics of the five drought indices. See text for more details.
Table 2. Characteristics of the five drought indices. See text for more details.
Start Date PDMax PDMin PD
DOct1Apr 1PD on Oct 10.00
DmaxApr 1Max between Apr 1 and Oct 10.00
DIApr1Apr 1Max between Apr 1 and Oct 1Min before Max
DIGDD1st day GDD > 440 °CMax between 1st day and Oct 1Min before Max
DIwetJan 1Max between Jan 1 and Oct 1Min before Max
Table 3. Five drought indices for the irrigation area, the date when the GDD reached a value of 440 °C, and the date when PD was at its maximum.
Table 3. Five drought indices for the irrigation area, the date when the GDD reached a value of 440 °C, and the date when PD was at its maximum.
Drought Index (mm)Date (mmdd)Drought Index (mm)Date (mmdd)
DOct1DmaxDIApr1DIGDDDIwet440max DOct1DmaxDIApr1DIGDDDIwet440max
20015124153153153Apr 7Aug 120122446757580Mar 26Sep 10
20026774799191May 17June 302013143207205186220Apr 26Sep 6
2003198202214211237Apr 12Sep 2720142049717175Mar 14Jul 4
2004580999999Apr 2Jun 172015101196202190202Apr 9Aug 13
20054889111111111Apr 2Jul 1820169697117117124Apr 3Sep 28
2006136192198180198Apr 25Jul 29201786159160161181Mar 30Jun 27
200715106103119119Mar 9May 62018328336342338361Apr 9Sep 20
200895132140140140Mar 16Jul 62019244280280294300Mar 22Sep 22
2009204205202186210Apr 11Sep 282020272301299333333Mar 10Sep 22
201052199210178210Apr 20Jul 2520218191103103110Mar 31Sep 26
201164170169169195Apr 2Jul 11
Table 4. Correlation (%) between drought indices; Spearman Rs (blue) above, Pearson R (red) below.
Table 4. Correlation (%) between drought indices; Spearman Rs (blue) above, Pearson R (red) below.
DOct181808181
89Dmax989899
8899DIApr19799
909898DIGDD99
89999999DIwet
Table 5. p-values from the permutation test; each row shows the p-values of an index with the other indices, with values lower than 0.05 colored red.
Table 5. p-values from the permutation test; each row shows the p-values of an index with the other indices, with values lower than 0.05 colored red.
DOct10.9090.8650.9990.993
0.091Dmax0.4920.9750.915
0.1350.571DIApr10.9920.952
0.0010.0250.008DIGDD0.000
0.0070.0850.0481.000DIwet
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Witte, J.-P.M.; van den Eertwegh, G.A.P.H.; Torfs, P.J.J.F. Absolute Meteorological Drought Indices Validated Against Irrigation Amounts. Water 2025, 17, 1056. https://doi.org/10.3390/w17071056

AMA Style

Witte J-PM, van den Eertwegh GAPH, Torfs PJJF. Absolute Meteorological Drought Indices Validated Against Irrigation Amounts. Water. 2025; 17(7):1056. https://doi.org/10.3390/w17071056

Chicago/Turabian Style

Witte, Jan-Philip M., Gé A. P. H. van den Eertwegh, and Paul J. J. F. Torfs. 2025. "Absolute Meteorological Drought Indices Validated Against Irrigation Amounts" Water 17, no. 7: 1056. https://doi.org/10.3390/w17071056

APA Style

Witte, J.-P. M., van den Eertwegh, G. A. P. H., & Torfs, P. J. J. F. (2025). Absolute Meteorological Drought Indices Validated Against Irrigation Amounts. Water, 17(7), 1056. https://doi.org/10.3390/w17071056

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop