Flow Pattern and Turbulent Kinetic Energy Analysis Around Tandem Piers: Insights from k-ε Modelling and Acoustic Doppler Velocimetry Measurements
Abstract
1. Introduction
2. Numerical Model
2.1. Hydrodynamic Model
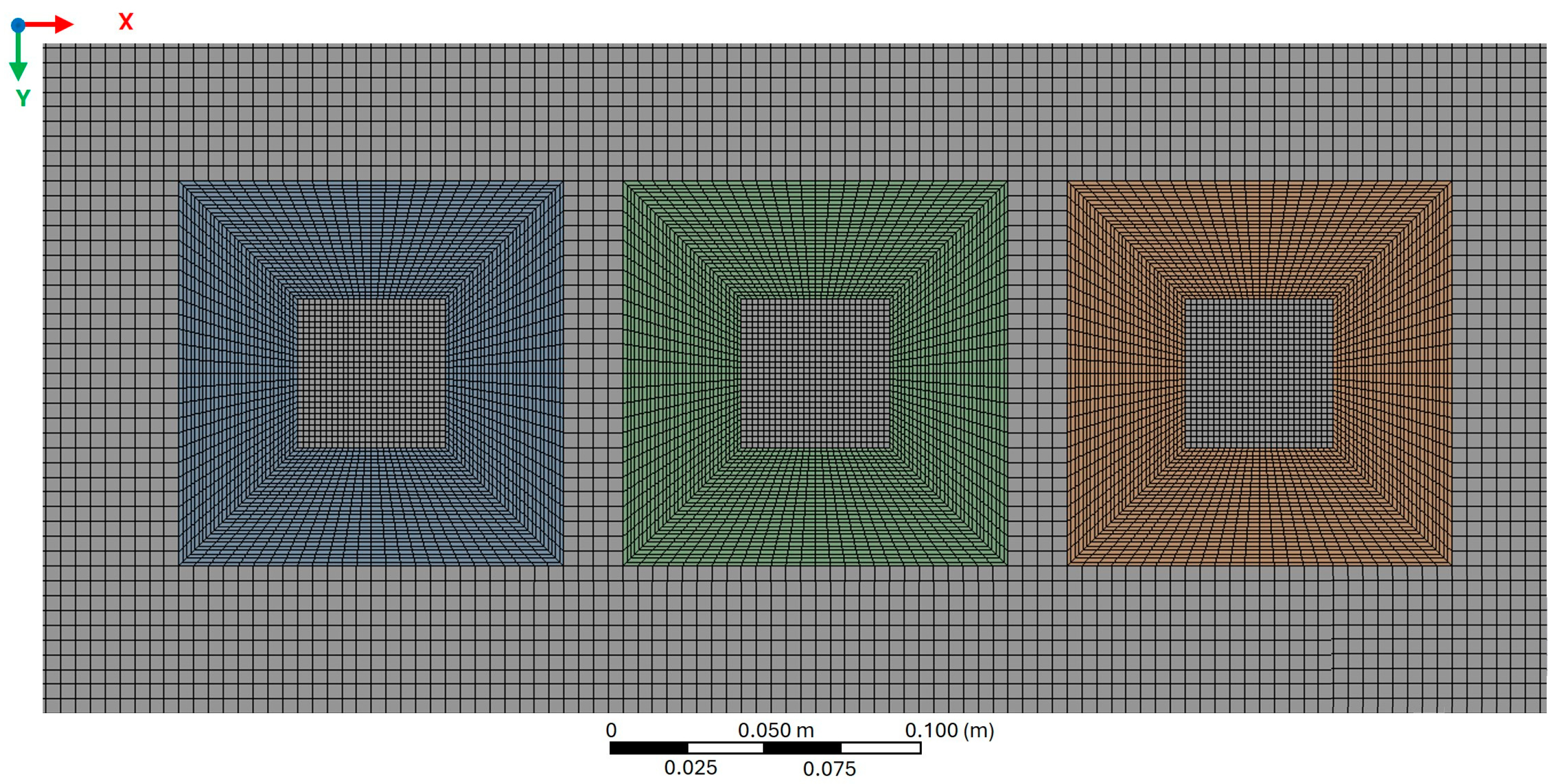
2.2. Numerical Setup
3. Experimental Setup
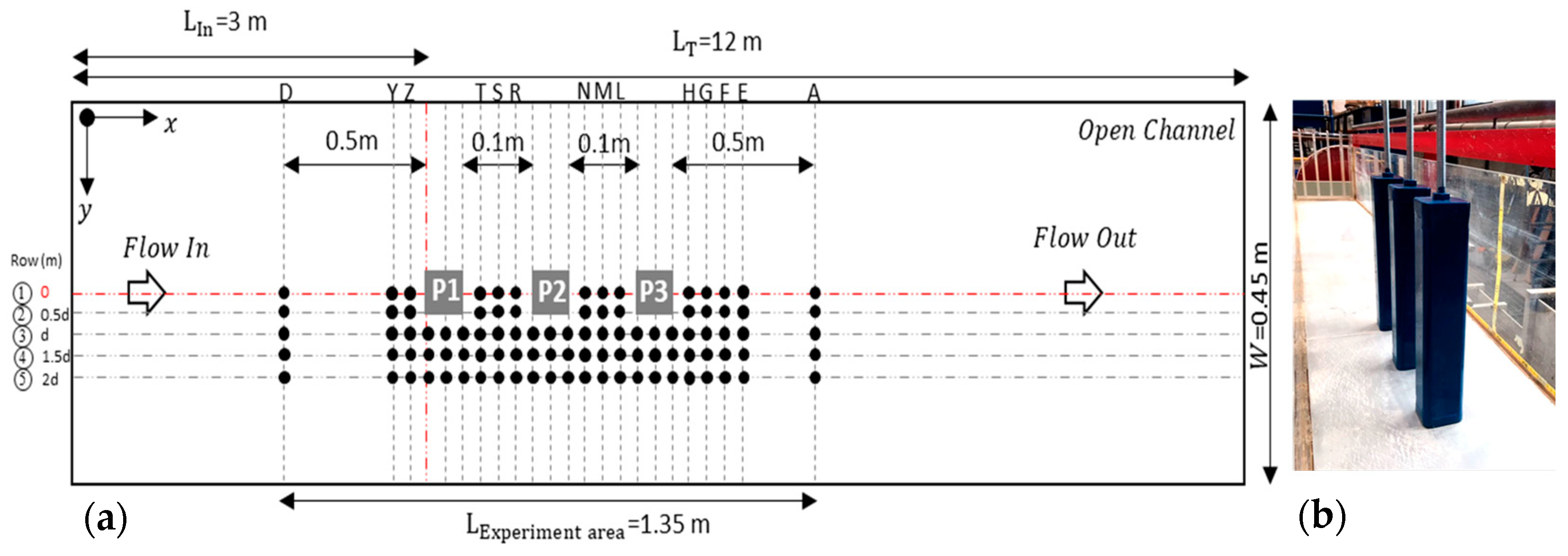
3.1. Hydraulic Model
3.2. Acoustic Doppler Velocimetry (ADV)
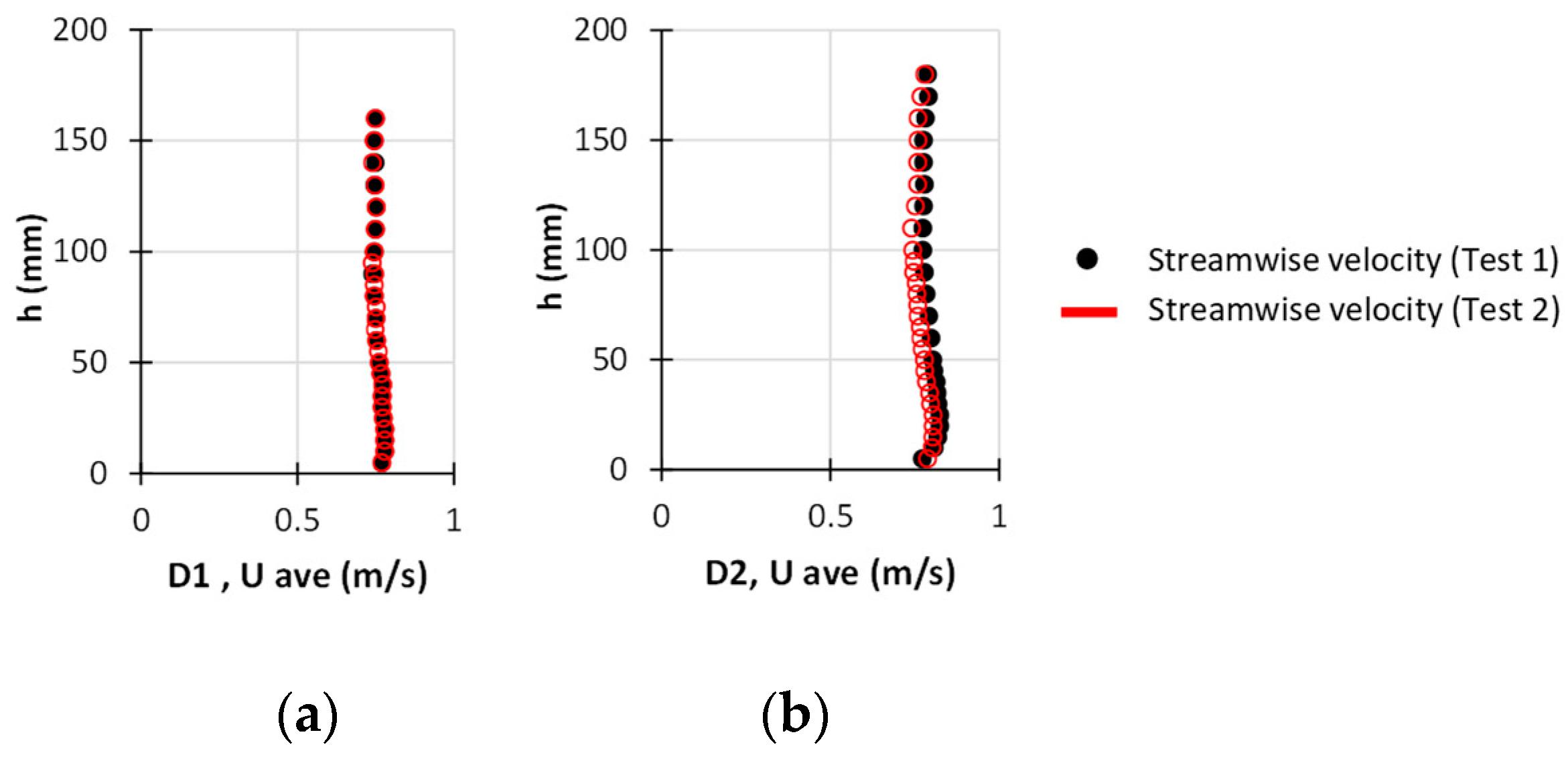
3.3. Uncertainty Analysis
4. Results and Discussion
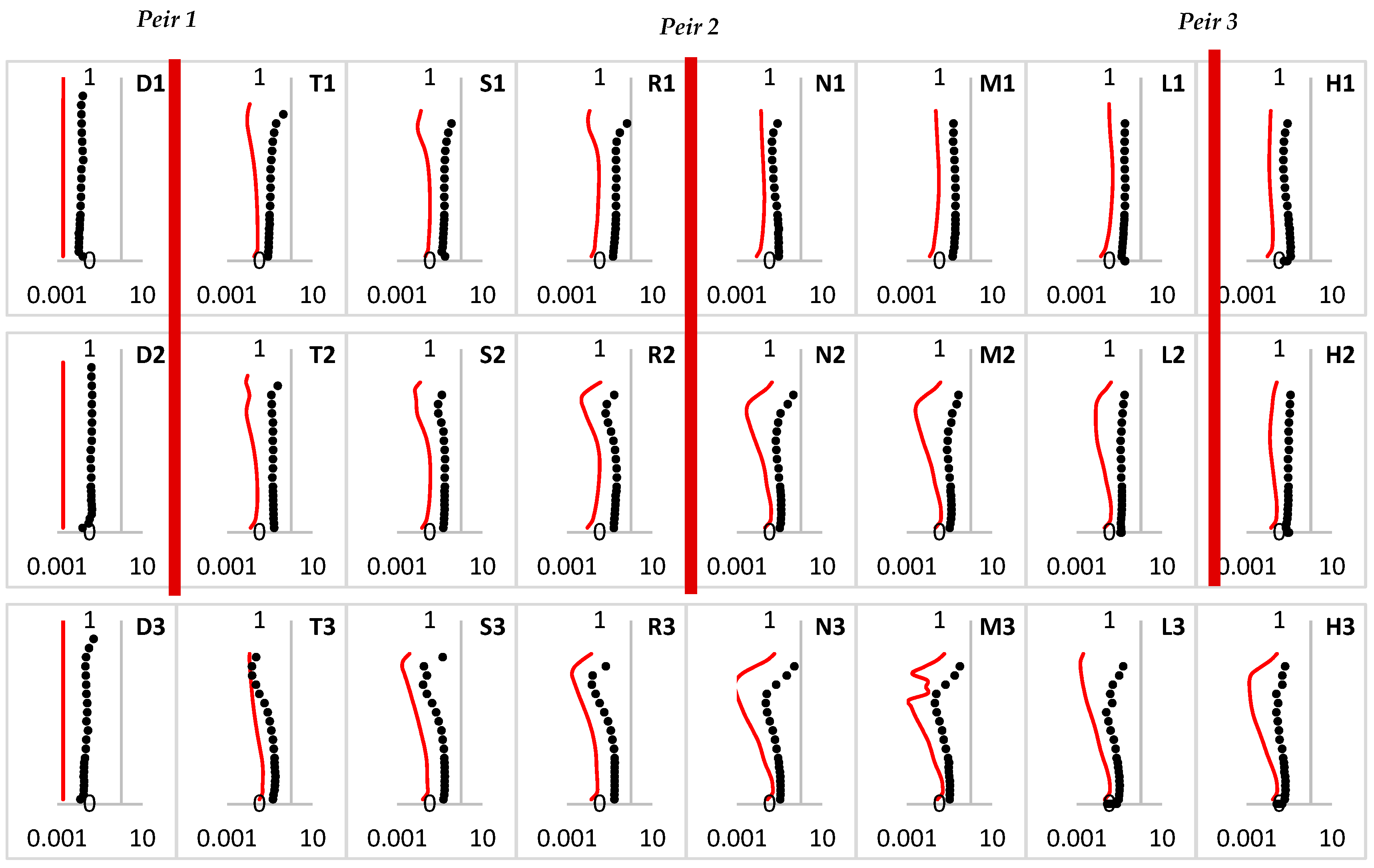
4.1. Validation Process
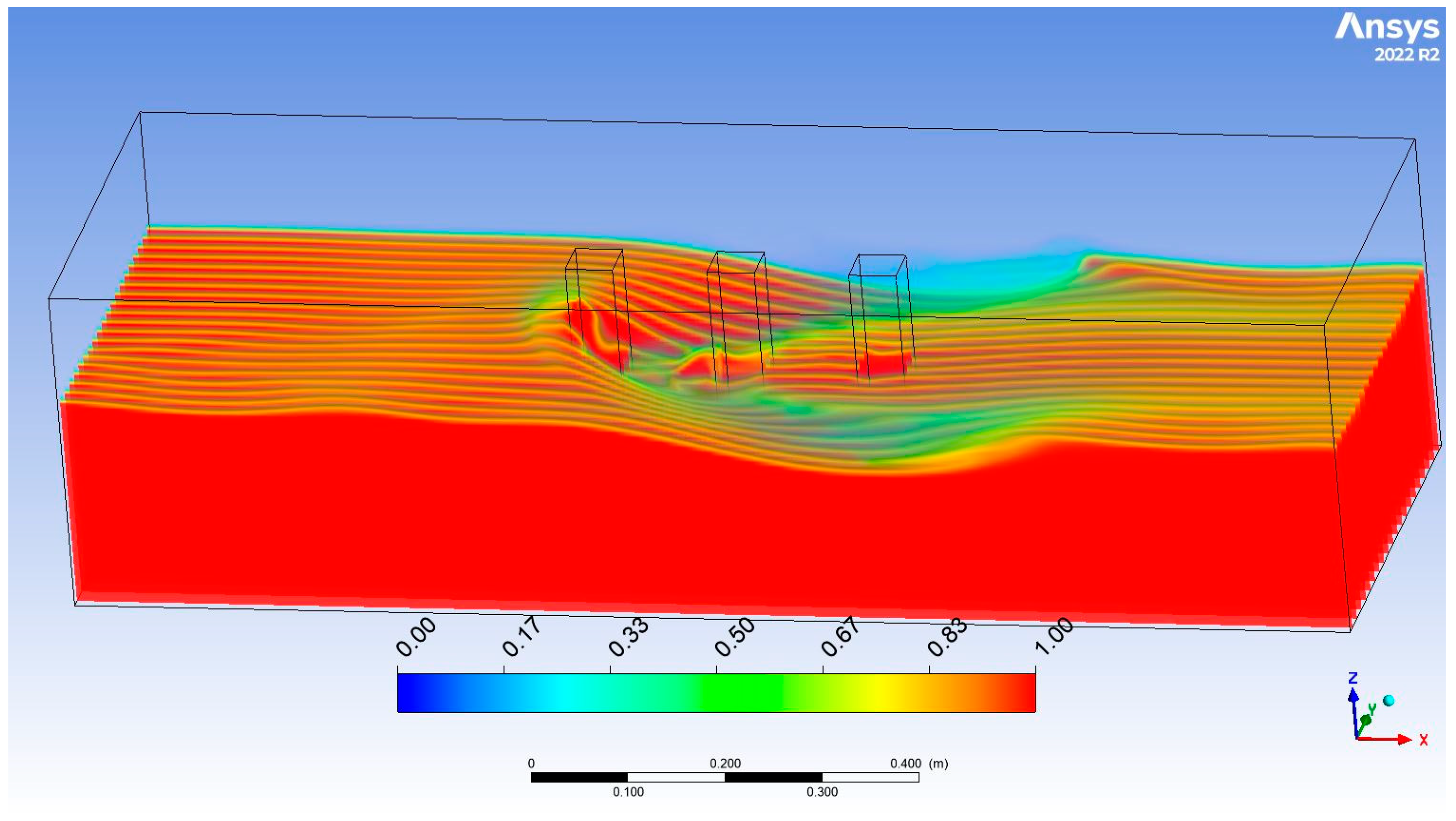
4.2. Numerical Analysis of Free-Surface Flow Around Three Tandem Piers
4.3. Turbulent Kinetic Energy (TKE) Distribution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, K.H.; Karim, O. Simulation of flow around piers. J. Hydraul. Res. 2002, 40, 161–174. [Google Scholar]
- Dey, S.; Barbhuiya, A.K. 3D flow field in a scour hole at a wing-wall abutment. J. Hydraul. Res. 2006, 44, 33–50. [Google Scholar]
- Mutlu Sumer, B. Mathematical modelling of scour: A review. J. Hydraul. Res. 2007, 45, 723–735. [Google Scholar] [CrossRef]
- Kocaman, S. Prediction of backwater profiles due to bridges in a compound channel using CFD. Adv. Mech. Eng. 2014, 6, 905217. [Google Scholar]
- Soori, S.; Karami, H. Laboratory study on relative energy loss and backwater rise at bridge piers and abutment. Model. Earth Syst. Environ. 2024, 10, 1359–1373. [Google Scholar]
- Pagliara, S.; Carnacina, I. Temporal scour evolution at bridge piers: Effect of wood debris roughness and porosity. J. Hydraul. Res. 2010, 48, 3–13. [Google Scholar]
- Soori, S.; Babaali, H.; Soori, N. An optimal design of the inlet and outlet obstacles at USBR II Stilling Basin. Int. J. Sci. Eng. Appl. 2017, 6, 134–142. [Google Scholar]
- Bressan, F.; Ballio, F.; Armenio, V. Turbulence around a scoured bridge abutment. J. Turbul. 2011, 12, N3. [Google Scholar] [CrossRef]
- Rodi, W.; Constantinescu, G.; Stoesser, T. Large-Eddy Simulation in Hydraulics; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Keylock, C.; Constantinescu, G.; Hardy, R. The application of computational fluid dynamics to natural river channels: Eddy resolving versus mean flow approaches. Geomorphology 2012, 179, 1–20. [Google Scholar] [CrossRef]
- Kara, S.; Kara, M.C.; Stoesser, T.; Sturm, T.W. Free-surface versus rigid-lid LES computations for bridge-abutment flow. J. Hydraul. Eng. 2015, 141, 04015019. [Google Scholar]
- Al-Jubouri, M.; Ray, R.P.; Abbas, E.H. Advanced numerical simulation of scour around bridge piers: Effects of pier geometry and debris on scour depth. J. Mar. Sci. Eng. 2024, 12, 1637. [Google Scholar] [CrossRef]
- Alvarez, L.V.; Grams, P.E. An Eddy-Resolving Numerical Model to Study Turbulent Flow, Sediment, and Bed Evolution Using Detached Eddy Simulation in a Lateral Separation Zone at the Field-Scale. J. Geophys. Res. Earth Surf. 2021, 126, e2021JF006149. [Google Scholar] [CrossRef]
- Ikani, N.; Pu, J.H.; Hanmaiahgari, P.R.; Kumar, B.; Al-Qadami, E.H.H.; Razi, M.A.M.; Zang, S.-Y. Computational and experimental analysis of flow velocity and complex vortex formation around a group of bridge piers. Water Sci. Eng. 2025; in press. [Google Scholar] [CrossRef]
- Huang, W.; Yang, Q.; Xiao, H. CFD modeling of scale effects on turbulence flow and scour around bridge piers. Comput. Fluids 2009, 38, 1050–1058. [Google Scholar] [CrossRef]
- Chatterjee, D.; Mazumder, B.S.; Ghosh, S.; Debnath, K. Turbulent flow characteristics over forward-facing obstacle. J. Turbul. 2021, 22, 141–179. [Google Scholar] [CrossRef]
- Uchida, T.; Ato, T.; Kobayashi, D.; Maghrebi, M.F.; Kawahara, Y. Hydrodynamic forces on emergent cylinders in non-uniform flow. Environ. Fluid Mech. 2022, 22, 1355–1379. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Ghzayel, A.; Beaudoin, A. Three-dimensional numerical study of a local scour downstream of a submerged sluice gate using two hydro-morphodynamic models, SedFoam and FLOW-3D. Comptes Rendus Mécanique 2023, 351, 525–550. [Google Scholar] [CrossRef]
- Lai, Y.G.; Liu, X.; Bombardelli, F.A.; Song, Y. Three-dimensional numerical modeling of local scour: A state-of-the-art review and perspective. J. Hydraul. Eng. 2022, 148, 03122002. [Google Scholar] [CrossRef]
- Calixto, N.C.; Zambrano, M.C.; Castaño, A.G.; Soto, G.C. Analysis of a three-dimensional numerical modeling approach for predicting scour processes in longitudinal walls of granular bedding rivers. EUREKA Phys. Eng. 2023, 4, 168–179. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Chatelain, M.; Proust, S. Open-channel flows through emergent rigid vegetation: Effects of bed roughness and shallowness on the flow structure and surface waves. Phys. Fluids 2021, 33, 106602. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W.H. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef]
- Sahin, B.; Ozturk, N.A. Behaviour of flow at the junction of cylinder and base plate in deep water. Measurement 2009, 42, 225–240. [Google Scholar] [CrossRef]
- Sahin, B.; Akilli, H.; Karakus, C.; Akar, M.; Ozkul, E. Qualitative and quantitative measurements of horseshoe vortex formation in the junction of horizontal and vertical plates. Measurement 2010, 43, 245–254. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Zang, Z. Experimental and numerical investigation of local scour around a submerged vertical circular cylinder in steady currents. Coast. Eng. 2010, 57, 709–721. [Google Scholar] [CrossRef]
- Ettema, R.; Kirkil, G.; Muste, M. Similitude of large-scale turbulence in experiments on local scour at cylinders. J. Hydraul. Eng. 2006, 132, 33–40. [Google Scholar] [CrossRef]
- Cheng, Z.; Koken, M.; Constantinescu, G. Approximate methodology to account for effects of coherent structures on sediment entrainment in RANS simulations with a movable bed and applications to pier scour. Adv. Water Resour. 2018, 120, 65–82. [Google Scholar] [CrossRef]
- Sinha, S.K.; Sotiropoulos, F.; Odgaard, A.J. Three-dimensional numerical model for flow through natural rivers. J. Hydraul. Eng. 1998, 124, 13–24. [Google Scholar] [CrossRef]
- Dargahi, B. Controlling mechanism of local scouring. J. Hydraul. Eng. 1990, 116, 1197–1214. [Google Scholar] [CrossRef]
- Xiong, W.; Cai, C.S.; Kong, B.; Kong, X. CFD simulations and analyses for bridge-scour development using a dynamic-mesh updating technique. J. Comput. Civ. Eng. 2016, 30, 04014121. [Google Scholar]
- Guemou, B.; Seddini, A.; Ghenim, A.N. Numerical investigations of the round-nosed bridge pier length effects on the bed shear stress. Prog. Comput. Fluid Dyn. Int. J. 2016, 16, 313–321. [Google Scholar]
- Soori, S.; Hajikandi, H. Numerical Computation of Flow Reattachment Lengthovera Backward-Facing Step at High Reynolds Number. Int. J. Res. Eng. 2017, 4, 145–149. [Google Scholar]
- Svsndl, P.; Suresh, K. Simulation of flow behavior around bridge piers using ANSYS–CFD. Int. J. Eng. Sci. Invent. (IJESI) 2018, 7, 13–22. [Google Scholar]
- Lahsaei, K.; Vaghefi, M.; Sedighi, F.; Chooplou, C.A. Numerical simulation of flow pattern at a divergent pier in a bend with different relative curvature radii using ansys fluent. Eng. Rev. 2022, 42, 63–85. [Google Scholar]
- Ahmed, A.A.; Ismael, A.A. Comparing the 3D Flow Behavior Around Different Bridge Pier Shapes Using CFD-Fluent: Implications for Reducing Local Scour. Math. Model. Eng. Probl. 2024, 11, 1315–1322. [Google Scholar]
- Mueller, D.S.; Abad, J.D.; García, C.M.; Gartner, J.W.; García, M.H.; Oberg, K.A. Errors in acoustic Doppler profiler velocity measurements caused by flow disturbance. J. Hydraul. Eng. 2007, 133, 1411–1420. [Google Scholar]
- Ikani, N.; Pu, J.H.; Taha, T.; Hanmaiahgarib, P.R.; Penna, N. Bursting phenomenon created by bridge piers group in open channel flow. Environ. Fluid Mech. 2023, 23, 125–140. [Google Scholar]
- Ikani, N.; Pu, J.H.; Zang, S.; Al-Qadami, E.H.H.; Razi, A. Detailed turbulent structures investigation around piers group induced flow. Exp. Therm. Fluid Sci. 2024, 152, 111112. [Google Scholar]
- Chanson, H.; Leng, X. Acoustic Doppler Velocimetry in Transient Free-Surface Flows: Field and Laboratory Experience with Bores and Surges. J. Hydraul. Eng. 2024, 150, 04024034. [Google Scholar]
- Roache, P. Verification and Validation in Computational Science and Engineering; Hermosa Publishers: Hermosa Beach, CA, USA, 1998. [Google Scholar]
- Babuska, I.; Oden, J.T. Verification and validation in computational engineering and science: Basic concepts. Comput. Methods Appl. Mech. Eng. 2004, 193, 4057–4066. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Trucano, T.G. Verification and validation in computational fluid dynamics. Prog. Aerosp. Sci. 2002, 38, 209–272. [Google Scholar]
- Mojtahedi, A.; Soori, N.; Mohammadian, M. Energy dissipation evaluation for stepped spillway using a fuzzy inference system. SN Appl. Sci. 2020, 2, 1466. [Google Scholar]
- Tu, J.; Yeoh, G.H.; Liu, C.; Tao, Y. Computational Fluid Dynamics: A Practical Approach; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Oveici, E.; Tayari, O.; Jalalkamali, N. Experimental (ADV & PIV) and numerical (CFD) comparisons of 3D flow pattern around intact and damaged bridge piers. Pertanika J. Sci. Technol. 2020, 28, 523–544. [Google Scholar]
- Abad, J.D.; Musalem, R.A.; García, C.M.; Cantero, M.I.; García, M.H. Exploratory study of the influence of the wake produced by acoustic Doppler velocimeter probes on the water velocities within measurement volume. Crit. Transit. Water Environ. Resour. Manag. 2004, 1–9. [Google Scholar] [CrossRef]
- Sarkardeh, H.; Zarrati, A.R.; Jabbari, E.; Marosi, M. Numerical simulation and analysis of flow in a reservoir in the presence of vortex. Eng. Appl. Comput. Fluid Mech. 2014, 8, 598–608. [Google Scholar]
- Quaresma, A.; Pinheiro, A.N. Analysis of flows in pool-type fishways using acoustic Doppler velocimetry (ADV) and computational fluid dynamics (CFD). In Proceedings of the 10th International Symposium on Ecohydraulics, Trodheim, Norway, 23–27 June 2014. [Google Scholar]
- Shaheed, R.; Mohammadian, A.; Gildeh, H.K. A comparison of standard k–ε and realizable k–ε turbulence models in curved and confluent channels. Environ. Fluid Mech. 2019, 19, 543–568. [Google Scholar] [CrossRef]
- Rodi, W. Turbulence modeling and simulation in hydraulics: A historical review. J. Hydraul. Eng. 2017, 143, 03117001. [Google Scholar] [CrossRef]
- Pu, J.H.; Hussain, K.; Tait, S.J. Simulation of turbulent free surface obstructed flow within channels. In Proceedings of the 32nd IAHR World Congress, Venice, Italy, 1–6 July 2007. [Google Scholar]
- Pu, J.H.; Cheng, N.-S.; Tan, S.K.; Shao, S. Source term treatment of SWEs using surface gradient upwind method. J. Hydraul. Res. 2012, 50, 145–153. [Google Scholar]
- Pu, J.H.; Shao, S.; Huang, Y. Numerical and experimental turbulence studies on shallow open channel flows. J. Hydro Environ. Res. 2014, 8, 9–19. [Google Scholar]
- Argyropoulos, C.D.; Markatos, N. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar]
- Rodi, W. Turbulence Models and Their Application in Hydraulics; Routledge: Oxford, UK, 2017. [Google Scholar]
- Graf, W.; Istiarto, I. Flow pattern in the scour hole around a cylinder. J. Hydraul. Res. 2002, 40, 13–20. [Google Scholar] [CrossRef]
- Pu, J.H. Turbulence modelling of shallow water flows using Kolmogorov approach. Comput. Fluids 2015, 115, 66–74. [Google Scholar] [CrossRef]
- Kim, S.-E.; Choudhury, D.; Patel, B. Computations of Complex Turbulent Flows Using the Commercial Code Fluent, in Modeling Complex Turbulent Flows; Springer: Berlin/Heidelberg, Germany, 1999; pp. 259–276. [Google Scholar]
- Fluent, A. Ansys Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2011; Volume 15317, pp. 724–746. [Google Scholar]
- Chiew, Y.-M. Mechanics of riprap failure at bridge piers. J. Hydraul. Eng. 1995, 121, 635–643. [Google Scholar] [CrossRef]
- Discetti, S.; Coletti, F. Volumetric velocimetry for fluid flows. Meas. Sci. Technol. 2018, 29, 042001. [Google Scholar] [CrossRef]
- Pu, J.H. Velocity profile and turbulence structure measurement corrections for sediment transport-induced water-worked bed. Fluids 2021, 6, 86. [Google Scholar] [CrossRef]
- Franca, M.J.R.P.d. A Field Study of Turbulent Flows in Shallow Gravel-Bed Rivers; EPFL: Lausanne, Switzerland, 2005. [Google Scholar]
- Yu, G.; Tan, S.-K. Errors in the bed shear stress as estimated from vertical velocity profile. J. Irrig. Drain. Eng. 2006, 132, 490–497. [Google Scholar] [CrossRef]
- Khaple, S.; Hanmaiahgari, P.R.; Gaudio, R.; Dey, S. Splitter plate as a flow-altering pier scour countermeasure. Acta Geophys. 2017, 65, 957–975. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharma, N.; Pu, J.; Aamir, M.; Pandey, M. Two-dimensional turbulent burst examination and angle ratio utilization to detect scouring/sedimentation around mid-channel bar. Acta Geophys. 2021, 69, 1335–1348. [Google Scholar] [CrossRef]
- Devi, K.; Mishra, S.; Hanmaiahgari, P.R.; Pu, J.H. Wake flow field of a wall-mounted pipe with spoiler on a rough channel bed. Acta Geophys. 2023, 71, 2865–2881. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikani, N.; Pu, J.H.; Soori, S. Flow Pattern and Turbulent Kinetic Energy Analysis Around Tandem Piers: Insights from k-ε Modelling and Acoustic Doppler Velocimetry Measurements. Water 2025, 17, 1100. https://doi.org/10.3390/w17071100
Ikani N, Pu JH, Soori S. Flow Pattern and Turbulent Kinetic Energy Analysis Around Tandem Piers: Insights from k-ε Modelling and Acoustic Doppler Velocimetry Measurements. Water. 2025; 17(7):1100. https://doi.org/10.3390/w17071100
Chicago/Turabian StyleIkani, Nima, Jaan H. Pu, and Saba Soori. 2025. "Flow Pattern and Turbulent Kinetic Energy Analysis Around Tandem Piers: Insights from k-ε Modelling and Acoustic Doppler Velocimetry Measurements" Water 17, no. 7: 1100. https://doi.org/10.3390/w17071100
APA StyleIkani, N., Pu, J. H., & Soori, S. (2025). Flow Pattern and Turbulent Kinetic Energy Analysis Around Tandem Piers: Insights from k-ε Modelling and Acoustic Doppler Velocimetry Measurements. Water, 17(7), 1100. https://doi.org/10.3390/w17071100








