Sensitivity Analysis of Dissolved Oxygen in Cold Region Rivers Through Numerical Modelling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Reach and Data Availability
2.2. Model Description and Setup
2.2.1. Hydrodynamic (HD)
2.2.2. Advection–Dispersion (AD) and Water Quality
2.2.3. Ice-Cover Effects
2.3. Sensitivity Analysis Methodology
3. Results and Discussion
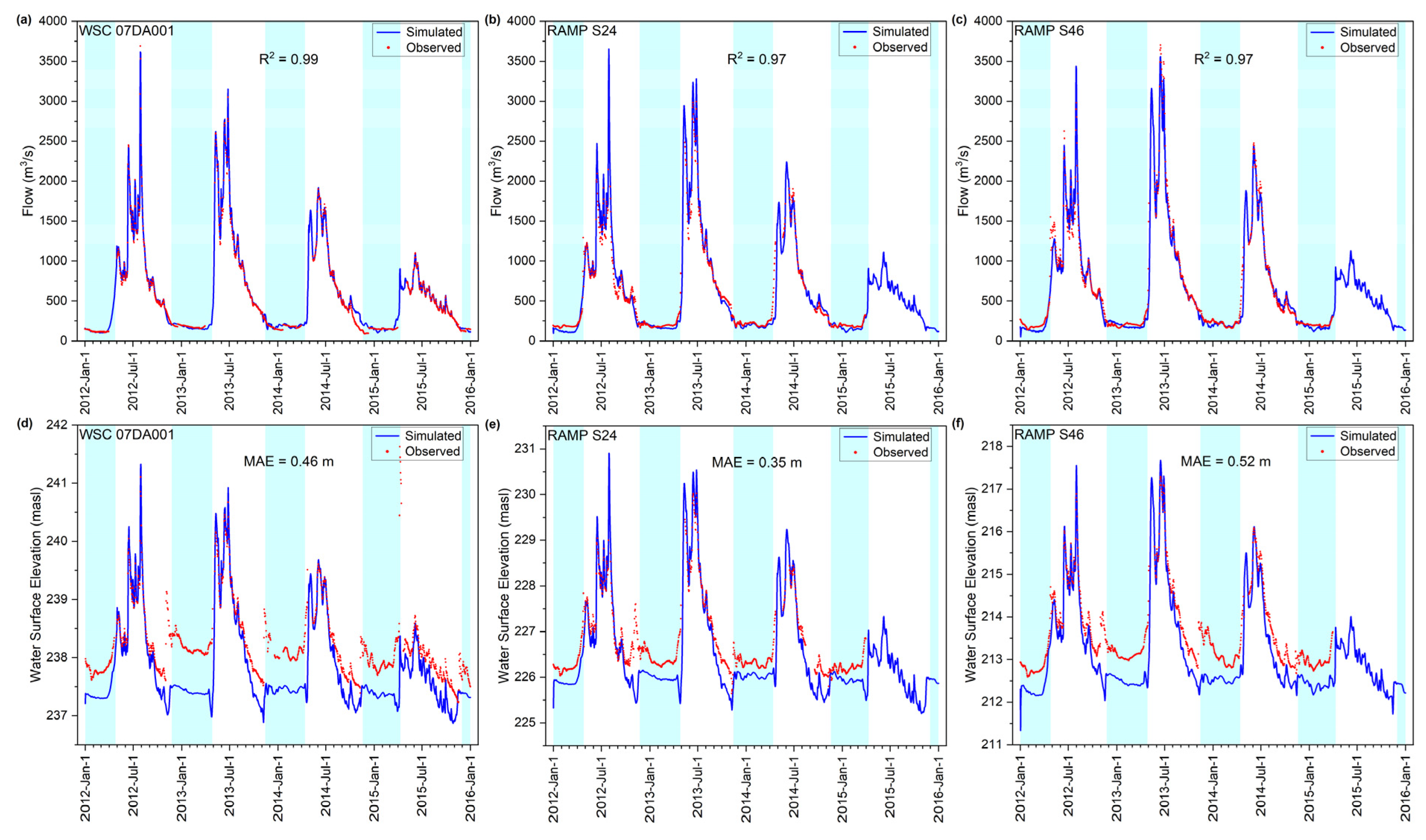
3.1. Calibration and Validation
3.1.1. Flow and Water Level
3.1.2. Water Temperature
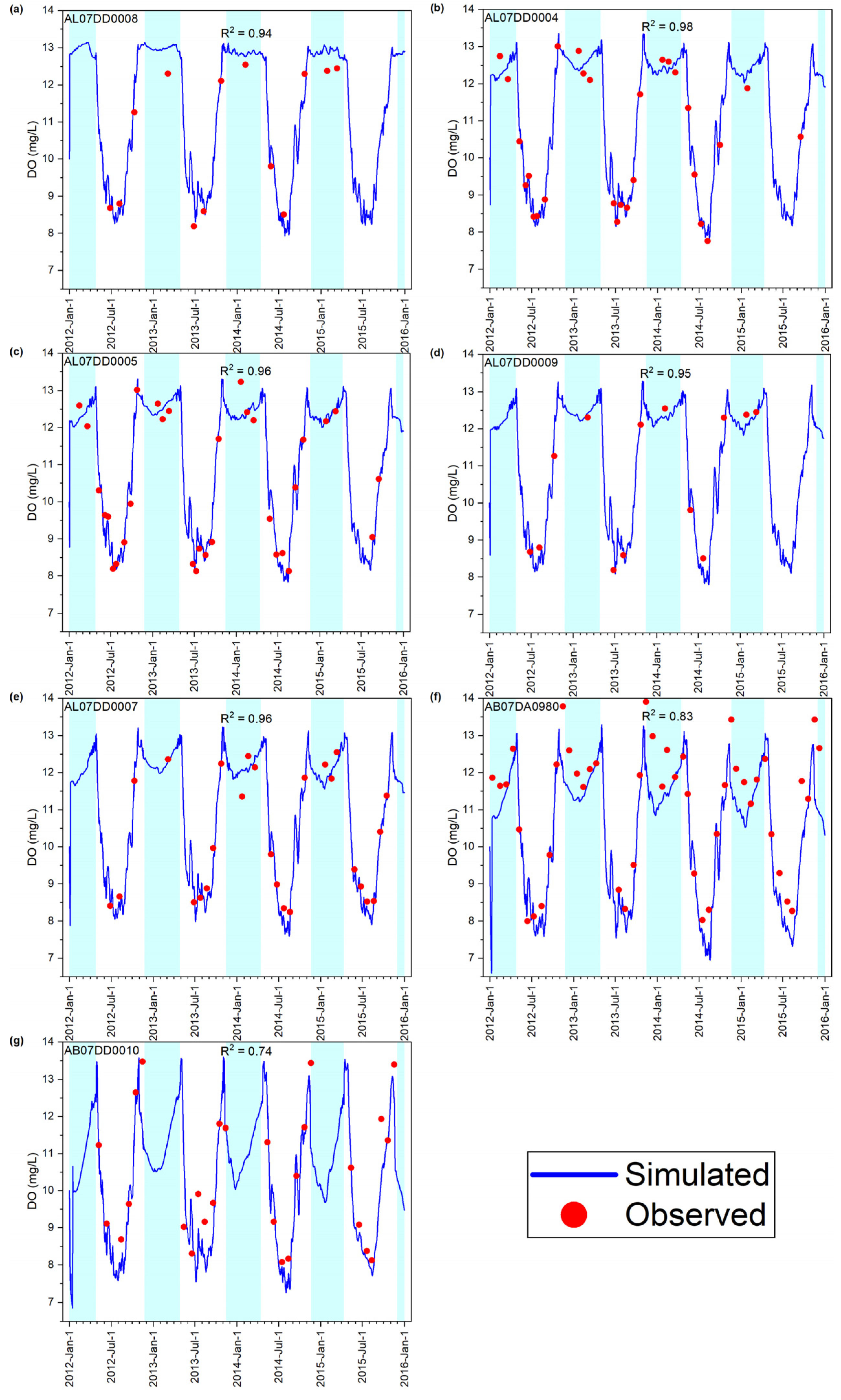
3.1.3. DO Concentration
3.2. Model Limitations
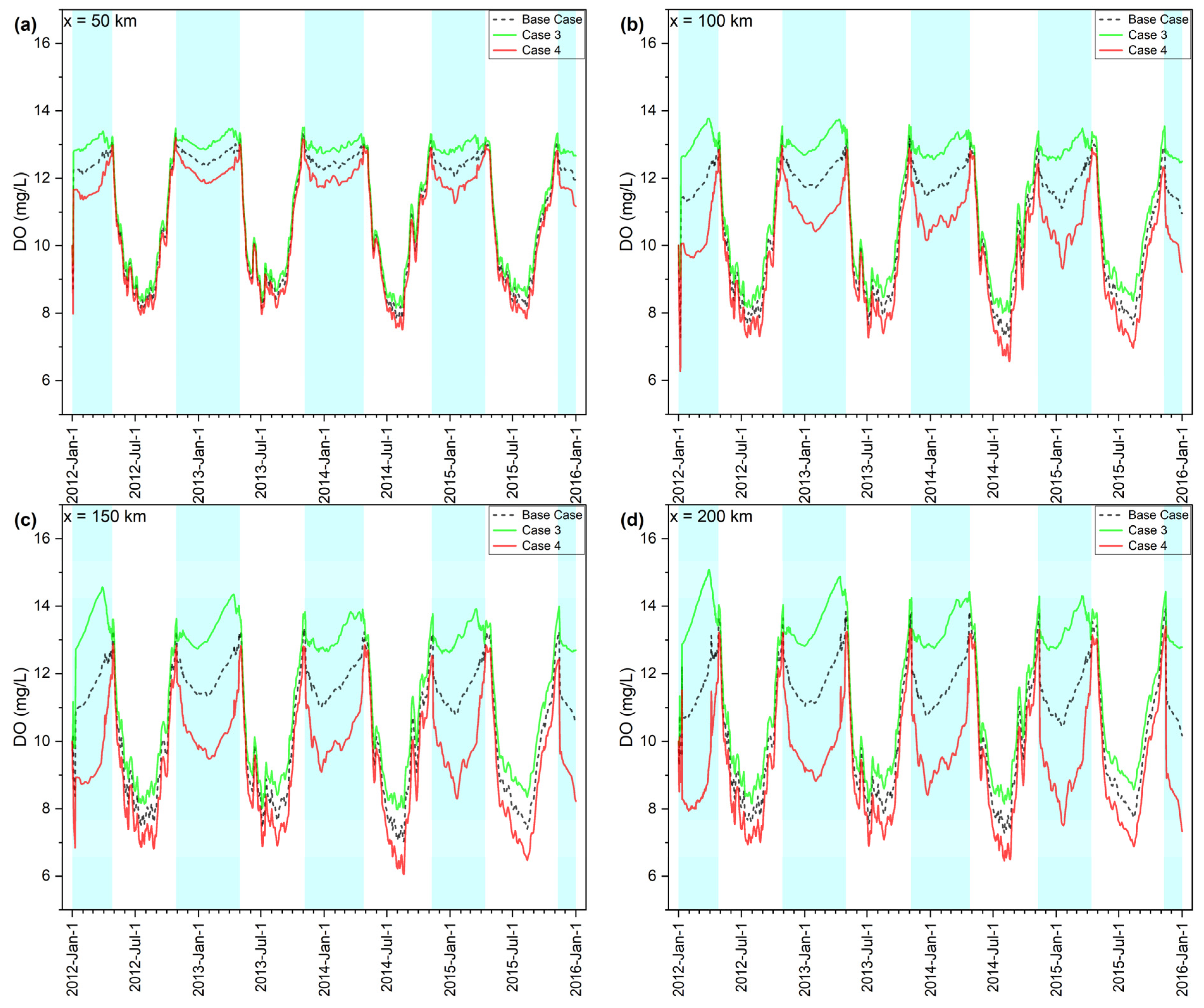
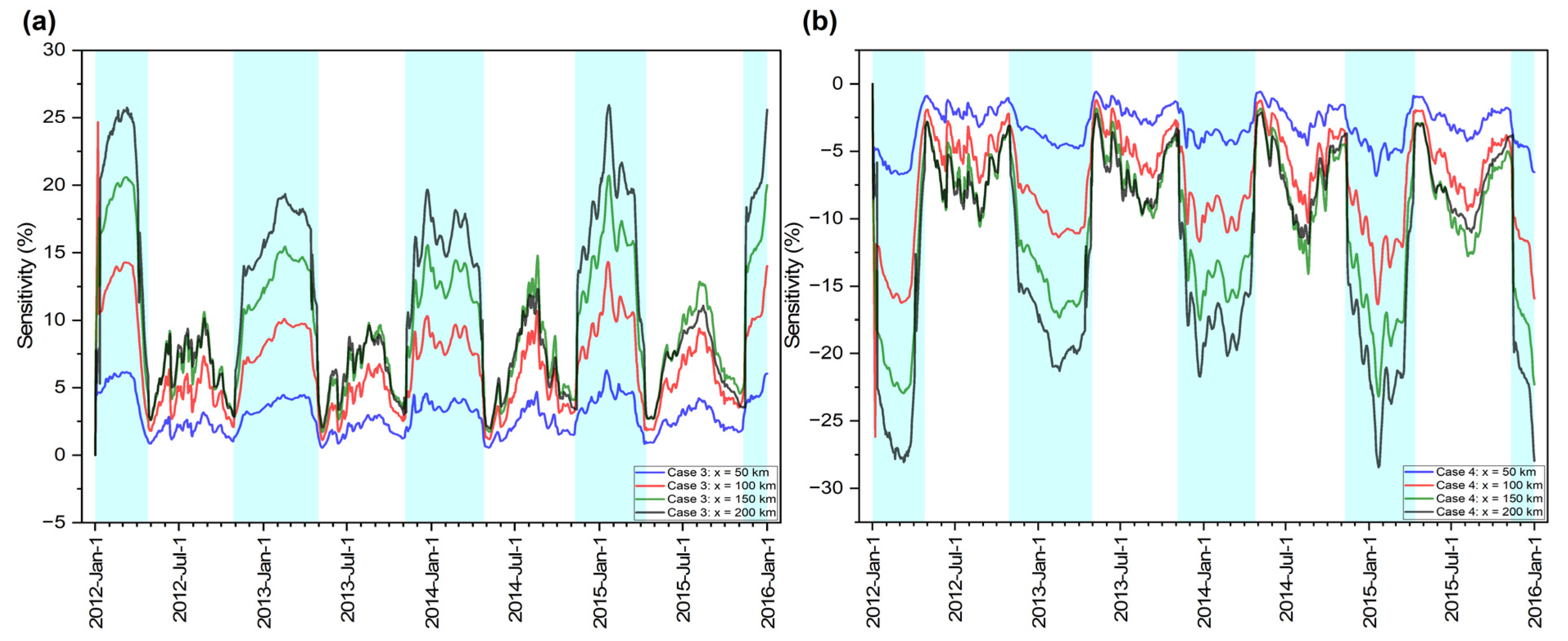
3.3. DO Sensitivity Analysis
4. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oveisy, A.; Rao, Y.R.; Leon, L.F.; Bocaniov, S.A. Three-dimensional winter modeling and the effects of ice cover on hydrodynamics, thermal structure and water quality in Lake Erie. J. Gt. Lakes Res. 2014, 40, 19–28. [Google Scholar] [CrossRef]
- Turcotte, B.; Morse, B.; Bergeron, N.E.; Roy, A.G. Sediment transport in ice-affected rivers. J. Hydrol. 2011, 409, 561–577. [Google Scholar] [CrossRef]
- Prowse, T.D. River-Ice Ecology. I: Hydrologic, Geomorphic, and Water-Quality Aspects. J. Cold Reg. Eng. 2001, 15, 1–16. [Google Scholar] [CrossRef]
- Prowse, T.; Alfredsen, K.; Beltaos, S.; Bonsal, B.R.; Bowden, W.B.; Duguay, C.R.; Korhola, A.; McNamara, J.; Vincent, W.F.; Vuglinsky, V.; et al. Effects of Changes in Arctic Lake and River Ice. AMBIO 2011, 40, 63–74. [Google Scholar] [CrossRef]
- Blackburn, J.; She, Y. A comprehensive public-domain river ice process model and its application to a complex natural river. Cold Reg. Sci. Technol. 2019, 163, 44–58. [Google Scholar] [CrossRef]
- Nafziger, J.; She, Y.; Hicks, F. Dynamic River ice processes in a river delta network. Cold Reg. Sci. Technol. 2019, 158, 275–287. [Google Scholar] [CrossRef]
- Hicks, F.E.; Phd, F.H. An Introduction to River Ice Engineering: For Civil Engineers and Geoscientists; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2016; ISBN 978-1-4927-8863-8. [Google Scholar]
- Chambers, P.A.; Brown, S.; Culp, J.M.; Lowell, R.B.; Pietroniro, A. Dissolved oxygen decline in ice-covered rivers of northern Alberta and its effects on aquatic biota. J. Aquat. Ecosyst. Stress Recovery 2000, 8, 27–38. [Google Scholar] [CrossRef]
- Martin, N.; McEachern, P.; Yu, T.; Zhu, D.Z. Model development for prediction and mitigation of dissolved oxygen sags in the Athabasca River, Canada. Sci. Total Environ. 2013, 443, 403–412. [Google Scholar] [CrossRef]
- Rajwa-Kuligiewicz, A.; Bialik, R.J.; Rowiński, P.M. Dissolved oxygen and water temperature dynamics in lowland rivers over various timescales. J. Hydrol. Hydromech. 2015, 63, 353–363. [Google Scholar] [CrossRef]
- Williams, R.J.; Boorman, D.B. Modelling in-stream temperature and dissolved oxygen at sub-daily time steps: An application to the River Kennet, UK. Sci. Total Environ. 2012, 423, 104–110. [Google Scholar] [CrossRef]
- Zdorovennova, G.; Palshin, N.; Golosov, S.; Efremova, T.; Belashev, B.; Bogdanov, S.; Fedorova, I.; Zverev, I.; Zdorovennov, R.; Terzhevik, A. Dissolved Oxygen in a Shallow Ice-Covered Lake in Winter: Effect of Changes in Light, Thermal and Ice Regimes. Water 2021, 13, 2435. [Google Scholar] [CrossRef]
- Zhi, W.; Ouyang, W.; Shen, C.; Li, L. Temperature outweighs light and flow as the predominant driver of dissolved oxygen in US rivers. Nat. Water 2023, 1, 249–260. [Google Scholar] [CrossRef]
- Whitfield, P.H.; McNaughton, B. Dissolved-oxygen depressions under ice cover in two Yukon rivers. Water Resour. Res. 1986, 22, 1675–1679. [Google Scholar] [CrossRef]
- Pietroniro, A.; Chambers, P.A.; Ferguson, M.E. Application of a Dissolved Oxygen Model to an Ice-Covered River. Can. Water Resour. J. Rev. Can. Ressour. Hydr. 1998, 23, 351–368. [Google Scholar] [CrossRef]
- Wool, T.; Ambrose, R.B.; Martin, J.L.; Comer, A. WASP 8: The Next Generation in the 50-year Evolution of USEPA’s Water Quality Model. Water 2020, 12, 1398. [Google Scholar] [CrossRef] [PubMed]
- Żelazny, M.; Bryła, M.; Ozga-Zielinski, B.; Walczykiewicz, T. Applicability of the WASP Model in an Assessment of the Impact of Anthropogenic Pollution on Water Quality—Dunajec River Case Study. Sustainability 2023, 15, 2444. [Google Scholar] [CrossRef]
- Terry, J.; Lindenschmidt, K.-E. Modelling Climate Change and Water Quality in the Canadian Prairies Using Loosely Coupled WASP and CE-QUAL-W2. Water 2023, 15, 3192. [Google Scholar] [CrossRef]
- Wells, S.A. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 4.5 User Manual: Part 1 Introduction; Portland State University: Portland, OR, USA, 2024. [Google Scholar]
- Shakibaeinia, A.; Kashyap, S.; Dibike, Y.B.; Prowse, T.D. An integrated numerical framework for water quality modelling in cold-region rivers: A case of the lower Athabasca River. Sci. Total Environ. 2016, 569–570, 634–646. [Google Scholar] [CrossRef]
- Shakibaeinia, A.; Dibike, Y.B.; Kashyap, S.; Prowse, T.D.; Droppo, I.G. A numerical framework for modelling sediment and chemical constituents transport in the Lower Athabasca River. J. Soils Sediments 2017, 17, 1140–1159. [Google Scholar] [CrossRef]
- DHI. A Modelling System for Rivers and Channels User Guide; DHI: Copenhagen, Denmark, 2012. [Google Scholar]
- Chen, F.; Shen, H.T.; Jayasundara, N.C. A One-Dimensional Comprehensive River Ice Model. In Proceedings of the 18th IAHR International Symposium on Ice, Clarkson University, Potsdam, NY, USA, 28 August–1 September 2006; pp. 61–68. [Google Scholar]
- Blackburn, J.; She, Y. One-dimensional channel network modelling and simulation of flow conditions during the 2008 ice breakup in the Mackenzie Delta, Canada. Cold Reg. Sci. Technol. 2021, 189, 103339. [Google Scholar] [CrossRef]
- Blackburn, J.; She, Y. The simulation of ice jam profiles in multi-channel systems using a one-dimensional network model. Cold Reg. Sci. Technol. 2023, 208, 103796. [Google Scholar] [CrossRef]
- Blackburn, J.; She, Y.; Zhang, W. Enhancing River1D for simulating water quality in ice-affected rivers. In Proceedings of the 27th IAHR International Symposium on Ice, Gdańsk, Poland, 9–13 June 2024. [Google Scholar]
- Sun, X.Y.; Newham, L.T.H.; Croke, B.F.W.; Norton, J.P. Three complementary methods for sensitivity analysis of a water quality model. Environ. Model. Softw. 2012, 37, 19–29. [Google Scholar] [CrossRef]
- Li, D.; Jiang, P.; Hu, C.; Yan, T. Comparison of local and global sensitivity analysis methods and application to thermal hydraulic phenomena. Prog. Nucl. Energy 2023, 158, 104612. [Google Scholar] [CrossRef]
- Qin, C.; Jin, Y.; Tian, M.; Ju, P.; Zhou, S. Comparative Study of Global Sensitivity Analysis and Local Sensitivity Analysis in Power System Parameter Identification. Energies 2023, 16, 5915. [Google Scholar] [CrossRef]
- Akomeah, E.; Chun, K.P.; Lindenschmidt, K.-E. Dynamic water quality modelling and uncertainty analysis of phytoplankton and nutrient cycles for the upper South Saskatchewan River. Environ. Sci. Pollut. Res. 2015, 22, 18239–18251. [Google Scholar] [CrossRef]
- Hosseini, N.; Chun, K.P.; Wheater, H.; Lindenschmidt, K.-E. Parameter Sensitivity of a Surface Water Quality Model of the Lower South Saskatchewan River—Comparison Between Ice-On and Ice-Off Periods. Environ. Model. Assess. 2017, 22, 291–307. [Google Scholar] [CrossRef]
- Hosseini, N.; Johnston, J.; Lindenschmidt, K.-E. Impacts of Climate Change on the Water Quality of a Regulated Prairie River. Water 2017, 9, 199. [Google Scholar] [CrossRef]
- Terry, J.A.; Sadeghian, A.; Lindenschmidt, K.-E. Modelling Dissolved Oxygen/Sediment Oxygen Demand under Ice in a Shallow Eutrophic Prairie Reservoir. Water 2017, 9, 131. [Google Scholar] [CrossRef]
- Akomeah, E.; Lindenschmidt, K.-E. Seasonal Variation in Sediment Oxygen Demand in a Northern Chained River-Lake System. Water 2017, 9, 254. [Google Scholar] [CrossRef]
- Palshin, N.I.; Zdorovennova, G.E.; Zdorovennov, R.E.; Efremova, T.V.; Gavrilenko, G.G.; Terzhevik, A.Y. Effect of Under-Ice Light Intensity and Convective Mixing on Chlorophyll a Distribution in a Small Mesotrophic Lake. Water Resour. 2019, 46, 384–394. [Google Scholar] [CrossRef]
- Canada-Alberta JOINT Oil Sands Environmental Monitoring Information Portal (JOSMP). Available online: https://www.canada.ca/en/environment-climate-change/services/oil-sands-monitoring.html (accessed on 10 December 2024).
- Regional Aquatics Monitoring Program (RAMP). Available online: http://www.ramp-alberta.org/data/ClimateHydrology/climate/dailyClimate.aspx (accessed on 10 December 2024).
- Alberta’s River Water Quality Monitoring Program (WQP). Available online: https://environment.extranet.gov.ab.ca/apps/WaterQuality/dataportal/ (accessed on 10 December 2024).
- DHI MIKE HYDRO River User Guide. Available online: https://manuals.mikepoweredbydhi.help/latest/Water_Resources/MIKEHydro_River_UserGuide.pdf (accessed on 3 February 2025).
- DHI. MIKE ECO Lab, Numerical Lab for Ecological and Agent Based Modelling User Guide. Available online: https://manuals.mikepoweredbydhi.help/latest/General/MIKE_ECO_Lab_UserGuide.pdf (accessed on 4 February 2025).
- DHI WQ Templates, Scientific Description. Available online: https://manuals.mikepoweredbydhi.help/latest/General/MIKE_ECO_Lab_ShortScientific.pdf (accessed on 6 February 2025).
- Chen, Q.S.; Xie, X.H.; Du, Q.Y.; Liu, Y. Parameters sensitivity analysis of DO in water quality model of QUAL2K. IOP Conf. Ser. Earth Environ. Sci. 2018, 191, 012030. [Google Scholar] [CrossRef]
- Beltaos, S. Resistance of river ice covers to mobilization and implications for breakup progression in Peace River, Canada. Hydrol. Process. 2023, 37, e14850. [Google Scholar] [CrossRef]
- Thornton, P.E.; Rosenbloom, N.A. Ecosystem model spin-up: Estimating steady state conditions in a coupled terrestrial carbon and nitrogen cycle model. Ecol. Model. 2005, 189, 25–48. [Google Scholar] [CrossRef]


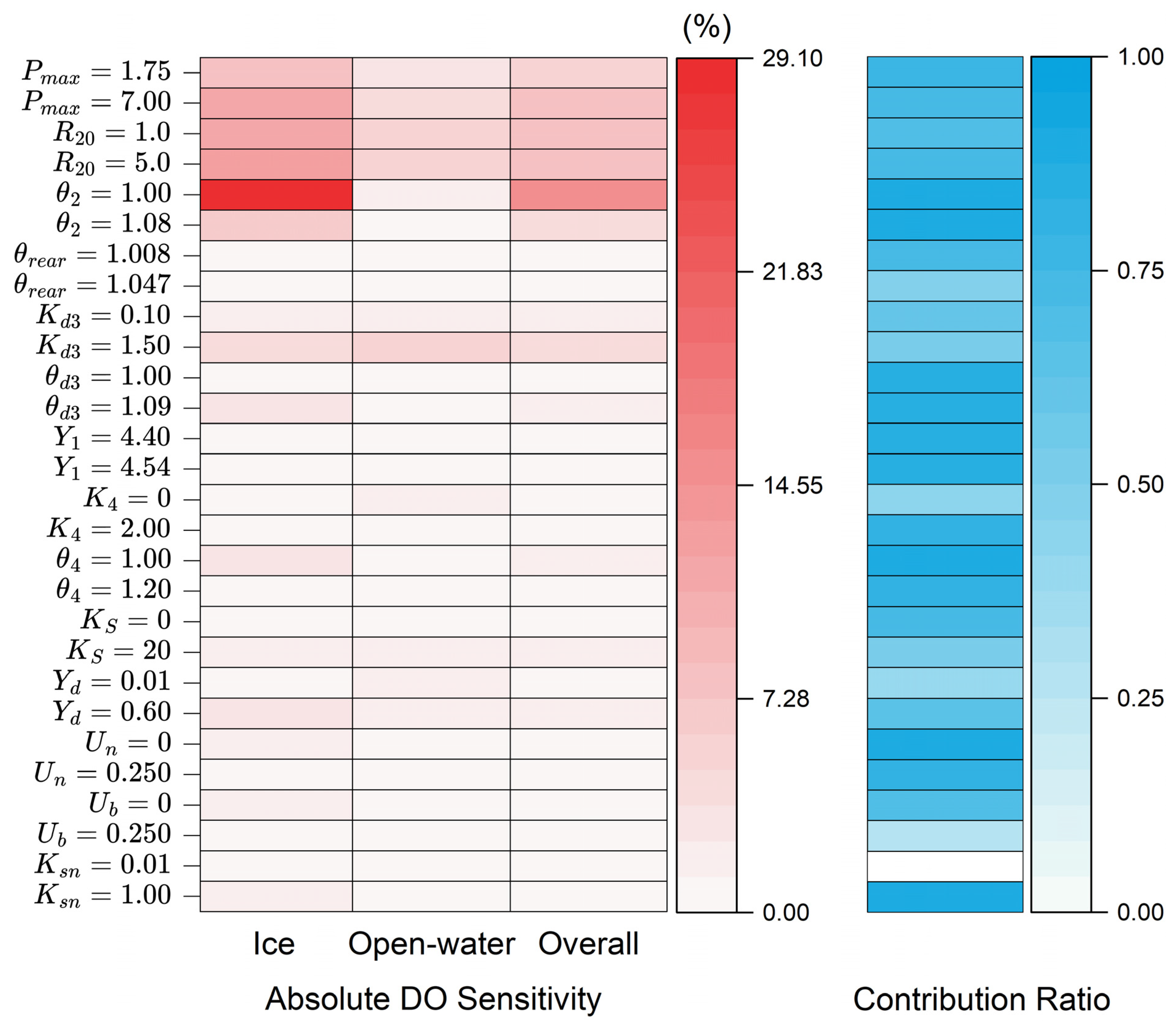
| Parameter | Unit | Calibrated Value | Testing Range |
|---|---|---|---|
| Maximum oxygen production by photosynthesis, Pmax | gO2/m2/day | 3.50 | 1.75–7.00 |
| Respiration of animals and plants, R20 | gO2/m2/day | 3.0 | 1.0–5.0 |
| Arrhenius temperature coefficient for respiration, Θ2 | - | 1.05 | 1.00–1.08 |
| Arrhenius temperature coefficient for reaeration, Θrear | - | 1.020 | 1.008–1.047 |
| Rate of BOD decay, Kd3 | 1/day | 0.25 | 0.10–1.50 |
| Arrhenius temperature coefficient for BOD decay, Θd3 | - | 1.02 | 1.00–1.09 |
| Oxygen demand by nitrification, Y1 | gO2/gNH4 | 4.47 | 4.40–4.54 |
| Rate of ammonia decay, K4 | 1/day | 1.54 | 0–2.00 |
| Arrhenius temperature coefficient for nitrification, Θ4 | - | 1.13 | 1.00–1.20 |
| Half-saturation oxygen concentration, Ks | mg/L | 2 | 0–20 |
| Ratio of ammonia released at BOD decay, Yd | gNH4/gBOD | 0.29 | 0.01–0.60 |
| Uptake of ammonia by plants, Un | - | 0.066 | 0–0.250 |
| Uptake of ammonia by bacteria, Ub | - | 0.109 | 0–0.250 |
| Half-saturation coefficient for ammonia, Ksn | mg/L | 0.05 | 0.01–1.00 |
| x = 50 km | x = 100 km | x = 150 km | x = 200 km | |
|---|---|---|---|---|
| Case | Sensitivity (%) | Sensitivity (%) | Sensitivity (%) | Sensitivity (%) |
| Case 1: Pmax = 1.75 | −1.83 (WS) * | −4.32 (WS) | −6.34 (S) | −7.54 (S) |
| Case 2: Pmax = 7.00 | 3.39 (WS) | 7.24 (S) | 10.48 (HS) | 12.62 (HS) |
| Case 3: R20 = 1.0 | 3.01 (WS) | 6.73 (S) | 9.91 (S) | 11.34 (HS) |
| Case 4: R20 = 5.0 | −3.16 (WS) | −7.38 (S) | −10.85 (HS) | −12.33 (HS) |
| Case 5: Θ2 = 1.00 | −5.70 (S) | −13.40 (HS) | −19.91 (HS) | −23.56 (HS) |
| Case 6: Θ2 = 1.08 | 1.45 (WS) | 3.21 (WS) | 4.80 (WS) | 5.74 (S) |
| Case 7: Θrear = 1.008 | −0.01 (I) | −0.19 (I) | −0.23 (I) | −0.22 (I) |
| Case 8: Θrear = 1.047 | −0.19 (I) | −0.53 (I) | −0.84 (I) | −0.98 (I) |
| Case 9: Kd3 = 0.10 | 1.04 (WS) | 2.04 (WS) | 2.20 (WS) | 2.01 (WS) |
| Case 10: Kd3 = 1.50 | −4.71 (WS) | −5.77 (S) | −4.72 (WS) | −3.69 (WS) |
| Case 11: Θd3 = 1.00 | −0.07 (I) | −0.31 (I) | −0.43 (I) | −0.46 (I) |
| Case 12: Θd3 = 1.09 | 1.04 (WS) | 1.98 (WS) | 2.10 (WS) | 2.04 (WS) |
| Case 13: Y1 = 4.40 | −0.07 (I) | −0.29 (I) | −0.41 (I) | −0.43 (I) |
| Case 14: Y1 = 4.54 | −0.08 (I) | −0.33 (I) | −0.46 (I) | −0.48 (I) |
| Case 15: K4 = 0 | 0.45 (I) | 1.06 (WS) | 1.25 (WS) | 1.13 (WS) |
| Case 16: K4 = 2.00 | −0.19 (I) | −0.54 (I) | −0.67 (I) | −0.67 (I) |
| Case 17: Θ4 = 1.00 | −1.22 (WS) | −2.07 (WS) | −2.28 (WS) | −2.26 (WS) |
| Case 18: Θ4 = 1.20 | 0.15 (I) | 0.23 (I) | 0.19 (I) | 0.15 (I) |
| Case 19: Ks = 0 | −0.18 (I) | −0.55 (I) | −0.77 (I) | −0.82 (I) |
| Case 20: Ks = 20 | 0.72 (I) | 1.49 (WS) | 2.06 (WS) | 2.22 (WS) |
| Case 21: Yd = 0.01 | 0.26 (I) | 1.02 (WS) | 1.38 (WS) | 1.29 (WS) |
| Case 22: Yd = 0.60 | −0.47 (I) | −2.09 (WS) | −3.01 (WS) | −3.05 (WS) |
| Case 23: Un = 0 | −0.19 (I) | −0.88 (I) | −1.33 (WS) | −1.49 (WS) |
| Case 24: Un = 0.250 | 0.12 (I) | 0.27 (I) | 0.30 (I) | 0.30 (I) |
| Case 25: Ub = 0 | −0.21 (I) | −0.91 (I) | −1.30 (WS) | −1.32 (WS) |
| Case 26: Ub = 0.250 | 0.10 (I) | 0.41 (I) | 0.56 (I) | 0.52 (I) |
| Case 27: Ksn = 0 | 0.00 (I) | 0.00 (I) | 0.00 (I) | 0.00 (I) |
| Case 28: Ksn = 1.00 | −0.18 (I) | −0.80 (I) | −1.20 (WS) | −1.33 (WS) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Blackburn, J.; She, Y.; Zhang, W. Sensitivity Analysis of Dissolved Oxygen in Cold Region Rivers Through Numerical Modelling. Water 2025, 17, 1135. https://doi.org/10.3390/w17081135
Wu Y, Blackburn J, She Y, Zhang W. Sensitivity Analysis of Dissolved Oxygen in Cold Region Rivers Through Numerical Modelling. Water. 2025; 17(8):1135. https://doi.org/10.3390/w17081135
Chicago/Turabian StyleWu, Yifan, Julia Blackburn, Yuntong She, and Wenming Zhang. 2025. "Sensitivity Analysis of Dissolved Oxygen in Cold Region Rivers Through Numerical Modelling" Water 17, no. 8: 1135. https://doi.org/10.3390/w17081135
APA StyleWu, Y., Blackburn, J., She, Y., & Zhang, W. (2025). Sensitivity Analysis of Dissolved Oxygen in Cold Region Rivers Through Numerical Modelling. Water, 17(8), 1135. https://doi.org/10.3390/w17081135







