Evaluation of Simulation Results of HEC-RAS Coupled 1D/2D and 2D Modeling Approaches Through Scenario-Based Analysis
Abstract
:1. Introduction
2. Data Collection, Materials, and Methods
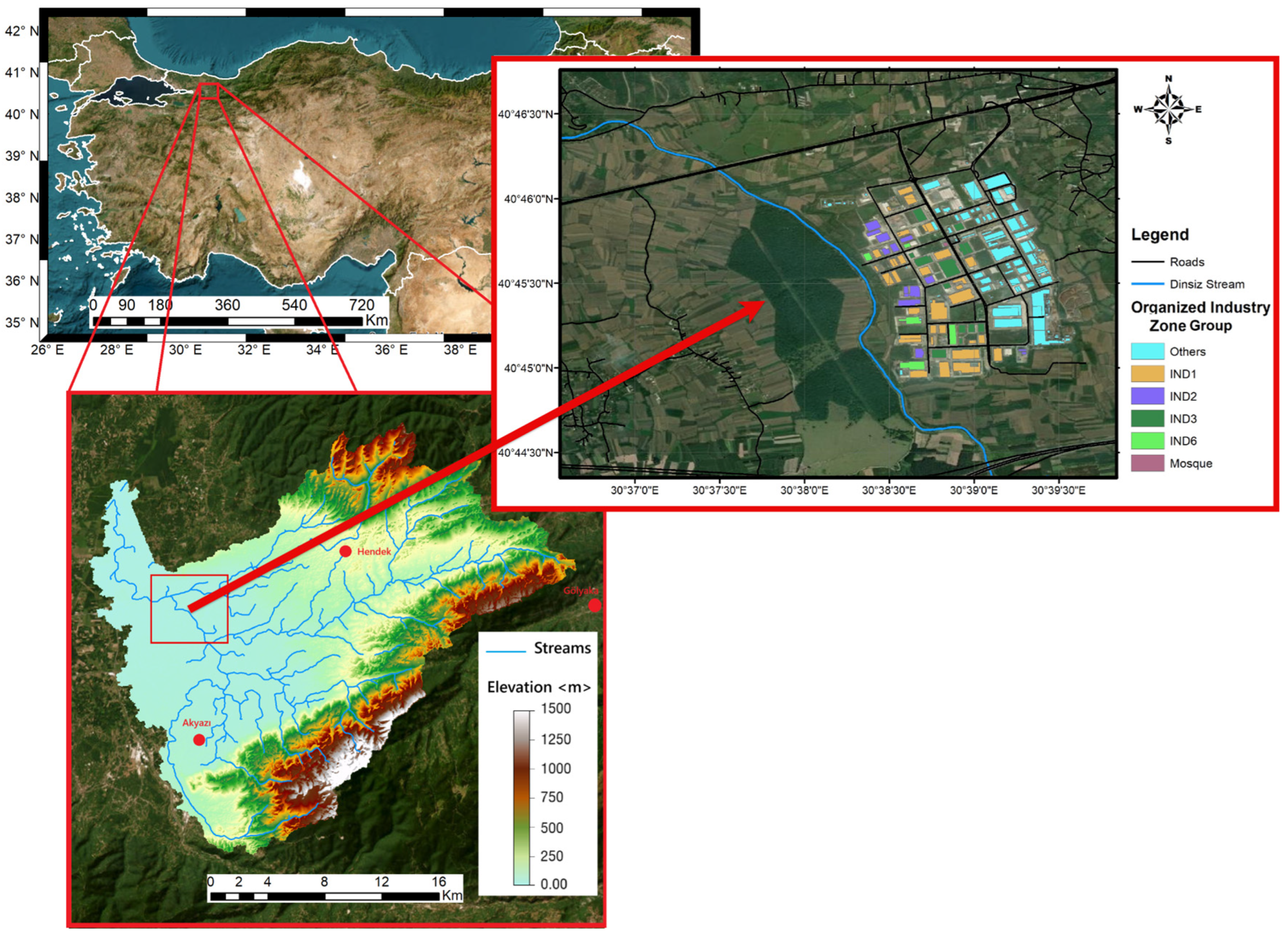
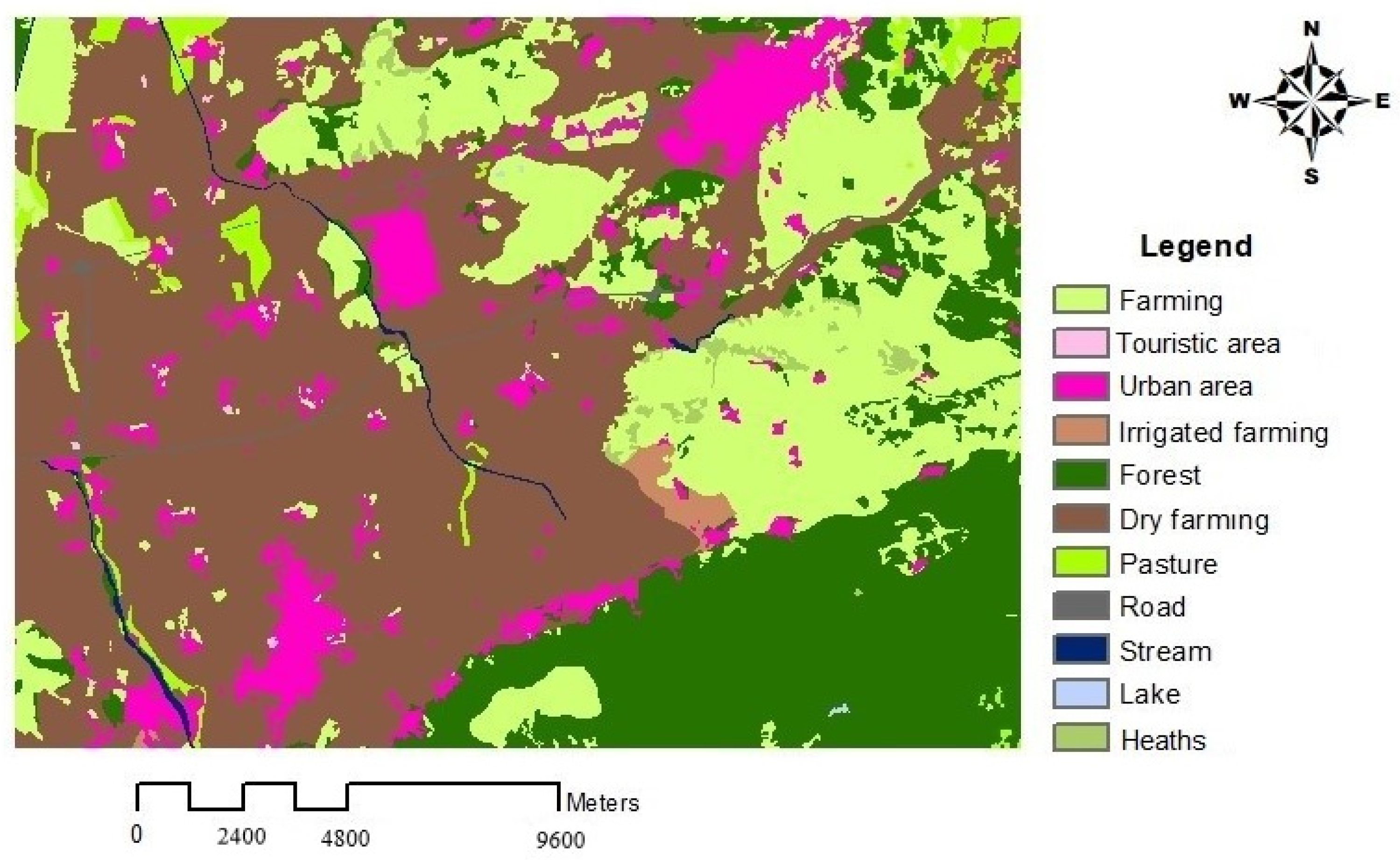
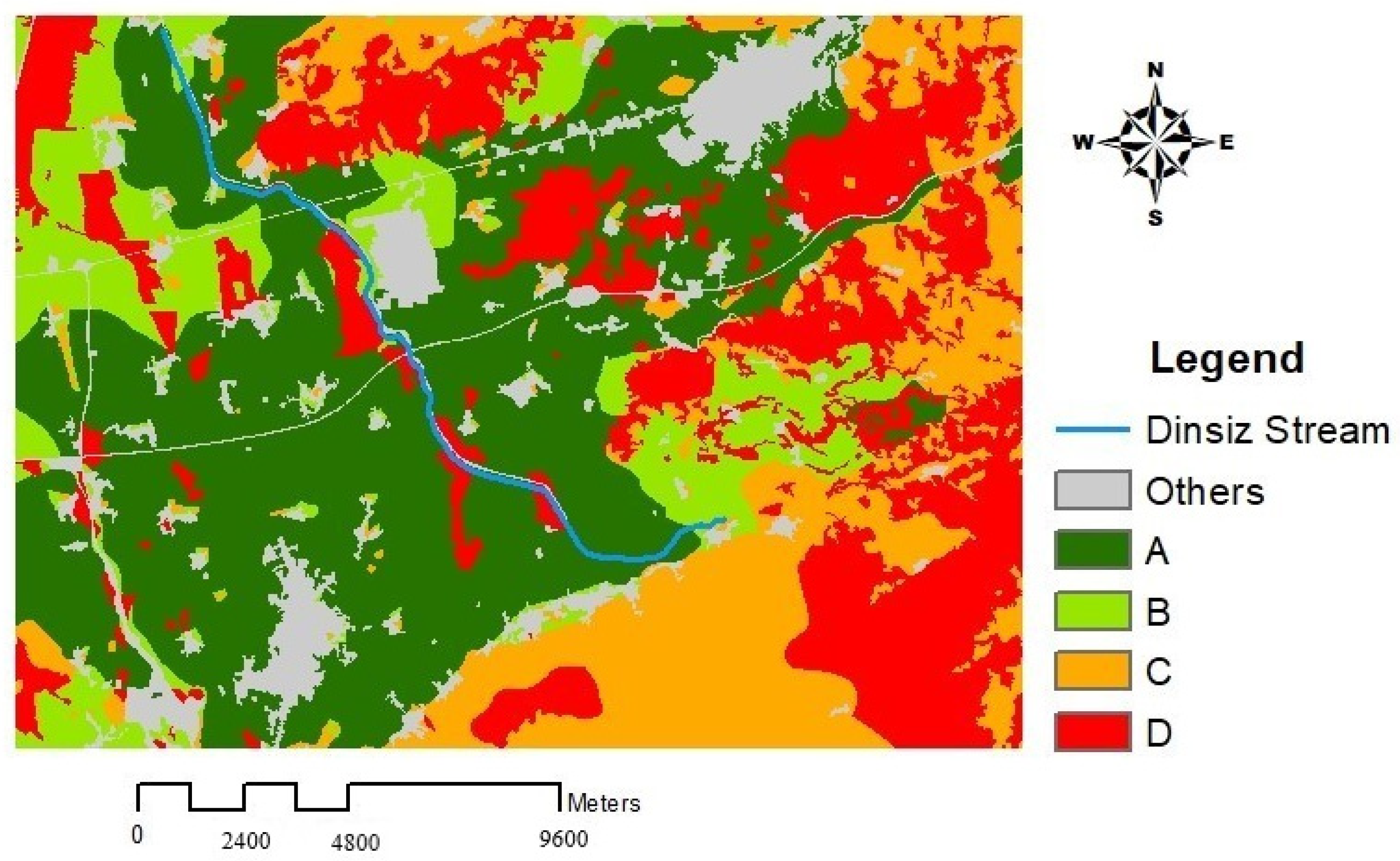
2.1. Study Area
2.2. Hydrological Steps
2.2.1. Rainfall Data
2.2.2. Creation of Hydrographs Using HEC-HMS (Hydrological Model)
2.3. Hydraulics Steps
2.3.1. HEC-RAS
2.3.2. 2D Model
2.3.3. Coupled 1D/2D Modelling
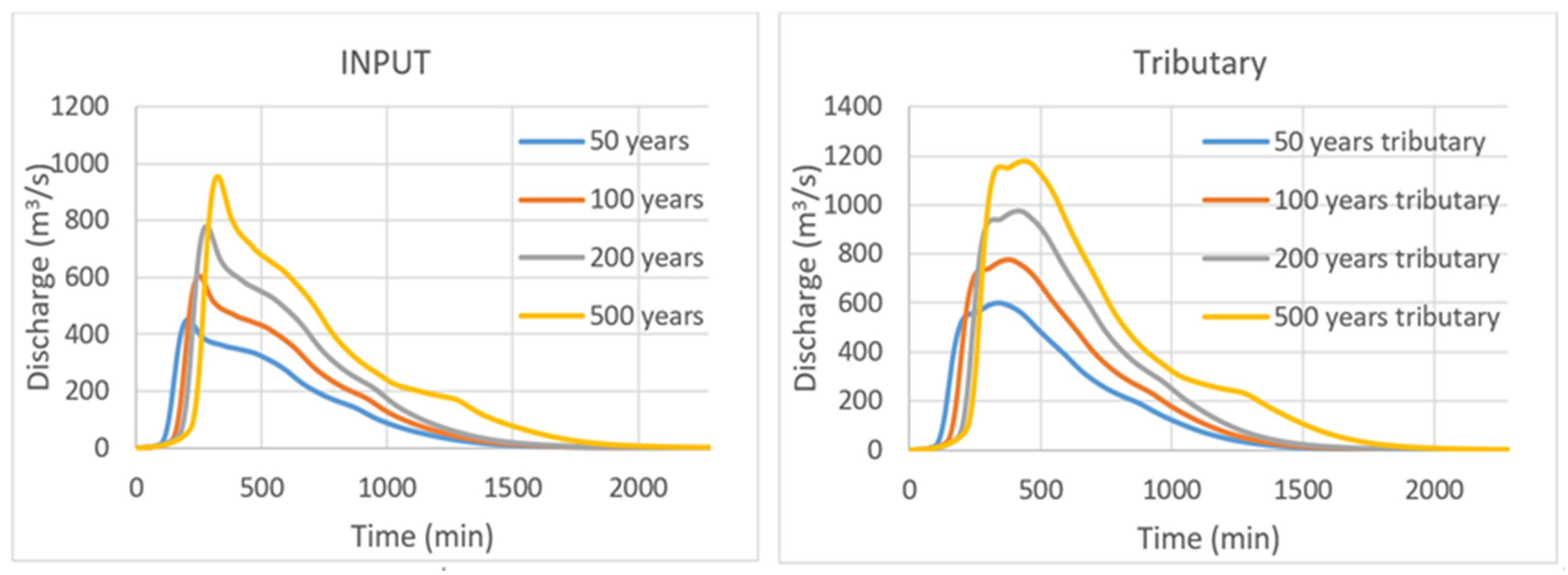
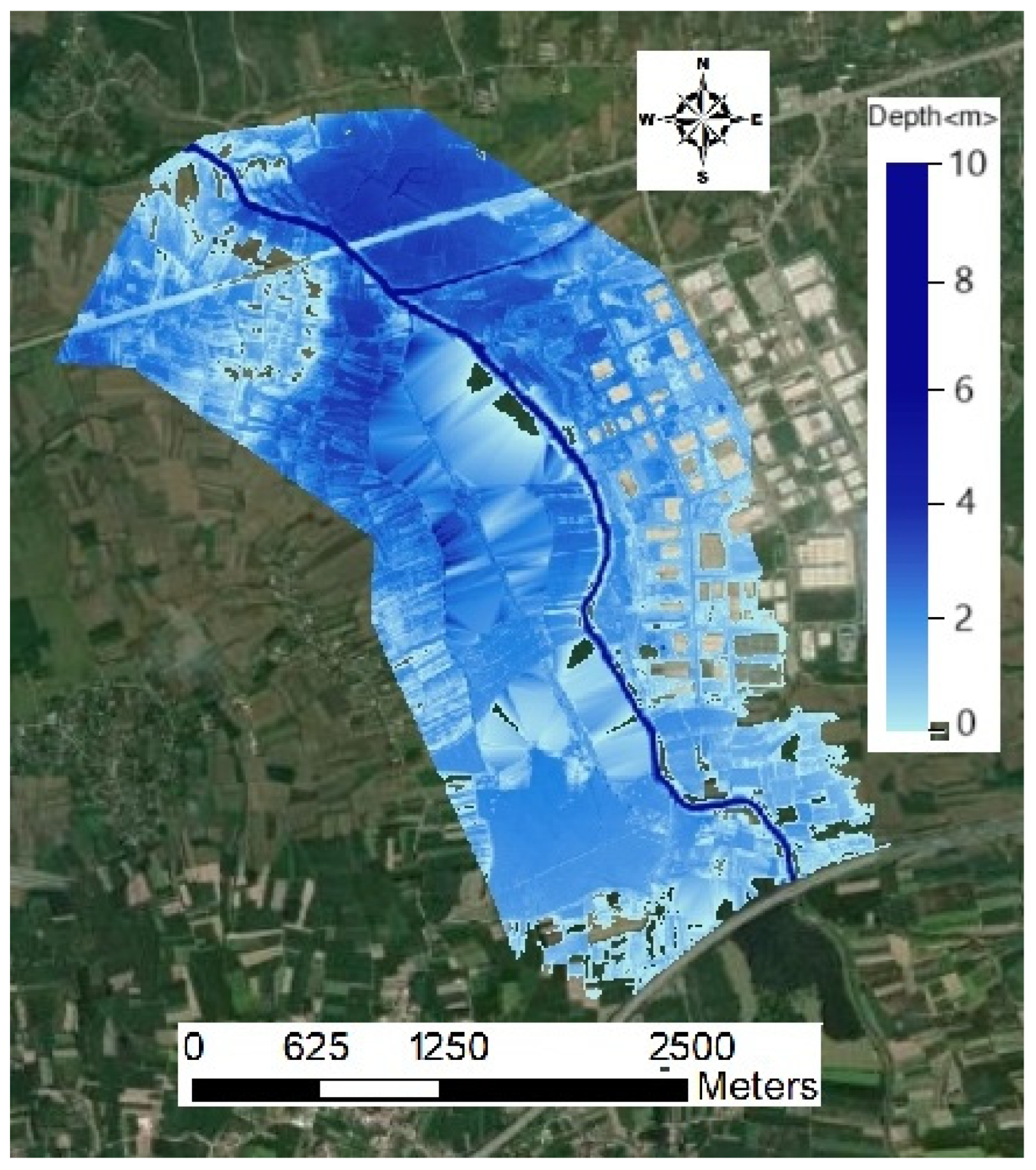
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kheradmand, S.; Seidou, O.; Konnte, D.; Batoure, M.B.B. Evaluation of adaptation options to flood risk in a probabilistic framework. J. Hydrol. Reg. Stud. 2018, 19, 1–16. [Google Scholar] [CrossRef]
- Munich Reinsurance Company. Natural Loss Events Worldwide 1980–2018 Nat. Cat. Service Munich Reinsurance Company. 2019. Available online: https://natcatservice.munichre.com (accessed on 5 October 2020).
- Azouagh, A.; El Bardai, R.; Hilal, I.; Stitou el Messari, J. Integration of GIS and HEC-RAS in floods modeling of Martil River (Northern Morocco). Eur. Sci. J. 2018, 14, 130. [Google Scholar] [CrossRef]
- Kishore, N.; Marqués, D.; Mahmud, A.; Kiang, M.V.; Rodriguez, I.; Fuller, A.; Ebner, P.; Sorensen, C.; Racy, F.; Lemery, J.; et al. Mortality in Puerto Rico after hurricane Maria. N. Engl. J. Med. 2018, 379, 162–170. [Google Scholar] [CrossRef]
- Malik, A.; Abdalla, R. Geospatial modeling of the impact of sea level rise on coastal communities: Application of Richmond, British Columbia, Canada. Model. Earth Syst. Environ. 2016, 2, 146. [Google Scholar] [CrossRef]
- Shrestha, M.N. Spatially distributed hydrological modelling considering land-use changes using remote sensing and GIS. In Proceedings of the Map Asia Conference, Kuala Lumpur, Malaysia, 13–15 October 2003. [Google Scholar]
- Wheater, H.; Evans, E. Land use, water management and future flood risk. Land Use Policy 2009, 26, 251–264. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Quiroga, V.M.; Kure, S.; Udo, K.; Mano, A. Application of 2D numerical simulation for the analysis of the February 2014 Bolivian Amazonia flood: Application of the new HEC-RAS version 5, RIBAGUA. Rev. Iberoam. Agua 2016, 3, 25–33. [Google Scholar] [CrossRef]
- Horritt, M.S. A linearized approach to flow resistance uncertainty in a 2-D finite volume model of flood flow. J. Hydrol. 2002, 316, 13–27. [Google Scholar] [CrossRef]
- Alho, P.; Aaltonen, J. Comparing a 1D hydraulic model with a 2D hydraulic model for the simulation of extreme glacial outburst floods. Hydrol. Process. Int. J. 2008, 22, 1537–1547. [Google Scholar] [CrossRef]
- Leedal, D.; Neal, J.; Beven, K.; Young, P.; Bates, P. Visualization approaches for communicating real-time flood forecasting level and inundation information. J. Flood Risk Manag. 2010, 3, 140–150. [Google Scholar] [CrossRef]
- Vozinaki, A.E.K.; Morianou, G.G.; Alexakis, D.D.; Tsanis, I.K. Comparing 1D and combined 1D/2D hydraulic simulations using high-resolution topographic data: A case study of the Koiliaris basin, Greece. Hydrol. Sci. J. 2017, 62, 642–656. [Google Scholar] [CrossRef]
- Anees, M.T.; Abdullah, K.; Nordin, M.N.M.; Ab Rahman, N.N.N.; Syakir, M.I.; Kadir, M.O.A. One- and Two-dimensional Hydrological Modelling and Their Uncertainties. Flood Risk Manag. 2016, 11, 221–244. [Google Scholar]
- Dutta, D.; Herath, S.; Musiake, K. An application of a flood risk analysis system for impact analysis of a flood control plan in a river basin. Hydrol. Process. 2006, 20, 1365–1384. [Google Scholar] [CrossRef]
- Banks, J.C.; Camp, J.V.; Abkowitz, M.D. Adaptation planning for floods: A review of available tools. Nat. Hazards 2014, 70, 1327–1337. [Google Scholar] [CrossRef]
- DHI. MIKE 21-2D Modelling of Coast and Sea; DHI Water & Environment Pty Ltd.: Hørsholm, Denmark, 2012. [Google Scholar]
- Roberts, S.; Nielsen, O.; Gray, D.; Sexton, J.; Davies, G. ANUGA User Manual; Commonwealth of Australia (Geoscience Australia) and the Australian National University: Canberra, Australia, 2015. [Google Scholar]
- An, H.; Yu, S.; Lee, G.; Ki, Y. Analysis of an open source quadtree grid shallow water solver for flood simulation. Quat. Int. 2015, 384, 118–128. [Google Scholar] [CrossRef]
- An, H.; Yu, S. Well-balanced shallow water flow simulation on quadtree cut cell grids. Adv. Water Resour. 2012, 39, 60–70. [Google Scholar] [CrossRef]
- Brunner, G.W. HEC-RAS River Analysis System Hydraulic Reference Manual Version 5.0. 2016. Available online: https://www.hec.usace.army.mil/software/hec-ras/documentation/HEC-RAS%205.0%20Reference%20Manual.pdf (accessed on 26 September 2021).
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Bladé, E.; Cea, L.; Coresteina, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber—River modelling simulation tool. Rev. Int. Métodos Numéricos Cálculo Diseño Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Neal, J.; Keef, C.; Bates, P.; Beven, K.; Leedal, D. Probabilistic flood risk mapping including spatial dependence. Hydrol. Process. 2012, 27, 1349–1363. [Google Scholar] [CrossRef]
- Sönmez, O.; Doğan, E. Determination of flood inundation area in Cedar River using calibrated and validated 1D and 1D/2D model. Sak. Univ. J. Sci. 2016, 20, 337–347. [Google Scholar] [CrossRef]
- Betsholtz, A.; Nordlöf, B. Potentials and Limitations of 1D, 2D and Coupled 1D–2D Flood Modeling in HEC-RAS. Master’s Thesis, Lund University, Lund, Sweden, 2017. [Google Scholar]
- Hammami, S.; Romdhane, H.; Soualmia, A.; Kourta, A. 1D/2D coupling model to assess the impact of dredging works on the Medjerda river floods, Tunisia. J. Mater. Environ. Sci. 2022, 13, 825–839. [Google Scholar]
- Kalra, A.; Joshi, N.; Baral, S.; Pradhan, S.N.; Mambepa, M.; Paudel, S.; Xia, C.; Gupta, R. Coupled 1D and 2D HEC-RAS floodplain modeling of Pecos River in New Mexico. In Proceedings of the 2021 World Environmental and Water Resources Congress, Virtual, 7–11 June 2021; pp. 165–178. [Google Scholar] [CrossRef]
- Dasallas, L.; Kim, Y.; An, H. Case study of HEC-RAS 1D–2D coupling simulation: 2002 Baeksan flood event in Korea. Water 2019, 11, 2048. [Google Scholar] [CrossRef]
- Bates, P.D. Flood inundation prediction. Annu. Rev. Fluid Mech. 2022, 54, 287–315. [Google Scholar] [CrossRef]
- Patel, D.; Ramirez, J.A.; Srivastava, P.K.; Bray, M.; Zhang, S. Assessment of flood inundation mapping of Surat city by coupled 1D/2D hydrodynamic modelling: A case application of the new HEC-RAS 5. Nat. Hazards 2017, 89, 93–130. [Google Scholar] [CrossRef]
- Tazin, T. Flood Hazard Mapping of Dharla River Floodplain Using HEC-RAS 1D/2D Coupled Model. Mater’s Thesis, Bangladesh University of Engineering and Technology (BUET), Dhaka, Bangladesh, 2017. [Google Scholar]
- Rubio, F. Flood Risk Assessment in the Vicinity of Kartena Town Using HEC-RAS 1D–2D Models. Master’s Thesis, Aleksandras Stulginskis University, Kaunas, Lithuania, 2018. [Google Scholar]
- Ucar, I.; Kapcak, M.; Sonmez, O.; Dogan, E.; Turan, B.; Dal, M.; Findik, S.B.; Yilmaz, M.; Sever, A. From Hazard Maps to Action Plans: Comprehensive Flood Risk Mitigation in the Susurluk Basin. Water 2025, 17, 860. [Google Scholar] [CrossRef]
- Kulkarni, A.D.; Kale, G.D. The Development of Coupled 1D–2D Hydrodynamic Flood Model by Using HEC-RAS: A Case Study of the Panchganga River Basin, Kolhapur District, Maharashtra, India. Water Resour. 2024, 51, 789–799. [Google Scholar] [CrossRef]
- Siakara, G.; Gourgouletis, N.; Baltas, E. Assessing the Efficiency of Fully Two-Dimensional Hydraulic HEC-RAS Models in Rivers of Cyprus. Geographies 2024, 4, 513–536. [Google Scholar] [CrossRef]
- Lim, M.; Ginting, B.M.; Senjaya, T.; Kieswant, C. Comparison of 1D, coupled 1D–2D, and 2D shallow water numerical modeling for dam-break flow analysis of Way-Ela dam, Indonesia. Acta Hydrotech. 2024, 37, 27–50. [Google Scholar] [CrossRef]
- Moghim, S.; Gharehtoragh, M.A.; Safaie, A. Performance of the flood models in different topographies. J. Hydrol. 2023, 620, 129446. [Google Scholar] [CrossRef]
- Özcan, O. Determination of Flood Risk Analysis of Sakarya River Sub-Basin with Remote Sensing and CBS. Master’s Thesis, Istanbul Technical University, Istanbul, Turkey, 2008. [Google Scholar]
- Koliokosta, E. Return Periods in Assessing Climate Change Risks: Uses and Misuses. Environ. Sci. Proc. 2023, 26, 75. [Google Scholar] [CrossRef]
- Van Campenhout, J.; Houbrechts, G.; Peeters, A.; Petit, F. Return Period of Characteristic Discharges from the Comparison between Partial Duration and Annual Series, Application to the Walloon Rivers (Belgium). Water 2020, 12, 792. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Montanari, A.; Lins, H.; Koutsoyiannis, D.; Brandimarte, L.; Blöschl, G. Flood fatalities in Africa: From diagnosis to mitigation. Geophys. Res. Lett. 2010, 37, L22402. [Google Scholar] [CrossRef]
- Jobe, A.; Bhandari, S.; Kalra, A.; Ahmad, S. Ice-Cover and jamming effects on inline structures and upstream water levels. In Proceedings of the 2017 World Environmental and Water Resources Congress, Sacramento, CA, USA, 21–25 May 2017; pp. 270–279. [Google Scholar] [CrossRef]
- Sagarika, S.; Kalra, A.; Ahmad, S. Interconnections between oceanic-atmospheric indices and variability in the U.S. streamflow. J. Hydrol. 2015, 525, 724–736. [Google Scholar] [CrossRef]
- Sagarika, S.; Kalra, A.; Ahmad, S. Pacific Ocean SST and Z500 climate variability and western U.S. seasonal streamflow. Int. J. Climatol. 2016, 36, 1515–1533. [Google Scholar] [CrossRef]
- United States Army Crops of Engineers (USACE). HEC-HMS Hydrologic Modelling System User’s Manual; Hydrologic Engineering Center: Davis, CA, USA, 2001.
- Feldman, A.D. Hydrologic Modelling System HEC-HMS Technical Reference Manual; CDP-74B; US Army Corps of Engineers: Washington, DC, USA, 2000.
- Scharffenberg, W.; Ely, P.; Daly, S.; Fleming, M.; Pak, J. Hydrologic modelling system (HEC-HMS): Physically-based simulation components. In Proceedings of the 2nd Joint Federal Interagency Conference, Las Vegas, NV, USA, 27 June–1 July 2010. [Google Scholar]
- Schulze, R.E.; Schmidt, E.J.; Smithers, J.C. SCS-SA User Manual PC Based SCS Design Flood Estimates for Small Catchments in Southern Africa; Department of Agricultural Engineering, University of Natal: Pietermaritzburg, South Africa, 1992. [Google Scholar]
- Katara, P.; Machiwal, D.; Mittal, H.K.; Dashora, Y.; Bhagat, A. Estimation of Runoff for Ahar River Catchment in Udaipur District. Integrated Remote Sensing and Geographical Information System; The Institute of Engineers (India) Udaipur Local Centre: Udaipur, India, 2013; pp. 169–175. [Google Scholar]
- United States Department of Agriculture (USDA). Estimation of direct runoff from storm rainfall, Part 630 Hydrology. In National Engineering Handbook; United States Department of Agriculture (USDA): Washington, DC, USA, 2004. [Google Scholar]
- Soil Conservation Service. Hydrology, National Engineering Handbook; Soil Conservation Service, USDA: Washington, DC, USA, 1985.
- Zhan, X.; Huang, M.L. ArcCN-Runoff: An ArcGIS tool for generating curve number and runoff maps. Environ. Model. Softw. 2004, 19, 875–879. [Google Scholar] [CrossRef]
- Cowan, W.L. Estimating hydraulic roughness coefficients. Agric. Eng. 1956, 37, 473–475. [Google Scholar]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains, Final Repo; U.S. Department of Transportation: Washington, DC, USA, 1984.
- Turkish State Hydraulic Works (DSI). Roughness Coefficient Determination Guide for Stream Beds; Ministry of Forestry and Water Affairs, General Directorate of State Hydraulic Works: Ankara, Turkey, 2016.
- Barnes, H.H. Roughness Characteristics of Natural Channels; Technical Report; U.S. Geological Survey Water-Supply; United States Government Printing Office: Washington, DC, USA, 1987.
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Nas, S.S.; Nas, E. Determination of flood areas with the help of geographic information systems and risk analysis: The example of Harşit Stream (Gümüşhane). In Proceedings of the Flood and Landslide, Trabzon, Türkiye, 24–26 October 2013. [Google Scholar]
- Brunner, G.W. Creating and Combined 1D/2D Model; US Army Corps of Engineers, Institute for Water Resources, Hydrologic Engineering Center: Davis, CA, USA, 2016. Available online: https://www.hec.usace.army.mil/confluence/rasdocs/hgt/latest/guides/creating-an-combined-1d-2d-model (accessed on 26 September 2021).







| Name of Station | Measurement Range | Measurement Year | Average (mm) | Standard Deviation | Skewness Coefficient |
|---|---|---|---|---|---|
| Akyazı | 1950–2019 | 50 | 48.2 | 16.39 | 1.25 |
| Hendek | 1950–2019 | 50 | 50.8 | 19.74 | 1.08 |
| Gölyaka | 2010–2020 | 10 | 46.5 | 12.18 | −0.52 |
| Distribution | Akyazı | Hendek | Gölyaka | |
|---|---|---|---|---|
| 1 | Gamma | 5 | 5 | 5 |
| 2 | Gamma (3P) | 8 | 7 | 4 |
| 3 | Gen. Gamma | 6 | 4 | 6 |
| 4 | Gumbel Max | 3 | 3 | 8 |
| 5 | Log-Pearson 3 | 2 | 2 | 1 |
| 6 | Lognormal | 4 | 1 | 7 |
| 7 | Lognormal (3P) | 1 | 6 | 3 |
| 8 | Normal | 7 | 8 | 2 |
| Station Name | 50 Years | 100 Years | 200 Years | 500 Years |
|---|---|---|---|---|
| Akyazı | 119.09 | 139.85 | 162.8 | 196.8 |
| Hendek | 136.8 | 157.63 | 179.94 | 212 |
| Gölyaka | 76.66 | 80.2 | 83.32 | 86.82 |
| Type of material on the river bed | Concrete Rock Soil Grit Fine gravel Gravel Coarse gravel Coarse stone Big rock | Median diameter (mm) | - - - 1–2 - 2–64 - 64–256 >256 | nb | 0.012–0.018 - 0.025–0.032 0.026–0.035 - 0.028–0.035 - 0.030–0.050 0.040–0.070 |
| Channel side slope | Smooth Minor Moderate Severe | --- Concrete wall Stone wall Stacking stone support Soil slope Stacked stone Tree slope | n1 | 0.000 0.003 0.005 0.008 0.010 0.015 0.020 | |
| Channel section change | Gradual Occasionally changing Frequently changing | n2 | 0.000 0.005 0.01–0.015 | ||
| Obstacles in the channel | Neglected Insignificant Noteworthy Severe | <5% 5–15% 15–50% >50% | n3 | 0.000 0.01–0.005 0.02–0.03 0.04–0.06 | |
| Vegetation in the channel | Low Middle High Very high | n4 | 0.005–0.010 0.010–0.025 0.025–0.050 0.050–0.100 | ||
| Channel fold | Insignificant Noteworthy Severe | 1–1.2 1.2–1.5 >1.5 | m | 1.00 1.150 1.300 | |
| 1D model 2D model | River channel Urban area and farming | 0.0805 0.013 and 0.04 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spor, P.; Paşa, Y.; Doğan, E. Evaluation of Simulation Results of HEC-RAS Coupled 1D/2D and 2D Modeling Approaches Through Scenario-Based Analysis. Water 2025, 17, 1163. https://doi.org/10.3390/w17081163
Spor P, Paşa Y, Doğan E. Evaluation of Simulation Results of HEC-RAS Coupled 1D/2D and 2D Modeling Approaches Through Scenario-Based Analysis. Water. 2025; 17(8):1163. https://doi.org/10.3390/w17081163
Chicago/Turabian StyleSpor, Pınar, Yasin Paşa, and Emrah Doğan. 2025. "Evaluation of Simulation Results of HEC-RAS Coupled 1D/2D and 2D Modeling Approaches Through Scenario-Based Analysis" Water 17, no. 8: 1163. https://doi.org/10.3390/w17081163
APA StyleSpor, P., Paşa, Y., & Doğan, E. (2025). Evaluation of Simulation Results of HEC-RAS Coupled 1D/2D and 2D Modeling Approaches Through Scenario-Based Analysis. Water, 17(8), 1163. https://doi.org/10.3390/w17081163





