Evaluation of Water-Richness and Risk Level of the Sandstone Aquifer in the Roof of the No. 3 Coal Seam in Hancheng Mining Area
Abstract
1. Introduction
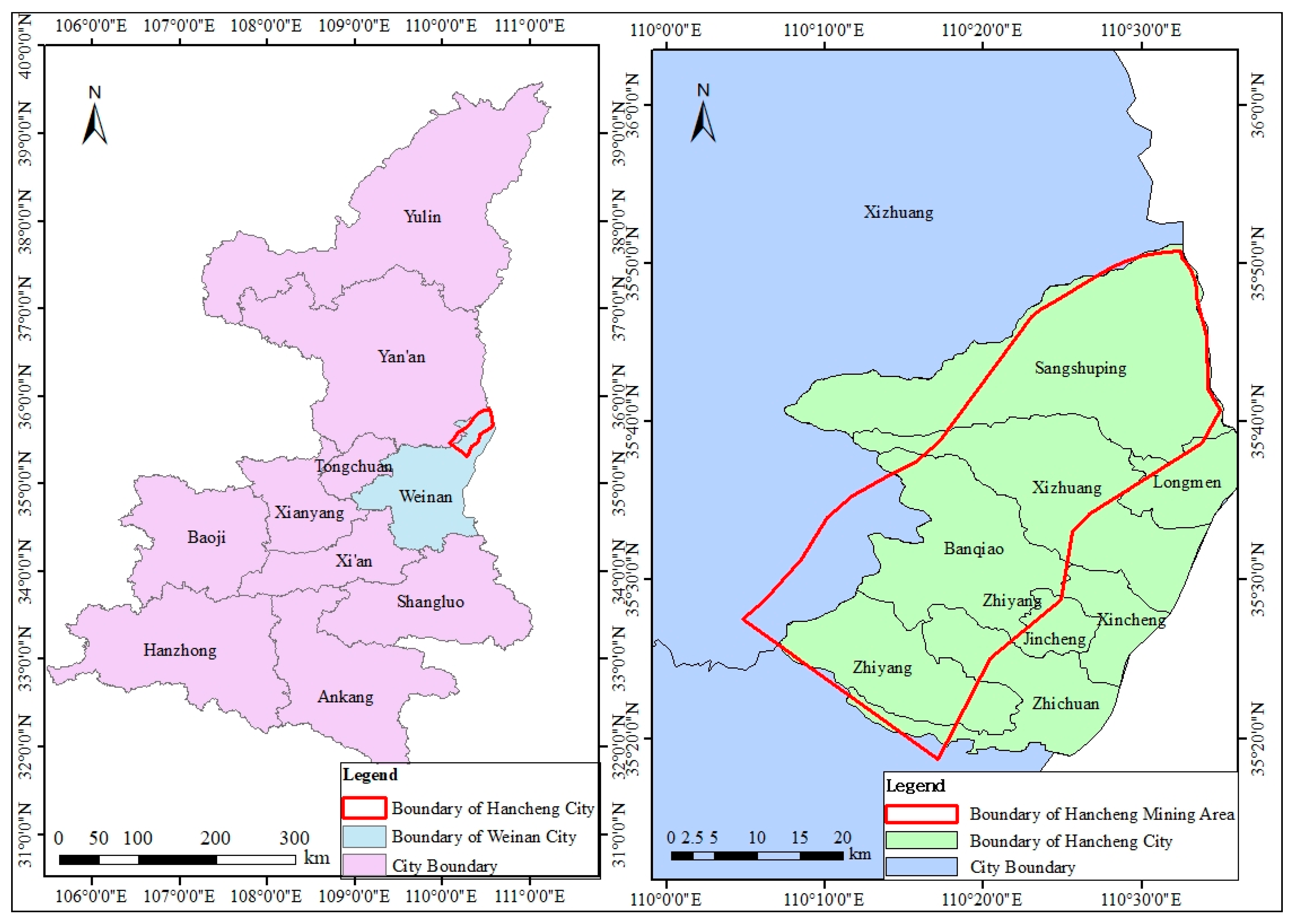
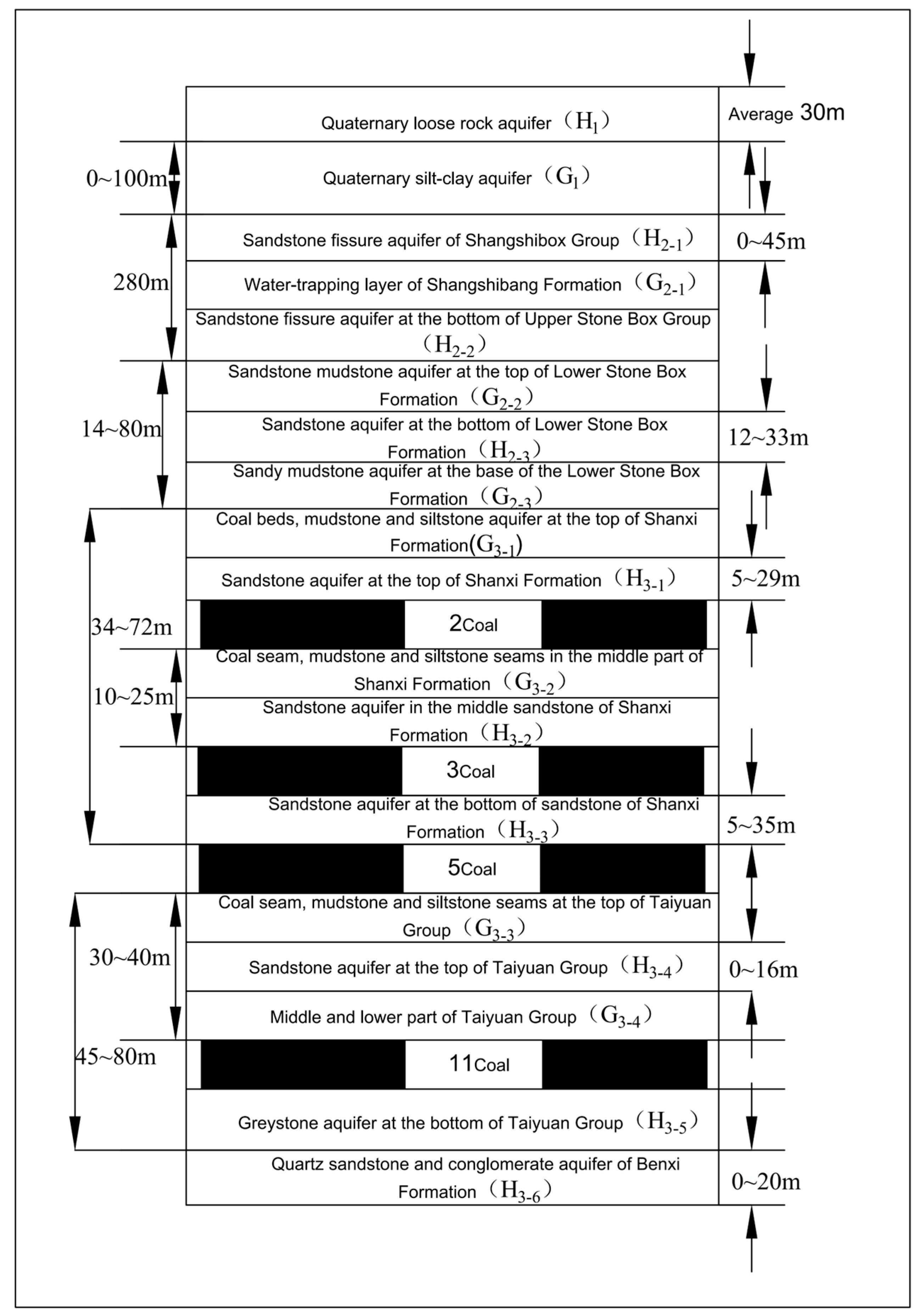
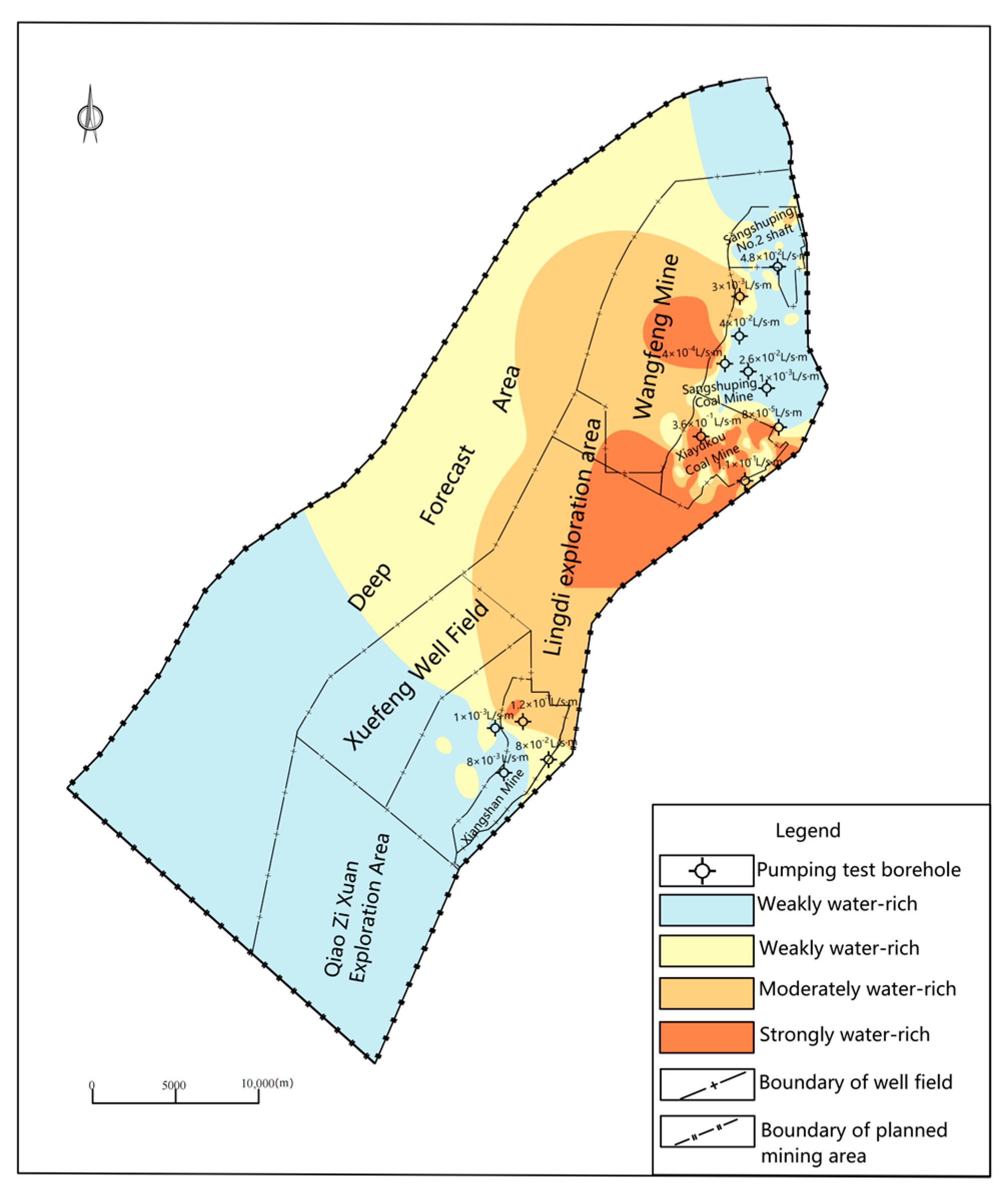
2. Overview of the Mining Area
3. Selection of Water-Richness Indicators
- (1)
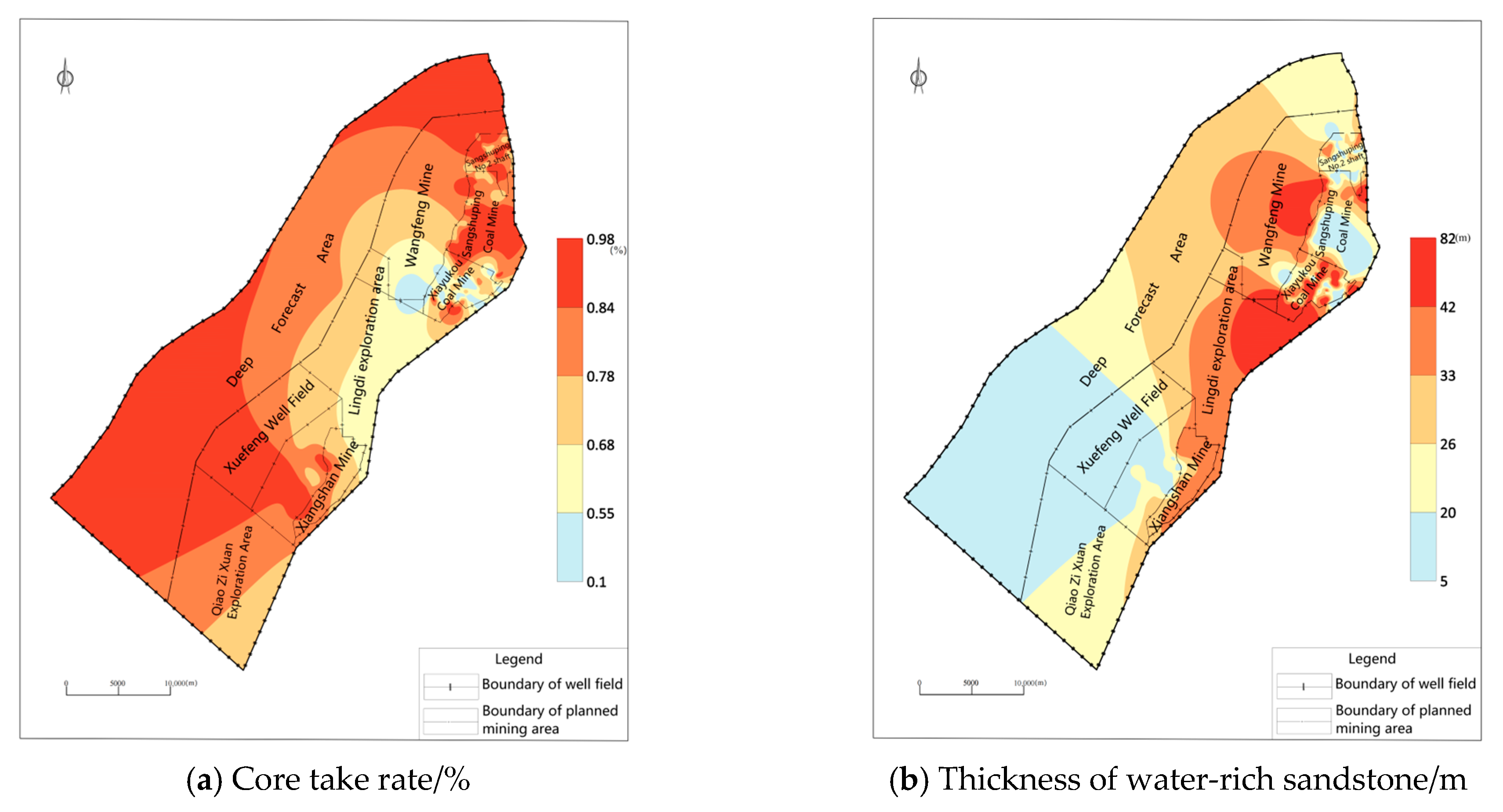
- Core take rate. The rock’s integrity can be inferred from the core take rate; the lower the take rate, the more fractured the rock, the greater the water-richness, and the larger the water storage space (Figure 3a).
- (2)
- Water-rich sandstone equivalent thickness. As per Equation (1) (Figure 3b), the scale factor of 1, 0.8, and 0.6 indicates that coarse [16], medium, and fine sandstones, respectively, are among the water-rich sandstones.Here, L is water-rich sandstone equivalent thickness, and a, b, and c represent the thickness of coarse, medium, and fine sandstones, respectively.
- (3)
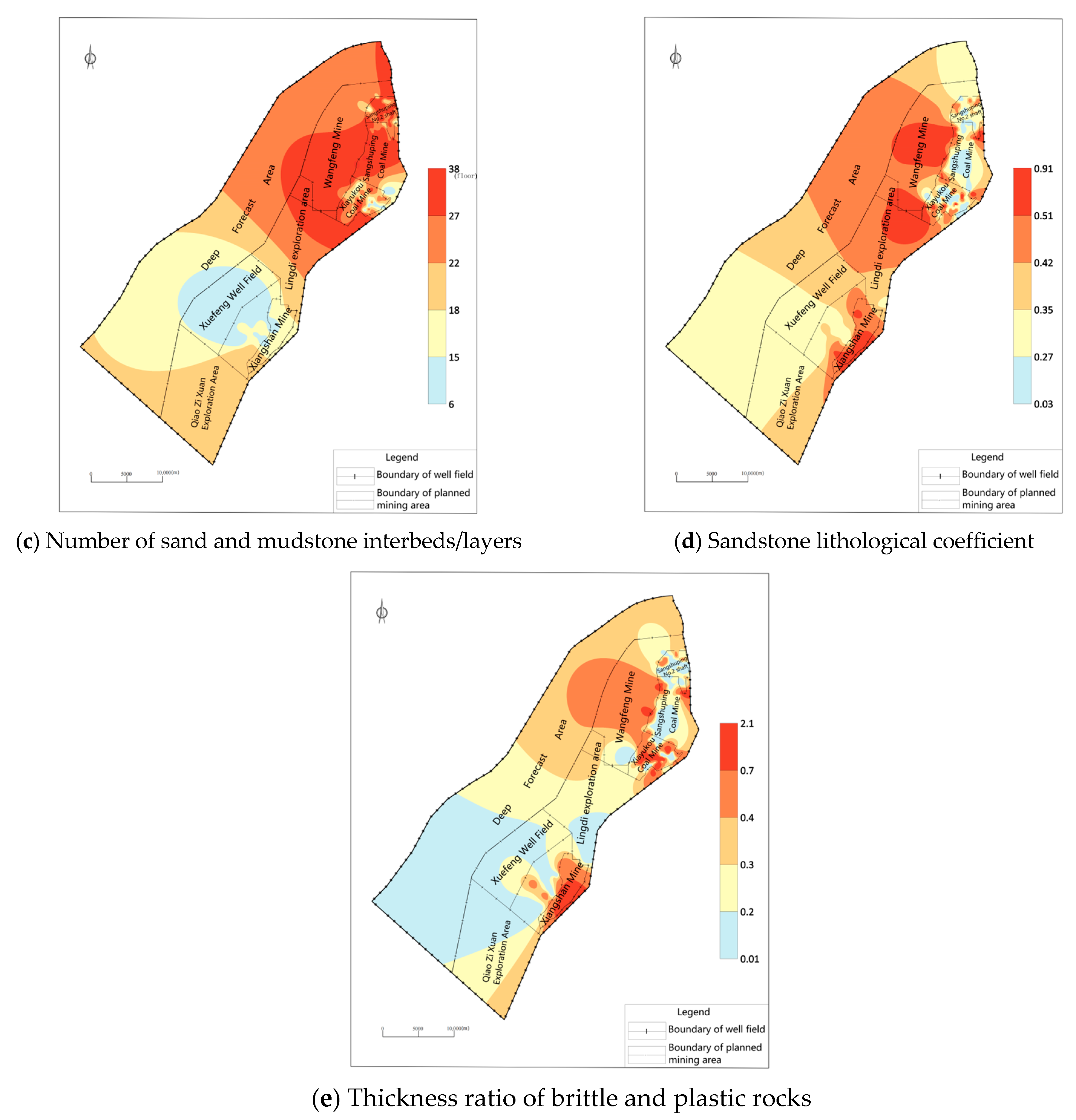
- The quantity of interbedded mudstone and sandstone strata. The amount of sand and mudstone interlayers in the aquifer has an impact on the aquifer’s permeability coefficient. The permeability coefficient decreases with increasing sand and mudstone interlayer density (Figure 3c).
- (4)
- The lithology coefficient of sandstone. The ratio of the aquifer’s water-rich sandstone thickness to its overall thickness is known as the sandstone lithology coefficient; the greater this ratio, the more strongly the aquifer is water-rich (Figure 3d).
- (5)
- Brittle plastic rock thickness ratio. Sandstone and siltstone make up the majority of the brittle and plastic rock layers, respectively. When subjected to force, the rock layers exhibit varying rupture characteristics. The brittle rock will crack more when forced, increasing the water-richness of the layer (Figure 3e).
4. Evaluation of Water-Richness
4.1. Evaluation of Water-Richness Zoning Based on Ordinal Relationship Analysis–Entropy Value Method
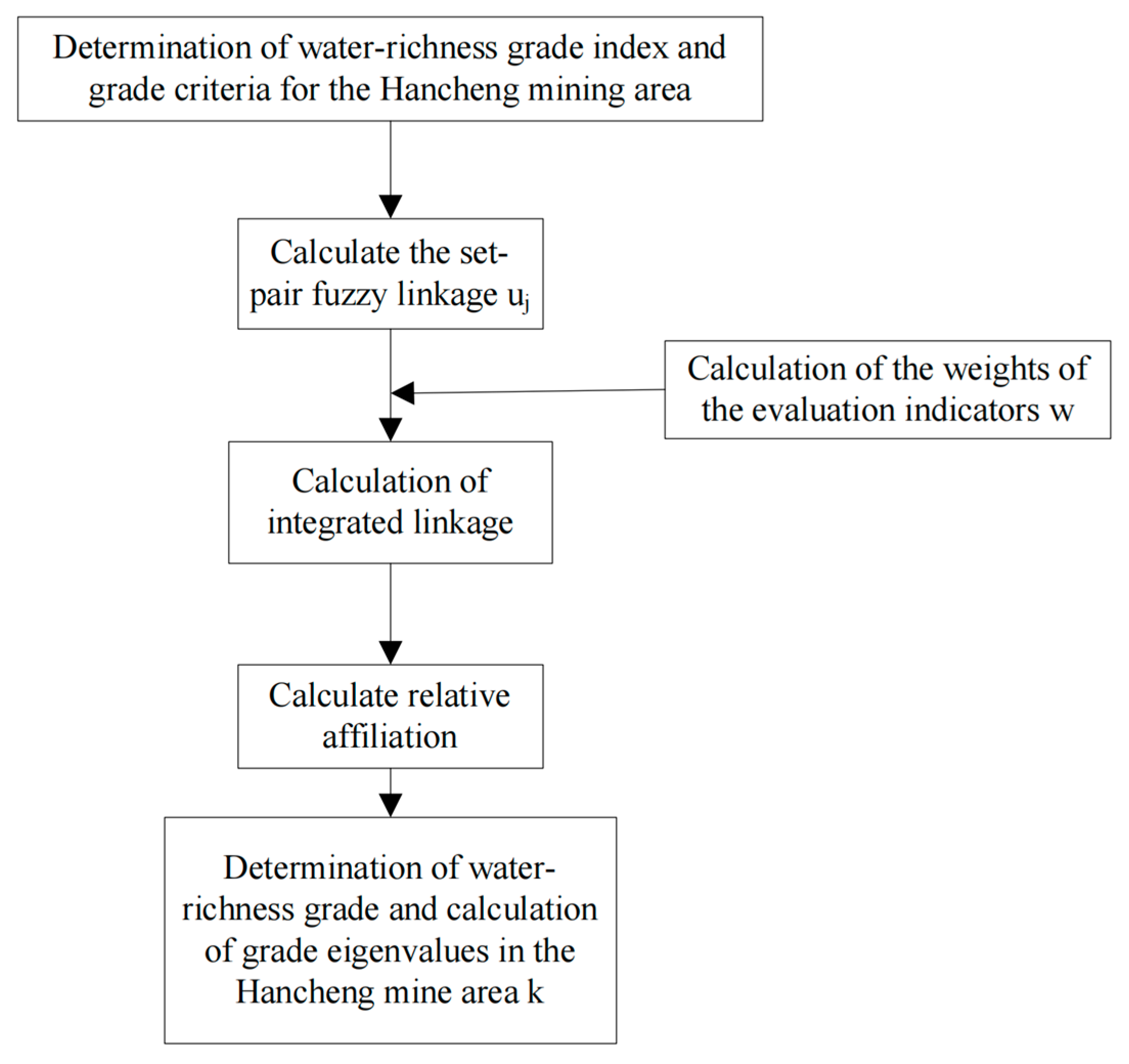
4.1.1. Model Construction Workflow
- 1.
- Order relationship analysis method [20]
- (1)
- Establish the order relationship between the indicators. To do this, first ascertain the significance of the first level of indicators for the target level. For example, if indicator X1 is significant in relation to indicator X2, it will be recorded as X1 > X2, and so on to determine the ordinal relationship between the indicators.
- (2)
- Ascertain the relative importance of the adjacent indicators. In the indicator system, Xk−1 and Xk are adjacent indicators, and the decision maker determines the importance of the two indicators, resulting in an indicator importance ratio Rk, as shown in Table 1.Here, the indicators Wk−1 and WK represent the importance of Xk−1 and Xk, respectively, and n is the number of indicators.
- (3)
- Calculate the weight coefficients. The weight coefficient of the nth indicator is Wn, which is defined and computed as follows in Equations (3) and (4).
- (4)
- Find out how much each indicator value is weighted in relation to the target level. Wp is the weight coefficient of the pth criterion under the objective layer, Wq is the weight coefficient of the qth indicator for the pth criterion under the pth criterion, and Wpq is the weight coefficient of the qth indicator under the pth criterion layer in the total objective layer. A questionnaire poll of five experts yielded a ratio of the indicators’ importance at one level (Table 2), which was based on Table 1.
- 2.
- (1)
- Build the initial matrix (5), choosing n boreholes and m indications, which displays the original matrix X with m rows and n columns:
- (2)
- Data standardization. The method of extreme difference is selected to remove the influence of the indicator’s outline because of the significant variations in each indicator’s data. When variables have different units or vastly varying numerical scales, standardization eliminates the impact of dimensionality and scale differences in the model, ensuring comparability across variables. Equations (6) and (7) for positive and negative indicators, respectively, will be dimensionless. The precise procedure is as follows,where max xij is the largest value in the indicators and max xij is the smallest one.
- (3)
- Calculation of specific gravity Pij:
- (4)
- Calculate the entropy value eiwhere K , then .
- (5)
- Calculate information entropy redundancy dj:
- (6)
- Calculate the weights of the indicators Wj:
- 3.
- Integrated subjective and objective empowerment
4.1.2. Zoning Evaluation Results
4.1.3. Validation of Evaluation Results
4.2. Evaluation of Water-Richness Risk Level
4.2.1. Theoretical Basis of Model Coupling
4.2.2. Risk Grading Evaluation Results
- 1.
- Calculation of linkage degree
- 2.
- Risk level standard and classification
4.2.3. Comprehensive Evaluation Results
5. Conclusions
- (1)
- The sandstone aquifer’s water-richness is dependent upon its connectivity and storage capacity. Five evaluation factors, including core taking rate, water-rich sandstone thickness, sand mudstone interlayer thickness, sandstone lithology coefficient, and brittle–plastic layer thickness ratio are chosen to construct the sandstone aquifer lithology influence index based on an analysis of the geological data of the mining area from the perspective of water-richness.
- (2)
- Based on the lithological and structural characteristics of the sandstone aquifer in the study area, an evaluation model for the water richness of the roof sandstone was established using the ordinal relationship analysis–entropy method, and the water richness of the Shanxi Formation aquifer was predicted. The relative grades of water richness and their zoning were delineated and compared with the pumping test results of the aquifer. It was determined that the water richness is strong in the northeastern part of the Hancheng mining area, moderate to weak in the southwestern part, and decreases from west to east across the mining area.
- (3)
- An evaluation model for the water richness of the aquifer was constructed based on the set pair analysis–variable fuzzy set evaluation method. According to the calculation results of characteristic values and the confidence criterion, it was judged that the water richness of the No. 3 coal seam roof in the Hancheng mining area is at a medium risk level. Combining the results of the comprehensive water richness evaluation model with subjective and objective weighting, the western part of the mining area has high water richness, while the northern and southern parts have low water richness. The mining company needs to strengthen precautions in the western region during coal seam mining to ensure safe extraction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Q.; Huang, X.; Dong, D.; Yin, Z.; Li, J.; Hong, Y.; Zhang, H. The “Three Maps-Double Forecast Method” for evaluating water inrush conditions in coal seam roof. J. China Coal Soc. 2000, 62–67. [Google Scholar] [CrossRef]
- Dong, F.; Yin, H.; Cheng, W.; Li, Y.; Qiu, M.; Zhang, C.; Tang, R.; Xu, G.; Zhang, L. Study on water inrush pattern of Ordovician limestone in North China Coalfield based on hydrochemical characteristics and evolution processes: A case study in Binhu and Wangchao Coal Mine of Shandong Province, China. J. Clean. Prod. 2022, 380, 134954. [Google Scholar] [CrossRef]
- Dai, G.; Xue, X.; Xu, K.; Niu, C.; Yang, T. Risk assessment of water inrush from No.11 coal seam floor in Hancheng mining area based on vulnerability index method. Coal Geol. Explor. 2017, 45, 112–117+125. [Google Scholar]
- Niu, C.; Tian, Q.; Xiao, L.; Xue, X.; Zhang, R.; Xu, D.; Luo, S. Principal causes of water damage in mining roofs under giant thick topsoil-lilou coal mine. Appl. Water Sci. 2024, 14, 146. [Google Scholar] [CrossRef]
- Xiao, L.; Li, F.; Niu, C.; Dai, G.; Qiao, Q.; Lin, C. Evaluation of Water Inrush Hazard in Coal Seam Roof Based on the AHP-CRITIC Composite Weighted Method. Energies 2022, 16, 114. [Google Scholar] [CrossRef]
- Ma, X.; Cheng, Z.; Cui, J.; Han, J.; Yin, C. Risk assessment of water inrush from the Jurassic Yan’an Formation No. 8 coal seam roof in the first mining area of Xinzhuang Coal Mine, Ningzheng mining area. Coal Sci. Technol. 2023, 51, 298–309. [Google Scholar]
- Liu, W.; Zheng, Q.; Pang, L.; Dou, W.; Meng, X. Study of roof water inrush forecasting based on EM-FAHP two-factor model. Math. Biosci. Eng. 2021, 18, 4987–5005. [Google Scholar] [CrossRef]
- Li, B.; Wei, T.; Liu, Z. Construction of water abundance evaluation index system for karst aquifer in coal seam roof and risk assessment of water inrush in Southwest China. J. China Coal Soc. 2022, 47, 152–159. [Google Scholar]
- Yang, L.; Lei, F.; Hou, E.; Lu, B.; Feng, D.; Zhao, K. Water abundance zoning of aquifer and segmented prediction of water inflow after mine drainage in working face. Coal Geol. Explor. 2023, 51, 114–123. [Google Scholar]
- Cheng, X.; Li, S.; Bian, K.; Yang, H.; Chang, J. Risk assessment of water inrush based on FAHP-EWM combined weighting method. Coal Mine Saf. 2024, 55, 184–193. [Google Scholar]
- Chen, Y.; Fan, G.; Yin, C.; Zhang, D.; Han, X. Evaluation and application of water abundance in roof of water-seepage roadway based on improved AHP-entropy weight coupling method. Coal Eng. 2023, 55, 141–146. [Google Scholar]
- Han, C.; Wei, J.; Xie, D.; Xu, J.; Zhang, W.; Zhao, Z. Water abundance evaluation of sandstone aquifer based on set pair analysis-variable fuzzy set coupling method: A case study of Jurassic Zhiluo Formation aquifer in Jinjiaqu Minefield, Ningdong mining area. J. China Coal Soc. 2020, 45, 2432–2443. [Google Scholar]
- Qiu, M.; Shao, Z.; Zhang, W.; Zheng, Y.; Yin, X.; Gai, G.; Han, Z.; Zhao, J. Water-richness evaluation method and application of clastic rock aquifer in mining seam roof. Sci. Rep. 2024, 14, 6465. [Google Scholar] [CrossRef]
- Kuo, W.; Li, X.; Zhang, Y.; Li, W.; Wang, Q.; Li, L. Prediction Model of Water Abundance of Weakly Cemented Sandstone Aquifer Based on Principal Component Analysis–Back Propagation Neural Network of Grey Correlation Analysis Decision Making. Water 2024, 16, 551. [Google Scholar] [CrossRef]
- Dai, X.; Li, X.; Zhang, Y.; Li, W.; Meng, X.; Li, L.; Han, Y. A Prediction Model of Coal Seam Roof Water Abundance Based on PSO-GA-BP Neural Network. Water 2023, 15, 4117. [Google Scholar] [CrossRef]
- Xiao, L.; Niu, C.; Dai, G.; Nie, W.; Zhang, H.; Gao, Y. Evaluation of water-richness of Zhiluo Formation based on water-richness structure index method. Coal Sci. Technol. 2018, 46, 207–213. [Google Scholar]
- Zhou, Q.; Zhang, H.; Jiao, Y.; Yu, B.; Guo, J. Risk assessment of water inrush from coal seam roof based on combined weighting method. Sci. Technol. Eng. 2022, 22, 3497–3503. [Google Scholar]
- Hou, E.; Yang, S.; Miao, Y.; Che, X.; Yang, L.; Lu, B.; Xie, X.; Wang, H.; Dang, B. Water abundance prediction of weathered bedrock based on Bayes discriminant analysis model. Coal Mine Saf. 2023, 54, 180–187. [Google Scholar]
- Li, P.; Hou, E.; Ji, Y. Water abundance evaluation of Luohe Formation aquifer based on subjective weight modified by standard deviation. China Energy Environ. Prot. 2023, 45, 25–31. [Google Scholar]
- Liu, J.; Yuan, X.; Liang, D.; Wang, C. Fire risk evaluation of energy storage power atstion based on G1-CRITIC combination weighting cloud model. J. Xi’an Univ. Sci. Technol. 2024, 44, 447–455. [Google Scholar]
- Tan, S.; Shen, Z. Safety evaluation of coal mine water penetration based on entropy method-mutation theory. J. Xi’an Univ. Sci. Technol. 2022, 42, 1064–1070. [Google Scholar]
- Zhang, H.; Wu, Q. Application of constant-weight vulnerability index method based on entropy method-FAHP for coal bed floor water breakage. Energy Environ. Prot. 2020, 42, 1–5+9. [Google Scholar]
- Zhao, K. A review of the application of set-pair analysis in system intelligent prediction. J. Intell. Syst. 2022, 17, 233–247. [Google Scholar]
- Pan, Q.; Zhou, R.; Wang, Y. Set-pair analysis and variable fuzzy set method for vulnerability assessment of regional water resources system. China Popul. Resour. Environ. 2016, 26, 198–202. [Google Scholar]
- Wang, M.; Li, L.; Jin, J. Set-pair analysis of mining building damage-variable fuzzy set comprehensive evaluation model. Coalf. Geol. Explor. 2008, 36, 39–41. [Google Scholar]
- Chen, S. Variable Fuzzy Set Theory and Methods for Water Resources and Flood Defence Systems. Dalian Univ. Technol. Dalian 2005, 22, 10–11, 16. [Google Scholar]
- Zhao, Z. Quantitative Evaluation of Geological Formations and Study on Water-Richness of Top Plate Sandstone Aquifer. Ph.D. Thesis, Shandong University of Science and Technology, Qingdao, China, 2021. [Google Scholar]
- Fan, J. Research on Evaluation of Sponge City Construction Based on Set-Pair Analysis-Variable Fuzzy Set Coupling. Ph.D. Thesis, Anhui University of Architecture, Hefei, China, 2018. [Google Scholar]
- Zhang, J. Research on Coal Mine Water Damage Risk Evaluation Based on Set-Pair Analysis-Variable Fuzzy Set Coupling. Ph.D. Thesis, Henan University of Science and Technology, Luoyang, China, 2023. [Google Scholar]
- Li, D. Research on Systematic Risk Evaluation Based on Generalized Set-Pair Analysis. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2010. [Google Scholar]
- Zhao, Y.; Wan, J. Risk evaluation of air traffic control operation based on set-pair analysis. J. Saf. Environ. 2018, 18, 871–875. [Google Scholar]

| Rk Value | Clarification |
|---|---|
| 1.0 | Indicators Xk−1 and Xk are equally important |
| 1.2 | Indicators Xk−1 and Xk marginally important |
| 1.4 | Indicators Xk−1 and Xk are clearly important |
| 1.6 | Indicators Xk−1 and Xk are strongly important |
| 1.8 | Extreme importance of indicators Xk−1 and Xk |
| 1.1, 1.3, 1.5, 1.7 | Intermediate cases between indicator judgements |
| Master | Serial Relationship | Ratio of Importance |
|---|---|---|
| R | ||
| 1 | X1 > X2 | 1.6 |
| 2 | X1 > X2 | 1.5 |
| 3 | X1 > X2 | 1.3 |
| 4 | X2 > X1 | 1.3 |
| 5 | X1 > X2 | 1.4 |
| Water-Richness Grade | Weak | Moderate | Strong | Extremely Strong |
|---|---|---|---|---|
| Unit water influx (L/s·m) | ≤0.1 | 0.1~1 | 1~5 | >5 |
| Controlling Factors | Core Take Rate (A1) | Thickness of Water-Rich Sandstone (A2) | Number of Sandstone-Mudstone Interbeds (A3) | Sandstone Lithological Coefficient (A4) | Thickness Ratio of Brittle and Plastic Rocks (A5) |
|---|---|---|---|---|---|
| Combined weight Ai | 0.2261 | 0.2071 | 0.2642 | 0.1485 | 0.1541 |
| Evaluation Criteria | Indicator Score |
|---|---|
| Core take rate | 4.1 |
| Thickness of water-rich sandstone | 3.6 |
| Number of sandstone and mudstone interlayers | 3.4 |
| Sandstone lithological coefficient | 4.3 |
| Thickness ratio of brittle and plastic rocks | 4.0 |
| Evaluation Indicators | Evaluation Level | ||||
|---|---|---|---|---|---|
| Low Risk | Low Risk | Medium Risk | Higher Risk | High Risk | |
| Core take rate | −0.2261 | 0.1243 | 0.2261 | −0.1244 | −0.2261 |
| Thickness of water-rich sandstone | −0.2071 | −0.0695 | 0.2071 | 0.0695 | −0.2071 |
| Number of sandstone-mudstone interbedded layers | −0.0198 | 0.2642 | 0.0198 | −0.2642 | −0.2642 |
| Sandstone lithological coefficient | −0.0195 | 0.1485 | 0.0195 | −0.1485 | −0.1485 |
| Thickness ratio of brittle and plastic rocks | 0.0222 | 0.1541 | −0.0222 | −0.1541 | −0.1541 |
| Low Risk | Lower Risk | Medium Risk | Higher Risk | High Risk | |
|---|---|---|---|---|---|
| Composite Affiliation | 0.1509 | 0.1056 | 0.0987 | −0.1293 | −0.2096 |
| Relative Affinity | 0.5755 | 0.5528 | 0.5494 | 0.4353 | 0.3952 |
| Normalized Affinity | 0.2294 | 0.2204 | 0.2190 | 0.1736 | 0.1576 |
| Eigenvalue | 2.8094 | ||||
| Risk Rating | Medium Risk | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, C.; Xu, X.; Dai, G.; Liu, K.; Xiao, L.; Luo, S.; Qian, W. Evaluation of Water-Richness and Risk Level of the Sandstone Aquifer in the Roof of the No. 3 Coal Seam in Hancheng Mining Area. Water 2025, 17, 1164. https://doi.org/10.3390/w17081164
Niu C, Xu X, Dai G, Liu K, Xiao L, Luo S, Qian W. Evaluation of Water-Richness and Risk Level of the Sandstone Aquifer in the Roof of the No. 3 Coal Seam in Hancheng Mining Area. Water. 2025; 17(8):1164. https://doi.org/10.3390/w17081164
Chicago/Turabian StyleNiu, Chao, Xin Xu, Gelian Dai, Kai Liu, Lele Xiao, Shoutao Luo, and Wanxue Qian. 2025. "Evaluation of Water-Richness and Risk Level of the Sandstone Aquifer in the Roof of the No. 3 Coal Seam in Hancheng Mining Area" Water 17, no. 8: 1164. https://doi.org/10.3390/w17081164
APA StyleNiu, C., Xu, X., Dai, G., Liu, K., Xiao, L., Luo, S., & Qian, W. (2025). Evaluation of Water-Richness and Risk Level of the Sandstone Aquifer in the Roof of the No. 3 Coal Seam in Hancheng Mining Area. Water, 17(8), 1164. https://doi.org/10.3390/w17081164





