Contrasting the Contributions of Climate Change and Greening to Hydrological Processes in Humid Karst and Non-Karst Areas
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data Preparation
3. Methodology
3.1. V2karst V1.1 Model
3.2. Model Calibration and Validation
- A bias of <20% between observed and simulated AET for calibration and validation:where is the set of daily timescales during the study period, is the simulated AET on day, and is the observed AET on day.
- The correlation coefficient between simulated and observed AET for calibration and validation > 0.6:
- The correlation coefficient between the simulated and observed soil moisture for the calibration and validation > 0.6:
- In karst regions, the total simulated surface runoff for the calibration and validation: <10% of total precipitation.
- The parameter values for soil and vegetation align with the a priori information.
- The NSE between simulated and observed AET for the calibration and validation > 0.6:where is the average of the observed AET.
3.3. Statistical Analyses
3.4. Correlation Analyses
3.5. Attribution Analysis
4. Results
4.1. Model Validation and Evaluation
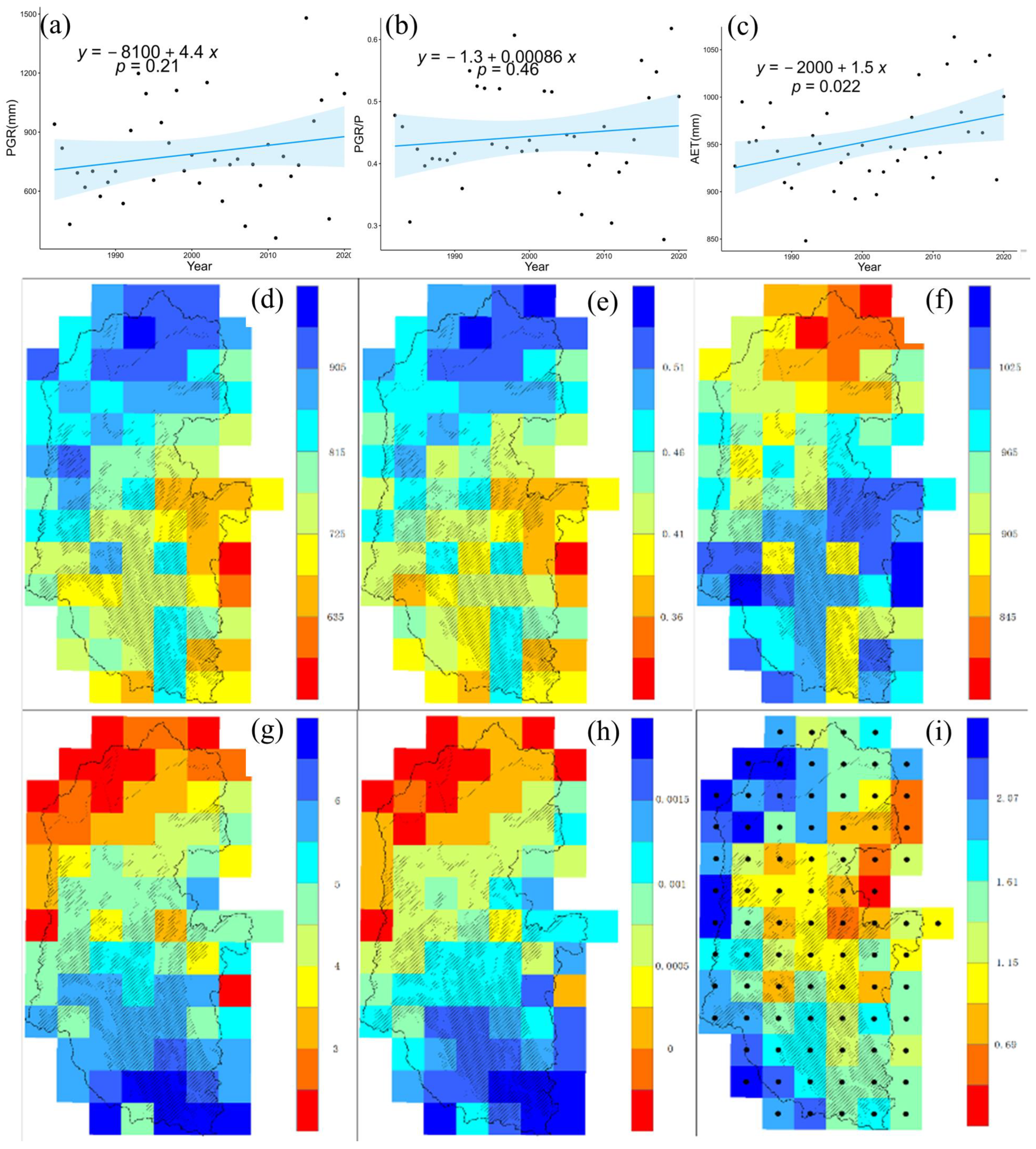
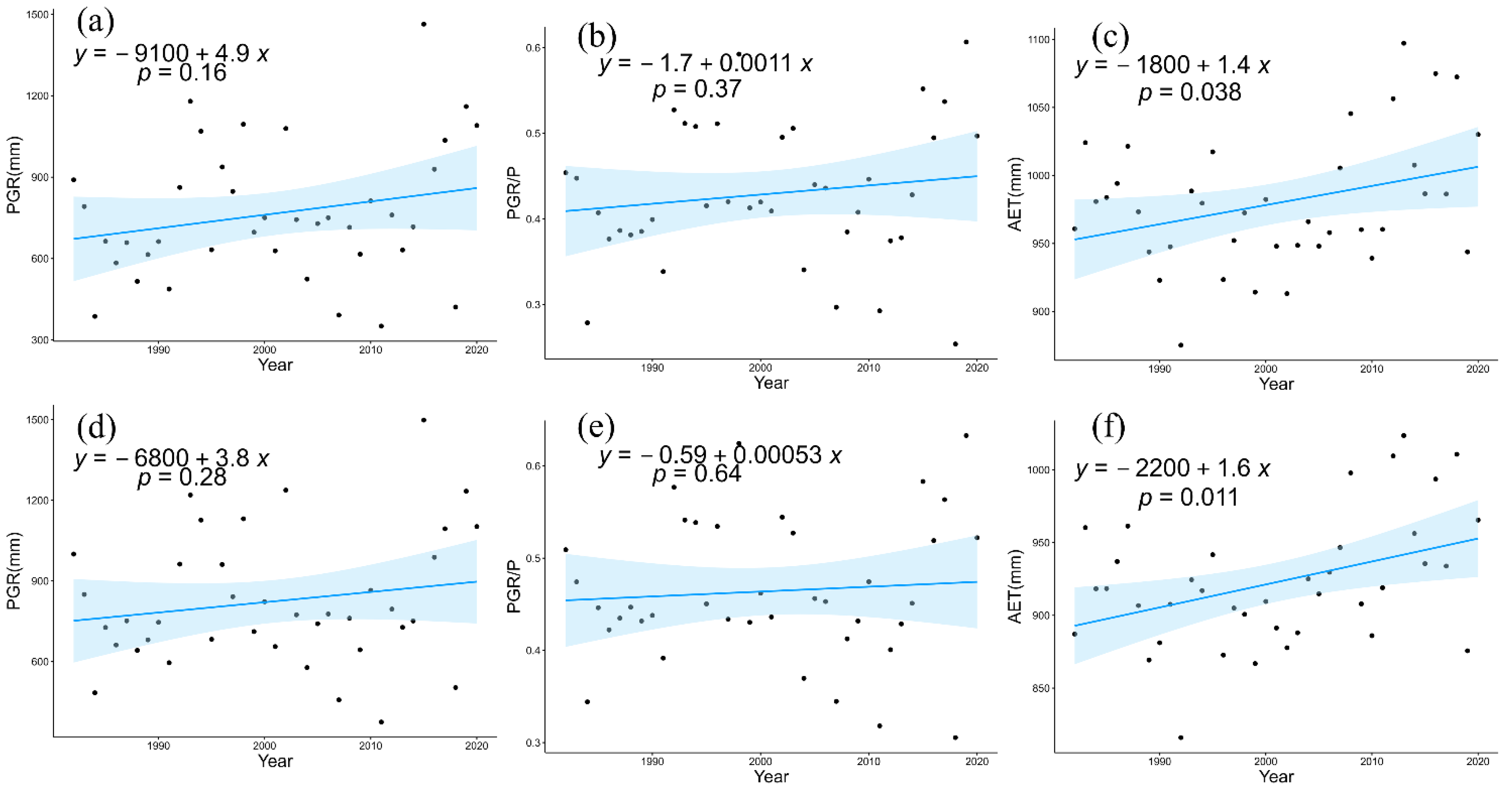
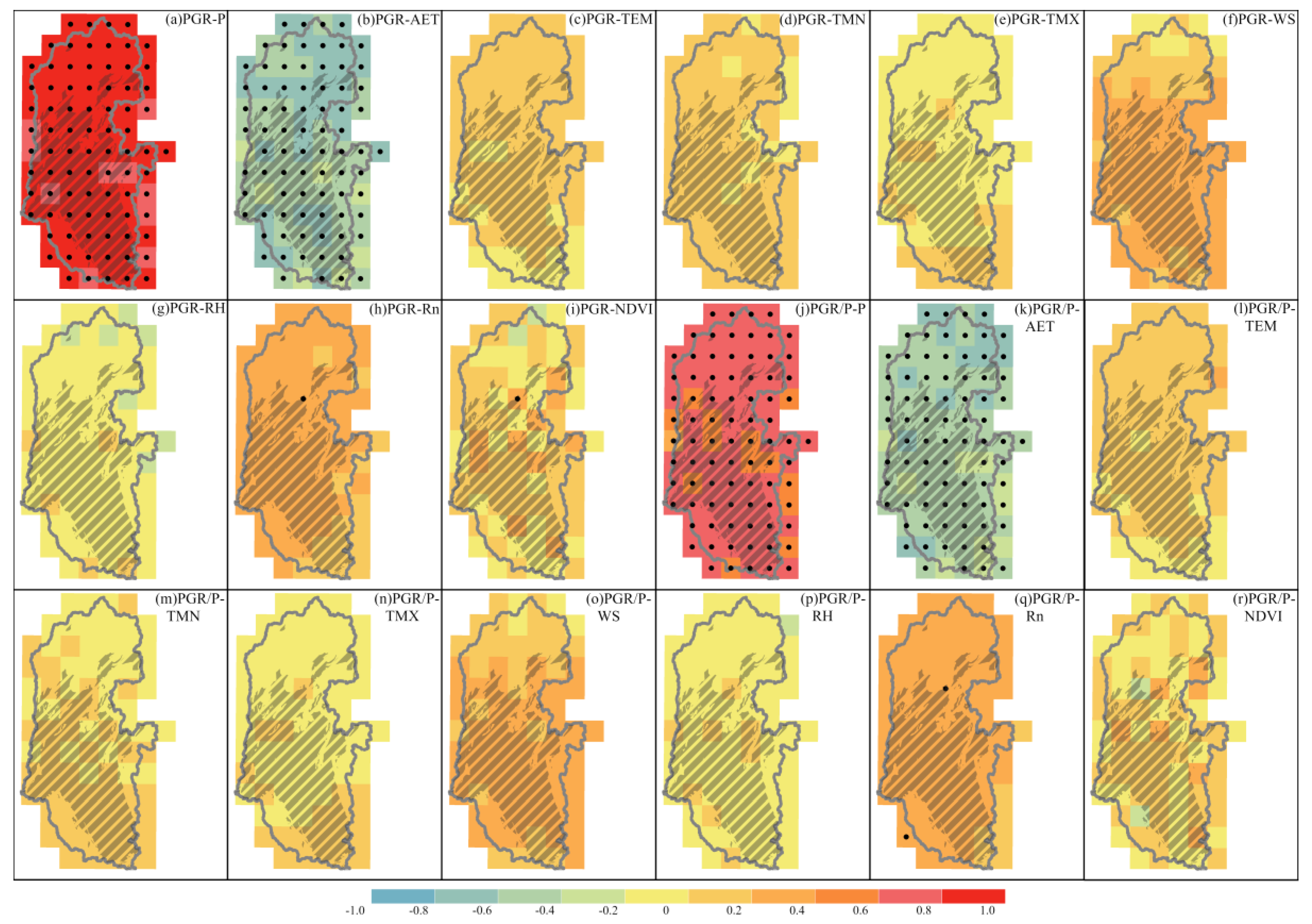
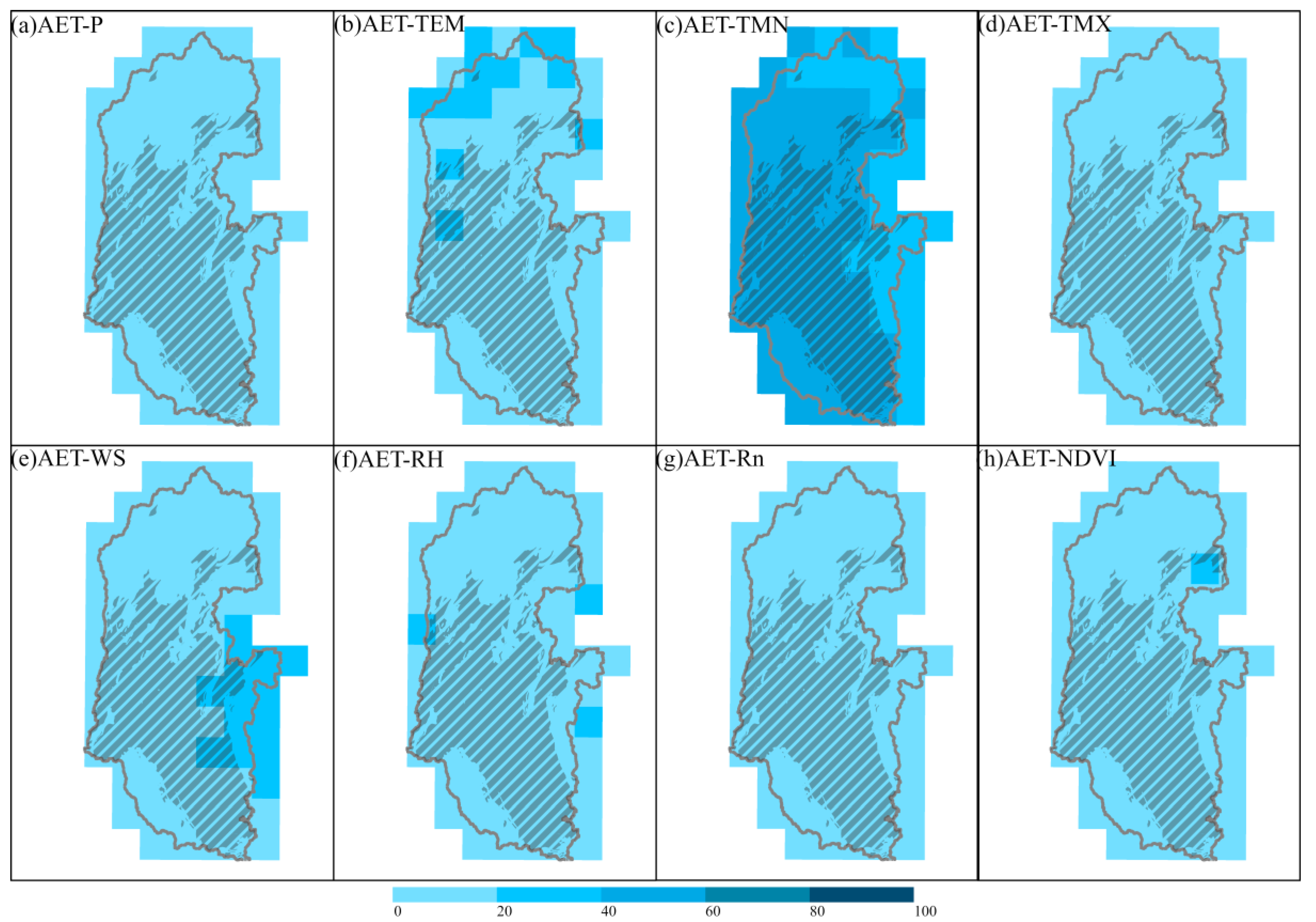
4.2. Spatiotemporal Variability of PGR, PGR/P, and AET
4.3. Responses of PGR, PGR/P, and AET to Climate Change and NDVI
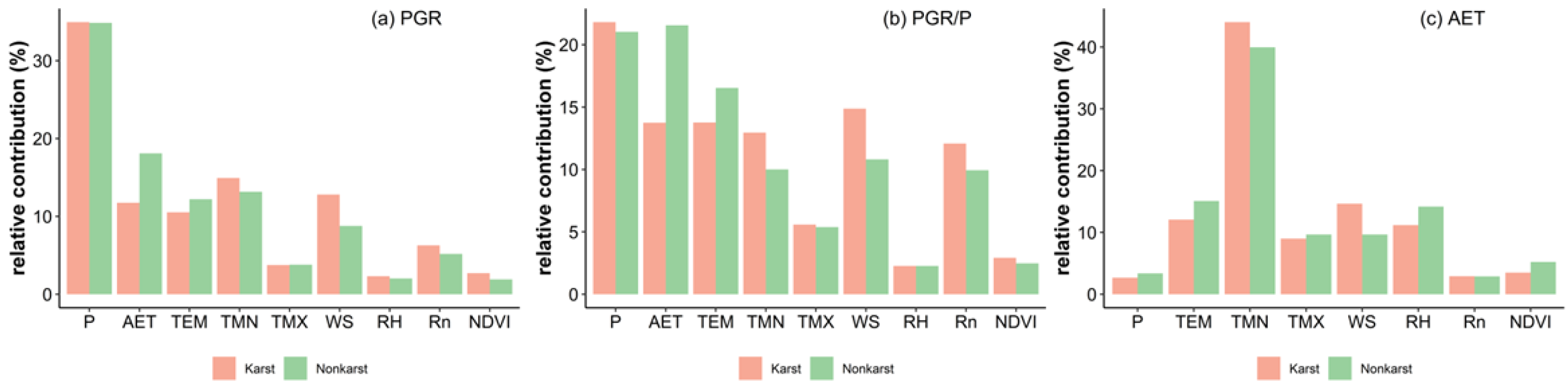
4.4. Causes of the Variability in PGR, PGR/P, and AET
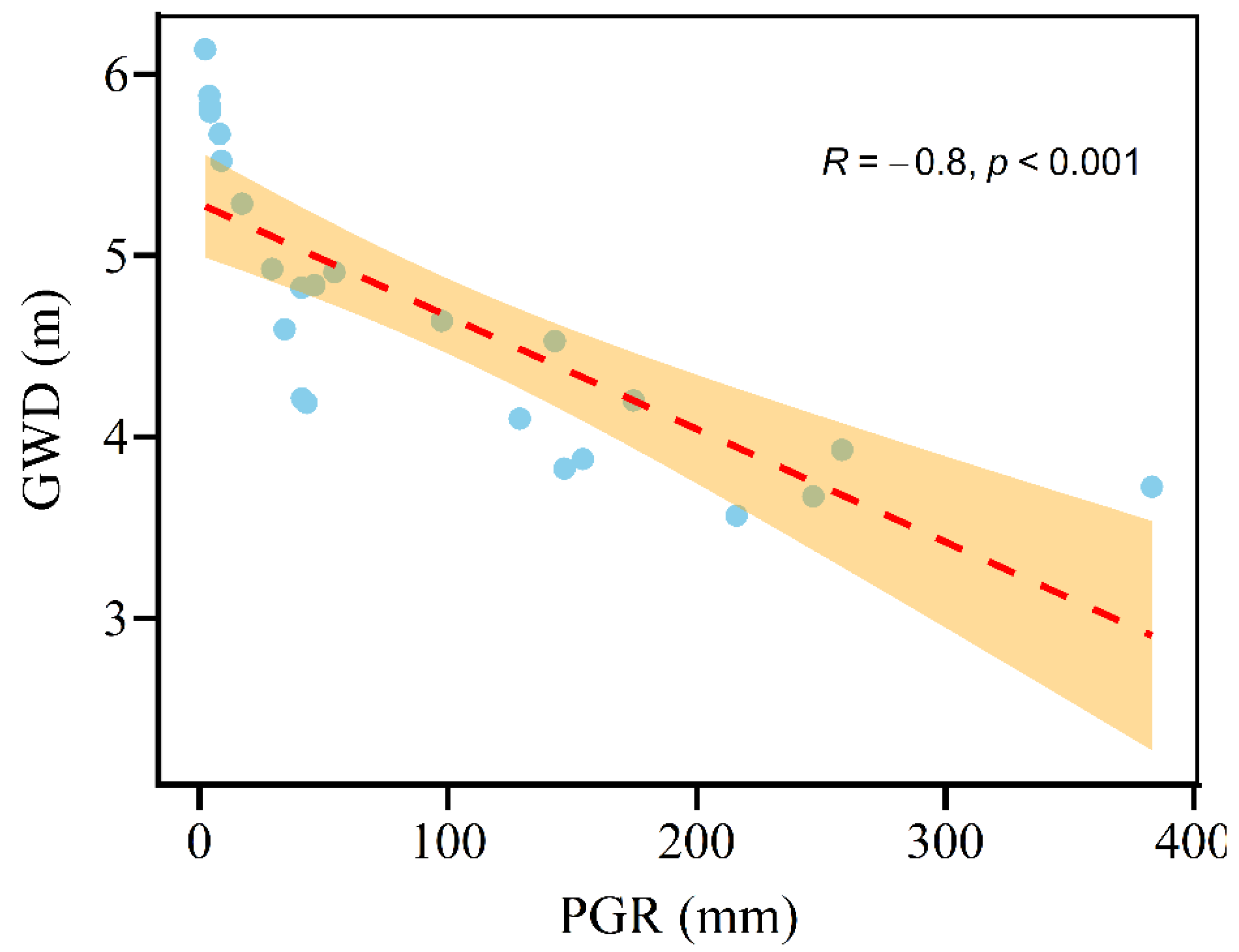
4.5. Temporal Variability of PGR and GWD
5. Discussion
5.1. Spatiotemporal Variations and Influencing Factors of PGR, PGR/P, and AET
5.2. Implications of Vegetation Restoration Activities
5.3. Uncertainty Analysis
6. Conclusions
- (1)
- During the study period, PGR, PGR/P, and AET exhibited increases at rates of 4.4 mm/y, 0.00086, and 1.6 mm/y, respectively. The growth rate of AET in non-karst areas was 14% faster than that in karst areas, and the growth rate of PGR in karst areas was 12.8% faster than that in non-karst areas.
- (2)
- In the case of a humid climate and stable LUCC, NDVI exhibited modest effects on PGR, PGR/P, and AET changes in humid catchments.
- (3)
- TMN was the key factor that determined the changes in AET in the LRB (42.14%). P and AET were the key factors that determined the changes in PGR and PGR/P in the LRB, where P was dominant (34.89%). Moreover, changes in the recharge and recharging rate in the non-karst region were more responsive to AET than in the karst region. Generally, climate change was the primary driving factor of hydrological processes in the basin, while vegetation restoration had a less significant impact.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PGR | Potential groundwater recharge |
| PGR/P | Potential groundwater recharge as a proportion of precipitation |
| AET | Actual evapotranspiration |
| PER | Potential evapotranspiration |
| GWD | Groundwater depth |
| P | Precipitation |
| TEM | Mean temperature |
| TMN | Minimum temperature |
| TMX | Maximum temperature |
| Rn | Net radiation |
| RH | Relative humidity |
| WS | Wind speed |
| NDVI | Normalized Difference Vegetation Index |
| LUCC | Land cover/use change |
| LRB | Lijiang River Basin |
References
- Ford, D.; Williams, P.W. Karst Hydrogeology and Geomorphology, rev. ed.; John Wiley & Sons: Chichester, UK; Hoboken, NJ, USA, 2007; ISBN 978-0-470-84996-5. [Google Scholar]
- Zeng, F.; Jiang, Z.; Shen, L.; Chen, W.; Yang, Q.; Zhang, C. Assessment of Multiple and Interacting Modes of Soil Loss in the Karst Critical Zone, Southwest China (SWC). Geomorphology 2018, 322, 97–106. [Google Scholar] [CrossRef]
- Deng, Y.; Jiang, Z.C. Characteristic of Rocky Desertification and Comprehensive Improving Model in Karst Peak-Cluster Depression in Guohua, Guangxi, China. Procedia Environ. Sci. 2011, 10, 2449–2452. [Google Scholar] [CrossRef]
- Chang, J.; Li, Q.; Zhai, L.; Liao, C.; Qi, X.; Zhang, Y.; Wang, K. Comprehensive Assessment of Rocky Desertification Treatment in Southwest China Karst. Land Degrad. Dev. 2024, 35, 3461–3476. [Google Scholar] [CrossRef]
- Yue, Y.; Qi, X.; Wang, K.; Liao, C.; Tong, X.; Brandt, M.; Liu, B. Large Scale Rocky Desertification Reversal in South China Karst. Prog. Phys. Geogr. Earth Environ. 2022, 46, 661–675. [Google Scholar] [CrossRef]
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst Water Resources in a Changing World: Review of Hydrological Modeling Approaches: KARST WATER RESOURCES PREDICTION. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- Chang, Y.; Liu, Y.; Liu, L. Contrasting Hydrological Responses to Climate Change in Two Adjacent Catchments Dominated by Karst and Nonkarst. J. Hydrol. 2023, 625, 130013. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground Water and Climate Change. Nat. Clim. Change 2013, 3, 322–329. [Google Scholar] [CrossRef]
- Hu, W.; Wang, Y.Q.; Li, H.J.; Huang, M.B.; Hou, M.T.; Li, Z.; She, D.L.; Si, B.C. Dominant Role of Climate in Determining Spatio-Temporal Distribution of Potential Groundwater Recharge at a Regional Scale. J. Hydrol. 2019, 578, 124042. [Google Scholar] [CrossRef]
- Muhumure, J.; Pohl, E.; Schulz, S. Assessing the Impact of Climate Change on Spring Discharge Using Hydrological Modelling in Musanze District, Rwanda. Hydrogeol. J. 2024, 32, 1909–1923. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Adeyeri, O.E.; Onojeghuo, A.O.; Ferreira, V.G.; Kalu, I.; Okwuashi, O. Understanding Global Groundwater-Climate Interactions. Sci. Total Environ. 2023, 904, 166571. [Google Scholar] [CrossRef]
- Klaas, D.K.S.Y.; Imteaz, M.A.; Sudiayem, I.; Klaas, E.M.E.; Klaas, E.C.M. Assessing Climate Changes Impacts on Tropical Karst Catchment: Implications on Groundwater Resource Sustainability and Management Strategies. J. Hydrol. 2020, 582, 124426. [Google Scholar] [CrossRef]
- Liu, M.; Xu, X.; Wang, D.; Sun, A.Y.; Wang, K. Karst Catchments Exhibited Higher Degradation Stress from Climate Change than the Non-Karst Catchments in Southwest China: An Ecohydrological Perspective. J. Hydrol. 2016, 535, 173–180. [Google Scholar] [CrossRef]
- Liu, Y.; Lian, J.; Luo, Z.; Chen, H. Spatiotemporal Variations in Evapotranspiration and Transpiration Fraction Following Changes in Climate and Vegetation in a Karst Basin of Southwest China. J. Hydrol. 2022, 612, 128216. [Google Scholar] [CrossRef]
- Ashraf, S.; Ali, M.; Shrestha, S.; Hafeez, M.A.; Moiz, A.; Sheikh, Z.A. Impacts of Climate and Land-Use Change on Groundwater Recharge in the Semi-Arid Lower Ravi River Basin, Pakistan. Groundw. Sustain. Dev. 2022, 17, 100743. [Google Scholar] [CrossRef]
- Salem, A.; Abduljaleel, Y.; Dezső, J.; Lóczy, D. Integrated Assessment of the Impact of Land Use Changes on Groundwater Recharge and Groundwater Level in the Drava Floodplain, Hungary. Sci. Rep. 2023, 13, 5061. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Sun, J.; Li, S.; Ning, T.; Li, Z. Indirect Effects of Revegetation Dominate Groundwater Recharge Change at the Basin Scale. J. Clean. Prod. 2024, 456, 142396. [Google Scholar] [CrossRef]
- Li, X.; Gentine, P.; Lin, C.; Zhou, S.; Sun, Z.; Zheng, Y.; Liu, J.; Zheng, C. A Simple and Objective Method to Partition Evapotranspiration into Transpiration and Evaporation at Eddy-Covariance Sites. Agric. For. Meteorol. 2019, 265, 171–182. [Google Scholar] [CrossRef]
- Lian, X.; Piao, S.; Huntingford, C.; Li, Y.; Zeng, Z.; Wang, X.; Ciais, P.; McVicar, T.R.; Peng, S.; Ottlé, C.; et al. Partitioning Global Land Evapotranspiration Using CMIP5 Models Constrained by Observations. Nat. Clim. Change 2018, 8, 640–646. [Google Scholar] [CrossRef]
- Li, R.; Zheng, H.; O’Connor, P.; Xu, H.; Li, Y.; Lu, F.; Robinson, B.E.; Ouyang, Z.; Hai, Y.; Daily, G.C. Time and Space Catch up with Restoration Programs That Ignore Ecosystem Service Trade-Offs. Sci. Adv. 2021, 7, eabf8650. [Google Scholar] [CrossRef]
- Lu, C.; Zhao, T.; Shi, X.; Cao, S. Ecological Restoration by Afforestation May Increase Groundwater Depth and Create Potentially Large Ecological and Water Opportunity Costs in Arid and Semiarid China. J. Clean. Prod. 2018, 176, 1213–1222. [Google Scholar] [CrossRef]
- Zhao, M.; Geruo, A.; Zhang, J.; Velicogna, I.; Liang, C.; Li, Z. Ecological Restoration Impact on Total Terrestrial Water Storage. Nat. Sustain. 2020, 4, 56–62. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, X.; Ding, Y.; Chen, D.; Qin, D.; Zhai, P. Understanding Human Influence on Climate Change in China. Natl. Sci. Rev. 2022, 9, nwab113. [Google Scholar] [CrossRef]
- Jeannin, P.-Y.; Artigue, G.; Butscher, C.; Chang, Y.; Charlier, J.-B.; Duran, L.; Gill, L.; Hartmann, A.; Johannet, A.; Jourde, H.; et al. Karst Modelling Challenge 1: Results of Hydrological Modelling. J. Hydrol. 2021, 600, 126508. [Google Scholar] [CrossRef]
- Anderson, M.; Woessner, W.; Hunt, R. Applied Ground Water Modeling: Simulation of Flow and Advective Transport; Academic Press: San Diego, CA, USA, 2015; ISBN 978-0-12-058103-0. [Google Scholar]
- Jourde, H.; Wang, X. Advances, Challenges and Perspective in Modelling the Functioning of Karst Systems: A Review. Environ. Earth Sci. 2023, 82, 396. [Google Scholar] [CrossRef]
- Al Aamery, N.; Adams, E.; Fox, J.; Husic, A.; Zhu, J.; Gerlitz, M.; Agouridis, C.; Bettel, L. Numerical Model Development for Investigating Hydrologic Pathways in Shallow Fluviokarst. J. Hydrol. 2021, 593, 125844. [Google Scholar] [CrossRef]
- Chen, L.; Deng, J.; Yang, W.; Chen, H. Hydrological Modelling of Large-Scale Karst-Dominated Basin Using a Grid-Based Distributed Karst Hydrological Model. J. Hydrol. 2024, 628, 130459. [Google Scholar] [CrossRef]
- Liu, Y.; Wagener, T.; Hartmann, A. Assessing Streamflow Sensitivity to Precipitation Variability in Karst-Influenced Catchments with Unclosed Water Balances. Water Resour. Res. 2021, 57, e2020WR028598. [Google Scholar] [CrossRef]
- Ollivier, C.; Olioso, A.; Carrière, S.D.; Boulet, G.; Chalikakis, K.; Chanzy, A.; Charlier, J.-B.; Combemale, D.; Davi, H.; Emblanch, C.; et al. An Evapotranspiration Model Driven by Remote Sensing Data for Assessing Groundwater Resource in Karst Watershed. Sci. Total Environ. 2021, 781, 146706. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Dowd, P.; Bosch, A.P.; Luque-Espinar, J.A.; Heredia, J.; Durán-Valsero, J.J. A Parsimonious Distributed Model for Simulating Transient Water Flow in a High-Relief Karst Aquifer. Hydrogeol. J. 2018, 26, 2617–2627. [Google Scholar] [CrossRef]
- Sarrazin, F.; Hartmann, A.; Pianosi, F.; Rosolem, R.; Wagener, T. V2Karst V1.1: A Parsimonious Large-Scale Integrated Vegetation–Recharge Model to Simulate the Impact of Climate and Land Cover Change in Karst Regions. Geosci. Model Dev. 2018, 11, 4933–4964. [Google Scholar] [CrossRef]
- Hartmann, A.; Gleeson, T.; Rosolem, R.; Pianosi, F.; Wada, Y.; Wagener, T. A Large-Scale Simulation Model to Assess Karstic Groundwater Recharge over Europe and the Mediterranean. Geosci. Model Dev. 2015, 8, 1729–1746. [Google Scholar] [CrossRef]
- Kovačič, G.; Petrič, M.; Ravbar, N. Evaluation and Quantification of the Effects of Climate and Vegetation Cover Change on Karst Water Sources: Case Studies of Two Springs in South-Western Slovenia. Water 2020, 12, 3087. [Google Scholar] [CrossRef]
- Wagener, T.; Sarrazin, F.; Hartmann, A.J.; Pianosi, F.; Rosolem, R. Data Mining a Large Ensemble of Groundwater Recharge Projections under Climate and Land Use Changes across Europe. In Proceedings of the AGU Fall Meeting Abstracts, Washington, DC, USA, 10–14 December 2018; Volume 2018, p. H31F-04. [Google Scholar]
- Duan, W.; Li, H.F.; Wang, J.; Zhao, L.; Li, G.; Wang, S. The Regulation Effect of Typical Forest on Rainfall-Runoff in Upper Reaches of Lijiang River. Shengtai Xuebao 2015, 35, 663–669. [Google Scholar]
- Yang, Y.; Zhai, L.; Jia, Y.; Xue, K. An Analysis of the Change of Rainfall-Runoff Characteristics in the Lijiang River Basin under Different Types of Landuse. China Rural Water Hydropower 2022, 8, 97–105. [Google Scholar]
- Hartmann, A.; Lange, J.; Weiler, M.; Arbel, Y.; Greenbaum, N. A New Approach to Model the Spatial and Temporal Variability of Recharge to Karst Aquifers. Hydrol. Earth Syst. Sci. 2012, 16, 2219–2231. [Google Scholar] [CrossRef]
- He, Y.; Fan, G.; Zhang, X.; Liu, M.; Gao, D. Variation of Vegetation NDVI and Its Response to Climate Change in Zhejiang Province. Shengtai Xuebao/Acta Ecol. Sin. 2012, 32, 4352–4362. [Google Scholar]
- Adeyeri, O.E.; Zhou, W.; Wang, X.; Zhang, R.; Laux, P.; Ishola, K.A.; Usman, M. The Trend and Spatial Spread of Multisectoral Climate Extremes in CMIP6 Models. Sci. Rep. 2022, 12, 21000. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Y.; Wu, C.; Li, G.; Ma, M.; Fan, L.; Zheng, H.; Song, L.; Tang, X. Exploring the Contribution of Environmental Factors to Evapotranspiration Dynamics in the Three-River-Source Region, China. J. Hydrol. 2023, 626, 130222. [Google Scholar] [CrossRef]
- Ruggieri, G.; Allocca, V.; Borfecchia, F.; Cusano, D.; Marsiglia, P.; De Vita, P. Testing Evapotranspiration Estimates Based on MODIS Satellite Data in the Assessment of the Groundwater Recharge of Karst Aquifers in Southern Italy. Water 2021, 13, 118. [Google Scholar] [CrossRef]
- Fu, J.; Gong, Y.; Zheng, W.; Zou, J.; Zhang, M.; Zhang, Z.; Qin, J.; Liu, J.; Quan, B. Spatial-Temporal Variations of Terrestrial Evapotranspiration across China from 2000 to 2019. Sci. Total Environ. 2022, 825, 153951. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Simmons, C.T.; Zhang, L.; Zhang, Q. Changes in Groundwater Levels across China from 2005 to 2016. J. Hydrol. 2023, 623, 129781. [Google Scholar] [CrossRef]
- Wu, W.-Y.; Lo, M.-H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.-F.; Ducharne, A.; Yang, Z.-L. Divergent Effects of Climate Change on Future Groundwater Availability in Key Mid-Latitude Aquifers. Nat. Commun. 2020, 11, 3710. [Google Scholar] [CrossRef] [PubMed]
- Stoy, P.C.; El-Madany, T.S.; Fisher, J.B.; Gentine, P.; Gerken, T.; Good, S.P.; Klosterhalfen, A.; Liu, S.; Miralles, D.G.; Perez-Priego, O.; et al. Reviews and Syntheses: Turning the Challenges of Partitioning Ecosystem Evaporation and Transpiration into Opportunities. Biogeosciences 2019, 16, 3747–3775. [Google Scholar] [CrossRef]
- Zhao, F.; Ma, S.; Wu, Y.; Qiu, L.; Wang, W.; Lian, Y.; Chen, J.; Sivakumar, B. The Role of Climate Change and Vegetation Greening on Evapotranspiration Variation in the Yellow River Basin, China. Agric. For. Meteorol. 2022, 316, 108842. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Huang, Y.; Zhang, Y. Effect of Catchment Properties on Runoff Coefficient in a Karst Area of Southwest China. Hydrol. Process. 2014, 28, 3691–3702. [Google Scholar] [CrossRef]
- Cai, L.; Xiong, K.; Liu, Z.; Li, Y.; Fan, B. Seasonal Variations of Plant Water Use in the Karst Desertification Control. Sci. Total Environ. 2023, 885, 163778. [Google Scholar] [CrossRef]
- Chen, Y.; Xue, Y.; Hu, Y. How Multiple Factors Control Evapotranspiration in North America Evergreen Needleleaf Forests. Sci. Total Environ. 2018, 622–623, 1217–1224. [Google Scholar] [CrossRef]
- Liu, Y.J.; Chen, J.; Pan, T. Analysis of Changes in Reference Evapotranspiration, Pan Evaporation, and Actual Evapotranspiration and Their Influencing Factors in the North China Plain During 1998–2005. Earth Space Sci. 2019, 6, 1366–1377. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Zhang, L.; Zhang, Q.; Gan, R.; Li, X. Attribution of Evapotranspiration Changes in Humid Regions of China from 1982 to 2016. J. Geophys. Res. Atmos. 2020, 125, e2020JD032404. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, C.; Qiu, B.; Wang, J.; Chen, J.; Zhang, Y.; Wu, C.; Liu, B.; Shu, L. Spatiotemporally Non-Stationary Evolution of Groundwater Levels in Poyang Lake Basin Driven by Meteorological and Hydrological Factors. Sci. Total Environ. 2024, 950, 175244. [Google Scholar] [CrossRef]
- Yifru, B.A.; Chung, I.-M.; Kim, M.-G.; Chang, S.W. Assessing the Effect of Land/Use Land Cover and Climate Change on Water Yield and Groundwater Recharge in East African Rift Valley Using Integrated Model. J. Hydrol. Reg. Stud. 2021, 37, 100926. [Google Scholar] [CrossRef]
- Anurag, H.; Ng, G.H.C.; Tipping, R.; Tokos, K. Modeling the Impact of Spatiotemporal Vegetation Dynamics on Groundwater Recharge. J. Hydrol. 2021, 601, 126584. [Google Scholar] [CrossRef]
- Mohan, C.; Western, A.W.; Wei, Y.; Saft, M. Predicting Groundwater Recharge for Varying Land Cover and Climate Conditions—A Global Meta-Study. Hydrol. Earth Syst. Sci. 2018, 22, 2689–2703. [Google Scholar] [CrossRef]
- Riedel, T.; Weber, T.K.D. Review: The Influence of Global Change on Europe’s Water Cycle and Groundwater Recharge. Hydrogeol. J. 2020, 28, 1939–1959. [Google Scholar] [CrossRef]
- Li, N.; Wang, J.; Wang, H.; Fu, B.; Chen, J.; He, W. Impacts of Land Use Change on Ecosystem Service Value in Lijiang River Basin, China. Environ. Sci Pollut Res 2021, 28, 46100–46115. [Google Scholar] [CrossRef]
- Douinot, A.; Tetzlaff, D.; Maneta, M.; Kuppel, S.; Schulte-Bisping, H.; Soulsby, C. Ecohydrological Modelling with EcH2O-iso to Quantify Forest and Grassland Effects on Water Partitioning and Flux Ages. Hydrol. Process. 2019, 33, 2174–2191. [Google Scholar] [CrossRef]
- Ellison, D.; Morris, C.E.; Locatelli, B.; Sheil, D.; Cohen, J.; Murdiyarso, D.; Gutierrez, V.; Noordwijk, M.V.; Creed, I.F.; Pokorny, J.; et al. Trees, Forests and Water: Cool Insights for a Hot World. Glob. Environ. Change 2017, 43, 51–61. [Google Scholar] [CrossRef]
- Yu, L.; Liu, Y.; Liu, T.; Yan, F. Impact of Recent Vegetation Greening on Temperature and Precipitation over China. Agric. For. Meteorol. 2020, 295, 108197. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, M.; Mildrexler, D.J.; Motesharrei, S.; Mu, Q.; Kalnay, E.; Zhao, F.; Li, S.; Wang, K. Potential and Actual Impacts of Deforestation and Afforestation on Land Surface Temperature. J. Geophys. Res. Atmos. 2016, 121, 14,372–14,386. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Liu, M.; Li, Z.; Zhang, Y.; Zhu, J.; Wang, K.; Chen, X.; Zhang, Z.; Peng, T. An Improved Optimization Scheme for Representing Hillslopes and Depressions in Karst Hydrology. Water Resour. Res. 2020, 56, e2019WR026038. [Google Scholar] [CrossRef]
- Yang, Y.; Lijuan, W.; Xiaoyan, H.; Yue, Q.; Rui, X. Analysis on Spatio-Temporal Variation of Evapotranspiration in the Yellow River Basin Based on ERA5-Land Products. J. Arid Meteorol. 2023, 41, 390. [Google Scholar]
- Abhishek; Kinouchi, T.; Sayama, T. A Comprehensive Assessment of Water Storage Dynamics and Hydroclimatic Extremes in the Chao Phraya River Basin during 2002–2020. J. Hydrol. 2021, 603, 126868. [Google Scholar] [CrossRef]
- Piao, S.; Wang, X.; Park, T.; Chen, C.; Lian, X.; He, Y.; Bjerke, J.W.; Chen, A.; Ciais, P.; Tømmervik, H.; et al. Characteristics, Drivers and Feedbacks of Global Greening. Nat. Rev. Earth Environ. 2019, 1, 14–27. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, Y. Increasing Tibetan Plateau Terrestrial Evapotranspiration Primarily Driven by Precipitation. Agric. For. Meteorol. 2022, 317, 108887. [Google Scholar] [CrossRef]

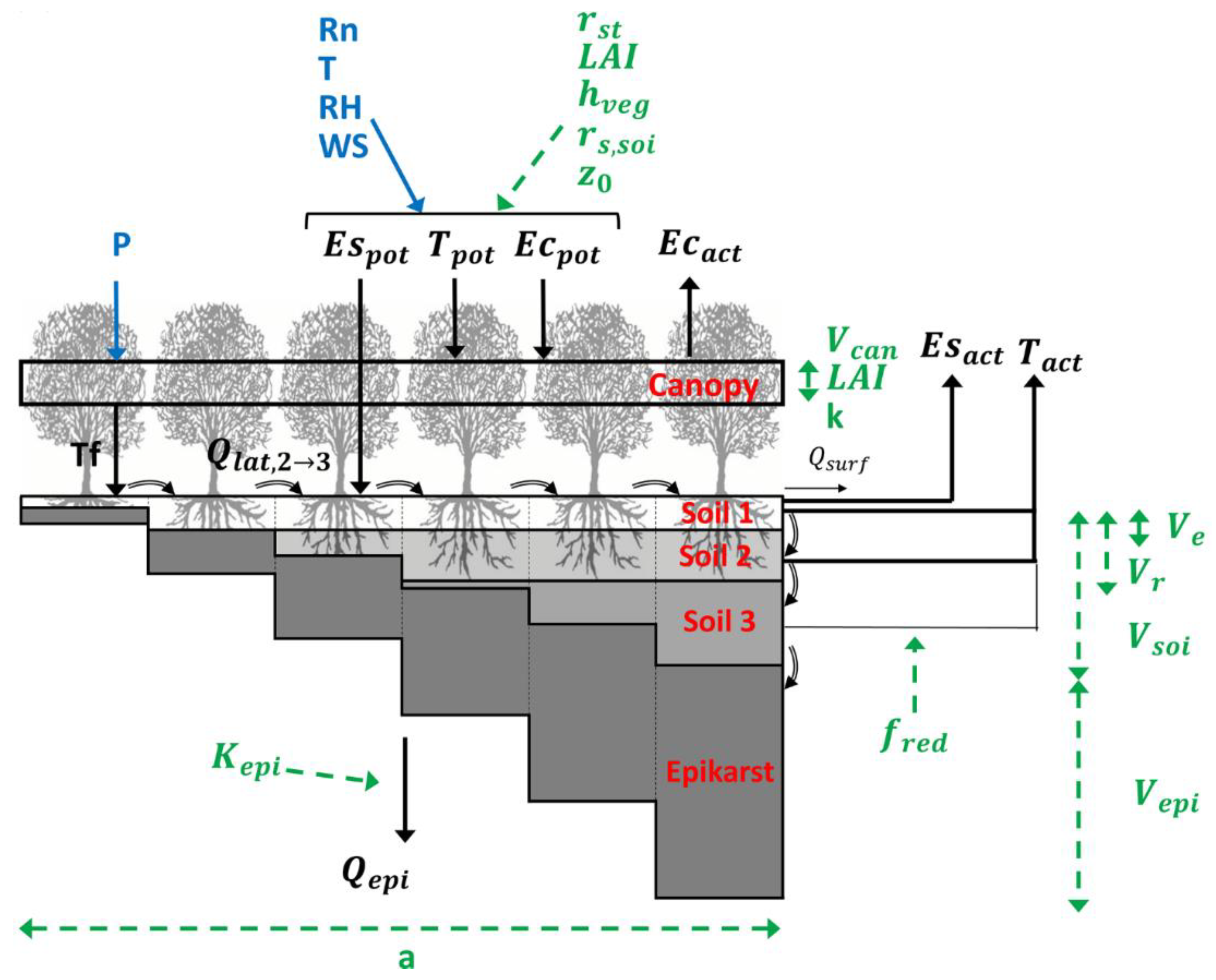




| Product | Spatial Resolution | Period | Source |
|---|---|---|---|
| ERA5_Land | 0.1° | 1980–2020 | https://cds.climate.copernicus.eu accessed on 23 April 2024 |
| Canopy height | 30 m | 2020 | https://www.3decology.org/2023/06/21/forest-tree-height-map-of-china-2 accessed on 23 April 2024 |
| NDVI | 1/12° | 1982–2020 | https://zenodo.org/records/8253971 accessed on 23 April 2024 |
| Meteorological data | - | 1980–2020 | https://data.cma.cn accessed on 23 April 2024 |
| DEM | 30 m | - | https://earthexplorer.usgs.gov accessed on 23 April 2024 |
| Prior information | 1 km | 1992 | https://www.usgs.gov/centers/eros/science/usgs-eros-archive-land-cover-products-global-land-cover-characterization-glcc accessed on 23 April 2024 |
| Groundwater depth data | 50 points | 2019–2020 | China Geological Survey, on-site measured data. |
| Parameter | Unit | Range |
|---|---|---|
| hveg | m | 0.2—site specific |
| rst | s/m | 20–600 |
| LAImin | % | 5–100 |
| LAImax | m2m−2 | 0.5–8 |
| Vr | mm | 20–500 |
| Vcan | mm/LAI | 0.1–0.5 |
| k | - | 0.4–0.7 |
| fred | - | 0–0.15 |
| z0 | m | 0.0003–0.013 |
| rs,soi | s/m | 0–100 |
| Ve | mm | 5–45 |
| a | - | 0–6 |
| Vsoi | mm | 20–800 |
| Vepi | mm | 200–700 |
| Kepi | d | 0–50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, X.; Deng, Y.; Wang, Y.; Pan, L.; Chen, Y.; Cai, J. Contrasting the Contributions of Climate Change and Greening to Hydrological Processes in Humid Karst and Non-Karst Areas. Water 2025, 17, 1258. https://doi.org/10.3390/w17091258
Tan X, Deng Y, Wang Y, Pan L, Chen Y, Cai J. Contrasting the Contributions of Climate Change and Greening to Hydrological Processes in Humid Karst and Non-Karst Areas. Water. 2025; 17(9):1258. https://doi.org/10.3390/w17091258
Chicago/Turabian StyleTan, Xiaoyu, Yan Deng, Yehao Wang, Linyan Pan, Yuanyuan Chen, and Junjie Cai. 2025. "Contrasting the Contributions of Climate Change and Greening to Hydrological Processes in Humid Karst and Non-Karst Areas" Water 17, no. 9: 1258. https://doi.org/10.3390/w17091258
APA StyleTan, X., Deng, Y., Wang, Y., Pan, L., Chen, Y., & Cai, J. (2025). Contrasting the Contributions of Climate Change and Greening to Hydrological Processes in Humid Karst and Non-Karst Areas. Water, 17(9), 1258. https://doi.org/10.3390/w17091258





