The Influence of Natural and Anthropogenic Forcing on Water and Energy Balance and on Photosynthesis
Abstract
:1. Introduction
2. Data and Methods
2.1. Data and Study Area
| Name | Descriptions | Periods |
|---|---|---|
| CMIP6 historical simulation | CMIP6 historical simulation (∼2014): WMGHGs, BC, OC, SO2, SO4, NOx, NH3, CO, NMVOC, nitrogen deposition, ozone, tratospheric aerosols, solar irradiance, and land use | 1850–2010 |
| hist-NAT | Natural-only historical simulations (solar irradiance and stratospheric aerosol) | 1850–2010 |
| hist-GHG | Well-mixed greenhouse-gas-only historical simulations (WMGHGs) | 1850–2010 |
| hist-AER | Anthropogenic-aerosol-only historical simulations (BC, OC, SO2, SO4, NOx, NH3, CO, and NMVOC) | 1850–2010 |
| Model | PR | T | ET, SH | GPP | SSM(TSM) | RUNOFF |
|---|---|---|---|---|---|---|
| ACCESS-ESM1-5 [33] | ∘ | ∘ | ∘ | ∘ | ||
| BCC-CSM2-MR [34] | ∘ | |||||
| CanESM5 [35] | ∘ | ∘ | ∘ | ∘ | ||
| CESM2 [36] | ∘ | ∘ | ∘ | ∘ | ||
| CNRM-ESM2-1 [37] | ∘ | ∘ | ∘ | ∘ | ||
| FGOALS-g3 [38] | ∘ | ∘ | ∘ | |||
| GFDL-ESM4 [39] | ∘ | ∘ | ∘ | |||
| GISS-E2-1-G [40] | ∘ | ∘ | ||||
| HadGEM3-GC31-LL [41] | ∘ | ∘ | ∘ | |||
| IPSL-CM6A-LR [42] | ∘ | ∘ | ∘ | ∘ | ∘ | |
| MIROC6 [43] | ∘ | ∘ | ∘ | ∘ | ∘ | |
| MRI-ESM2-0 [44] | ∘ | ∘ | ∘ | ∘ | ∘ | |
| NorESM2-LM [45] | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ |
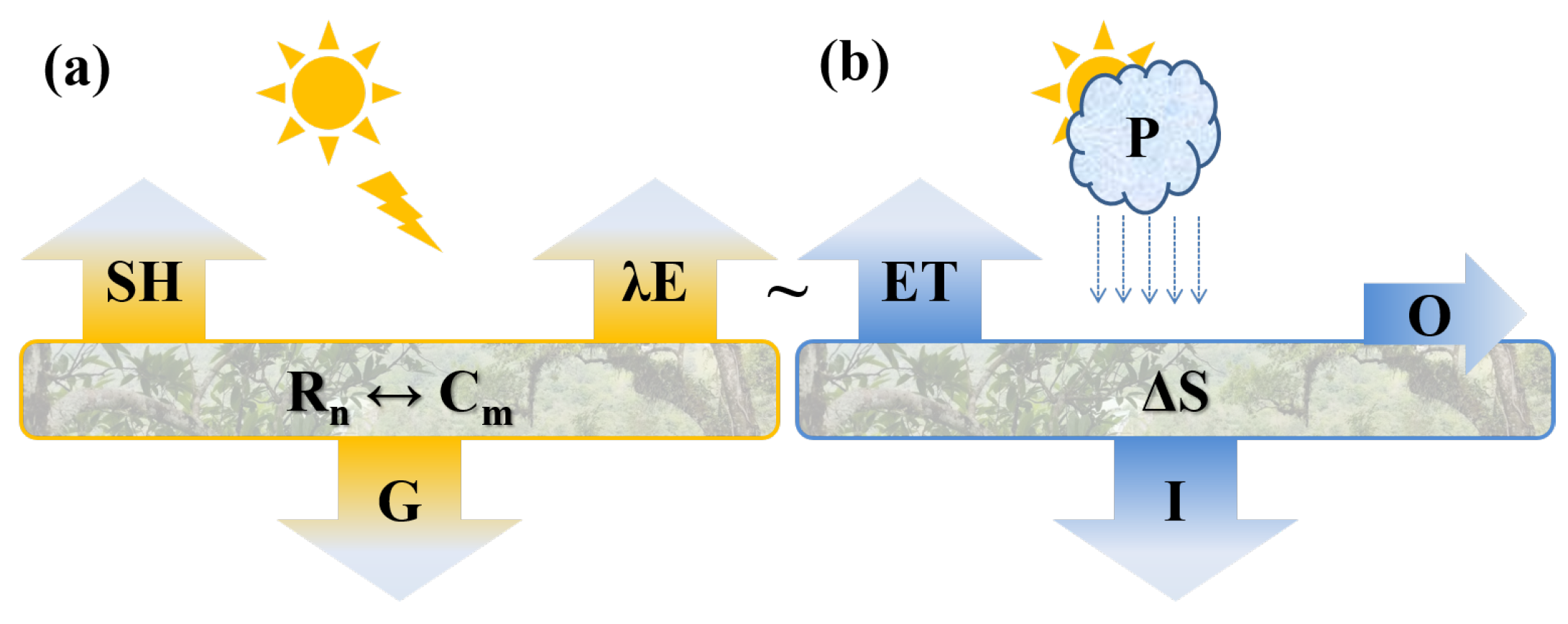
2.2. Energy and Water Balance
2.3. Analysis Method
3. Results
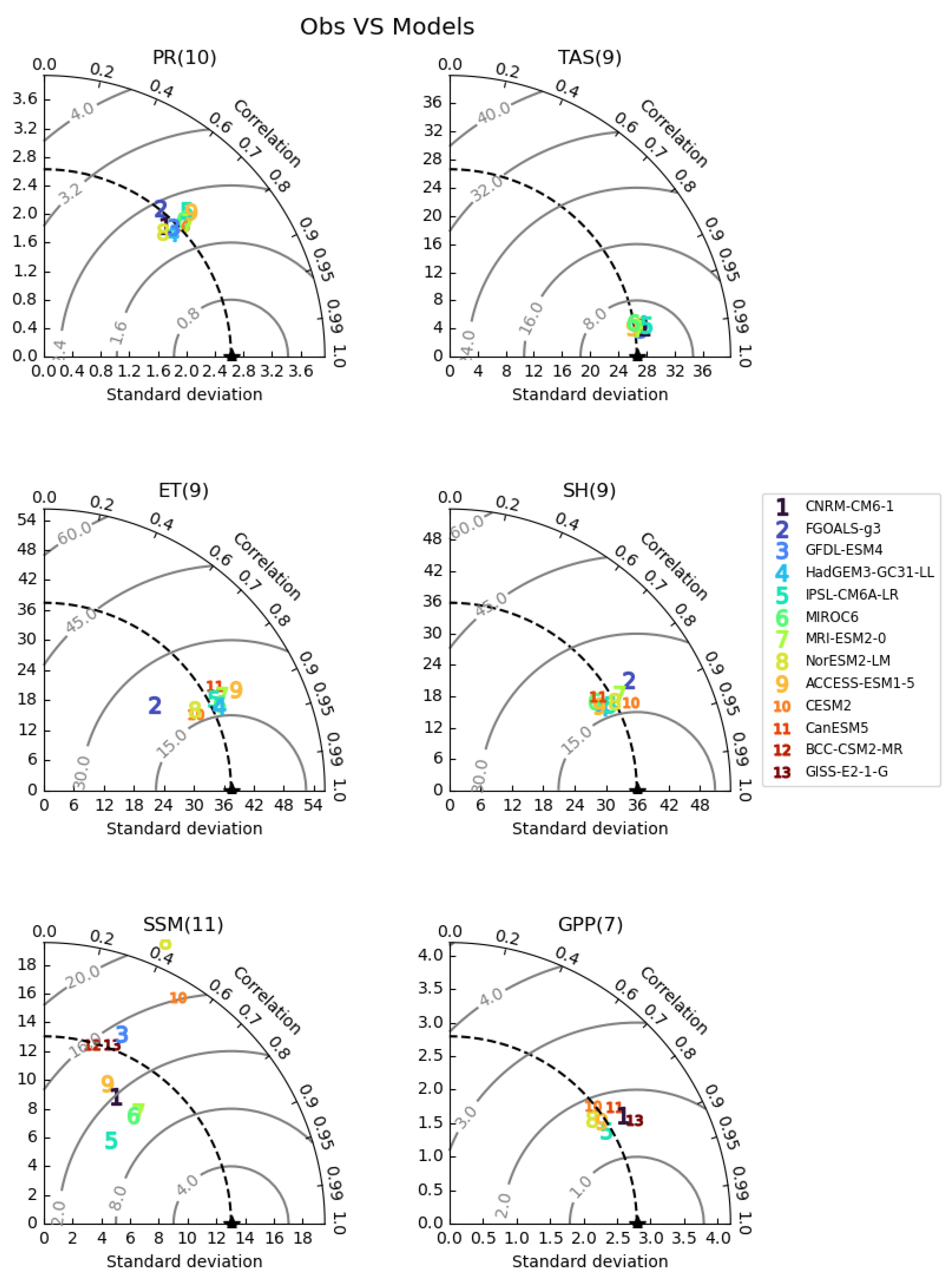
3.1. Precipitation and Temperature
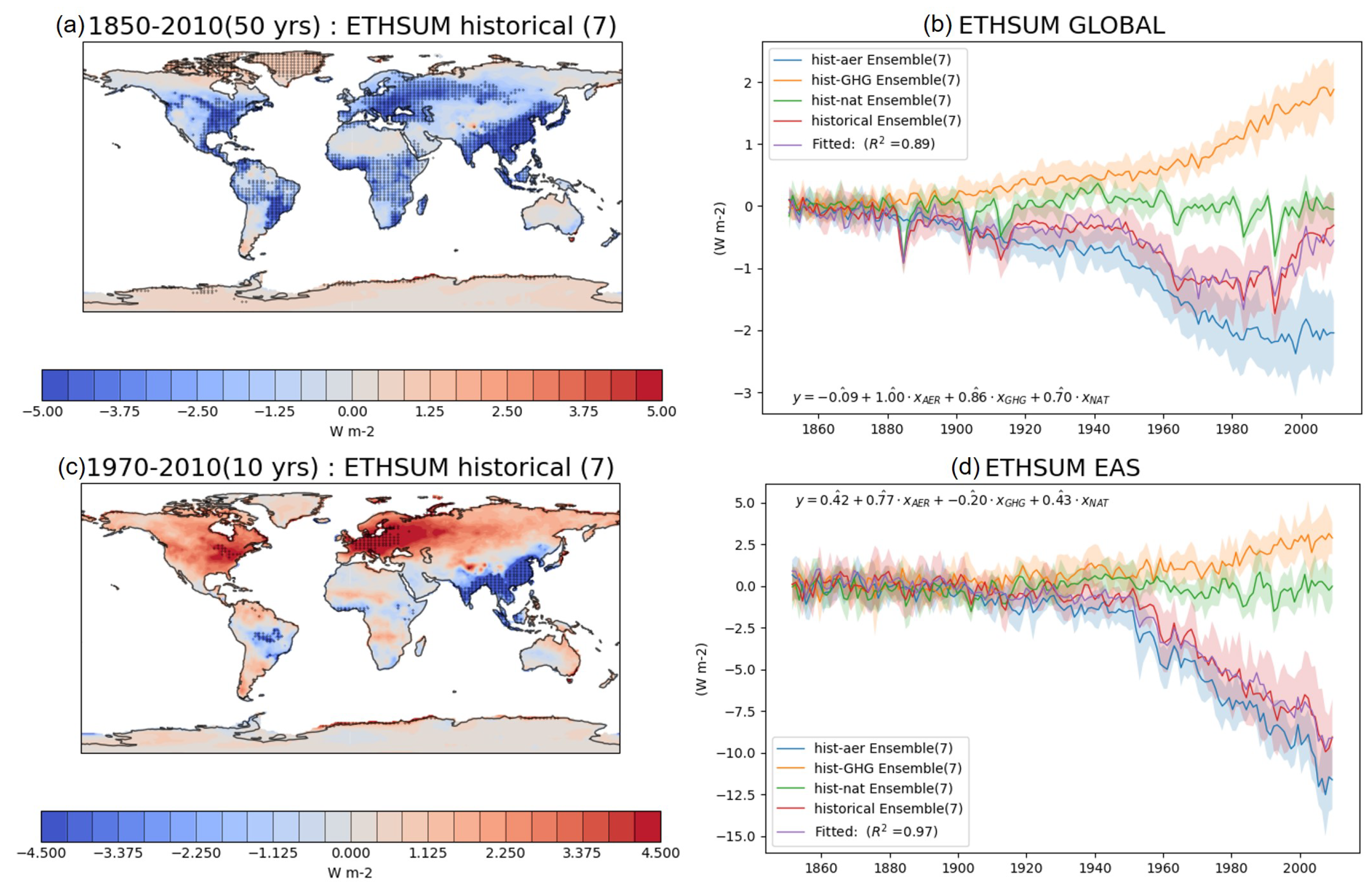
3.2. Energy Balance
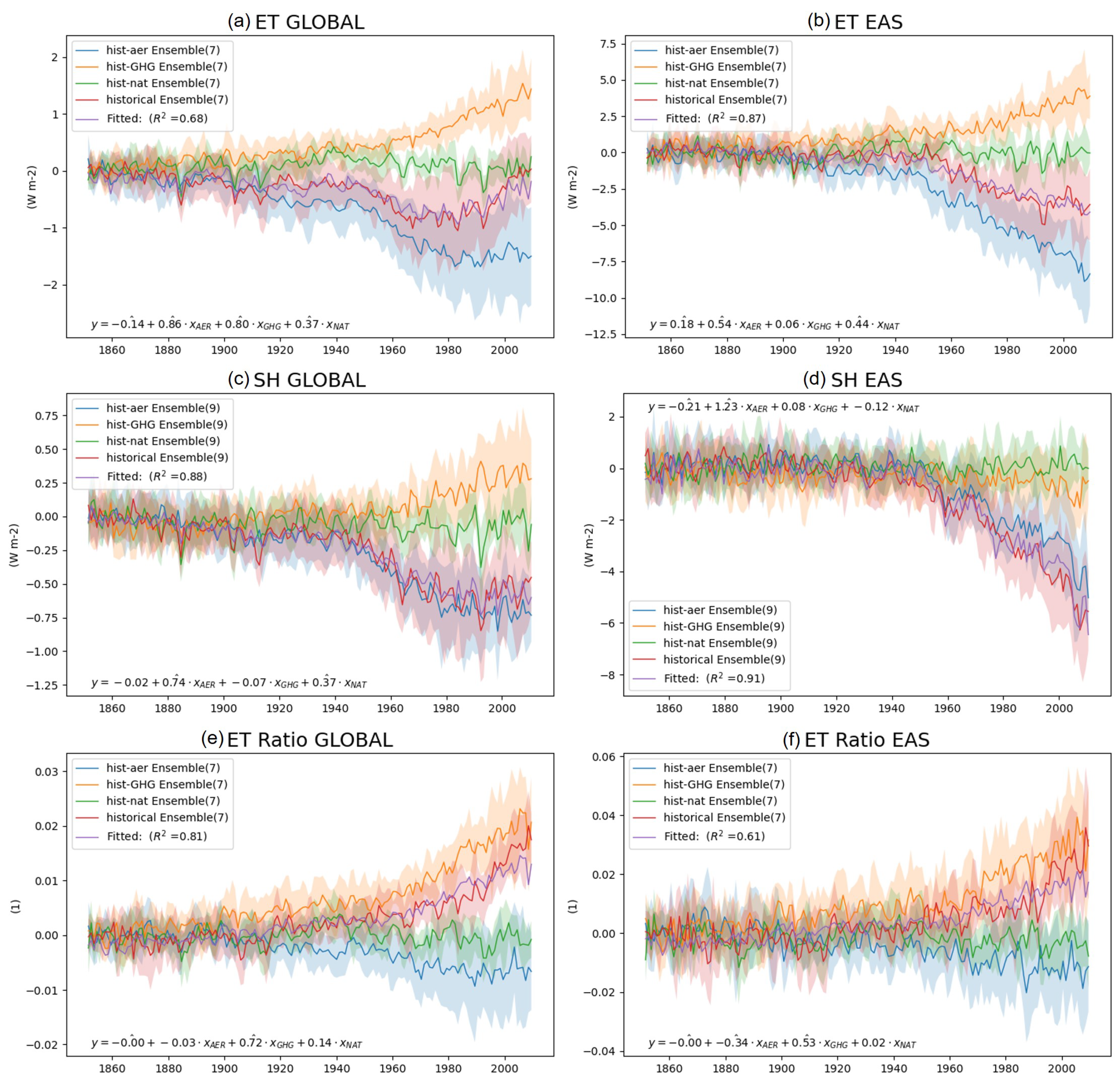
3.3. Water Balance
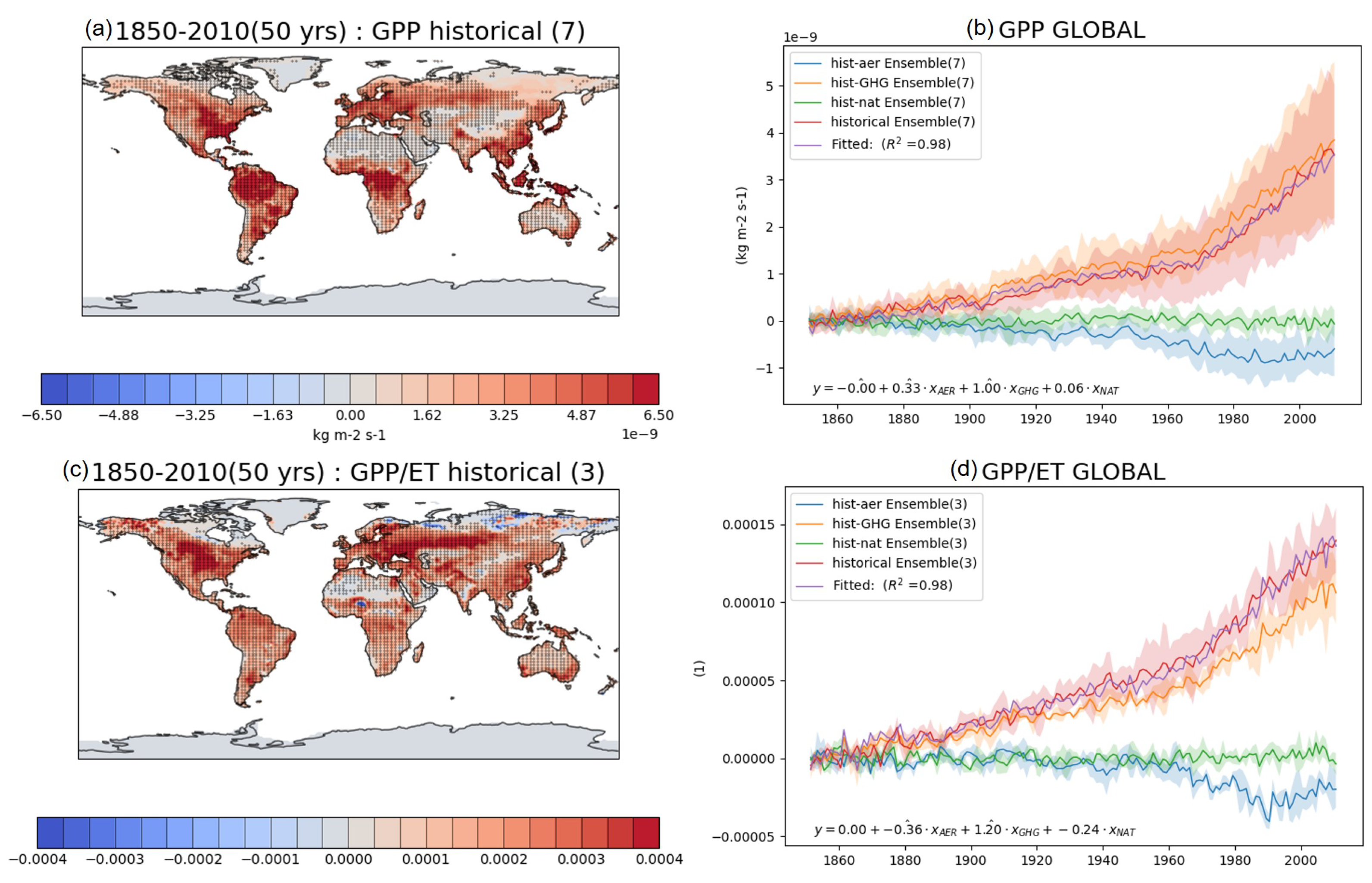
3.4. GPP and Water Use Efficiency
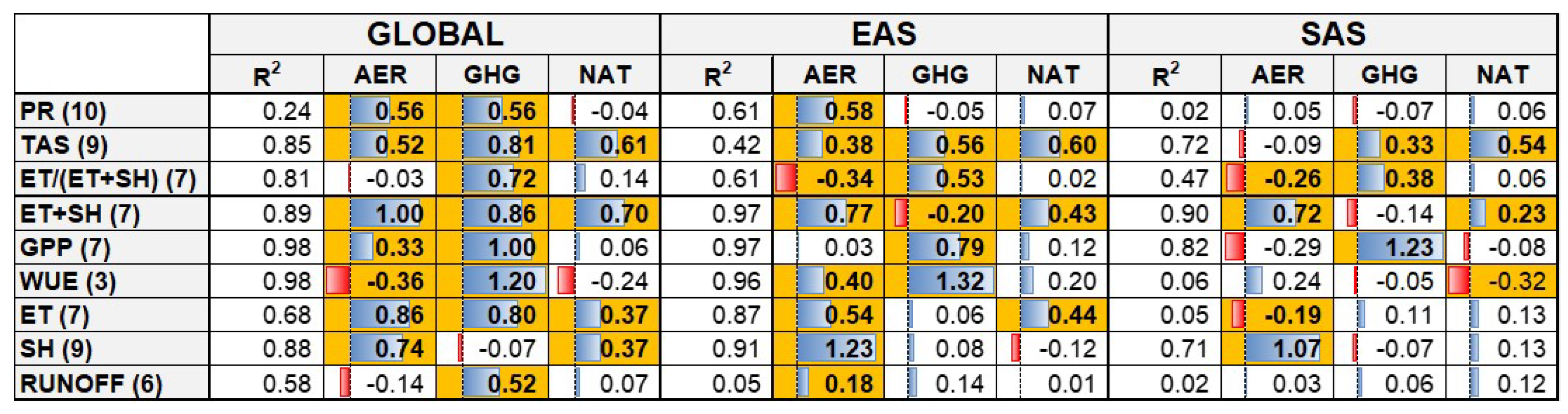
3.5. Parameter Table
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, Y.H.; Min, S.K.; Zhang, X.; Sillmann, J.; Sandstad, M. Evaluation of the CMIP6 multi-model ensemble for climate extreme indices. Weather. Clim. Extrem. 2020, 29, 100269. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef] [Green Version]
- Gillett, N.P.; Shiogama, H.; Funke, B.; Hegerl, G.; Knutti, R.; Matthes, K.; Santer, B.D.; Stone, D.; Tebaldi, C. The Detection and Attribution Model Intercomparison Project (DAMIP v1.0) contribution to CMIP6. Geosci. Model Dev. 2016, 9, 3685–3697. [Google Scholar] [CrossRef] [Green Version]
- Ribes, A.; Terray, L. Application of regularised optimal fingerprinting to attribution. Part II: Application to global near-surface temperature. Clim. Dyn. 2013, 41, 2837–2853. [Google Scholar] [CrossRef]
- Ribes, A.; Gillett, N.P.; Zwiers, F.W. Designing Detection and Attribution Simulations for CMIP6 to Optimize the Estimation of Greenhouse Gas–Induced Warming. J. Clim. 2015, 28, 3435–3438. [Google Scholar] [CrossRef]
- Ha, K.J.; Kim, B.H.; Chung, E.S.; Chan, J.C.L.; Chang, C.P. Major factors of global and regional monsoon rainfall changes: Natural versus anthropogenic forcing. Environ. Res. Lett. 2020, 15, 034055. [Google Scholar] [CrossRef]
- Moseid, K.O.; Schulz, M.; Storelvmo, T.; Julsrud, I.R.; Olivié, D.; Nabat, P.; Wild, M.; Cole, J.N.S.; Takemura, T.; Oshima, N.; et al. Bias in CMIP6 models as compared to observed regional dimming and brightening. Atmos. Chem. Phys. 2020, 20, 16023–16040. [Google Scholar] [CrossRef]
- Irving, D.B.; Wijffels, S.; Church, J.A. Anthropogenic Aerosols, Greenhouse Gases, and the Uptake, Transport, and Storage of Excess Heat in the Climate System. Geophys. Res. Lett. 2019, 46, 4894–4903. [Google Scholar] [CrossRef] [Green Version]
- Stott, P.A.; Gillett, N.P.; Hegerl, G.C.; Karoly, D.J.; Stone, D.A.; Zhang, X.; Zwiers, F. Detection and attribution of climate change: A regional perspective. WIREs Clim. Chang. 2010, 1, 192–211. [Google Scholar] [CrossRef]
- Ribes, A.; Zwiers, F.W.; Azaïs, J.M.; Naveau, P. A new statistical approach to climate change detection and attribution. Clim. Dyn. 2017, 48, 367–386. [Google Scholar] [CrossRef]
- Gillett, N.P.; Kirchmeier-Young, M.; Ribes, A.; Shiogama, H.; Hegerl, G.C.; Knutti, R.; Gastineau, G.; John, J.G.; Li, L.; Nazarenko, L.; et al. Constraining human contributions to observed warming since the pre-industrial period. Nat. Clim. Chang. 2021, 11, 207–212. [Google Scholar] [CrossRef]
- Song, J.; Miller, G.R.; Cahill, A.T.; Aparecido, L.M.T.; Moore, G.W. Modeling land surface processes over a mountainous rainforest in Costa Rica using CLM4.5 and CLM5. Geosci. Model Dev. 2020, 13, 5147–5173. [Google Scholar] [CrossRef]
- Song, J.; Miller, G.R.; Cahill, A.T.; Aparecido, L.M.T.; Moore, G.W. Modeling Profiles of Micrometeorological Variables in a Tropical Premontane Rainforest Using Multi-Layered CLM (CLM-ML). J. Adv. Model. Earth Syst. 2021, 13, e2020MS002259. [Google Scholar] [CrossRef]
- Sheil, D. Forests, atmospheric water and an uncertain future: The new biology of the global water cycle. For. Ecosyst. 2018, 5, 19. [Google Scholar] [CrossRef] [Green Version]
- Song, J.Y. Improving Predictions of Soil and Plant Evapotranspiration in Vadose Zone and Land Surface Models. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2019. [Google Scholar]
- Harris, R.M.B.; Loeffler, F.; Rumm, A.; Fischer, C.; Horchler, P.; Scholz, M.; Foeckler, F.; Henle, K. Biological responses to extreme weather events are detectable but difficult to formally attribute to anthropogenic climate change. Sci. Rep. 2020, 10, 14067. [Google Scholar] [CrossRef] [PubMed]
- Stott, P. How climate change affects extreme weather events. Science 2016, 352, 1517–1518. [Google Scholar] [CrossRef]
- Mann, M.E.; Rahmstorf, S.; Kornhuber, K.; Steinman, B.A.; Miller, S.K.; Coumou, D. Influence of Anthropogenic Climate Change on Planetary Wave Resonance and Extreme Weather Events. Sci. Rep. 2017, 7, 45242. [Google Scholar] [CrossRef] [Green Version]
- Allan, C.; Xia, J.; Pahl-Wostl, C. Climate change and water security: Challenges for adaptive water management. Curr. Opin. Environ. Sustain. 2013, 5, 625–632. [Google Scholar] [CrossRef]
- Turral, H.; Burke, J.; Faurès, J.M. Climate Change, Water and Food Security; Number 36; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2011. [Google Scholar]
- Misra, A.K. Climate change and challenges of water and food security. Int. J. Sustain. Built Environ. 2014, 3, 153–165. [Google Scholar] [CrossRef] [Green Version]
- Kayiranga, A.; Chen, B.; Trisurat, Y.; Ndayisaba, F.; Sun, S.; Tuankrua, V.; Wang, F.; Karamage, F.; Measho, S.; Nthangeni, W.; et al. Water Use Efficiency-Based Multiscale Assessment of Ecohydrological Resilience to Ecosystem Shifts Over the Continent of Africa During 1992–2015. J. Geophys. Res. Biogeosci. 2020, 125, e2020JG005749. [Google Scholar] [CrossRef]
- Neher, I.; Buchmann, T.; Crewell, S.; Evers-Dietze, B.; Pfeilsticker, K.; Pospichal, B.; Schirrmeister, C.; Meilinger, S. Impact of atmospheric aerosols on photovoltaic energy production Scenario for the Sahel zone. Energy Procedia 2017, 125, 170–179. [Google Scholar] [CrossRef]
- Jones, C.D.; Arora, V.; Friedlingstein, P.; Bopp, L.; Brovkin, V.; Dunne, J.; Graven, H.; Hoffman, F.; Ilyina, T.; John, J.G.; et al. C4MIP—The Coupled Climate–Carbon Cycle Model Intercomparison Project: Experimental protocol for CMIP6. Geosci. Model Dev. 2016, 9, 2853–2880. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, D.M.; Hurtt, G.C.; Arneth, A.; Brovkin, V.; Calvin, K.V.; Jones, A.D.; Jones, C.D.; Lawrence, P.J.; de Noblet-Ducoudré, N.; Pongratz, J.; et al. The Land Use Model Intercomparison Project (LUMIP) contribution to CMIP6: Rationale and experimental design. Geosci. Model Dev. 2016, 9, 2973–2998. [Google Scholar] [CrossRef] [Green Version]
- Hoffman, F.M.; Covey, C.C.; Fung, I.Y.; Randerson, J.T.; Thornton, P.E.; Lee, Y.H.; Rosenbloom, N.A.; Stöckli, R.C.; Running, S.W.; Bernholdt, D.E.; et al. Results from the carbon-land model intercomparison project (C-LAMP) and availability of the data on the earth system grid (ESG). J. Phys. Conf. Ser. 2007, 78, 012026. [Google Scholar] [CrossRef]
- Hoffman, F.M.; Koven, C.D.; Keppel-Aleks, G.; Lawrence, D.M.; Riley, W.J.; Randerson, J.T.; Ahlström, A.; Abramowitz, G.; Baldocchi, D.D.; Best, M.J.; et al. 2016 International Land Model Benchmarking (ILAMB) Workshop Report; U.S. Department of Energy, Office of Science: Germantown, MD, USA, 2017. [CrossRef] [Green Version]
- Friedlingstein, P.; Cox, P.; Betts, R.; Bopp, L.; von Bloh, W.; Brovkin, V.; Cadule, P.; Doney, S.; Eby, M.; Fung, I.; et al. Climate—Carbon Cycle Feedback Analysis: Results from the C4MIP Model Intercomparison. J. Clim. 2006, 19, 3337–3353. [Google Scholar] [CrossRef]
- Prentice, I.; Farquhar, G.; Fasham, M.; Goulden, M.; Heimann, M.; Jaramillo, V.; Kheshgi, H.; Quéré, C.L.; Scholes, R.; Wallace, D.; et al. The carbon cycle and atmospheric carbon dioxide. In Climate Change 2001: The Scientific Basis, Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001; pp. 183–237. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Jung, M.; Koirala, S.; Weber, U.; Ichii, K.; Gans, F.; Camps-Valls, G.; Papale, D.; Schwalm, C.; Tramontana, G.; Reichstein, M. The FLUXCOM ensemble of global land-atmosphere energy fluxes. Sci. Data 2019, 6, 74. [Google Scholar] [CrossRef] [Green Version]
- Yuan, S.; Quiring, S.M.; Leasor, Z.T. Historical Changes in Surface Soil Moisture Over the Contiguous United States: An Assessment of CMIP6. Geophys. Res. Lett. 2021, 48, e2020GL089991. [Google Scholar] [CrossRef]
- Ziehn, T.; Chamberlain, M.A.; Law, R.M.; Lenton, A.; Bodman, R.W.; Dix, M.; Stevens, L.; Wang, Y.P.; Srbinovsky, J. The Australian Earth System Model: ACCESS-ESM1.5. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 193–214. [Google Scholar] [CrossRef]
- Wu, T.; Lu, Y.; Fang, Y.; Xin, X.; Li, L.; Li, W.; Jie, W.; Zhang, J.; Liu, Y.; Zhang, L.; et al. The Beijing Climate Center Climate System Model (BCC-CSM): The main progress from CMIP5 to CMIP6. Geosci. Model Dev. 2019, 12, 1573–1600. [Google Scholar] [CrossRef] [Green Version]
- Swart, N.C.; Cole, J.N.S.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Hanna, S.; et al. The Canadian Earth System Model version 5 (CanESM5.0.3). Geosci. Model Dev. 2019, 12, 4823–4873. [Google Scholar] [CrossRef] [Green Version]
- Danabasoglu, G.; Lamarque, J.F.; Bacmeister, J.; Bailey, D.A.; DuVivier, A.K.; Edwards, J.; Emmons, L.K.; Fasullo, J.; Garcia, R.; Gettelman, A.; et al. The Community Earth System Model Version 2 (CESM2). J. Adv. Model. Earth Syst. 2020, 12, e2019MS001916. [Google Scholar] [CrossRef] [Green Version]
- Seferian, R.; Nabat, P.; Michou, M.; Saint-Martin, D.; Voldoire, A.; Colin, J.; Decharme, B.; Delire, C.; Berthet, S.; Chevallier, M.; et al. Evaluation of CNRM Earth System Model, CNRM-ESM2-1: Role of Earth System Processes in Present-Day and Future Climate. J. Adv. Model. Earth Syst. 2019, 11, 4182–4227. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Yu, Y.; Tang, Y.; Lin, P.; Xie, J.; Song, M.; Dong, L.; Zhou, T.; Liu, L.; Wang, L.; et al. The Flexible Global Ocean-Atmosphere-Land System Model Grid-Point Version 3 (FGOALS-g3): Description and Evaluation. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002012. [Google Scholar] [CrossRef]
- Dunne, J.P.; Horowitz, L.W.; Adcroft, A.J.; Ginoux, P.; Held, I.M.; John, J.G.; Krasting, J.P.; Malyshev, S.; Naik, V.; Paulot, F.; et al. The GFDL Earth System Model Version 4.1 (GFDL-ESM 4.1): Overall Coupled Model Description and Simulation Characteristics. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002015. [Google Scholar] [CrossRef]
- Kelley, M.; Schmidt, G.A.; Nazarenko, L.S.; Bauer, S.E.; Ruedy, R.; Russell, G.L.; Ackerman, A.S.; Aleinov, I.; Bauer, M.; Bleck, R.; et al. GISS-E2.1: Configurations and Climatology. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002025. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.D.; Copsey, D.; Blockley, E.W.; Bodas-Salcedo, A.; Calvert, D.; Comer, R.; Davis, P.; Graham, T.; Hewitt, H.T.; Hill, R.; et al. The Met Office Global Coupled Model 3.0 and 3.1 (GC3.0 and GC3.1) Configurations. J. Adv. Model. Earth Syst. 2018, 10, 357–380. [Google Scholar] [CrossRef]
- Hourdin, F.; Rio, C.; Grandpeix, J.Y.; Madeleine, J.B.; Cheruy, F.; Rochetin, N.; Jam, A.; Musat, I.; Idelkadi, A.; Fairhead, L.; et al. LMDZ6A: The Atmospheric Component of the IPSL Climate Model With Improved and Better Tuned Physics. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001892. [Google Scholar] [CrossRef] [Green Version]
- Tatebe, H.; Ogura, T.; Nitta, T.; Komuro, Y.; Ogochi, K.; Takemura, T.; Sudo, K.; Sekiguchi, M.; Abe, M.; Saito, F.; et al. Description and basic evaluation of simulated mean state, internal variability, and climate sensitivity in MIROC6. Geosci. Model Dev. 2019, 12, 2727–2765. [Google Scholar] [CrossRef] [Green Version]
- Yukimoto, S.; Kawai, H.; Koshiro, T.; Oshima, N.; Yoshida, K.; Urakawa, S.; Tsujino, H.; Deushi, M.; Tanaka, T.; Hosaka, M.; et al. The Meteorological Research Institute Earth System Model Version 2.0, MRI-ESM2.0: Description and Basic Evaluation of the Physical Component. J. Meteorol. Soc. Jpn. Ser. II 2019, 97, 931–965. [Google Scholar] [CrossRef] [Green Version]
- Seland, Ø.; Bentsen, M.; Olivié, D.; Toniazzo, T.; Gjermundsen, A.; Graff, L.S.; Debernard, J.B.; Gupta, A.K.; He, Y.C.; Kirkevåg, A.; et al. Overview of the Norwegian Earth System Model (NorESM2) and key climate response of CMIP6 DECK, historical, and scenario simulations. Geosci. Model Dev. 2020, 13, 6165–6200. [Google Scholar] [CrossRef]
- Iturbide, M.; Gutiérrez, J.M.; Alves, L.M.; Bedia, J.; Cerezo-Mota, R.; Cimadevilla, E.; Cofiño, A.S.; Di Luca, A.; Faria, S.H.; Gorodetskaya, I.V.; et al. An update of IPCC climate reference regions for subcontinental analysis of climate model data: Definition and aggregated datasets. Earth Syst. Sci. Data 2020, 12, 2959–2970. [Google Scholar] [CrossRef]
- Wang, A.; Zeng, X.; Guo, D. Estimates of global surface hydrology and heat fluxes from the Community Land Model (CLM4.5) with four atmospheric forcing datasets. J. Hydrometeorol. 2016, 17, 2493–2510. [Google Scholar] [CrossRef] [Green Version]
- Heidkamp, M.; Chlond, A.; Ament, F. Closing the energy balance using a canopy heat capacity and storage concept—A physically based approach for the land component JSBACHv3.11. Geosci. Model Dev. 2018, 11, 3465–3479. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J.; Unsworth, M. Principles of Environmental Physics: Plants, Animals, and the Atmosphere; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Brutsaert, W. Hydrology: An Introduction; Cambridge Univeristy Press: Cambridge, UK, 2005. [Google Scholar]
- Shim, S.; Sung, H.; Kwon, S.; Kim, J.; Lee, J.; Sun, M.; Song, J.; Ha, J.; Byun, Y.; Kim, Y.; et al. Regional Features of Long-Term Exposure to PM2.5 Air Quality over Asia under SSP Scenarios Based on CMIP6 Models. Int. J. Environ. Res. Public Health 2021, 18, 6817. [Google Scholar] [CrossRef]
- Seo, J.; Shim, S.; Kwon, S.H.; Boo, K.O.; Kim, Y.H.; O’Connor, F.; Johnson, B.; Dalvi, M.; Folberth, G.; Teixeira, J.; et al. The Impacts of Aerosol Emissions on Historical Climate in UKESM1. Atmosphere 2020, 11, 1095. [Google Scholar] [CrossRef]
- Angell, J.K.; Korshover, J. Surface temperature changes following the six major volcanic episodes between 1780 and 1980. J. Clim. Appl. Meteorol. 1985, 24, 937–951. [Google Scholar] [CrossRef] [Green Version]
- Han, B.; Lü, S.; Li, R.; Wang, X.; Zhao, L.; Zhao, C.; Wang, D.; Meng, X. Global land surface climate analysis based on the calculation of a modified Bowen ratio. Adv. Atmos. Sci. 2017, 34, 663–678. [Google Scholar] [CrossRef]
- Chanzy, A.; Bruckler, L. Significance of soil surface moisture with respect to daily bare soil evaporation. Water Resour. Res. 1993, 29, 1113–1125. [Google Scholar] [CrossRef]
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A Biochemical Model of Photosynthetic CO2 Assimilation in Leaves of C3 Species; Springer: Berlin, Germany, 1980. [Google Scholar] [CrossRef] [Green Version]
- Evans, J. Improving photosynthesis. Plant Physiol. 2013, 162, 1780–1793. [Google Scholar] [CrossRef] [Green Version]
- Medlyn, B.E.; Dreyer, E.; Ellsworth, D.; Forstreuter, M.; Harley, P.C.; Kirschbaum, M.U.F.; Le Roux, X.; Montpied, P.; Strassemeyer, J.; Walcroft, A.; et al. Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data. Plant Cell Environ. 2002, 25, 1167–1179. [Google Scholar] [CrossRef] [Green Version]
- Bonan, G.B.; Lawrence, P.J.; Oleson, K.W.; Levis, S.; Jung, M.; Reichstein, M.; Lawrence, D.M.; Swenson, S.C. Improving canopy processes in the Community Land Model version 4 (CLM4) using global flux fields empirically inferred from FLUXNET data. J. Geophys. Res. Biogeosci. 2011, 116, G02014. [Google Scholar] [CrossRef] [Green Version]
- Bonan, G.B.; Oleson, K.W.; Fisher, R.A.; Lasslop, G.; Reichstein, M. Reconciling leaf physiological traits and canopy flux data: Use of the TRY and FLUXNET databases in the Community Land Model version 4. J. Geophys. Res. Biogeosci. 2012, 117, G02026. [Google Scholar] [CrossRef]
- Neumann, R.B.; Cardon, Z.G. The magnitude of hydraulic redistribution by plant roots: A review and synthesis of empirical and modeling studies. New Phytol. 2012, 194, 337–352. [Google Scholar] [CrossRef] [PubMed]
- Bonan, G.B.; Williams, M.; Fisher, R.A.; Oleson, K.W. Modeling stomatal conductance in the earth system: Linking leaf water-use efficiency and water transport along the soil–plant–atmosphere continuum. Geosci. Model Dev. 2014, 7, 2193–2222. [Google Scholar] [CrossRef] [Green Version]
- Medvigy, D.; Wofsy, S.C.; Munger, J.W.; Hollinger, D.Y.; Moorcroft, P.R. Mechanistic scaling of ecosystem function and dynamics in space and time: Ecosystem Demography model version 2. J. Geophys. Res. Biogeosci. 2009, 114, G01002. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.; Liu, J.; Zuo, Y.; Guo, Z.; Wang, N.; Song, C.; Wang, Z.; Sun, L.; Guo, Y.; Song, Y.; et al. Rising vegetation activity dominates growing water use efficiency in the Asian permafrost region from 1900 to 2100. Sci. Total. Environ. 2020, 736, 139587. [Google Scholar] [CrossRef]
- Lavergne, A.; Graven, H.; De Kauwe, M.G.; Keenan, T.F.; Medlyn, B.E.; Prentice, I.C. Observed and modelled historical trends in the water-use efficiency of plants and ecosystems. Glob. Chang. Biol. 2019, 25, 2242–2257. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Shim, S.; Kim, J.-S.; Lee, J.-H.; Byun, Y.-H.; Kim, Y.-H. The Influence of Natural and Anthropogenic Forcing on Water and Energy Balance and on Photosynthesis. Land 2021, 10, 1151. https://doi.org/10.3390/land10111151
Song J, Shim S, Kim J-S, Lee J-H, Byun Y-H, Kim Y-H. The Influence of Natural and Anthropogenic Forcing on Water and Energy Balance and on Photosynthesis. Land. 2021; 10(11):1151. https://doi.org/10.3390/land10111151
Chicago/Turabian StyleSong, Jaeyoung, Sungbo Shim, Ji-Sun Kim, Jae-Hee Lee, Young-Hwa Byun, and Yeon-Hee Kim. 2021. "The Influence of Natural and Anthropogenic Forcing on Water and Energy Balance and on Photosynthesis" Land 10, no. 11: 1151. https://doi.org/10.3390/land10111151
APA StyleSong, J., Shim, S., Kim, J.-S., Lee, J.-H., Byun, Y.-H., & Kim, Y.-H. (2021). The Influence of Natural and Anthropogenic Forcing on Water and Energy Balance and on Photosynthesis. Land, 10(11), 1151. https://doi.org/10.3390/land10111151






