Next Article in Journal
Dynamics of the Condition of Reclaimed Agricultural Lands in the Russian Federation
Next Article in Special Issue
Influence of Anthropogenic Load in River Basins on River Water Status: A Case Study in Lithuania
Previous Article in Journal
Strengthening Local Governance of Secondary Forest in Peru
Previous Article in Special Issue
Use of Pedotransfer Functions in the Rosetta Model to Determine Saturated Hydraulic Conductivity (Ks) of Arable Soils: A Case Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Land
Volume 10
Issue 12
10.3390/land10121287
land-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Rate of Fen-Peat Soil Subsidence Near Drainage Ditches (Central Poland)

by
Ryszard Oleszczuk
1,
Ewelina Zając
2,*,
Janusz Urbański
3 and
Jan Jadczyszyn
4
1
Institute of Environmental Engineering, Warsaw University of Life Sciences—SGGW, Nowoursynowska 166 St., 02-787 Warsaw, Poland
2
Department of Land Reclamation and Environmental Development, Faculty of Environmental Engineering and Land Surveying, University of Agriculture in Krakow, Al. Mickiewicza 21, 31-120 Krakow, Poland
3
Institute of Civil Engineering, Warsaw University of Life Sciences—SGGW, Nowoursynowska 166 St., 02-787 Warsaw, Poland
4
Institute of Soil Science and Plant Cultivation—State Research Institute, Czartoryskich 8 St., 24-100 Puławy, Poland
*
Author to whom correspondence should be addressed.
Land 2021, 10(12), 1287; https://doi.org/10.3390/land10121287
Submission received: 11 October 2021 / Revised: 17 November 2021 / Accepted: 18 November 2021 / Published: 24 November 2021
(This article belongs to the Special Issue Effects of Land Use on the Ecohydrology of River Basin in Accordance with Climate Change)
Browse Figures
Review Reports Versions Notes

Abstract

:
This study analyzed design depths (to), post-subsidence depths (t), shallowing magnitudes (d = to − t) and ratio values (d/t) of 12 drainage ditches in a fragment of the drained Solec fen-peat (central Poland) over a period of 47 years between 1967 and 2014. A significant decrease of the designed depth of the ditches to was shown, from the average designed value of 0.97 m to their average depth after subsidence, t = 0.71 m. The ratio (d/t) of 0.41, which is associated with the degree of organic matter decomposition, indicated medium degree of peat decomposition. The average values of bank and bottom subsidence of the ditches during the analyzed period, 1967–2014, were 0.43 m and 0.17 m, respectively. The values of the average annual rate of land surface subsidence in the vicinity of the ditches were varied and within the range of 0.09 cm year−1 to 1.70 cm year−1, with an average of 0.92 cm year−1. Two linear empirical equations were proposed to calculate the amount of subsidence and the average annual rate of subsidence of peat soil surface near the drainage ditch route, based on the knowledge of the initial thickness of the peat deposit. The results of calculations using the equations proposed by the authors were compared with calculations of the same parameters using 10 equations published in the literature. The results obtained using the proposed equations were mostly larger than those calculated with literature-published equations.

1. Introduction

In excessively humid areas (e.g., river valleys), the high groundwater table and low air content in the soil are conducive to the formation of peat soils, which are characterized by a high organic carbon content. Peat deposits covering only approximately 4% of the world are estimated to accumulate approximately 30% of the global organic carbon of all soils in their deposits [1,2,3]. In Europe, about 16% of peat soils are used for agricultural purposes (arable land and grassland), including the vast majority in Western European countries [4]. The area of organic soils and soils of organic origin in Poland estimated on the basis of the soil-agricultural map at a scale of 1:25,000 occupies 13.3% of agricultural land, wherein 5.6% are peat soils, 1.6% are sited peat soils, and 6.1% are moorsh soils [5]. These areas, used by many disciplines (including agriculture, horticulture, and forestry), have been drained in numerous cases [6]. This has resulted in the interruption of the existing organic matter accumulation process due to incomplete decomposition under conditions of very high humidity and lack of air access. In their natural state, these soils absorb carbon dioxide as a result of the assimilation and photosynthesis processes of the vegetation living in these areas. The change in air–water relations that accompanies the drainage of peatlands has caused the initiation of mucking and mineralization processes in organic matter, and the conversion of organic forms of nitrogen into mineral compounds and emission of greenhouse gases, such as carbon dioxide and nitrous oxide, into the atmosphere [7,8,9]. The ongoing climate change, significant increase in air temperature, and reduction in precipitation during the growing season lead to extreme weather phenomena, as well as increased frequency of agricultural drought [10,11,12]. The foregoing weather phenomena contribute to the intensification of mucking processes and permanent degradation of drained peat soils. Changes occur in their physical properties, i.e., retention, hydraulic properties, and soil compaction due to the shrinkage process, as do changes in their chemical properties, specifically reduction in organic carbon content and increase in ash content. All these phenomena contribute to the lowering of the surface (shallowing of the profile) in drained peat deposits, i.e., subsidence. This leads to a decrease in the thickness, as well as surface area, of these deposits and a permanent reduction in their agricultural production potential. It may even contribute to the total disappearance of peat soils in the natural environment and their transformation into typical mineral soils in the long run. This is an extremely unfavorable phenomenon, taking into consideration the numerous functions that peatlands play in the natural environment (e.g., accumulation of organic carbon, water retention, and biodiversity).
In the past, using peatlands for agricultural purposes (mainly meadows and pastures) required lowering the groundwater level to reduce moisture in the root zone (0–30 cm) in view of the water needs of grassland vegetation. These drainages were done in stages by constructing a network of deep draining channels, usually followed by a dense network of drainage ditches after several years (typically spaced about 100 m apart) and, as needed, an additional network of drainage pipes (spaced about 30 m apart). The foregoing drainage network parameters depend on the drainage depth (usually about 0.8–1.0 m) and the hydraulic properties of the peat soils, specifically the filtration coefficient [13]. Drainage of these soils for agricultural purposes, as opposed to drainage of mineral soils, has resulted in many negative physical, chemical, and biological processes, due to a decrease in the moisture content of the top layers, and a consequent increase in air content. Among the physical processes, the shrinkage process is observed due to a decrease in the moisture content of these soils, which consequently leads to increased compaction, reduced retention capacity, and changes in the hydraulic properties of these soils [14,15,16,17,18,19]. The disappearance of the buoyancy force and the pressure of the drained peat layers on the underlying layers results in the lowering of the surface of the drained peatland, which assumes the highest annual rate in the initial 15–20 years after drainage and is called the first subsidence phase [20,21,22,23,24,25,26]. The magnitude and rate of peatland surface subsidence depends mainly on the physical properties of the soil, peat type, and drainage depth. Despite the stabilization of the soil water level at a certain reduced level, the rate of the soil surface subsidence decreases but does not cease and passes into the second phase of subsidence [20,22,27,28,29]. Mainly chemical and biological processes occur in Phase II, resulting in partial (humification) and complete (mineralization) decomposition of organic matter. During these processes, the resulting greenhouse gas, carbon dioxide, is emitted from the atmosphere and dissolved in groundwater [2,7,30,31,32,33,34,35,36]. Consequently, this leads to a decrease in organic carbon in the surface peat layers, and an increase in nitrogen, both in the soil and in the water into which it is leached. This leads to upsetting the natural C:N ratio and causing it to narrow, which is a measure of the degradation processes of these soils. As a result of degradation, the mineral content, i.e., ash content, increases [16,29,37,38,39].
The processes of surface subsidence in drained peat soils, the decrease of their thickness, and even disappearance of these areas from the natural environment have been quite well described in the world literature based on field studies around the world at single measurement points. These phenomena have been monitored over many years at single measurement points, along cross sections, or on the surface of entire peatlands [27,28,40,41,42,43,44,45,46]. For example, for drained peat soils located in the Groot-Mijdrecht Polder near Amsterdam (The Netherlands), surface subsidence measurements were made at 1423 locations between 1954 and 1968 [43]. However, less attention has been paid to areas located near drainage channels and ditches where intensification of the surface subsidence process of drained soils is the greatest due to the lowest groundwater table in their vicinity during the drainage process [37,47,48,49]. In the literature there is much less research related to the effects of described processes on functioning and technical parameters of drainage systems, such as the decreasing depth of ditches and position of drainage pipelines as a result of the subsidence process. Undoubtedly, this creates a threat to the proper functioning of such systems and the necessity of their modernization in terms of conducting proper water management on such areas (irrigation of these areas).
Measurement results for banks and bottoms of 12 ditches located in a drained fen peat are analyzed in this paper and available archival data from the project of this object are used. Based on 1967 (designed) and 2014 (measured) elevation data, the following objectives are undertaken:
  • Determination of the depth of ditches after subsidence (t) in relation to the designed depth (to), determination of the amount of their shallowing (d = to − t), and the ratio (d/t) in the analyzed period;
  • Determination of the magnitude and average annual rate of subsidence of the peat soil surface near the measurement points along the analyzed ditches;
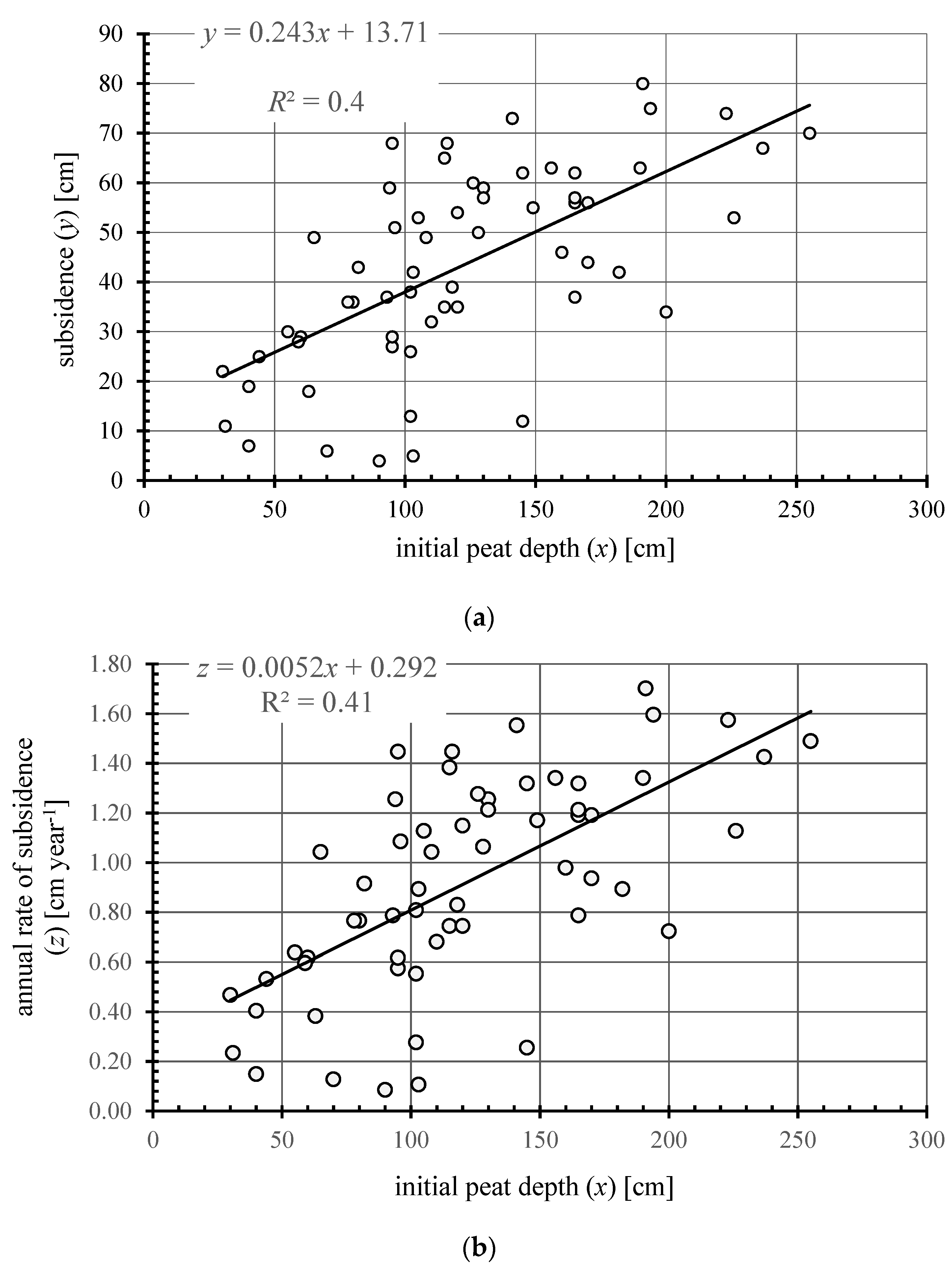
  • Development of empirical relationships between the amount of subsidence (y) and the rate of average annual surface subsidence of a drained peat deposit (z), and its original (initial) thickness (x) in the vicinity of drainage ditches;
  • Comparison of the results of calculating the amount of subsidence/subsidence rate using the proposed empirical relationships with the results obtained from 10 empirical equations of this type published in the literature.

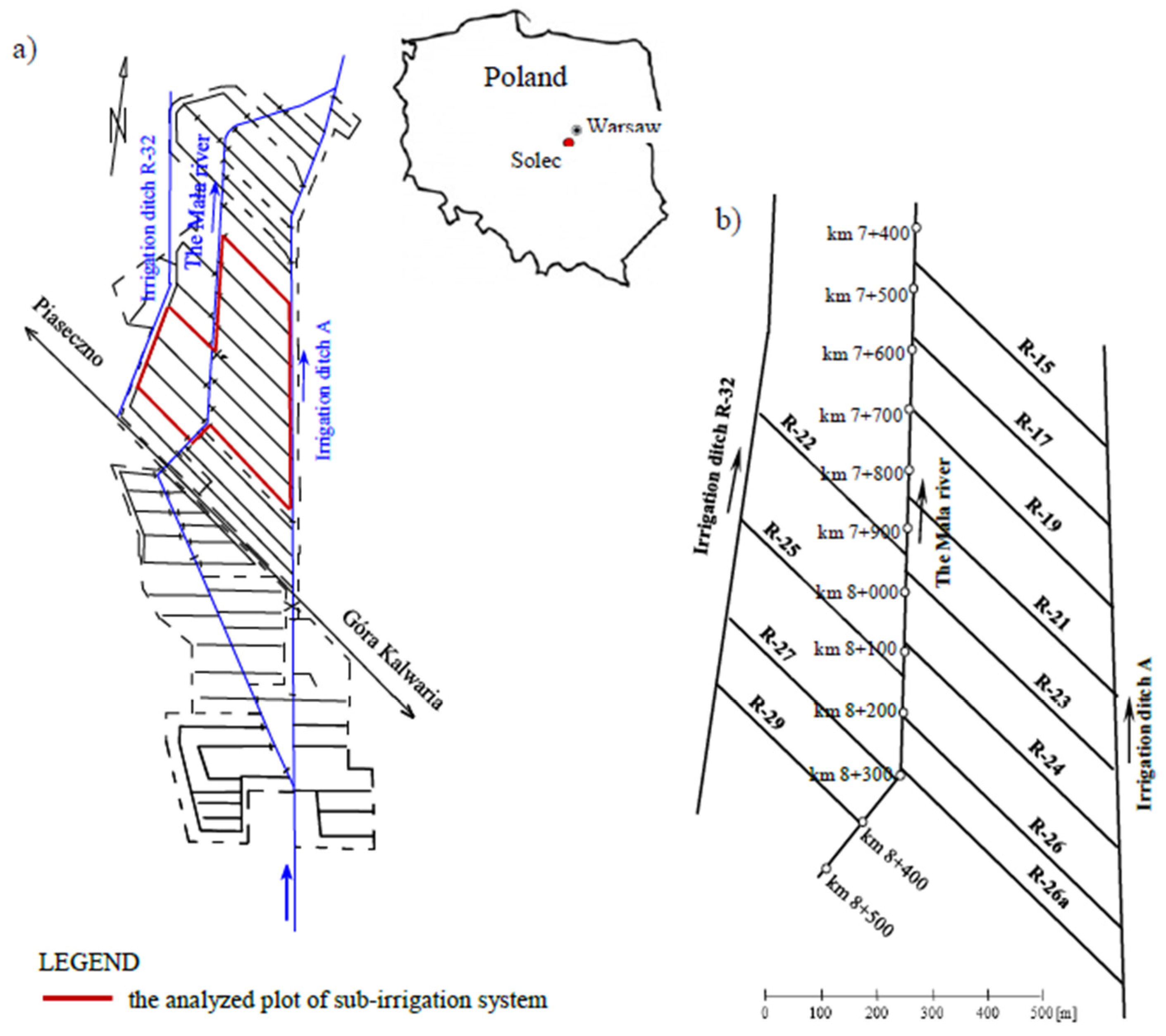
2. Material and Methods

The study was conducted on a fragment of the Solec fen-peatland (Góra Kalwaria Commune, Piaseczyński Poviat, Masovian Voivodeship, Central Poland (52°2′16.345″ N, 21°6′14.622″ E). The 220-ha peat deposit is made up of quaternary formations up to about 50 m thick. The aquifer consists of sands, and in the upper part there are organic soils, sedge, and sedge-reed peats of medium degree of decomposition [50,51]. In the vicinity of the site boundaries, the peat thickness is approximately 30–40 cm, while in its central part it varies within approximately 130–180 cm, and locally up to 250 cm. The first land draining works at the site were conducted between 1941 and 1943 and consisted mainly of a new section of the Mała River running through the center of the site [52] (Figure 1a). In 1967, a project for a drainage system was created that called for the construction of 62 ditches and about 80 communication and damming structures [52]. Draining works according to the project were carried out in 1967–1971. The site was subdivided into 13 plots in which sub-irrigation system was implemented. The main source of irrigation water was the Mała River and feeder A and R-32 (Figure 1b). Most of the site was in agricultural use as meadows and pastures. Since about 1985, irrigation has no longer been implemented, no damming devices are in place, and the ditches only drain adjacent land, discharging into the Mała River. Most of the area has not been used for agriculture since about 2000.The Mała River drains water in the range of about 100 m on each side. In the growing season the ditches are usually dry, and after short-term intensive rainfall the depth of water in the ditches is about 15–20 cm.
The study covered a fragment of the Solec fen with an area of about 50 ha, on which there are 12 drainage ditches: R-15, R-17, R-19, R-21, R-22, R-23, R-24, R-25, R-26, R-26a, R-27, and R-29. Ditch spacing in most cases is 90 m, while ditches R-22 and R-25 are spaced 140 m apart, with lengths ranging from 250 m to about 540 m (Figure 1b). Geodetic measurements of the ordinates of both their banks and bottom were made in cross sections located every 100 m on the ditches in 2014, and the thickness of the peat deposit on both banks was measured. Measurements were taken with a NI 050 levelling device from Carl Zeiss Jena, with reference to the existing state geodetic network.
Changes in bank and bottom ordinates of ditches from 1967 to 2014 were analyzed and ditch depths as designed (to) (1967), ditch depths after subsidence (t) (2014), ditch shallowing magnitudes (d = to − t), ratio (d/t), and subsidence magnitudes/average annual rate of land surface subsidence near ditches were calculated. The values of the d/t ratio were included in ranges depending on the degree of peat decomposition [53,54]. For peat with a low degree of decomposition (H1–H4), the values of this ratio range from 1.28–0.57, for a medium degree of decomposition (H5–H6), the ratio (d/t) is 0.39, and for peat with a high degree of decomposition (H7–H10), it is 0.27–0.19. Based on the results, two empirical relationships were developed between the amount of subsidence (y) (cm) and the rate of average annual subsidence (z) (cm year−1) of the surface of the drained peat deposit and its initial thickness (x) near the drainage ditches. The calculation results obtained using the proposed equations were compared with the calculation results of these quantities obtained using 10 empirical equations developed for the second phase of subsidence of large areas (not only for near-ditch locations) of drained fens published in the literature, summarized in Table 1.

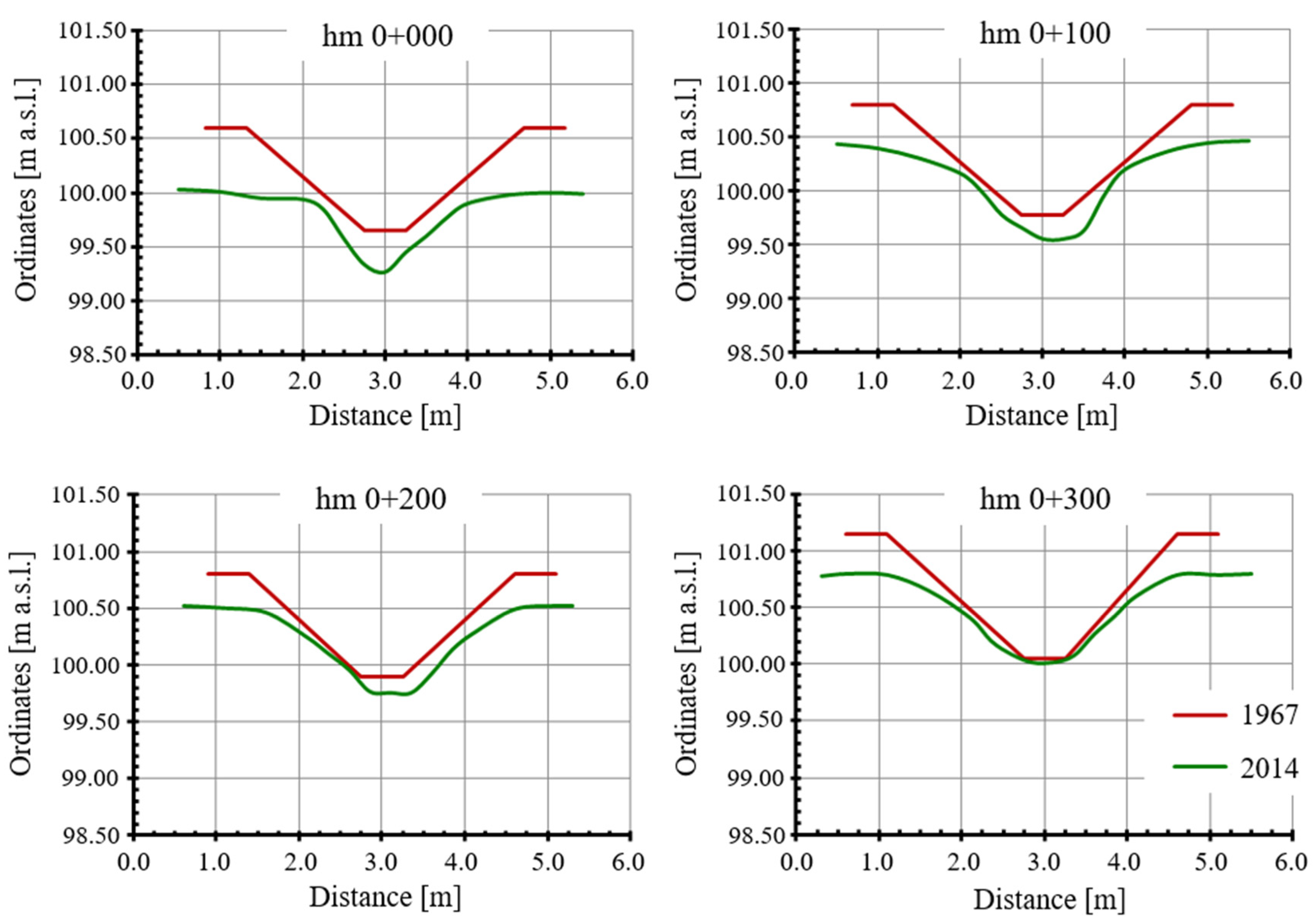
3. Results

The example longitudinal profile of the selected ditch R-29 (Figure 2) and the cross-sections (Figure 3) show the archival (1967) averaged ordinates of both ditch banks and its bottom, and the results of measurements of the same parameters in 2014, as well as the ordinates of the mineral subsoil. The profiles of 12 ditches included in the drainage system [52] were analyzed. Based on the ordinates of the banks and bottom of the ditches at each hectometer, it was found that the design depth of the ditches (to) was within 0.73–1.35 m, with an average of 1.0 m. This indicates a medium-to-high intensity of drainage in the area [55]. The wide range of ditch depths was probably due to the slope of the terrain and the level of the designed bottom. As a result of the dewatering process, it was observed that the depth of the ditches decreased after subsidence (t) in 2014 to an average depth of about 0.74 m, and their shallowing averaged about 0.26 m (Table 2 and Table S1). The values of the ratio of the magnitude of ditch shallowing (d) to its depth after subsidence (t) vary within very large limits from about 0.01 to 1.16, with an average of 0.40. During the analysis period of 47 years (1967–2014), significantly higher values of subsidence were observed on the banks of the ditches compared to the subsidence of their bottoms. The ordinates of the ditch banks decreased by about 0.43 m on average (0.04–0.80 m) compared with the 1967 ordinates, whereas the ditch bottom decreased to a much smaller extent (by about 0.17 m on average), i.e., about 40% in comparison with the amount of their bank subsidence (Table 2 and Table S1). This is also an effect of siltation, the contribution of which is difficult to estimate.
The variability of the initial peat thickness in 1967 along the route of the analyzed ditches was quite large and ranged from about 30 cm to about 255 cm, with an average of about 122 cm (Table 3 and Table S2). The deposit was the shallowest along the route of ditch R-25, and the deepest along ditches R-19 and R-21. As a rule, the highest deposit thicknesses were found in the middle part of the trench route, while the lowest thicknesses were found at the ends of the trenches, near feeders A and R-32.
Based on the magnitude of bank subsidence of the analyzed 12 ditches over 47 years (1967–2014), it was found that the highest subsidence values were observed in the central part of their route, slightly smaller at the mouth of the ditches feeding into the Mała River, and the lowest near the end of the ditches, which may be related to the variable thickness of the deposit along the route of the ditches (Table 3 and Table S2). The amount of land surface subsidence in the vicinity of the ditches during the analysis period ranged from about 4 cm to 80 cm with an average of 43 cm. This corresponds to a reduction in the thickness of the peat deposit relative to the initial thickness of 4% to 75% (43% on average). The mean annual subsidence rate during the 47-year period analyzed was also variable, ranging from 0.08 to 1.7 cm year−1, with an average of 0.92 cm year−1 (Table 3 and Table S2). The results of land surface subsidence measurements from 1967 to 2014 along the analyzed drainage ditches are presented in Figure 4a in relation to the initial thickness of the peat deposit. The average annual subsidence rate of the peat surface depended on the same parameter, as shown in Figure 4b.
Based on the results obtained (Figure 4a,b), two empirical Equations (11) and (12) were developed, which make the amount of subsidence of the drained peat deposit surface (y) (cm) near the ditches and the average annual rate of peatland surface subsidence (z) (cm year−1) dependent on the initial thickness of the peat deposit (x) (cm) (explanation of symbols and units used in the text):
y = 0.243 x + 13.71
z = 0.0052 x + 0.292
The relationships developed are linear, with correlation coefficient r values of 0.65 in both cases. Using the proposed Equations (11) and (12), calculations were performed for the amount of subsidence (y) (Figure 4a) and the average annual subsidence rate (z) (Figure 5b) depending on the initial thickness of the peat deposit (x) within the range of its values from 30 cm to 250 cm (the range of the actual thickness of the deposit in the analyzed fragment of the site). The values of the same parameters (y) and (z) were calculated using Equations (1)–(10) given in Table 1 (Figure 5a,b). The subsidence values calculated according to Equation (11) were larger over the entire range of thicknesses considered than the subsidence volumes calculated by Equations (1), (2), (4), and (7). Equations (1) and (2) were developed for low (0.4–0.6 m) and medium (0.6–1.0 m) drainage intensity conditions, respectively (Table 1). When calculated with Equations (5) and (6), the results coincide with those obtained using Equation (11) in the thickness range from 30 cm to 100 cm. Next, as the thickness increases, the calculation results of the proposed Equation (11) increase significantly with respect to the other equations. In the case of Equation (3) (high drainage intensity, i.e., 1.0–1.2 m) for thickness changes within 30–100 cm, the calculations exceed the settling calculated by Equation (11). In the range of larger thicknesses of the peat deposit (above 100 cm), the results of the subsidence calculation by Equation (3) are similar to those obtained by Equations (5) and (6) (Figure 5a).
In the case of the equations for the average annual subsidence rate (Figure 4b), the calculation of this parameter with the proposed equation (12) outperforms the results of calculations using Equations (8)–(10) (Table 1) in the prevailing range of soil thickness changes, i.e., from 70 cm to 250 cm. Equations (11) and (12) were developed based on the results of settling measurements of the drainage ditch banks, where the intensity of drainage is locally the highest and consequently causes the greatest settling of the soil surface.

4. Discussion of Results

The lowering of the water table as a result of dewatering causes the buoyancy force to disappear and the pressure of the dewatered layers on the lower lying layers to disappear, resulting in the subsidence of the peat deposit at depth. The land surface, which is composed of the sum of the subsidence of the individual layers and, to a lesser extent, the bottom of the trenches, decreases the most [22,25,26,28]. When conducting long-term studies (1965–1998) on subsidence of peat soils in northern Poland, it was found that drainage pipelines initially located about 1 m below the ground surface decreased their depth by about 40–50 cm due to surface and bottom subsidence. The average annual rate of decrease in their depth was contained in the range of 1.21–1.51 cm year−1. In the conditions of the northern Netherlands, according to Van den Akker et. al. [26,56], the position of the water table in the ditches on peat soils used as pastures was mostly maintained at about 60 cm below the ground surface. In these soils, there was a decrease in the water table in the ditches and their bottoms observed as a result of the subsidence process, by about 10 cm on average over a period of 10 years. Maintaining the ditch water table between 0.30 and 1.20 m below ground surface on these soils results in an average annual subsidence rate ranging from 0.50 to 2.20 cm year−1 [26,56]. Grzywna [57,58], Gąsowska [37], Oleszczuk et al. [49] observed a decrease in the designed ditch depth of 1.00 m on average to a post-subsidence depth of 0.20–0.60 m over a period of about 40–50 years on this type of site (drained peat soils, grassland use) in central and eastern Poland. In the case analyzed in this work, the design depth of the 12 ditches in 1967 ranging from 0.73 to 1.35 m (average depth of about 0.97 m) decreased over a period of 47 years to post-subsidence depths ranging from 0.40 to 1.05 m, with an average of 0.71 m.
Ostromęcki [53] and Pierzgalski [54] determined the ranges for the values of the ditch shallowing post-subsidence depth ratio (d/t) in relation to the degree of organic matter decomposition in peat soil. In the studied peatland, the values of this coefficient varied over a very wide range, with an average of 0.41, which indicates that most of these soils had an average degree of organic matter decomposition. This is confirmed by independent physical tests conducted under laboratory conditions on soil samples from this site [37,39,45,50,51].
The value of subsidence of the drained organic soils surface is usually expressed in cm and quite often related as a percentage of its initial thickness. However, average annual rate of subsidence expressed in cm year−1 or mm year−1 allows the results obtained from this process to be compared across many countries and continents in the world [27].
The average annual subsidence rate in the vicinity of drainage ditches in the study area of Solec peatland was 0.92 cm year−1. Similar studies of the subsidence rates conducted on a section of this peatland by Oleszczuk et al. [45] over a 40-year period (1978–2018) indicated an average annual subsidence rate of 0.62 cm year−1. The authors then showed that the subsidence rate also depended on the location of the measurement points in relation to the existing drainage system. Out of the 14 measurement points analyzed, four of them were located in the immediate vicinity of drainage ditches and the Mała River. The average annual rate was relatively varied across these points and amounted to 0.25 cm year−1, 0.48 cm year−1, 1.20 cm year−1, and 1.45 cm year−1, respectively [45]. It can be concluded that typically the surface settles most along localized drainage facilities (canals, ditches, drains) because the depression curve of the groundwater table near these facilities assumes the greatest depths [37]. This results in a significant decrease in the initial depth of channels and ditches, and a decrease in the depth of drain location. When peatlands are used agriculturally, this poses a threat to the continued proper functioning of drainage systems in these areas [49,59], and requires upgrading such systems by, e.g., dredging the existing ditch network [43,56,60,61,62]. On the other hand, on sites where agricultural use has already been withdrawn, subsidence and shallowing of this infrastructure may contribute to limiting the functioning of these systems, resulting in a positive effect of inhibiting or blocking water runoff, limiting the degradation of peat soils [62,63,64]. These topics have been widely reported in the literature. In this context, the authors of this paper emphasize that they focus only on the technical aspect related to the subsidence effects on drainage systems.
The amount of settling of drained peat soils and its rate depends on numerous factors: the depth of drainage of the peat deposit, its initial thickness, the botanical composition of peat and its decomposition degree, physical and chemical properties, the time elapsed since drainage, the type of use, and the climatic conditions in the area [20, 2540]. In order to develop empirical relationships expressing the magnitude/average annual subsidence rate of a drained peat soil surface of practical dimension, it is not possible to consider all these factors. Relationships presented in the literature expressing the magnitude/rate of subsidence have considered the initial thickness of the peat deposit, the length of time since dewatering, the depth/intensity of dewatering, and the position of the groundwater table [20,21,22,25,27,42,45,58,61,65,66]. Most commonly, simple empirical relationships between the magnitude/rate of annual subsidence and the initial thickness of the peat deposit are found in the literature (see Table 1). Some results of measurements of this type published in the literature show a large variation in the amount of subsidence of peat soils, depending on their initial thickness. For example, in case of an area of fen-peat soils from the Noteć area, Ilnicki [55] showed that with an initial peat deposit thickness of 300 cm, the amount of surface subsidence varied from about 4 cm to about 80 cm over a period of 43 to 66 years. Consequently, the correlation coefficients of this type of linear relationship are r = 0.56 for low drainage intensity (0.40 m–0.60 m), r = 0.25 for medium drainage intensity (0.60 m–1.00 m), and r = 0.58 for high drainage intensity (1.00 m–1.20 m). Based on the results obtained in the peatlands of the Biebrza Marshes, Krzywonos [23] developed a similar linear relationship with a correlation coefficient of r = 0.624.
Comparison of the magnitude of subsidence/average annual rate of subsidence over a period of 47 years against the magnitude of the initial thickness of the peat deposit shows a rather large range of field results, which demonstrates the high degree of difficulty in determining this type of relationship. Nevertheless, the correlation coefficients obtained (0.65) are consistent with results published in the literature (e.g., [55]). The analysis of the calculation results for the magnitude and subsidence rate by empirical formulas proposed by different authors indicates that Equations (11) and (12) proposed in this paper can be used to estimate the magnitude of subsidence or the average annual subsidence rate of the drained fen-peat soil surface, with a medium degree of decomposition near drainage ditches in areas with an initial deposit thickness of up to 250 cm.

5. Conclusions

  • Over the period of 47 years (1967–2014) in the analyzed fragment of the Solec fen drainage site near the route of 12 ditches, there were significant changes in the position of their banks and bottoms in relation to the initial values. The effect of these changes reduced the depth of the ditches from their design depths. As a result of the subsidence processes of their banks and bottom, the designed depth of the ditches within the range of 0.73–1.35 m decreased to the values within the range of 0.40–1.05 m. The ditch banks have subsided by about 42 cm on average, and the bottom by about 17 cm on average. As a result, they have been shallowed by about 26 cm on average over a period of 47 years.
  • The ratio of the amount of ditch shallowing to its depth after subsidence (d/t), which is associated with the degree of peat decomposition, was 0.41 in the analyzed peatland section, indicating a medium degree of decomposition. This was confirmed by the results of previous independent, long-term field and laboratory studies at the site.
  • The mean annual subsidence rate of 0.92 cm year−1 in the fen-peat soil studied along the route of the drainage ditches was about 48% higher compared to the average of the entire area, confirming the higher intensity of drainage and subsidence of soils near the ditches.
  • The two empirical equations proposed to estimate the amount of subsidence and the average annual subsidence rate of the peatland surface near the route of drainage ditches were applied to a fen with an average degree of organic matter decomposition in area with an initial peat deposit thickness of up to 250 cm.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/land10121287/s1, Table S1: Results of field measurements (2014) and archival data (1967) of the analyzed ditches on a part of the Solec peatland; Table S2: Values of initial thickness of the peat deposit (1967) and the size of the subsidence and the average annual rate of subsidence in the years 1967–2014.

Author Contributions

Conceptualization: R.O., E.Z., J.U.; methodology: J.U., R.O., E.Z., validation: R.O., E.Z., J.J.; formal analysis: R.O., E.Z., J.U.; investigation: R.O., J.U.; data curation: R.O., J.U., J.J.; writing—original draft preparation: R.O., E.Z., J.J.; writing review and editing: E.Z., J.J.; visualization: J.U., E.Z.; project administration: E.Z., J.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Moore, P.D. The future of cool temperate bogs. Environ. Conserv. 2002, 29, 3–20. [Google Scholar] [CrossRef]
  2. Oleszczuk, R.; Regina, K.; Szajdak, L.; Höper, H.; Maryganowa, V. Impacts of agricultural utilization of peat soils on the greenhouse gas balance. In Peatlands and Climate Change; Strack, M., Ed.; International Peat Society: Jyväskylä, Finland, 2008; pp. 70–97. [Google Scholar]
  3. Post, W.M.; Emanuel, W.R.; Zinke, P.J.; Stangenberger, A.G. Soil carbon pools and world life zones. Nature 1982, 298, 156–159. [Google Scholar] [CrossRef]
  4. Byrne, K.A.; Chonjicki, B.; Christensen, T.R.; Drosler, M.; Freibauer, A.; Friborg, T.; Frolking, S.; Lindroth, A.; Mailhammer, J.; Malmer, N.; et al. EU peatlands: Current carbon stocks and trace gas fluxes. In Report 4/2004 to ‘Concerted Action: Synthesis of the European Greenhouse Gas Budget’; Geosphere-Biosphere Centre, University of Lund: Lund, Sweden, 2004; p. 58. [Google Scholar]
  5. Jadczyszyn, J.; Bartosiewicz, B. Soil drainage and degradation processes. Studia i Raporty IUNG-PIB. Puławy 2020, 64, 49–60. [Google Scholar]
  6. Kudlicki, Ł. Desertification threat in Poland. Bezpieczeństwo Nar. 2006, 1, 201–211. [Google Scholar]
  7. Couwenberg, J. Greenhouse gas emissions from managed peat soils: Is the IPCC reporting guidance realistic? Mires Peat 2011, 8, 1–10. [Google Scholar]
  8. Okruszko, H. The effect of land reclamation on organic soils within Poland conditions. Zesz. Probl. Post Nauk. Roln. 1976, 177, 159–204. [Google Scholar]
  9. Okruszko, H.; Ilnicki, P. The moorsh horizons as quality indicators of reclaimed organic soils. In Organic Soils and Peat Materials for Sustainable Agriculture. Parent, L.E., Ilnicki, P., Eds.; CRC Press: Boca Raton, FL, USA, 2003; p. 205. [Google Scholar]
  10. Doroszewski, A.; Jóźwicki, T.; Wróblewska, W.; Kozyra, J. Agricultural drought in Poland in the years 1961–2010; Institute of Soil Science and Plant Cultivation. State Reaserch Institute: Puławy, Poland, 2014; p. 144. [Google Scholar]
  11. Fenner, N.; Freeman, C. Drought-induced carbon loss in peatlands. Nature Geosci. 2011, 4, 895–900. [Google Scholar] [CrossRef]
  12. Koza, P.; Łopatka, A.; Jadczyszyn, J.; Wawer, R.; Doroszewski, A.; Siebielec, G. Raport IUNG-PIB: Delimitation of Areas at Varying Degrees of risk of Drought in Poland for the Purposes of Implementing the Operation “Modernization of Agricultural Farms” in the Rural Development Program for 2014–2020; IUNG: Puławy, Poland, 2019; p. 43. [Google Scholar]
  13. Brandyk, T.; Szatyłowicz, J.; Oleszczuk, R.; Gnatowski, T. Water–related physical attributes of organic soils. In Organic Soils and Peat Materials for Sustainable, Agriculture; Parent, L.E., Ilnicki, P., Eds.; CRC Press: Boca Raton, FL, USA, 2003; pp. 33–66. [Google Scholar]
  14. Gebhard, S.; Fleige, H.; Horn, R. Anisotropic shrinkage of mineral and organic soils and its impact on soil hydraulic properties. Soil Till. Res. 2012, 125, 96–104. [Google Scholar] [CrossRef]
  15. Hooijer, A.; Page, S.; Jauhiainen, J.; Lee, W.A.; Lu, X.X.; Idris, A.; Anshari, G. Subsidence and carbon loss in drained tropical peatlands. Biogeosciences 2012, 9, 1053–1071. [Google Scholar] [CrossRef] [Green Version]
  16. Okruszko, H. Transformation of fen-peat soils under the impact of draining. Zesz. Probl. Post. Nauk. Roln. 1993, 40, 3–73. [Google Scholar]
  17. Peng, X.; Horn, R. Anisotropic shrinkage and swelling of some organic and inorganic soils. Eur. J. Soil Sci. 2007, 58, 98–107. [Google Scholar] [CrossRef]
  18. Silins, U.; Rothwell, R.L. Forest peatland drainage and subsidence affect soil water retention and transport properties in an Alberta peatland. Soil Sci. Soc. Am. J. 1998, 62, 1048–1056. [Google Scholar] [CrossRef]
  19. Snyder, G.H. Everglades agricultural area soil subsidence and land use projections. Annu. Proc. Soil Crop Sci. Soc. Fla. 2005, 64, 44–51. [Google Scholar]
  20. Eggelsmann, R. Subsidence of peatland caused by drainage, evaporation and oxidation. In Land Subsidence, Proceedings of the Third International Symposium on Land Subsidence Held in Venice, Italy, 19–25 March 1984; IAHS Publication No. 151; Johnson, A.I., Carbognin, L., Ubertini, L., Eds.; Institute of Hydrology, Wallingford: Oxfordshire, UK, 1986; pp. 497–505. [Google Scholar]
  21. Hillman, G.H. Effects of engineered drainage on water tables and peat subsidence in an Alberta Treed Fen. In Northern Forested Wetlands Ecology and Management; Carl, C., Ed.; CRC Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 253–272. [Google Scholar]
  22. Jurczuk, S. The influence of water regulations on subsidence and mineralisation of organic soils. In Biblioteczka Wiadomości IMUZ; IMUZ: Falenty, Poland, 2000; Volume 96, p. 120. [Google Scholar]
  23. Krzywonos, K. The subsidence of peatlands after drainage near ZD IMUZ Biebrza. Wiadomości IMUZ Falenty 1974, 12, 151–169. [Google Scholar]
  24. Lipka, K.; Zając, E.; Wdowik, W. The effect of land use on the disappearance of peat-moorsh soils in the Mrowla River valley near Rzeszów. Zesz Probl Post Nauk Roln 2005, 507, 349–355. [Google Scholar]
  25. Schothorst, C.J. Subsidence of low moor peat soils in the western Netherlands. Geoderma 1977, 17, 265–291. [Google Scholar] [CrossRef]
  26. Wösten, J.H.M.; Ismail, A.B.; van Wijk, A.L.M. Peat subsidence and its practical implications: A case study in Malaysia. Geoderma 1997, 78, 25–36. [Google Scholar] [CrossRef]
  27. Ikkala, L.; Ronkanen, A.-K.; Utriainen, O.; Kløve, B.; Marttila, H. Peatland subsidence enhances cultivated lowland flood risk. Soil Till Res 2021, 212, 105078. [Google Scholar] [CrossRef]
  28. Lipka, K.; Zając, E.; Hlotov, V.; Siejka, Z. Disappearance rate of a peatland in Dublany near Lviv (Ukraine) drained in 19th century. Mires Peat 2017, 19, 1–15. [Google Scholar]
  29. Maslov, B.S.; Kolganov, A.V.; Kreshtapova, V.N. Peat Soils and Their Change under Amelioration; Rossel’khozizdat: Moskva, Russia, 1996. [Google Scholar]
  30. Berglund, Ö.; Berglund, K. Distribution and cultivation intensity of agricultural peat and gyttja soils in Sweden and estimation of greenhouse gas emissions from cultivated peat soils. Geoderma 2010, 154, 173–180. [Google Scholar] [CrossRef] [Green Version]
  31. Camporese, M.; Gamolati, G.; Putti, M.; Teatini, P. Peatland Susidence in the Venice Watershed. In Peatlands: Evolution and Records of Environmental and Climate Changes; Martini, I.P., Martinez Cortizas, A., Chesworth, W., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 529–550. [Google Scholar]
  32. Ilnicki, P. Restoration of Carbon Sequestrating Capacity and Biodiversity in Abandoned Grassland on Peatland in Poland. Monography; August Cieszkowski Agricultural University Press of Poznań: Poznań, Poland, 2002; p. 170. [Google Scholar]
  33. Kasimir-Klemedtsson, A.; Klemedtsson, L.; Berglund, K.; Martikainen, P.; Silvola, J.; Oenema, O. Greenhouse gas emissions from farmed organic soils: A review. Soil Use Manag. 1997, 13, 245–250. [Google Scholar] [CrossRef]
  34. Kechavarzi, C.; Dawson, Q.; Leeds-Harrison, P.B.; Szatyłowicz, J.; Gnatowski, T. Water–table management in lowland UK peat soils and its potential impact on CO2 emission. Soil Use Manag. 2007, 23, 359–367. [Google Scholar] [CrossRef]
  35. Schipper, L.A.; McLeod, M. Subsidence rates and carbon loss in peat soils following conversion to pasture in the Waikato region, New Zealand. Soil Use Manag. 2002, 18, 91–93. [Google Scholar] [CrossRef]
  36. Van den Akker, J.J.H.; Jansen, P.C.; Hendriks, R.F.A.; Hoving, I.; Pleijter, M. Submerged infiltration to halve subsidence and GHG emissions of agricultural peat soils. In Proceedings of the 14th International Peat Congress, Extended abstract No. 383, Stockholm, Sweden, 3–8 June 2012; p. 6. [Google Scholar]
  37. Gąsowska, M. The Influence of Change in Meadow Use on Physical–Water Properties of Organic Soils. Case Study: Łąki Soleckie. Ph.D. Thesis, Warsaw University of Life Sciences–SGGW, Warsaw, Poland, 2017. [Google Scholar]
  38. Organic Soils and Peat Materials for Sustainable Agriculture; Parent, L.E.; Ilnicki, P. (Eds.) CRC Press: Boca Raton, FL, USA, 2003; p. 205. [Google Scholar]
  39. Truba, M.; Oleszczuk, R. An analysis of some basic chemical and physical properties of drained fen peat and moorsh soil layers. Ann Wars. Univ. Life Sci.-SGGW Land Reclam. 2014, 46, 69–78. [Google Scholar] [CrossRef]
  40. Dawson, Q.; Kechavarzi, C.; Leeds-Harrison, P.B.; Burton, R.G.O. Subsidence and degradation of agricultural peatlands in the Fenlands of Norfolk, UK. Geoderma 2010, 154, 181–187. [Google Scholar] [CrossRef]
  41. Deverel, S.J.; Ingrum, T.; Leighton, D. Present-day oxidative subsidence of organic soils and mitigation in the Sacramento-San Joaquin Delta, California, USA. Hydrogeol. J. 2016, 24, 569–586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  42. Evans, C.D.; Williamson, J.M.; Kacaribu, F.; Irawan, D.; Suardiwerianto, Y.; Hidayat, M.F.; Laurén, A.; Page, S.E. Rates and spatial variability of peat subsidence in Acacia plantation and forest landscapes in Sumatra, Indonesia. Geoderma 2019, 338, 410–421. [Google Scholar] [CrossRef]
  43. Hoogland, T.; van den Akker, J.J.H.; Brus, D.J. Modeling the subsidence of peat soils in the Dutch coastal area. Geoderma 2012, 171–172, 92–97. [Google Scholar] [CrossRef]
  44. Ilnicki, P.; Szajdak, L.W. Peatland Disappearance; PTPN Press: Poznań, Poland, 2016; p. 312. [Google Scholar]
  45. Oleszczuk, R.; Zając, E.; Urbański, J. Verification of empirical equations describing subsidence rate of peatland in Central Poland. Wetl. Ecol Manag. 2020, 2, 495–507. [Google Scholar] [CrossRef]
  46. Zanello, F.; Teatini, P.; Putti, M.; Gambolati, J. Long term peatland subsidence: Experimental study and modeling scenarios in the Venice coastland. J. Geophys. Res. 2011, 116, 1–14. [Google Scholar] [CrossRef]
  47. Ciepielowski, A.; Włodarczyk, A. Hydrotechnical structures in protected areas. Acta Sci. Pol. Arch. 2004, 3, 3–21. [Google Scholar]
  48. Murat-Błażejewska, S.; Zbierska, J.; Ławniczak, A.; Kanclerz, J.; Kupiec, J.; Sojka, M. Exploitation of water infrastructure in aspect of water resources of lowland river catchment. Acta Sci. Pol. Arch. 2008, 7, 13–22. [Google Scholar]
  49. Oleszczuk, R.; Gąsowska, M.; Guz, G.; Urbański, J.; Hewelke, E. The influence of subsidence and disappearance of organic moorsh soils on longitudinal sub-irrigation ditch profiles. Acta Sci Pol. Cir. 2017, 16, 3–13. [Google Scholar] [CrossRef] [Green Version]
  50. Brandyk, T. Principles of Moisture Management for Shallow Water Table Soils. In Treatises and Monographs; Warsaw Agricultural University Press: Warsaw, Poland, 1990; Volume 116, p. 120. [Google Scholar]
  51. Kaca, E. Mathematical Model of Ground Water Rising in Sub-Irrigation System. Ph.D. Thesis, Institute of Land Reclamation and Water Management, Warsaw Agricultural Unviersity, Warsaw, Poland, 1981; p. 192. [Google Scholar]
  52. Brożek, W. The Description of the Technical Project of Land Reclamation of the Grassland Mała River Site; CBSiPWM: Warsaw, Poland, 1967; p. 45, unpublished work. [Google Scholar]
  53. Ostromęcki, J. The Drainage of Grasslands. Guide–Book. Warsaw Agricultural University Press: Warsaw, Poland, 1971; p. 163. [Google Scholar]
  54. Pierzgalski, E. Land Reclamation of Grassland–Sub-Irrigation Systems. Guide–Book; Warsaw Agricultural University Press: Warsaw, Poland, 1996; p. 200. [Google Scholar]
  55. Ilnicki, P. Subsidence of Fenland Areas in the Noteć Valley under Longterm Agricultural Use Depending on Their Structure and Drainage Intensity. Doctoral Dissertation, Agricultural University, Szczecin, Poland, 1972; p. 63. [Google Scholar]
  56. Van den Akker, J.J.H.; Hendriks, R.F.A.; Pleijter, M. CO2 emissions from peat soils in agricultural use: Calculation and prevention. Agrociencia 2012, 16, 43–50. [Google Scholar]
  57. Grzywna, A. Peatlands surface subsidence in drainage grassland Polesie Lubelskie. Acta Sci. Pol. Cir. 2016, 15, 81–89. [Google Scholar] [CrossRef] [Green Version]
  58. Grzywna, A. The degree of peatland subsidence resulting from drainage of land. Environ. Earth Sci. 2017, 76, 1–8. [Google Scholar] [CrossRef] [Green Version]
  59. Brandyk, A.; Oleszczuk, R.; Urbański, J. Estimation of organic soils subsidence in the vicinity of hydraulic structures—Case study of a subirrigation system in Central Poland. J. Ecol. Eng. 2020, 21, 64–74. [Google Scholar] [CrossRef]
  60. Querner, E.P.; Jansen, P.C.; van den Akker, J.J.H.; Kwakernaak, C. Analysing water level strategies to reduce soil subsidence in Dutch peat meadows. J. Hydrol. 2012, 446–447, 59–69. [Google Scholar] [CrossRef]
  61. Van den Hardeveld, H.A.; Driessen, P.P.J.; Schot, P.P.; Wassen, M.J. An integrated modelling framework to assess long-term impacts of water management strategies steering soil subsidence in peatlands. Environ. Impact Asses. Rev. 2017, 66, 66–77. [Google Scholar] [CrossRef]
  62. Van den Hardeveld, H.A.; de Jong, H.; Knepfle, M.; de Lange, T.; Schot, P.P.; Spanjers, B.; Teurlincx, S. Integrated impact assessment of adaptive management strategies in a Dutch peatland polder. In Proceedings of IAHS Proceedings of the International Association of Hydrological Sciences (PIAHS), Copernicus Publications, Gottingen, Germany, 2020; Volume 382, pp. 553–557.
  63. Clark, D.; Rieley, J. (Eds.) Strategy for Responsible Peatland Management; International Peat Society: Jyväskylä, Finland, 2010; p. 39. [Google Scholar]
  64. Joosten, H.; Clarke, D. Wise Use of Mires and Peatlands-Background and Principles Including a Framework for Decision-Making; International Mire Conservation Group and International Peat Society: Saarijärvi, Finland, 2002; p. 304. [Google Scholar]
  65. Urzainki, I.; Laurén, A.; Palviainen, M.; Haahti, K.; Budiman, A.; Basuki, I.; Netzer, M.; Hökkä, H. Canal blocking optimization in restoration of drained peatlands. Biogeosciences 2020, 17, 4769–4784. [Google Scholar] [CrossRef]
  66. Gąsowska, M.; Oleszczuk, R.; Urbański, J. The estimation of the subsidence rate of drained peatland and verification of empirical equations of this process. Sci. Rev.—Eng. Environ. Sci. 2019, 28, 95–104. [Google Scholar]
Land 10 01287 g001 550
Figure 1. Location of the study site, its schematic (a), and the analyzed parts of it (b).
Figure 1. Location of the study site, its schematic (a), and the analyzed parts of it (b).
Land 10 01287 g001
Land 10 01287 g002 550
Figure 2. Longitudinal profile of the R-29 ditch.
Figure 2. Longitudinal profile of the R-29 ditch.
Land 10 01287 g002
Land 10 01287 g003 550
Figure 3. Cross-sections of the R-29 ditch in the year 1967 (designed) and 2014 (measured).
Figure 3. Cross-sections of the R-29 ditch in the year 1967 (designed) and 2014 (measured).
Land 10 01287 g003
Land 10 01287 g004 550
Figure 4. Relationship between the amount of surface subsidence of a drained peat deposit (a), and the average annual rate of peat deposit surface subsidence (b) on the initial thickness of the peat deposit.
Figure 4. Relationship between the amount of surface subsidence of a drained peat deposit (a), and the average annual rate of peat deposit surface subsidence (b) on the initial thickness of the peat deposit.
Land 10 01287 g004
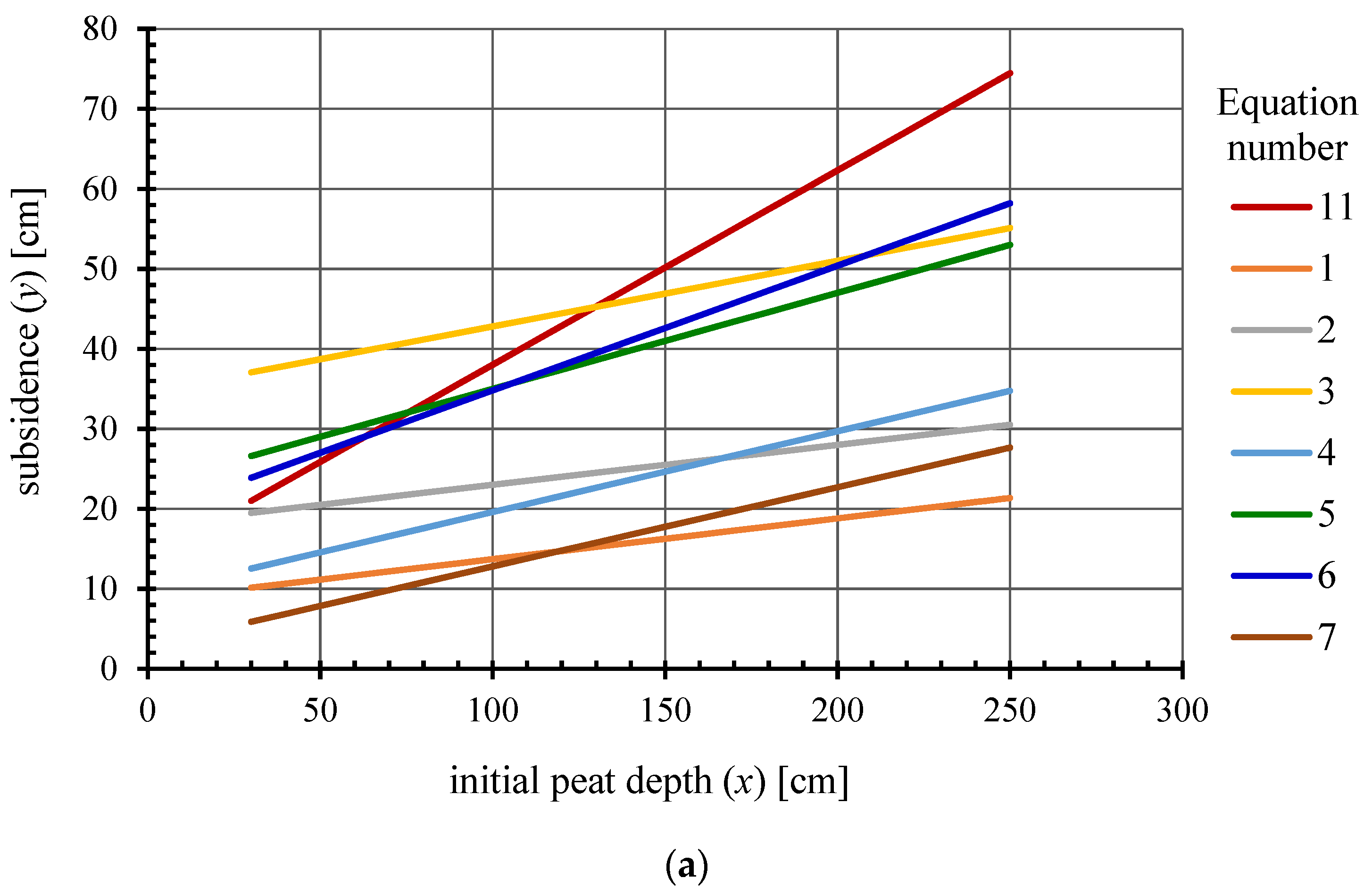
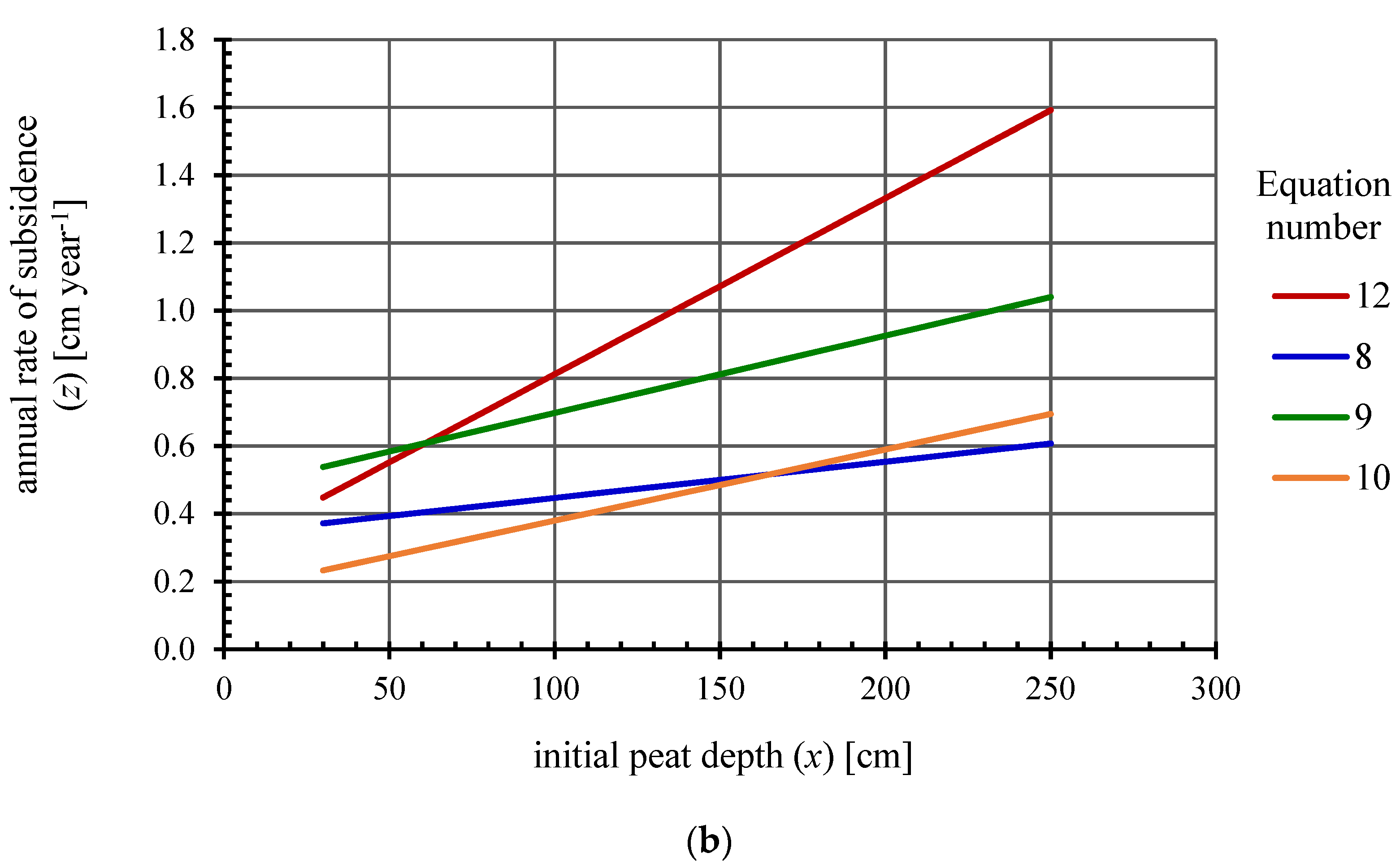
Land 10 01287 g005a 550Land 10 01287 g005b 550
Figure 5. Comparison of the results of calculating the amount of surface subsidence using proposed Equation (11) (a) and the amount of average annual rate of subsidence using proposed Equation (12) (b) with the results of calculating these parameters with equations published in the literature.
Figure 5. Comparison of the results of calculating the amount of surface subsidence using proposed Equation (11) (a) and the amount of average annual rate of subsidence using proposed Equation (12) (b) with the results of calculating these parameters with equations published in the literature.
Land 10 01287 g005aLand 10 01287 g005b
Table
Table 1. Empirical equations for the second phase of peat surface subsidence based on initial peat deposit depth and soil surface subsidence or annual peat subsidence rates published by various authors.
Table 1. Empirical equations for the second phase of peat surface subsidence based on initial peat deposit depth and soil surface subsidence or annual peat subsidence rates published by various authors.
Site (Source)Equation (Number)Explanations of Symbols
acc. to Sources
Noteć River Valley; drainage intensity of peatlands:
-
low (0.4–0.6 m),
-
medium (0.6–1.0 m),
-
high (1.0–1.2 m),
-
total (Ilnicki 1972)

y = 0.051 x + 8.6
y = 0.05 x + 18
y = 0.082 x + 34.6
y = 0.101 x + 9.5
(1)
(2)
(3)
(4)
y—surface subsidence [cm]
x—initial peat depth [cm]


Peatlands in Central Europe (Ilnicki 1972) y = 0.12 x + 23 (5)y—surface subsidence [cm]
x—initial peat depth [cm]
Peatland of Moscow Research Station (Stankiewicz and Karelin 1965 after Ilnicki 1972) y = 0.156 x + 19.2 (6)y—surface subsidence [cm]
x—initial peat depth [cm]
Biebrza River Valley; Kuwasy I fen (Krzywonos 1974) y = 0.099 x + 2.9 (7)y—surface subsidence [cm]
x—initial peat depth [cm]
Noteć River Valley; drainage intensity of peatlands:
-
medium (0.6–1.0 m),
-
high (1.0–1.2 m),
-
total (Ilnicki 1972)

z = 0.00107 x + 0.34
z = 0.00228 x + 0.47
z = 0.0021 x + 0.17
(8)
(9)
(10)
z—average annual rate of soil surface subsidence [cm year−1]
x—initial peat depth [cm]
Table
Table 2. Mean values and range (min–max) parameters describing subsidence of drainage ditches (banks and bottom).
Table 2. Mean values and range (min–max) parameters describing subsidence of drainage ditches (banks and bottom).
Ditch No.Peat Depth
(cm)		Ditch Shallowing (cm)d/t Ratio
(cm)		Subsidence
(cm)
1967 t02014 td = t0 − tBanksBottom
R 150.89 (0.73–1.15)0.55 (0.40–0.75)0.35 (0.19–0.44)0.66 (0.35–1.00)0.63 (0.51–0.70)0.29 (0.24–0.32)
R 170.94 (0.81–1.09)0.75 (0.63–0.82)0.20 (0.09–0.34)0.27 (0.13–0.54)0.40 (0.26–0.63)0.20 (0.04–0.36)
R 191.10 (1.03–1.15)0.71 (0.56–0.94)0.38 (0.20–0.56)0.59 (0.22–0.95)0.61 (0.49–0.75)0.23 (0.00–0.38)
R 211.02 (0.93–1.06)0.71 (0.57–1.00)0.31 (0.05–0.40)0.47 (0.05–0.70)0.59 (0.42–0.80)0.28 (0.19–0.41)
R 221.18 (0.94–1.35)0.69 (0.50–0.85)0.49 (0.44–0.53)0.73 (0.59–0.88)0.55 (0.49–0.5900.06 (0.05–0.07)
R 230.97 (0.88–1.13)0.58 (0.42–0.72)0.39 (0.21–0.51)0.73 (0.31–1.67)0.60 (0.42–0.74)0.21 (0.04–0.40)
R 240.98 (0.76–1.12)0.83 (0.65–1.05)0.15 (0.01–0.38)0.20 (0.01–0.58)0.23 (0.04–0.50)0.08 (0.03–0.12)
R 250.81 (0.73–0.89)0.72 (0.68–0.77)0.10 (0.04–0.12)0.14 (0.06–0.18)0.21 (0.11–0.29)0.11 (0.07–0.17)
R 260.99 (0.79–1.10)0.75 (0.54–0.94)0.23 (0.02–0.46)0.36 (0.03–0.85)0.35 (0.06–0.56)0.11 (0.03–0.21)
R 26a0.92 (0.85–1.00)0.71 (0.60–0.85)0.21 (0.07–0.30)0.31 (0.09–0.43)0.34 (0.22–0.44)0.13 (0.10–0.15)
R 270.85 (0.75–0.95)0.75 (0.61–0.93)0.10 (0.02–0.16)0.15 (0.02–0.25)0.26 (0.07–0.36)0.16 (0.05–0.27)
R 290.98 (0.90–1.10)0.79 (0.76–0.87)0.19 (0.03–0.32)0.24 (0.03–0.41)0.40 (0.28–0.57)0.20 (0.04–0.38)
Total0.97 (0.73–1.35)0.71 (0.40–1.05)0.26 (0.01–0.56)0.41 (0.01–1.17)0.43 (0.04–0.80)0.18 (0.00–0.41)
Table
Table 3. Mean values and range (min–max) of initial peat depth and average rate of subsidence of drainage ditches.
Table 3. Mean values and range (min–max) of initial peat depth and average rate of subsidence of drainage ditches.
Ditch No.L
(m)		Peat Depth 1967SubsidenceAverage Annual Subsidence Rate
(cm)y (cm)y(%) (%)z (cm year−1)
R 15450141.2 (95–255)63.2 (51–70)50.3 (27.5–71.6)1.34 (1.09–1.49)
R 17470135.6 (102–200)40.0 (26–63)30.6 (17.0–40.4)0.85 (0.55–1.34)
R 19490163.6 (108–226)61.0 (49–75)39.2 (23.5–62.8)1.30 (1.04–1.60)
R 21500152.0 (82–237)58.5 (42–80)42.7 (23.1–62.8)1.24 (0.89–1.70)
R 22260120.0 (65–165)55.0 (49–59)51.8 (34.5–75.4)1.17 (1.04–1.26)
R 23500150.3 (103–223)60.3 (42–74)42.3 (33.2–58.6)1.28 (0.89–1.57)
R 24510114.8 (63–160)22.5 (4–50)19.0 (4.4–39.1)0.48 (0.09–1.06)
R 2531052.5 (31–95)21.0 (11–29)42.6 (30.5–56.8)0.45 (0.23–0.62)
R 26510120.3 (70–170)35.3 (6–56)26.9 (8.6–45.0)0.75 (0.13–1.19)
R 26a540109.2 (30–170)33.8 (22–44)39.3 (22.4–73.3)0.72 (0.47–0.94)
R 2737072.5 (40–110)26.0 (7–36)35.0 (17.5–48.3)0.55 (0.15–0.77)
R 2932490.0 (59–130)39.5 (28–57)44.3 (39.8–47.5)0.84 (0.60–1.21)
Total-121.7 (30–255)43.3 (4–80)37.7 (4.4–75.4)0.92 (0.09–1.70)
Explanations: L—total length of the ditch.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Oleszczuk, R.; Zając, E.; Urbański, J.; Jadczyszyn, J. Rate of Fen-Peat Soil Subsidence Near Drainage Ditches (Central Poland). Land 2021, 10, 1287. https://doi.org/10.3390/land10121287

AMA Style

Oleszczuk R, Zając E, Urbański J, Jadczyszyn J. Rate of Fen-Peat Soil Subsidence Near Drainage Ditches (Central Poland). Land. 2021; 10(12):1287. https://doi.org/10.3390/land10121287

Chicago/Turabian Style

Oleszczuk, Ryszard, Ewelina Zając, Janusz Urbański, and Jan Jadczyszyn. 2021. "Rate of Fen-Peat Soil Subsidence Near Drainage Ditches (Central Poland)" Land 10, no. 12: 1287. https://doi.org/10.3390/land10121287

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop