Normalizing the Local Incidence Angle in Sentinel-1 Imagery to Improve Leaf Area Index, Vegetation Height, and Crop Coefficient Estimations
Abstract
:1. Introduction
2. Materials and Methods
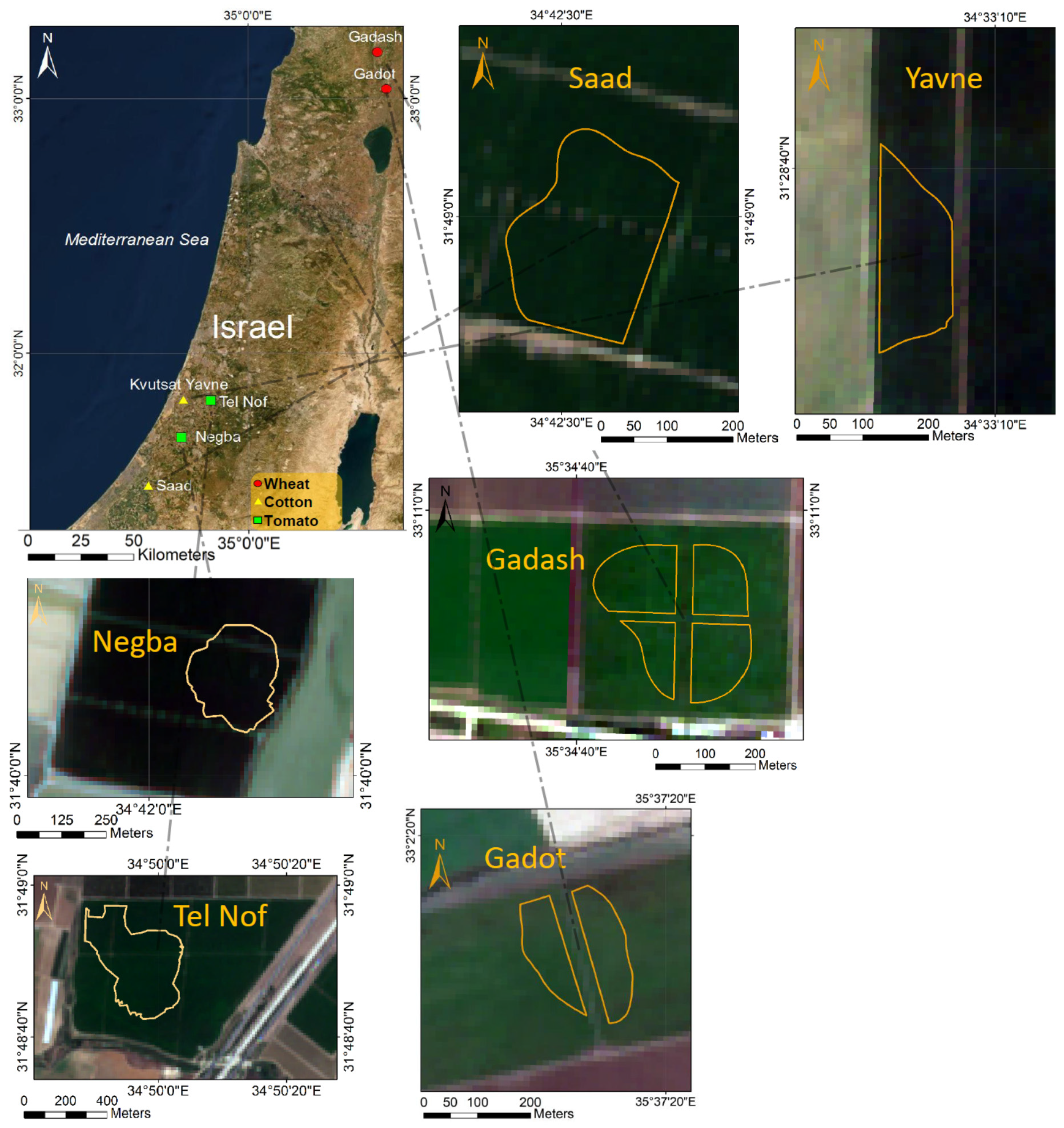
2.1. Test Sites and Field Measurements
2.2. Agro-Meteorological Measurements
2.3. Satellite Imagery
2.4. Image Processing
2.5. Dual-Polarized RVI Algorithm
2.6. σ0-Based Local Incidence Angle Normalization
2.7. β0-Based Local Incidence Angle Normalization Method for Tomato and Cotton Height, LAI, and Kc Estimation
2.8. Calibration and Validation of Empirical Vegetation Variable Estimation Models
3. Results
3.1. Wheat, Processing Tomato, and Cotton Height, LAI, and Kc Models Based on the σ0 Normalization Method
3.2. Processing Tomato and Cotton Height, LAI, and Kc Models Based on the β0 Normalization Method
3.3. Performance of the Dual-Polarized RVI
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Broge, N.H.; Thomsen, A.G.; Andersen, P.B. Comparison of Selected Vegetation Indices as Indicators of Crop Status. Available online: http://www.earsel.org/symposia/2002-symposium-Prague/pdf/083.pdf (accessed on 24 June 2021).
- González-Dugo, M.P.; Mateos, L. Spectral vegetation indices for benchmarking water productivity of irrigated cotton and sugarbeet crops. Agric. Water Manag. 2008, 95, 48–58. [Google Scholar] [CrossRef]
- Johnson, L.F.; Trout, T.J. Satellite NDVI Assisted Monitoring of Vegetable Crop Evapotranspiration in California’s San Joaquin Valley. Remote Sens. 2012, 4, 439–455. [Google Scholar] [CrossRef] [Green Version]
- Mróz, M.; Sobieraj, A. Comparison of several vegetation indices calculated on the basis of a seasonal SPOT XS time series, and their suitability for land cover and agricultural crop identification. Technol. Sci. 2004, 7, 39–66. [Google Scholar] [CrossRef]
- Purevdorj, T.S.; Tateishi, R.; Ishiyama, T.; Honda, Y. Relationships between percent vegetation cover and vegetation indices. Int. J. Remote Sens. 1998, 19, 3519–3535. [Google Scholar] [CrossRef]
- Rozenstein, O.; Haymann, N.; Kaplan, G.; Tanny, J. Estimating cotton water consumption using a time series of Sentinel-2 imagery. Agric. Water Manag. 2018, 207, 44–52. [Google Scholar] [CrossRef]
- Santos, C.L.M.d.O.; Lamparelli, R.A.C.; Figueiredo, G.K.D.A.; Dupuy, S.; Boury, J.; Luciano, A.C.d.S.; Torres, R.d.S.; le Maire, G. Classification of crops, pastures, and tree plantations along the season with multi-sensor image time series in a subtropical agricultural region. Remote Sens. 2019, 11, 334. [Google Scholar] [CrossRef] [Green Version]
- Viña, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.L.; Peng, Y.; Gitelson, A.A.; Arkebauer, T.J. Agricultural and Forest Meteorology Estimating green LAI in four crops Potential of determining optimal spectral bands for a universal algorithm. Agric. For. Meteorol. J. 2014, 192–193, 140–148. [Google Scholar] [CrossRef]
- Rozenstein, O.; Qin, Z.; Derimian, Y.; Karnieli, A. Derivation of land surface temperature for Landsat-8 TIRS using a split window algorithm. Sensors 2014, 14, 5768–5780. [Google Scholar] [CrossRef]
- Manivasagam, V.S.; Kaplan, G.; Rozenstein, O. Developing Transformation Functions for VENμS and Sentinel-2 Surface Reflectance over Israel. Remote Sens. 2019, 11, 1710. [Google Scholar] [CrossRef] [Green Version]
- Flood, N. Continuity of reflectance data between Landsat-7 ETM+ and Landsat-8 OLI, for both top-of-atmosphere and surface reflectance: A study in the Australian landscape. Remote Sens. 2014, 6, 7952–7970. [Google Scholar] [CrossRef] [Green Version]
- Bannari, A. Synergy Between Sentinel-MSI and Landsat-OLI to Support High Temporal Frequency for Soil Salinity Monitoring in an Arid Landscape. Res. Dev. Saline Agric. 2019. [Google Scholar] [CrossRef]
- Padró, J.C.; Pons, X.; Aragonés, D.; Díaz-Delgado, R.; García, D.; Bustamante, J.; Pesquer, L.; Domingo-Marimon, C.; González-Guerrero, Ò.; Cristóbal, J.; et al. Radiometric correction of simultaneously acquired Landsat-7/Landsat-8 and Sentinel-2A imagery using Pseudoinvariant Areas (PIA): Contributing to the Landsat time series legacy. Remote Sens. 2017, 9, 1319. [Google Scholar] [CrossRef] [Green Version]
- Kaplan, G.; Fine, L.; Lukyanov, V.; Manivasagam, V.S.; Malachy, N.; Tanny, J.; Rozenstein, O. Estimating Processing Tomato Water Consumption, Leaf Area Index, and Height Using Sentinel-2 and VENµS Imagery. Remote Sens. 2021, 13, 1046. [Google Scholar] [CrossRef]
- Asrar, G.; Fuchs, M.; Kanemasu, E.T.; Hatfield, J.L. Estimating Absorbed Photosynthetic Radiation and Leaf Area Index from Spectral Reflectance in Wheat. Agron. J. 1984, 76, 300. [Google Scholar] [CrossRef]
- Reichenau, T.G.; Korres, W.; Montzka, C.; Fiener, P.; Wilken, F.; Stadler, A.; Waldhoff, G.; Schneider, K. Spatial heterogeneity of Leaf Area Index (LAI) and its temporal course on arable land: Combining field measurements, remote sensing and simulation in a Comprehensive Data Analysis Approach (CDAA). PLoS ONE 2016, 11, 1–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Y.; Qin, Q.; Ren, H.; Zhang, T.; Chen, S. Red-Edge Band Vegetation Indices for Leaf Area Index Estimation from Sentinel-2/MSI Imagery. IEEE Trans. Geosci. Remote Sens. 2020, 58, 826–840. [Google Scholar] [CrossRef]
- Wang, C.; Feng, M.C.; Yang, W.D.; Ding, G.W.; Sun, H.; Liang, Z.Y.; Xie, Y.K.; Qiao, X.X. Impact of spectral saturation on leaf area index and aboveground biomass estimation of winter wheat. Spectrosc. Lett. 2016, 49, 241–248. [Google Scholar] [CrossRef]
- Kaplan, G.; Rozenstein, O. Spaceborne Estimation of Leaf Area Index in Cotton, Tomato, and Wheat Using Sentinel-2. Land 2021, 10, 505. [Google Scholar] [CrossRef]
- Simic Milas, A.; Romanko, M.; Reil, P.; Abeysinghe, T.; Marambe, A. The importance of leaf area index in mapping chlorophyll content of corn under different agricultural treatments using UAV images. Int. J. Remote Sens. 2018, 39, 5415–5431. [Google Scholar] [CrossRef]
- Ewert, F. Modelling plant responses to elevated CO2: How important is leaf area index? Ann. Bot. 2004, 93, 619–627. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, I.; Pimstein, A.; Karnieli, A.; Cohen, Y.; Alchanatis, V.; Bonfil, D.J. LAI assessment of wheat and potato crops by VENμS and Sentinel-2 bands. Remote Sens. Environ. 2011, 115, 2141–2151. [Google Scholar] [CrossRef]
- Heuvelink, E.; Bakker, M.J.; Elings, A.; Kaarsemaker, R.; Marcelis, L.F.M. Effect of leaf area on tomato yield. Acta Hortic. 2005, 691, 43–50. [Google Scholar] [CrossRef]
- Sadeh, Y.; Zhu, X.; Dunkerley, D.; Walker, J.P.; Zhang, Y.; Rozenstein, O.; Manivasagam, V.S.; Chenu, K. Fusion of Sentinel-2 and PlanetScope time-series data into daily 3 m surface reflectance and wheat LAI monitoring. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102260. [Google Scholar] [CrossRef]
- Manivasagam, V.S.; Rozenstein, O. Practices for upscaling crop simulation models from field scale to large regions. Comput. Electron. Agric. 2020, 175, 105554. [Google Scholar] [CrossRef]
- Manivasagam, V.S.; Sadeh, Y.; Kaplan, G.; Bonfil, D.J.; Rozenstein, O. Studying the Feasibility of Assimilating Sentinel-2 and PlanetScope Imagery into the SAFY Crop Model to Predict Within-Field Wheat Yield. Remote Sens. 2021, 13, 2395. [Google Scholar] [CrossRef]
- Qi, J.; Wang, C.; Inoue, Y.; Zhang, R.; Gao, W. Synergy of optical and radar remote sensing in agricultural applications. Ecosyst. Dyn. Agric. Remote Sens. Model. Site-Specific Agric. 2004, 5153, 153. [Google Scholar] [CrossRef]
- Luo, P.; Liao, J.; Shen, G. Combining Spectral and Texture Features for Estimating Leaf Area Index and Biomass of Maize Using Sentinel-1/2, and Landsat-8 Data. IEEE Access 2020, 8, 53614–53626. [Google Scholar] [CrossRef]
- Jin, X.; Yang, G.; Xu, X.; Yang, H.; Feng, H.; Li, Z.; Shen, J.; Zhao, C.; Lan, Y. Combined multi-temporal optical and radar parameters for estimating LAI and biomass in winter wheat using HJ and RADARSAR-2 data. Remote Sens. 2015, 7, 13251–13272. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.; Steiner, J.; Doughty, R.B.; Chang, Q. Estimating leaf area index and aboveground biomass of grazing pastures using Sentinel-1, Sentinel-2 and Landsat images. ISPRS J. Photogramm. Remote Sens. 2019, 154, 189–201. [Google Scholar] [CrossRef] [Green Version]
- Reamer, R.E.; Stockton, W.O.; Stromfors, R.D. New military uses for Synthetic Aperture Radar (SAR). Airborne Reconnaiss. XVI 1993, 113–119. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Dirk, R.; Smith, M. Crop Evapotranspiration-Guidelines For Computing Crop Water Requirements-FAO Irrigation And Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. Available online: http://www.fao.org/3/X0490E/X0490E00.htm (accessed on 24 June 2021).
- Pereira, L.S.; Paredes, P.; Hunsaker, D.J.; López-Urrea, R.; Mohammadi Shad, Z. Standard single and basal crop coefficients for field crops. Updates and advances to the FAO56 crop water requirements method. Agric. Water Manag. 2021, 243, 1–35. [Google Scholar] [CrossRef]
- Trevisan, R.G.; Junior, N.d.S.V.; Portz, G.; Eitelwein, M.T.; Molin, J.P. Use of crop height and optical sensor readings to predict mid-season cotton biomass. In Proceedings of the Precision agriculture ’15, Volcani Center, Israel, 12–16 July 2015; p. 8. [Google Scholar]
- Asilo, S.; Nelson, A.; Bie, K.D.; Skidmore, A.; Laborte, A.; Maunahan, A.; Quilang, E.J.P. Relating X-band SAR Backscattering to Leaf Area Index of Rice in Different Phenological Phases. Remote Sens. 2019, 11, 1462. [Google Scholar] [CrossRef] [Green Version]
- Canisius, F.; Shang, J.; Liu, J.; Huang, X.; Ma, B.; Jiao, X.; Geng, X.; Kovacs, J.M.; Walters, D. Tracking crop phenological development using multi-temporal polarimetric Radarsat-2 data. Remote Sens. Environ. 2018, 210, 508–518. [Google Scholar] [CrossRef]
- McNairn, H.; Champagne, C.; Shang, J.; Holmstrom, D.; Reichert, G. Integration of optical and Synthetic Aperture Radar (SAR) imagery for delivering operational annual crop inventories. ISPRS J. Photogramm. Remote Sens. 2009, 64, 434–449. [Google Scholar] [CrossRef]
- Hosseini, M.; McNairn, H.; Merzouki, A.; Pacheco, A. Estimation of Leaf Area Index (LAI) in corn and soybeans using multi-polarization C- and L-band radar data. Remote Sens. Environ. 2015, 170, 77–89. [Google Scholar] [CrossRef]
- Kim, Y.; Jackson, T.; Bindlish, R.; Lee, H.; Hong, S. Radar vegetation index for estimating the vegetation water content of rice and soybean. IEEE Geosci. Remote Sens. Lett. 2012, 9, 564–568. [Google Scholar] [CrossRef]
- Small, D. Flattening Gamma: Radiometric Terrain Correction for SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Makynen, M.; Karvonen, J. Incidence angle dependence of first-year sea ice backscattering coefficient in Sentinel-1 SAR imagery over the Kara Sea. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6170–6181. [Google Scholar] [CrossRef]
- Widhalm, B.; Bartsch, A.; Goler, R. Simplified normalization of C-band synthetic aperture radar data for terrestrial applications in high latitude environments. Remote Sens. 2018, 10, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Van Tricht, K.; Gobin, A.; Gilliams, S.; Piccard, I. Synergistic Use of Radar Sentinel-1 and Optical Sentinel-2 Imagery for Crop Mapping: A Case Study for Belgium. Remote Sens. 2018, 10, 1642. [Google Scholar] [CrossRef] [Green Version]
- Inoue, Y.; Sakaiya, E.; Wang, C. Capability of C-band backscattering coefficients from high-resolution satellite SAR sensors to assess biophysical variables in paddy rice. Remote Sens. Environ. 2014, 140, 257–266. [Google Scholar] [CrossRef]
- Veloso, A.; Mermoz, S.; Bouvet, A.; Le Toan, T.; Planells, M.; Dejoux, J.F.; Ceschia, E. Understanding the temporal behavior of crops using Sentinel-1 and Sentinel-2-like data for agricultural applications. Remote Sens. Environ. 2017, 199, 415–426. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; Lili-Chabaane, Z.; Baghdadi, N.; El Hajj, M.; Gao, Q.; Mougenot, B. Potential of Sentinel-1 Radar Data for the Assessment of Soil and Cereal Cover Parameters. Sensors 2017, 17, 2617. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nasirzadehdizaji, R.; Balik Sanli, F.; Abdikan, S.; Cakir, Z.; Sekertekin, A.; Ustuner, M. Sensitivity Analysis of Multi-Temporal Sentinel-1 SAR Parameters to Crop Height and Canopy Coverage. Appl. Sci. 2019, 9, 655. [Google Scholar] [CrossRef] [Green Version]
- Navarro, A.; Rolim, J.; Miguel, I.; Catalão, J.; Silva, J.; Painho, M.; Vekerdy, Z. Crop Monitoring Based on SPOT-5 Take-5 and Sentinel-1A Data for the Estimation of Crop Water Requirements. Remote Sens. 2016, 8, 525. [Google Scholar] [CrossRef] [Green Version]
- Inglada, J.; Vincent, A.; Arias, M.; Marais-Sicre, C. Improved early crop type identification by joint use of high temporal resolution SAR and optical image time series. Remote Sens. 2016, 8, 362. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, M.; McNairn, H.; Mitchell, S.; Davidson, A.; Robertson, L.D. Combination of optical and SAR sensors for monitoring biomass over corn fields. Int. Geosci. Remote Sens. Symp. 2018, 2018, 5952–5955. [Google Scholar] [CrossRef]
- Phan, H.; Le Toan, T.; Bouvet, A. Understanding Dense Time Series of Sentinel-1 Backscatter from Rice Fields: Case Study in a Province of the Mekong Delta, Vietnam. Remote Sens. 2021, 13, 921. [Google Scholar] [CrossRef]
- Molijn, R.; Iannini, L.; Vieira Rocha, J.; Hanssen, R. Sugarcane Productivity Mapping through C-Band and L-Band SAR and Optical Satellite Imagery. Remote Sens. 2019, 11, 1109. [Google Scholar] [CrossRef] [Green Version]
- Demarez, V.; Helen, F.; Marais-Sicre, C.; Baup, F. In-Season Mapping of Irrigated Crops Using Landsat 8 and Sentinel-1 Time Series. Remote Sens. 2019, 11, 118. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, H.S.; Sivasankar, T. Potential of C-Band Hybrid Polarimetric RISAT-1 SAR Data To Estimate Wheat Crop Height. In Proceedings of the ISPRS-GEOGLAM-ISRS International Workshop on ‘Earth Observations for Agricultural Monitoring’, New Delhi, India, 18–20 February 2019. [Google Scholar]
- Srivastava, H.S.; Sivasankar, T.; Patel, P. The sensitivity of C-band hybrid polarimetric RISAT-1 SAR data to leaf area index of paddy crop. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Benabdelouahab, T.; Dominique, D.; Hayat, L.; Hadria, R.; Tychon, B.; Boudhar, A.; Balaghi, R.; Lebrini, Y.; Maaroufi, H.; Barbier, C. Using SAR Data to Detect Wheat Irrigation Supply in an Irrigated Semi-arid Area. J. Agric. Sci. 2018, 11, 1916–9760. [Google Scholar] [CrossRef]
- Han, D.; Liu, S.; Du, Y.; Xie, X.; Fan, L.; Lei, L.; Li, Z.; Yang, H.; Yang, G. Crop Water Content of Winter Wheat Revealed with Sentinel-1 and Sentinel-2 Imagery. Sensors 2019, 19, 4013. [Google Scholar] [CrossRef] [Green Version]
- Yadav, V.P.; Prasad, R.; Bala, R. Leaf area index estimation of wheat crop using modified water cloud model from the time-series SAR and optical satellite data. Geocarto Int. 2019, 36, 791–802. [Google Scholar] [CrossRef]
- Chauhan, S.; Srivastava, H.S.; Patel, P. Wheat crop biophysical parameters retrieval using hybrid-polarized RISAT-1 SAR data. Remote Sens. Environ. 2018, 216, 28–43. [Google Scholar] [CrossRef]
- Harfenmeister, K.; Spengler, D.; Weltzien, C. Analyzing temporal and spatial characteristics of crop parameters using Sentinel-1 backscatter data. Remote Sens. 2019, 11, 1569. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Wang, J. Mapping Winter Wheat Planting Area and Monitoring Its Phenology Using Sentinel-1 Backscatter Time Series. Remote Sens. 2019, 11, 449. [Google Scholar] [CrossRef] [Green Version]
- Ashmitha, M.N.; Ahamed, M.J.; Pazhanivelan, S.; Kumaraperumal, R.; Ganesha Raj, K. Estimation of cotton and maize crop area in Perambalur district of Tamil Nadu using multi-date Sentinel-1A SAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2019, 42, 67–71. [Google Scholar] [CrossRef] [Green Version]
- Vreugdenhil, M.; Wagner, W.; Bauer-Marschallinger, B.; Pfeil, I.; Teubner, I.; Rüdiger, C.; Strauss, P. Sensitivity of Sentinel-1 backscatter to vegetation dynamics: An Austrian case study. Remote Sens. 2018, 10, 1396. [Google Scholar] [CrossRef] [Green Version]
- Topouzelis, K.; Singha, S. Incidence angle Normalization of Wide Swath SAR Data for Oceanographic Applications. Open Geosci. 2016, 8, 450–464. [Google Scholar] [CrossRef] [Green Version]
- Mladenova, I.E.; Jackson, T.J.; Bindlish, R.; Hensley, S. Incidence Angle Normalization of Radar Backscatter Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1791–1804. [Google Scholar] [CrossRef]
- Revill, A.; Florence, A.; Macarthur, A.; Hoad, S.; Rees, R.; Williams, M. Quantifying uncertainty and bridging the scaling gap in the retrieval of leaf area index by coupling Sentinel-2 and UAV observations. Remote Sens. 2020, 12, 1843. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef] [Green Version]
- Corbari, C.; Ravazzani, G.; Galvagno, M.; Cremonese, E.; Mancini, M. Assessing crop coefficients for natural vegetated areas using satellite data and eddy covariance stations. Sensors 2017, 17, 2664. [Google Scholar] [CrossRef] [Green Version]
- Rozenstein, O.; Haymann, N.; Kaplan, G.; Tanny, J. Validation of the cotton crop coefficient estimation model based on Sentinel-2 imagery and eddy covariance measurements. Agric. Water Manag. 2019, 223, 105715. [Google Scholar] [CrossRef]
- Huang, C.; Zheng, X.; Tait, A.; Dai, Y.; Yang, C.; Chen, Z.; Li, T.; Wang, Z. On using smoothing spline and residual correction to fuse rain gauge observations and remote sensing data. J. Hydrol. 2014, 508, 410–417. [Google Scholar] [CrossRef]
- Wright, J.; Lillesand, T.M.; Kiefer, R.W. Remote Sensing and Image Interpretation, 5th ed.; Flahive, R., Powell, D., Eds.; Wiley: Hoboken, NJ, USA, 2004; ISBN 0471026093. [Google Scholar]
- Stateczny, A.; Kazimierski, W.; Kulpa, K. Radar and Sonar Imaging and Processing. Remote Sens. 2020, 12, 1811. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 44. [Google Scholar] [CrossRef] [Green Version]
- Inoue, Y.; Sakaiya, E.; Wang, C. Potential of X-Band Images from High-Resolution Satellite SAR Sensors to Assess Growth and Yield in Paddy Rice. Remote Sens. 2014, 6, 5995–6019. [Google Scholar] [CrossRef] [Green Version]
- Ndikumana, E.; Minh, D.H.T.; Nguyen, H.T.D.; Baghdadi, N.; Courault, D.; Hossard, L.; Moussawi, I. El Estimation of rice height and biomass using multitemporal SAR Sentinel-1 for Camargue, Southern France. Remote Sens. 2018, 10, 1394. [Google Scholar] [CrossRef] [Green Version]
- Flores, A.; Herndon, K.; Thapa, R.; Cherrington, E. SAR Handbook: Comprehensive Methodologies for Forest Monitoring and Biomass Estimation, 1st ed.; SERVIR Global: Huntsville, AL, USA, 2019. [Google Scholar]
- Kumar, D.; Rao, S.; Sharma, J.R. Radar Vegetation Index as an Alternative to NDVI for Monitoring of Soyabean and Cotton. In Proceedings of the XXXIII INCA International Congress, Jodhpur, India, 19–21 September 2013; pp. 91–96. [Google Scholar]
- Trudel, M.; Charbonneau, F.; Leconte, R. Using RADARSAT-2 polarimetric and ENVISAT-ASAR dual-polarization data for estimating soil moisture over agricultural fields. Can. J. Remote Sens. 2012, 38, 514–527. [Google Scholar] [CrossRef]
- Holtgrave, A.-K.; Röder, N.; Ackermann, A.; Erasmi, S.; Kleinschmit, B. Comparing Sentinel-1 and -2 Data and Indices for Agricultural Land Use Monitoring. Remote Sens. 2020, 12, 2919. [Google Scholar] [CrossRef]
- Richards, M. Fundamentals of Radar Signal Processing; McGraw-Hill: New York, NY, USA, 2005; ISBN 0-07-144474-2. [Google Scholar]
- Mäkynen, M.P.; Manninen, A.T.; Similä, M.H.; Karvonen, J.A.; Hallikainen, M.T. Incidence angle dependence of the statistical properties of C-band HH-polarization backscattering signatures of the Baltic Sea ice. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2593–2605. [Google Scholar] [CrossRef]
- Sabel, D.; Pathe, C.; Wagner, W.; Hasenauer, S.; Bartsch, A.; Künzer, C.; Scipal, K. Using ENVISAT ScanSAR data for characterising scaling properties of scatterometer derived soil moisture information over Southern Africa. In Proceedings of the ENVISAT Symposium, Montreux, Switzerland, 23–27 April 2007. [Google Scholar]
- Lecomte, P.; Wagner, W. ERS Wind Scatterometer Commissioning and In-Flight Calibration. Available online: https://earth.esa.int/documents/10174/1602497/WSC12.pdf (accessed on 25 June 2021).
- Skolnik, M. Radar Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 2008; ISBN 978-0-07-148547-0. [Google Scholar]
- Rozenstein, O.; Siegal, Z.; Blumberg, D.G.; Adamowski, J. Investigating the backscatter contrast anomaly in synthetic aperture radar (SAR) imagery of the dunes along the Israel—Egypt border. Int. J. Appl. Earth Obs. Geoinf. 2016, 46, 13–21. [Google Scholar] [CrossRef]
- Srivastava, H.S.; Patel, P.; Sharma, K.P.; Krishnamurthy, Y.V.N.; Dadhwal, V.K. A semi-empirical modelling approach to calculate two-way attenuation in radar backscatter from soil due to crop cover. Curr. Sci. 2011, 100, 1871–1874. [Google Scholar]
- Ulaby, F. Radar response to vegetation. IEEE Trans. Antennas Propag. 1975, 23, 36–45. [Google Scholar] [CrossRef]
- Da Silva, A.d.Q.; Paradella, W.R.; Freitas, C.C.; Oliveira, C.G. Evaluation of digital classification of polarimetric SAR data for iron-mineralized laterites mapping in the Amazon region. Remote Sens. 2013, 5, 3101–3122. [Google Scholar] [CrossRef] [Green Version]
- Carver, K.R.; Elachi, C.; Ulaby, F.T. Microwave remote sensing from space. Proc. IEEE 1985, 73, 970–996. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing with Imaging Radar; Signals and Communication Technology; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-642-02019-3. [Google Scholar]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Small, D.; Rohner, C.; Miranda, N.; Ruetschi, M.; Schaepman, M.E. Wide-Area Analysis-Ready Radar Backscatter Composites. IEEE Trans. Geosci. Remote Sens. 2021, 1–14. [Google Scholar] [CrossRef]
- Frey, O.; Santoro, M.; Werner, C.L.; Wegmüller, U. DEM-based SAR pixel-area estimation for enhanced geocoding refinement and radiometric normalization. IEEE Geosci. Remote Sens. Lett. 2013, 10, 48–52. [Google Scholar] [CrossRef]
- Raney, R.K.; Freeman, T.; Hawkins, R.W.; Bamler, R. A plea for radar brightness. In Proceedings of the Proceedings of IGARSS ’94—1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; Volume 2, pp. 1090–1092. [Google Scholar]
- El-Darymli, K.; Mcguire, P. Understanding the Significance of Radiometric Calibration for Synthetic Aperture Radar Imagery. In Proceedings of the 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), Toronto, ON, Canada, 4–7 May 2014; 2014; pp. 1–6. [Google Scholar]
- Kreslavsky, M. Venera-15,-16 radar brightness of Venus surface: Comparison with Magellan data. Abstr. Lunar Planet. Sci. Conf. 1995, 26, 799. [Google Scholar]
- Goldstein, R.M.; Melbourne, W.G.; Morris, G.A.; Downs, G.S.; Handley, D.A.O. Preliminary radar results of Mars. Radio Sci. 1970, 5, 475–478. [Google Scholar] [CrossRef]
- Meyer, F.; Hinz, S. Automatic ship detection in space-borne SAR imagery. Int. Arch. Photogram. Remote Sens. Spat. Inform. Sci. 2009, 38, 1–6. [Google Scholar]
- Maître, H. Processing of Synthetic Aperture Radar Images; Matre, H., Ed.; ISTE: London, UK, 2008; ISBN 9780470611111. [Google Scholar]
- Steiger, J.H. Tests for comparing elements of a correlation matrix. Psychol. Bull. 1980, 87, 245–251. [Google Scholar] [CrossRef]
- Fisher, R.A. On the Probable Error of a Coefficient of Correlation Deduced from a Small Sample. Metron 1921, 1, 3–32. [Google Scholar]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biometrics Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Button, K.S.; Ioannidis, J.P.A.; Mokrysz, C.; Nosek, B.A.; Flint, J.; Robinson, E.S.J.; Munafò, M.R. Power failure: Why small sample size undermines the reliability of neuroscience. Nat. Rev. Neurosci. 2013, 14, 365–376. [Google Scholar] [CrossRef] [Green Version]
- Bréda, N.J.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef]
- El-Shirbeny, M.A.; Abutaleb, K. Sentinel-1 Radar Data Assessment to Estimate Crop Water Stress. World J. Eng. Technol. 2017, 05, 47–55. [Google Scholar] [CrossRef] [Green Version]
- Beeri, O.; Netzer, Y.; Munitz, S.; Mintz, D.F.; Pelta, R.; Shilo, T.; Horesh, A.; Mey-tal, S. Kc and LAI Estimations Using Optical and SAR Remote Sensing Imagery for Vineyards Plots. Remote Sens. 2020, 12, 3478. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2010; ISBN 978-0-19-956973-1. [Google Scholar]
- Verba, V.S.; Neronskiy, L.B.; Osipov, V.E.; Turuk, I.G. Spaceborne Earth Surveillance Radar Systems; Radiotechnika: Moscow, Russia, 2010. [Google Scholar]
- Léonard, A.; Bériaux, E.; Defourny, P. Complementarity of Linear Polarizations in C-Band SAR Imagery to Estimate Leaf Area Index for Maize and Winter Wheat. Available online: https://ftp.space.dtu.dk/pub/Ioana/papers/s444_1leon.pdf (accessed on 25 June 2021).
- Naval Air Systems Command Electronic Warfare and Radar Systems Engineering Handbook, 2nd ed.; Naval Air Warfare Center: Point Mugu, CA, USA, 1999.
- Skolnik, M. Introduction to Radar Systems, 2nd ed.; McGraw-Hili Book Co.: New York, NY, USA, 1981; ISBN 9786069276969. [Google Scholar]
- Zikidis, K. Early Warning Against Stealth Aircraft, Missiles and Unmanned Aerial Vehicles. In Surveillance in Action. Advanced Sciences and Technologies for Security Applications; Karampelas, P., Bourlai, T., Eds.; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-68532-8. [Google Scholar]
- Shoshany, M.; Svoray, T.; Svoray, T.; Curran, P.J.; Foody, G.M.; Perevolotsky, A. The relationship between ERS-2 SAR backscatter and soil moisture: Generalization from a humid to semi-arid transect. Int. J. Remote Sens. 2000, 21, 2337–2343. [Google Scholar] [CrossRef]
- Filgueiras, R.; Mantovani, E.C.; Althoff, D.; Fernandes Filho, E.I.; Cunha, F.F. da Crop NDVI Monitoring Based on Sentinel-1. Remote Sens. 2019, 11, 1441. [Google Scholar] [CrossRef] [Green Version]
- Dinevich, L. Improving the accuracy of selection of bird radar echoes against a background of atomized clouds and atmospheric inhomogeneities. Ring 2016, 37, 3–18. [Google Scholar] [CrossRef] [Green Version]
- NAWCWD Avionics Department. Electronic Warfare and Radar Systems. Engineering Handbook, 4th ed.; Naval Air Warfare Center: Point Mugu, CA, USA, 2013; ISBN 9781608077052. [Google Scholar]
- Fenn, A.J. Adaptive Antennas and Phased Arrays for Radar and Communications; Artech House: Norwood, MA, USA, 2008; ISBN 9781596932739. [Google Scholar]









| Study | Incidence Angle (°) | Satellite | Crop | Application |
|---|---|---|---|---|
| Van Tricht et al. (2018) [44] | 32–42 | Sentinel-1 | Many crops | Crop classification |
| Inoue et al. (2014) [45] | 25–35 | RADARSAT-2 | Paddy rice | Various biophysical variables |
| Veloso et al. (2017) [46] | 38–41 | Sentinel-1 | Wheat, rapeseed, maize, soybean, sunflower | Temporal behavior |
| Bousbih et al. (2017) [47] | 39–40 | Sentinel-1 | Cereals | Crop height and LAI |
| Nasirzadehdizaji et al. (2019) [48] | 39–40 | Sentinel-1 | Maize, sunflower, wheat | Crop height and canopy coverage |
| Navarro et al. (2016) [49] | 38.87–39.26 | Sentinel-1 | Maize, soybean, bean, pasture | Crop water requirements |
| Inglada et al. (2016) [50] | 38.89–39.05 | Sentinel-1 | Wheat, rapeseed, barley, corn, sunflower | Crop classification |
| Hosseini et al. (2018) [51] | 20.63–28.16 | RADARSAT-2 | Corn | Biomass |
| Phan et al. (2021) [52] | 42–44 | Sentinel-1 | Rice | Various biophysical variables |
| Molijn et al. (2019) [53] | 36.0–36.6 | Sentinel-1 | Sugarcane | Productivity mapping |
| Demarez et al. (2019) [54] | 30 | Sentinel-1 | Maize | Crop mapping |
| Srivastava et al. (2019) [55] | 31 | RISAT-1 | Wheat | Crop height |
| Srivastava et al. (2018) [56] | 32 | RISAT-1 | Paddy | LAI |
| Benabdelouahab et al. (2018) [57] | 23.3 | ERS-1 | Wheat | Irrigation supply detection |
| Han et al. (2019) [58] | 42.5 | Sentinel-1 | Wheat | Crop water content |
| Yadav et al. (2019) [59] | 40 | Sentinel-1 | Wheat | LAI |
| Chauhan et al. (2018) [60] | 38 | RISAT-1 | Wheat | Various biophysical variables |
| Harfenmeister et al. (2019) [61] | Constant. Undisclosed. | Sentinel-1 | Wheat, barley | Various biophysical variables |
| Song and Wang (2019) [62] | Constant. Undisclosed. | Sentinel-1 | Wheat | Crop classification and phenology monitoring |
| Nihar et al. (2019) [63] | Constant. Undisclosed. | Sentinel-1 | Cotton, maize | Crop classification |
| Vreugdenhil et al. (2018) [64] | Constant. Undisclosed. | Sentinel-1 | Corn, cereals, oilseed rape | Various biophysical variables |
| Experiment Area | Crop | Period * | # Crop Height Measurements | # LAI Measurements | Area Size (# Sentinel-1 Pixels) | Nearest Meteorological Station ET0 Data | Distance and Bearing to the Meteorological Station |
|---|---|---|---|---|---|---|---|
| Saad | Wheat | 1-Jan-2018 9-Apr-2018 | 8 | 6 | 260 | Dorot | 9.5 km NE |
| Yavne | Wheat | 18-Dec-2018 10-Apr-2019 | 7 | 7 | 550 | - | - |
| Tel Nof | Cotton | 6-Jun-2016 17-Sep-2016 | 7 | - | 1300 | Revadim | 5 km S |
| Negba | Cotton | 25-Jul-2017 11-Sep-2017 | - | - | 460 | Negba | 2.5 km SW |
| Gadash | Processing tomatoes | 9-May-2018 30-Jul-2018 | 8 | - | 250 | - | - |
| Gadash | Processing tomatoes | 3-May-2019 24-Jul-2019 | 7 | 6 | 500 | Gadash | 250 m SE |
| Gadot | Processing tomatoes | 25-Apr-2019 14-Aug-2019 | 11 | 11 | 300 | Gadot | 1.5 km SW |
| Model | # Images | R2 | RMSE | R2 Improvement | RMSE Improvement (%) |
|---|---|---|---|---|---|
| Wheat height | 38 | 0.8566 | 6 cm | 0.0738 * | 2 cm, (25%) |
| Wheat LAI | 34 | 0.7194 | 0.6 | 0.1639 * | 0.2, (25%) |
| Wheat Kc | 11 | 0.6722 | 0.073 | 0.1601 | 0.016, (18%) |
| Tomato Kc σ0-based | 59 | 0.8549 | 0.0871 | 0.0172 | 0.005, (5%) * |
| Tomato LAI σ0-based | 50 | 0.7881 | 1.0 | 0.1001 | 1.1, (52%) * |
| Tomato height σ0-based | 94 | 0.4201 | 11 cm | 0.0446 | 1 cm, (8%) |
| Tomato Kc β0-based | 59 | 0.871 | 0.0821 | 0.1143 * | 0.0307, (27%) |
| Tomato LAI β0-based | 50 | 0.8341 | 0.9 | 0.352 * | 0.7, (44%) |
| Tomato height β0-based | 94 | 0.8107 | 9 cm | 0.3442 * | 2 cm, (18%) |
| Cotton height σ0-based | 11 | 0.8721 | 5 cm | 0.367 * | 5 cm, (50%) |
| Cotton Kc σ0-based | 12 | 0.3742 | 0.0511 | 0.3543 * | 0.0128, (21%) * |
| Cotton height β0-based | 11 | 0.9467 | 8 cm | 0.668 * | 5 cm, (38%) |
| Cotton Kc β0-based | 12 | 0.707 | 0.1293 | 0.6353 | 0.0379, (23%) * |
| Height | LAI | Kc | |
|---|---|---|---|
| Wheat | |||
| Overpass | Asc | Asc | Asc |
| # SAR images used | 26 | 25 | 6 |
| Local incidence angle (°) | 35.3–36.6 | 35.3–36.6 | 47.7 |
| R2 | 0.4248 | 0.1389 | 0.2912 |
| R2 difference | −0.2626 | −0.5805 | −0.381 |
| RMSE | 13 cm | 1.6 | 0.102 |
| RMSE difference | −4 cm | −1.0 | −0.029 |
| (%) | (−44) | (−167) | (−40) |
| Processing tomatoes | |||
| Overpass | Asc | Asc | Asc |
| # SAR images used | 25 | 31 | 27 |
| Local incidence angle (°) | 42.0–43.1 | 42.0–43.1 | 42.0–43.1 |
| R2 | 0.1584 | 0.3425 | 0.5635 |
| R2 difference | −0.6523 | −0.4916 | −0.3075 |
| RMSE | 14 cm | 1.9 | 0.2488 |
| RMSE difference | −5 cm | −1.0 | −0.1667 |
| (%) | (−56) | (−111) | (−203) |
| Cotton | |||
| Overpass | Asc | ||
| # SAR images used | 5 | ||
| Local incidence angle (°) | 35.9 | ||
| R2 | 0.3297 | ||
| R2 difference | −0.5424 | ||
| RMSE | 12 cm | ||
| RMSE difference | −7 cm | ||
| (%) | (−140) | ||
| Model | Satellite | Crop | Incidence Angle (°) | R2 | Accuracy (RMSE) |
|---|---|---|---|---|---|
| Wheat (this study) | Sentinel-1 | Wheat | 34.6–45.8 | 0.8566 | 6 cm |
| Processing tomatoes σ0-based (this study) | Sentinel-1 | Tomato | 30.8–43.1 | 0.4201 | 11 cm |
| Processing tomatoes β0-based (this study) | Sentinel-1 | Tomato | 30.8–43.1 | 0.8107 | 9 cm |
| Bousbih et al. (2017) [47] | Sentinel-1 | Cereals | 39–40 | 0.54 | Not given |
| Nasirzadehdizaji et al. (2019) [48] | Sentinel-1 | Wheat | 39–40 | 0.67 (<53 cm) 0.07 (≥53 cm) | Not given |
| Srivastava (2019) [55] | RISAT-1 | Wheat | 31 | 0.37 | 18 cm |
| Vreugdenhil et al. (2018) [64] | Sentinel-1 | Cereals | Constant | 0.68 | Not given |
| Harfenmeister et al. (2019) [61] | Sentinel-1 | Wheat | Constant | 0.41 | Not given |
| Model | Satellite | Crop | Incidence Angle (°) | R2 | Accuracy (RMSE) |
|---|---|---|---|---|---|
| Wheat (this study) | Sentinel-1 | Wheat | 34.6–45.8 | 0.7225 | 0.6 |
| Processing tomatoes σ0-based (this study) | Sentinel-1 | Tomato | 30.8–43.0 | 0.7881 | 1.0 |
| Processing tomatoes β0-based (this study) | Sentinel-1 | Tomato | 30.8–43.0 | 0.8341 | 0.9 |
| Chauhan et al. (2018) [60] | RISAT-1 | Wheat | 38 | 0.76 | 0.4 |
| Bousbih et al. (2017) [47] | Sentinel-1 | Cereals | 39–40 | 0.25 | Not given |
| Vreugdenhil et al. (2018) [64] | Sentinel-1 | Cereals | Constant | 0.30 | Not given |
| Harfenmeister et al. (2019) [61] | Sentinel-1 | Wheat | Constant | 0.48 | Not given |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaplan, G.; Fine, L.; Lukyanov, V.; Manivasagam, V.S.; Tanny, J.; Rozenstein, O. Normalizing the Local Incidence Angle in Sentinel-1 Imagery to Improve Leaf Area Index, Vegetation Height, and Crop Coefficient Estimations. Land 2021, 10, 680. https://doi.org/10.3390/land10070680
Kaplan G, Fine L, Lukyanov V, Manivasagam VS, Tanny J, Rozenstein O. Normalizing the Local Incidence Angle in Sentinel-1 Imagery to Improve Leaf Area Index, Vegetation Height, and Crop Coefficient Estimations. Land. 2021; 10(7):680. https://doi.org/10.3390/land10070680
Chicago/Turabian StyleKaplan, Gregoriy, Lior Fine, Victor Lukyanov, V. S. Manivasagam, Josef Tanny, and Offer Rozenstein. 2021. "Normalizing the Local Incidence Angle in Sentinel-1 Imagery to Improve Leaf Area Index, Vegetation Height, and Crop Coefficient Estimations" Land 10, no. 7: 680. https://doi.org/10.3390/land10070680
APA StyleKaplan, G., Fine, L., Lukyanov, V., Manivasagam, V. S., Tanny, J., & Rozenstein, O. (2021). Normalizing the Local Incidence Angle in Sentinel-1 Imagery to Improve Leaf Area Index, Vegetation Height, and Crop Coefficient Estimations. Land, 10(7), 680. https://doi.org/10.3390/land10070680








