Modeling of the 1783 Tsunami Event in Scilla Generated by Landslide
Abstract
:1. Introduction
2. Modeling Landslide and Tsunami
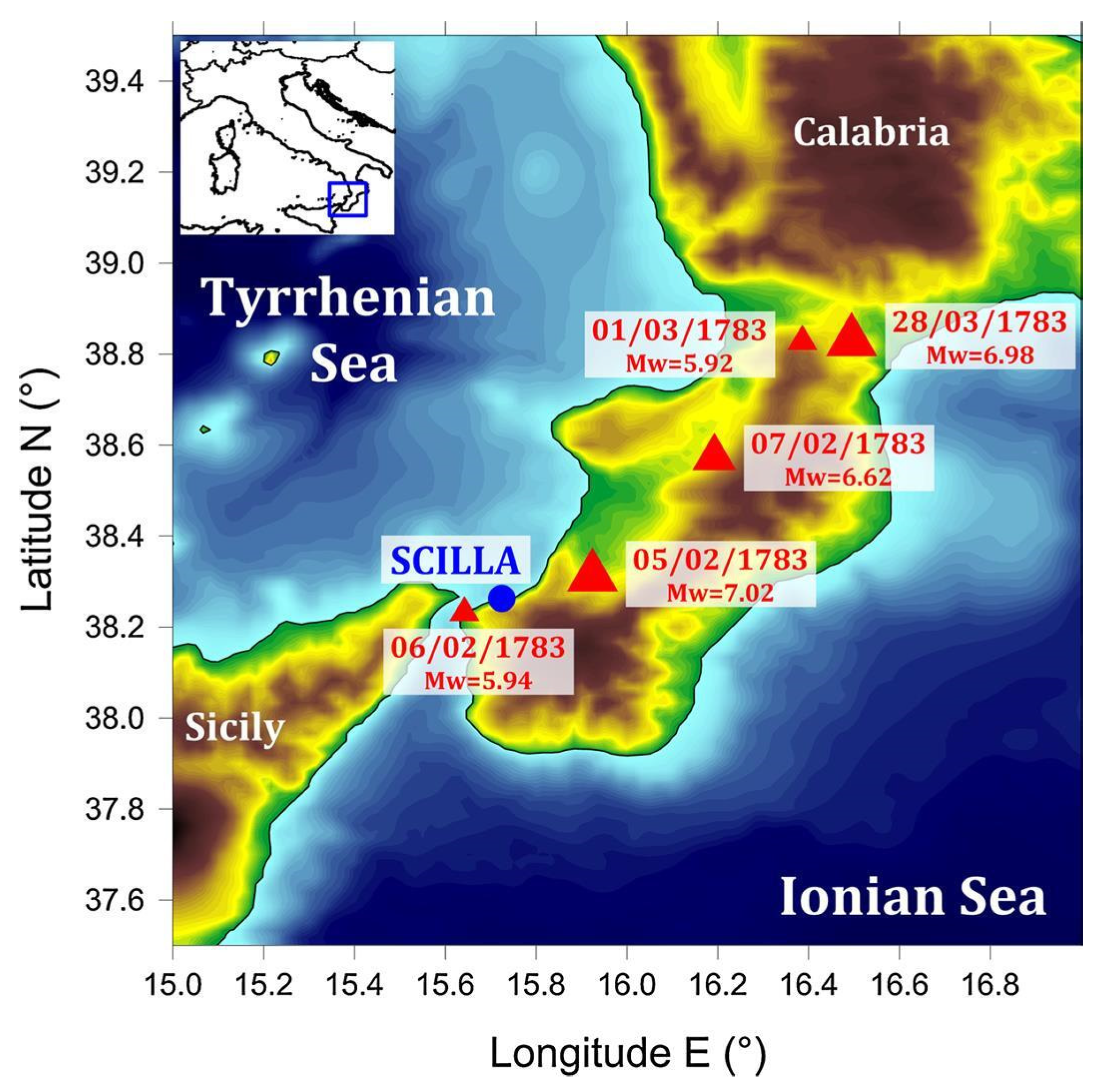
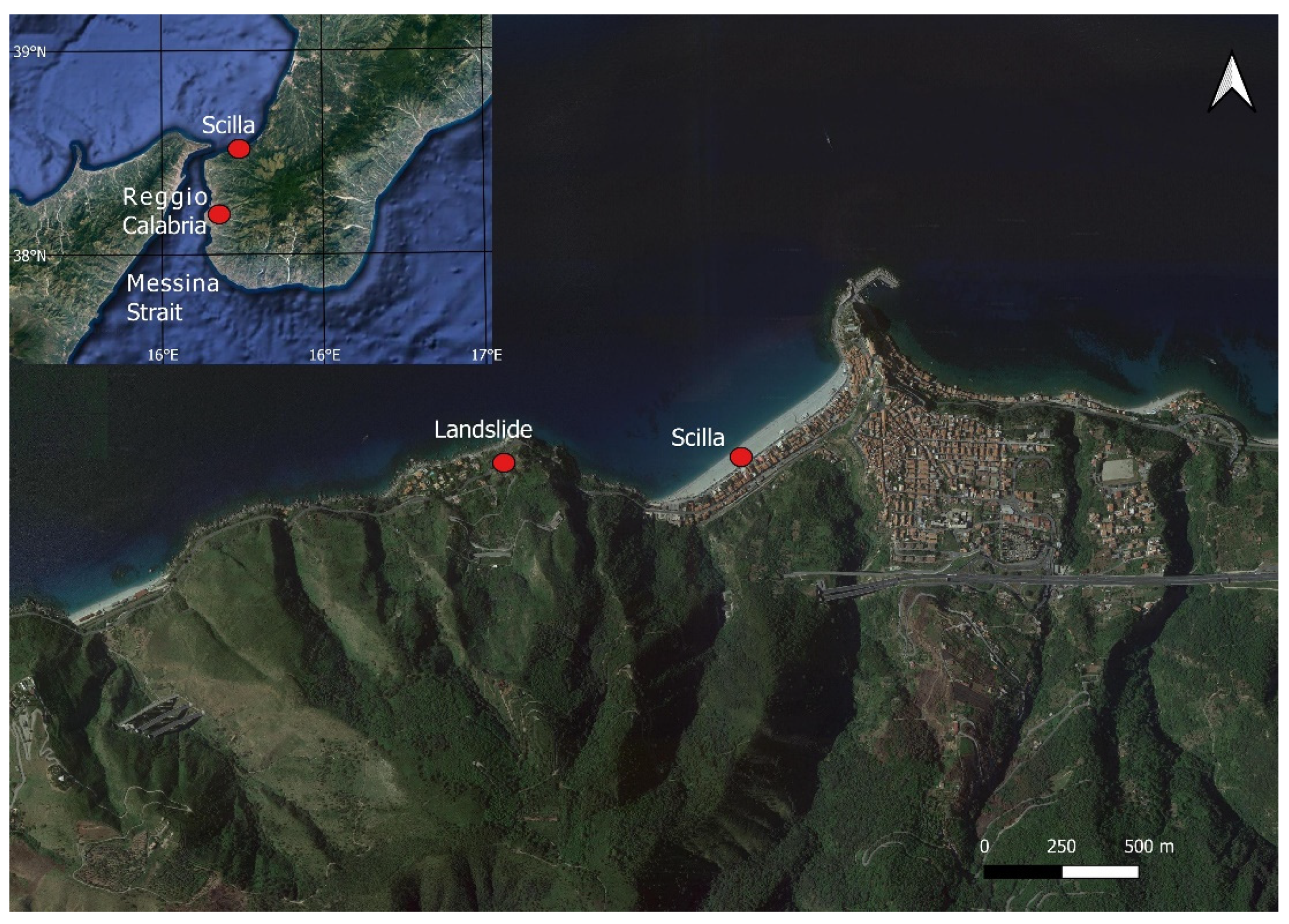
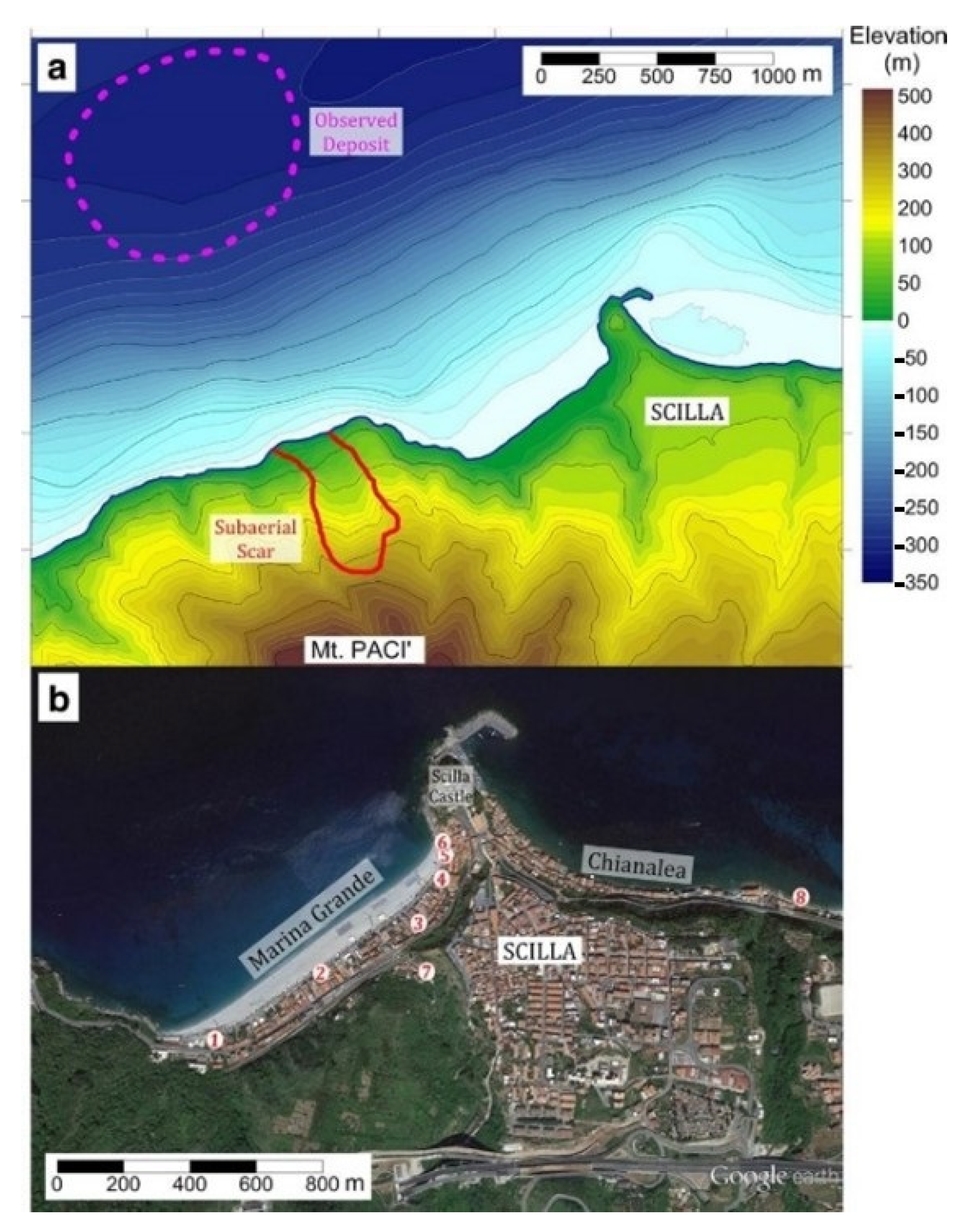
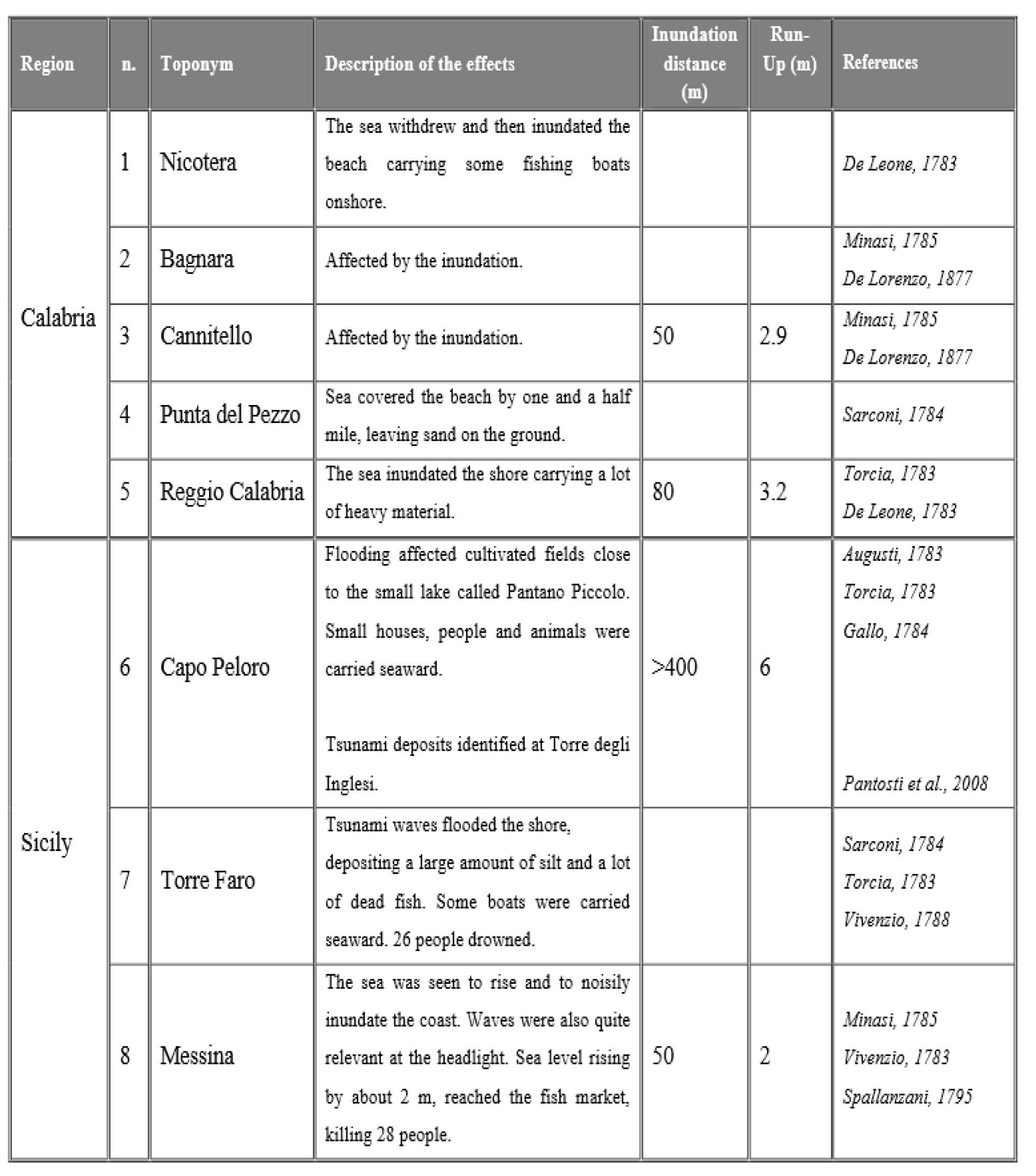
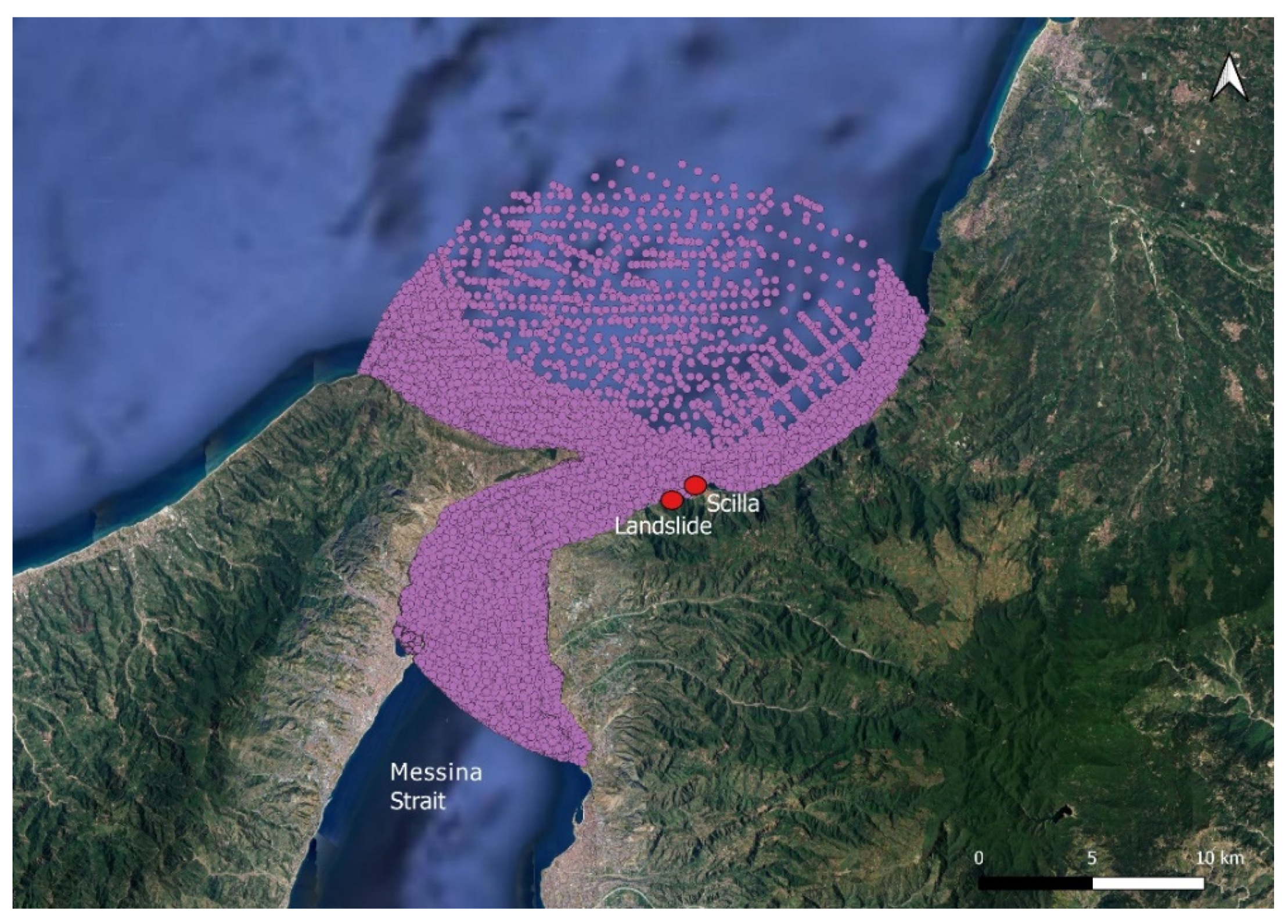
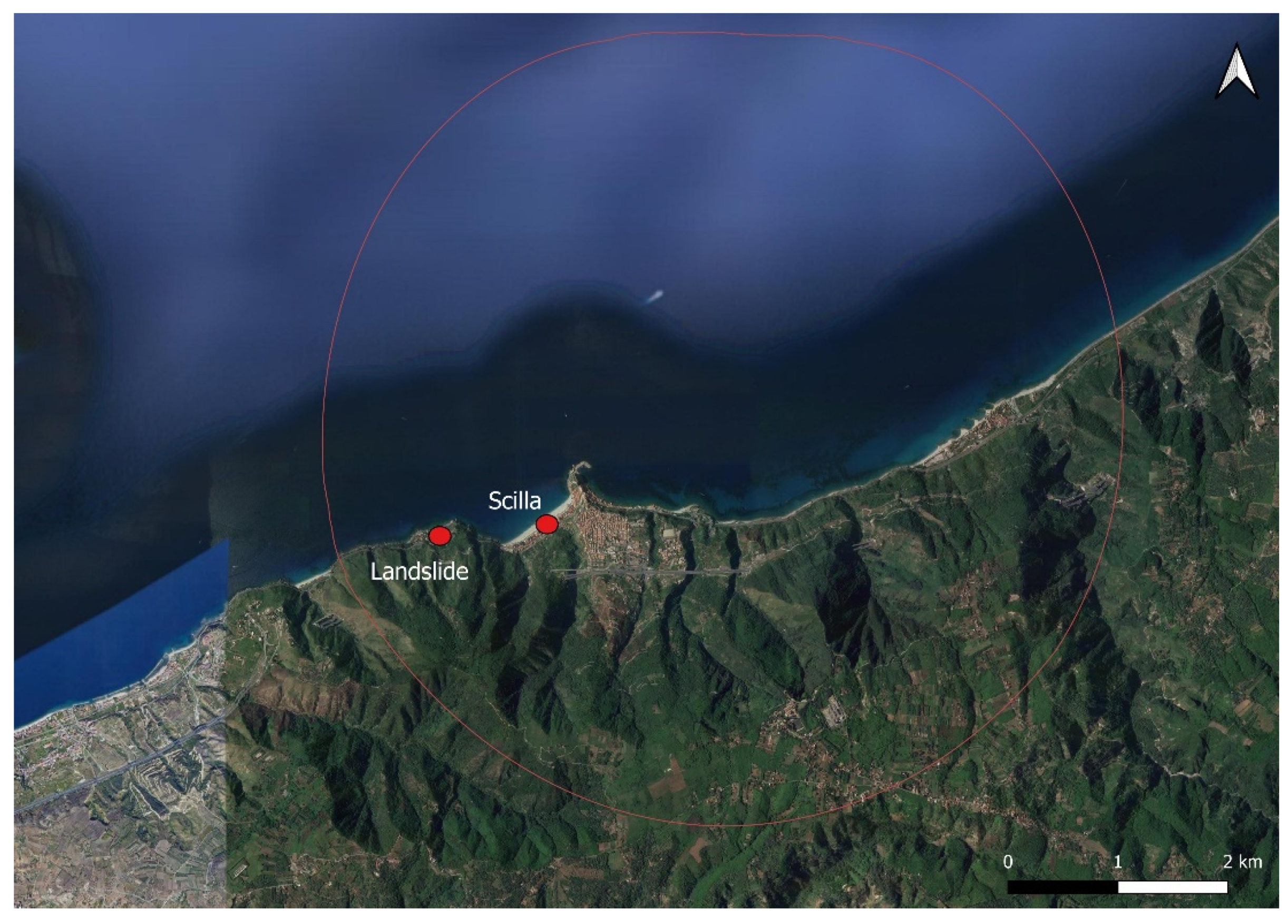
2.1. The Scilla 1783 Case
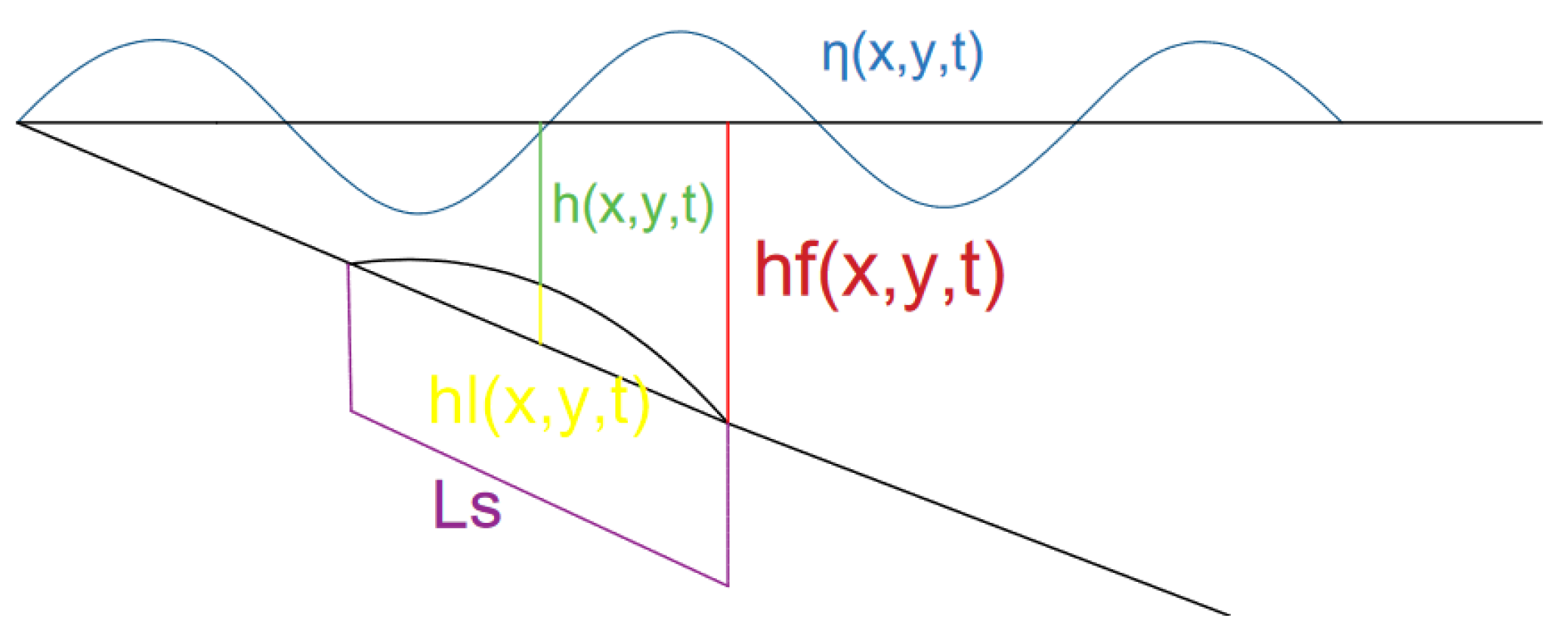
2.2. Depth Integrated Wave Model
2.3. Methodology
- Acquisition of geographic data from IGM (Military Geographic Institute). The IGM (Military Geographic Institute) provided the bathymetry as 80 vector files with unstructured data. The original reference system was WGS 84/UTM zone 33N, so each file was first converted to a shapefile using QGIS while maintaining the same georeferencing.
- Construction of the geographical domain by using QGIS;
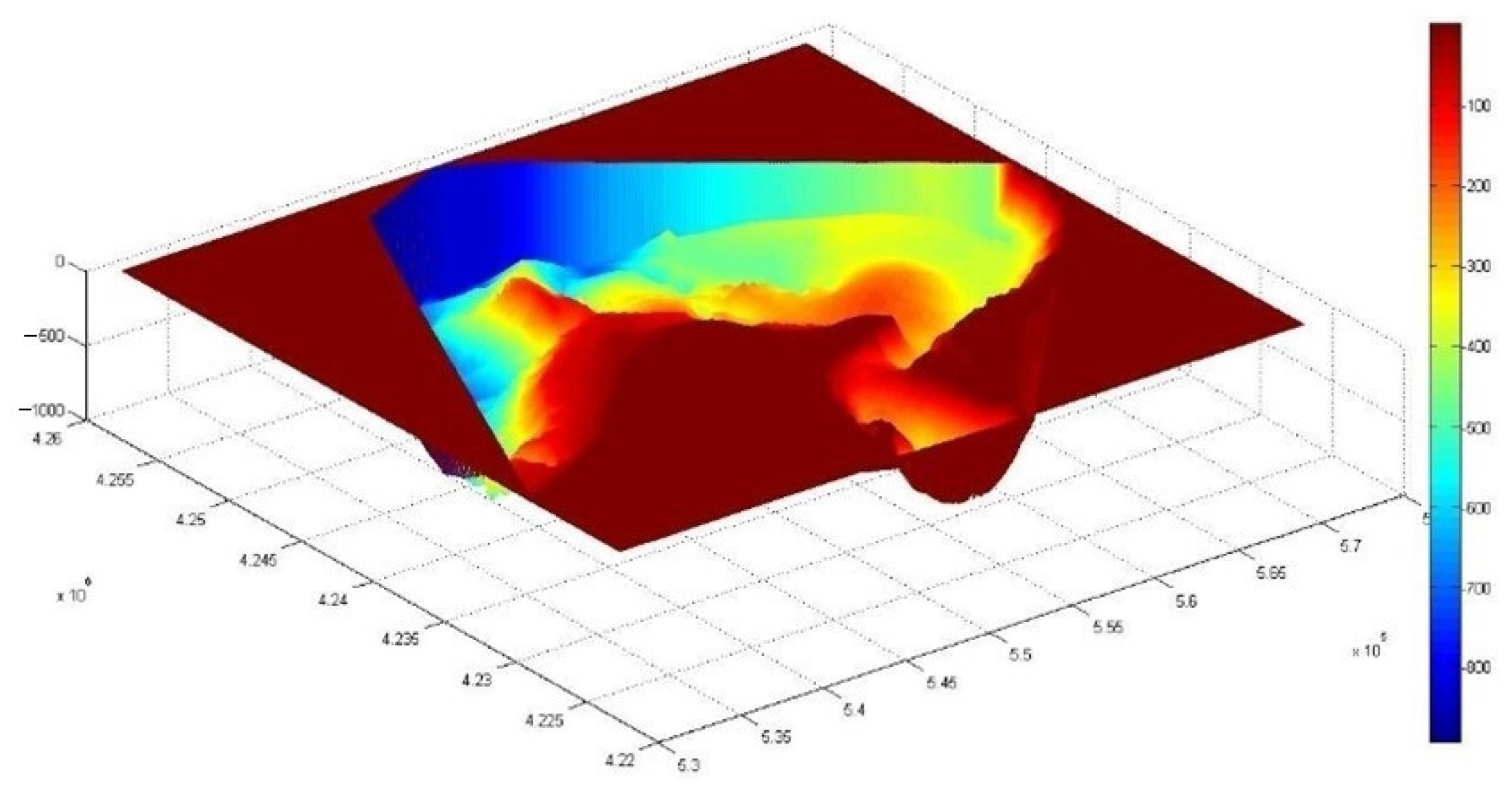
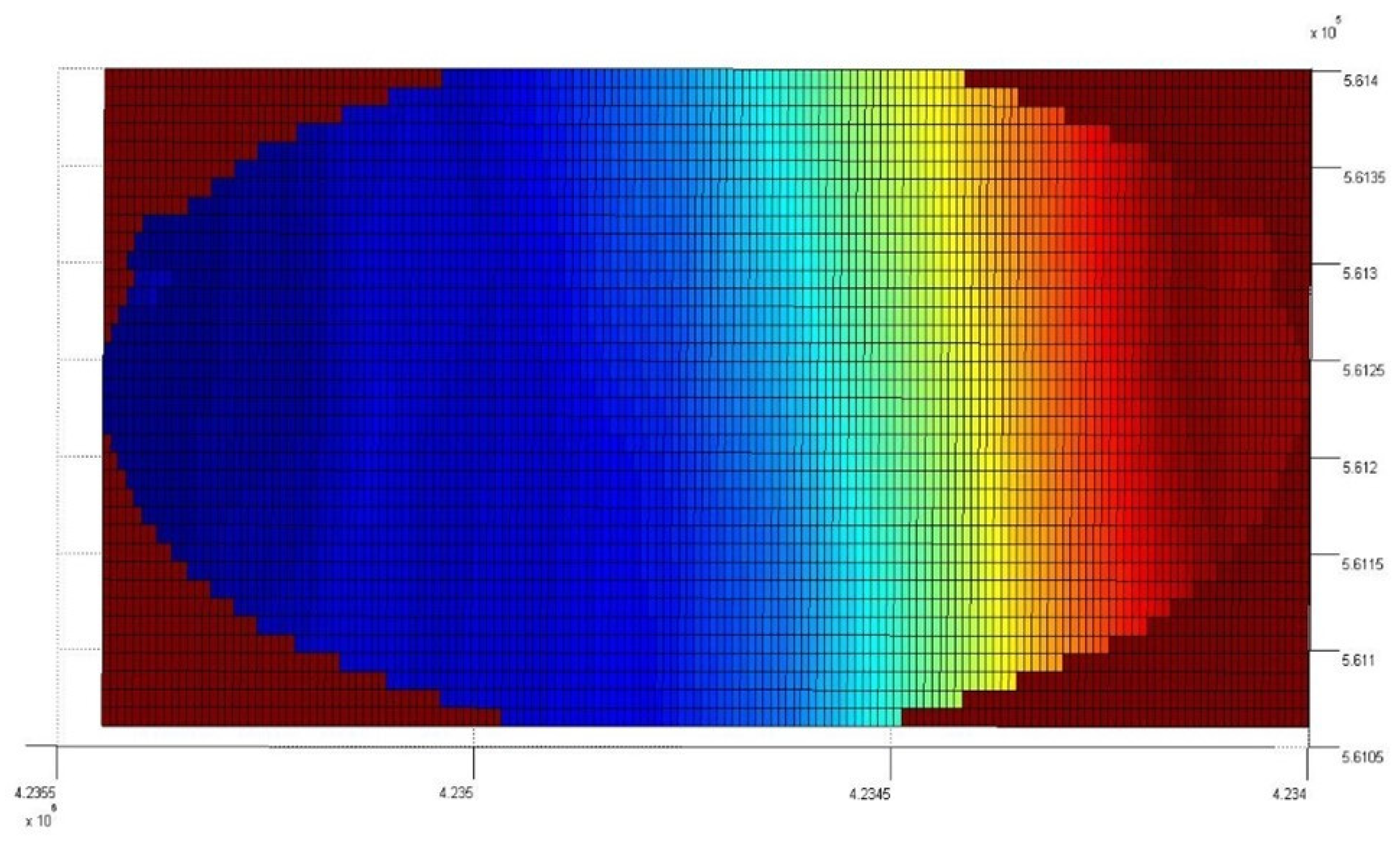
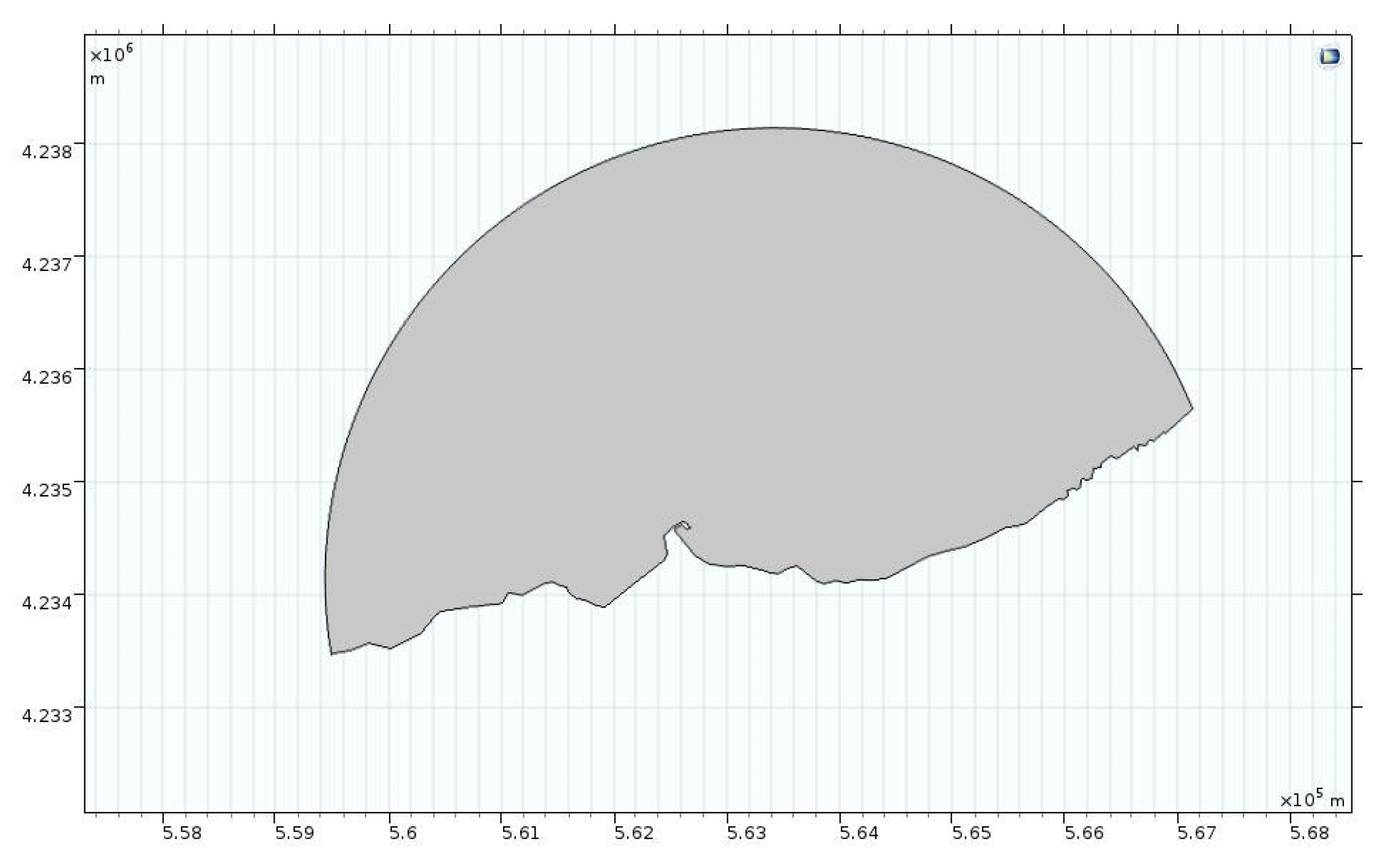
- Creation of a single file with all the georeferenced bathymetric data available and importation into MATLAB to be processed. A grid was created to interpolate the data, which were not structured, with Δx = Δy = 10 m, where Δx and Δy are the spatial nodes into which the grid is divided, the interpolation concerned the three coordinates x, y and z;
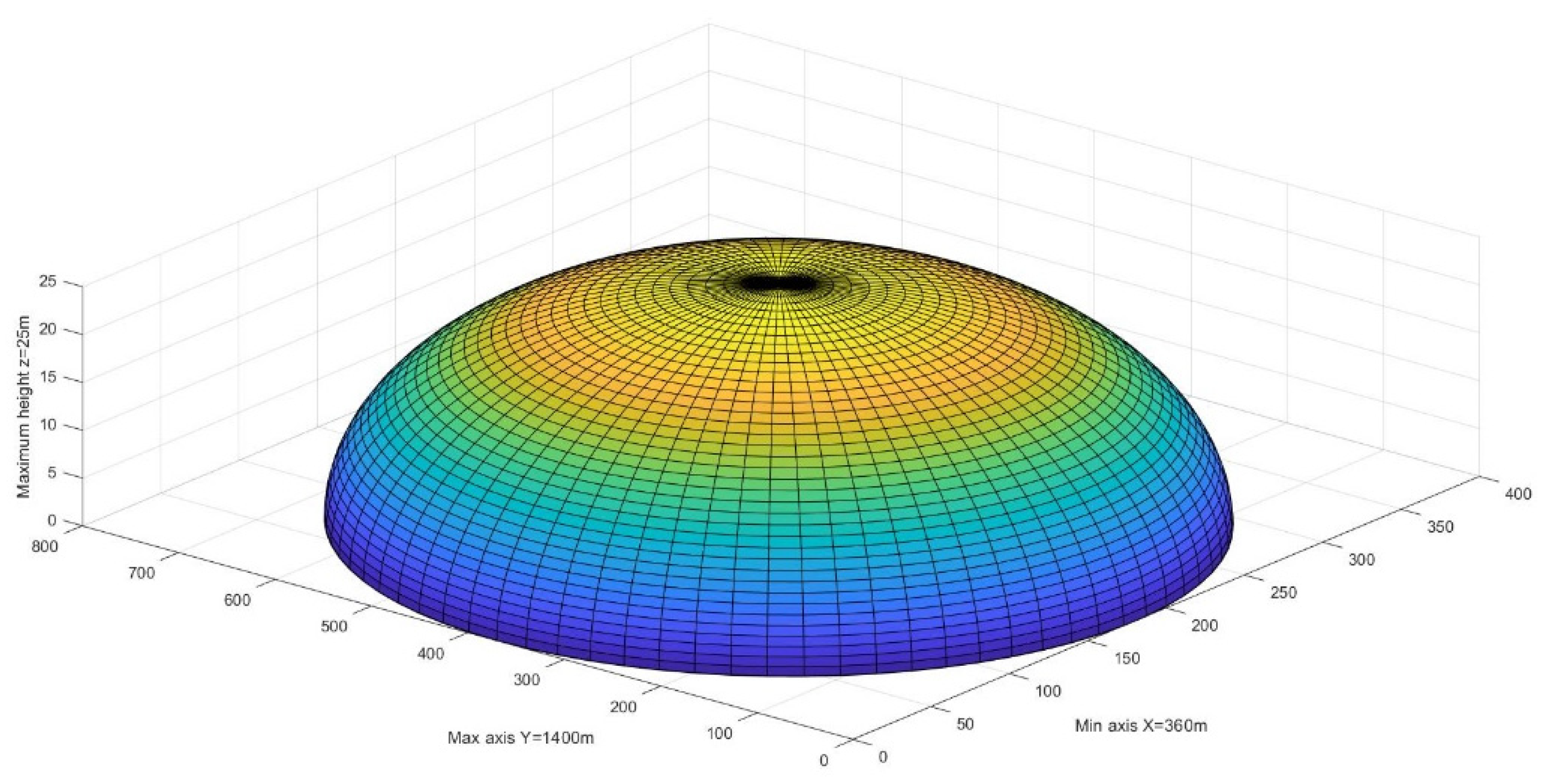
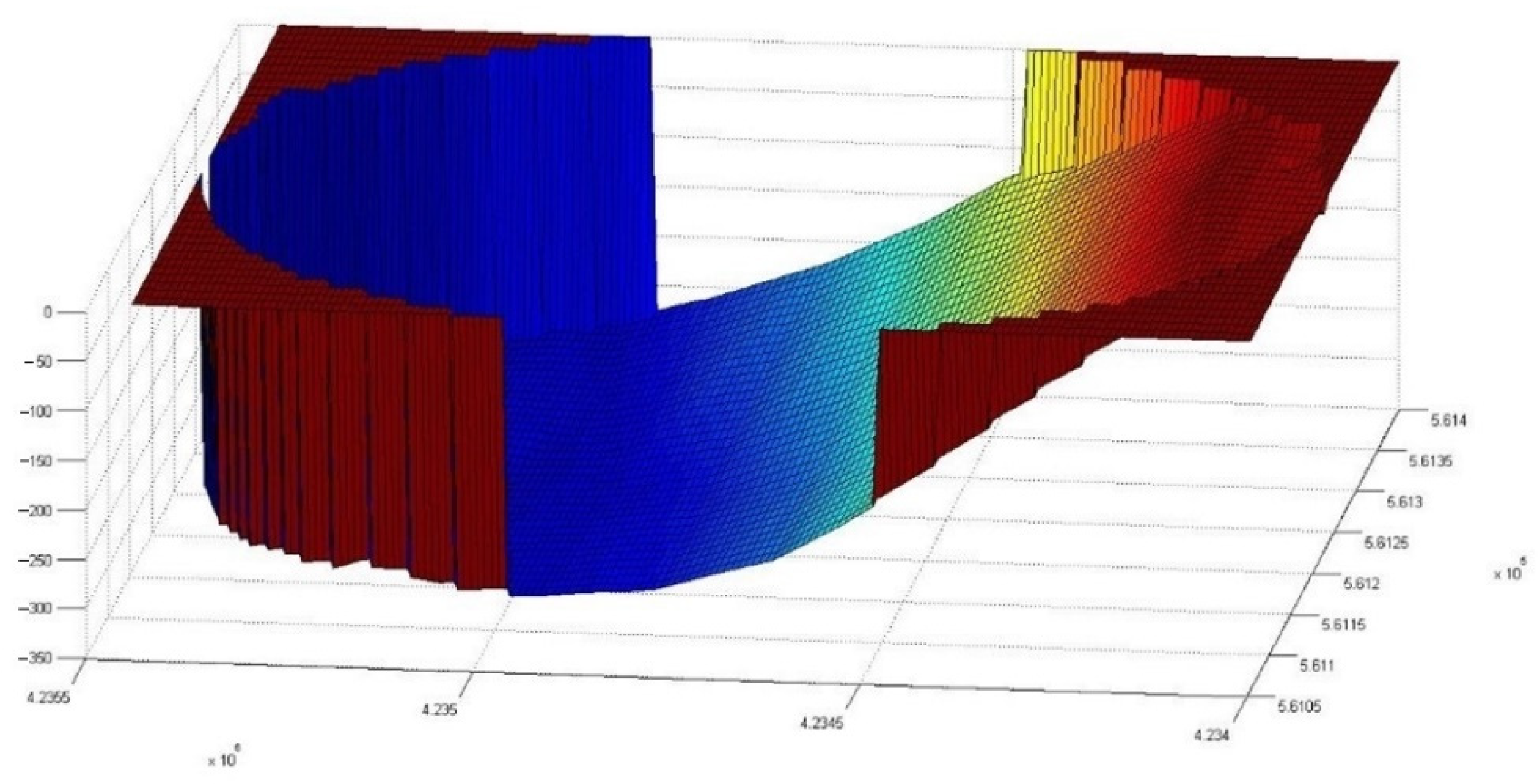
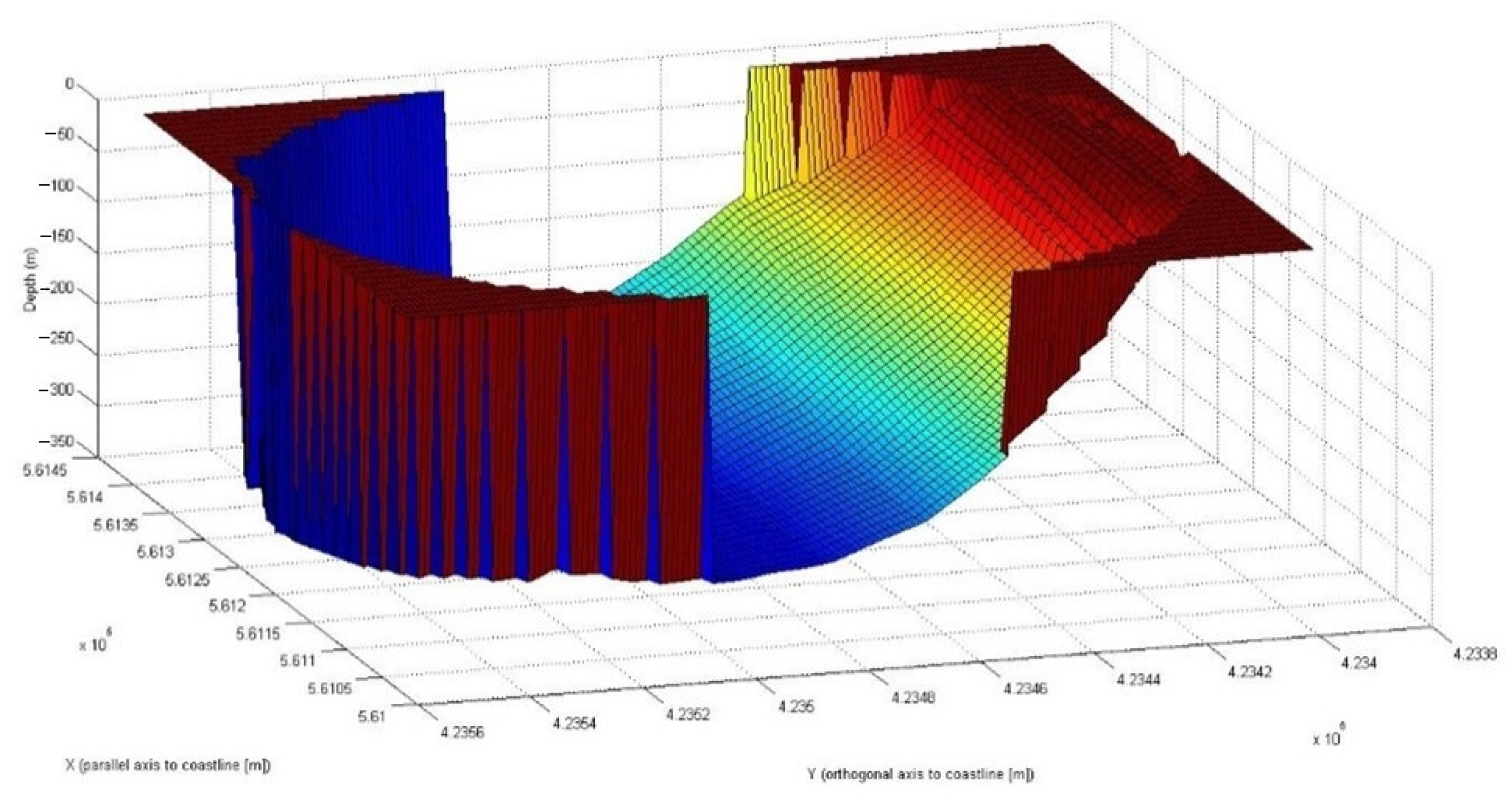
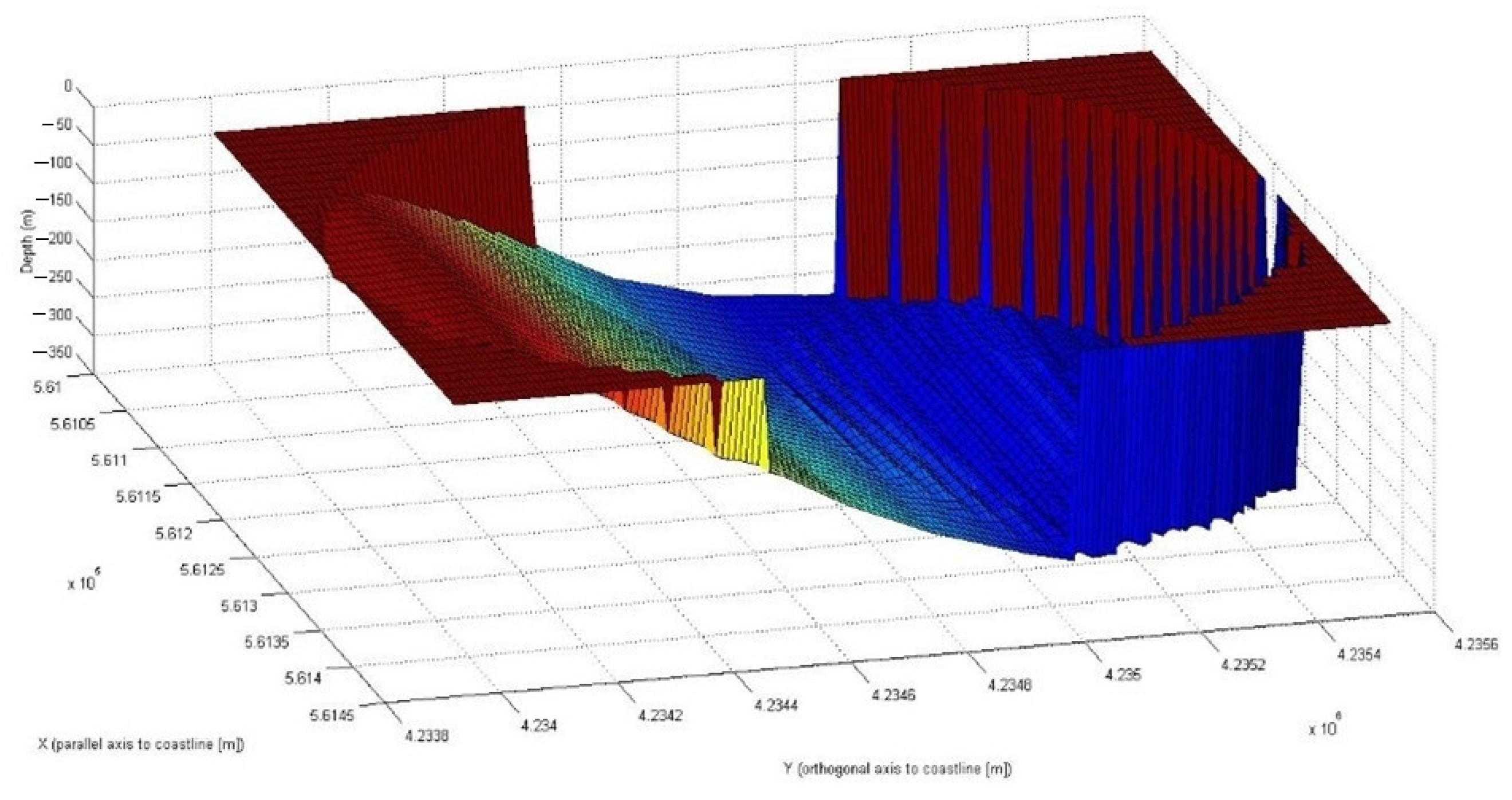
- Extrapolation of a subdomain, the one corresponding to the passage of the landslide, to evaluate its displacement over time. The domain concerned had dimensions of X = 360 m axis parallel to the coast and Y = 1400 m approximately orthogonal axis to the coast and reached a depth of −300 m in which the landslide was deposited in its final position;
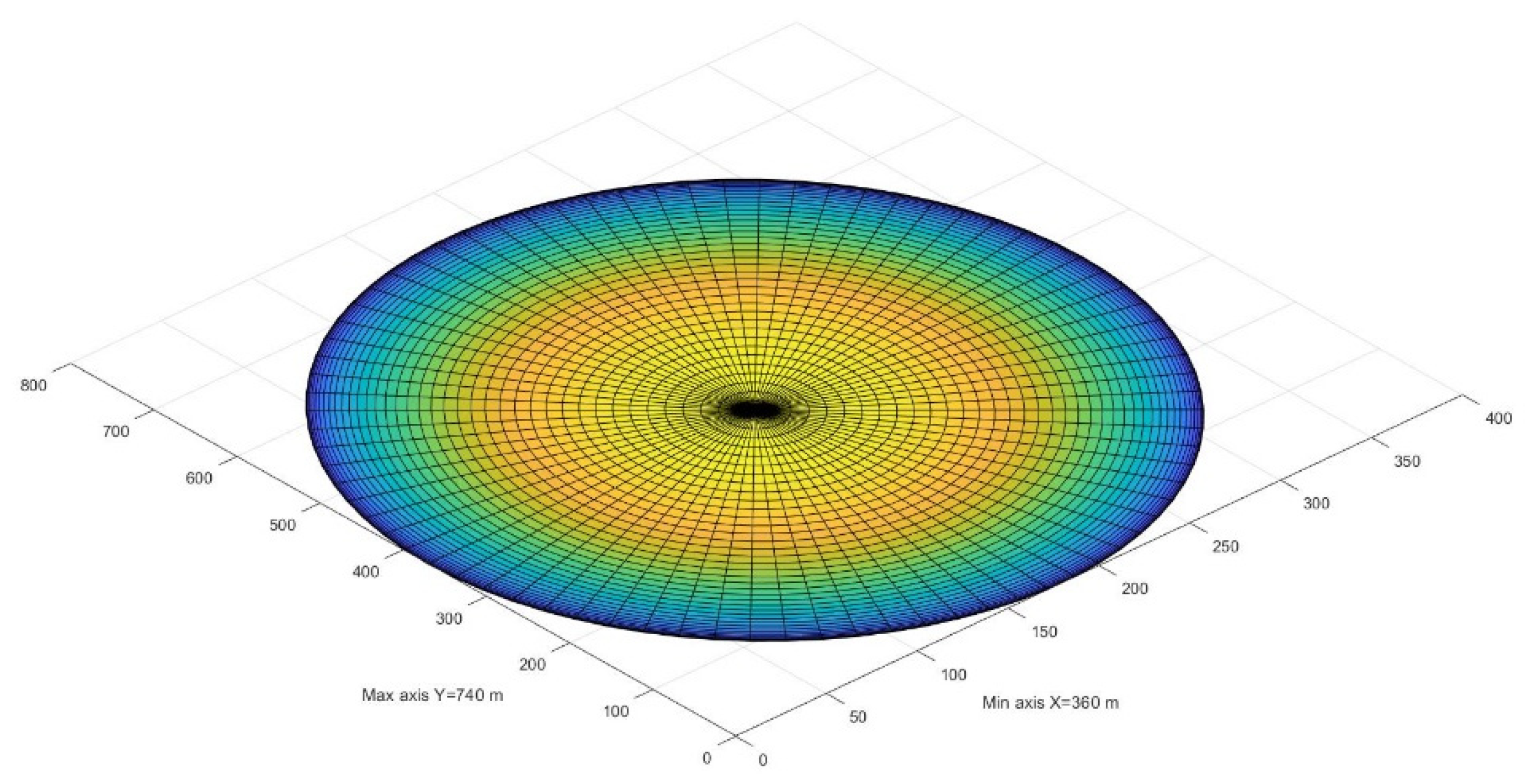
- The bathymetric subdomain extracted, corresponding to the passage of the landslide, is reworked in MATLAB in order to create an ellipsoidal grid;
- Estimation of the simulation of the displacement of the landslide at different time points;
- Identification of the geographic domain to be included in COMSOL, where the characteristics of the model were then assigned;
- Creation in MATLAB of an array that represents the position of the landslide in the spatial dimensions x and y at various time points. The result was, therefore, a set of matrices that represent the spatial position, and in the third dimension, there was spatial variation over time.
- Insertion of boundary conditions and COMSOL mesh;
- Wave propagation simulation in COMSOL software and extrapolation of the results.
2.4. Geographic Data and Domain
2.5. Landslide Modeling
2.6. Fully Dispersion Model Derivation
2.7. Numerical Simulation
3. Results
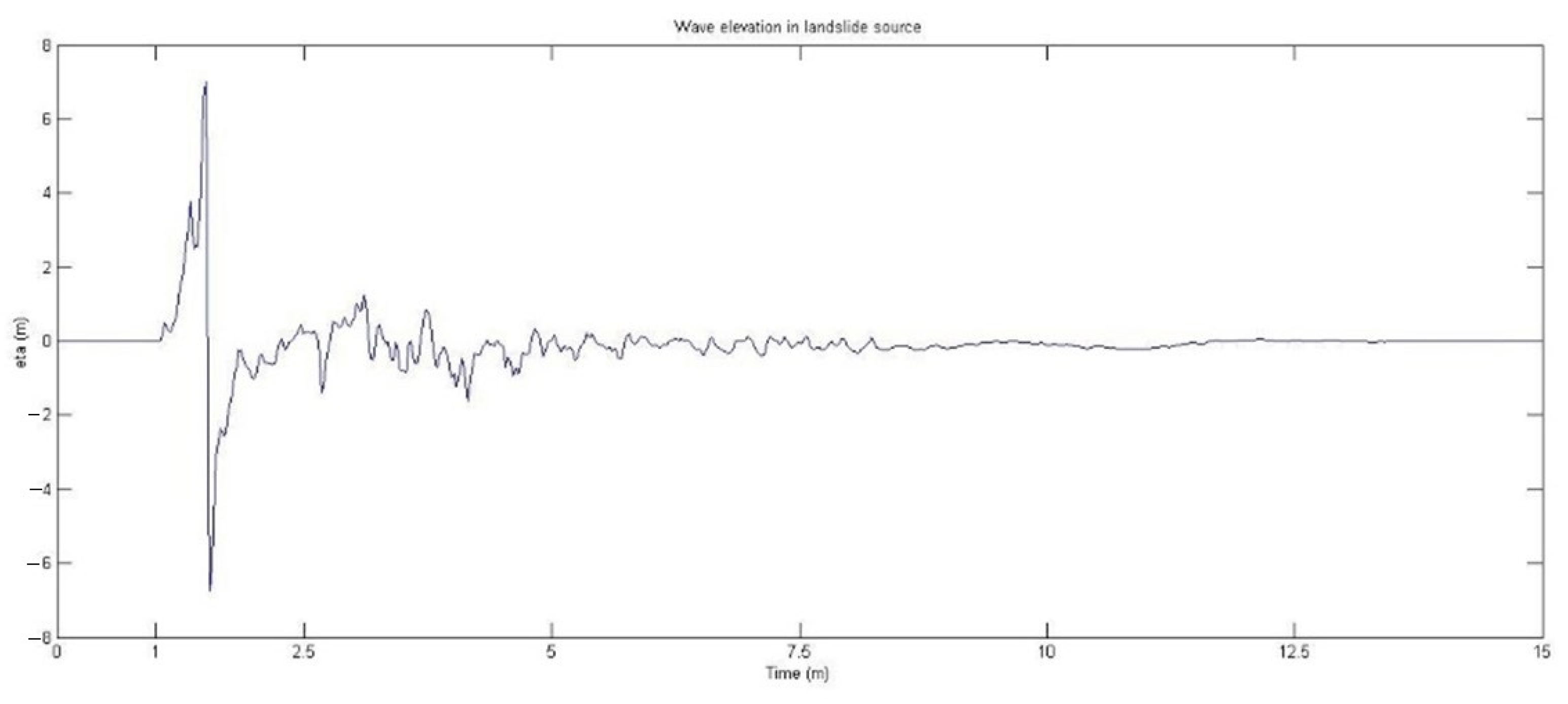
3.1. Landslide Movement
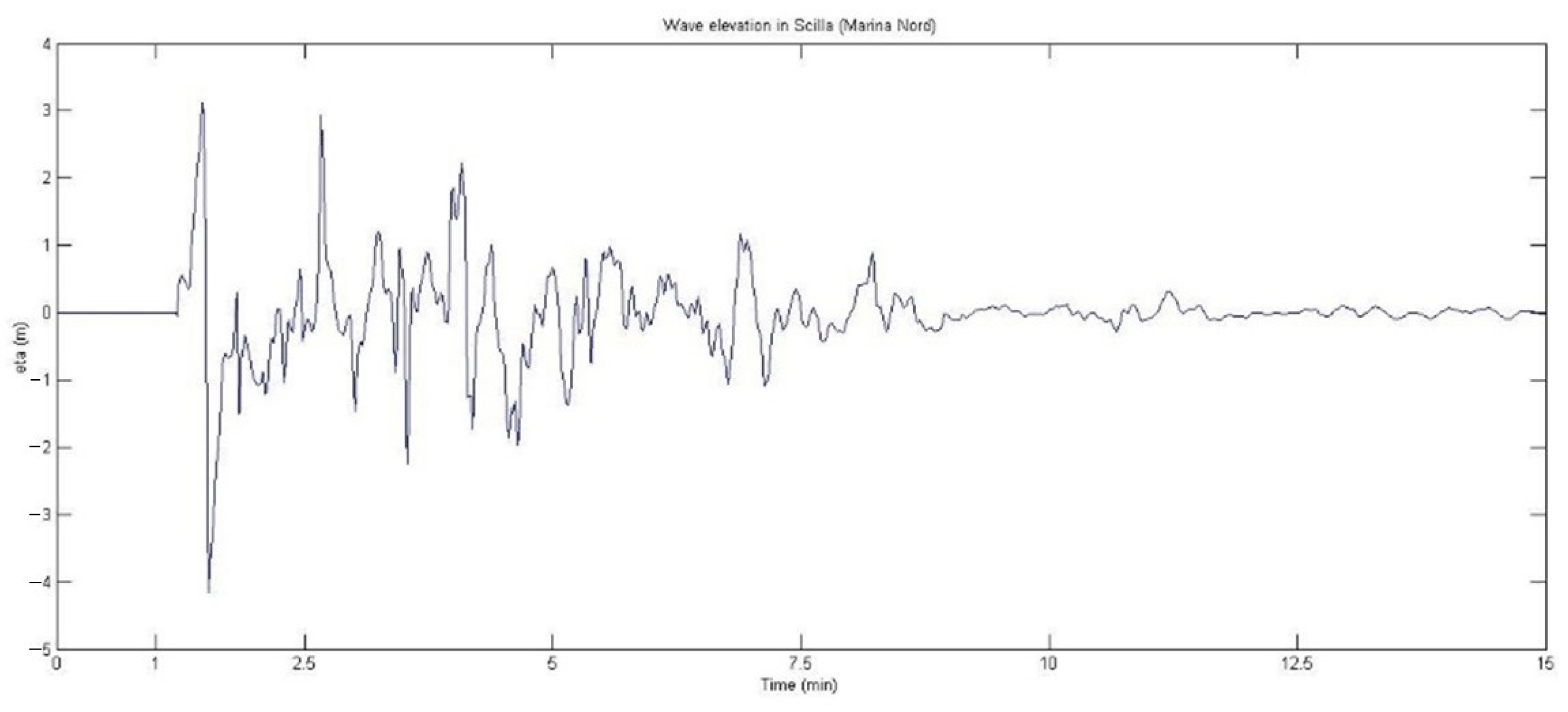
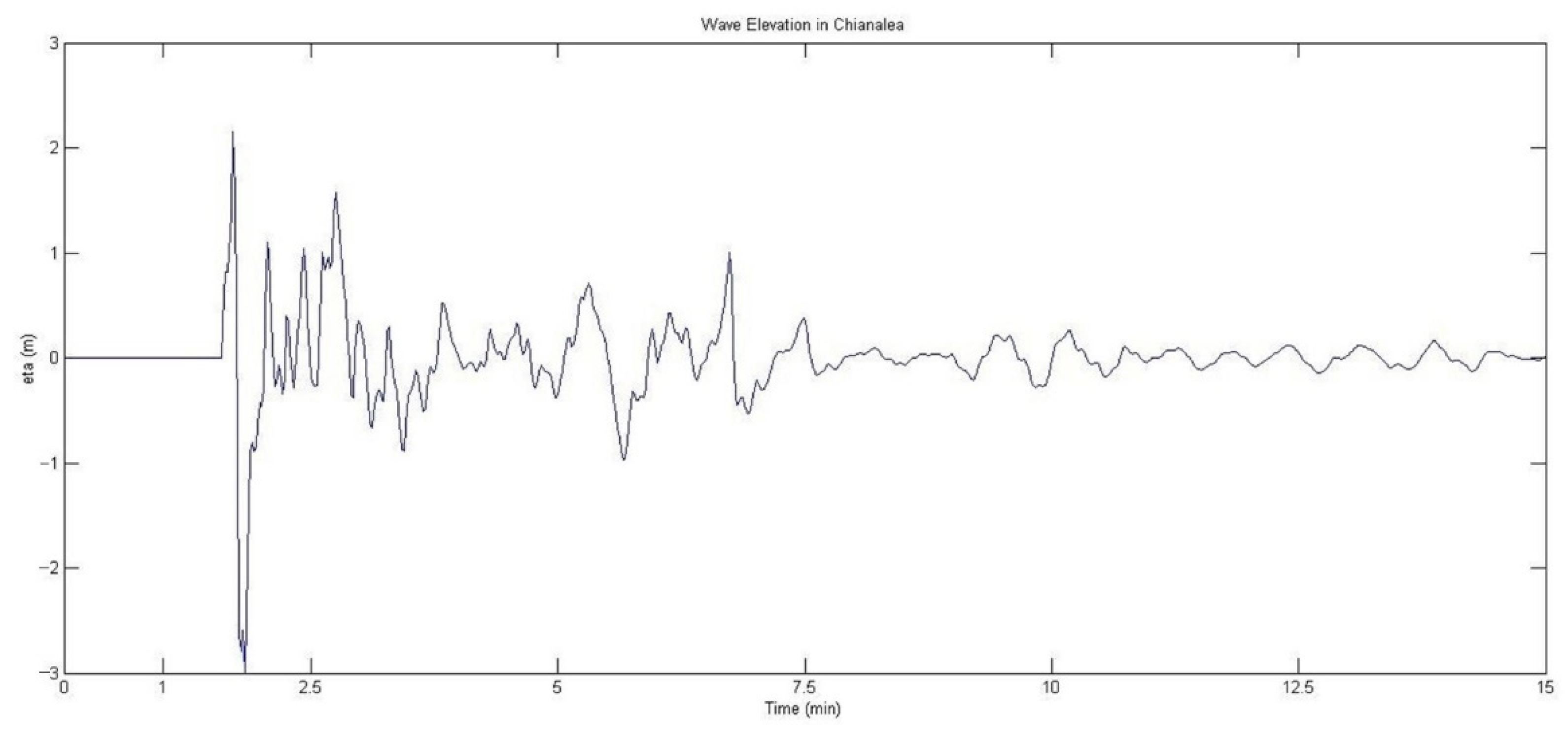
3.2. Wave Propagation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Grilli, S.T.; Vogelmann, S.; Watts, P. Development of a 3D numerical wave tank for modeling tsunami generation by underwater landslides. Eng. Anal. Bound. Elem. 2002, 26, 301–313. [Google Scholar] [CrossRef]
- Grilli, S.T.; Watts, P. Modeling of waves generated by a moving submerged body. Applications to underwater landslides. Eng. Anal. Bound. Elem. 1999, 23, 645–656. [Google Scholar] [CrossRef]
- Tinti, S.; Maramai, A.; Graziani, L. The new catalogue of Italian tsunamis. Nat. Hazards 2004, 33, 439–465. [Google Scholar] [CrossRef]
- Schambach, L.; Grilli, S.T.; Tappin, D.R.; Gangemi, M.D.; Barbaro, G. New simulations and understanding of the 1908 Messina tsunami for a dual seismic and deep submarine mass failure source. Mar. Geol. 2020, 421, 106093. [Google Scholar] [CrossRef]
- Schambach, L.; Grilli, S.T.; Tappin, D.R.; Gangemi, M.D.; Barbaro, G. Response to: Comment on “New simulations and understanding of the 1908 Messina tsunami for a dual seismic and deep submarine mass failure source”. Mar. Geol. 2021, 442, 106636. [Google Scholar] [CrossRef]
- Minasi, G. Continuazione ed Appendice Sopra I Tremuoti Descritti Nella Relazione Colla Data di Scilla de 30 Settembre 1783, con Altro che Accadde in Progresso; Di Stefano G.: Messina, Italy, 1785. (In Italian) [Google Scholar]
- Sarconi, M. Istoria de’ Fenomeni del Tremuoto Avvenuto nelle Calabrie e nel Valdemone Nell’anno 1783; Reale Accademia delle Scienze e delle Belle Lettere di Napoli: Napoli, Italy, 1784. (In Italian) [Google Scholar]
- Vivenzio, G. Historia dei Tremuoti Avvenuti Nella Provincia di Calabria Ulteriore e nella citta ‘di Messina Nell’anno 1783; Stamperia Regale: Napoli, Italy, 1788. (In Italian) [Google Scholar]
- Hamilton, W. Relazione Dell’ultimo Terremoto Delle Calabrie e della Sicilia; Stamperia della Rovere: Firenze, Italy, 1783. (In Italian) [Google Scholar]
- De Lorenzo, A. Memorie da Servire alla Storia Sacra e Civile di Reggio e delle Calabrie; Stamperia Siclari: Reggio Calabria, Italy, 1877; Volume I. [Google Scholar]
- Zaniboni, F.; Armigliato, A.; Tinti, S. A numerical investigation of the 1783 landslide induced catastrophic tsunami in Scilla, Italy. Nat. Hazards 2016, 84, 455–470. [Google Scholar] [CrossRef]
- Tinti, S.; Tonini, R. The UBO-TSUFD tsunami inundation model: Validation and application to a tsunami case study focused on the city of Catania, Italy. Nat. Hazards Earth Syst. Sci. 2013, 13, 1795–1816. [Google Scholar] [CrossRef] [Green Version]
- Zaniboni, F.; Pagnoni, G.; Gallotti, G.; Paparo, M.A.; Armigliato, A.; Tinti, S. Assessment of the 1783 Scilla landslide-tsunami effects on Calabria and Sicily coasts through numerical modeling. Nat. Hazards Earth Syst. Sci. 2019, 19, 1585–1600. [Google Scholar] [CrossRef] [Green Version]
- Bellotti, G.; Cecioni, C.; De Girolamo, P. Simulation of small-amplitude frequency-dispersive transient waves by means of the mild-slope equation. Coast. Eng. 2008, 55, 447–458. [Google Scholar] [CrossRef]
- Bellotti, G.; Di Risio, M.; De Girolamo, P. Feasibility of Tsunami Early Warning Systems for small volcanic islands. Nat. Hazards Earth Syst. Sci. 2009, 9, 1911–1919. [Google Scholar] [CrossRef] [Green Version]
- Bellotti, G.; Beltrami, G.M.; De Girolamo, P. Internal generation of waves in 2D fully-elliptic mild-slope equation FEM models. Coast. Eng. 2003, 49, 71–81. [Google Scholar] [CrossRef]
- Barbaro, G.; Petrucci, O.; Canale, C.; Foti, G.; Mancuso, P.; Puntorieri, P. Contemporaneity of floods and storms. A case study of Metropolitan Area of Reggio Calabria in Southern Italy. In Proceedings of the 3rd International Symposium New Metropolitan Perspectives Smart Innovation, Systems and Technologies, Reggio Calabria, Italy, 22–25 May 2020; Volume 101, pp. 614–620. [Google Scholar] [CrossRef]
- Barbaro, G.; Foti, G.; Nucera, A.; Barillà, G.C.; Canale, C.; Puntorieri, P.; Minniti, F. Risk mapping of coastal flooding areas. Case studies: Scilla and Monasterace (Italy). Int. J. Saf. Secur. Eng. 2020, 10, 59–67. [Google Scholar] [CrossRef]
- Barbaro, G.; Gangemi, M.D.; Foti, G. An agent-based tsunami alert system. In Proceedings of the 18th Workshop “From Objects to Agents”, Scilla, Italy, 15–17 June 2017; Volume 1867, pp. 102–107. [Google Scholar]
- Canale, C.; Barbaro, G.; Petrucci, O.; Fiamma, V.; Foti, G.; Barillà, G.C.; Puntorieri, P.; Minniti, F.; Bruzzaniti, L. Analysis of floods and storms: Concurrent conditions. Ital. J. Eng. Geol. Environ. 2020, 1, 23–29. [Google Scholar] [CrossRef]
- Foti, G.; Barbaro, G.; Bombino, G.; Fiamma, V.; Puntorieri, P.; Minniti, F.; Pezzimenti, C. Shoreline changes near river mouth: Case study of Sant’Agata River (Reggio Calabria, Italy). Eur. J. Remote Sens. 2019, 52, 102–112. [Google Scholar] [CrossRef]
- Minniti, F.; Foti, G.; Barbaro, G. Analysis of areas inundated by tsunamis induced by earthquakes and landslides in the region of Calabria, Italy. In Proceedings of the 12th International Conference on Risk Analysis and Hazard Mitigation, Online. 23–25 June 2020; Volume 129, pp. 135–146. [Google Scholar] [CrossRef]
- Baratta, M. I Terremoti d’Italia. Saggio di Storia, Geografia e Bibliografia Sismica Italiana; F.lli Boccal: Turin, Italy, 1901. (In Italian) [Google Scholar]
- Tinti, S.; Guidoboni, E. Revision of the tsunamis occurred in 1783 In Calabria and Sicily (Italy). Sci Tsunami Hazards 1988, 6, 17–22. [Google Scholar]
- Graziani, L.; Maramai, A.; Tinti, S. A revision of the 1783–1784 Calabrian (southern Italy) 5 tsunamis. Nat. Hazards Earth Syst. Sci. 2006, 6, 1053–1060. [Google Scholar] [CrossRef] [Green Version]
- Tinti, S.; Maramai, A.; Graziani, L. The Italian Tsunami Catalogue (ITC), Version 2. 2007. Available online: http://www.ingv.it/servizi-e risorse/BD/catalogotsunami/catalogo-degli-tsunami-italiani (accessed on 15 October 2021).
- Tinti, S.; Pagnoni, G.; Zaniboni, F. The landslides and tsunamis of the 30th of December 2002 in Stromboli analyzed through numerical simulations. Bull. Volcanol. 2006, 68, 462–479. [Google Scholar] [CrossRef]
- Cecioni, C.; Bellotti, G. Inclusion of landslide tsunamis generation into a depth integrated wave model. Nat. Hazards Earth Syst. Sci. 2010, 10, 2259–2268. [Google Scholar] [CrossRef] [Green Version]
- Cecioni, C.; Bellotti, G. Modeling tsunamis generated by submerged landslides using depth integrated equations. Appl. Ocean. Res. 2010, 32, 343–350. [Google Scholar] [CrossRef]
- Mazzanti, P. Studio integrato subaereo-subacqueo di frane in ambiente costiero: I casi di Scilla (RC) e del lago di Albano (RM). G. Geol. Appl. 2008, 8, 245–261. [Google Scholar]
- Mazzanti, P.; Bozzano, F. Revisiting the February 6th 1783 Scilla (Calabria, Italy) landslide and tsunami by numerical simulation. Mar. Geophys Res. 2011, 32, 273–286. [Google Scholar] [CrossRef]







| Δx (m) | Δy (m) | Nx | Ny | Xmin (m) | Xmax (m) | Ymin (m) | Ymax (m) |
|---|---|---|---|---|---|---|---|
| 10 | 10 | 2500 | 2650 | 5.4730 × 105 | 5.7247 × 105 | 4.2229 × 106 | 4.2494 × 106 |
| Δx (m) | Δy (m) | Nx | Ny | Xmin (m) | Xmax (m) | Ymin (m) | Ymax (m) |
|---|---|---|---|---|---|---|---|
| 10 | 10 | 37 | 158 | 5.6105 × 105 | 5.6150 × 105 | 4.2340 × 106 | 4.2356 × 106 |
| Total Time of Displacement (s) | ΔT (s) | Nt |
|---|---|---|
| 30 | 0.5 | 79 |
| Total Time of Displacement (s) | ΔT (s) | Nt |
|---|---|---|
| 40 | 0.4 | 79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minniti, F.; Barbaro, G.; Foti, G. Modeling of the 1783 Tsunami Event in Scilla Generated by Landslide. Land 2022, 11, 69. https://doi.org/10.3390/land11010069
Minniti F, Barbaro G, Foti G. Modeling of the 1783 Tsunami Event in Scilla Generated by Landslide. Land. 2022; 11(1):69. https://doi.org/10.3390/land11010069
Chicago/Turabian StyleMinniti, Francesca, Giuseppe Barbaro, and Giandomenico Foti. 2022. "Modeling of the 1783 Tsunami Event in Scilla Generated by Landslide" Land 11, no. 1: 69. https://doi.org/10.3390/land11010069
APA StyleMinniti, F., Barbaro, G., & Foti, G. (2022). Modeling of the 1783 Tsunami Event in Scilla Generated by Landslide. Land, 11(1), 69. https://doi.org/10.3390/land11010069








