Effects of Polycentricity on Economic Performance and Its Dependence on City Size: The Case of China
Abstract
:1. Introduction
2. Literature Review and Hypotheses
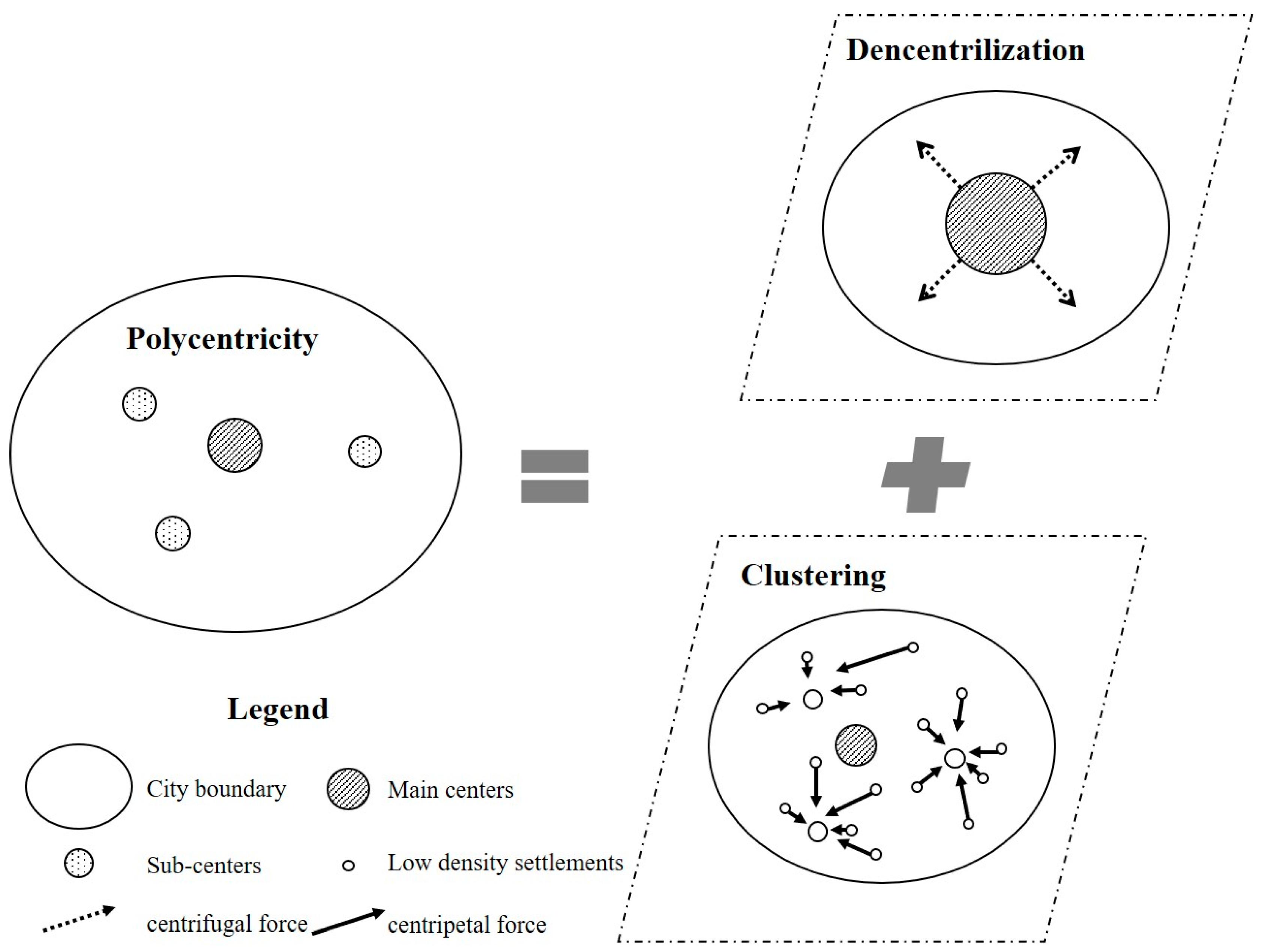
2.1. Concept of Urban Spatial Structure
2.2. Relation between Economic Performance and Urban Spatial Structure
2.3. Moderating Effect of City Size
2.4. Existing Gaps
2.5. Our Hypotheses
3. Methods and Data
3.1. Data Sources and Research Scale
3.2. Measurement of Urban Spatial Structure
3.3. Models
4. Empirical Results
4.1. Basic Models
4.2. Robustness Tests
4.3. Discussion
4.3.1. Discussion 1: Comparing Our Results with Those of Previous Studies
4.3.2. Discussion 2: City Size Threshold for a Positive Influence from Polycentricity
4.3.3. Discussion 3: Optimal City Size Constrained by Different Spatial Structures
4.3.4. Discussion 4: The Economic Significance of Urban Spatial Structure
5. Conclusions and Policy Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Sun, B.; Zhang, T.; Zhang, Z. Polycentric spatial structure and its economic performance: Evidence from meta-analysis. Reg. Sci. 2022, 1–15. [Google Scholar] [CrossRef]
- Meijers, E.J.; Burger, M.J. Spatial structure and productivity in US metropolitan areas. Environ. Plan. A 2010, 42, 1383–1402. [Google Scholar] [CrossRef]
- Kwon, K.; Seo, M. Does the polycentric urban region contribute to economic performance? The case of korea. Sustainability 2018, 10, 4157. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, B.; Li, W. The economic performance of urban structure: From the perspective of Polycentricity and Monocentricity. Cities 2017, 68, 18–24. [Google Scholar] [CrossRef]
- Wang, M.; Derudder, B.; Liu, X. Polycentric urban development and economic productivity in china: A multiscalar analysis. Environ. Plan. A 2019, 51, 1622–1643. [Google Scholar] [CrossRef]
- Fujita, M.; Thisse, J.F.; Zenou, Y. On the endogeneous formation of secondary employment centers in a city. J. Urban Econ. 1997, 41, 337–357. [Google Scholar] [CrossRef]
- Parr, J. The polycentric urban region: A closer inspection. Reg. Stud. 2004, 38, 231–240. [Google Scholar] [CrossRef]
- Camagni, R.P.; Salone, C. Network urban structures in northern Italy: Elements for a theoretical framework. Urban Stud. 1993, 30, 1053–1064. [Google Scholar] [CrossRef]
- Capello, R. The city network paradigm: Measuring urban network externalities. Urban Stud. 2000, 37, 1925–1945. [Google Scholar] [CrossRef]
- Meijers, E.J.; Burger, M.J. Stretching the concept of ‘borrowed size’. Urban Stud. 2017, 54, 269–291. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X. How did urban polycentricity and dispersion affect economic productivity? A case study of 306 Chinese cities. Landsc. Urban Plan. 2018, 173, 51–59. [Google Scholar] [CrossRef]
- Lee, B.; Gordon, P. Urban spatial structure and economic growth in US metropolitan areas. In Proceedings of the 46th Annual Meetings of the Western Regional Science Association, Newport Beach, CA, USA, 21–24 February 2007. [Google Scholar]
- Meijers, E.J.; Burger, M.J.; Hoogerbrugge, M.M. Borrowing size in networks of cities: City size, network connectivity and metropolitan functions in Europe. Pap. Reg. Sci. 2016, 95, 181–198. [Google Scholar] [CrossRef]
- Burger, M.J.; Meijers, E.J. Agglomerations and the rise of urban network externalities. Pap. Reg. Sci. 2016, 95, 5–15. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Liu, D. How does urban spatial structure affect economic growth? Evidence from landsat data in China. J. Econ. Issues 2020, 54, 798–812. [Google Scholar] [CrossRef]
- Li, W.; Sun, B.; Zhang, T. Spatial structure and labour productivity: Evidence from prefectures in China. Urban Stud. 2019, 56, 1516–1532. [Google Scholar] [CrossRef]
- Xiao, W.; Liu, W.; Li, C. Can the urban spatial structure accelerate urban employment growth? Evidence from China. Growth Change 2021. [Google Scholar] [CrossRef]
- Anas, A.; Arnott, R.; Small, K.A. Urban spatial structure. J. Econ. Lit. 1998, 36, 1426–1464. [Google Scholar]
- Lee, B. “Edge” or “edgeless” cities? Urban spatial structure in US metropolitan areas, 1980 to 2000. J. Reg. Sci. 2007, 47, 479–515. [Google Scholar] [CrossRef]
- Sun, B.; Li, W. City Size Distribution and Economic Performance: Evidence from City-Regions in China. Sci. Geogr. Sin. 2016, 36, 328–334. [Google Scholar]
- Cervero, R. Efficient urbanisation: Economic performance and the shape of the metropolis. Urban Stud. 2001, 38, 1651–1671. [Google Scholar] [CrossRef]
- Veneri, P.; Burgalassi, D. Spatial Structure and Productivity in Italian NUTS-3 Regions; Università Politecnica delle Marche, Dipartimento di Scienze Economiche e Sociali: Ancona, Italy, 2011. [Google Scholar]
- Glaeser, E.L.; Kahn, M.E. Sprawl and urban growth. In Handbook of Regional and Urban Economics; Elsevier: Amsterdam, The Netherlands, 2004; Volume 4, pp. 2481–2527. [Google Scholar]
- Fallah, B.N.; Partridge, M.D.; Olfert, M.R. Urban sprawl and productivity: Evidence from US metropolitan areas. Pap. Reg. Sci. 2011, 90, 451–472. [Google Scholar] [CrossRef]
- Qin, M.; Liu, X. Does urban sprawl lead to urban productivity losses in China? Empirical study based on nighttime light data. J. Financ. Econ. 2015, 41, 28–40. [Google Scholar]
- Friedmann, J. Regional Development Policy: A Case Study of Venezuela; MIT Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Fujita, M.; Ogawa, H. Multiple equilibria and structural transition of non-monocentric urban configurations. Reg. Sci. Urban Econ. 1982, 12, 161–196. [Google Scholar] [CrossRef]
- McMillen, D.P.; Smith, S.C. The number of subcenters in large urban areas. J. Urban Econ. 2003, 53, 321–338. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, B.; Zhang, T. Do polycentric urban regions promote functional spillovers and economic performance? Evidence from China. Reg. Stud. 2020, 56, 63–74. [Google Scholar] [CrossRef]
- Duranton, G.; Puga, D. Micro-foundations of urban agglomeration economies. In Handbook of Regional and Urban Economics; Elsevier: Amsterdam, The Netherlands, 2004; Volume 4, pp. 2063–2117. [Google Scholar]
- Wheaton, W.C. Commuting, congestion, and employment dispersal in cities with mixed land use. J. Urban Econ. 2004, 55, 417–438. [Google Scholar] [CrossRef]
- Galster, G.; Hanson, R.; Ratcliffe, M.R.; Wolman, H.; Coleman, S.; Freihage, J. Wrestling sprawl to the ground: Defining and measuring an elusive concept. Hous. Policy Debate 2001, 12, 681–717. [Google Scholar] [CrossRef]
- Massey, D.S.; Denton, N.A. The dimensions of residential segregation. Soc. Forces 1988, 67, 281–315. [Google Scholar] [CrossRef]
- Gordon, P.; Richardson, H.W.; Wong, H.L. The distribution of population and employment in a polycentric city: The case of Los Angeles. Environ. Plan. A 1986, 18, 161–173. [Google Scholar] [CrossRef]
- Small, K.A.; Song, S. Population and employment densities: Structure and change. J. Urban Econ. 1994, 36, 292–313. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Qin, M. Urban spatial structure and regional economic efficiency: The choice of urbanization path mode in China. Manag. World 2017, 1, 51–64. (In Chinese) [Google Scholar]
- Dong, L.; Pan, J.; Feng, Y.; Wang, W. Spatial difference pattern of house vacancy in china from nighttime light view. Econ. Geogr. 2017, 37, 62–69, 176. (In Chinese) [Google Scholar]
- Wang, X.; Xia, X. Optimize city scale and promote economic growth. Econ. Res. 1999, 9, 22–29. (In Chinese) [Google Scholar]
- Chen, W.; Jiang, H. City Size Economics and Policy. Financ. Econ. 2000, 4, 67–70. (In Chinese) [Google Scholar]
- Ma, S.; Song, L. Analysis and Comparative Study on Development of City Scales of China. Stat. Res. 2003, 7, 30–34. (In Chinese) [Google Scholar]
- Au, C.C.; Henderson, J.V. Are Chinese Cities Too Small? Rev. Econ. Stud. 2006, 73, 549–576. [Google Scholar] [CrossRef] [Green Version]
- Liu, B. The Empirical Research on the Optimum City Size in China; Northeast Normal University: Changchun, China, 2007. (In Chinese) [Google Scholar]
- Zhang, J.; Xie, Y.; Qian, F. Optimal City Size in China:An Extended Empirical Study from the Perspective of Energy Consumption. China City Plan. Rev. 2017, 26, 22–28. [Google Scholar]





| Centralization indices | |
| Modified Wheaton index [31] | |
| Modified weighted average distance from the CBD [32] | |
| Clustering indices | |
| Delta index [32,33] | |
| Gini coefficient [34,35] | |
| Variable Name | Description | Mean | S.D. | Min | Max |
|---|---|---|---|---|---|
| GDP per worker in yuan (ln) | 11.62 | 0.527 | 9.527 | 13.95 | |
| Physical capital stock per worker in 104 yuan (ln) | 2.516 | 0.579 | 0.469 | 4.787 | |
| Number of middle school student per 104 persons | 6.868 | 0.395 | 4.904 | 8.017 | |
| G | Ratio of government consumption to GDP | 100% | 0.113 | 0.0720 | 0.0200 |
| Population in 104 persons | 4.558 | 0.774 | 2.654 | 7.499 | |
| lnMWI | Centralization index 1 | 0.484 | 0.169 | −0.69 | 0.688 |
| lnMADC | Centralization index 2 | 0.579 | 0.084 | 0.111 | 0.688 |
| lnDELTA | Clustering index 1 | 0.461 | 0.109 | 0.0250 | 0.646 |
| lnGINI | Clustering index 2 | 0.517 | 0.111 | 0.0250 | 0.666 |
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Dependent Variable: ln(GDP/L) | FE | FE | FE | FE | FE |
| ln(K/L) | 0.5816 *** | 0.5828 *** | 0.5817 *** | 0.5807 *** | 0.5860 *** |
| (0.035) | (0.035) | (0.035) | (0.035) | (0.034) | |
| ln(H/L) | 0.0830 ** | 0.0834 ** | 0.0841 ** | 0.0869 *** | 0.0873 *** |
| (0.033) | (0.034) | (0.034) | (0.033) | (0.033) | |
| G | −0.7232 * | −0.7189 * | −0.7224 * | −0.7120 * | −0.6919 * |
| (0.375) | (0.374) | (0.375) | (0.377) | (0.374) | |
| lnPOP | 1.1806 *** | 1.2396 *** | 1.1816 *** | 0.9285 ** | 1.0014 *** |
| (0.317) | (0.372) | (0.316) | (0.362) | (0.355) | |
| lnPOP × lnPOP | −0.0993 *** | −0.1027 *** | −0.0993 *** | −0.0883 *** | −0.0961 *** |
| (0.030) | (0.032) | (0.029) | (0.031) | (0.032) | |
| lnMWI | −0.0283 | 0.2361 | 1.3465 * | ||
| (0.079) | (0.619) | (0.693) | |||
| lnPOP × lnMWI | −0.0619 | −0.3322 ** | |||
| (0.139) | (0.166) | ||||
| lnDELTA | −0.0248 | −1.4951 * | −2.7848 *** | ||
| (0.137) | (0.858) | (1.062) | |||
| lnPOP × lnDELTA | 0.3338 * | 0.6525 *** | |||
| (0.189) | (0.246) | ||||
| Time FE | Y | Y | Y | Y | Y |
| City FE | Y | Y | Y | Y | Y |
| Constant | 6.5128 *** | 6.3167 *** | 6.4983 *** | 7.3782 *** | 7.1902 *** |
| (0.933) | (1.127) | (0.918) | (1.085) | (1.058) | |
| Observations | 734 | 734 | 734 | 734 | 734 |
| R-squared | 0.873 | 0.873 | 0.873 | 0.874 | 0.875 |
| Number of cities | 273 | 273 | 273 | 273 | 273 |
| Hausman test Prob > chi2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| lnMWI | lnMADC | lnDELTA | lnGINI | |
|---|---|---|---|---|
| First-stage coefficients on the IVs | 0.3014 *** (0.0319) | 2.7629 *** (0.7746) | 0.3525 *** (0.0386) | 1.1047 *** (0.4376) |
| Shea partial R2 | 0.1645 | 0.0273 | 0.1559 | 0.0139 |
| Anderson canon. corr. LM statistics | 75.848 *** | 12.591 *** | 71.690 *** | 6.396 ** |
| Cragg–Donald Wald F statistics | 89.209 | 12.720 | 83.419 | 6.374 |
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Dependent Variable: ln(GDP/L) | TSLS | TSLS | TSLS | TSLS | TSLS |
| lnPOP | 1.1767 *** | 1.9634 *** | 1.1790 *** | −1.1453 | −1.4068 |
| (0.345) | (0.503) | (0.354) | (1.731) | (1.791) | |
| lnPOP × lnPOP | −0.0991 *** | −0.1448 *** | −0.0993 *** | 0.0017 | 0.0146 |
| (0.033) | (0.040) | (0.034) | (0.090) | (0.101) | |
| lnMWI | −0.1272 | 3.4557 ** | −0.6968 | ||
| (0.215) | (1.592) | (2.874) | |||
| lnPOP × lnMWI | −0.8217 ** | 0.1124 | |||
| (0.380) | (0.642) | ||||
| lnDELTA | −0.6979 | −14.2572 | −14.9520 ** | ||
| (0.862) | (9.214) | (7.302) | |||
| lnPOP × lnDELTA | 3.0653 | 3.2583 * | |||
| (2.144) | (1.663) | ||||
| Others | Y | Y | Y | Y | Y |
| Time FE | Y | Y | Y | Y | Y |
| City FE | Y | Y | Y | Y | Y |
| Observations | 714 | 714 | 714 | 714 | 714 |
| R-squared | 0.872 | 0.860 | 0.864 | 0.795 | 0.777 |
| Number of cities | 253 | 253 | 253 | 253 | 253 |
| Hausman Prob > chi2 | 1.0000 | 0.7408 | 0.9990 | 0.9407 | 0.9708 |
| (1) | (2) | (3) | |
|---|---|---|---|
| Dependent Variable: ln(GDP/L) | FE | FE | FE |
| lnPOP | 1.1375 ** | 0.9224 ** | 1.1242 *** |
| (0.446) | (0.361) | (0.422) | |
| lnPOP × lnPOP | −0.0978 *** | −0.0909 *** | −0.0955 *** |
| (0.032) | (0.031) | (0.032) | |
| lnMADC | −0.3233 | 2.1723 | |
| (1.377) | (1.813) | ||
| lnPOP × lnMADC | 0.0495 | −0.5319 | |
| (0.306) | (0.426) | ||
| lnGINI | −1.6431 * | −2.7654 ** | |
| (0.864) | (1.273) | ||
| lnPOP × lnGINI | 0.3561 * | 0.6315 ** | |
| (0.193) | (0.301) | ||
| Others | Y | Y | Y |
| Time FE | Y | Y | Y |
| City FE | Y | Y | Y |
| Constant | 6.7249 *** | 7.4470 *** | 6.6762 *** |
| (1.486) | (1.092) | (1.377) | |
| Observations | 734 | 734 | 734 |
| R-squared | 0.873 | 0.874 | 0.875 |
| Number of cities | 273 | 273 | 273 |
| Table 3 Model 5 | |
|---|---|
| (lnMWI) | 1.3465 |
| (lnpop × lnMWI) | −0.3322 |
| the threshold of city size for MWI | 575,800 |
| (lnDELTA) | −2.7848 |
| (lnpop × lnDELTA) | 0.6525 |
| the threshold of city size for DELTA | 713,700 |
| Peak Population Size | Dispersed | Clustered | ||
|---|---|---|---|---|
| DELTA in Q1 | DELTA in Q2 | DELTA in Q3 | ||
| Decentralized | MWI in Q1 | 340.72 | 424.08 | 584.13 |
| MWI in Q2 | 286.60 | 356.72 | 417.04 | |
| Centralized | MWI in Q3 | 253.86 | 324.48 | 379.36 |
| Authors (Year) | Optimal City Size (in 10,000 Persons) |
|---|---|
| Wang and Xia (1999) [38] | 100–400 |
| Chen and Jiang (2002) [39] | 100–400 |
| Ma and Song (2003) [40] | 100–200 |
| Au and Henderson (2006) [41] | 54.4–144 |
| Liu (2007) [42] | 270 |
| Zhang and Xie (2017) [43] | 200–500 |
| City | Jiayuguan | Suizhou | Weinan | Wuhan | Tianjin |
|---|---|---|---|---|---|
| Population (million persons) | 0.2 | 0.5 | 1 | 5.1 | 8.2 |
| GDP per capita (thousand yuan/person) | 311 | 93.8 | 157.2 | 195.2 | 293.1 |
| Change in GDP per capita with a 1% decrease in centralization (thousand yuan/person) | −1.1 | −0.04 | 0.3 | 1.4 | 2.6 |
| Change in GDP per capita with a 1% increase in clustering (thousand yuan/person) | −2.6 | −0.2 | 0.3 | 2.5 | 4.7 |
| Change in GDP per capita with a decrease of one standard deviation in centralization (thousand yuan/person) | −18.5 | −0.7 | 0 | 0.2 | 43.7 |
| Change in GDP per capita with a decrease of one standard deviation in clustering (thousand yuan/person) | −28.1 | −2.4 | 3.7 | 27.4 | 50.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Zhang, T.; Li, W.; Song, Y. Effects of Polycentricity on Economic Performance and Its Dependence on City Size: The Case of China. Land 2022, 11, 1546. https://doi.org/10.3390/land11091546
Sun B, Zhang T, Li W, Song Y. Effects of Polycentricity on Economic Performance and Its Dependence on City Size: The Case of China. Land. 2022; 11(9):1546. https://doi.org/10.3390/land11091546
Chicago/Turabian StyleSun, Bindong, Tinglin Zhang, Wan Li, and Yan Song. 2022. "Effects of Polycentricity on Economic Performance and Its Dependence on City Size: The Case of China" Land 11, no. 9: 1546. https://doi.org/10.3390/land11091546
APA StyleSun, B., Zhang, T., Li, W., & Song, Y. (2022). Effects of Polycentricity on Economic Performance and Its Dependence on City Size: The Case of China. Land, 11(9), 1546. https://doi.org/10.3390/land11091546






