Abstract
The analysis and modeling of spatial and temporal changes in land use can reveal changing urban spatial patterns and trends. In this paper, we introduce a linear transformation optimization Markov (LTOM) model that can be exploited to estimate the state transition probability matrix of land use, building a loosely coupled ANN-CA-LTOM model for simulating and predicting land use changes. The advantages of this model are that it is flexible and high expansibility; it can maintain semantic coupling between the Artificial Neural Networks (ANN), Cellular Automata (CA), and LTOM model and enhance their functions; and it can break the limitation of requiring two periods of land use data when calculating the transition probability matrix. We also construct a suitability atlas of land use as the transition rules into the CA-LTOM model, taking into account the regional natural and socioeconomic driver factors, by exploiting the ANN model. The ANN-CA-LTOM model is employed to simulate the distribution of the three major types of land use, i.e., construction land, agricultural land, and unused land, in the Nansha District, China, in 2018 and 2020. The results show that the model performs well and the overall accuracy of the land use simulation was 97.72%, with a kappa coefficient of 0.962761. Furthermore, the simulated and predicted results of land use changes from 2021 to 2023 in Nansha District show changing trends in construction, agricultural, and unused land use. This study provides an approach for estimating a Markov transition probability matrix and a coupled mode of the models for simulating and predicting land use changes.
1. Introduction
Over the past three decades, China’s rapid expansion of economic growth and increasing population have driven industrialization and urbanization in many cities. Pursuing a single land use space no longer satisfies the needs of people to improve living conditions and shape their futures. As a result of this situation, land use and land management have undergone significant changes [,]. Accurate prediction for land use can support the government in strengthening the supervision and scientific regulation of urban land use changes []. Therefore, it is necessary to explore and summarize the spatial–temporal change characteristics of urban land use and to simulate future changes.
Researchers have successfully built many models to analyze and simulate Land Use and Land-Cover Change (LUCC) at national [,,] and regional [,,] scales. The models are referred to as numerical simulation models, spatial simulation models, or coupling models according to the simulation methods.
Numerical simulation models are based on mathematical theoretical frameworks used to predict quantitative changes in land use, including the Markov model, logistic regression, back-propagation neural networks [], and the system dynamic model (SD) []. The simulation results of these models only reflect the amount of urban land and do not simulate the characteristics of the spatial distribution pattern [,]. Common spatial simulation models include the cellular automaton (CA) model [], CLUE-S model [], and future land use simulation (FLUS) model []. The CA model has the advantage of simplicity and the flexibility of integration with other models [], but it relies solely on spatial data and has poor simulation accuracy. The CLUE-S model works well for simulating land use changes in small-scale areas but can be limited by the spatial resolution []. In general, the accuracy of spatial simulation models alone is not ideal and is improved when combined with numerical models. Thus, the coupled models for quantitative and spatial simulation have been proposed for research on land use simulation, such as the CA-Markov, CA-SD, and CA-SVM models [,].
The CA-Markov model is currently the most widely used simulation model for land use changes [,], and is capable of predicting not only the total changes in various land use types and the state transition probability matrix, but also the spatial distribution of land use through inter-neighborhood analysis [,]. In general, the CA-Markov model is most suitable for short-term simulation. Marwa Waseem et al. used the CA-Markov model to predict the LUCC changes in parts of the northwestern desert of Egypt in 2023, revealing the potential and merit of this method in predicting future land use changes []. However, the causes and trends of land use changes in such regions are poorly understood. During the process of a city’s development, there are always some driving factors that dominate the speed and direction of change in urban spatial land use []. The traditional CA-Markov model can only simulate the linear evolution process of land use without considering the dynamic and regulatory power of the driving factors of land use patterns.
In order to improve the validity and rationality of land use simulation, the key to improving the CA-Markov model is to transform the complex nonlinear driving factor data into land use transition rules. The logistic model can be used to calculate the regression coefficients of multiple driving factors of land use distribution and then generate regional probability maps of each type of land use. The atlas can be incorporated into the CA-Markov model to achieve multi-scenario simulations of land use changes in the future [,,]. Multiple criteria evaluation (MCE) can be applied to score the suitability of drivers. Li et al. [] predicted the land use patterns in small and medium cities based on the MCE-CA-Markov model, and the accuracy of the simulation was significantly improved compared with the traditional model. However, determining the weight of driving factors was vulnerable to subjective influence. Fu et al. improved the MCE method based on historical data so that the selection of factors, scores, and weights are determined to reflect actual historical trends, but the limitation of the model was obvious because it assumed that the spatial–temporal variation in land use is a linearly changing trend [].
With the development of artificial intelligence, machine learning and deep learning methods have been applied to land use simulation. Zhou et al. used the random forest algorithm to explore the transition rules of the CA-Markov model and constructed the RF-CA-Markov model, which can improve prediction accuracy without significantly increasing the calculation cost []. Artificial neural networks (ANNs) are some of the most powerful artificial-intelligence-based tools. Since ANNs are adept at handling complex nonlinear relationships through learning, the transition suitability atlases generated by them can obtain better simulation accuracy when being integrated into the CA-Markov model [,].
The land use transition rules based on the CA-Markov model include not only the land use suitability atlas but also the transition probability matrix of the Markov chain, which directly determines the transition rules and quantitative change trends between each type of land use. Most existing studies calculate the transition probability matrix based on two-period historical data of land use [,]. This method limits the simulation to the time interval of the data period [,]. Based on historical statistical data in respect of land use, the linear transformation optimization Markov (LTOM) model proposed in this paper can estimate the transition probability matrix of a Markov chain by building a linear programming model. It breaks the restriction of time intervals and is less affected by data with respect to abnormal land use changes, which is conducive to improving the performance and stability of the model. Coupling the LTOM mathematical prediction model, ANN model, and CA spatial simulation model in the land use simulation and prediction can achieve satisfactory simulation accuracy under the comprehensive consideration of multiple driving factors.
In this paper, we took the Nansha District in Guangzhou City, China, as the study area and collected historical land use data, DEM, traffic and road data, arable land data, and socioeconomic data for this area. Two time periods, 2010–2018 and 2018–2020, were chosen as the research period. Taking 2014 and 2019 as base periods, respectively, we employed the ANN-CA-LTOM-coupled model to simulate the land use changes in 2018 and 2020, compared the prediction results with the observed land use data, and verified the simulation accuracy with kappa coefficients. Finally, taking 2020 as the base period, we simulated and predicted the land use changes from 2021 to 2023 and analyzed the spatial–temporal evolution of the simulated land use structure and distribution. We explored the spatial–temporal dynamic changes of the three major types of land use in Nansha District, aiming to discover the law of land use changes, so as to assist in optimizing the spatial layout of three major types of land use and achieve harmonious human–land relationships and sustainable economic, social, and ecological development.
2. Methodology
2.1. ANN-CA-LTOM Model
Based on the statistical results of the proportion of the three major land use types from 2010 to 2019, the CA-LTOM model constructs a linear programming model through the LTOM model to estimate the transition probability matrix of the Markov chain, which is one of the transition rules of the CA model. Furthermore, the ANN model is introduced to build the urban land suitability atlas based on land use maps of the base period (2014/2019) and the data of various driving factors. The urban land suitability atlas is another transition rule of the CA model. Subsequently, we loosely couple the CA-LTOM model with ANN model to simulate and predict the distribution and changes of land use. Finally, we verify the simulation accuracy of the model, and modify the suitability atlas to achieve satisfactory simulation accuracy. Figure 1 shows the research framework and each of the above models is explained in the following sections.
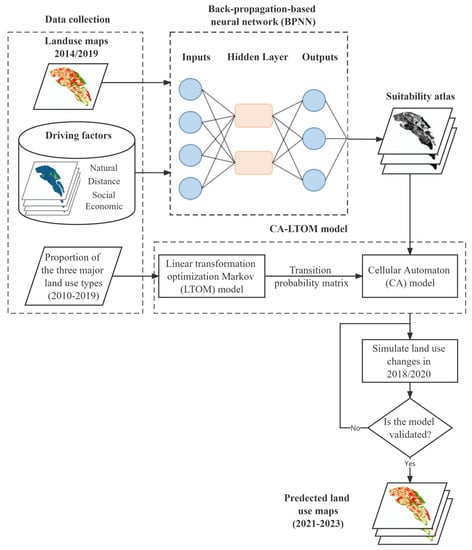
Figure 1.
The framework of the loosely coupled ANN-CA-LTOM model.
2.1.1. LTOM Model
The Markov chain (MC) is a discrete stochastic process with Markovian properties, i.e., the probability distribution of the system in the next and all future steps depends only on the current state of the system and not additionally on the state of the system in the previous steps []. It has a wide range of applications in urban expansion and land use changes. MC describes the probability of transition between land use types through a transition probability matrix. Each item in the matrix represents the probability of transferring from one land use state to another. The transition probability matrix between states can be used to predict the future land use state and development trends. Determining the state transition probability matrix is the key to the Markov prediction model []. The expressions are as follows:
where and denote the state of the land use structure at times t and t + 1, respectively. is the state transition probability matrix and has the following properties:
According to previous studies, the determination of the state transition probability matrix for the same region at different times requires at least two periods of land use data, and the matrix is calculated from a multifaceted cross-tabulation between a pair of land use images from two historical observation years. The time period of state transition is limited to the time interval of two periods of land use data. In this paper, the linear transformation optimization Markov (LTOM) model is introduced to estimate the state transition probability matrix of land use types at any time interval based on the statistics of the area proportion by constructing linear programming equations.
The LTOM model takes the minimum relative error as the objective function to build an optimization model to solve the Markov state transition probability matrix, and transforms the nonlinear problem into a linear problem by variable substitution []. Assuming that the relative fitting error between the estimated value and the actual value of state j at time t is after one-step transfer, then []:
The relative error value is replaced by the following variables:
For m stages, the objective function can be expressed as []:
By building the following linear programming model, the estimated state transition probability matrix can be obtained.
2.1.2. ANN Model
The transition rule is the core part of the ANN-CA-LTOM model, but the nonlinear relationship between driving factors and land use types makes it difficult to determine the transition rule. Artificial neural networks (ANNs) can form a complex network structure through the connection of a large number of neurons to simulate the structure and function of the human brain []; they are able to self-organize, self-adapt, self-learn, and simulate complex nonlinear problems []. Back-propagation-based neural networks (BPNNs) are neural networks trained by a backward propagation algorithm, including an input layer, a hidden layer, and an output layer. These constantly adjust the weights of neuronal connections through training to obtain a network model with minimum errors []. The change in urban land use is affected by many factors, and is a complex process. Based on the characteristics of BPNNs, they are suitable for the suitability assessment of urban land use types and can generate an urban land use suitability atlas, which can be used as the transition rule of the CA-Markov model. This quantitative method allows us to effectively calibrate the CA-Markov model by adjusting different factors. The comprehensive transformation law of the ANN-CA-LTOM model obtained using this method is more scientific, reliable, and in line with the real-life development situation.
2.1.3. CA-LTOM Model
The cellular automaton (CA) [] model is a dynamical model consisting of six parts: cell, cellular space, cellular state, cellular neighborhood, transition rule, and discrete time. The ability of CA to simulate proximity makes it suitable for modeling land use dynamics. The state of a cell depends on itself and the previous state of its neighboring cells. Based on certain transition rules, the CA model simulates the cellular state transition within discrete time and space dimensions, and then simulates the complex spatial–temporal evolution process of land use. Its expression is as follows:
where S is a finite and discrete state set of the cell, t and t + 1 represent different discrete times, N is the cellular neighborhood, and f represents the state transition rule.
In terms of land use change simulation, the MC model can only predict the total amount of each type of land use and the transition probability matrix; it cannot explain the impact of neighboring cells and driving factors on land use change simulation, and it also cannot simulate spatial change. In contrast, CA includes spatial information and has a strong spatial evolution prediction ability. The CA-LTOM coupling model combines the advantages of both to realize the complex dynamic simulation of land use over the long-term.
Based on the above model, ANN-CA-LTOM modeling in this paper comprises the following four steps: First, we statistically analyze the historical land use data and build a linear programming model to generate the transition probability matrix and the transition area matrix. Secondly, according to the natural, economic, and social drivers of land use change, the ANN model is employed to generate a land use suitability atlas, which determines the transition rules of land use changes. Third, the transition area matrix and the suitability atlas generated via the above steps are used as input data to realize the simulation of land use change using the built-in CA-Markov module in IDRISI 17.0. Finally, the simulated land use map is compared with the observed land use map. If the comparison results are unacceptable, the transition area matrix and suitability atlas are modified until the simulation results reach satisfactory accuracy. After accuracy verification, the model can predict the future land use map.
2.2. Accuracy Evaluation
Before simulating the future land use distribution, it is necessary to verify the simulation accuracy of the model. In addition to the visual comparison method, the kappa coefficient and pixel confusion matrix are used to quantitatively evaluate the accuracy of simulation results. The kappa coefficient is an index for consistency testing and is commonly used to check whether a model’s prediction results are consistent with the observed classification results. The formula is as follows []:
The producer accuracy refers to the ratio between the number of correctly classified pixels and the total number of actual pixels of a certain land use type. The calculation method is as follows []:
The user accuracy refers to the ratio between the number of correctly classified pixels and the total number of classified pixels of a certain land use type. The calculation method is as follows []:
where is the number of correctly predicted pixels of class i, N is the total number of pixels, and is the overall classification accuracy, that is, the accuracy rate. is the true number of pixels of class i, is the predicted number of pixels of class i, and indicates the proportion of pixels that are simulated consistently under the random state. The kappa value is in the range 0~1, and if its value is closer to 1, then the accuracy of the model calculation and simulation is higher. In general, the simulation effect will be better when its value is greater than 0.75.
Since large areas of land in Nansha District did not change during the simulation period, the kappa coefficient may overestimate the agreement between the simulated results and the observed results. In order to compare the changes in the simulated results and the observed results, the concept of “figure of merit” is introduced in this paper. Figure of merit refers to the ratio of the intersection of observed and predicted area of one land use type to the union of observed and predicted area, that is, the proportion of correctly predicted area in the total area. It can be calculated as follows []:
where is the predicted area and is the observed area. The value of the figure of merit ranges from 0% to 100%, meaning the proportion of overlap between the observed and predicted area of one land use type.
3. Case Study
3.1. Study Area
The Nansha District (Figure 2) is located in the southernmost part of Guangzhou, Guangdong Province, China. The Nansha District includes nine townships, namely, Lanhe Town, Dongyong Town, Dagang Town, Huangge Town, Hengli Town, Nansha Street, Zhujiang Street, Longxue Street, and Wanqingsha Town. The total area of the administrative division is about 803 km2, of which the sea area occupies a quarter. The overall topography of the Nansha District is gentle, and the landform types include low hills, basins, plains, and tidal flats. Currently, Guangzhou is in the deepening stage of industrialization and urbanization, and Nansha District’s economic aggregates and permanent population are growing steadily and continuously. As of November 2020, the resident population of Nansha District was 846,584, which is 3.26-times the resident population in the sixth national population census in 2010, and the average annual growth rate of the resident population from 2010 to 2020 was 12.53%, which is 3.19-times the city’s average annual growth rate (3.93%) in the same period. Driven by the dual role of the urban economy and population growth, the demand for natural resources in Nansha District is showing an apparent increase, and the total amount of construction land has a fluctuating upward trend.
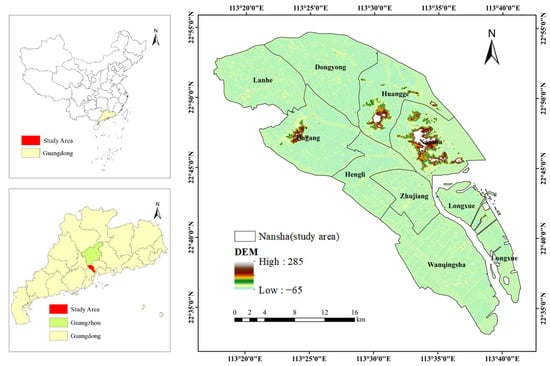
Figure 2.
The study area located in Guangzhou, Guangdong Province, China.
3.2. Data Sources and Pre-Processing
In this study, the land use classification follows the three major categories of construction land, agricultural land, and unused land. Guangzhou carried out its first national land survey, second national land survey, and third national land survey from 1984 to 1997, 2009 to 2012, and 2018 to 2021, respectively, and has conducted annual surveys of land change. The land use data in this study are derived from the data of the third national land survey (2019–2021) and the land change survey data (2010–2018). Compared with the conventional methods of identifying, interpreting, and extracting land use information from remote sensing images, our data ensure higher accuracy and reliability of land use classification.
The driving factors include terrain and social economy. Digital elevation model (DEM) data were derived from Shuttle Radar Topography Mission (SRTM) data with a spatial resolution of 30 m × 30 m. The slope map and aspect map of the study area were generated based on DEM data. The population density data originated from the 1000 m resolution raster dataset of WorldPop (https://www.worldpop.org/, accessed on 4 August 2022), and the population density raster was resampled to 30 m × 30 m resolution using the bilinear interpolation method. Vector data for railways and main highways originated from OpenStreetMap (https://www.openstreetmap.org/, accessed on 4 August 2022). The water area, urban, and rural data were extracted from national land survey data and change survey data. According to the Nansha statistical yearbook data, we calculated the proportion of the cultivated land area in the prime farmland protection area and the industrial output value of each street and town in the Nansha District, and then obtained the corresponding raster data.
In order to facilitate the processing and analysis of the spatial data, all the data in this study were converted into a unified geographic coordinate system (GCS_China_Geodetic_Coordinate_System_2000) and Gauss–Kruger projection (CGCS2000_3_Degree_GK_Zone_38). All the raster data were unified to 30 m spatial resolution and were extracted according to the land survey boundary of Nansha District using a mask.
3.3. Estimating the Transition Probability Matrix
We calculated and counted the area percentages of construction land, agricultural land, and unused land in the Nansha District from 2010 to 2019, and the results are listed in Table 1. It can be seen from the table that the proportion of construction land shows a fluctuating upward trend, while the proportion of agricultural land and unused land shows a fluctuating downward trend. It should be noted that the proportion of construction land decreased significantly in the period 2018–2019, while the proportion of agricultural land and unused land increased. The primary reason for this is that the data for 2019 were generated from the third national land survey, which has a somewhat different classification system compared to the land change survey data for the period 2010–2018.

Table 1.
The area percentage of three types of land use in Nansha District from 2010 to 2019.
According to Equation (10), a linear programming solution model with the objective function of minimizing the sum of relative errors was built. Based on the above data from 2010 to 2019 (Table 1), the state transition probability matrix of three types of land use in the Nansha district was estimated as follows:
The value of each item in the matrix is between 0 and 1, and the closer the value is to 1, the more likely it is to shift from one type to another type. The values on the main diagonal of the matrix indicate the probability that the land cover type will remain in its original state. In contrast, the values on the off-diagonal indicate the probability that the land cover type will be converted into another type. According to the matrix, it can be seen that each land use type has the highest probability of remaining unchanged, which is above 98%. Construction land is the most stable category, and the probability of conversion into agricultural land and unused land is small, which is consistent with the actual situation. The conversion probability from agricultural land into construction land is about 1%. This indicates that the increase in construction land comes at the cost of a decrease in agricultural land.
Taking 2015 and 2019 as the base periods, respectively, the estimated state transition probability matrix using the LTOM model was used to predict the area percentage of three major land categories in Nansha District in 2020, and the relative error and average relative error of the prediction results were calculated and compared with the results of the proportion in 2020 predicted by the estimated state transition probability matrix using the Markov model (Table 2 and Table 3). In Table 2, the average relative error of the predicted value calculated by the estimated state transition probability matrix is only 1.93%, which is significantly lower than the average relative error of the predicted value calculated by the estimated state transition probability matrix using the Markov model (7.95%). Table 3 shows similar results. The LTOM model performs well with high reliability of the prediction results.

Table 2.
Prediction results and accuracy of the area percentage of three types of land use in Nansha District in 2020 with 2019 as the base period (1-year interval).

Table 3.
Prediction results and accuracy of the area percentage of three types of land use in Nansha District in 2020 with 2015 as the base period (5-year interval).
3.4. Transition Suitability Atlas
Building the transition suitability atlas of land use classification is the key to implementing the ANN-CA-LTOM model for land use simulation. There is a complex relationship between the spatial distribution pattern of land use and regional site conditions. Land use is not only limited by environmental factors but is also influenced by social and economic factors. Taking into account the characteristics of the natural and social environment of the study area, we chose three natural factors (the digital elevation model (DEM), slope, and aspect), four distance factors (the distance from water (Dis_water), the distance from the city (Dis_city), the distance from villages (Dis_village), and the distance from railways/main highways (Dis_traffic)), and three socioeconomic factors (population density (Pop), industrial output value (Industry), and the proportion of farmland in the prime farmland protection area (Farmland)), as the factors for building a transition suitability atlas of land use classification (Figure 3) based on the principles of accessibility, continuity, reliability, diversity, and representativeness of the driving factors. Table 4 lists the details of all driving factors such as the year of data, data source, etc. We normalized the above ten driving factors, and took the land use classification data of 2019 and the normalized driving factors as the input data of ANN. The training samples were sampled in the way of uniform sampling, and the number of hidden layers of the neural network was set to 12. After training, the probability suitability map of the spatial distribution of each land use type in 2019 was output, as shown in Figure 4. The value of suitability ranges from 0 to 1. Being closer to 1 indicates the higher suitability of specific land use in this region, and being closer to 0 indicates lower suitability. Finally, the Collection Editor tool of the IDRISI software package was used to generate a land use transition suitability atlas from the suitability maps of the three land use types obtained from the ANN model, which was used for the transition rules of the CA model.
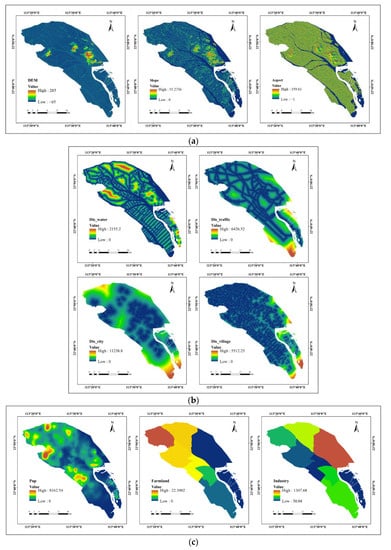
Figure 3.
The main driving factors of land use change in Nansha District in 2019: (a) Natural factors; (b) Distance factors; (c) Socioeconomic factors.

Table 4.
The meaning and data source of each driving factor in 2014, 2019, and 2020.
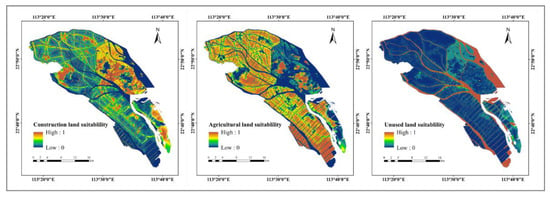
Figure 4.
Spatial patterns of the suitability of construction land, agricultural land, and unused land in Nansha in 2019.
3.5. Simulation Result Analysis and Model Validation
Based on the raster data of three major types of land use in the Nansha District in 2014 and 2019, we used the CA-Markov model in IDRISI to import the estimated transition probability matrix of land use and the suitability atlas obtained by the ANN model. At the same time, we set the standard 5 × 5 grid-cell contiguity filter to constitute the CA model filter [] and the number of iterations to be a multiple of the time interval between the base period and the end time. Figure 5 and Figure 6, respectively, show the observed and simulated land use distributions in the Nansha District in 2018 and 2020. We randomly and evenly select five areas which are distributed in Lanhe Town, Dongchong Town, Dagang Town, Huangge Town, Hengli Town, Zhujiang Street, Longxue Street, and Wanqingsha Town. The results show that the simulated results are highly similar to the spatial patches of the observed land use patterns in Parts 1 to 5. It is worth stating that the simulation results in Part 4 in Figure 5 are different from the spatial patches of the observed land use pattern. The reason for the inconsistency is that a factory has been built in Part 4 according to the government’s plan, which is difficult to simulate with the existing driving factors. Planning data should be introduced to the model in the future to avoid such inconsistencies. Once authoritative planning data have been obtained, it is straightforward to introduce them into the model of this paper as a driving factor.
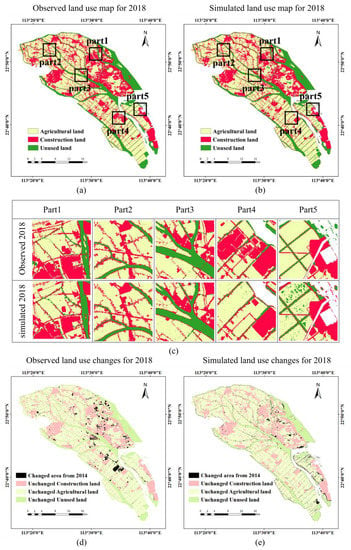
Figure 5.
Comparison of observed land use map and simulated map for 2018: (a) Observed land use map for 2018; (b) Simulated land use map for 2018; (c) Comparison of observed map and simulated map from part1 to part5; (d) Observed land use changes for 2018; (e) Simulated land use changes for 2018.
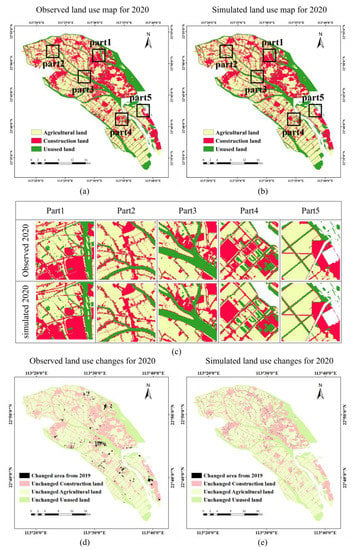
Figure 6.
Comparison of observed land use map and simulated map for 2020: (a) Observed land use map for 2020; (b) Simulated land use map for 2020; (c) Comparison of observed map and simulated map from part1 to part5; (d) Observed land use changes for 2020; (e) Simulated land use changes for 2020.
To further validate the model and assess its reliability in predicting land use classification in future years, we compared the maps of the observed distributions of three major land use types in 2018 and 2020 with the simulated maps for the same periods. Then, a quantitative accuracy test and confusion matrix were used to test the consistency between the observed and simulated land use. According to the confusion matrix in Table 5, the overall accuracy between the simulated cell number and the actual cell number of the three types of land use in 2018 was 94.22% and the kappa value was 0.904565. According to the confusion matrix in Table 6, the overall accuracy between the simulated cell number and the observed cell number of the three land use types in 2020 was 97.72% and the kappa value was 0.962761. In addition, I calculated the figure of merit for the simulation results of the three land use types in 2018 and 2020 (Table 7). According to the table, the value of figure of merit in 2018 is above 80%, and that in 2019 is above 90%. The results show that the simulation accuracy of the model is high. This also indicates that the model has a high confidence level.

Table 5.
The confusion matrix of observed and simulated land use types in 2018.

Table 6.
The confusion matrix of observed and simulated land use types in 2020.

Table 7.
The figure of merit for the simulation results of the three land use types in 2018 and 2020.
3.6. Model Comparison
In order to compare the performance of our model with the CA-Markov model and CA-LTOM model, we used the distribution map of the three land use types in 2019 as the base period data and the three models to simulate the distribution of land use in Nansha District in 2020. Among them, the transition suitability atlas used in the CA-Markov model and CA-LTOM model was generated by the Markov tool in the IDRISI software. The tool generates a suitability atlas based on two periods of historical land use data without incorporating actual economic and social driving factors. However, the transition suitability atlas used in the ANN-CA-LTOM model was output by the ANN model based on ten driving factors. The quantitative accuracy test and confusion matrix were used to test the consistency of land use classification between the observed and simulated results from different models in 2020. The accuracy statistics of the simulation results are listed in Table 8. According to the table, the overall simulation accuracy of three models is high, which verifies the CA-Markov model’s excellent performance in land use simulation. Comparatively, the traditional CA-Markov model has the lowest simulation accuracy of 95.50%, with a kappa coefficient of 0.926538. The overall simulation accuracy of the CA-LTOM model is significantly improved, with a value of 97.71% and a kappa coefficient of 0.96256. From the estimated results, the overall accuracy of the ANN-CA-LTOM model built in this paper is slightly higher than the CA-LTOM model. Furthermore, the artificial neural network detects the potential interdependencies and captures different variables and dynamics behind land conversion []. Thus, our model is flexible by coupling ANN. We will consider more practical driving factors to enhance the simulation accuracy and achieve more meaningful prediction under different incentives or limited development policies in the future.

Table 8.
Consistency between simulations using different models and observed land use classification in Nansha District in 2020.
3.7. Simulation and Prediction of Land Use Changes in the Period 2021–2023
In our study, we assume that there is no significant change in the natural and socioeconomic factors and land use policy of Nansha District from 2020 to 2023. The land use changes from 2021 to 2023 can be simulated and predicted according to the land use transition rules from 2010 to 2020. The land use simulation maps of the Nansha District from 2021 to 2023 are shown in Figure 7. In order to quantitatively analyze land use changes from 2020 to 2023, Table 9 lists the area and change of observed land use in 2020 and simulated land use types from 2021 to 2023. As shown in Table 9, during the period 2020–2023, the proportion of agricultural land is the largest, exceeding 50% of the total area of the study area, followed by the construction land and unused land. The area of construction land will continue to increase from 191.01 km2 (28.16%) in 2020 to 200.07 km2 (29.49%) in 2023, but the increase will slow down year by year. The area of agricultural land and unused land will continue to decline. The proportions will decrease from 51.50% (349.34 km2) and 20.35% (138.04 km2) in 2020 to 50.35% (341.60 km2) and 20.15% (136.72 km2) in 2023, respectively, with the decline also slowing down year by year.
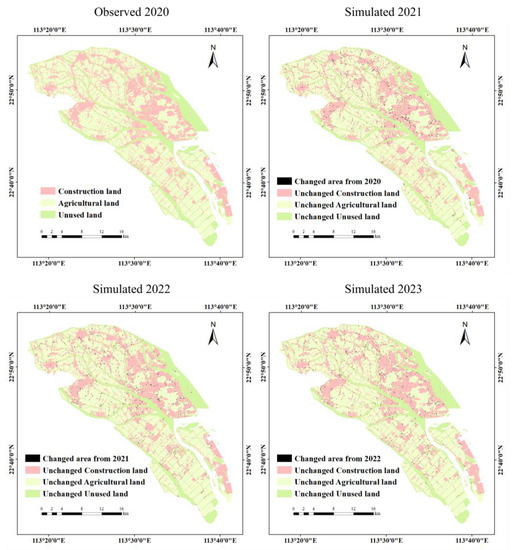
Figure 7.
Land use maps in Nansha for 2020 (observed), 2021 (simulated), 2022 (simulated), and 2023 (simulated).

Table 9.
Changes in area of the three major land use types in the Nansha District from 2020 to 2023.
According to the simulation results, although agricultural land occupies the most significant proportion among the three types of land use, with the expansion of construction land, the proportion of agricultural land will gradually decline, similar to results reported by Anne Gharaibeh []. From the simulated map, the expansion mode of construction land is mainly spreading and filling [], extending inward or outward along the edge of the original construction land, and the area adjacent to the leading road network is more likely to change into construction land. This result is also the same as the previous study, probably because the cost of developing and building a city based on the original construction land is the lowest. The flat terrain is also conducive to horizontal expansion and change of construction land. Without restrictions, agricultural land in the future may be covered by linear urban areas along the main roads. In addition, the unused land in Nansha District mainly includes rivers and wetlands. According to the simulation results, the proportion of unused land presents a slowly decreasing trend. As an essential hub node connecting the Pearl River port city cluster and Hong Kong and Macao, it is necessary to implement protection and restoration measures for water bodies in Nansha District. Strengthening wetland protection is also an essential part of regional ecological protection. Our research results show that the urbanization process of urban areas in the Nansha District will slow down during 2020–2023. Based on this situation, cities should focus on agricultural protection policies and high-quality urban development, limiting the spatial changes that may lead to urban expansion. Under the finite incremental index, planning departments should reasonably use the construction land index, promote economical and intensive land use, focus on the optimization and structural adjustment of territorial space layout in the urban construction area, and tap the potential of land resource utilization to realize improved functions of land use.
The case study in this paper only divides Nansha into three primary types of land use. However, other case studies may include more changes in land use. Our model is easy to apply to other case studies by adding more land use types into the model. This will not significantly increase data requirements or time costs.
4. Conclusions
In this paper, we aim to develop an efficient coupled model for simulating future urban land use changes. Firstly, the linear transformation optimization Markov (LTOM) model is employed to estimate the state transition probability matrix of land use types at any time interval. Secondly, based on the historical statistics and various driving factors of land use changes, we loosely couple a LTOM quantitative prediction model, CA spatial prediction model, and artificial neural network to improve the prediction accuracy with respect to future land use changes. Such a coupled model is flexible and high expansibility. It can reduce the limitations of a single model and enhance the advantages of each model. Taking Nansha District as the research area, we used national land survey data and change survey data to ensure the correctness and authority of the original experimental data. The model only needs historical statistical data of land use without the limitation of requiring two periods of land use data. Furthermore, the estimation results are rarely affected by abnormal data. The results show that the ANN-CA-LTOM model performs well in regional land use simulation with an overall accuracy of 97.72% and a kappa value of 0.962761. The study results can reveal the trends in regional land use change in the future and provide a reference for the formulation of land-planning policies and thus the optimal control of national land space.
However, the approach in our study does have certain limitations in its present state, and these limitations will mark the directions of our future research. The driving factor of the proportion of farmland in prime farmland protection areas is introduced in the study of land use suitability, but it is still not deeply integrated with regional policies, and the driving factors selected from natural conditions and socioeconomic perspectives are not comprehensive enough. In future research, regional planning and policies should be considered, so that the simulated results will conform to the urban development to improve the validity and accuracy of the simulation.
Author Contributions
Conceptualization, C.H.; methodology, J.L.; validation, J.L., C.H. and X.K.; formal analysis, C.H.; investigation, J.L.; data curation, J.L., X.K. and F.C.; Resources, J.L. and C.H.; writing—original draft preparation, J.L. and C.H.; writing—review and editing, J.L. and C.H.; visualization, J.L.; supervision, C.H.; project administration, C.H.; funding acquisition, C.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Hubei Province of China under grant number 2022CFB194.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
The related work on data processing was supported by the Research on Guangzhou Natural Resources Investigation, Monitoring and Evaluation System (Evaluation Pilot) project.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Wang, Q.; Wang, H. Dynamic simulation and conflict identification analysis of production–living–ecological space in Wuhan, Central China. Integr. Environ. Assess. Manag. 2022, 18, 1578–1596. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Luo, T.; Liu, Z.; Kong, X.; Li, J.; Tan, R. A comparative analysis of urban and rural construction land use change and driving forces: Implications for urban–rural coordination development in Wuhan, Central China. Habitat Int. 2015, 47, 113–125. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Song, W. Simulating Urban Sprawl in China Based on the Artificial Neural Network-Cellular Automata-Markov Model. Sustainability 2020, 12, 4341. [Google Scholar] [CrossRef]
- Yin, H.; Kong, F.; Yang, X.; James, P.; Dronova, I. Exploring zoning scenario impacts upon urban growth simulations using a dynamic spatial model. Cities 2018, 81, 214–229. [Google Scholar] [CrossRef]
- Wei, Y.D.; Ye, X. Urbanization, urban land expansion and environmental change in China. Stoch. Environ. Res. Risk Assess. 2014, 28, 757–765. [Google Scholar] [CrossRef]
- Zhang, J.; Hou, Y.; Dong, Y.; Wang, C.; Chen, W. Land Use Change Simulation in Rapid Urbanizing Regions: A Case Study of Wuhan Urban Areas. Int. J. Environ. Res. Public Health 2022, 19, 8785. [Google Scholar] [CrossRef]
- Karimi, H.; Jafarnezhad, J.; Khaledi, J.; Ahmadi, P. Monitoring and prediction of land use/land cover changes using CA-Markov model: A case study of Ravansar County in Iran. Arab. J. Geosci. 2018, 11, 592. [Google Scholar] [CrossRef]
- Mansour, S.; Al-Belushi, M.; Al-Awadhi, T. Monitoring land use and land cover changes in the mountainous cities of Oman using GIS and CA-Markov modelling techniques. Land Use Policy 2020, 91, 104414. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, Y.; Wang, X.; Lin, Q.; Li, L. A new approach to land use optimization and simulation considering urban development sustainability: A case study of Bortala, China. Sustain. Cities Soc. 2022, 87, 104135. [Google Scholar] [CrossRef]
- Geng, B.; Zheng, X.; Fu, M. Scenario analysis of sustainable intensive land use based on SD model. Sustain. Cities Soc. 2017, 29, 193–202. [Google Scholar] [CrossRef]
- Li, Y.; Yao, S.; Yan, F.; Chen, L.; Qi, Y. Improved Cellular Automata-Markov model-based simulation and prediction on evolution of land use pattern: A case of Xinyu City. Water Resour. Hydropower Eng. 2022, 53, 71–83. [Google Scholar]
- Huang, Y.; Yang, B.; Wang, M.; Liu, B.; Yang, X. Analysis of the future land cover change in Beijing using CA–Markov chain model. Environ. Earth Sci. 2020, 79, 60. [Google Scholar] [CrossRef]
- Liu, G.; Jin, Q.; Li, J.; Li, L.; He, C.; Huang, Y.; Yao, Y. Policy factors impact analysis based on remote sensing data and the CLUE-S model in the Lijiang River Basin, China. Catena 2017, 158, 286–297. [Google Scholar] [CrossRef]
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Gharaibeh, A.; Shaamala, A.; Obeidat, R.; Al-Kofahi, S. Improving land-use change modeling by integrating ANN with Cellular Automata-Markov Chain model. Heliyon 2020, 6, e5092. [Google Scholar] [CrossRef]
- Chotchaiwong, P.; Wijitkosum, S. Predicting Urban Expansion and Urban Land Use Changes in Nakhon Ratchasima City Using A CA-Markov Model under Two Different Scenarios. Land 2019, 8, 140. [Google Scholar] [CrossRef]
- Zhao, Z.; Guan, D.; Du, C. Urban growth boundaries delineation coupling ecological constraints with a growth-driven model for the main urban area of Chongqing, China. GeoJournal 2020, 85, 1115–1131. [Google Scholar] [CrossRef]
- Hamad, R.; Balzter, H.; Kolo, K. Predicting Land Use/Land Cover Changes Using a CA-Markov Model under Two Different Scenarios. Sustainability 2018, 10, 3421. [Google Scholar] [CrossRef]
- Jia, J.; Sun, Z.; Gui, X.; Mao, L. Simulation of Landscape Pattern of Agricultural and Forestry Land in Hegang City Based on Ann-CA-Markov Model. For. Resour. Manag. 2022, 3, 81–88. [Google Scholar]
- Halmy, M.W.A.; Gessler, P.E.; Hicke, J.A.; Salem, B.B. Land use/land cover change detection and prediction in the north-western coastal desert of Egypt using Markov-CA. Appl. Geogr. 2015, 63, 101–112. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, X.; Wu, B. Spatial distribution simulation of urban construction land expansion in Zhangzhou city. J. Fuzhou Univ. 2012, 40, 63–69. [Google Scholar]
- Xu, T.; Gao, J. Directional multi-scale analysis and simulation of urban expansion in Auckland, New Zealand using logistic cellular automata. Comput. Environ. Urban Syst. 2019, 78, 101390. [Google Scholar] [CrossRef]
- Guan, D.; Zhao, Z.; Tan, J. Dynamic simulation of land use change based on logistic-CA-Markov and WLC-CA-Markov models: A case study in three gorges reservoir area of Chongqing, China. Environ. Sci. Pollut. Res. 2019, 26, 20669–20688. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Y.; Liang, Y. Simulation and spatiotemporal evolution analysis of biocapacity in Xilingol based on CA-Markov land simulation. Environ. Sustain. Indic. 2021, 11, 100136. [Google Scholar] [CrossRef]
- Fu, X.; Wang, X.; Yang, Y.J. Deriving suitability factors for CA-Markov land use simulation model based on local historical data. J. Environ. Manag. 2018, 206, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Dang, X.; Sun, Q.; Wang, S. Multi-scenario simulation of urban land change in Shanghai by random forest and CA-Markov model. Sustain. Cities Soc. 2020, 55, 102045. [Google Scholar] [CrossRef]
- Xing, R.; Zhou, Q. Predictive Simulation of Ecological Spatial Evolution Based on Ann-CA-Markov Model: A Case Study of Wanzhou District, Chongqing. J. Ecol. Rural. Environ. 2021, 37, 740–750. [Google Scholar]
- Baqa, M.F.; Chen, F.; Lu, L.; Qureshi, S.; Tariq, A.; Wang, S.; Jing, L.; Hamza, S.; Li, Q. Monitoring and Modeling the Patterns and Trends of Urban Growth Using Urban Sprawl Matrix and CA-Markov Model: A Case Study of Karachi, Pakistan. Land 2021, 10, 700. [Google Scholar] [CrossRef]
- Zhou, D.; Lin, Z.; Liu, L. Regional land salinization assessment and simulation through cellular automaton-Markov modeling and spatial pattern analysis. Sci. Total Environ. 2012, 439, 260–274. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, B.; Jiang, W.; Qiu, H. Identification and scenario prediction of degree of wetland damage in Guangxi based on the CA-Markov model. Ecol. Indic. 2021, 127, 107764. [Google Scholar] [CrossRef]
- Xu, Z. Research of Method to Estimate Markov State Transition Probability Matrix. Master’s Thesis, Northeast Agricultural University, Harbin, Heilongjiang Province, China, 2013. [Google Scholar]
- Zhao, J.; Ma, Y.; Shi, Y.; Hao, S.; Ma, X. Prediction of soil erosion evolution in counties in the loess hilly region based on ANN-CA model. Sci. Soil Water Conserv. 2021, 19, 60–68. [Google Scholar]
- Soares-Filho, B.S.; Cerqueira, G.C.; Pennachin, C.L. dinamica—A stochastic cellular automata model designed to simulate the landscape dynamics in an Amazonian colonization frontier. Ecol. Model. 2002, 154, 217–235. [Google Scholar] [CrossRef]
- Wang, H.; He, S.; Liu, X.; Dai, L.; Pan, P.; Hong, S.; Zhang, W. Simulating urban expansion using a cloud-based cellular automata model: A case study of Jiangxia, Wuhan, China. Landsc. Urban Plan. 2013, 110, 99–112. [Google Scholar] [CrossRef]
- Gao, J.; Chen, J.; Yuan, F.; Wei, Y.; Chen, W. Patterns, functions and underlying mechanisms of urban land expansion in Nanjing. Geogr. Res. 2014, 33, 1892–1907. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).