Physical Urban Area Identification Based on Geographical Data and Quantitative Attribution of Identification Threshold: A Case Study in Chongqing Municipality, Southwestern China
Abstract
:1. Introduction
2. Materials and Methods
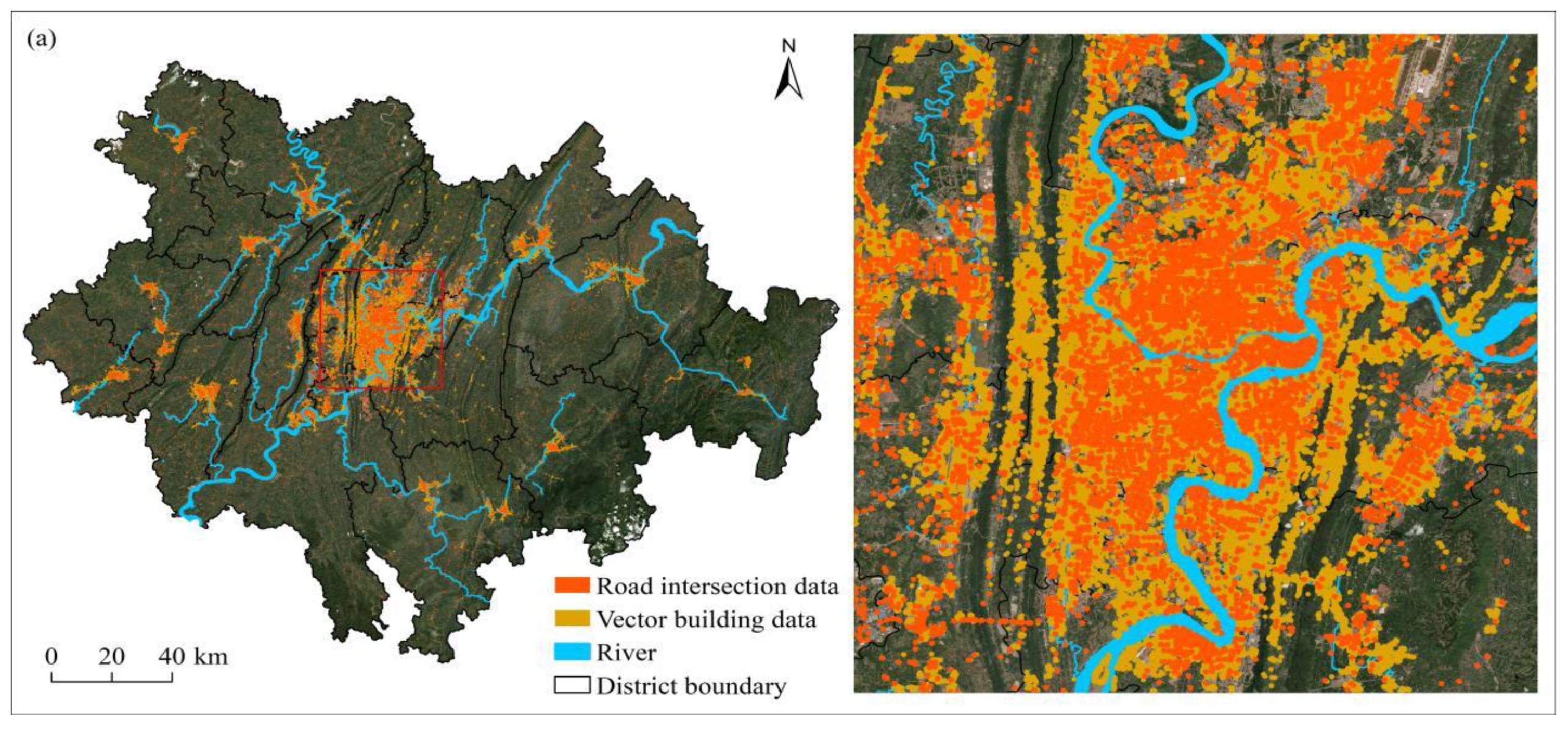
2.1. Study Area and Data Sources
2.2. Research Methods
2.2.1. Urban Expansion Curve Method
2.2.2. Geographical Detector Method
3. Results
3.1. Identification of Optimal Distance Threshold
3.2. Identification of Physical Urban Area
3.3. Analysis of Driving Factors of Optimal Distance Threshold
3.3.1. Factor Detection Analysis
3.3.2. Ecological Detection Analysis
3.3.3. Interactive Detection Analysis
3.3.4. Adaptiveness of Optimal Distance Threshold
4. Discussion
4.1. Accuracy Verification of Physical Urban Area
4.2. Quantitative Attribution of Optimal Distance Threshold
5. Conclusions
- (1)
- The physical urban area of the Chongqing municipality based on two geographical data have a similar distribution pattern. However, the vector building data can better reflect the urban pattern and has a higher accuracy than road intersection data. The optimal distance threshold based on vector building data was 146 m, and the physical urban area was 1598.43 km2. While the optimal distance threshold based on road intersection data was 156 m, and the physical urban area was 1112.79 km2. The area error of vector building data was 13.18%, which was smaller than -21.2% of road intersection data. The urban pattern of the Chongqing municipality is characterized by core-periphery distribution and the distribution along the water corridor.
- (2)
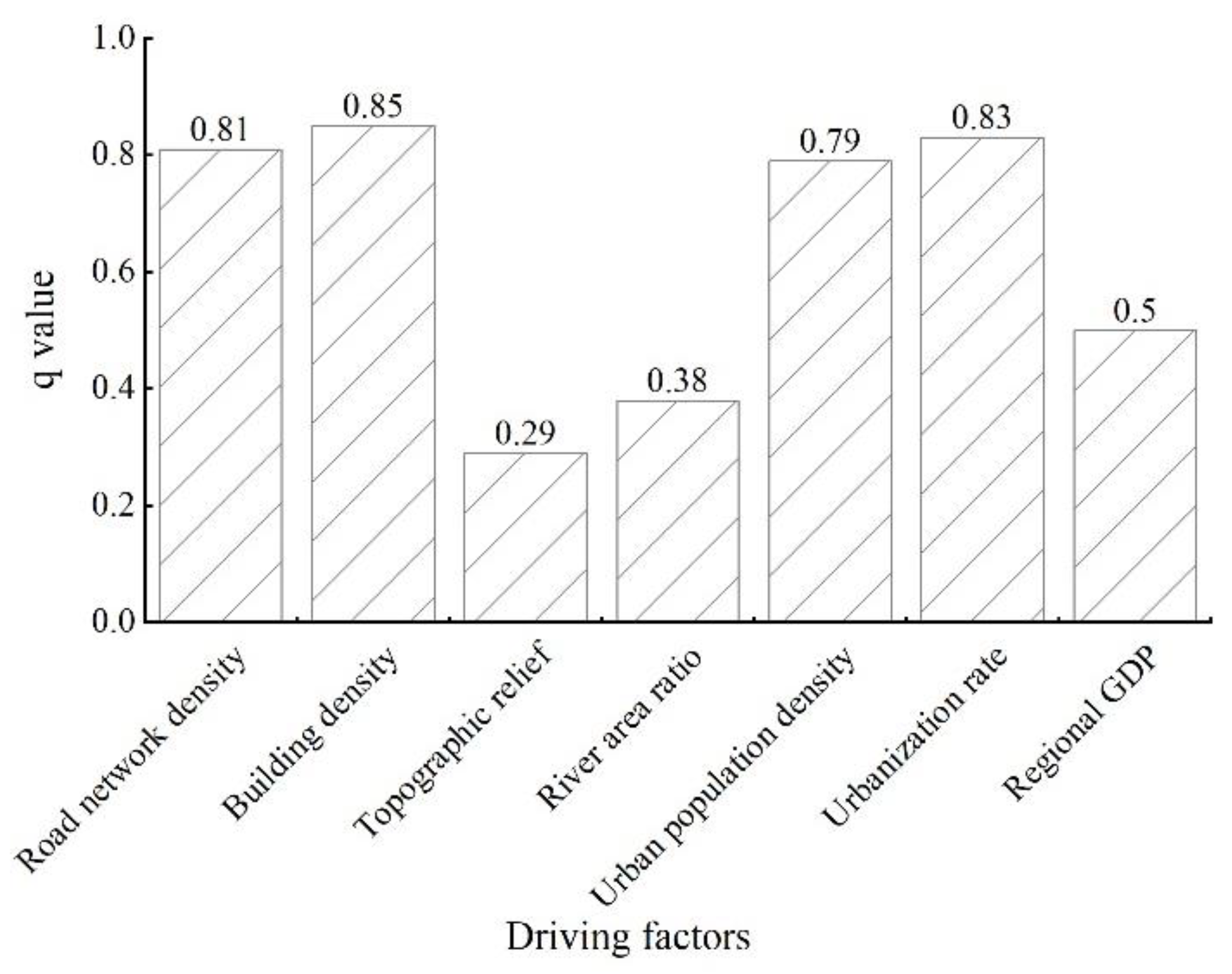
- Based on the factor detection analysis, the compactness of urban spatial structure, the scale of a city and the flow of urban population had the greatest influence on the optimal distance threshold for identifying physical urban area, with the index value of influence degree ≥0.79. Among them, there was no significant difference in the influence of the four factors of road network density, building density, urban population density and urbanization rate on the optimal distance threshold. The regional GDP, river area ratio and topographic relief that had little influence on the optimal distance threshold also show insignificant difference. Based on the interaction detection analysis, the pairwise interaction of the three groups of driving factors was greater than the influence of a single factor on the optimal distance threshold. The interaction relationship between any two factors included nonlinear enhancement and bilinear enhancement. Where the synergistic effect of the compactness of urban spatial structure, the scale of a city and the flow of urban population with regional GDP of economic indicator had the most significant impact on the optimal distance threshold, the index value of influence degree is ≥0.93.
- (3)
- Under the synergistic influence of the 7 various factors, the explanatory power of the optimal distance threshold was greatly enhanced and the optimal distance threshold regularly corresponded to different stages of buffer radius in the process of expansion, which had the characteristics of self-adaptation. In addition to the Ba’nan district and the Beibei district, the optimal distance thresholds of the Chongqing central districts were between 100–1000 m, and the optimal distance threshold of peripheral districts were at the stage of 20–100 m.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Land Space Planning Bureau; Ministry of Natural Resources. Scientific Identification of Urban Areas to Enhance Spatial Governance Capacity; China Natural Resources News: Shenzhen, China, 2021; pp. 7–22. [Google Scholar]
- Qi, W.; Wang, K.Y. Spatial differences and optimization integration between urban administrative areas and physical areas in China. Geogr. Res. 2019, 38, 207–220. [Google Scholar]
- Zhou, Y.X.; Shi, Y.L. The concept of physical area for the establishment of Chinese cities. Acta Geogr. Sin. 1995, 4, 289–301. [Google Scholar]
- Chen, X.X.; Feng, J. Discrimination and Research Progress of Urban Regional Concept. Urban Dev. Stud. 2020, 27, 62–69. [Google Scholar]
- Kong, L.; He, Z.W.; Chen, Z.S.; Luo, M.L.; Du, Z.; Zhu, F.Q.; He, L. Spatial distribution and morphological identification of regional urban settlements based on road intersections. ISPRS Int. J. Geo-Inf. 2021, 10, 201. [Google Scholar] [CrossRef]
- Department of the Ministry of Construction of the People’s Republic of China. Standards for Basic Terms of Urban Planning; China Construction Industry Press: Beijing, China, 1999. [Google Scholar]
- Zhou, Y.X. Urban Geography; The commercial Press: Beijing, China, 1995. [Google Scholar]
- Chen, Y.G. Fractal Urban System: Scale Symmetry Spatial Complexity; Science Press: Beijing, China, 2008. [Google Scholar]
- Fang, C.L. Research progress and basic judgment of urban agglomeration spatial scope identification standard. Urban Plan. Forum 2009, 4, 6. [Google Scholar]
- Rozenfeld, H.; Rybski, D.; Gabaix, X.; Makse, H. The area and population of cities: New insights from a different perspective on cities. Am. Econ. Rev. 2010, 101, 2205–2225. Available online: https://www.aeaweb.org/articles?id=10.1257/aer.101.5.2205 (accessed on 1 January 2021). [CrossRef] [Green Version]
- Cao, F.J.; Qiu, Y.; Zou, Y. Fast extraction method of built-up area based on H/T fracture method and POI data. Geogr. Geo-Inf. Sci. 2020, 36, 7. [Google Scholar]
- Zhang, H.C.; Ning, X.G.; Shao, Z.F.; Wang, H. Spatiotemporal pattern analysis of china’s cities based on high-resolution imagery from 2000 to 2015. ISPRS Int. J. Geo-Inf. 2019, 8, 241. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Tu, M.G.; Wang, S.X.; Liu, W.L. A novel approach for identifying urban built-up area boundaries using high-resolution remote-sensing data based on the scale effect. ISPRS Int. J. Geo-Inf. 2018, 7, 135. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.T.; Xie, Z.W.; You, Y.C.; Xuan, X. Research on Rapid Extraction Method of Urban Built-Up Area with Multiple Remote Sensing Indexes. In Book Geoinformatics in Sustainable Ecosystem and Society; Springer: Guangzhou, China, 2020; pp. 199–209. [Google Scholar]
- Xu, T.T.; Coco, G.; Gao, J. Extraction of urban built-up areas from nighttime lights using artificial neural network. Geocarto Int. 2018, 35, 1049–1066. [Google Scholar] [CrossRef]
- Yu, B.L.; Tang, M.; Wu, Q.S.; Yang, C.S.; Deng, S.Q.; Shi, K.F.; Peng, C.; Wu, J.P.; Chen, Z.Q. Urban built-up area extraction from log-transformed NPP-VIIRS nighttime light composite data. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1279–1283. Available online: https://ieeexplore.ieee.org/document/8358755 (accessed on 1 January 2021). [CrossRef]
- Su, Y.X.; Chen, X.Z.; Wang, C.Y.; Zhang, H.O.; Liao, J.S.; Ye, Y.Y. A new method for extracting built-up urban areas using DMSP-OLS nighttime stable lights: A case study in the pearl river delta, southern china. Giscience Remote Sens. 2015, 52, 218–238. [Google Scholar] [CrossRef]
- Lin, X.J.; Fang, S.F.; Xu, Y.L.; Zou, B.Y.; Luo, M.L. Urban Boundary Identification Based on Neighborhood Expansion Curve of Road Intersection Points—Taking Chengdu, Xi’an, Wuhan, Nanjing and Changsha as Examples. Prog. Geogr. 2018, 37, 781–789. [Google Scholar]
- Jiang, B.; Jia, T. Zipf’s law for all the natural cities in the united states: A geospatial perspective. Int. J. Geogr. Inf. Sci. 2011, 25, 1269–1281. [Google Scholar] [CrossRef]
- Jia, T.; Jiang, B. Measuring Urban Sprawl Based on Massive Street Nodes and the Novel Concept of Natural Cities. Physics 2012. Available online: https://arxiv.org/abs/1010.0541 (accessed on 1 November 2021).
- Jiang, B. Natural cities generated from all building locations in America. Data 2019, 4, 59. [Google Scholar] [CrossRef] [Green Version]
- Tannier, C.; Thomas, I.; Vuidel, G.; Frankhauser, P. A fractal approach to identifying urban boundaries. Geogr. Anal. 2011, 43, 211–227. [Google Scholar] [CrossRef]
- Tannier, C.; Thomas, I. Defining and characterizing urban boundaries: A fractal analysis of theoretical cities and Belgian cities. Comput. Environ. Urban Syst. 2013, 41, 234–248. [Google Scholar] [CrossRef]
- Chen, Y.G. How high is urbanization in China? Why do urban geography research draw on fractal geometry? City Plan. Review 2003, 7, 12–17. [Google Scholar]
- Chen, Y.G.; Wang, J.J. Multifractal characterization of urban form and growth: The case of Beijing. Environ. Plan. B Urban Anal. City Sci. 2013, 40, 884–904. [Google Scholar] [CrossRef]
- Ogoke, U. Correlational analysis of someinfectious diseases. IOSR J. Math. 2022, 14, 54–57. [Google Scholar]
- Zhou, Y.; Zhao, C. Research on government subsidy, internal control and overinvestment in enterprises by multiple regression analysis method: Based on multiple regression analysis method. In Proceedings of the Management Science Informatization and Economic Innovation Development Conference, Guangzhou, China, 18–20 December 2020; pp. 285–288. [Google Scholar]
- Yu, G. The influencing factors of drug addiction based on principal component analysis model. IOP Conf. Ser. Mater. Sci. Eng. 2019, 612, 022002. [Google Scholar] [CrossRef]
- Wang, J.F.; Xu, C.D. Geodetector: Principle and prospect. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar]
- Ahmadpoor, N.; Smith, A.D.; Heath, T. Rethinking legibility in the era of digital mobile maps: An empirical study. J. Urban Des. 2020, 26, 296–318. [Google Scholar] [CrossRef]
- Jokar Arsanjani, J.; Mooney, P.; Zipf, A.; Helbich, M. OpenStreetMap in GIScience: Experiences, Research, Applications; Springer: New York, NY, USA, 2015. [Google Scholar]
- Mandelbrot, B.B. The fractal geometry on nature. Am. J. Phys. 1983, 51, 468. [Google Scholar] [CrossRef]
- Minkowski, H. Volumen und Oberfläche. Math. Ann. 1903, 57, 447–495. [Google Scholar] [CrossRef] [Green Version]
- Lowe, D.G. Organization of smooth image curves at multiple scales. Int. J. Comput. Vis. 1988, 3, 119–130. [Google Scholar] [CrossRef]
- Huang, J.X.; Wang, J.F.; Bo, Y.C.; Xu, C.D.; Hu, M.G.; Huang, D.C. Identification of health risks of hand, foot and mouth disease in china using the geographical detector technique. Int. J. Environ. Res. Public Health 2014, 11, 3407–3423. [Google Scholar] [CrossRef]
- Tung Chi University; Xi’an University of Architecture and Technology; Southeast University; Chongqing University. Fourth Edition of Housing Architecture; China Construction Industry Press: Beijing, China, 2005. [Google Scholar]
- Shi, F.; Yin, H.W. Research on Dynamic Optimization Method of Urban Road Grade Structure. In Book Annual Meeting of Asian Transportation Society and ‘Transportation and Logistics’ Symposium; Science and Technology of China Press: Dalian, China, 2007. [Google Scholar]
- Huang, X.; Li, J.Y.; Jie, Y.; Zhang, Z.; Li, D.R.; Liu, X.P. 30 m global impervious surface area dynamics and urban expansion pattern observed by landsat satellites: From 1972 to 2019. Sci. China Earth Sci. 2021, 64, 1922–1933. Available online: https://link.springer.com/article/10.1007/s11430-020-9797-9 (accessed on 1 December 2021). [CrossRef]
- Zhao, M.; Cheng, C.X.; Zhou, Y.Y.; Li, X.C.; Shen, S.; Song, C.Q. A global dataset of annual urban extents (1992–2020) from harmonized nighttime lights. Earth Syst. Sci. Data 2022, 14, 517–534. Available online: https://essd.copernicus.org/articles/14/517/2022/ (accessed on 1 October 2022). [CrossRef]
- Portugali, J. Self-organizing cities. Futures 1997, 29, 353–380. [Google Scholar] [CrossRef]
- Portugali, J. Self-Organization and the City; Springer: New York, NY, USA, 1999. [Google Scholar]
- Wu, K.H.; Li, C.K.; Liu, J.J.; Hao, H.J. Development boundary identification of urban agglomeration core area based on spatial syntax theory. Geogr. Res. 2020, 39, 1418–1426. [Google Scholar]
- Zhan, D.S.; Zhang, W.Z.; Yu, J.H.; Meng, B.; Dang, Y.X. The impact mechanism of Beijing residents’ livable satisfaction based on geographical detectors. Prog. Geogr. 2015, 34, 966–975. [Google Scholar]
- Li, J. Urban Design Theory and Method; Wuhan University Press: Wuhan, China, 2010. [Google Scholar]
- Tan, X.Y.; Huang, B. Identifying urban agglomerations in china based on density—Density correlation functions. Ann. Am. Assoc. Geogr. 2022, 112, 1666–1684. [Google Scholar] [CrossRef]
- Long, H.L.; Wu, X.Q.; Wang, W.J.; Dong, G.H. Analysis of urban-rural land-use change during 1995–2006 and its policy dimensional driving forces in Chongqing, china. Sensors 2008, 8, 681–699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, D.H. Third Edition of Urban Planning Principle; China Construction Industry Press: Beijing, China, 2001. [Google Scholar]
- Wu, Z.Q.; Li, D.H. Urban Planning Principle; China Construction Industry Press: Beijing, China, 2010. [Google Scholar]
- Liang, L.; Chen, M.; Lu, D. Revisiting the relationship between urbanization and economic development in china since the reform and opening-up. Chin. Geogr. Sci. 2022, 32, 1–15. Available online: https://link.springer.com/article/10.1007/s11769-022-1255-7 (accessed on 1 October 2022). [CrossRef]

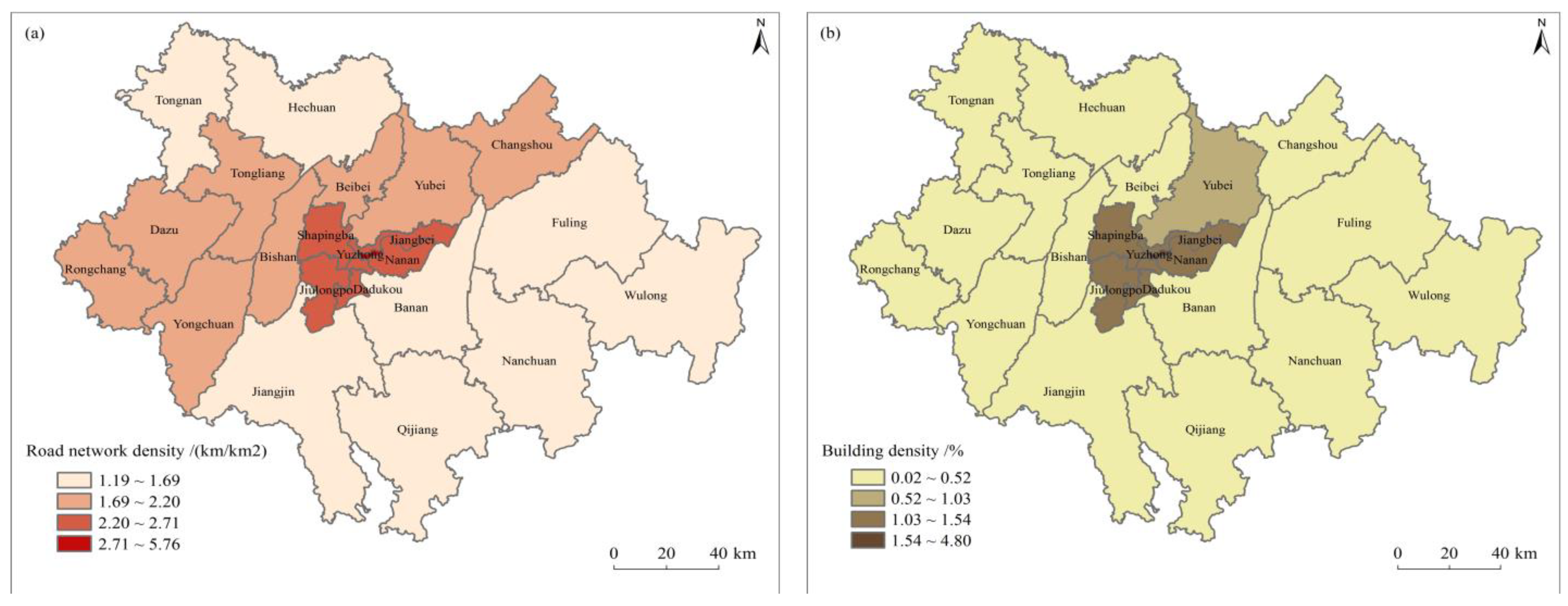


| District | Built-Up Area/km2 | Road Network Density/(km/km2) | Building Density/% | Topographic Relief/m | River Area Ratio/% | Urban Population Density/(Million People/km2) | Urbanization Rate/% | Regional GDP/(Billion Yuan) |
|---|---|---|---|---|---|---|---|---|
| Ba’nan | 105.38 | 1.64 | 0.23 | 148 | 2.31 | 0.05 | 82.71 | 875 |
| Beibei | 65.66 | 1.72 | 0.48 | 104 | 2.32 | 0.09 | 84.50 | 606 |
| Bishan | 33.73 | 1.96 | 0.22 | 62 | 0.57 | 0.05 | 60.20 | 681 |
| Dadukou | 35.99 | 2.56 | 1.54 | 69 | 11.16 | 0.34 | 97.71 | 254 |
| Dazu | 30.09 | 1.75 | 0.15 | 95 | 0.34 | 0.03 | 60.05 | 646 |
| Fuling | 72.01 | 1.64 | 0.07 | 200 | 3.28 | 0.03 | 69.77 | 1179 |
| Hechuan | 49.02 | 1.44 | 0.09 | 158 | 3.67 | 0.04 | 70.59 | 913 |
| Jiangbei | 101.12 | 2.58 | 1.43 | 118 | 10.07 | 0.39 | 96.50 | 1240 |
| Jiangjin | 87.6 | 1.27 | 0.05 | 199 | 3.17 | 0.03 | 69.76 | 1037 |
| Jiulongpo | 132.09 | 2.56 | 1.54 | 58 | 2.65 | 0.27 | 94.14 | 1463 |
| Nan’an | 90.88 | 2.71 | 1.36 | 111 | 8.31 | 0.34 | 96.03 | 771 |
| Nanchuan | 26.55 | 1.19 | 0.04 | 273 | 0.22 | 0.01 | 62.35 | 334 |
| Qijiang | 26.89 | 1.53 | 0.07 | 198 | 0.53 | 0.03 | 64.08 | 683 |
| Rongchang | 21.68 | 1.94 | 0.15 | 63 | 0.47 | 0.04 | 58.36 | 653 |
| Shapingba | 121.08 | 2.67 | 1.46 | 64 | 1.71 | 0.28 | 95.97 | 977 |
| Tongliang | 20.46 | 1.95 | 0.12 | 79 | 0.78 | 0.03 | 58.36 | 617 |
| Tongnan | 30.46 | 1.60 | 0.06 | 72 | 0.80 | 0.03 | 55.56 | 451 |
| Wulong | 6.58 | 1.57 | 0.02 | 288 | 0.69 | 0.01 | 45.55 | 210 |
| Yongchuan | 80.4 | 1.92 | 0.14 | 114 | 1.00 | 0.05 | 71.27 | 953 |
| Yubei | 202.44 | 1.91 | 0.53 | 119 | 1.62 | 0.1 | 84.22 | 1848 |
| Yuzhong | 17.62 | 5.76 | 4.80 | 74 | 21.13 | 2.89 | 100.00 | 1301 |
| Changshou | 54.5 | 1.82 | 0.17 | 109 | 1.96 | 0.04 | 67.82 | 701 |
| Driving Factors | Number of Partitions | Partition Description |
|---|---|---|
| Road network density/(km/km2) | 1~4 | 1. 1.19~1.69; 2. 1.69~2.20; 3. 2.20~2.71; 4. 2.71~5.76 |
| Building density/% | 1~4 | 1. 0.02~0.52; 2. 0.52~1.03; 3. 1.03~1.54; 4.1.54~4.80 |
| Topographic relief/m | 1~6 | 1. 58~96; 2. 96~134; 3. 134~173; 4. 173~211; 5. 211~249; 6. 249~288 |
| River area ratio/% | 1~6 | 1. 0.22~3.70; 2. 3.70~7.19; 3. 7.19~10.67; 4. 10.67~14.16; 5. 14.16~17.64; 6. 17.64~21.13 |
| Urban population density/(million people/km2) | 1~4 | 1. 0.01~0.13; 2. 0.13~0.26; 3. 0.26~0.39; 4. 0.39~2.89 |
| Urbanization rate/% | 1~5 | 1. 45.55~56.44; 2. 56.44~67.33; 3. 67.33~78.22; 4. 78.22~89.11; 5. 89.11~100 |
| Regional GDP/(billion yuan) | 1~5 | 1. 210~537; 2. 537~865; 3. 865~1192; 4. 1192~1520; 5. 1520~1848 |
| Description | Intersection |
|---|---|
| q(A∩B) > max(q(A), q(B)) | Enhance, bivariate |
| q(A∩B) < min(q(A), q(B)) | Weaken, nonlinear |
| q(A∩B) = q(A) + q(B) | Independent |
| q(A∩B) > q(A) + q(B) | Enhance, nonlinear |
| min(q(A), q(B)) < q(A∩B) < max(q(A), q(B)) | Weaken, bivariate |
| Region | Principal Curvature Point | Optimal Distance Threshold/m |
|---|---|---|
| Chongqing Municipality | 0.36 | 146 |
| Ba’nan | −0.12 | 46 |
| Beibei | 0.03 | 89 |
| Bishan | −0.26 | 57 |
| Dadukou | −0.14 | 102 |
| Dazu | −0.28 | 45 |
| Fuling | −0.96 | 36 |
| Hechuan | −0.06 | 52 |
| Jiangbei | 0.08 | 176 |
| Jiangjin | −0.25 | 50 |
| Jiulongpo | 0.10 | 169 |
| Nan’an | 0.06 | 132 |
| Nanchuan | −0.58 | 39 |
| Qijiang | −0.22 | 52 |
| Rongchang | −0.31 | 38 |
| Shapingba | 0.04 | 149 |
| Tongliang | −0.20 | 42 |
| Tongnan | 0.01 | 52 |
| Wulong | −0.81 | 32 |
| Yongchuan | 0.02 | 49 |
| Yubei | 0.11 | 104 |
| Yuzhong | −0.06 | 111 |
| Changshou | −0.14 | 64 |
| Driving Factors | Road Network Density | Building Density | Topographic Relief | River Area Ratio | Urban Population Density | Urbanization Rate |
|---|---|---|---|---|---|---|
| Building density | N | |||||
| Topographic relief | Y | Y | ||||
| River area ratio | Y | Y | N | |||
| Urban population density | N | N | Y | Y | ||
| Urbanization rate | N | N | Y | Y | N | |
| Regional GDP | Y | Y | N | N | Y | Y |
| Driving Factors | Road Network Density | Building Density | Topographic Relief | River Area Ratio | Urban Population Density | Urbanization Rate | Regional GDP |
|---|---|---|---|---|---|---|---|
| Road network density | 0.81 | ||||||
| Building density | 0.87 | 0.85 | |||||
| Topographic relief | 0.88 | 0.90 | 0.29 | ||||
| River area ratio | 0.88 | 0.91 | 0.52 | 0.38 | |||
| Urban population density | 0.82 | 0.86 | 0.88 | 0.85 | 0.79 | ||
| Urbanization rate | 0.90 | 0.88 | 0.90 | 0.91 | 0.86 | 0.83 | |
| Regional GDP | 0.95 | 0.95 | 0.87 | 0.76 | 0.95 | 0.93 | 0.50 |
| Data | Optimal Distance Threshold/m | Physical Urban Area/km2 | Built-Up Area/km2 | Area Error Rate/% |
|---|---|---|---|---|
| Vector building | 146 | 1598.43 | 1412.23 | 13.18% |
| Road intersection | 156 | 1112.79 | −21.2% | |
| Landsat satellite | none | 2081.85 | 47.42% | |
| Harmonized nighttime light | none | 1948.17 | 37.95% |
| Region | Physical Urban Area/km2 | Area Error Rate/% |
|---|---|---|
| Ba’nan | 112.82 | 7.06% |
| Beibei | 80.1 | 21.99% |
| Bishan | 25.57 | −24.19% |
| Dadukou | 37.95 | 5.45% |
| Dazu | 23.31 | −22.53% |
| Fuling | 47.97 | −33.38% |
| Hechuan | 39.26 | −19.91% |
| Jiangbei | 84.27 | −16.66% |
| Jiangjin | 60.86 | −30.53% |
| Jiulongpo | 164.57 | 24.59% |
| Nan’an | 101.76 | 11.97% |
| Nanchuan | 22.68 | −14.58% |
| Qijiang | 28.47 | 5.88% |
| Rongchang | 16.09 | −25.78% |
| Shapingba | 151.99 | 25.53% |
| Tongliang | 16.47 | −19.50% |
| Tongnan | 21.56 | −29.22% |
| Wulong | 7.86 | 19.45% |
| Yongchuan | 50.48 | −37.21% |
| Yubei | 155.23 | −23.32% |
| Yuzhong | 18.29 | 3.80% |
| Changshou | 41.02 | −24.73% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Kong, L.; Chen, Z.; Yang, X.; Luo, M. Physical Urban Area Identification Based on Geographical Data and Quantitative Attribution of Identification Threshold: A Case Study in Chongqing Municipality, Southwestern China. Land 2023, 12, 30. https://doi.org/10.3390/land12010030
Wang D, Kong L, Chen Z, Yang X, Luo M. Physical Urban Area Identification Based on Geographical Data and Quantitative Attribution of Identification Threshold: A Case Study in Chongqing Municipality, Southwestern China. Land. 2023; 12(1):30. https://doi.org/10.3390/land12010030
Chicago/Turabian StyleWang, Dan, Liang Kong, Zhongsheng Chen, Xia Yang, and Mingliang Luo. 2023. "Physical Urban Area Identification Based on Geographical Data and Quantitative Attribution of Identification Threshold: A Case Study in Chongqing Municipality, Southwestern China" Land 12, no. 1: 30. https://doi.org/10.3390/land12010030







