U-Net-LSTM: Time Series-Enhanced Lake Boundary Prediction Model

Abstract

Change detection of natural lake boundaries is one of the important tasks in remote sensing image interpretation. In an ordinary fully connected network, or CNN, the signal of neurons in each layer can only be propagated to the upper layer, and the processing of samples is independent at each moment. However, for time-series data with transferability, the learned change information needs to be recorded and utilized. To solve the above problems, we propose a lake boundary change prediction model combining U-Net and LSTM. The ensemble of LSTMs helps to improve the overall accuracy and robustness of the model by capturing the spatial and temporal nuances in the data, resulting in more precise predictions. This study selected Lake Urmia as the research area and used the annual panoramic remote sensing images from 1996 to 2014 (Lat: 37°00′ N to 38°15′ N, Lon: 46°10′ E to 44°50′ E) obtained by Google Earth Professional Edition 7.3 software as the research data set. This model uses the U-Net network to extract multi-level change features and analyze the change trend of lake boundaries. The LSTM module is introduced after U-Net to optimize the predictive model using historical data storage and forgetting as well as current input data. This method enables the model to automatically fit the trend of time series data and mine the deep information of lake boundary changes. Through experimental verification, the model’s prediction accuracy for lake boundary changes after training can reach 89.43%. Comparative experiments with the existing U-Net-STN model show that the U-Net-LSTM model used in this study has higher prediction accuracy and lower mean square error.

1. Introduction

With the deepening of environmental science research [1,2,3], the research on the trend prediction of natural lake boundaries has become a research direction with potential value [4,5,6]. The combination of optical remote sensing images and deep learning technology provides a favorable tool for the research and development of lake boundary change prediction research [4,7,8]. In addition, to better predict lake boundary changes, change detection is one of the most important prerequisites for predicting lake boundaries based on remote sensing images [9,10,11]. For change detection, it is necessary to learn the time series data of optical remote sensing images and record the learned change information, and then use it for time series data with transferability. Traditional models, such as manual and satellite-based mapping, rely heavily on human input and thus are only suitable for certain steps in the prediction task [12]. In the final decision stage [13,14], an integrated and independent change detection method is needed to detect changes more extensively and conveniently without auxiliary tasks, such as threshold selection or classification. In order to solve the above problems, it is necessary to reduce the dependence on humans in the learning process. In recent years, with the development of deep learning and remote sensing technology, many researchers have applied these strategies to land cover prediction, greatly reducing the manual workload in the model.

In 2018, Liu et al. [15] applied a convolutional neural network (CNN) to multi-temporal polarimetric synthetic Aperture radar (SAR) images to detect and predict land cover change trends. This model first employs a CNN with only convolutional layers for change detection and then forms an LRCNN by imposing spatial constraints called local restrictions on the output layer of the CNN. LRCNN can not only identify different types of changed and unchanged data, but can also ensure noise insensitivity without losing details of changed regions. In 2020, Li et al. [16] designed a land cover classification model by using a CNN classifier to extract high-resolution features of land from Google Earth images and combining traditional machine learning classifiers, random forest (RF) and support vector machine (SVM), to extract spectral features from 30-m Landsat data. In the same year, Giang et al. [17] used the U-Net convolutional network to design a land cover classification model based on multispectral unmanned aerial vehicle (UAV) images. A total of 7 optimizer function types were used, and an area of 0.5 km × 0.8 km was used to train and test seven U-Net models. The experimental results show that the two models using the Nadam and Adadelta optimizer functions achieved higher than 83% accuracy in classifying the six land cover types, especially in open-pit mining areas and polluted streams that flow from mining areas.

However, current land cover prediction models based on CNN has great limitations when detecting time-series data such as land cover change [18,19,20,21]. However, we expect that the land cover prediction model can detect changes in all available information using complete and independent change rules and can transform the change rules into new target multi-temporal images. Simply stated, an effective change rule should have the ability to represent the change information reliably, and the learned change rule can be transferred to the new target image without any additional learning process, which shows its transferability [22].

Recently, recurrent neural network (RNN) has shown its ability to help solve the problem above [23]. In RNN, the output of neurons can act directly on itself in the next timestamp. For change detection, RNN uses hidden layers or storage units to learn the time evolution characteristics of changes and model the dynamic changes of input continuous time series data [24]. RNN, especially the long-term–short-term memory (LSTM) model, has shown its ability to solve many challenging problems involving time series data [25,26,27]. In the RNN learning framework, learning the appropriate representations of sequence data is essential to realizing artificial intelligence. It perfectly matches the requirement of change detection, i.e., the model must be able to extract and detect changes from the change information representation reliably. Therefore, the RNN model is a representative method for learning reliable difference information and providing memorability of change detection in temporal remote sensing data [28,29,30]. It might be possible to directly detect the change information with migration ability of land cover by designing a dynamic change rule with LSTM and extracting the change information characteristics of time series data.

In this study, a lake boundary change prediction model based on U-Net-LSTM is proposed. The model analyzes lake boundary change trends and extracts multi-level change characteristics using the U-Net network. After U-Net, the LSTM module is added to enhance the prediction model utilizing both recent input data and previous data storage and forgetting. The ability of LSTMs to capture temporal patterns enables combined networks to adapt to changing conditions or learn time-varying interactions. This work discusses the fundamental procedure for predicting lake boundary in remote sensing images using U-Net-LSTM. The ensemble of LSTMs helps to improve the overall accuracy and robustness of the model by capturing the spatial and temporal nuances in the data, resulting in more precise predictions. After that, a comparison with a model that just uses U-Net [31] is completed to confirm the usefulness of the LSTM module. Multiple sets of control experiments were conducted to compare and analyze the impact of the timing length of a single input image on the prediction results on two data sets, verifying the effectiveness of the proposed method.

2. Dataset

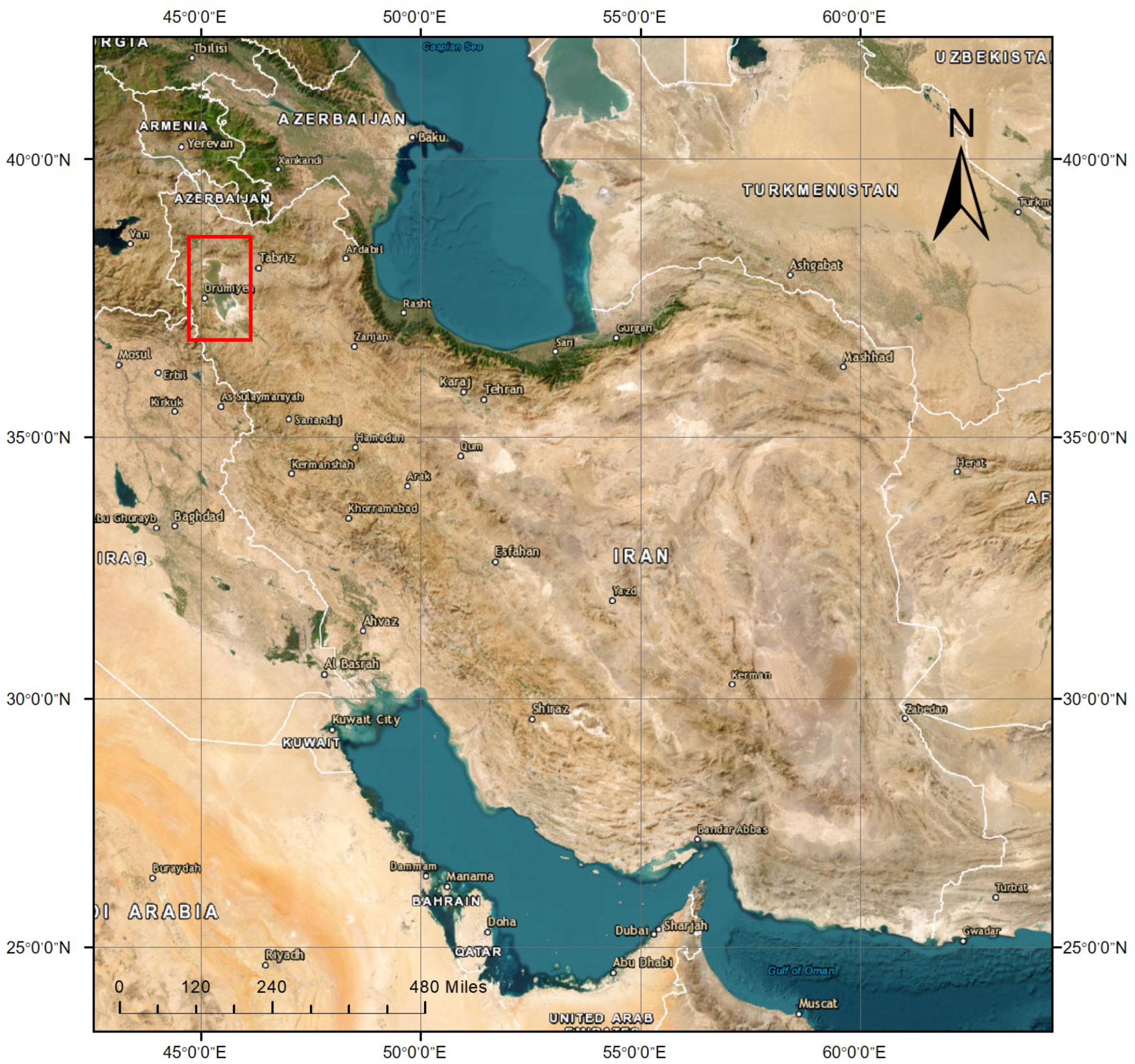
2.1. Data Source

Lake Urmia is a salty lake in northwestern Iran, close to Turkey, between East Azerbaijan Province and West Azerbaijan Province. The coordinates of Lake Urmia are located at 37°42′ north latitude and 45°22′ east longitude. Figure 1 shows the geographical location of Lake Urmia in Iran (red box).

Lake Urmia is the largest lake in Iran and the second largest saltwater lake on the Earth. Its surface area was about 5180 square kilometers, its longest point was about 140.01 km, and its widest was about 54.72 km. However, in recent years, the lake has faced significant environmental challenges, including shrinking water levels and increased salinity, making its conservation an important concern. This study selects Lake Urmia as the research area and uses its historical remote sensing images to study the rules of its boundary changes. Figure 2 shows satellite images from 1984 and 2020.

By observing historical data from 1984 to 2020, the boundaries of the lake show a trend of shrinking year by year [32]. Figure 3 presents comparative diagram of boundary reduction using images from 1984, 2000, and 2020.

This article obtained yearly images of the selected area from Google Earth Pro Version 7.3 from the years 1996 to 2014 and used them as analysis data. Each image was taken on December 30 of that year.

This study constructed two data sets for experiments. Dataset 1 is a panoramic remote sensing image of Lake Urmia to verify the effectiveness of this model at predicting the overall evolution trend of cover. Dataset 2 is a remote sensing image of part of Lake Urmia, used to test the ability of this model to capture changes in regional details. The data set information is shown in

Table 1. Dataset information.

Name	Time Period	Spatial Coverage	Image Size	Number
Dataset 1	1996–2014	Lat: 37°00′ N to 38°15′ N Lon: 46°10′ E to 44°50′ E	560 × 640	19
Dataset 2	2000–2014	Lat: 38°05′ N to 38°15′ N Lon: 45°30′ E to 44°20′ E	1280 × 560	15

[31].

2.2. Data Preprocessing

The data preprocessing process is shown in Figure 4.

2.2.1. Image Segmentation

Image segmentation and binarization are the key steps in image preprocessing [33]. The main purpose of image segmentation is to divide an image into several segments, making it easier to extract information from the segmentation and reducing the computational cost of processing large images. This technique is conducive to displaying the evolution process of lake boundaries and is of great help to the subsequent model in learning the evolution process of coverage [34]. Binarization reduces the complexity of an image by converting it into a binary form, making it easier to analyze and process.

In this study, taking dataset 2 as an example, 15 remote sensing images were segmented, and the lake was successfully distinguished from other areas, which provided help for the visualization of land coverage and the subsequent extraction and prediction of land coverage change features. Figure 5 shows the result of the remote sensing images from 2000 after segmentation and binarization.

2.2.2. Image Grayscale Gradient Filling

To facilitate the spatial transformation module in extracting the evolution characteristics of the cover according to the movement of the image pixels, this paper proposes a novel method of grayscale gradual filling based on the above binarized image [35]. The steps of this method are as follows:

Step one: The cover boundary in the image is gradually and smoothly shrunk to the center of the cover by multiple consecutive erosion operations, and the intermediate results after each contraction are saved. The formula for the erosion of image A using the erosion operator B is given in Equation (1).

$$A\ominus B=\left\{z|{\left(B\right)}_z\subset A\right\},$$

(1)

where $\ominus$ is the erosion operation, and the erosion operator B is also called the structuring element, which can generally be identified with a cross, rectangle, circle, or oval. In this section, the images from the year 2000 in the second dataset segmented by the above image are taken as an example, and the circular operator with radius 3 is used to erode the images 50 times in turn.

Step 2: According to the order of erosion, the difference image of two adjacent shrinkage images is obtained by subtracting sequentially, that is, the pixel value corresponding to the result of the ith corrosion and the result of the i + 1th corrosion is subtracted. The point set with the difference value of 255 is the pixel set deleted in the i + 1 corrosion, and the result is displayed as the lake boundary.

Step 3: The obtained difference image set is sorted in turn, and the gray level is filled according to the linear change from front to back, changing the pixel value of the point shown as white in the difference image. The set of pixels in the first difference image has the highest gray value and is close to white, while the set of pixels in the last difference image has the lowest gray value and is close to black.

Figure 6 shows the result of Figure 5 after grayscale gradient filling.

2.2.3. Filtering

The filtering operation can smooth the gray level change of the image after the grayscale gradients filling. Such a trend is beneficial to the model to obtain the optimal solution in the gradient descent algorithm. Common filtering algorithms are Gaussian filtering, mean filtering, and median filtering. Grayscale images often contain continuous variations in intensity, and Gaussian filtering can preserve these variations while reducing noise and unwanted details. This can result in a smoother and more natural appearance [36]. To better smooth the gray level change of the image, the two-dimensional Gaussian filter is selected for filtering in this paper. The formula for calculating the weight of the neighboring pixels in the two-dimensional Gaussian filter is shown in Equation (2) [37]:

$$G\left(x,y\right)=\frac{1}{2\pi {\sigma }^2}{e}^{-(x^2+y^2)/2{\sigma }^2},$$

(2)

The size of the Gaussian kernel is 5 × 5. Figure 7 shows the results of Figure 6 after filtering.

3. Method

This study proposes a dynamic evolution prediction model for land cover in remote sensing images based on the U-Net model [31] with an added LSTM module to capture the multi-dimensional change characteristics of time-series remote sensing data. The model is depicted in Figure 8 and consists of sequence image preprocessing, sequence image evolution feature extraction, evolution field fitting, spatial variation, and coverage prediction.

The specific steps of this model are as follows:

(1) Sequence image preprocessing. In this section, $N$ consecutive time series images ${[P}_1$,$P_2\dots \dots P_{n-1},P_n]$ are preprocessed, filled with gray levels in sequence, and input into the evolution feature extraction module in chronological order.

(2) Evolutionary feature extraction. After each convolutional layer, an LSTM module is added, and the input is the preprocessed $N$ consecutive time series images in step (1). For example, suppose the image width is $\mathrm{W}$ and the height is H, and the time-series images are spliced into a tensor of size $N\times W\times H$ according to the time dimension. LSTM saves the intermediate output results of $N$ time steps, and it is possible to return the output results of all time steps or the last time step.

(3) In the feature fusion stage, the Nth or last time step of the multi-scale time series characteristics passed through the LSTM module is selected, and it is combined with the output of the symmetrically upsampled layer. The resulting output is then forwarded to the next upsampled layer. The width and height of the output image of the final upsampled layer are the same as that of a single input image. Additionally, the first M sequential images are selected and sent to step (4).

(4) Evolution field. The evolution field estimates the displacement in two directions from the image at the Nth time step to the image at the $N+1$-th time step, and the size is $W\times H\times 2$.

(5) Spatial transformation. Each pixel of the N-th time series image is spatially transformed based on the evolving field of step (4) to fit the time series image of the $N+1$th time step, namely $P_{n+1}\_pred$.

(6) Cover prediction. Calculate the similarity loss between the $P_{n+1}\_pred$ output in step (5) and the actual image $P_{n+1}$, and add it to the regular term of the evolution field gradient to form the loss function, which is based on backpropagation Gradient descent loss and update network parameters.

Step (1) of the above was described in detail in the data preprocessing section, so it will not be addressed here. Steps (2), (3), and (4) are the evolution feature extraction and fusion module. Step (5) is the space transformation module. Step (6) is the loss function. This article will introduce these three modules in detail.

3.1. Evolutionary Feature Extraction and Fusion Module

This section presents the use of LSTM to build a multi-layer U-Net-LSTM network model for remote sensing image time series coverage prediction. Figure 9 illustrates the schematic diagram of the deep stack U-Net-LSTM model, which can be divided into the following components: input, encoder, LSTM timing processing, decoder, and evolution field.

(1) Input. Suppose there are N+M+1 images ${[P}_1,P_2\dots \dots P_{n+m},P_{n+m+1}]$ in the dataset. Take the image in size $W\times H$; for example, N sequential images of the same size are spliced in chronological order $N\times W\times H\times 1.$ The N + 1 image is taken as the ground truth. According to this, the data set can be divided into m + 1 samples, i.e., ${[P}_1,P_2\dots \dots P_n/P_{n+1}]$, ${[P}_2,P_3\dots \dots P_{n+1}/P_{n+2}]$,……, ${[P}_m,P_{m+1}\dots \dots P_{m+n-1}/P_{m+n}]$, ${[P}_{m+1},P_{m+2}\dots \dots P_{m+n}/P_{m+n+1}]$.

The first M samples are training sets, which can be spliced into $M\times N\times W\times H\times 1$ tensor direct input model.

(2) Encoder. Taking M = 1 as an example, this section adds the LSTM module behind each convolution layer and the activation function of the encoder. The size of the convolution core is 3 × 3, and the number of channels is 16, 32, 32, and 32 in turn. The input of each LSTM is the multi-scale feature of N time steps, and the output can be selected as the output sequence of N time steps, with the size of $N\times W\times H\times 1$, or as only the output of the last time step, size $1\times W\times H\times 1$. The jump connection’s output of LSTM is connected with the upper sampling layer’s output with the same U-Net dimension.

(3) Decoder. Taking LSTM only outputs the result of the last time step as an example; the decoding stage includes four upper sampling layers, convolution layers, and activation functions, the convolution kernel size is 3 × 3, and the number of channels is 32, 32, 32, and 32 in turn. Before the first convolution operation of the encoder, the input image is connected to the upper sampling layer of the last layer through LSTM. After up sampling, the output of the last convolution layer of the encoder passes through LSTM as the input of the subsequent up sampling layer. The number of hidden layer nodes and activation functions can be adjusted according to the dimension and size of input features, and the time series length determines the time step parameters of LSTM.

(4) Evolution field. Before evolving the field, multiple convolutional layers and activation function layers can be appropriately added to extract the timing sequence information further. The evolution field predicts the displacement of the image from the $N-th$ time step to the $N+1-th$ time step in the two directions by learning the evolution information of the previous N time steps. The size is $W\times H\times 2$.

(5) Initialization mode. To improve accuracy, the general batch normalization (BN) layer is added between the convolution layer and the activation function layer of the encoder and decoder. This scheme optimizes the adverse effects caused by the initialization mode. The method performs Gaussian normalization and linear transformation on the output value of the convolution layer before activating the function. The execution flow of the BN algorithm is shown in Algorithm 1.

Algorithm 1: BN algorithm

Input: Sample values of a mini-batch: $X=\{x_1,\dots ,x_m\},$

BN layer parameters to be learned: β, γ.

Output: $y_i=\left\{{BN}_{\gamma ,\beta }\right(x_i\left)\right\}$.

Calculate the sample mean ${\mu }_X$ according to Equation (3);

Calculate the sample variance ${\sigma }_X^2$ according to Equation (4);

The sample values are normalized according to Equation (5);

γ and β are introduced to translate and scale the sample values, and the sample values are updated according to Equation (6) during backpropagation.

$${\mu }_X=\frac{1}{m}{\sum }_{i=1}^m{x}_i,$$

(3)

$${\sigma }_X^2=\frac{1}{m}\sum _{i=1}^m{(x_i-{\mu }_X)}^2$$

(4)

$${\widehat{x}}_i=\frac{x_i-{\mu }_X}{\sqrt{{\sigma }_X^2}}$$

(5)

$$y_i=\gamma {\widehat{x}}_i+\beta =B{N}_{\gamma ,\beta }\left(x_i\right)$$

(6)

During training, the mean and variance are calculated from the current batch. When testing, the mean and variance of the previous training should be used instead of the new batch of data during the test. Figure 10 shows the output value distribution diagram of the random normal distribution initialization combined with the BN algorithm.

3.2. Space Transformation Module

The spatial transformation module receives the output from the evolution feature module, which is the evolution field, and outputs the predicted image $z\_pred$ after spatial transformation of the second image y in the time series image pair $x, y$. The model adjusts the network parameters by minimizing $y · \phi$, that is, the difference between $z\_pred$ and $z$. In order to use the gradient descent method to minimize the loss function, this paper constructs a differentiable operation based on a spatial transformation network to calculate it.

For each pixel $p$ of $z\_pred$, the sub-pixel position of the pixel before the evolution field transformation is calculated as $p^{\prime }=p+\phi \left(p\right)$. Because pixels are only defined in integer, the model uses the values of eight neighboring pixels for linear interpolation:

$$y·\phi ={\sum }_{q\in Z\left(p^{\prime }\right)}Z\left(q\right){\prod }_{d\in \{m,n\}}(1-\left|{p^{\prime }}_d-q_d\right|),$$

(7)

where $Z(p’)$ is the set of domain pixels of pixel $p\prime$, d is the dimension of the image, including the m and n dimensions, and $·$ represents the spatial transformation operation.

3.3. Loss Function

The model is trained with a differentiable loss function. The loss function of this model is composed of the following parts:

(1)

Similarity loss $l_{sim}$ is shown in Equation (8):

$$MSE\left(P_n,{\tilde{P}}_n\right)=\frac{1}{\left|\omega \right|}{\sum }_{(u,v)\in \omega }{‖P_n\left(u,v\right)-{\tilde{P}}_n(u,v)‖}^2,$$

(8)

(2)

Term of penalty $l_{smooth}(\varnothing )$ is shown in Equation (9):

$$l_{smooth}\left(\mathrm{\varnothing }\right)={\sum }_{(u,v)\in \omega }{‖{\nabla }_2\mathrm{\varnothing }(u,v)‖}^2+{‖{\nabla }_2\mathrm{\varnothing }(u,v)‖}^2,$$

(9)

where ${\tilde{P}}_n=P_n · \varnothing$ is the nth image predicted by the model, where · represents the spatial transformation operation, $P_n$ is the real nth image, $w$ is the set of image pixels, and $(u, v)$ is the pixel coordinate of any point. $l_{sim}$ is the mean square value of pixel values at all pixels of the predicted image and the real image, and $l_{smooth}\left(\phi \right)$ is used to smooth the cover evolution field.

The final loss function is shown in Equation (10):

$$loss=l_{sim}+\alpha l_{smooth}\left(\mathrm{\varnothing }\right),$$

(10)

where $\alpha$ is the regularization parameter.

4. Experiment and Results

4.1. Experiment Setting

In this section, Dataset 1, a total of 19 images ${[P}_1,P_2\dots \dots P_{18},P_{19}]$ are divided into 20-T samples according to time step T, as the experiment 1 and experiment 3 data sets ${Col}_1$.

For example, when T = 10, there are a total of 10 samples, which are ${[P}_1$,$P_2\cdots P_8,P_9/P_{10}]$, ${[P}_2$,$P_3\cdots P_9,P_{10}/P_{11}]\dots \dots {[P}_{10}$,$P_{11}\cdots P_{17},P_{18}/P_{19}]$. The first nine images in each sample are input data, and the last image is ground truth. The first nine samples are used as the training set, and the last group is used as the test set to evaluate their performance.

Dataset 2 has a total of 15 images, which are similarly split into 15-T samples as the data sets ${Col}_2$ of Experiment 2 and Experiment 4.

Experiment 1 used the U-Net-LSTM model proposed in this article to predict the time series images of the first 4 years, 7 years, 10 years, 14 years, and 18 years in ${Col}_1$.

Experiment 2 used the U-Net-LSTM model proposed in this article to predict the time series images of the first 5–7 years in ${Col}_2$.

Experiments 3 and 4 compared and analyzed the influence of the time series length of a single input image on the prediction results of the data sets of ${Col}_1$ and ${Col}_2$.

The experimental environment and parameter settings are shown in

Table 2. Experimental environment parameters.

Component	Specification
CPU	Intel® Core™ i9-10900K
RAM	32 G
GPU	GeForce RTX 2080 ∗ 2
Operating System	Ubuntu 18.04 LTS
Development Language	Python 3.6
Framework	PyTorch 1.5.0
Training Method	Batch Gradient Descent (BGD)
Learning Rate	1 × 10−4 (0.0001)
Training Epochs	10,000

.

4.2. Evaluating Indicators

This study uses ACC, MSE, MAE, and DICE as the experimental evaluation indicators. ACC is the accuracy of coverage prediction, MSE is the mean square error, and MAE is the average absolute error. DICE is an ensemble similarity measurement index, usually used to calculate the similarity of two samples. The image difference between the predicted and actual results is evaluated to visually show the gap.

MSE is calculated as shown in Equation (8). $ACC$, $MAE$, and $DICE$ are calculated as shown in Equations (11)–(13).

$$ACC=\frac{N_{correct}}{N_{total}},$$

(11)

$$MAE\left(P_n,{\tilde{P}}_n\right)=\sqrt{\frac{1}{\left|\omega \right|}{\sum }_{(u,v)\in \omega }{‖P_n(u,v)-{\tilde{P}}_n(u,v)‖}^2},$$

(12)

$$DICE\left(T,P\right)=\frac{\left|T_1\cap P_1\right|}{(\left|P_1\right|+\left|T_2\right|)/2}=\frac{2N_{TP}}{N_{FP}+2N_{TP}+{2N}_{FN}},$$

(13)

4.3. LSTM Effectiveness Analysis in Experiments 1 and 2

The model proposed in this section adds an LSTM module. Compared with a separate U-net model, the U-Net-LSTM model can input time series data at multiple time steps simultaneously. In order to verify the effectiveness of the LSTM module, the following is a comparison of the prediction results of the U-Net model and the U-Net-LSTM model after training using T time series data. The U-Net model inputs two images each time, and the U-Net-LSTM model can input image time steps each time. In Experiments 1 and 2, to verify the LSTM module’s effectiveness, the control variable input step length is the same.

4.3.1. Experiment 1

In experiment 1, the training set is 20-T samples of T time steps before 2014 in ${Col}_1$, and the test set is [2012, 2013 | 2014]. Figure 11 and

Table 3. U-Net and U-Net-LSTM different time step prediction results in ${Col}_1$.

Predict 2014	ACC	MSE	DICE
8 years U-Net [31]	0.8855	410.01	0.9537
8 years U-Net-LSTM	0.8876	392.37	0.9581
12 years U-Net [31]	0.8879	402.41	0.9574
12 years U-Net-LSTM	0.8929	373.38	0.9599
18 years U-Net [31]	0.8900	377.20	0.9576
18 years U-Net-LSTM	0.8943	234.79	0.9608

show the comparison of experimental results for T = 8, 12, and 18.

These images and difference images are used to compare the predictions made by the U-Net and U-Net-LSTM models at different time steps with the actual images from 2013 and 2014, as well as to assess the accuracy of the predictions. The results show that, after adding LSTM, the model predicts fewer difference image areas and has higher accuracy.

4.3.2. Experiment 2

In Experiment 2, the training set consists of T time steps before 2014 in ${Col}_2$, while the test set is [2012, 2013 | 2014]. Figure 12 and Figure 13 show the comparison of experimental results for T = 6, 7, and 8. The first row (10a, 10b, 10c, 11a, 11b, and 11c) of Figure 10 and Figure 11 uses the remote sensing image from 2003 to 2008 as the training set and the remote sensing image from 2009 as the ground truth for comparison. The second row (10d, 10e, 10f, 11d, 11e, and 11f) compares the prediction results using the first seven time steps, with the training set consisting of the remote sensing image from 2003 to 2009, and the ground truth being the remote sensing image from 2010. The third row (10g, 10h, 10i, 11g, 11h, and 11i) compares the prediction results using the first eight time steps, with the training set consisting of the remote sensing image from 2003 to 2010 and the ground truth being the remote sensing image from 2011.

Table 4. U-Net and U-Net-LSTM different time step prediction results in ${Col}_2$.

Predict 2014	ACC	MSE	DICE
6 years U-Net [31]	0.7425	1487.35	0.9268
6 years U-Net-LSTM	0.7646	1405.79	0.9297
7 years U-Net [31]	0.7810	1475.24	0.9574
7 years U-Net-LSTM	0.7893	1555.08	0.9673
8 years U-Net [31]	0.7873	1169.98	0.9680
8 years U-Net-LSTM	0.8022	918.82	0.9743

shows the prediction evaluation indicators for time steps T = 6, 7, and 8.

4.4. Time Series Length and Sample Number Analysis

The number of input samples of the U-Net-LSTM model is M, and the time step of each sample is N. To test the impact of the number of samples and the length of the training data on the prediction results. In Experiments 3 and 4, T is unchanged. In such a case, by changing the input sample time step N, the number of samples M will also change.

4.4.1. Experiment 3

Experiment 3 uses the first 18 time steps of 2014 in ${Col}_1$, and the test set is [2012, 2013 | 2014]. Figure 14 and

Table 5. Results for different combinations of sample length and number of samples in ${Col}_1$.

Sample Length/Number of Samples	ACC	MSE	DICE
18/1	0.8855	377.20	0.9595
13/5	0.8906	369.67	0.9627
8/10	0.8922	271.11	0.9709
2/16	0.8913	323.35	0.9630

compare the experimental results when N = 18, 13, 8, 2, and the corresponding M = 1, 5, 10, and 16, respectively.

When N = 18, the prediction result of the model is almost the same as that of the covering image in 2013, indicating that the migration ability of the model is not strong at this time. As N decreases, the prediction result of the model gradually changes and approaches the actual image of 2014, indicating that the model’s prediction ability has been improved. However, when N is reduced to a certain value, the model’s prediction accuracy gradually decreases, and some situations, such as the covering boundary, cannot be closed, and too much noise occurs.

4.4.2. Experiment 4

Experiment 4 uses the data from 2004 to 2013 in ${Col}_2$ as the training set, and the data in 2014 are ground truth. Figure 15 lists the prediction results when the sample length is 5, 6, 7, and 8.

Table 6. Results for different combinations of sample length and number of samples in ${Col}_2$.

Sample Length/Number of Samples	ACC	MSE	DICE
5/5	0.7914	1645.64	0.9329
6/4	0.7930	1323.35	0.9360
7/3	0.7948	1293.69	0.9407
8/2	0.7930	1411.99	0.9347

shows their respective evaluation index values.

As N increases, the prediction accuracy is improved. However, when N increases to a certain extent, the number of samples is too small, and the model is easily over-fitted, making it difficult for the learned change rules to be applied to brand-new data, resulting in reduced prediction accuracy.

The results show that the number and length of training samples will have a greater impact on the prediction results, which is consistent with the results of Experiment 3. As the sample length N increases, the accuracy of predicting coverage details is improved. However, when N increases to a certain extent, the number of samples is too small, which leads to insufficient mobility of the model. As a result, the prediction accuracy is reduced when the model is applied to brand-new data. Comparing Experiments 2 and 4 with Experiments 1 and 3, the model’s accuracy in predicting changes in detail coverage is slightly lower than that of predicting overall coverage.

5. Discussion

The results of Experiments 1 and 2, which verified the effectiveness of the model, showed that, after adding LSTM, the model has higher prediction accuracy than the U-Net model. When t is consistent, the contours predicted by the U-Net-LSTM model are closer to the coverage of the original image compared to the U-Net model. Both the accuracy index of the prediction results and the similarity measurement index verify the effectiveness of the introduced LSTM module.

Experiments 3 and 4 show that the choice of N and M greatly affects the prediction of coverage changes by the model. However, there is no uniform standard or obvious rule for the selected scheme, which must be tested repeatedly according to the actual situation. When T is the same, the control variable method cannot be used to control the consistency of any variable in M and N. As the length N of each sample increases, the number of samples M must decrease accordingly. From the experimental results, we can see that the prediction accuracy improves initially as N decreases. However, when N is reduced to a certain level, the model cannot extract more temporal information, the role of the LSTM module is not fully utilized, and the prediction accuracy is reduced. As the sample length N increases, the accuracy of the predicted coverage details improves. However, when N increases to a certain extent, the number of samples is too small, resulting in insufficient mobility for the model. As a result, the prediction accuracy decreases when the model is applied to completely new data. Therefore, it is necessary to choose the appropriate M and N for experiments to achieve the best prediction.

Overall, the U-Net-LSTM model proposed in this study can realize differential memory and forgetting of historical data and different levels of utilization of current input data. This method can customize a prediction model of boundary changes for natural areas, such as lakes, with a small data set and provide valuable reference results. Using LSTM for prediction can extract the state changes of land cover from remote sensing image time series and generate migration change rules, which is of great significance for natural lake boundary prediction. However, this study also has notable limitations. It solely relies on remote sensing imagery as the sole basis for predicting changes in lake boundaries and the results lack interpretability. In future research, we aspire to follow the lead of previous scholars [32] by incorporating additional factors, such as temperature, precipitation, population changes, and industrial shifts, to explore a more comprehensive set of variables related to lake changes. By leveraging multimodal data, we aim to construct more precise and real-time prediction models that can provide superior solutions to water body protection issues.

6. Conclusions

U-Net performs well in an encoder–decoder architecture by capturing spatial features and hierarchical relationships and is able to detect changes in lake boundaries, but it lacks sensitivity to time-series data. To address this limitation, this paper proposes a novel method combining U-Net and LSTM in an end-to-end lake boundary prediction model. The U-Net network is used to extract multi-level change features and analyze land cover change trends. The LSTM module is introduced after U-Net, using historical data storage and forgetting and current input data to optimize the prediction model. This method enables the model to automatically fit the trend of time series data and mine the spatio-temporal fusion information of lake boundary changes. To further optimize the prediction model, various model optimization algorithms are used in this paper. These methods help to ensure the validity of the model and prevent overfitting, allowing continuous optimization through experimental methods. Compared with traditional prediction models such as Markov and cellular automata, this model can simultaneously detect and predict lake boundary rate changes, provide more comprehensive and accurate predictions, and provide a valuable tool for natural lake management planning and decision-making. The introduction of the LSTM module allows the extraction of state changes in land cover from a time series of remote sensing images. LSTM introduces memory cells that enable the network to retain and selectively update information over long sequences. New movement rules can then be generated, which is crucial for accurate lake boundary predictions. By integrating LSTM with U-Net, the fusion of spatio-temporal information can be achieved. This is useful in tasks that involve both spatial structure and temporal dependencies. This paper demonstrates in detail the feasibility and advantages of introducing the LSTM module h by comparing it with the existing U-net-STN model.