Coupling Fuzzy Bi-Level Chance Constraint Programming and Spatial Analysis for Urban Ecological Management
Abstract
:1. Introduction
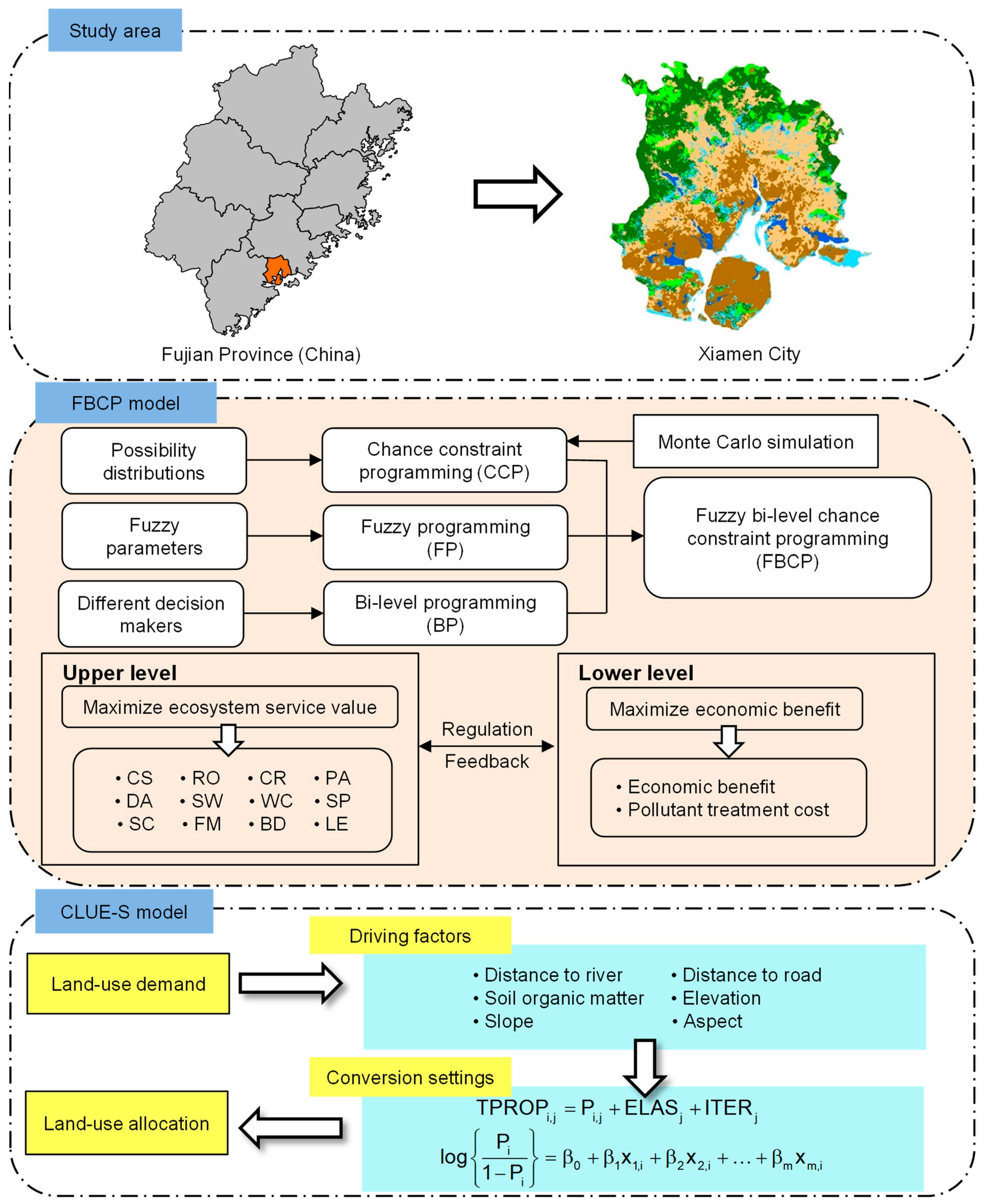
2. Case Study
3. Methodology
3.1. Fuzzy Bi-Level Chance Constraint Programming (FBCP)
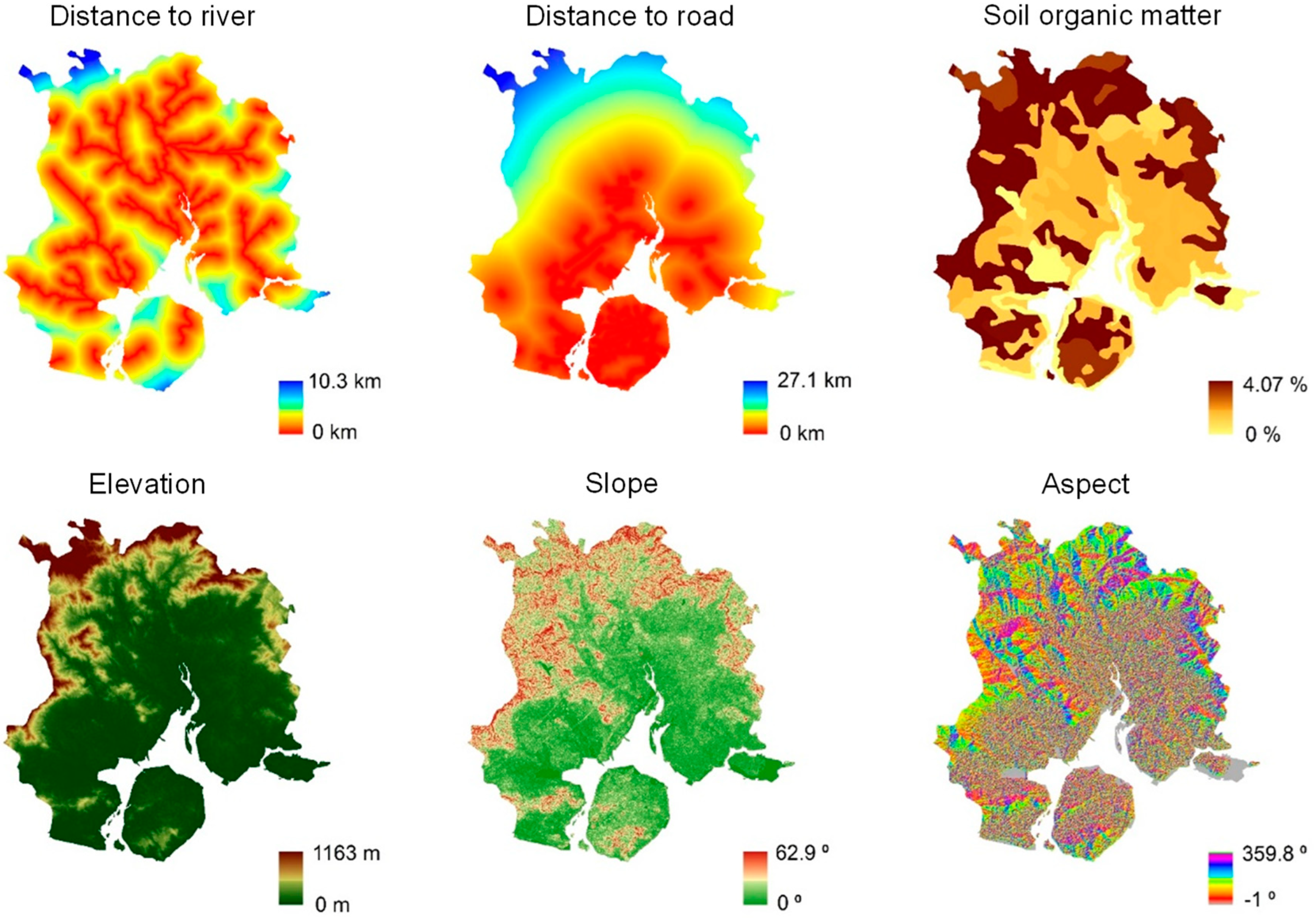
3.2. The Conversion of Land Use and Its Effects at Small Regional Extent (CLUE-S)
3.3. Modelling Formulation
- 1.
- Reallocated land constraints:
- 2.
- Ecological water constraint:
- 3.
- Water resource constraints:
- 4.
- Carbon emission constraint:
- 5.
- Solid waste emission constraint:
- 6.
- COD discharge constraint:
- 7.
- NH3-N discharge constraint:
- 8.
- SO2 discharge constraint:
- 9.
- Sewage discharge constraint:
- 10.
- Percentage of the forestry and grass coverage constraint:
- 11.
- Soil erosion constraint:
- 12.
- Population constraint:
- 13.
- Non-negative constraint:
3.4. Data Acquisition Method
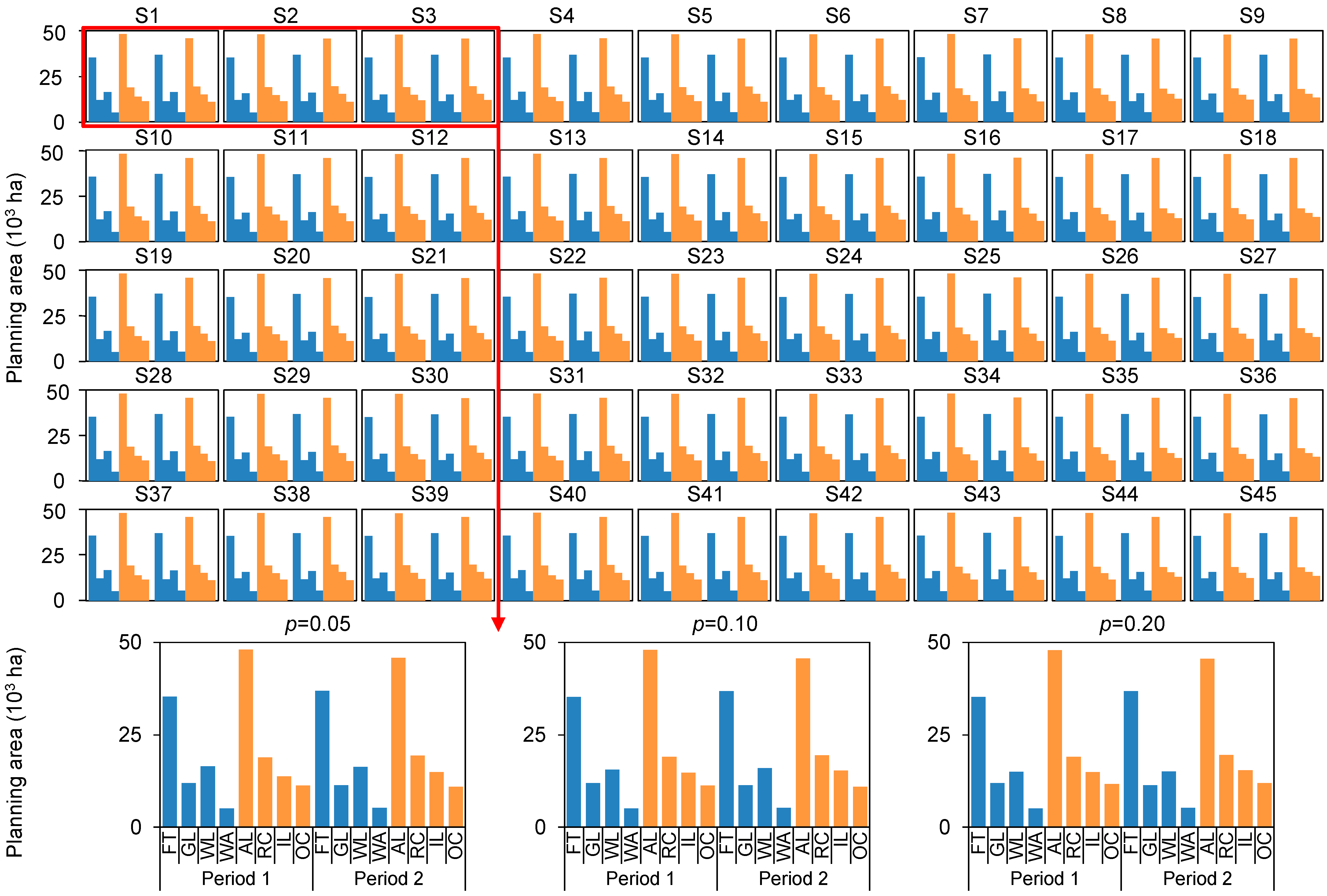
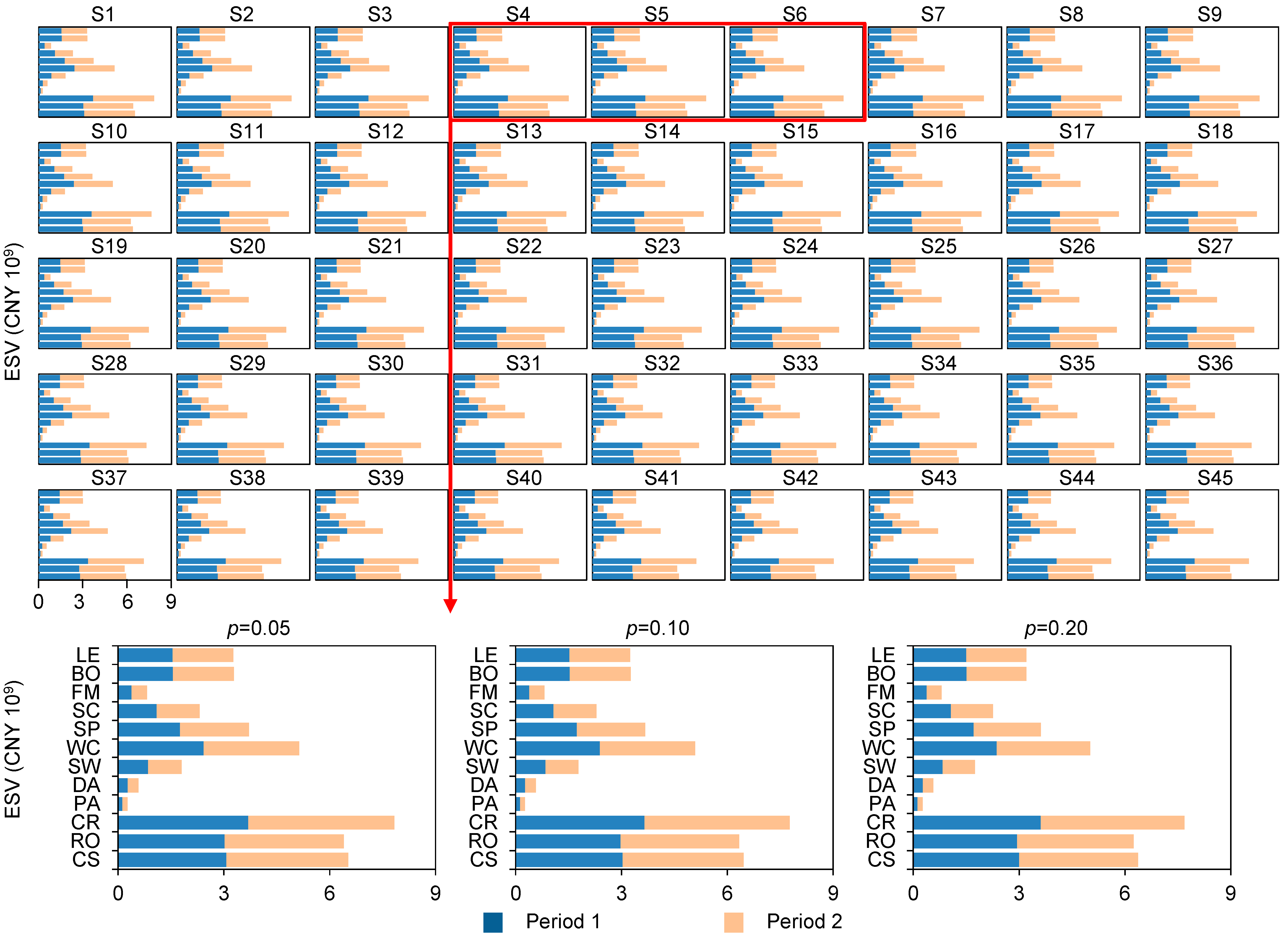
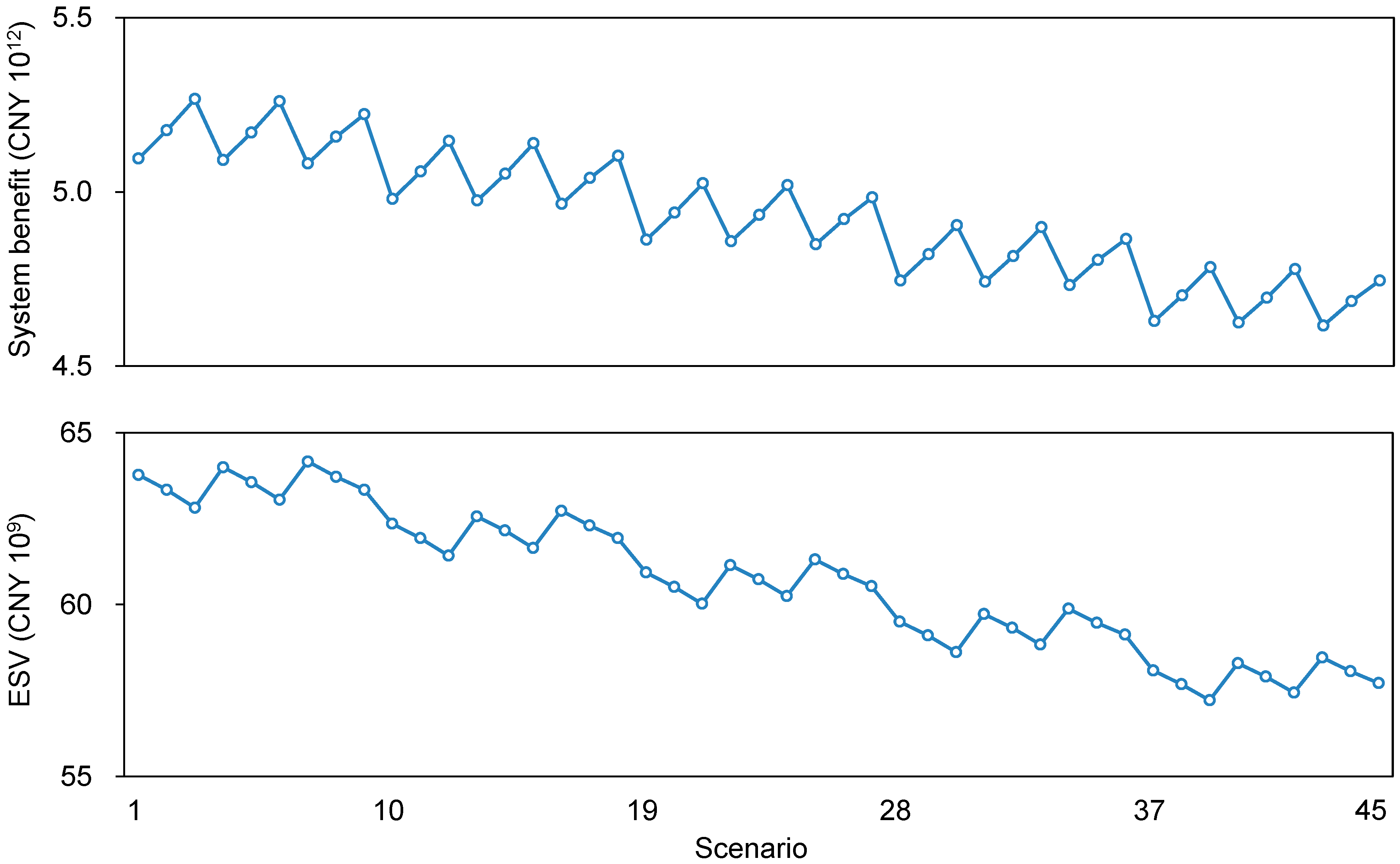
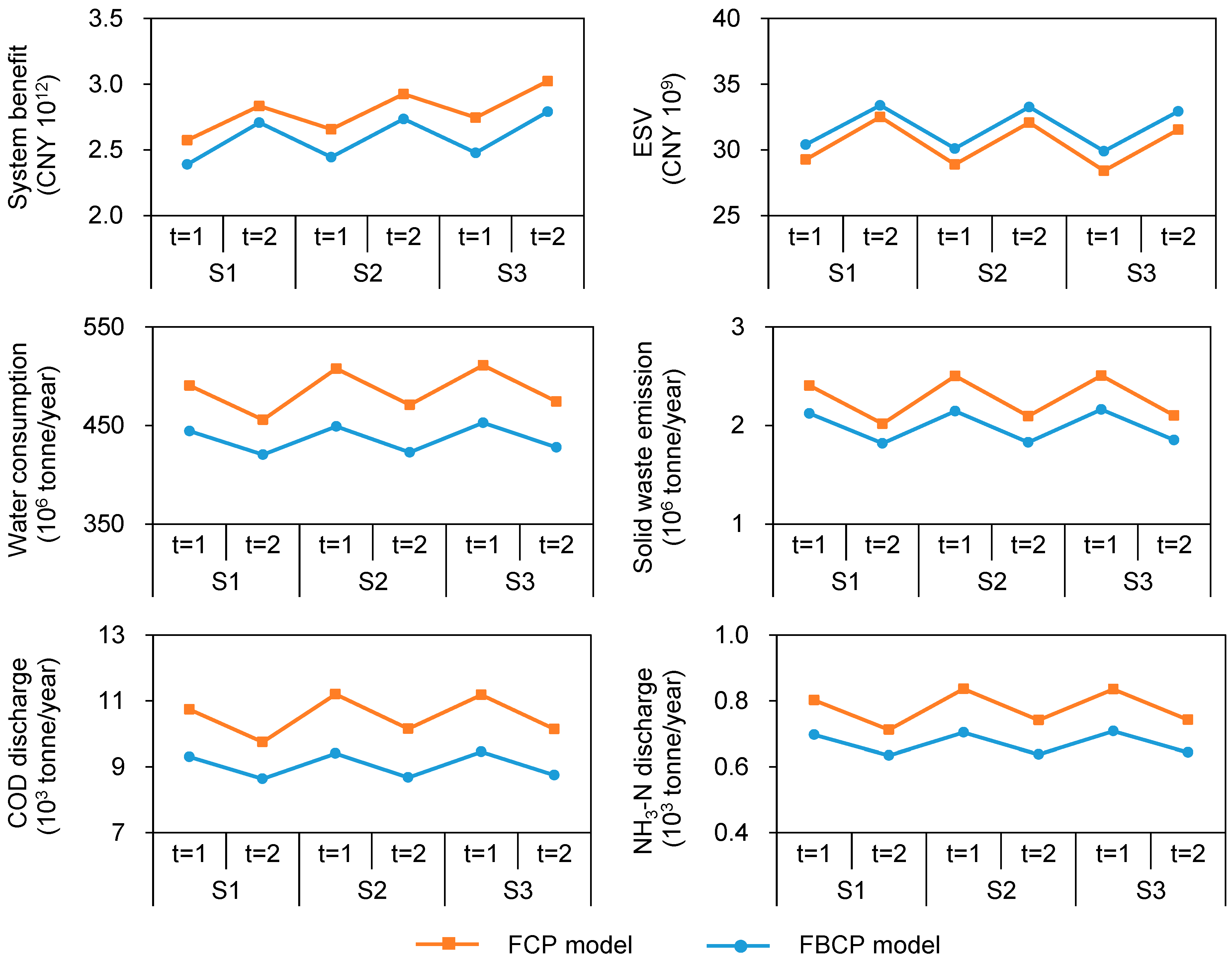
4. Result Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| f1 | expected ecosystem service value (CNY) |
| f2 | expected economic benefit (CNY) |
| i | ecological land; i = 1, 2, 3, 4 (for forest, bushland, wetlands, water area) |
| j | human activities land; j = 1, 2, 3, 4 (for agricultural land, commercial and residential land, industrial land, public land) |
| t | time periods; t = 1, 2 (for years of 2024–2028, years of 2029–2033) |
| n | element; n = 1, 2, 3 (for N, P, K) |
| PEi,t | planning area of ecological land i (ha) |
| PIj,t | planning area of human activities land j (ha) |
| L | year of the planning period (a) |
| St | total planning area (ha) |
| CACi,t | CO2 absorption amount of ecological land i (t/ha) |
| CT,t | carbon tax (CNY/t) |
| OPt | oxygen price (CNY/t) |
| CREi,t | climate regulation value of ecological land i (CNY/ha) |
| CASi,t | SO2 absorption amount of ecological land i (t/ha) |
| CSRt | SO2 removal cost (CNY/t) |
| ADEi,t | dust absorption amount of ecological land i (t/ha) |
| CDAt | dust removal cost (CNY/t) |
| SWEi,t | solid waste purification amount of ecological land i (t/ha) |
| CWTt | solid waste treatment cost (CNY/t) |
| CCEi,t | water conservation volume of ecological land i (m3/ha) |
| SREi,t | surface runoff coefficient of ecological land i (%) |
| RCt | water price (CNY/m3) |
| CWEi,t | sewage purification amount of ecological land i (t/ha) |
| CSTt | sewage treatment cost (CNY/t) |
| SEEi,t | soil conservation quantity of ecological land i (t/(ha·a)) |
| CESt | soil transportation cost (CNY/t) |
| NCn,t | content of n element in the soil (%) |
| FPn,t | price of fertilizer n (CNY/t) |
| VBEi,t | biodiversity value of ecological land i (CNY/ha) |
| ETVi,t | leisure and entertainment value of ecological land i (CNY/ha) |
| ISVt | ecosystem service value of afforest (CNY) |
| IEBj,t | benefit of human activities land j (CNY/ha) |
| EBEi,t | agricultural products of ecological land i (CNY/ha) |
| WCIj,t | water consumption of human activities land j (ton/ha) |
| AWt | available water resources (t) |
| CPIj,t | COD discharge of human activities land j (t/ha) |
| CPRj,t | COD removal rate of human activities land j (%) |
| CAEi,t | COD purification amount of ecological land i (t/ha) |
| ACDt | COD discharge threshold (t) |
| NPIj,t | NH3-N discharge of human activities land j (t/ha) |
| NPRj,t | NH3-N removal rate of human activities land j (%) |
| NAEi,t | NH3-N purification amount of ecological land i (t/ha) |
| ANDt | NH3-N discharge threshold (t) |
| CEIj,t | carbon emissions of human activities land j (t/ha) |
| ACEt | carbon emissions threshold (t) |
| SWIj,t | solid waste discharge of human activities land j (t/ha) |
| SIRj,t | solid waste recovery rate of human activities land j (%) |
| ASWt | solid waste discharge threshold (t) |
| VAEi,t | vegetation coverage of ecological land i (%) |
| VAIj,t | vegetation coverage of human activities land j (%) |
| PFGt | forestry and grass coverage (%) |
| EREi,t | soil erosion area of ecological land i (ha/ha) |
| ERIj,t | soil erosion area of human activities land j (ha/ha) |
| ASEt | soil erosion threshold (ha) |
| SDIk,t | sewage discharge of human activities land j (t/ha) |
| AWDt | sewage discharge threshold (t) |
| DDIj,t | SO2 emissions of human activities land j (t/ha) |
| DIRj,t | SO2 removal rate of human activities land j (%) |
| ASDt | SO2 discharge threshold (t) |
| MOEi,t | moisturizing coefficient (%) |
| T | conversion coefficient, T = 31.536 × 106 |
| Y | year statistics (a) |
| Qemin | minimum monthly runoff (m3/s) |
| UPj,t | amount of the population of human activities land j (person/ha) |
| TPt | planned total population (person) |
| MINEi,t | minimum area of ecological land i (ha) |
| MINIj,t | minimum area of human activities land j (ha) |
| MAXEi,t | maximum area of ecological land i (ha) |
| MAXIj,t | maximum area of human activities land j (ha) |
References
- Magalhães Filho, L.; Roebeling, P.; Villasante, S.; Bastos, M.I. Ecosystem services values and changes across the Atlantic coastal zone: Considerations and implications. Mar. Policy 2022, 145, 105265. [Google Scholar] [CrossRef]
- Yan, F.Q.; Zhang, S.W. Ecosystem service decline in response to wetland loss in the Sanjiang Plain, Northeast China. Ecol. Eng. 2019, 130, 117–121. [Google Scholar] [CrossRef]
- Li, C.W.; Fang, S.B.; Geng, X.L.; Yuan, Y.; Zheng, X.W.; Zhang, D.; Li, R.X.; Sun, W.; Wang, X.R. Coastal ecosystem service in response to past and future land use and land cover change dynamics in the Yangtze river estuary. J. Clean. Prod. 2023, 385, 135601. [Google Scholar] [CrossRef]
- Fahad, S.; Li, W.; Lashari, A.H.; Islam, A.; Khattak, L.H.; Rasool, U. Evaluation of land use and land cover Spatio-temporal change during rapid Urban sprawl from Lahore, Pakistan. Urban Clim. 2021, 39, 100931. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, H.J. Spatiotemporal dynamics and evolution relationships between land-use/land cover change and landscape pattern in response to rapid urban sprawl process: A case study in Wuhan, China. Ecol. Eng. 2022, 182, 106716. [Google Scholar] [CrossRef]
- Rong, Q.Q.; Zeng, J.N.; Su, M.R.; Yue, W.C.; Cai, Y.P. Prediction and optimization of regional land-use patterns considering nonpoint-source pollution control under conditions of uncertainty. J. Environ. Manag. 2022, 306, 114432. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Guo, X.W.; Yin, H.J.; Zhang, W.G.; Li, Q.K. Spatially distributed footprint families-based simulation–optimization approach for agricultural-ecological resources management under uncertainty. J. Hydrol. 2022, 613, 128319. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Wang, T.T.; Ding, Z.L.; Zhang, X.Q.; Han, L.W. Uncertainty analysis of impact factors of eco-environmental vulnerability based on cloud theory. Ecol. Indic. 2020, 110, 105864. [Google Scholar] [CrossRef]
- Laskookalayeh, S.S.; Najafabadi, M.M.; Shahnazari, A. Investigating the effects of management of irrigation water distribution on farmers’ gross profit under uncertainty: A new positive mathematical programming model. J. Clean. Prod. 2022, 351, 131277. [Google Scholar] [CrossRef]
- Fallahi, F.; Bakir, I.; Yildirim, M.; Ye, Z. A chance-constrained optimization framework for wind farms to manage fleet-level availability in condition based maintenance and operations. Renew. Sustain. Energ. Rev. 2022, 168, 112789. [Google Scholar] [CrossRef]
- Molavi, A.; Shi, J.; Wu, Y.; Lim, G.J. Enabling smart ports through the integration of microgrids: A two-stage stochastic programming approach. Appl. Energy 2020, 258, 114022. [Google Scholar] [CrossRef]
- Xu, Y.; Tan, J.Y.; Wang, X.; Li, W.; He, X.; Hu, X.G.; Fan, Y.R. Synergetic management of water-energy-food nexus system and GHG emissions under multiple uncertainties: An inexact fractional fuzzy chance constraint programming method. Agric. Water Manag. 2022, 262, 107323. [Google Scholar] [CrossRef]
- Ou, G.L.; Tan, S.K.; Zhou, M.; Lu, S.S.; Tao, Y.H.; Zhang, Z.; Zhang, L.; Yan, D.P.; Guan, X.L.; Wu, G. An interval chance-constrained fuzzy modeling approach for supporting land-use planning and eco-environment planning at a watershed level. J. Environ. Manag. 2017, 204, 651–666. [Google Scholar] [CrossRef]
- Lv, J.P.; Li, Y.P.; Sun, J. Monte Carlo simulation based interval chance-constrained programming for regional ecosystem management–A case study of Zhuhai, China. Ecol. Indic. 2018, 85, 214–228. [Google Scholar] [CrossRef]
- Jia, Q.M.; Li, Y.P.; Liu, Y.R. Modeling urban eco-environmental sustainability under uncertainty: Interval double-sided chance-constrained programming with spatial analysis. Ecol. Indic. 2020, 115, 106438. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Li, Z.; Huang, W. Simulation-based interval chance-constrained quadratic programming model for water quality management: A case study of the central Grand River in Ontario, Canada. Environ. Res. 2021, 192, 110206. [Google Scholar] [CrossRef]
- Baudry, G.; Macharis, C.; Vallée, T. Range-based Multi-Actor Multi-Criteria Analysis: A combined method of Multi-Actor Multi-Criteria Analysis and Monte Carlo simulation to support participatory decision making under uncertainty. Eur. J. Oper. Res. 2018, 264, 257–269. [Google Scholar] [CrossRef]
- Chen, B.; Li, P.; Wu, H.J.; Husain, T.; Khan, F. MCFP: A Monte Carlo Simulation-based Fuzzy Programming Approach for Optimization under Dual Uncertainties of Possibility and Continuous Probability. J. Environ. Inform. 2017, 29, 88–97. [Google Scholar] [CrossRef]
- Liu, H.X.; Li, Y.P.; Yu, L. Urban agglomeration (Guangzhou-Foshan-Zhaoqing) ecosystem management under uncertainty: A factorial fuzzy chance-constrained programming method. Environ. Res. 2019, 173, 97–111. [Google Scholar] [CrossRef]
- Zaeimi, M.B.; Rassafi, A.A. Designing an integrated municipal solid waste management system using a fuzzy chance-constrained programming model considering economic and environmental aspects under uncertainty. Waste Manag. 2021, 125, 268–279. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.P.; Huang, G.H.; You, L.; Jin, S.W. Modeling for regional ecosystem sustainable development under uncertainty-A case study of Dongying, China. Sci. Total Environ. 2015, 533, 462–475. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Xiao, Y.; Jiang, S.; Li, Y.P.; Fan, Y.R.; Huang, G.H.; Lv, J.; Zuo, Q.T.; Wang, F.Q. A copula-based fuzzy interval-random programming approach for planning water-energy nexus system under uncertainty. Energy 2020, 196, 117063. [Google Scholar] [CrossRef]
- Guo, M.H.; Wang, W.; Chen, R.H.; Li, Y. Research on bi-level model power dispatch considering the uncertainty of source and load. Sustain. Energy Technol. Assess. 2022, 53, 102689. [Google Scholar] [CrossRef]
- Gan, L.; Li, G.Y.; Lin, J.; Zhou, M. A bi-level probabilistic transmission planning with intermittent generations based on life cycle cost. Int. J. Electr. Power Energy Syst. 2017, 90, 306–314. [Google Scholar] [CrossRef]
- Khanchehzarrin, S.; Panah, M.G.; Mahdavi-Amiri, N.; Shiripour, S. A bi-level multi-objective location-routing optimization model for disaster relief operations considering public donations. Socio-Econ. Plan. Sci. 2022, 80, 101165. [Google Scholar] [CrossRef]
- Jin, S.W.; Li, Y.P.; Nie, S. An integrated bi-level optimization model for air quality management of Beijing’s energy system under uncertainty. J. Hazard Mater. 2018, 350, 27–37. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y.P.; Huang, G.H. A bi-level chance-constrained programming method for quantifying the effectiveness of water-trading to water-food-ecology nexus in Amu Darya River basin of Central Asia. Environ. Res. 2020, 183, 109229. [Google Scholar] [CrossRef]
- Su, S.; Li, Z.N.; Jin, X.L.; Yamashita, K.; Xia, M.; Chen, Q. Bi-level energy management and pricing for community energy retailer incorporating smart buildings based on chance-constrained programming. Int. J. Electr. Power Energy Syst. 2022, 138, 107894. [Google Scholar] [CrossRef]
- Lv, J.; Li, Y.P.; Huang, G.H.; Nie, S.; Gong, J.W.; Ma, Y.; Li, Y. Synergetic management of energy-water nexus system under uncertainty: An interval bi-level joint-probabilistic programming method. J. Clean. Prod. 2021, 292, 125942. [Google Scholar] [CrossRef]
- Kucsicsa, G.; Popovici, E.A.; Bălteanu, D.; Grigorescu, I.; Dumitraşcu, M.; Mitrică, B. Future land use/cover changes in Romania: Regional simulations based on CLUE-S model and CORINE land cover database. Landsc. Ecol. Eng. 2019, 15, 75–90. [Google Scholar] [CrossRef]
- Chasia, S.; Olang, L.O.; Sitoki, L. Modelling of land-use/cover change trajectories in a transboundary catchment of the Sio-Malaba-Malakisi Region in East Africa using the CLUE-s model. Ecol. Modell. 2023, 476, 110256. [Google Scholar] [CrossRef]
- Peng, K.F.; Jiang, W.G.; Deng, Y.; Liu, Y.; Wu, Z.; Chen, Z. Simulating wetland changes under different scenarios based on integrating the random forest and CLUE-S models: A case study of Wuhan Urban Agglomeration. Ecol. Indic. 2020, 117, 106671. [Google Scholar] [CrossRef]
- Akin, A.; Erdoğan, N.; Berberoğlu, S.; Çilek, A.; Erdoğan, A.; Donmez, C.; Şatir, O. Evaluating the efficiency of future crop pattern modelling using the CLUE-S approach in an agricultural plain. Ecol. Inform. 2022, 71, 101806. [Google Scholar] [CrossRef]
- You, L.; Li, Y.P.; Huang, G.H. Modeling regional ecosystem development under uncertainty: A case study for New Binhai District of Tianjin. Ecol. Modell. 2014, 288, 127–142. [Google Scholar] [CrossRef]
- Mianaei, P.K.; Aliahmadi, M.; Faghri, S.; Ensaf, M.; Ghasemi, A.; Abdoos, A.A. Chance-constrained programming for optimal scheduling of combined cooling, heating, and power-based microgrid coupled with flexible technologies. Sustain. Cities Soc. 2022, 77, 103502. [Google Scholar] [CrossRef]
- Wang, Y.M.; Zhu, G.C. Inexact left-hand side two-stage chance-constrained programming for booster optimization in water distribution system. J. Environ. Manag. 2021, 298, 113372. [Google Scholar] [CrossRef]
- Wu, H.; Yue, Q.; Guo, P.; Pan, Q.; Guo, S.S. Sustainable regional water allocation under water-energy nexus: A chance-constrained possibilistic mean-variance multi-objective programming. J. Clean. Prod. 2021, 313, 127934. [Google Scholar] [CrossRef]
- Yu, L.; Li, Y.P. A flexible-possibilistic stochastic programming method for planning municipal-scale energy system through introducing renewable energies and electric vehicles. J. Clean. Prod. 2019, 207, 772–787. [Google Scholar] [CrossRef]
- Inuiguchi, M.; Ramık, J. Possibilistic linear programming: A brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem. Fuzzy Sets Syst. 2000, 111, 3–28. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, G.H.; Nie, X. Robust stochastic fuzzy possibilistic programming for environmental decision making under uncertainty. Sci. Total Environ. 2009, 408, 192–201. [Google Scholar] [CrossRef]
- Van Dijk, D.; Hendrix, E.M.; Haijema, R.; Groeneveld, R.A.; Van Ierland, E.C. On solving a bi-level stochastic dynamic programming model for analyzing fisheries policies: Fishermen behavior and optimal fish quota. Ecol. Modell. 2014, 272, 68–75. [Google Scholar] [CrossRef]
- Beykal, B.; Avraamidou, S.; Pistikopoulos, E.N. Data-driven optimization of mixed-integer bi-level multi-follower integrated planning and scheduling problems under demand uncertainty. Comput. Chem. Eng. 2022, 156, 107551. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.F.; Li, Y.P.; Huang, G.H.; Ma, Y.; Zhou, X. Planning a water-food-energy-ecology nexus system toward sustainability: A Copula bi-level fractional programming method. ACS Sustain. Chem. Eng. 2021, 9, 15212–15228. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y.P.; Huang, G.H.; Liu, Y.R. Water-energy nexus under uncertainty: Development of a hierarchical decision-making model. J. Hydrol. 2020, 591, 125297. [Google Scholar] [CrossRef]
- Gong, J.W.; Li, Y.P.; Lv, J.; Huang, G.H.; Suo, C.; Gao, P.P. Development of an integrated bi-level model for China’s multi-regional energy system planning under uncertainty. Appl. Energy 2022, 308, 118299. [Google Scholar] [CrossRef]
- Lv, Y.; Huang, G.H.; Li, Y.P.; Yang, Z.F.; Liu, Y.; Cheng, G.H. Planning regional water resources system using an interval fuzzy bi-level programming method. J. Environ. Inform. 2010, 16, 43–56. [Google Scholar] [CrossRef]
- Jin, S.W.; Li, Y.P.; Xu, L.P. Development of an integrated model for energy systems planning and carbon dioxide mitigation under uncertainty–Tradeoffs between two-level decision makers. Environ. Res. 2018, 164, 367–378. [Google Scholar] [CrossRef]
- Luo, G.P.; Yin, C.Y.; Chen, X.; Xu, W.; Lu, L. Combining system dynamic model and CLUE-S model to improve land use scenario analyses at regional scale: A case study of Sangong watershed in Xinjiang, China. Ecol. Complex 2010, 7, 198–207. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Chao, B.X.; Dong, P.; Zhang, D.; Yu, W.W.; Hu, W.J.; Ma, Z.Y.; Chen, G.C.; Liu, Z.H.; Chen, B. Simulating spatial change of mangrove habitat under the impact of coastal land use: Coupling MaxEnt and Dyna-CLUE models. Sci. Total Environ. 2021, 788, 147914. [Google Scholar] [CrossRef]
- Jiang, W.G.; Deng, Y.; Tang, Z.H.; Lei, X.; Chen, Z. Modelling the potential impacts of urban ecosystem changes on carbon storage under different scenarios by linking the CLUE-S and the InVEST models. Ecol. Modell. 2017, 345, 30–40. [Google Scholar] [CrossRef]

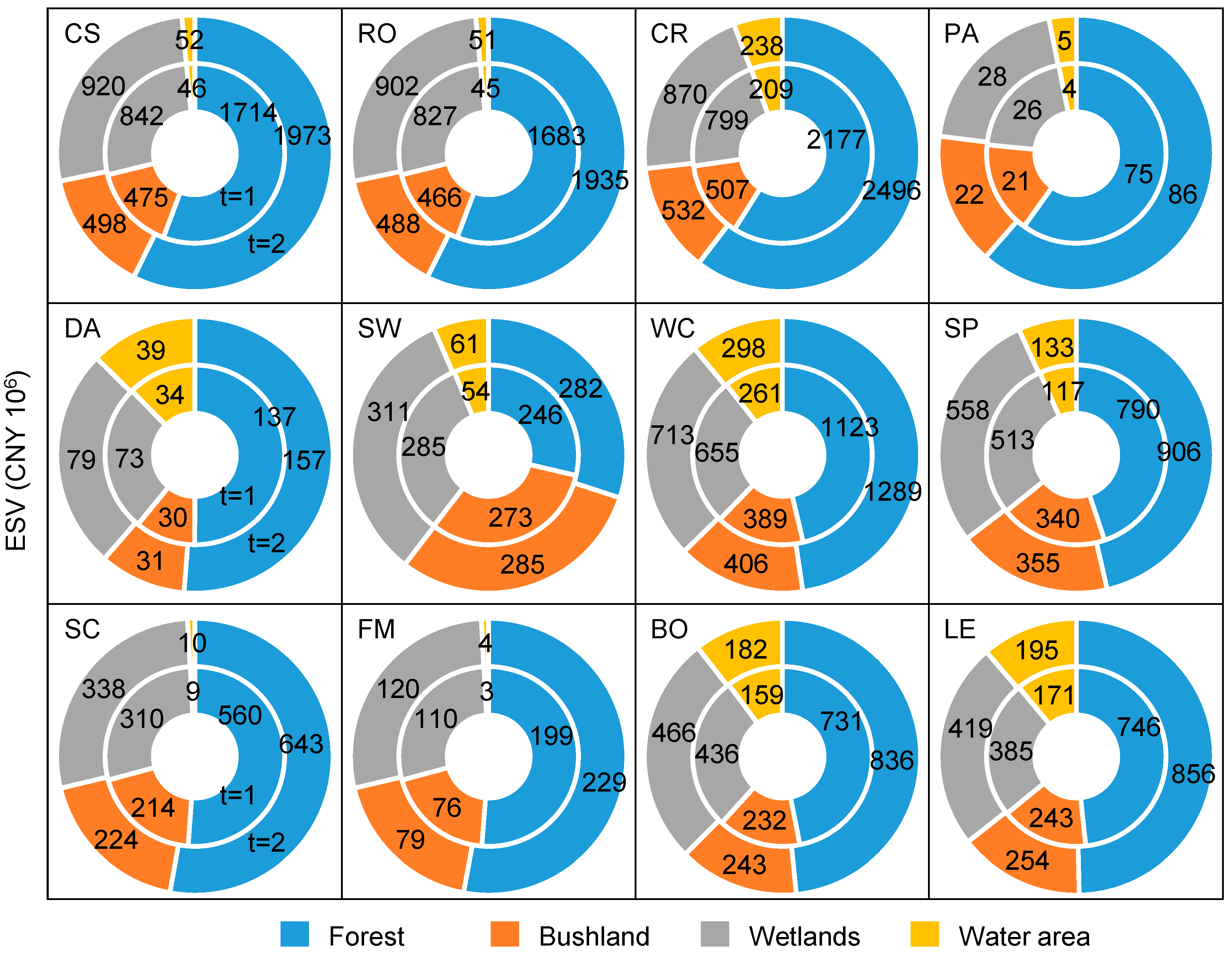
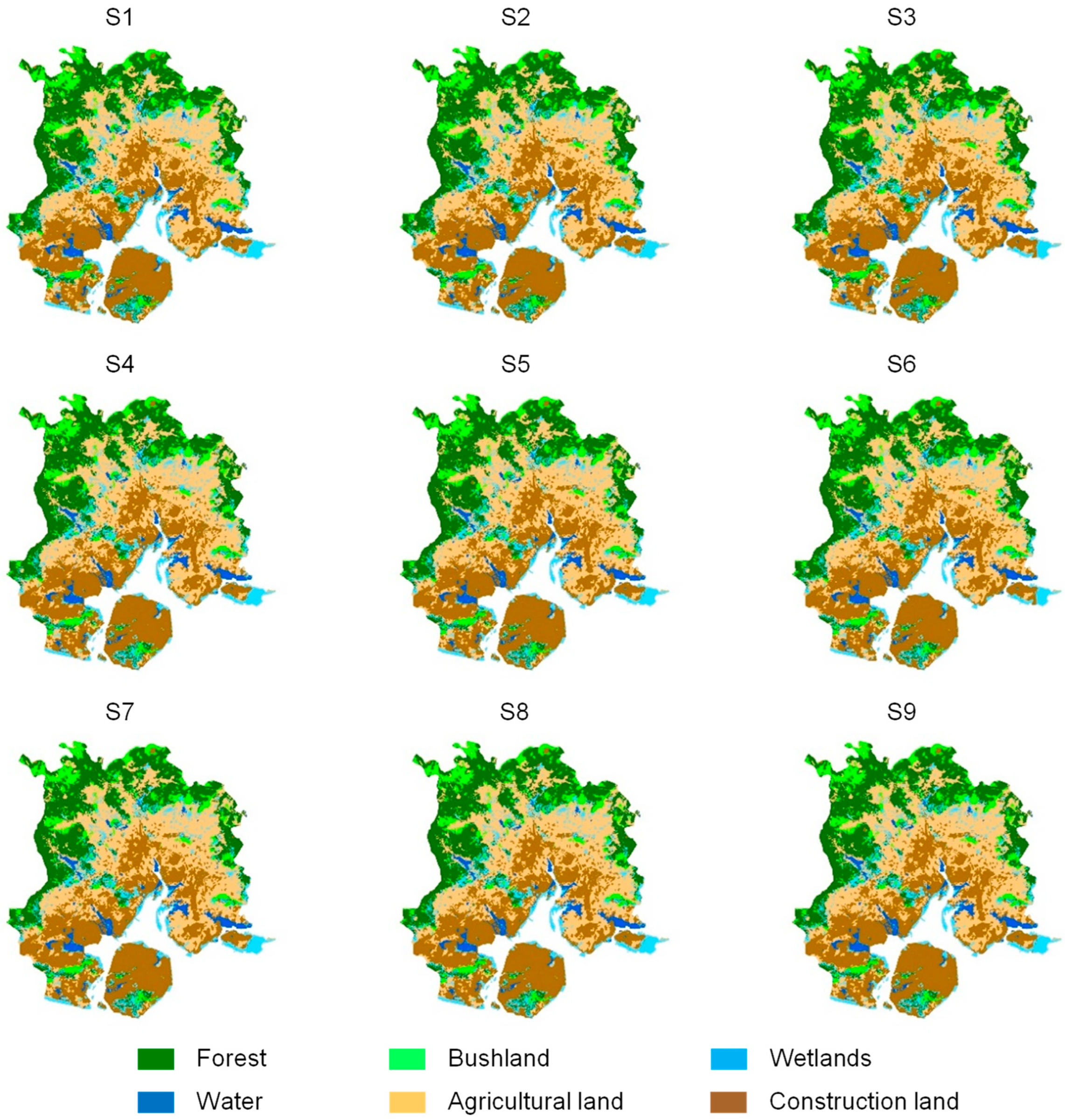
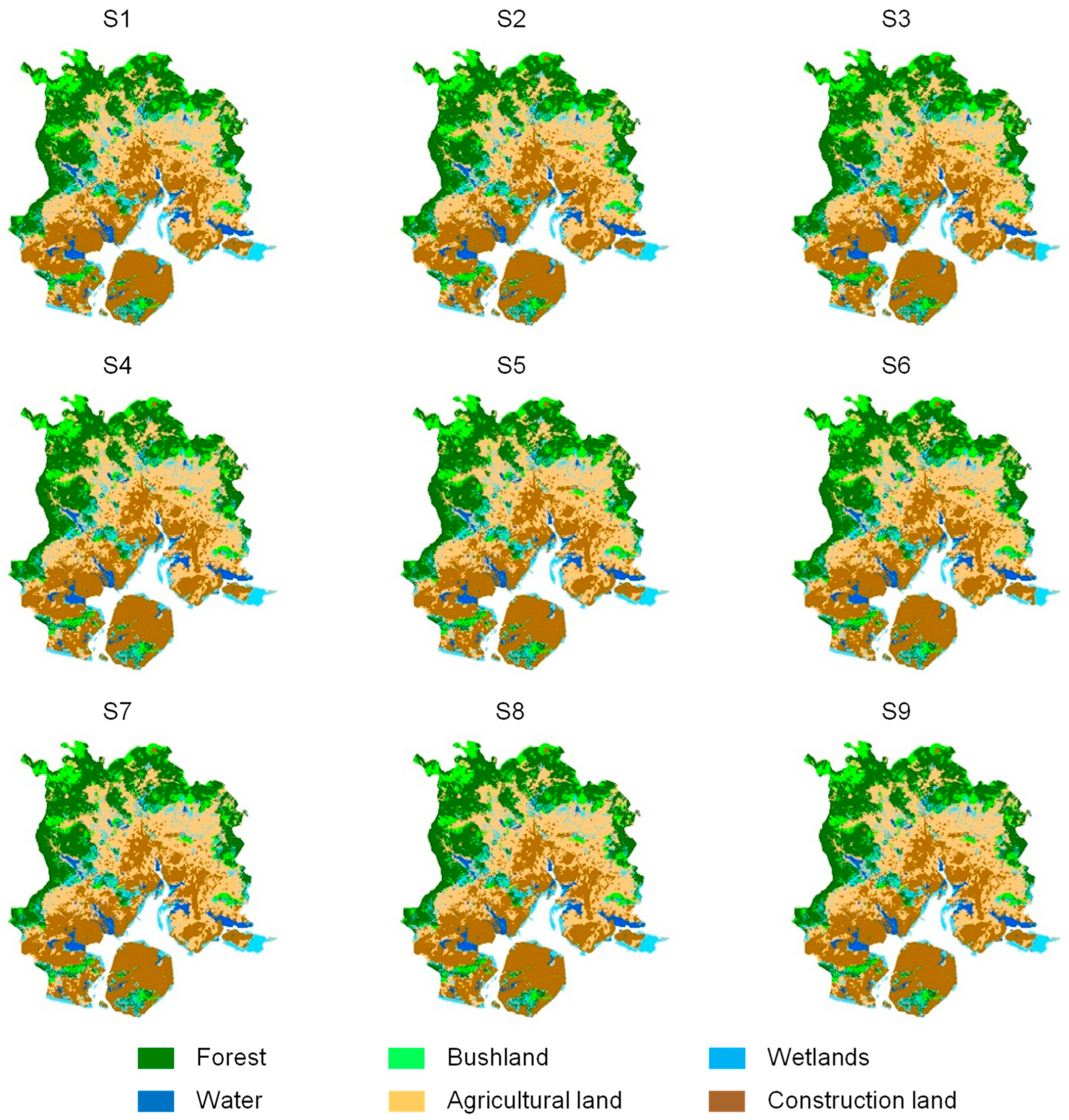
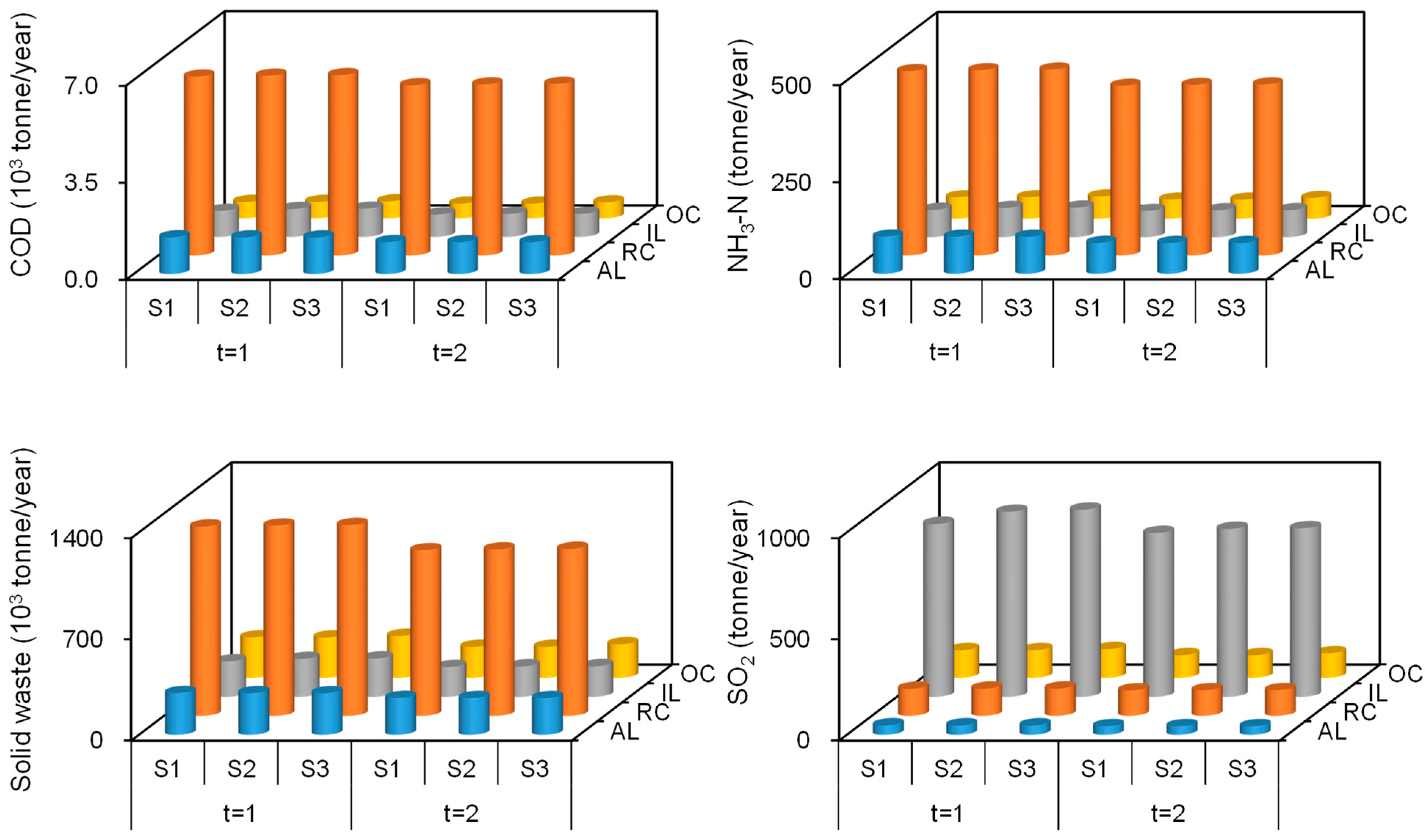
| Forest | Bushland | Wetlands | Water Area | |
|---|---|---|---|---|
| Carbon sequestration (t/ha) | 380 | 310 | 400 | 70 |
| SO2 sequestration (t/ha) | 0.022 | 0.018 | 0.016 | 0.008 |
| COD absorption (t/ha) | 0.008 | 0.009 | 0.015 | 0.012 |
| NH3-N absorption (t/ha) | 0.0009 | 0.0010 | 0.0024 | 0.0016 |
| Solid waste treatment (t/ha) | 3.7 | 12.1 | 9.2 | 5.6 |
| Dust absorption (t/ha) | 0.14 | 0.09 | 0.16 | 0.24 |
| Surface runoff coefficient | 0.42 | 0.40 | 0.46 | 0.57 |
| Water conservation capacity (t/ha) | 8600 | 9200 | 9800 | 10,200 |
| Water purification (t/ha) | 410 | 520 | 570 | 420 |
| Soil erosion modules | 16 | 18 | 19 | 1.8 |
| Period 1 | Period 2 | |
|---|---|---|
| CO2 (106 t) | 9.90 | 8.16 |
| COD (t) | 10,620 | 9560 |
| NH3-N (t) | 810 | 730 |
| SO2 (t) | 1050 | 945 |
| Solid waste (106 t) | 2.32 | 2.09 |
| Sewage (106 t) | 210 | 190 |
| Period 1 | Period 2 | |
|---|---|---|
| Forest and grass coverage (%) | ||
| p = 0.05 | 60.0 | 60.5 |
| p = 0.10 | 59.3 | 59.8 |
| p = 0.20 | 58.4 | 58.9 |
| Soil erosion (103 ha) | ||
| p = 0.05 | 11.88 | 10.44 |
| p = 0.10 | 12.41 | 10.96 |
| p = 0.20 | 13.06 | 11.61 |
| Forest | Bushland | Wetlands | Water Area | Agricultural Land | Construction Land | |
|---|---|---|---|---|---|---|
| Distance to river | −0.00006 | 0.00009 | 0.00022 | −0.00055 | −0.00017 | 0.00018 |
| Distance to road | 0.00004 | 0.00008 | −0.00022 | 0.00009 | 0.00016 | −0.00025 |
| Soil organic matter | 0.39577 | 0.07774 | −1.43912 | −0.52353 | 0.03868 | 0.10686 |
| Elevation | 0.00167 | 0.00156 | −0.24532 | −0.01900 | −0.00912 | −0.00908 |
| Slope | 0.11326 | 0.00843 | 0.06507 | −0.04303 | −0.03655 | −0.04231 |
| Aspect | 0.00065 | 0.00037 | −0.00116 | −0.00186 | 0.00083 | 0.00002 |
| Constant | −4.03193 | −3.87450 | −0.70530 | −0.66455 | −0.68941 | 0.50263 |
| ROC | 0.891 | 0.795 | 0.973 | 0.851 | 0.742 | 0.854 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, L.; Gao, P.; Wang, S.; Ma, Z. Coupling Fuzzy Bi-Level Chance Constraint Programming and Spatial Analysis for Urban Ecological Management. Land 2023, 12, 901. https://doi.org/10.3390/land12040901
Fang L, Gao P, Wang S, Ma Z. Coupling Fuzzy Bi-Level Chance Constraint Programming and Spatial Analysis for Urban Ecological Management. Land. 2023; 12(4):901. https://doi.org/10.3390/land12040901
Chicago/Turabian StyleFang, Licheng, Pangpang Gao, Shuguang Wang, and Zhenhao Ma. 2023. "Coupling Fuzzy Bi-Level Chance Constraint Programming and Spatial Analysis for Urban Ecological Management" Land 12, no. 4: 901. https://doi.org/10.3390/land12040901
APA StyleFang, L., Gao, P., Wang, S., & Ma, Z. (2023). Coupling Fuzzy Bi-Level Chance Constraint Programming and Spatial Analysis for Urban Ecological Management. Land, 12(4), 901. https://doi.org/10.3390/land12040901







