Simulating Urban Agglomeration Expansion in Henan Province, China: An Analysis of Driving Mechanisms Using the FLUS Model with Considerations for Urban Interactions and Ecological Constraints
Abstract
:1. Introduction
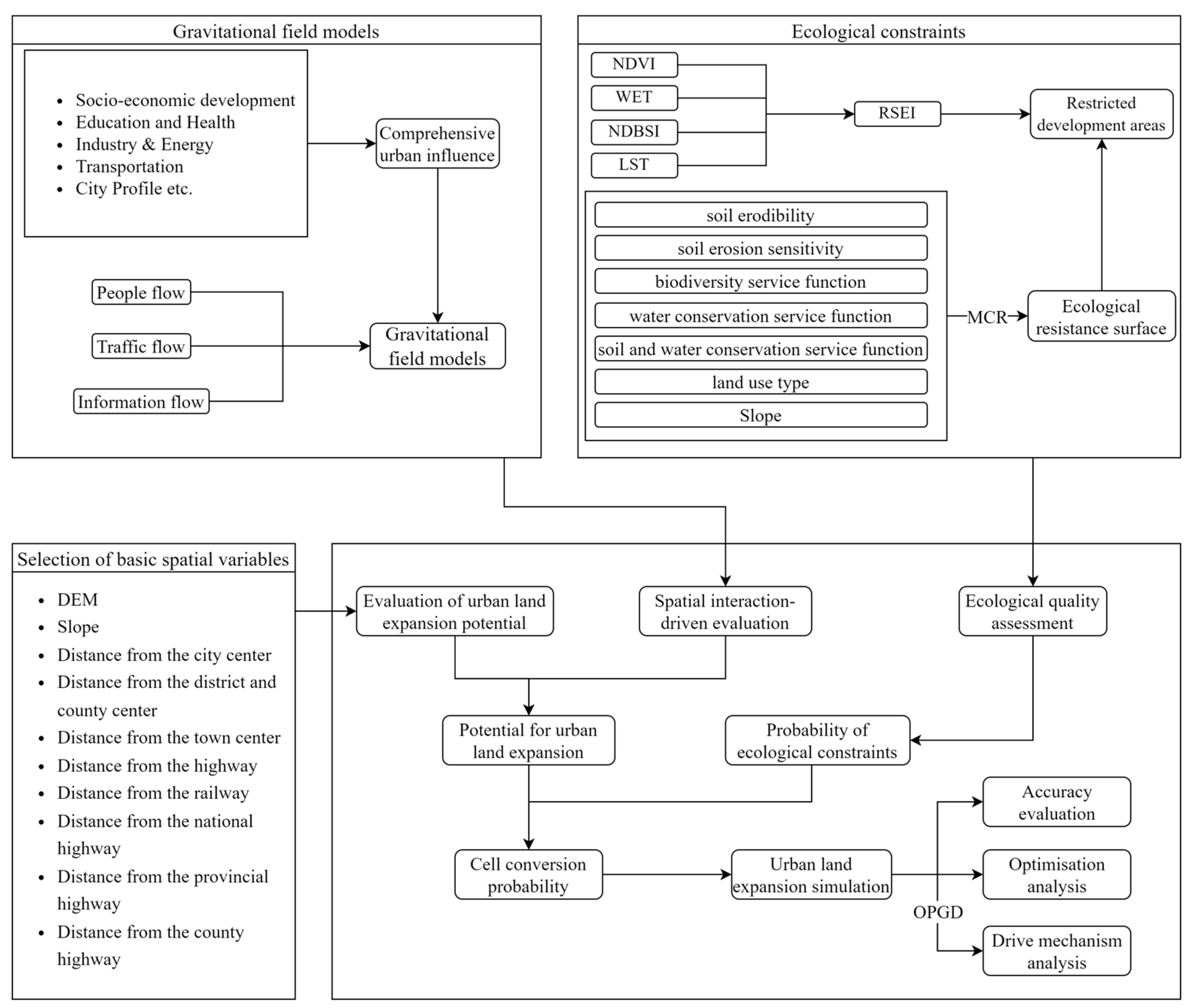
2. Research Methodology
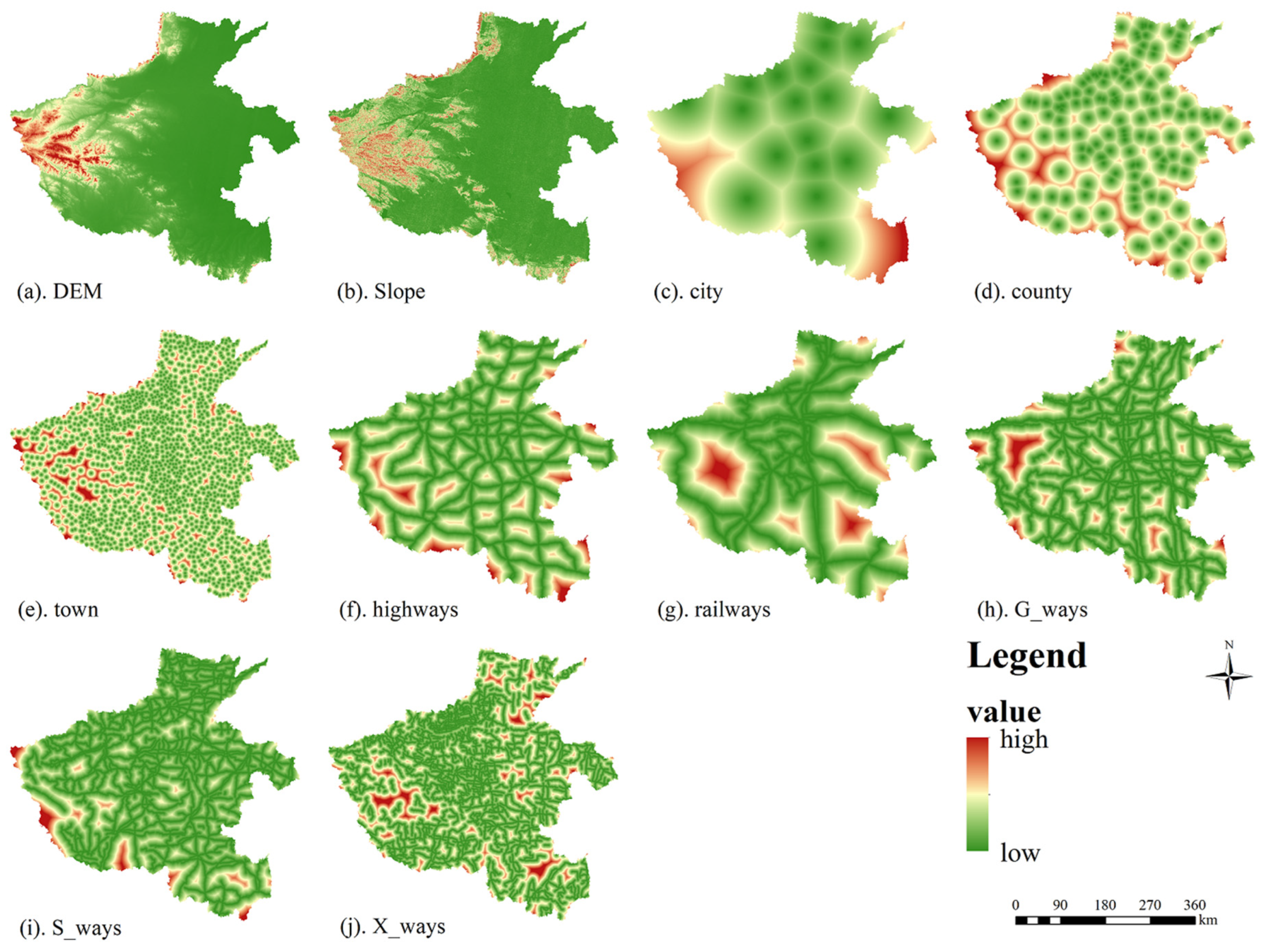
- Selection of basic spatial variables. Based on extensive research related to the FLUS model and previous studies on the land-use status of urban agglomerations, we selected ten drivers that significantly impact land-use change for this study;
- Construction of a gravitational field model that integrates socioeconomic data, other statistical data, and flow data, such as the Baidu index, population migration, traffic flow, and time–cost distance. We designated the urban spatial interaction intensity as a driving factor for the demand-driven FLUS model, subsequently simulating urban expansion in metropolitan areas;
- Evaluation of ecological quality. Ecological quality was assessed using the RSEI and ERS coefficients, and this was used to determine the restricted development area, which was set as a constraint for the expansion of urban clusters;
- Creation of a coupled model for urban agglomeration expansion simulation experiments. The accuracy of the simulation results was evaluated using the model validation method;
- Analysis of the driving mechanism of urban agglomeration expansion. Factor analysis and interaction analysis were performed for each driver using the OPGD model.
2.1. Gravitational Field Model
2.2. Ecological Quality Assessment
2.2.1. RSEI
2.2.2. ERS
2.3. Future Land Use Simulation (FLUS) Model
2.3.1. Introduction to the Model
2.3.2. FLUS Model Parameter Settings
2.4. The OPGD Model
3. Study Area and Data
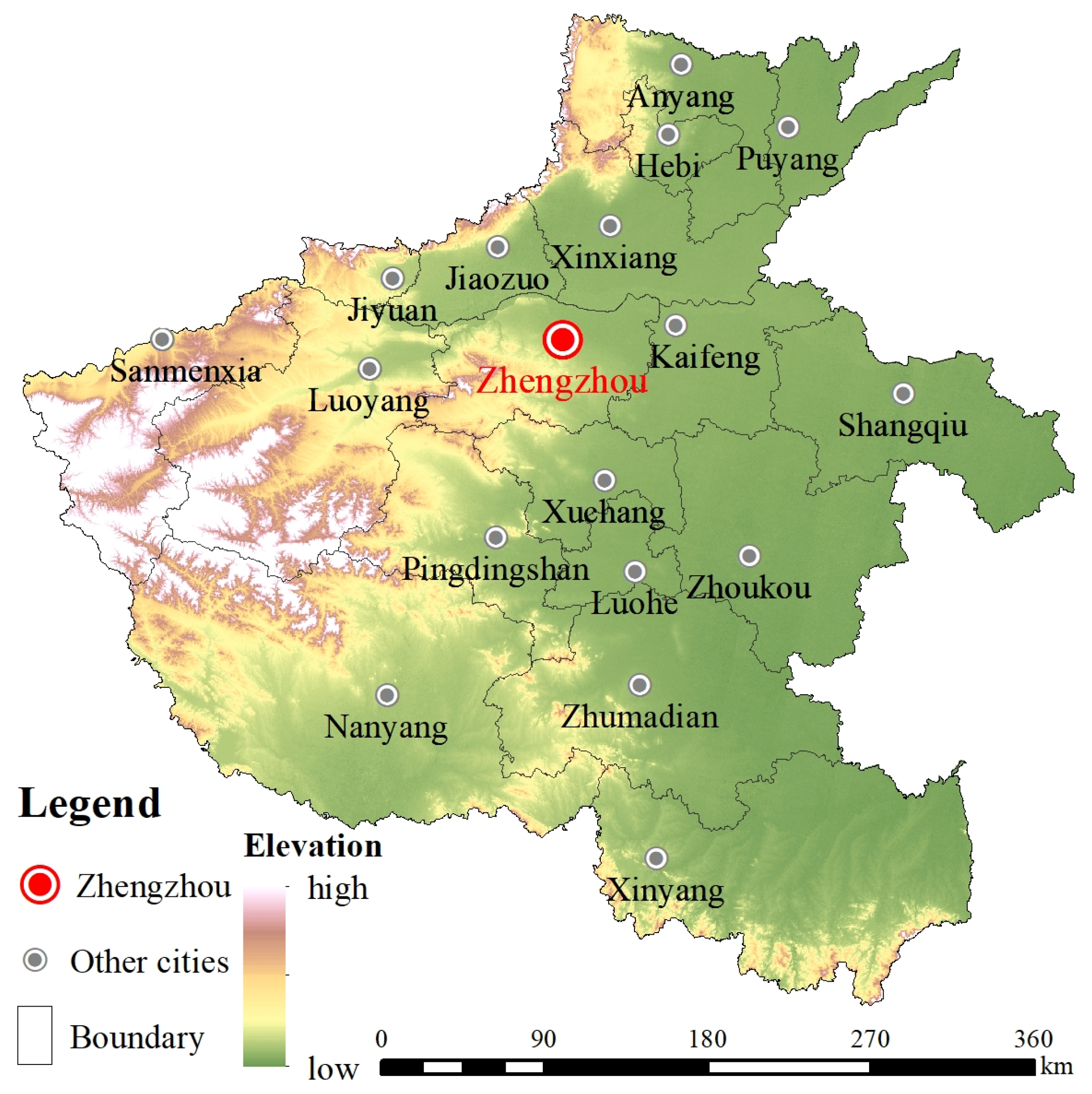
3.1. Overview of the Study Area
3.2. Data Sources and Processing
4. Results and Analysis
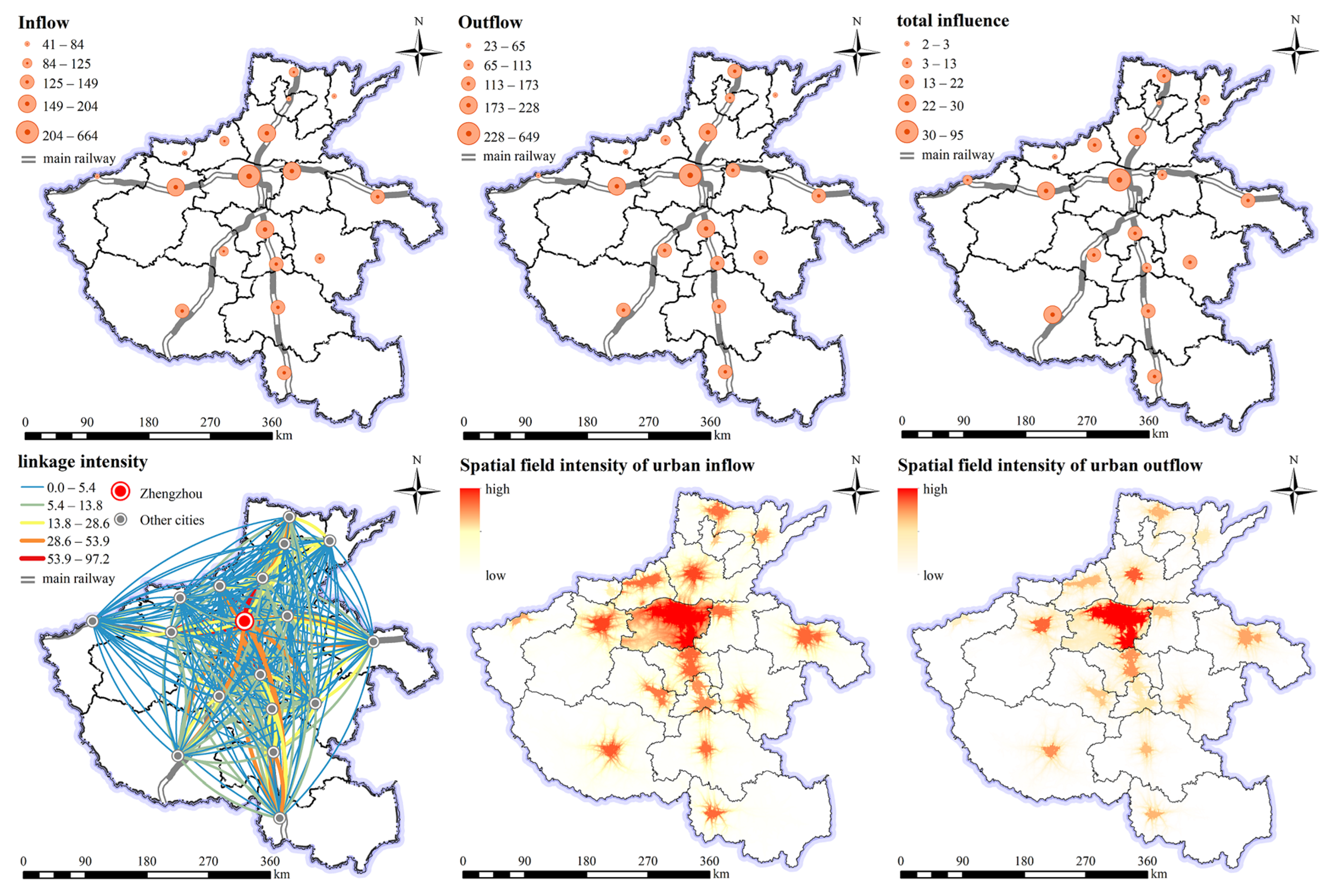
4.1. Urban Spatial Field Strength
4.2. Comprehensive Evaluation of Ecological Constraints
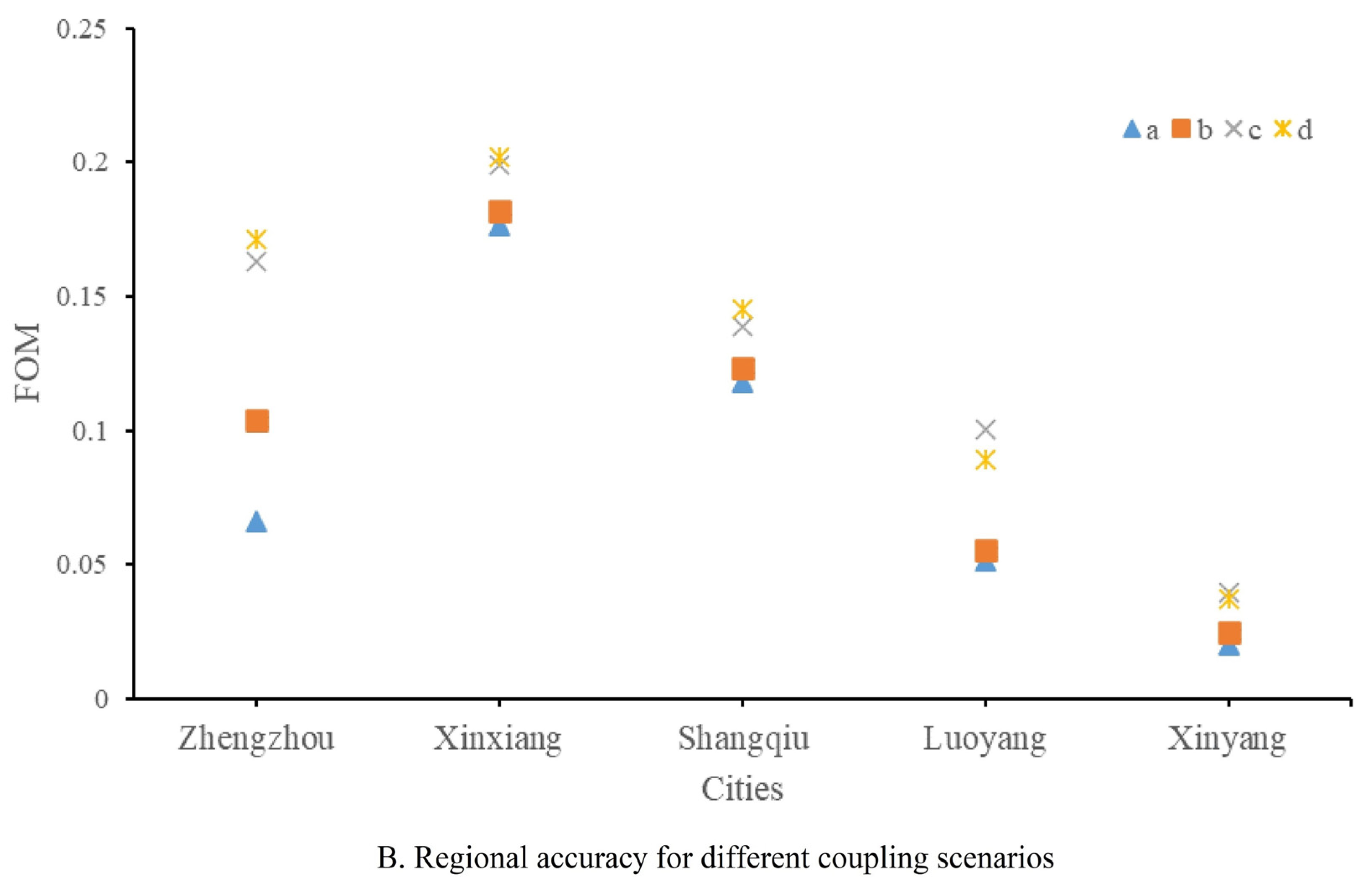
4.3. Simulation Accuracy Assessment
4.4. Simulation of Urban Expansion for 2020–2030
4.5. Analysis of the Various Factor-Driven Mechanisms
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, C.; Zhou, C.; Gu, C.; Chen, L.; Li, S. A proposal for the theoretical analysis of the interactive coupled effects between urbanization and the eco-environment in mega-urban agglomerations. J. Geogr. Sci. 2017, 27, 1431–1449. [Google Scholar] [CrossRef]
- Ye, Y.; Su, Y.; Zhang, H.-O.; Liu, K.; Wu, Q. Construction of an ecological resistance surface model and its application in urban expansion simulations. J. Geogr. Sci. 2015, 25, 211–224. [Google Scholar] [CrossRef]
- Zhang, M.; Kafy, A.-A.; Ren, B.; Zhang, Y.; Tan, S.; Li, J. Application of the Optimal Parameter Geographic Detector Model in the Identification of Influencing Factors of Ecological Quality in Guangzhou, China. Land 2022, 11, 1303. [Google Scholar] [CrossRef]
- Lopes, N.D.R.; Li, T.; Zhang, P.; Matomela, N.; Ikhumhen, H.O.; Sá, R.M. Predicting future coastal land use/cover change and associated sea-level impact on habitat quality in the Northwestern Coastline of Guinea-Bissau. J. Environ. Manag. 2022, 327, 116804. [Google Scholar] [CrossRef] [PubMed]
- Chang, D.; Li, S.; Lai, Z.; Fu, F.; Qi, X. Integrated effects of co-evolutions among climate, land use and vegetation growing dynamics to changes of runoff quantity and quality. J. Environ. Manag. 2023, 331, 117195. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Bai, Y.; Che, L.; Qiao, F.; Xie, L. Incorporating ecological constraints into urban growth boundaries: A case study of ecologically fragile areas in the Upper Yellow River. Ecol. Indic. 2021, 124, 107436. [Google Scholar] [CrossRef]
- Ma, Q. Integrating ecological correlation into cellular automata for urban growth simulation: A case study of Hangzhou, China. Urban For. Urban Green. 2020, 51, 126697. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, X.; Fu, Y.; Lu, Z.; Shen, X. Urban spatial growth modeling using logistic regression and cellular automata: A case study of Hangzhou. Ecol. Indic. 2020, 113, 106200. [Google Scholar] [CrossRef]
- Yao, Y.; Ma, L.; Che, X.; Dou, H. Simulation study of urban expansion under ecological constraint—Taking Yuzhong County, China as an example. Urban For. Urban Green. 2021, 57, 126933. [Google Scholar] [CrossRef]
- Jiao, L.M.; Tang, X.; Liu, X.P. Spatial linkage and urban expansion: An urban agglomeration view. ISPRS-Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2017, XLII-2/W7, 1203–1211. [Google Scholar] [CrossRef] [Green Version]
- Cuiking, L.; Ying, L. Urban expansion simulation and analysis in the Beijing-Tianjin-Hebei Region. Prog. Geogr. 2015, 34, 217–228. [Google Scholar]
- Li, X.; Chen, Y.; Liu, X.; Li, D.; He, J. Concepts, methodologies, and tools of an integrated geographical simulation and optimization system. Int. J. Geogr. Inf. Sci. 2011, 25, 633–655. [Google Scholar] [CrossRef] [Green Version]
- Couclelis, H. Cellular Worlds: A Framework for Modeling Micro—Macro Dynamics. Environ. Plan. A 1985, 17, 585–596. [Google Scholar] [CrossRef]
- Verburg, P.H.; Soepboer, W.; Veldkamp, A.; Limpiada, R.; Espaldon, V.; Mastura, S.S.A. Modeling the Spatial Dynamics of Regional Land Use: The CLUE-S Model. Environ. Manag. 2002, 30, 391–405. [Google Scholar] [CrossRef]
- He, C.; Shi, P.; Chen, J.; Li, X.; Pan, Y.; Li, J.; Li, Y.; Li, J. Developing land use scenario dynamics model by the integration of system dynamics model and cellular automata model. Sci. China Ser. D Earth Sci. 2005, 48, 1979–1989. [Google Scholar] [CrossRef]
- Parker, D.C.; Manson, S.M.; Janssen, M.A.; Hoffmann, M.J.; Deadman, P. Multi-Agent Systems for the Simulation of Land-Use and Land-Cover Change: A Review. Ann. Assoc. Am. Geogr. 2003, 93, 314–337. [Google Scholar] [CrossRef] [Green Version]
- Santé, I.; García, A.M.; Miranda, D.; Crecente, R. Cellular automata models for the simulation of real-world urban processes: A review and analysis. Landsc. Urban Plan. 2010, 96, 108–122. [Google Scholar] [CrossRef]
- Aburas, M.M.; Ho, Y.M.; Ramli, M.F.; Ash’aari, Z.H. The simulation and prediction of spatio-temporal urban growth trends using cellular automata models: A review. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 380–389. [Google Scholar] [CrossRef]
- Castro, M.L.; Machado, P.; Santos, I.; Rodriguez-Fernandez, N.; Torrente-Patiño, A.; Carballal, A. State of the Art on Artificial Intelligence in Land Use Simulation. Complexity 2022, 2022, 2291508. [Google Scholar] [CrossRef]
- Qiang, Y.; Lam, N.S.N. Modeling land use and land cover changes in a vulnerable coastal region using artificial neural networks and cellular automata. Environ. Monit. Assess. 2015, 187, 57. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Liu, Y.; Batty, M. Modeling urban growth with GIS based cellular automata and least squares SVM rules: A case study in Qingpu–Songjiang area of Shanghai, China. Stoch. Environ. Res. Risk Assess. 2016, 30, 1387–1400. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, Y.; Pontius, R.G. Spatially-Explicit Simulation of Urban Growth through Self-Adaptive Genetic Algorithm and Cellular Automata Modelling. Land 2014, 3, 719–738. [Google Scholar] [CrossRef] [Green Version]
- Liao, J.; Tang, L.; Shao, G.; Qiu, Q.; Wang, C.; Zheng, S.; Su, X. A neighbor decay cellular automata approach for simulating urban expansion based on particle swarm intelligence. Int. J. Geogr. Inf. Sci. 2014, 28, 720–738. [Google Scholar] [CrossRef]
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Lin, J.; He, P.; Yang, L.; He, X.; Lu, S.; Liu, D. Predicting future urban waterlogging-prone areas by coupling the maximum entropy and FLUS model. Sustain. Cities Soc. 2022, 80, 103812. [Google Scholar] [CrossRef]
- Gu, C.; Hu, L.; Zhang, X.; Wang, X.; Guo, J. Climate change and urbanization in the Yangtze River Delta. Habitat Int. 2011, 35, 544–552. [Google Scholar] [CrossRef]
- Limtanakool, N.; Schwanen, T.; Dijst, M. Ranking functional urban regions: A comparison of interaction and node attribute data. Cities 2007, 24, 26–42. [Google Scholar] [CrossRef]
- Lv, J.; Wang, Y.; Liang, X.; Yao, Y.; Ma, T.; Guan, Q. Simulating urban expansion by incorporating an integrated gravitational field model into a demand-driven random forest-cellular automata model. Cities 2021, 109, 103044. [Google Scholar] [CrossRef]
- Derudder, B.; Taylor, P. The cliquishness of world cities. Glob. Networks 2005, 5, 71–91. [Google Scholar] [CrossRef]
- Cao, H.; Wang, S. Analysis on the intensity of urban flow in the urban compact area of east Heilongjiang. Hum. Geogr. 2007, 22, 81–86. [Google Scholar]
- Yu, D.; Yanxu, L.; Bojie, F. Urban growth simulation guided by ecological constraints in Beijing city: Methods and implications for spatial planning. J. Environ. Manag. 2019, 243, 402–410. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Q.; Song, Y.; Han, H. Bringing conservation priorities into urban growth simulation: An integrated model and applied case study of Hangzhou, China. Resour. Conserv. Recycl. 2019, 140, 324–337. [Google Scholar] [CrossRef]
- Han, N.; Hu, K.; Yu, M.; Jia, P.; Zhang, Y. Incorporating Ecological Constraints into the Simulations of Tropical Urban Growth Boundaries: A Case Study of Sanya City on Hainan Island, China. Appl. Sci. 2022, 12, 6409. [Google Scholar] [CrossRef]
- He, C.; Zhao, Y.; Tian, J.; Shi, P. Modeling the urban landscape dynamics in a megalopolitan cluster area by incorporating a gravitational field model with cellular automata. Landsc. Urban Plan. 2013, 113, 78–89. [Google Scholar] [CrossRef]
- Chuanglin, F. Progress and the future direction of research into urban agglomeration in China. Acta Geogr. Sin. 2014, 69, 1130–1144. [Google Scholar]
- Tian, G.; Qiao, Z.; Zhang, Y. The investigation of relationship between rural settlement density, size, spatial distribution and its geophysical parameters of China using Landsat TM images. Ecol. Model. 2012, 231, 25–36. [Google Scholar] [CrossRef]
- Poelmans, L.; Van Rompaey, A. Detecting and modelling spatial patterns of urban sprawl in highly fragmented areas: A case study in the Flanders–Brussels region. Landsc. Urban Plan. 2009, 93, 10–19. [Google Scholar] [CrossRef]
- You, H.; Yang, X. Urban expansion in 30 megacities of China: Categorizing the driving force profiles to inform the urbanization policy. Land Use Policy 2017, 68, 531–551. [Google Scholar] [CrossRef]
- Colantoni, A.; Grigoriadis, E.; Sateriano, A.; Venanzoni, G.; Salvati, L. Cities as selective land predators? A lesson on urban growth, deregulated planning and sprawl containment. Sci. Total Environ. 2016, 545–546, 329–339. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Hu, S.; Frazier, A.E.; Liu, Y. Multi-order urban development model and sprawl patterns: An analysis in China, 2000–2010. Landsc. Urban Plan. 2017, 167, 386–398. [Google Scholar] [CrossRef]
- Lin, J.; Li, X. Simulating urban growth in a metropolitan area based on weighted urban flows by using web search engine. Int. J. Geogr. Inf. Sci. 2015, 29, 1721–1736. [Google Scholar] [CrossRef]
- James, P.E.; Martin, G.J. History of Geographical Thought; Xudan, L., Ed.; The Commercial Press: Beijing, China, 1989; pp. 481–482. [Google Scholar]
- Peng, G.; Ruihua, X. The Relationship between Urban Rail Transit and Urban Development Based on Gravitation Field Model. Syst. Eng. 2006, 1, 36–40. [Google Scholar]
- He, J.; Li, C.; Yu, Y.; Liu, Y.; Huang, J. Measuring urban spatial interaction in Wuhan Urban Agglomeration, Central China: A spatially explicit approach. Sustain. Cities Soc. 2017, 32, 569–583. [Google Scholar] [CrossRef]
- Hanqiu, X. A remote sensing urban ecological index and its application. Acta Ecol. Sin. 2013, 33, 7853–7862. [Google Scholar]
- Liping, H.; Ji, J. Remote Sensing Dynamic Monitoring on Temporal and Spatial Changes of Vegetation Coverage in Sichuan Province from 2009 to 2020. Bull. Soil Water Conserv. 2022, 42, 203–209. [Google Scholar]
- Liang, X.; Liu, X.; Li, X.; Chen, Y.; Tian, H.; Yao, Y. Delineating multi-scenario urban growth boundaries with a CA-based FLUS model and morphological method. Landsc. Urban Plan. 2018, 177, 47–63. [Google Scholar] [CrossRef]
- Baosheng, W.; Jiangfu, L.; Wei, Z.; Lin, Q.Q.W.; Lina, T. The weight of neighborhood setting of the FLUS model based on a historical scenario: A case study of land use simulation of urban agglomeration of the Golden Triangle of Southern Fujian in 2030. Acta Ecol. Sin. 2019, 39, 4284–4298. [Google Scholar]
- Jinfeng, W.; Chengdong, X. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar]
- Peng, W.; Fan, Z.; Duan, J.; Gao, W.; Wang, R.; Liu, N.; Li, Y.; Hua, S. Assessment of interactions between influencing factors on city shrinkage based on geographical detector: A case study in Kitakyushu, Japan. Cities 2022, 131, 103958. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, Y.; Qian, M.; Zeng, Z. Land Use Transition and Driving Forces in Chinese Loess Plateau: A Case Study from Pu County, Shanxi Province. Land 2021, 10, 67. [Google Scholar] [CrossRef]
- Tong, Z.; Jialin, W. On Driving Mechanism of Urban Expansion Based on Multi-source Nighttime Light Data: A Case Study of Three Urban Agglomerations in the Yangtze River Economic Belt. Sci. Technol. Manag. Land Resour. 2022, 39, 24–35. [Google Scholar]
- Song, Y.; Wang, J.; Ge, Y.; Xu, C. An optimal parameters-based geographical detector model enhances geographic characteristics of explanatory variables for spatial heterogeneity analysis: Cases with different types of spatial data. GISci. Remote Sens. 2020, 57, 593–610. [Google Scholar] [CrossRef]
- Peng, W.; Kuang, T.; Tao, S. Quantifying influences of natural factors on vegetation NDVI changes based on geographical detector in Sichuan, western China. J. Clean. Prod. 2019, 233, 353–367. [Google Scholar] [CrossRef]
- Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Miaomiao, Y.; Qinke, Y.; Keli, Z.; Yuru, L.; Chunmei, W.; Guowei, P. Effects of Content of Soil Rock Fragments on Calculating of Soil Erodibility. Acta Pedol. Sin. 2021, 58, 1157–1168. [Google Scholar]
- Yang, Q. Soil Erodibility Dataset of Pan-Third Pole 20 countries (2020, with a resolution of 7.5 arc second). Natl. Tibet. Plateau Data Cent. 2021, 58, 1157–1167. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef] [Green Version]
- McHale, M.R.; Pickett, S.T.; Barbosa, O.; Bunn, D.N.; Cadenasso, M.L.; Childers, D.L.; Gartin, M.; Hess, G.R.; Iwaniec, D.M.; McPhearson, T.; et al. The New Global Urban Realm: Complex, Connected, Diffuse, and Diverse Social-Ecological Systems. Sustainability 2015, 7, 5211–5240. [Google Scholar] [CrossRef] [Green Version]
- Xia, C.; Zhang, A.; Wang, H.; Zhang, B.; Zhang, Y. Bidirectional urban flows in rapidly urbanizing metropolitan areas and their macro and micro impacts on urban growth: A case study of the Yangtze River middle reaches megalopolis, China. Land Use Policy 2018, 82, 158–168. [Google Scholar] [CrossRef]
- Tan, R.; Zhou, K.; He, Q.; Xu, H. Analyzing the Effects of Spatial Interaction among City Clusters on Urban Growth—Case of Wuhan Urban Agglomeration. Sustainability 2016, 8, 759. [Google Scholar] [CrossRef] [Green Version]
- Dock, J.P.; Song, W.; Lu, J. Evaluation of dine-in restaurant location and competitiveness: Applications of gravity modeling in Jefferson County, Kentucky. Appl. Geogr. 2015, 60, 204–209. [Google Scholar] [CrossRef]
- Natale, F.; Borrello, A.; Motova, A. Analysis of the determinants of international seafood trade using a gravity model. Mar. Policy 2015, 60, 98–106. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, A.; Wang, H.; Zhang, B. Modeling urban growth in a metropolitan area based on bidirectional flows, an improved gravitational field model, and partitioned cellular automata. Int. J. Geogr. Inf. Sci. 2019, 33, 877–899. [Google Scholar] [CrossRef]
- Huang, A.; Xu, Y.; Liu, C.; Lu, L.; Zhang, Y.; Sun, P.; Zhou, G.; Du, T.; Xiang, Y. Simulated town expansion under ecological constraints: A case study of Zhangbei County, Heibei Province, China. Habitat Int. 2019, 91, 101986. [Google Scholar] [CrossRef]



| City Impact Evaluation Indicator System | Indicators |
|---|---|
| Socioeconomic development | Total GDP (X1), total retail sales of consumer goods (X2), average employee wages (X3), population (X4) |
| Education and Health | Number of students enrolled in higher education (X5), number of health institutions (X6), number of higher education institutions (X7) |
| Industry and Energy | Number of industrial enterprise units above scale (X8), electricity consumption of the entire society (X9) |
| Transportation | Passenger transport volume (X10), freight transport volume (X11), total post and telecommunications services (X12) |
| City overview | Area of built-up urban areas (X13), parkland area per capita (X14), greening coverage of built-up areas (X15) |
| Value of Ecological Resistance to Urban Expansion | Type of Land Use | Slope (Degree) |
|---|---|---|
| 1 | Urban building land | 0–3 |
| 3 | Bare land, facility land | 3–8 |
| 5 | Arable land, grassland | 8–15 |
| 7 | Woodland | 15–25 |
| 9 | Water areas, nature reserves | >25 |
| Cultivated Land | Forest | Grassland | Shrubland | Wetland | Water Body | Artificial Surfaces | Bare Land | |
|---|---|---|---|---|---|---|---|---|
| Cultivated Land | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| Forest | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| Grass Land | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| Shrubland | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| Wetland | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| Water Body | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| Artificial Surfaces | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Bare Land | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Data | Type | Resolution | Source | |
|---|---|---|---|---|
| Basic data | Basic geospatial data (including administrative areas, urban points, roads, etc.) | Vector | — | National Geomatics Centre of China (http://www.ngcc.cn/ngcc/) (accessed on 24 August 2022) |
| Land use data | Raster | 30 m | GlobeLand30 (http://www.globallandcover.com/)(accessed on 24 August 2022) | |
| DEM | Raster | 30 m | Geospatial Data Cloud (http://www.gscloud.cn/search) (accessed on 24 August 2022) | |
| Gravitational field model data | City Impact Evaluation Indicators | Properties | year | Henan Statistical Yearbook 2020 |
| Baidu Index Data | Properties | 1 January 2020–31 December 2020 | Baidu Index official website (https://index.baidu.com/v2/index.html#/) | |
| Traffic Flow Data | Properties | — | http://www.114piaowu.com, 12306 China railway (accessed on 3 September 2022) | |
| Population migration data | Properties | 1 January 2020–31 December 2020 | AutoNavi Maps Traffic Big Data (https://trp.autonavi.com/home.html) (accessed on 3 September 2022) | |
| Ecological constraints data | RESI (NDVI, WET, NDBSI, LST) | Raster | 30 m | Landsat-8 (obtained from Google Earth Engine platform processing) |
| Soil erodibility (K) [56,57] | Raster | 7.5 arc s | National Tibetan Plateau Data Center (http://data.tpdc.ac.cn) (accessed on 9 September 2022) | |
| Rainfall data and temperature data [58] | Raster | 1 km | National Earth System Science Data Center, National Science & Technology Infrastructure of China. (http://www.geodata.cn) (accessed on 9 September 2022) | |
| Average annual net primary productivity of vegetation | Raster | 500 m | National Aeronautics and Space Administration (https://ladsweb.modaps.eosdis.nasa.gov/search/) (accessed on 9 September 2022) | |
| Soil infiltration factor data | Raster | 1 km | Global Soil Database |
| Cultivated Land | Forest | Grassland | Shrubland | Wetland | Water Body | Artificial Surfaces | Bareland | |
|---|---|---|---|---|---|---|---|---|
| Weight | 0.5 | 0.71 | 0.75 | 0.74 | 0.76 | 0.76 | 1.0 | 0.75 |
| Kappa Coefficient | Overall Accuracy | FOM | |
|---|---|---|---|
| A | 0.723529 | 0.844612 | 0.068728 |
| B | 0.724108 | 0.845181 | 0.071257 |
| C | 0.730133 | 0.848536 | 0.082824 |
| D | 0.730844 | 0.848676 | 0.083005 |
| Q-Statistic | |
|---|---|
| ERS | 0.5064 ** |
| IN | 0.152 ** |
| OUT | 0.1495 ** |
| county | 0.1148 ** |
| RSEI | 0.0992 ** |
| city | 0.0735 ** |
| Slope | 0.0678 ** |
| dem | 0.0661 ** |
| railways | 0.0593 ** |
| S_ways | 0.0489 ** |
| G_ways | 0.0469 ** |
| highways | 0.0338 ** |
| town | 0.0332 ** |
| X_ways | 0.0104 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Wang, J.; Wang, M.; Zhang, Y. Simulating Urban Agglomeration Expansion in Henan Province, China: An Analysis of Driving Mechanisms Using the FLUS Model with Considerations for Urban Interactions and Ecological Constraints. Land 2023, 12, 1189. https://doi.org/10.3390/land12061189
Gao C, Wang J, Wang M, Zhang Y. Simulating Urban Agglomeration Expansion in Henan Province, China: An Analysis of Driving Mechanisms Using the FLUS Model with Considerations for Urban Interactions and Ecological Constraints. Land. 2023; 12(6):1189. https://doi.org/10.3390/land12061189
Chicago/Turabian StyleGao, Chaoran, Jinxin Wang, Manman Wang, and Yan Zhang. 2023. "Simulating Urban Agglomeration Expansion in Henan Province, China: An Analysis of Driving Mechanisms Using the FLUS Model with Considerations for Urban Interactions and Ecological Constraints" Land 12, no. 6: 1189. https://doi.org/10.3390/land12061189
APA StyleGao, C., Wang, J., Wang, M., & Zhang, Y. (2023). Simulating Urban Agglomeration Expansion in Henan Province, China: An Analysis of Driving Mechanisms Using the FLUS Model with Considerations for Urban Interactions and Ecological Constraints. Land, 12(6), 1189. https://doi.org/10.3390/land12061189








