Estimation and Climate Impact Analysis of Terrestrial Vegetation Net Primary Productivity in China from 2001 to 2020
Abstract
:1. Introduction
2. Materials and Methods
2.1. The CASA Model
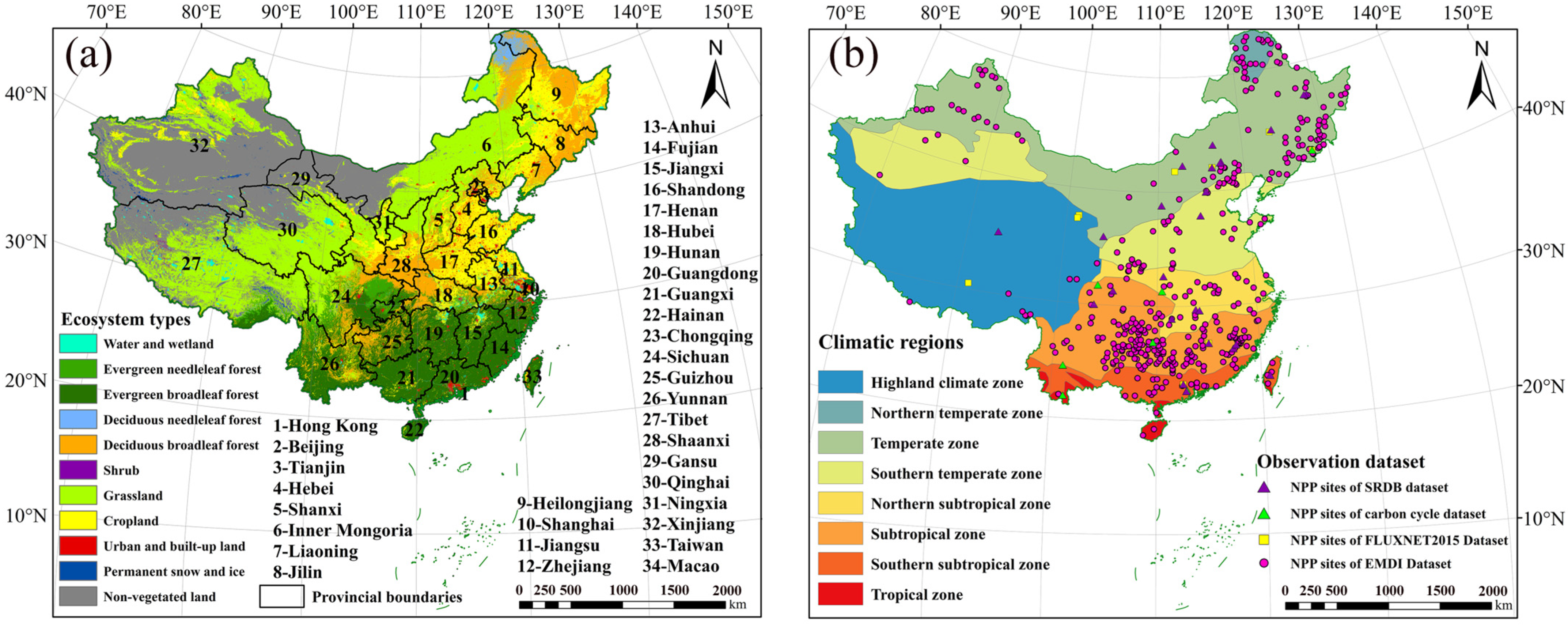
2.2. Data
2.3. Evaluation Methods for Model Estimation Results
2.3.1. Uncertainty Evaluation
2.3.2. Correlation Analysis
2.4. Data Analysis
2.4.1. Trend Analysis
2.4.2. Correlation between the NPP and Climatic Factors
2.4.3. Quantitative Relationship Analysis of Climatic Factors and NPP
3. Results
3.1. Validation and Consistency Analysis of Estimated NPP
3.1.1. Consistency Analysis with MOD17 and GLO-PEM NPP
3.1.2. Validation with Observation Site Dataset
3.2. Distribution of NPP
3.3. Trends of NPP
3.4. Response of NPP to Climate Factors
3.5. Perturbations of Temperature and Precipitation Changes on Grassland NPP
4. Discussion
4.1. Applicability and Limitations of the CASA Model
4.2. Limitations of Quantitative Statistical Method
4.3. Impacts of Land Use Change and Phenology on NPP
4.4. Impact of Temperature and Precipitation on the Trend of NPP
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, M.; Zhou, X.; Yang, Q.; Li, H.; Luo, Y.; Fang, C.; Chen, J.; Yang, X.; Li, B. Responses of Ecosystem Carbon Cycle to Experimental Warming: A Meta-Analysis. Ecology 2013, 94, 726–738. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fung, I.Y.; Doney, S.C.; Lindsay, K.; John, J. Evolution of Carbon Sinks in a Changing Climate. Proc. Natl. Acad. Sci. USA 2005, 102, 11201–11206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chapin, F.S.; Woodwell, G.M.; Randerson, J.T.; Rastetter, E.B.; Lovett, G.M.; Baldocchi, D.D.; Clark, D.A.; Harmon, M.E.; Schimel, D.S.; Valentini, R.; et al. Reconciling Carbon-Cycle Concepts, Terminology, and Methods. Ecosystems 2006, 9, 1041–1050. [Google Scholar] [CrossRef] [Green Version]
- Ji, Y.; Zhou, G.; Luo, T.; Dan, Y.; Zhou, L.; Lv, X. Variation of Net Primary Productivity and Its Drivers in China’s Forests during 2000–2018. For. Ecosyst. 2020, 7, 15. [Google Scholar] [CrossRef] [Green Version]
- Potter, C.; Klooster, S.; Myneni, R.; Genovese, V.; Tan, P.N.; Kumar, V. Continental-Scale Comparisons of Terrestrial Carbon Sinks Estimated from Satellite Data and Ecosystem Modeling 1982–1998. Glob. Planet. Chang. 2003, 39, 201–213. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Bounoua, L.; DeFries, R.; Lawrence, W.T.; Stutzer, D.; Tucker, C.J.; Ricketts, T. The Consequences of Urban Land Transformation on Net Primary Productivity in the United States. Remote Sens. Environ. 2004, 89, 434–443. [Google Scholar] [CrossRef]
- Haberl, H.; Erb, K.H.; Krausmann, F.; Gaube, V.; Bondeau, A.; Plutzar, C.; Gingrich, S.; Lucht, W.; Fischer-Kowalski, M. Quantifying and Mapping the Human Appropriation of Net Primary Production in Earth’s Terrestrial Ecosystems. Proc. Natl. Acad. Sci. USA 2007, 104, 12942–12947. [Google Scholar] [CrossRef] [Green Version]
- Shiga, Y.P.; Michalak, A.M.; Fang, Y.; Schaefer, K.; Andrews, A.E.; Huntzinger, D.H.; Schwalm, C.R.; Thoning, K.; Wei, Y. Forests Dominate the Interannual Variability of the North American Carbon Sink. Environ. Res. Lett. 2018, 13, 084015. [Google Scholar] [CrossRef]
- Ni, J.; Zhang, X.S.; Scurlock, J.M.O. Synthesis and Analysis of Biomass and Net Primary Productivity in Chinese Forests. Ann. For. Sci. 2001, 58, 351–384. [Google Scholar] [CrossRef]
- Guan, X.; Shen, H.; Gan, W.; Yang, G.; Wang, L.; Li, X.; Zhang, L. A 33-Year NPP Monitoring Study in Southwest China by the Fusion of Multi-Source Remote Sensing and Station Data. Remote Sens. 2017, 9, 1082. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J.L. Solar Radiation and Productivity in Tropical Ecosystems. Br. Ecol. Soc. 1972, 9, 747–766. [Google Scholar] [CrossRef] [Green Version]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial Ecosystem Production: A Process Model Based on Global Satellite and Surface Data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global Primary Production: A Remote Sensing Approach. J. Biogeogr. 1995, 22, 815. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a Light Use Efficiency Model from Eddy Covariance Flux Data for Predicting Daily Gross Primary Production across Biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Lal, R.; Zhao, Y.; Jiang, W.; Chen, Q. Estimating Net Primary Production of Natural Grassland and Its Spatio-Temporal Distribution in China. Sci. Total Environ. 2016, 553, 184–195. [Google Scholar] [CrossRef]
- Guo, D.; Song, X.; Hu, R.; Cai, S.; Zhu, X.; Hao, Y. Grassland Type-Dependent Spatiotemporal Characteristics of Productivity in Inner Mongolia and Its Response to Climate Factors. Sci. Total Environ. 2021, 775, 145644. [Google Scholar] [CrossRef]
- Yan, Y.; Wu, C.; Wen, Y. Determining the Impacts of Climate Change and Urban Expansion on Net Primary Productivity Using the Spatio-Temporal Fusion of Remote Sensing Data. Ecol. Indic. 2021, 127, 107737. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, X.; Huang, L.; Yang, G.; Fan, L.; Wei, P.; Chen, G. An Improved CASA Model for Estimating Winter Wheat Yield from Remote Sensing Images. Remote Sens. 2019, 11, 1088. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, X. Estimation of Net Primary Productivity of Different Forest Types Based on Improved CASA Model in Jing-Jin-Ji Region, China. J. Sustain. For. 2017, 36, 568–582. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Q.; Zou, F. Spatio-Temporal Changes of Vegetation Net Primary Productivity and Its Driving Factors on the Qinghai-Tibetan Plateau from 2001 to 2017. Remote Sens. 2021, 13, 1566. [Google Scholar] [CrossRef]
- Pei, Y.; Huang, J.; Wang, L.; Chi, H.; Zhao, Y. An Improved Phenology-Based CASA Model for Estimating Net Primary Production of Forest in Central China Based on Landsat Images. Int. J. Remote Sens. 2018, 39, 7664–7692. [Google Scholar] [CrossRef]
- Yang, H.; Hu, D.; Peng, F.; Wang, Y. Exploring the Response of Net Primary Productivity Variations to Land Use/Land Cover Change: A Case Study in Anhui, China. Polish J. Environ. Stud. 2019, 28, 3971–3984. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, X.; Nazieh, S.; Wang, X.; Nkrumah, T.; Hong, S. Spatiotemporal Distribution of Grassland NPP in Gansu Province, China from 1982 to 2011 and Its Impact Factors. PLoS ONE 2020, 15, e0242609. [Google Scholar] [CrossRef]
- Jiang, Y.; Guo, J.; Peng, Q.; Guan, Y.; Zhang, Y.; Zhang, R. The Effects of Climate Factors and Human Activities on Net Primary Productivity in Xinjiang. Int. J. Biometeorol. 2020, 64, 765–777. [Google Scholar] [CrossRef]
- Feng, Y.; Zhu, J.; Zhao, X.; Tang, Z.; Zhu, J.; Fang, J. Changes in the Trends of Vegetation Net Primary Productivity in China between 1982 and 2015. Environ. Res. Lett. 2019, 14, 124009. [Google Scholar] [CrossRef]
- Li, H.; Wu, Y.; Liu, S.; Xiao, J. Regional Contributions to Interannual Variability of Net Primary Production and Climatic Attributions. Agric. For. Meteorol. 2021, 303, 108384. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Guo, Q.H. Application of Casa Model To the Estimation of Chinese Terrestrial Net Primary Productivity. Acta Phytoecol. Sin. 2001, 25, 603–608. [Google Scholar]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global Net Primary Production: Combining Ecology and Remote Sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Pan, Y.; He, H.; Yu, D.; Hu, H. Simulation of Maximum Light Use Efficiency for Some Typical Vegetation Types in China. Chin. Sci. Bull. 2006, 51, 457–463. [Google Scholar] [CrossRef]
- Yu, D.; Shi, P.; Shao, H.; Zhu, W.; Pan, Y. Modelling Net Primary Productivity of Terrestrial Ecosystems in East Asia Based on an Improved CASA Ecosystem Model. Int. J. Remote Sens. 2009, 30, 4851–4866. [Google Scholar] [CrossRef]
- Zhou, G.S.; Zhang, X.S. Feedback of Vegetation on Climate. Acta Bot. Sin. 1996, 38, 1–7. [Google Scholar]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Sun, W.; Sun, Y.; Li, X.; Wang, T.; Wang, Y.; Qiu, Q.; Deng, Z. Evaluation and Correction of GPM IMERG Precipitation Products over the Capital Circle in Northeast China at Multiple Spatiotemporal Scales. Adv. Meteorol. 2018, 2018, 4714173. [Google Scholar] [CrossRef]
- Maghsood, F.F.; Hashemi, H.; Hosseini, S.H.; Berndtsson, R. Ground Validation of GPM IMERG Precipitation Products over Iran. Remote Sens. 2020, 12, 48. [Google Scholar] [CrossRef] [Green Version]
- Fensholt, R.; Rasmussen, K.; Nielsen, T.T.; Mbow, C. Evaluation of Earth Observation Based Long Term Vegetation Trends—Intercomparing NDVI Time Series Trend Analysis Consistency of Sahel from AVHRR GIMMS, Terra MODIS and SPOT VGT Data. Remote Sens. Environ. 2009, 113, 1886–1898. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Wang, Z.; Chen, Y.; Gang, C.; An, R.; Li, J. Vegetation Dynamics and Its Driving Forces from Climate Change and Human Activities in the Three-River Source Region, China from 1982 to 2012. Sci. Total Environ. 2016, 563–564, 210–220. [Google Scholar] [CrossRef]
- Cao, M.; Prince, S.D.; Small, J.; Goetz, S.J. Remotely Sensed Interannual Variations and Trends in Terrestrial Net Primary Productivity 1981–2000. Ecosystems 2004, 7, 233–242. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 Dataset and the ONEFlux Processing Pipeline for Eddy Covariance Data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- Jian, J.R.; Vargas, K.J.; Anderson-Teixeira, E.S. A Global Database of Soil Respiration Data. Biogeosciences 2010, 7, 1915–1926. [Google Scholar] [CrossRef] [Green Version]
- Olson, R.J.; Scurlock, J.M.O.; Prince, S.D.; Zheng, D.L.; Johnson, K.R. NPP Multi-Biome: NPP and Driver Data for Ecosystem Model-Data Intercomparison, R2 Data Set. ORNL DAAC 2013, 1, 1–23. [Google Scholar] [CrossRef]
- He, H.; Ge, R.; Ren, X.; Zhang, L.; Chang, Q.; Xu, Q.; Zhou, G.; Xie, Z.; Wang, S.; Wang, H.; et al. Reference Carbon Cycle Dataset for Typical Chinese Forests via Colocated Observations and Data Assimilation. Sci. Data 2021, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG Satellite-Based Precipitation Products and the Hydrological Utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; Yang, Y.; Zhou, W.; Gang, C.; Zhang, Y.; Li, J.; An, R.; Wang, K.; Odeh, I.; et al. Quantitative Assess the Driving Forces on the Grassland Degradation in the Qinghai-Tibet Plateau, in China. Ecol. Inform. 2016, 33, 32–44. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, R.; Ren, H.; Zhang, W.; Zhang, Z.; Zhang, Z.; Wen, Z. Evaluating the Dynamics of Grassland Net Primary Productivity in Response to Climate Change in China. Glob. Ecol. Conserv. 2021, 28, e01574. [Google Scholar] [CrossRef]
- Li, X.; Luo, Y.; Wu, J. Decoupling Relationship between Urbanization and Carbon Sequestration in the Pearl River Delta from 2000 to 2020. Remote Sens. 2022, 14, 526. [Google Scholar] [CrossRef]
- Cao, S.; Sanchez-Azofeifa, G.A.; Duran, S.M.; Calvo-Rodriguez, S. Estimation of Aboveground Net Primary Productivity in Secondary Tropical Dry Forests Using the Carnegie-Ames-Stanford Approach (CASA) Model. Environ. Res. Lett. 2016, 11, 075004. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Wolf, S.; Wu, J.; Wu, X.; Gioli, B.; Wohlfahrt, G.; Cescatti, A.; van der Tol, C.; Zhou, S.; et al. Spatio-Temporal Convergence of Maximum Daily Light-Use Efficiency Based on Radiation Absorption by Canopy Chlorophyll. Geophys. Res. Lett. 2018, 45, 3508–3519. [Google Scholar] [CrossRef]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS Terrestrial Gross and Net Primary Production Global Data Set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Mu, S.; Zhou, S.; Chen, Y.; Li, J.; Ju, W.; Odeh, I.O.A. Assessing the Impact of Restoration-Induced Land Conversion and Management Alternatives on Net Primary Productivity in Inner Mongolian Grassland, China. Glob. Planet. Chang. 2013, 108, 29–41. [Google Scholar] [CrossRef]
- Wang, M.; Hu, C.; Barnes, B.B.; Mitchum, G.; Lapointe, B.; Montoya, J.P. The Great Atlantic Sargassum Belt. Science 2019, 364, 83–87. [Google Scholar] [CrossRef]
- Ji, R.; Tan, K.; Wang, X.; Pan, C.; Xin, L. Spatiotemporal Monitoring of a Grassland Ecosystem and Its Net Primary Production Using Google Earth Engine: A Case Study of Inner Mongolia from 2000 to 2020. Remote Sens. 2021, 13, 4480. [Google Scholar] [CrossRef]
- Yu, H.; Ding, Q.; Meng, B.; Lv, Y.; Liu, C.; Zhang, X.; Sun, Y.; Li, M.; Yi, S. The Relative Contributions of Climate and Grazing on the Dynamics of Grassland Npp and Pue on the Qinghai-Tibet Plateau. Remote Sens. 2021, 13, 3424. [Google Scholar] [CrossRef]






| Vegetation Type | εmax (gC·MJ−1) | NDVImax | NDVImin | SRmax | SRmin |
|---|---|---|---|---|---|
| EBF | 0.985 | 0.676 | 0.023 | 5.17 | 1.05 |
| DBF | 0.692 | 0.747 | 0.023 | 6.91 | 1.05 |
| ENF | 0.389 | 0.647 | 0.023 | 4.67 | 1.05 |
| DNF | 0.485 | 0.738 | 0.023 | 6.63 | 1.05 |
| Grassland | 0.542 | 0.634 | 0.023 | 4.46 | 1.05 |
| Cropland | 0.542 | 0.634 | 0.023 | 4.46 | 1.05 |
| Shrub | 0.429 | 0.636 | 0.023 | 4.49 | 1.05 |
| Inputs | Spatial Resolution | Time Resolution | Source |
|---|---|---|---|
| Temperature | 0.1° | 1 month | The ERA5-Land dataset provided by (ECMWF) |
| Solar radiation | 0.2° | 6 h | Climate Forecast System (CFS) dataset provided by (NCEP) |
| Precipitation | 0.1° | 1 month | Global Precipitation Measurement (GPM) |
| NDVI | 500 m | 16 days | The MOD13A1 V6 product |
| Vegetation type | 500 m | 1 year | The MCD12Q1 V6 product |
| CASA NPP and Observed NPP | MOD17 NPP and Observed NPP | ||||||
|---|---|---|---|---|---|---|---|
| Vegetation Type | EMDI | Carbon Cycle Dataset | FLUX NET2015 | SRDB | Carbon Cycle Dataset | FLUXNET2015 | SRDB |
| ENF | 92.6 | 77.35 | 46.9 | 35.5 | 122.6 | ||
| EBF | 238.9 | 336.2 | 443.5 | 470.2 | 276.3 | 508.9 | 504.9 |
| DNF | 70.1 | 125.0 | 178.9 | ||||
| DBF | 138.4 | 146.6 | 229.3 | 282.4 | 94.10 | 132.3 | 317.9 |
| Shrub | 42.2 | 74.9 | |||||
| Grassland | 46.3 | 95.4 | 56.4 | 98.9 | |||
| Forest Type | Climatic Region | Number of Sites | Mean Observed NPP | Mean CASA NPP | MAE | RMSE |
|---|---|---|---|---|---|---|
| EBF | Tropical | 3 | 1186.6 | 1351.00 | 394.64 | 430.88 |
| Southern subtropical | 25 | 848.40 | 1084.00 | 405.36 | 461.49 | |
| Subtropical | 180 | 915.44 | 900.93 | 218.34 | 274.10 | |
| Northern subtropical | 32 | 674.53 | 597.60 | 186.48 | 238.82 | |
| Southern temperate | 5 | 636.00 | 595.90 | 132.10 | 162.74 | |
| Highland | 9 | 751.11 | 423.23 | 348.09 | 412.26 | |
| DBF | Southern temperate | 12 | 567.91 | 569.64 | 109.27 | 147.93 |
| Temperate | 29 | 638.79 | 553.03 | 135.68 | 175.15 | |
| Northern temperate | 5 | 494.00 | 526.50 | 224.1 | 229.71 | |
| ENF | Southern temperate | 4 | 452.50 | 471.25 | 60.00 | 83.76 |
| Temperate | 6 | 480.00 | 503.02 | 96.89 | 120.15 | |
| Northern temperate | 5 | 320.00 | 427.00 | 109.00 | 127.89 | |
| DNF | Temperate | 4 | 422.50 | 538.25 | 124.68 | 177.38 |
| Northern temperate | 9 | 452.77 | 485.27 | 49.88 | 70.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Chen, J.; Xu, G.; Sha, Z.; Yin, J.; Li, Z. Estimation and Climate Impact Analysis of Terrestrial Vegetation Net Primary Productivity in China from 2001 to 2020. Land 2023, 12, 1223. https://doi.org/10.3390/land12061223
Chen Z, Chen J, Xu G, Sha Z, Yin J, Li Z. Estimation and Climate Impact Analysis of Terrestrial Vegetation Net Primary Productivity in China from 2001 to 2020. Land. 2023; 12(6):1223. https://doi.org/10.3390/land12061223
Chicago/Turabian StyleChen, Zhaotong, Jiangping Chen, Gang Xu, Zongyao Sha, Jianhua Yin, and Zijian Li. 2023. "Estimation and Climate Impact Analysis of Terrestrial Vegetation Net Primary Productivity in China from 2001 to 2020" Land 12, no. 6: 1223. https://doi.org/10.3390/land12061223







