Nonlinear Flood Responses to Tide Level and Land Cover Changes in Small Watersheds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Model Data
2.2.1. Topography
2.2.2. Land Cover
2.2.3. Rainfall and Tide Levels
2.3. Model Setup
2.3.1. HEC-HMS
2.3.2. HEC-RAS
2.4. Model Calibration
2.4.1. Inundation Depths
2.4.2. Roughness Coefficients
2.4.3. Parameter Optimization
2.5. Scenarios Design
2.5.1. Rainfall Scenarios
2.5.2. Tide Level Scenarios
2.5.3. Land Cover Scenarios
2.6. Perturbation Analysis
3. Results
3.1. Model Performance
3.2. Responses to Rainfall Intensity Change
3.3. Responses to Tide Level Change
3.4. Responses to Land Cover Change
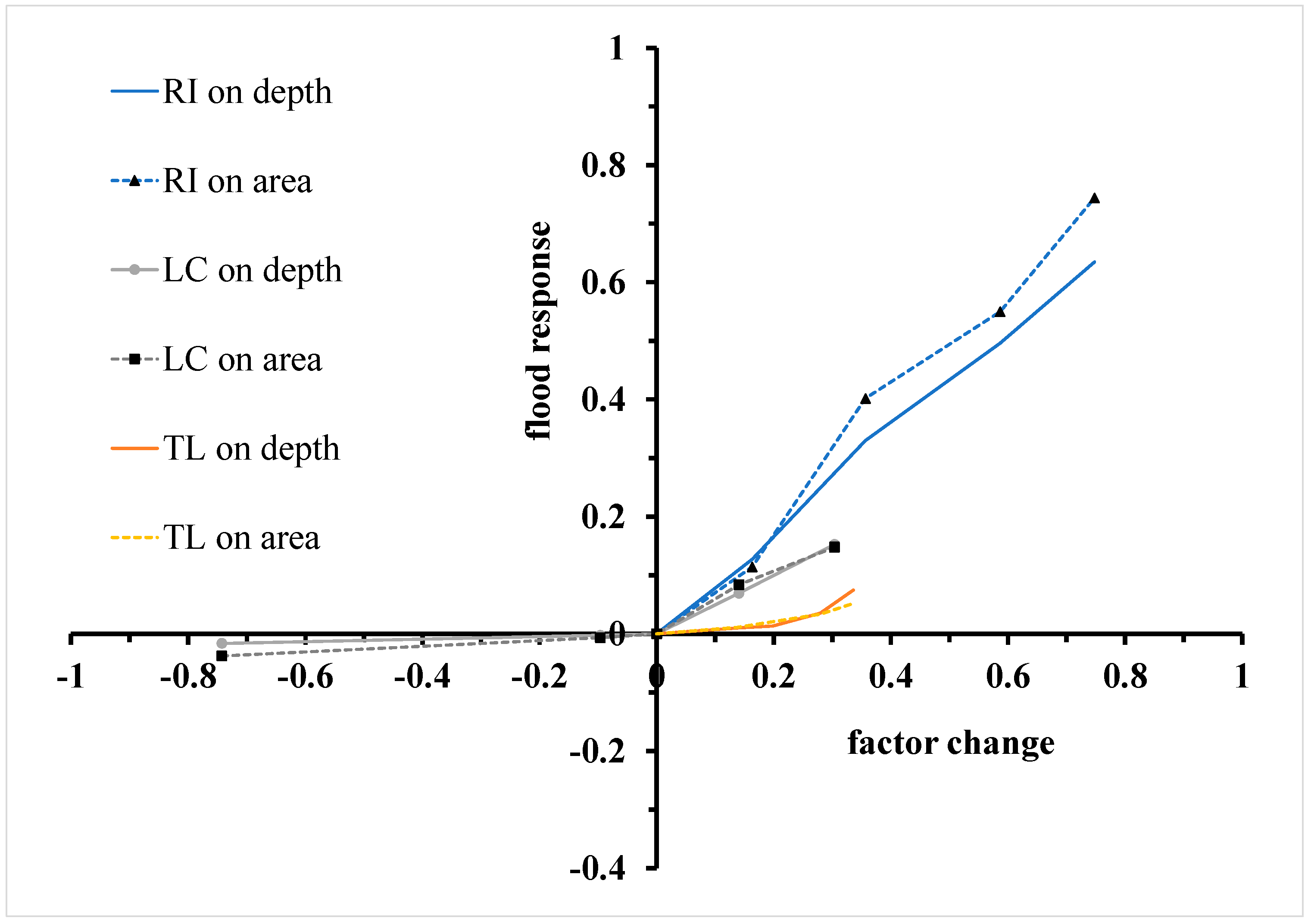
3.5. Comparison of Nonlinear Responses
4. Discussion
4.1. Impact of Tides on River-Dominated Watersheds
4.2. Timing for Flood Risk Management in Developing Regions
4.3. Uncertainties and Limitations
4.4. Benefits and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- UNDRR (United Nations Office for Disaster Risk Reduction). Human Cost of Disasters: An Overview of the Last 20 Years 2000–2019. 2020. Available online: https://www.undrr.org/publication/human-cost-disasters-overview-last-20-years-2000-2019 (accessed on 12 March 2021).
- IPCC (Intergovernmental Panel on Climate Change). Climate Change 2021: The Physical Science Basis; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Couasnon, A.; Eilander, D.; Muis, S.; Veldkamp TI, E.; Haigh, I.D.; Wahl, T.; Winsemius, H.C.; Ward, P.J. Measuring compound flood potential from river discharge and storm surge extremes at the global scale. Nat. Hazards Earth Syst. Sci. 2020, 20, 489–504. [Google Scholar] [CrossRef]
- Hendry, A.; Haigh, I.D.; Nicholls, R.J.; Winter, H.; Neal, R.; Wahl, T.; Joly-Laugel, A.; Darby, S.E. Assessing the characteristics and drivers of compound flooding events around the UK coast. Hydrol. Earth Syst. Sci. 2019, 23, 3117–3139. [Google Scholar] [CrossRef]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.D.; Luther, M.E. Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Chang. 2015, 5, 1093–1097. [Google Scholar] [CrossRef]
- Ward, P.J.; Couasnon, A.; Eilander, D.; Haigh, I.D.; Hendry, A.; Muis, S.; Veldkamp TI, E.; Winsemius, H.C.; Wahl, T. Dependence between high sea-level and high river discharge increases flood hazard in global deltas and estuaries. Environ. Res. Lett. 2018, 13, 084012. [Google Scholar] [CrossRef]
- Wu, W.; McInnes, K.; O’Grady, J.; Hoeke, R.; Leonard, M.; Westra, S. Mapping Dependence Between Extreme Rainfall and Storm Surge. J. Geophys. Res.-Ocean. 2018, 123, 2461–2474. [Google Scholar] [CrossRef]
- Zellou, B.; Rahali, H. Assessment of the joint impact of extreme rainfall and storm surge on the risk of flooding in a coastal area. J. Hydrol. 2019, 569, 647–665. [Google Scholar] [CrossRef]
- Zheng, F.; Westra, S.; Leonard, M.; Sisson, S.A. Modeling dependence between extreme rainfall and storm surge to estimate coastal flooding risk. Water Resour. Res. 2014, 50, 2050–2071. [Google Scholar] [CrossRef]
- Gori, A.; Lin, N.; Smith, J. Assessing Compound Flooding from Landfalling Tropical Cyclones on the North Carolina Coast. Water Resour. Res. 2020, 56, e2019WR026788. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, F.; Yu, H.C.; Sun, W.L.; Moghimi, S.; Myers, E.; Nunez, K.; Zhang, R.Y.; Wang, H.; Roland, A.; et al. Simulating compound flooding events in a hurricane. Ocean. Dyn. 2020, 70, 621–640. [Google Scholar] [CrossRef]
- Nasr, A.A.; Wahl, T.; Rashid, M.M.; Camus, P.; Haigh, I.D. Assessing the dependence structure between oceanographic, fluvial, and pluvial flooding drivers along the United States coastline. Hydrol. Earth Syst. Sci. 2021, 25, 6203–6222. [Google Scholar] [CrossRef]
- Ghanbari, M.; Arabi, M.; Kao, S.; Obeysekera, J.; Sweet, W. Climate Change and Changes in Compound Coastal-Riverine Flooding Hazard Along the US Coasts. Earths Future 2021, 9, e2021EF002055. [Google Scholar] [CrossRef]
- Bevacqua, E.; Maraun, D.; Vousdoukas, M.I.; Voukouvalas, E.; Vrac, M.; Mentaschi, L.; Widmann, M. Higher probability of compound flooding from precipitation and storm surge in Europe under anthropogenic climate change. Sci. Adv. 2019, 5, eaaw5531. [Google Scholar] [CrossRef]
- Faccini, F.; Luino, F.; Paliaga, G.; Roccati, A.; Turconi, L. Flash Flood Events along the West Mediterranean Coasts: Inundations of Urbanized Areas Conditioned by Anthropic Impacts. Land. 2021, 10, 620. [Google Scholar] [CrossRef]
- Fang, J.; Wahl, T.; Fang, J.; Sun, X.; Kong, F.; Liu, M. Compound flood potential from storm surge and heavy precipitation in coastal China: Dependence, drivers, and impacts. Hydrol. Earth Syst. Sci. 2021, 25, 4403–4416. [Google Scholar] [CrossRef]
- Didier, D.; Baudry, J.; Bernatchez, P.; Dumont, D.; Sadegh, M.; Bismuth, E.; Bandet, M.; Dugas, S.; Sevigny, C. Multihazard simulation for coastal flood mapping: Bathtub versus numerical modelling in an open estuary, Eastern Canada. J. Flood Risk Manag. 2019, 12, e12505. [Google Scholar] [CrossRef]
- Bakhtyar, R.; Maitaria, K.; Velissariou, P.; Trimble, B.; Mashriqui, H.; Moghimi, S.; Abdolali, A.; Van der Westhuysen, A.J.; Ma, Z.; Clark, E.P.; et al. A New 1D/2D Coupled Modeling Approach for a Riverine-Estuarine System Under Storm Events: Application to Delaware River Basin. J. Geophys. Res.-Ocean. 2020, 125, e2019JC015822. [Google Scholar] [CrossRef]
- Bilskie, M.V.; Hagen, S.C. Defining Flood Zone Transitions in Low-Gradient Coastal Regions. Geophys. Res. Lett. 2018, 45, 2761–2770. [Google Scholar] [CrossRef]
- Santiago-Collazo, F.L.; Bilskie, M.V.; Hagen, S.C. A comprehensive review of compound inundation models in low-gradient coastal watersheds. Environ. Model. Softw. 2019, 119, 166–181. [Google Scholar] [CrossRef]
- Cai, H.Y.; Savenije HH, G.; Toffolon, M. Linking the river to the estuary: Influence of river discharge on tidal damping. Hydrol. Earth Syst. Sci. 2014, 18, 287–304. [Google Scholar] [CrossRef]
- Feng, D.; Tan, Z.; Engwirda, D.; Liao, C.; Xu, D.; Bisht, G.; Zhou, T.; Li, H.; Leung, L.R. Investigating coastal backwater effects and flooding in the coastal zone using a global river transport model on an unstructured mesh. Hydrol. Earth Syst. Sci. 2022, 26, 5473–5491. [Google Scholar] [CrossRef]
- Juarez, B.; Stockton, S.A.; Serafin, K.A.; Valle-Levinson, A. Compound Flooding in a Subtropical Estuary Caused by Hurricane Irma 2017. Geophys. Res. Lett. 2022, 49, e2022GL099360. [Google Scholar] [CrossRef]
- Savenije HH, G.; Toffolon, M.; Haas, J.; Veling EJ, M. Analytical description of tidal dynamics in convergent estuaries. J. Geophys. Res. 2008, 113, C10025. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, X.; Guan, X.; Wang, T.; Ma, C.; Yan, D. Amplification of Flood Risks by the Compound Effects of Precipitation and Storm Tides Under the Nonstationary Scenario in the Coastal City of Haikou, China. Int. J. Disaster Risk Sci. 2022, 13, 602–620. [Google Scholar] [CrossRef]
- Guo, L.; Zhu, C.; Wu, X.; Wan, Y.; Jay, D.A.; Townend, I.; Wang, Z.B.; He, Q. Strong Inland Propagation of Low-Frequency Long Waves in River Estuaries. Geophys. Res. Lett. 2020, 47, e2020GL089112. [Google Scholar] [CrossRef]
- Yang, L.; Scheffran, J.; Qin, H.; You, Q. Climate-related flood risks and urban responses in the Pearl River Delta, China. Reg. Environ. Change 2015, 15, 379–391. [Google Scholar] [CrossRef]
- GBWA (Guangzhou Bureau of Water Authority). The Rainstorm Formula and Calculation Chart in Guangzhou Downtown; GBWA: Guangzhou, China, 2011. [Google Scholar]
- Keifer, C.J.; Chu, H.H. Synthetic Storm Pattern for Drainage Design. J. Hydraul. Div. 1957, 83, 1–25. [Google Scholar] [CrossRef]
- Wang, X. Storm Surge Disaster Risk Assessment and Impact Forecasting Research. Ph.D. Thesis, Wuhan University, Wuhan, China, 2016. [Google Scholar]
- Zhao, L.; Liu, X.; Liu, P.; Chen, G.; He, J. Urban Expansion Simulation and Early Warning based on Geospatial Partition and FLUS Model. J. Geo-Inf. Sci. 2020, 22, 517–530. [Google Scholar]
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Ren, J. The Coupling Effect of Flood Discharge and Storm Surge on Extreme Flood Stages: A Case Study in the Pearl River Delta, South China. Int. J. Disaster Risk Sci. 2021, 12, 495–509. [Google Scholar] [CrossRef]
- Qiu, J.; Liu, B.; Yang, F.; Wang, X.; He, X. Quantitative Stress Test of Compound Coastal-Fluvial Floods in China’s Pearl River Delta. Earth’s Future 2022, 10, e2021EF002638. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, Y.; Chen, Y.; Xu, C.Y.; Gao, Y.; Du, J. Hydrological response to urbanization at different spatio-temporal scales simulated by coupling of CLUE-S and the SWAT model in the Yangtze River Delta region. J. Hydrol. 2013, 485, 113–125. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhu, Y.; Wan, D.; Yu, Y.; Lu, Y. Similarity Analysis of Small- and Medium-Sized Watersheds Based on Clustering Ensemble Model. Water 2020, 12, 69. [Google Scholar] [CrossRef]
- Li, H.; Wang, R.; Huang, Q.; Xiang, J.; Qin, G. Advances on Flood Forecasting of Small-Medium Rivers. J. China Hydrol. 2020, 40, 16–23. [Google Scholar]


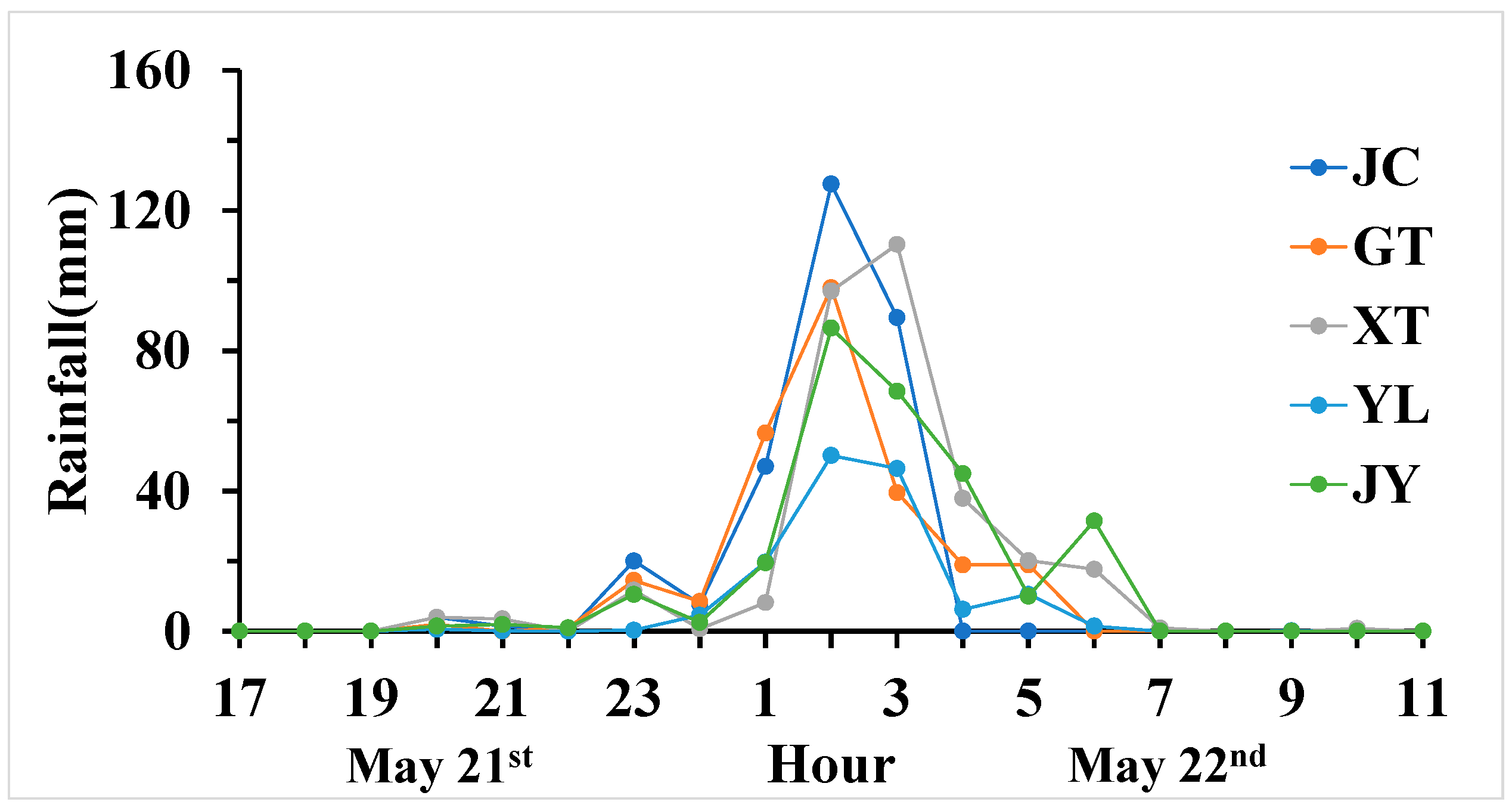

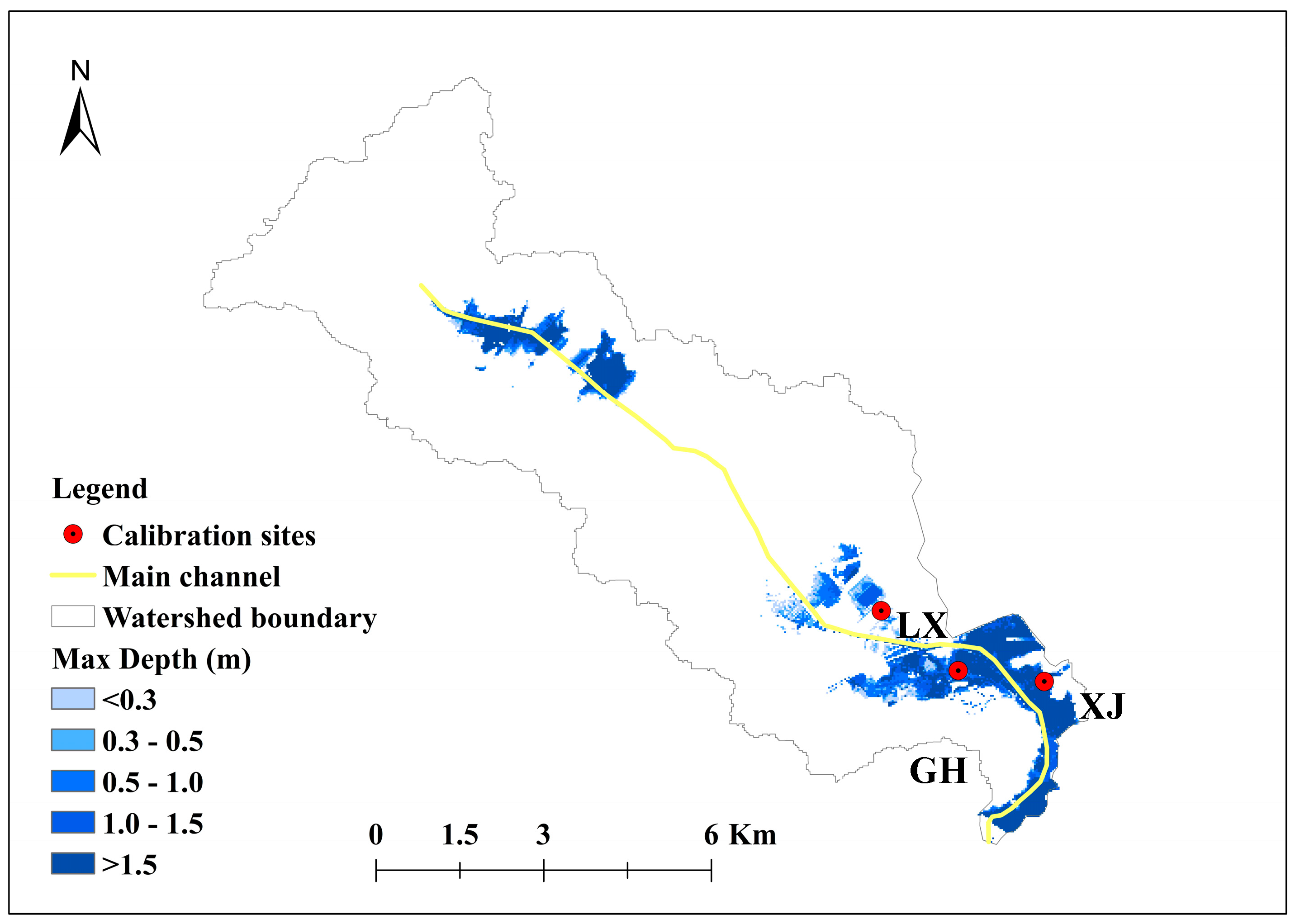

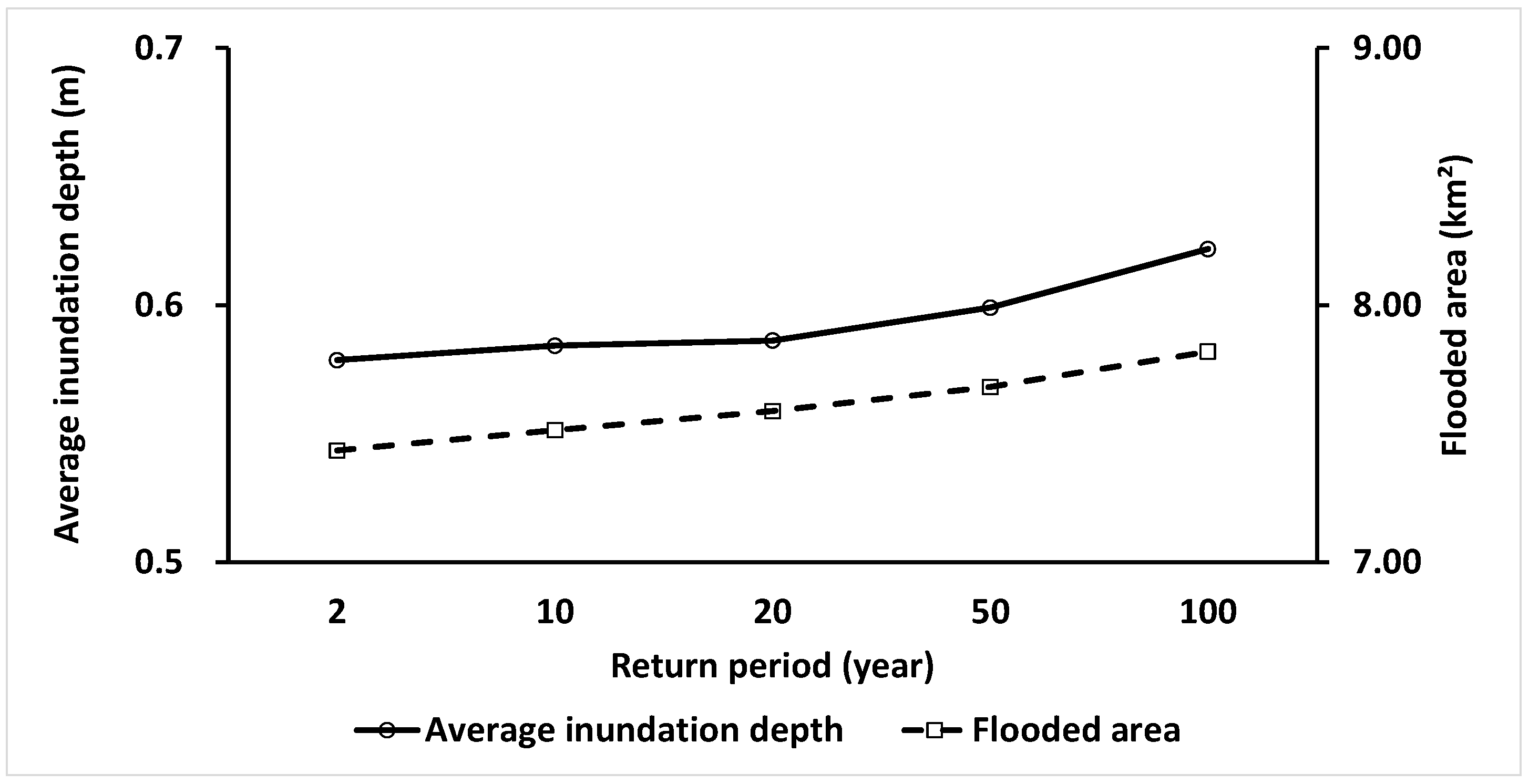
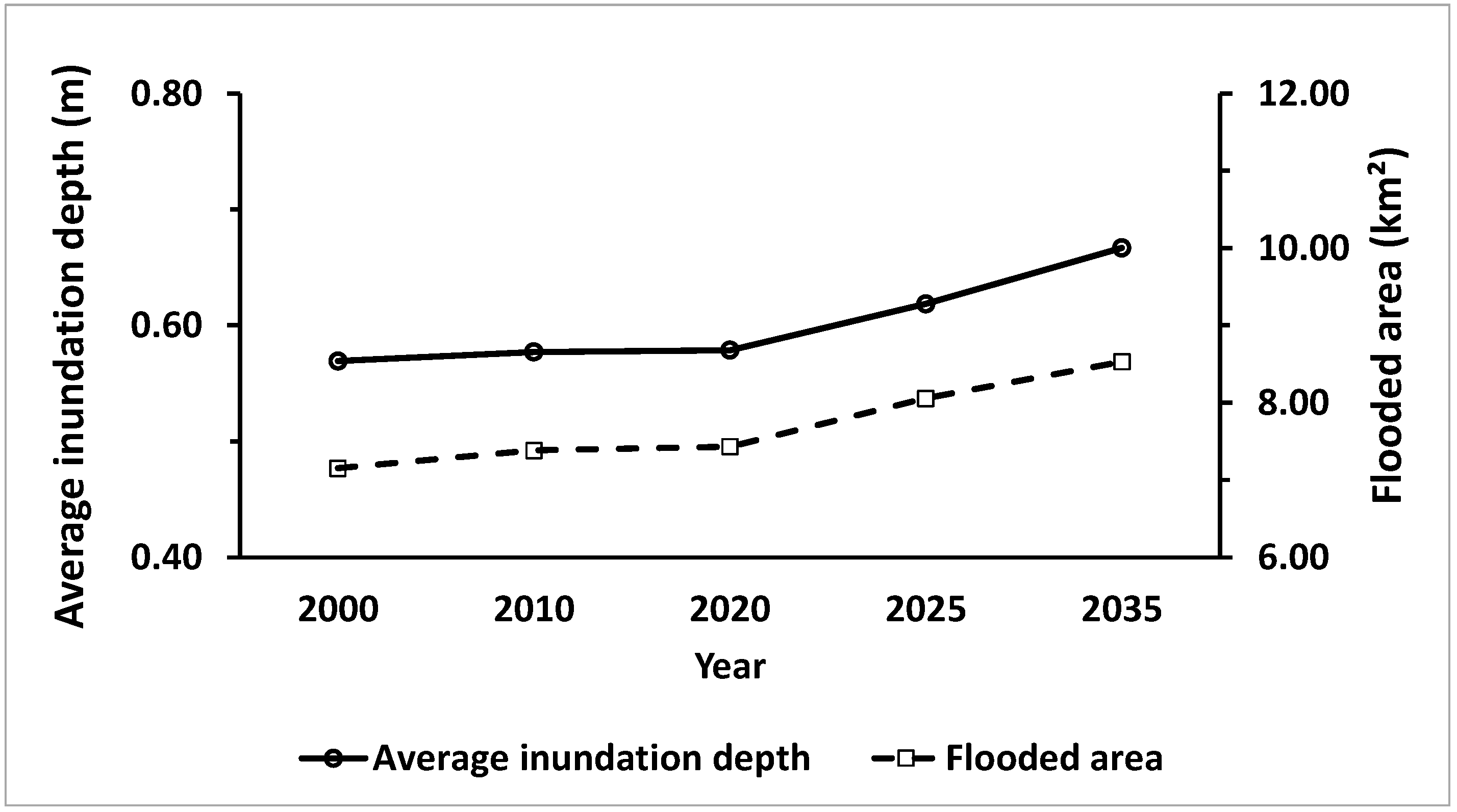
| Weather Station | Total Rainfall (mm) | Max Three-Hour Rainfall (mm) |
|---|---|---|
| Xintang (XT) | 312.8 | 245.0 |
| Jiancun (JC) | 297.2 | 264.0 |
| Jiuyu (JY) | 278.5 | 200.0 |
| Guangzhou Toyota (GT) | 258.0 | 194.0 |
| Yeling (YL) | 140.1 | 116.0 |
| Subarea | Range | Number of Samples |
|---|---|---|
| Upstream left floodplain | 0.011–0.080 | 4 |
| Upstream right floodplain | 0.011–0.080 | 4 |
| Main channel | 0.025–0.033 | 3 |
| Downstream left floodplain | 0.011–0.017 | 3 |
| Downstream right floodplain | 0.011–0.017 | 3 |
| Return Period (Year) | Average Intensity (L/(ha.s)) | Rainfall Depth (mm) |
|---|---|---|
| 5 | 100.255 | 108.3 |
| 10 | 116.64 | 126.0 |
| 20 | 136.011 | 146.9 |
| 50 | 159.062 | 171.8 |
| 100 | 175.228 | 189.2 |
| Return Period (Year) | 2 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|
| Tide level (m) | 2.47 | 2.81 | 2.96 | 3.16 | 3.30 |
| Roughness Coefficient | Deviation of Inundation Depth (m) | Mean Deviation (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| Upstream | Main Channel | Downstream | GH | XJ | LX | |||
| Left | Right | Left | Right | |||||
| 0.034 | 0.034 | 0.033 | 0.011 | 0.014 | 0.04 | 0.02 | 0.12 | 0.06 |
| Year | Imperviousness | Annual Growth | ||
|---|---|---|---|---|
| Upstream | Downstream | Total | ||
| 2000 | 14.3% | 13.2% | 13.9% | - |
| 2010 | 41.0% | 63.3% | 48.8% | 3.5% |
| 2020 | 42.3% | 76.9% | 54.4% | 0.6% |
| 2025 | 51.1% | 81.0% | 61.6% | 1.4% |
| 2035 | 58.5% | 92.7% | 70.4% | 0.9% |
| Phase | Rainfall Intensity | Land Cover | Tide Level | |||
|---|---|---|---|---|---|---|
| Depth | Area | Depth | Area | Depth | Area | |
| S1–S2 | 0.78 | 0.70 | 0.02 | 0.05 | 0.07 | 0.08 |
| S2–S3 | 1.05 | 1.49 | 0.03 | 0.07 | 0.06 | 0.16 |
| S3–S4 | 0.72 | 0.64 | 0.49 | 0.60 | 0.27 | 0.16 |
| S4–S5 | 0.86 | 1.21 | 0.51 | 0.39 | 0.70 | 0.33 |
| Overall S1–S5 | 0.85 | 1.00 | 0.50 | 0.49 | 0.22 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Pan, Y.; Wang, C.; Wang, X. Nonlinear Flood Responses to Tide Level and Land Cover Changes in Small Watersheds. Land 2023, 12, 1743. https://doi.org/10.3390/land12091743
Huang H, Pan Y, Wang C, Wang X. Nonlinear Flood Responses to Tide Level and Land Cover Changes in Small Watersheds. Land. 2023; 12(9):1743. https://doi.org/10.3390/land12091743
Chicago/Turabian StyleHuang, Huabing, Yu Pan, Changpeng Wang, and Xianwei Wang. 2023. "Nonlinear Flood Responses to Tide Level and Land Cover Changes in Small Watersheds" Land 12, no. 9: 1743. https://doi.org/10.3390/land12091743
APA StyleHuang, H., Pan, Y., Wang, C., & Wang, X. (2023). Nonlinear Flood Responses to Tide Level and Land Cover Changes in Small Watersheds. Land, 12(9), 1743. https://doi.org/10.3390/land12091743








