County-Level Spatiotemporal Dynamics and Driving Mechanisms of Carbon Emissions in the Pearl River Delta Urban Agglomeration, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials for Spatial Simulation of Carbon Emissions
2.2. Trend Analysis Based on SLOPE
2.3. Exploratory Spatial Data Analysis
2.4. Geodetector
3. Results
3.1. Spatial–Temporal Patterns and Trends of Carbon Emissions in the Pearl River Delta Urban Agglomeration
3.1.1. The Temporal Dynamics of Carbon Emissions in the Pearl River Delta Urban Agglomeration
3.1.2. Spatial Distribution Pattern of Carbon Emissions in the Pearl River Delta Urban Agglomeration
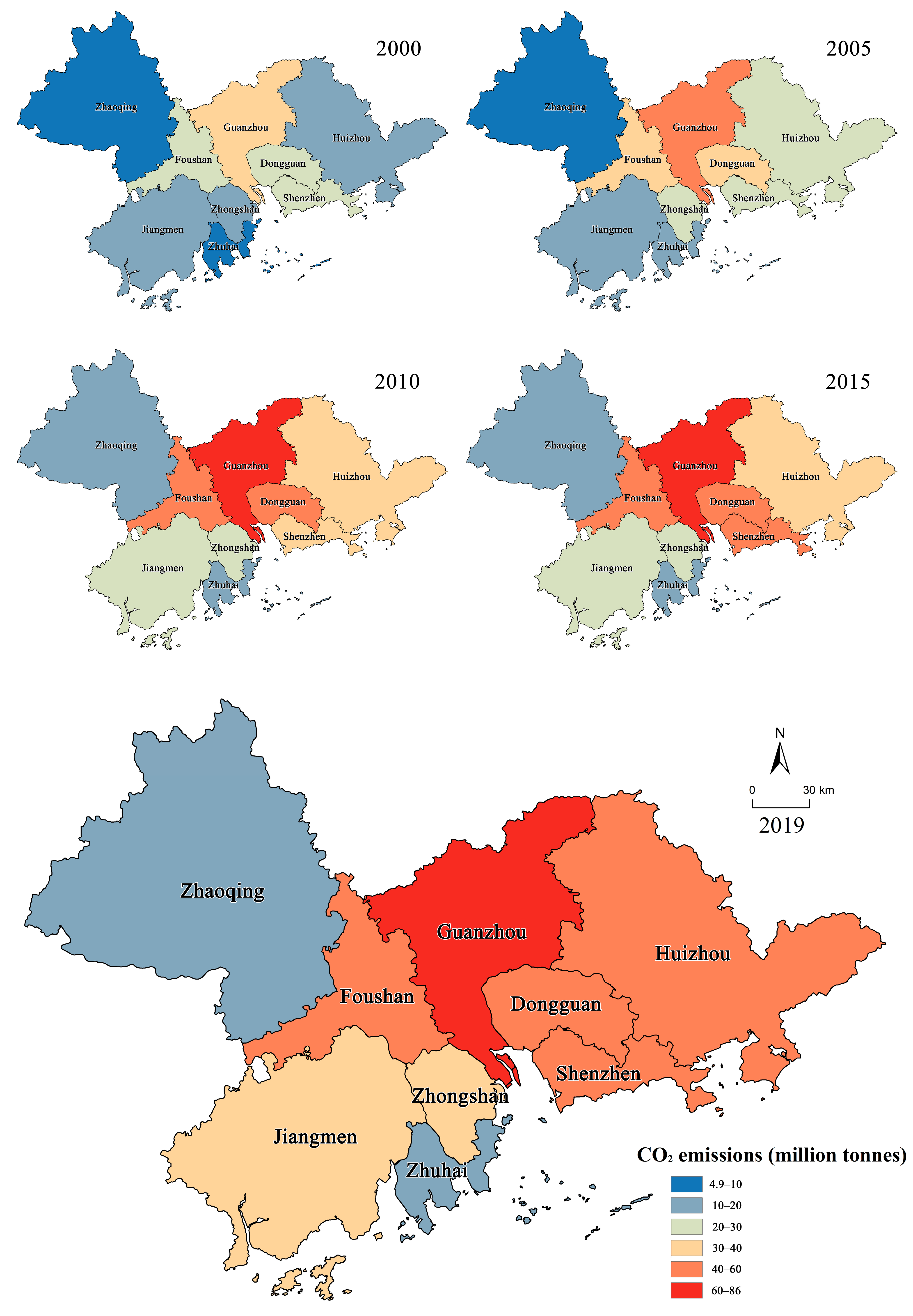
3.1.3. Evolution of City-Scale Carbon Emission Patterns in the Pearl River Delta Urban Agglomeration
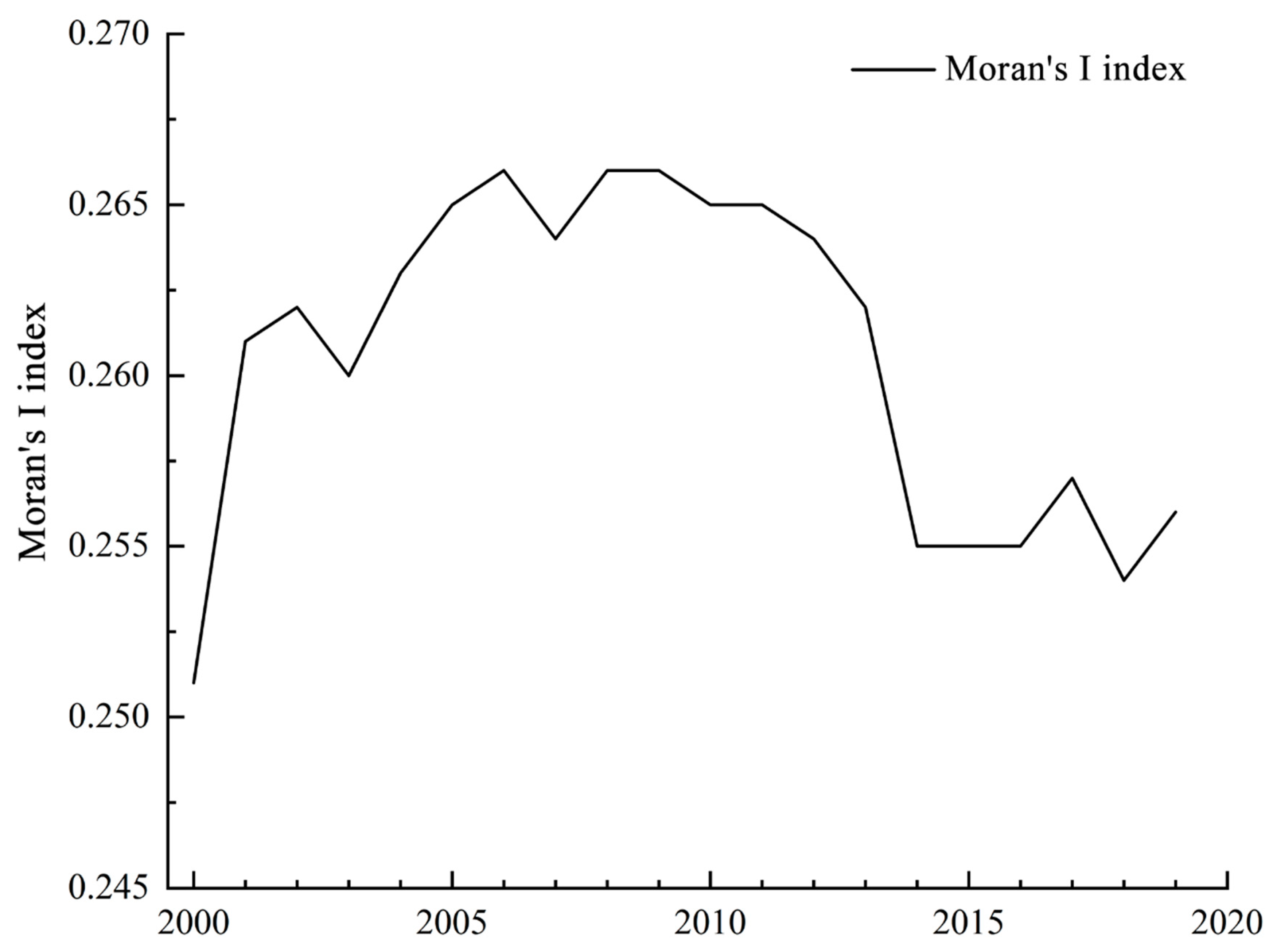
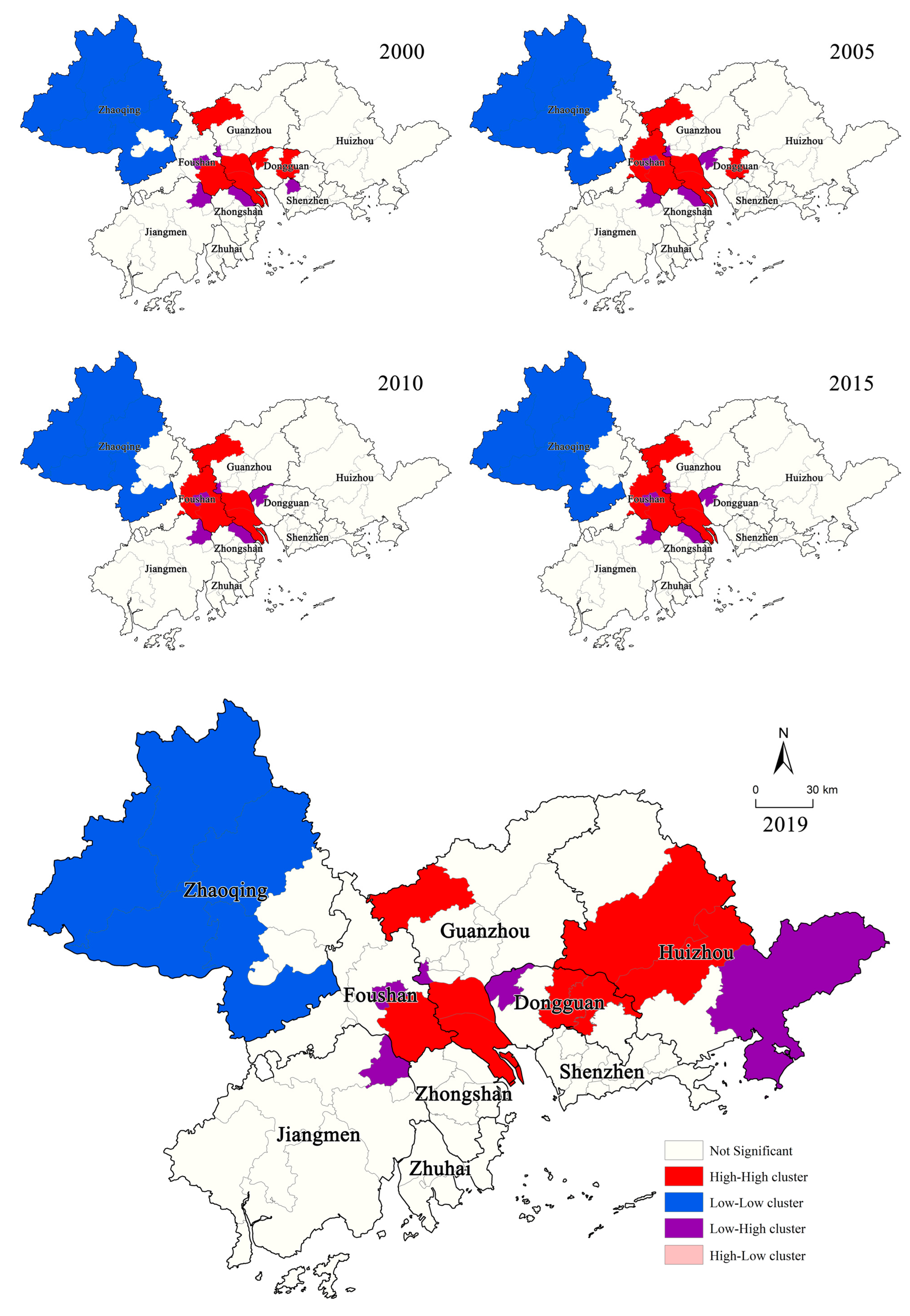
3.1.4. Spatial Pattern Analysis of Carbon Emissions at the County Level in the Pearl River Delta Urban Agglomeration
3.2. Driving Mechanisms of Carbon Emissions in the Pearl River Delta Urban Agglomeration
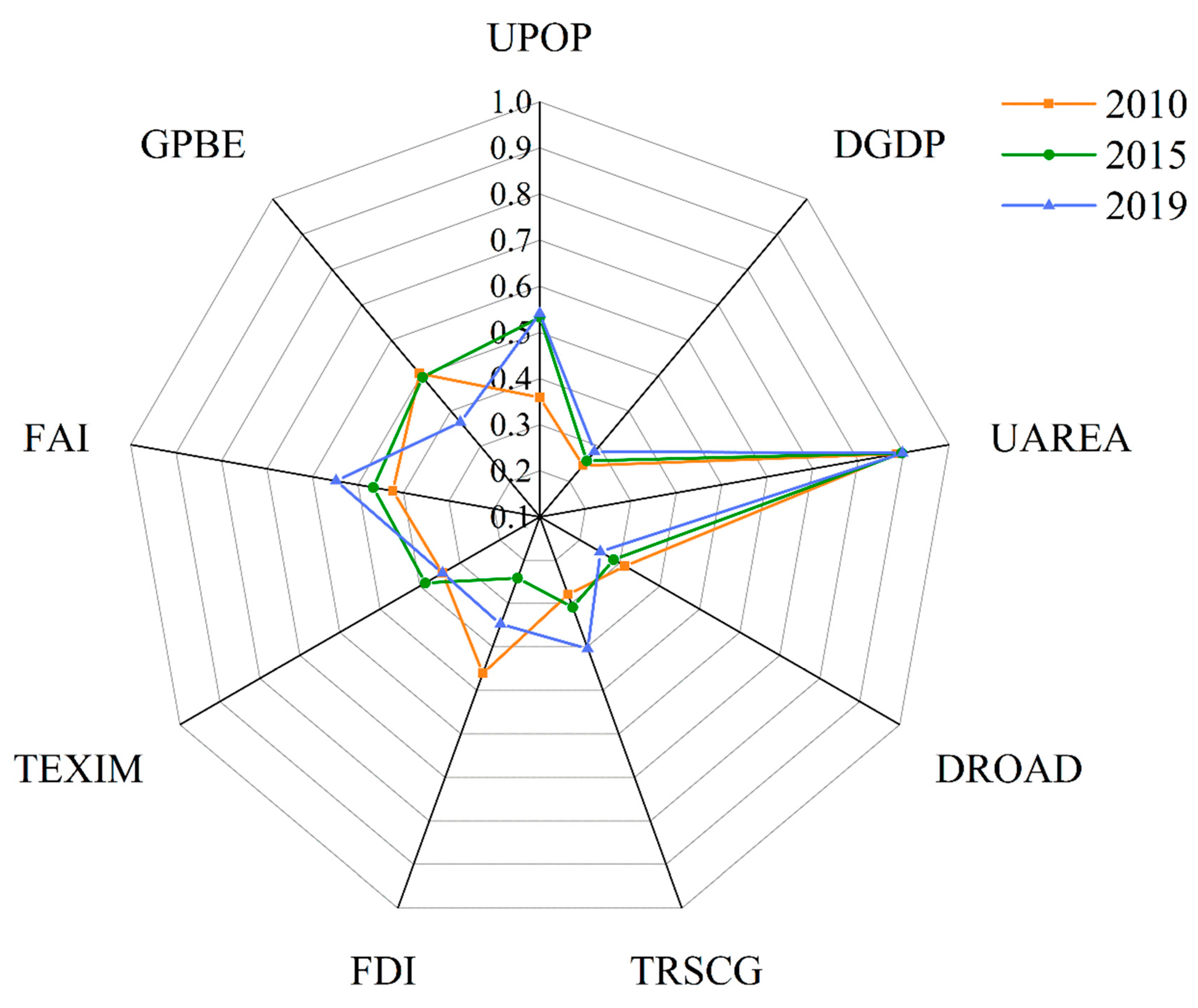
3.2.1. Single-Factor Detection Results
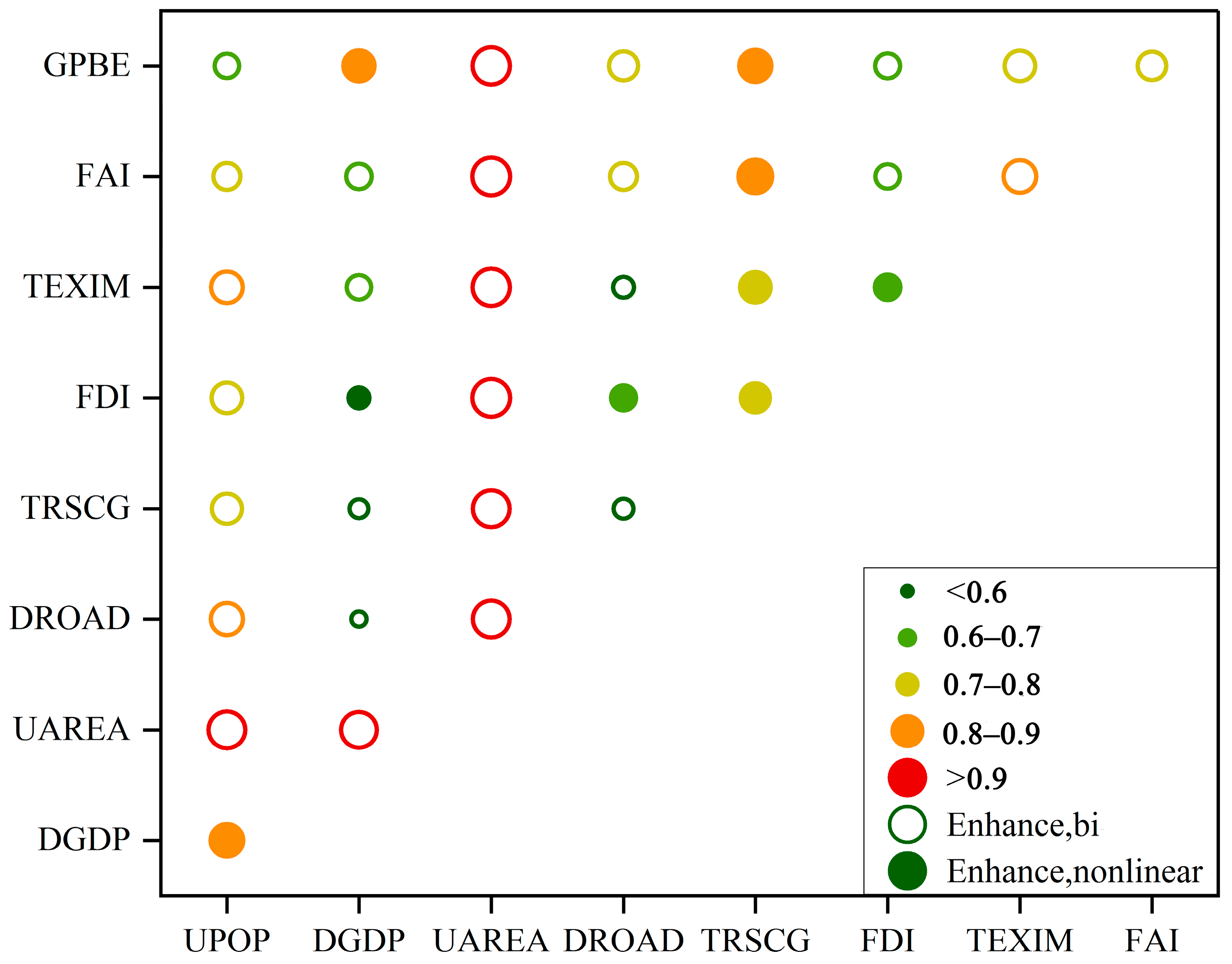
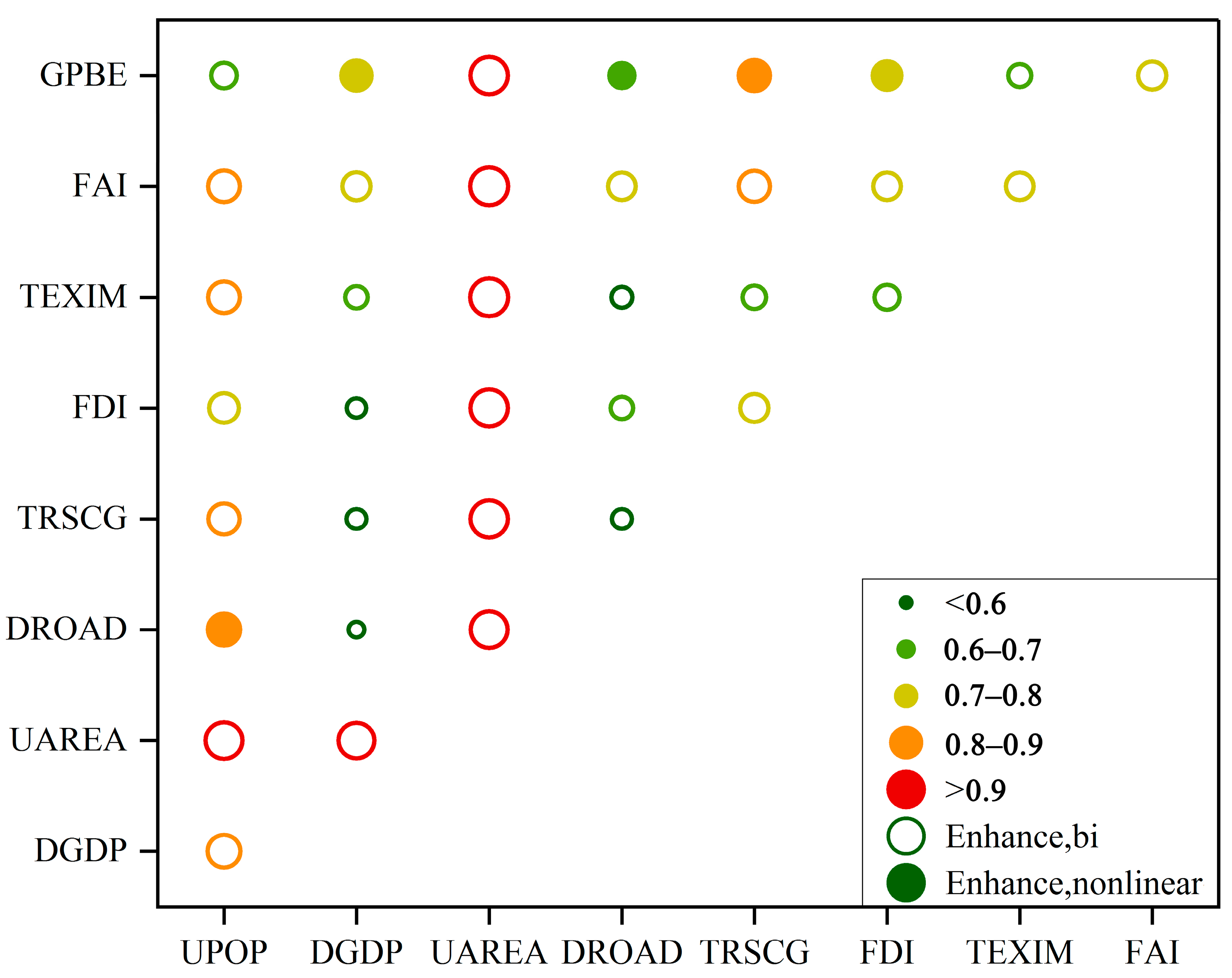
3.2.2. Multifactor Interaction Detection Results
4. Conclusions
5. Discussion
- (1)
- The spatial simulation of carbon emissions primarily relies on a top-down approach. Despite the coupling of high-precision population and economic spatial data, there is still room for further improvement in the spatial accuracy of carbon emissions data. In future studies, it is recommended to consider incorporating a combination of bottom-up and top-down approaches to enhance the integration of multi-source POI data, big data from industrial enterprises, high-precision land use data, etc., thereby enhancing the accuracy of spatial simulations for carbon emissions.
- (2)
- Energy consumption, energy structure, and other factors directly impact carbon emissions. However, obtaining data on energy consumption is challenging due to the varying statistical caliber at the city, district, and county levels. To enhance the accuracy of statistical accounting for carbon emissions in future research, it is recommended to conduct field surveys on energy consumption data at the district and county levels, as well as the enterprise and household levels.
- (3)
- The driving mechanisms of carbon emissions identified in this study primarily focused on the internal influencing factors of urban agglomerations. With the implementation of the new dual-cycle development pattern, there is increased connectivity between the internal and external aspects of urban agglomerations. Therefore, it is essential to enhance research on the impact of external influencing factors on local carbon emissions in urban agglomerations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- McNutt, M. Time’s up, CO2. Science 2019, 365, 411. [Google Scholar] [CrossRef] [PubMed]
- Bulkeley, H. Governing climate change: The politics of risk society? Trans. Inst. Br. Geogr. 2001, 26, 430–447. [Google Scholar] [CrossRef]
- Adger, W.N. Social Capital, Collective Action, and Adaptation to Climate Change. Econ. Geogr. 2003, 79, 387–404. [Google Scholar] [CrossRef]
- Thomas, C.D.; Cameron, A.; Green, R.E.; Bakkenes, M.; Beaumont, L.J.; Collingham, Y.C.; Erasmus, B.F.N.; de Siqueira, M.F.; Grainger, A.; Hannah, L.; et al. Extinction risk from climate change. Nature 2004, 427, 145–148. [Google Scholar] [CrossRef] [PubMed]
- Nordhaus, W.D. A Review of the Stern Review on the Economics of Climate Change. J. Econ. Lit. 2007, 45, 686–702. [Google Scholar] [CrossRef]
- Meinshausen, M.; Lewis, J.; McGlade, C.; Gütschow, J.; Nicholls, Z.; Burdon, R.; Cozzi, L.; Hackmann, B. Realization of Paris Agreement pledges may limit warming just below 2 °C. Nature 2022, 604, 304–309. [Google Scholar] [CrossRef]
- Roelfsema, M.; van Soest, H.L.; Harmsen, M.; van Vuuren, D.P.; Bertram, C.; den Elzen, M.; Höhne, N.; Iacobuta, G.; Krey, V.; Kriegler, E.; et al. Taking stock of national climate policies to evaluate implementation of the Paris Agreement. Nat. Commun. 2020, 11, 2096. [Google Scholar] [CrossRef]
- Schneider, L.; Duan, M.; Stavins, R.; Kizzier, K.; Broekhoff, D.; Jotzo, F.; Winkler, H.; Lazarus, M.; Howard, A.; Hood, C. Double counting and the Paris Agreement rulebook. Science 2019, 366, 180–183. [Google Scholar] [CrossRef]
- Rogelj, J.; Huppmann, D.; Krey, V.; Riahi, K.; Clarke, L.; Gidden, M.; Nicholls, Z.; Meinshausen, M. A new scenario logic for the Paris Agreement long-term temperature goal. Nature 2019, 573, 357–363. [Google Scholar] [CrossRef]
- Tanaka, K.; O’Neill, B.C. The Paris Agreement zero-emissions goal is not always consistent with the 1.5 °C and 2 °C temperature targets. Nat. Clim. Chang. 2018, 8, 319–324. [Google Scholar] [CrossRef]
- Acuto, M.; Parnell, S.; Seto, K.C. Building a global urban science. Nat. Sustain. 2018, 1, 2–4. [Google Scholar] [CrossRef]
- Dhakal, S. Urban energy use and carbon emissions from cities in China and policy implications. Energy Policy 2009, 37, 4208–4219. [Google Scholar] [CrossRef]
- Li, Z.; Wang, F.; Kang, T.; Wang, C.; Chen, X.; Miao, Z.; Zhang, L.; Ye, Y.; Zhang, H. Exploring differentiated impacts of socioeconomic factors and urban forms on city-level CO2 emissions in China: Spatial heterogeneity and varying importance levels. Sustain. Cities Soc. 2022, 84, 104028. [Google Scholar] [CrossRef]
- Streets, D.G.; Jiang, K.; Hu, X.; Sinton, J.E.; Zhang, X.-Q.; Xu, D.; Jacobson, M.Z.; Hansen, J.E. Recent Reductions in China’s Greenhouse Gas Emissions. Science 2001, 294, 1835–1837. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Xu, L.; Ye, S. Spatio-temporal Variations and Influencing Factors of Energy Efficiency in Fujian Province. J. Fujian Norm. Univ. Nat. Sci. Ed. 2024, 40, 20–29. [Google Scholar]
- Zhang, Q.; Lin, J.; Wang, Q.; Chen, D.; Zhou, T.; Dang, N.; Zhuang, X.; Li, Y.; Luo, D. The Impact of Main Functional Area Strategy on Regional Energy Consumption Carbon Emission: A Case Study of Fujian Province. J. Fujian Norm. Univ. Nat. Sci. Ed. 2024, 40, 30–43. [Google Scholar]
- Qi, X.; Huang, R.; Jia, Y.; Huang, Q. Analysis of Spatial and Temporal Characteristics and Driving Factors of Carbon Emissions at the County Level in Coal Resource-Based Areas:Take Shanxi Province as an Example. J. North China Inst. Water Conserv. Hydroelectr. Power Soc. Sci. Ed. 2024, 40, 1–11. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R.; Davis, C.W. Relation between satellite observed visible-near infrared emissions, population, economic activity and electric power consumption. Int. J. Remote Sens. 1997, 18, 1373–1379. [Google Scholar] [CrossRef]
- Doll, C.N.H.; Muller, J.P.; Elvidge, C.D. Night-time imagery as a tool for global mapping of socioeconomic parameters and greenhouse gas emissions. Ambio 2000, 29, 157–162. [Google Scholar] [CrossRef]
- Ghosh, T.; Elvidge, C.D.; Sutton, P.C.; Baugh, K.E.; Ziskin, D.; Tuttle, B.T. Creating a global grid of distributed fossil fuel CO2 emissions from nighttime satellite imagery. Energies 2010, 3, 1895–1913. [Google Scholar] [CrossRef]
- Oda, T.; Maksyutov, S. A very high-resolution (1 km × 1 km) global fossil fuel CO2 emission inventory derived using a point source database and satellite observations of nighttime lights. Atmos. Chem. Phys. 2011, 11, 543–556. [Google Scholar] [CrossRef]
- Su, Y.; Chen, X.; Li, Y.; Liao, J.; Ye, Y.; Zhang, H.; Huang, N.; Kuang, Y. China‘s 19-year city-level carbon emissions of energy consumptions, driving forces and regionalized mitigation guidelines. Renew. Sustain. Energy Rev. 2014, 35, 231–243. [Google Scholar] [CrossRef]
- Shi, K.; Yu, B.; Huang, Y.; Hu, Y.; Yin, B.; Chen, Z.; Chen, L.; Wu, J. Evaluating the Ability of NPP-VIIRS Nighttime Light Data to Estimate the Gross Domestic Product and the Electric Power Consumption of China at Multiple Scales: A Comparison with DMSP-OLS Data. Remote Sens. 2014, 6, 1705–1724. [Google Scholar] [CrossRef]
- Zhang, L.; Lei, J.; Wang, C.; Wang, F.; Geng, Z.; Zhou, X. Spatio-temporal variations and influencing factors of energy-related carbon emissions for Xinjiang cities in China based on time-series nighttime light data. J. Geogr. Sci. 2022, 32, 1886–1910. [Google Scholar] [CrossRef]
- Chen, J.; Gao, M.; Cheng, S.; Hou, W.; Song, M.; Liu, X.; Liu, Y.; Shan, Y. County-level CO2 emissions and sequestration in China during 1997–2017. Sci. Data 2020, 7, 391. [Google Scholar] [CrossRef]
- Chen, J.; Gao, M.; Cheng, S.; Liu, X.; Hou, W.; Song, M.; Li, D.; Fan, W. China’s city-level carbon emissions during 1992–2017 based on the inter-calibration of nighttime light data. Sci. Rep. 2021, 11, 3323. [Google Scholar] [CrossRef]
- Zhu, N.; Li, X.; Yang, S.; Ding, Y.; Zeng, G. Spatio-temporal dynamics and influencing factors of carbon emissions (1997–2019) at county level in mainland China based on DMSP-OLS and NPP-VIIRS Nighttime Light Datasets. Heliyon 2024, 10, e37245. [Google Scholar] [CrossRef]
- Xiang, C.; Mei, Y.; Liang, A. Analysis of Spatiotemporal Changes in Energy Consumption Carbon Emissions at District and County Levels Based on Nighttime Light Data—A Case Study of Jiangsu Province in China. Remote Sens. 2024, 16, 3514. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, L.; Wu, Q.; Zhang, X. How does extreme heat affect carbon emission intensity? Evidence from county-level data in China. Econ. Model. 2024, 139, 106814. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, L.; Zhao, R.; Xiao, L.; Ding, M.; Yao, S.; Chuai, X.; Rong, P. County-level carbon budget and carbon compensation in the Yellow River Basin: A perspective with balancing efficiency and equity. Environ. Dev. Sustain. 2024. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, S. Examining the determinants and the spatial nexus of city-level CO2 emissions in China: A dynamic spatial panel analysis of China’s cities. J. Clean. Prod. 2018, 171, 917–926. [Google Scholar] [CrossRef]
- Ke, N.; Lu, X.; Kuang, B.; Zhang, X. Regional disparities and evolution trend of city-level carbon emission intensity in China. Sustain. Cities Soc. 2023, 88, 104288. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Z.; Ye, X.; Wei, Y.D. Spatiotemporal dynamics of carbon intensity from energy consumption in China. J. Geogr. Sci. 2014, 24, 631–650. [Google Scholar] [CrossRef]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Brizga, J.; Feng, K.; Hubacek, K. Drivers of CO2 emissions in the former Soviet Union: A country level IPAT analysis from 1990 to 2010. Energy 2013, 59, 743–753. [Google Scholar] [CrossRef]
- Wang, H.; Ang, B.W.; Su, B. Assessing drivers of economy-wide energy use and emissions: IDA versus SDA. Energy Policy 2017, 107, 585–599. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Zhang, X.; Yang, Y.; Su, Y.; Ye, Y.; Zhang, H. Examining the driving factors of energy related carbon emissions using the extended STIRPAT model based on IPAT identity in Xinjiang. Renew. Sustain. Energy Rev. 2017, 67, 51–61. [Google Scholar] [CrossRef]
- Wang, F.; Wang, C.; Chen, J.; Li, Z.; Li, L. Examining the determinants of energy-related carbon emissions in Central Asia: Country-level LMDI and EKC analysis during different phases. Environ. Dev. Sustain. 2020, 22, 7743–7769. [Google Scholar] [CrossRef]
- Li, Z.; Chen, X.; Ye, Y.; Wang, F.; Liao, K.; Wang, C. The impact of digital economy on industrial carbon emission efficiency at the city level in China: Gravity movement trajectories and driving mechanisms. Environ. Technol. Innov. 2024, 33, 103511. [Google Scholar] [CrossRef]
- Xu, L.; Du, H.; Zhang, X. Driving forces of carbon dioxide emissions in China’s cities: An empirical analysis based on the geodetector method. J. Clean. Prod. 2021, 287, 125169. [Google Scholar] [CrossRef]
- Liao, K.; Huang, W.; Wang, C.; Wu, R.; Hu, Y. Spatio-Temporal Evolution Features and Impact Factors of Urban Expansion in Underdeveloped Cities: A Case Study of Nanchang, China. Land 2022, 11, 1799. [Google Scholar] [CrossRef]
- Su, Y.; Wu, J.; Ciais, P.; Zheng, B.; Wang, Y.; Chen, X.; Li, X.; Li, Y.; Wang, Y.; Wang, C.; et al. Differential impacts of urbanization characteristics on city-level carbon emissions from passenger transport on road: Evidence from 360 cities in China. Build. Environ. 2022, 219, 109165. [Google Scholar] [CrossRef]
- Liu, S.; Shen, J.; Liu, G.; Wu, Y.; Shi, K. Exploring the effect of urban spatial development pattern on carbon dioxide emissions in China: A socioeconomic density distribution approach based on remotely sensed nighttime light data. Comput. Environ. Urban Syst. 2022, 96, 101847. [Google Scholar] [CrossRef]
- Wang, S.; Liu, X.; Zhou, C.; Hu, J.; Ou, J. Examining the impacts of socioeconomic factors, urban form, and transportation networks on CO2 emissions in China’s megacities. Appl. Energy 2017, 185, 189–200. [Google Scholar] [CrossRef]
- Shi, K.; Xu, T.; Li, Y.; Chen, Z.; Gong, W.; Wu, J.; Yu, B. Effects of urban forms on CO2 emissions in China from a multi-perspective analysis. J. Environ. Manag. 2020, 262, 110300. [Google Scholar] [CrossRef]
- Li, Y.; Lv, C.; Yang, N.; Liu, H.; Liu, Z. A study of high temporal-spatial resolution greenhouse gas emissions inventory for on-road vehicles based on traffic speed-flow model: A case of Beijing. J. Clean. Prod. 2020, 277, 122419. [Google Scholar] [CrossRef]
- Duan, C.; Zhu, W.; Wang, S.; Chen, B. Drivers of global carbon emissions 1990–2014. J. Clean. Prod. 2022, 371, 133371. [Google Scholar] [CrossRef]
- Khan, M.K.; Teng, J.-Z.; Khan, M.I.; Khan, M.O. Impact of globalization, economic factors and energy consumption on CO2 emissions in Pakistan. Sci Total Environ. 2019, 688, 424–436. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S. The impacts of GDP, trade structure, exchange rate and FDI inflows on China’s carbon emissions. Energy Policy 2018, 120, 347–353. [Google Scholar] [CrossRef]
- Lin, H.; Wang, X.; Bao, G.; Xiao, H. Heterogeneous Spatial Effects of FDI on CO2 Emissions in China. Earths Future 2022, 10, e2021EF002331. [Google Scholar] [CrossRef]
- Hertwich, E.G. Increased carbon footprint of materials production driven by rise in investments. Nat. Geosci. 2021, 14, 151–155. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, X.; Shao, S. Decoupling CO2 emissions and industrial growth in China over 1993–2013: The role of investment. Energy Econ. 2016, 60, 275–292. [Google Scholar] [CrossRef]
- Cheng, S.; Chen, Y.; Meng, F.; Chen, J.; Liu, G.; Song, M. Impacts of local public expenditure on CO2 emissions in Chinese cities: A spatial cluster decomposition analysis. Resour. Conserv. Recycl. 2021, 164, 105217. [Google Scholar] [CrossRef]
- Xu, C.; Xu, Y.; Chen, J.; Huang, S.; Zhou, B.; Song, M. Spatio-temporal efficiency of fiscal environmental expenditure in reducing CO2 emissions in China’s cities. J. Environ. Manag. 2023, 334, 117479. [Google Scholar] [CrossRef]
- Wang, Q. Effects of urbanisation on energy consumption in China. Energy Policy 2014, 65, 332–339. [Google Scholar] [CrossRef]
- Wu, S.; Lei, Y.; Li, S. CO2 emissions from household consumption at the provincial level and interprovincial transfer in China. J. Clean. Prod. 2019, 210, 93–104. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y.; Su, B.; Zhang, Y.; Wang, S.; Liu, Y.; Li, H. Embodied carbon in China’s foreign trade: An online SCI-E and SSCI based literature review. Renew. Sustain. Energy Rev. 2017, 68, 492–510. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Y. Identification of the driving factors’ influences on regional energy-related carbon emissions in China based on geographical detector method. Environ. Sci. Pollut. Res. 2018, 25, 9626–9635. [Google Scholar] [CrossRef]
- Su, Y.; Chen, X.; Wang, C.; Zhang, H.; Liao, J.; Ye, Y.; Wang, C. A new method for extracting built-up urban areas using DMSP-OLS nighttime stable lights: A case study in the Pearl River Delta, southern China. GISci. Remote Sens. 2015, 52, 218–238. [Google Scholar] [CrossRef]
- Chen, J.; Liu, J.; Qi, J.; Gao, M.; Cheng, S.; Li, K.; Xu, C. City- and county-level spatio-temporal energy consumption and efficiency datasets for China from 1997 to 2017. Sci. Data 2022, 9, 101. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, Y.; Hang, Y.; Zheng, H.; Li, Y.; Guan, D.; Li, J.; Zhou, Y.; Li, L.; Hubacek, K. City-level emission peak and drivers in China. Sci. Bull. 2022, 67, 1910–1920. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Ruan, J.; Zhang, Z.; Qin, Z.; Lei, Z.; Cai, B.; Wang, S.; Tang, L. City-level pathways to carbon peak and neutrality in China. Cell Rep. Sustain. 2024, 1, 100102. [Google Scholar] [CrossRef]
- Cai, B.; Liang, S.; Zhou, J.; Wang, J.; Cao, L.; Qu, S.; Xu, M.; Yang, Z. China high resolution emission database (CHRED) with point emission sources, gridded emission data, and supplementary socioeconomic data. Resour. Conserv. Recycl. 2018, 129, 232–239. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, K.; Liang, S.; Zeng, X.; Cai, Y.; Meng, J.; Shan, Y.; Guan, D.; Yang, Z. Trends, Drivers, and Mitigation of CO2 Emissions in the Guangdong–Hong Kong–Macao Greater Bay Area. Engineering 2023, 23, 138–148. [Google Scholar] [CrossRef]
- Zhou, Y.; Shan, Y.; Liu, G.; Guan, D. Emissions and low-carbon development in Guangdong-Hong Kong-Macao Greater Bay Area cities and their surroundings. Appl. Energy 2018, 228, 1683–1692. [Google Scholar] [CrossRef]
- Song, Y.; Ma, M.; Veroustraete, F. Comparison and conversion of AVHRR GIMMS and SPOT VEGETATION NDVI data in China. Int. J. Remote Sens. 2010, 31, 2377–2392. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models. J. Am. Stat. Assoc. 1990, 85, 160. [Google Scholar]
- Haining, R. Spatial data analysis in the social and environmental sciences. Environ. Int. 1991, 17, 618. [Google Scholar]
- Liu, Q.; Wang, S.; Zhang, W.; Zhan, D.; Li, J. Does foreign direct investment affect environmental pollution in China’s cities? A spatial econometric perspective. Sci Total Environ. 2018, 613–614, 521–529. [Google Scholar] [CrossRef]
- Anselin, L. Local Indications of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Wang, J.F.; Li, X.H.; Christakos, G.; Liao, Y.L.; Zhang, T.; Gu, X.; Zheng, X.Y. Geographical Detectors-Based Health Risk Assessment and its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]

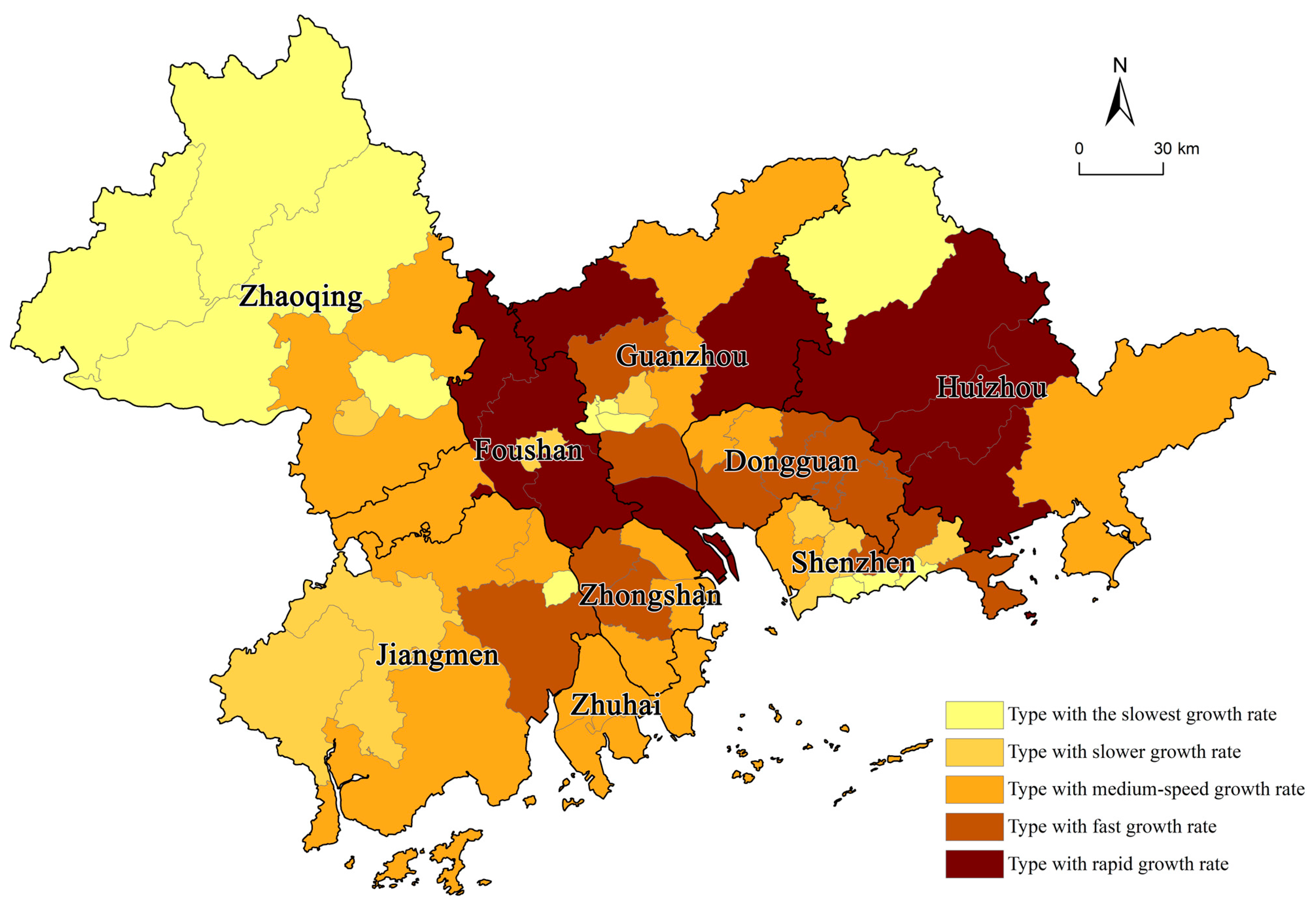


| Growth Type | During 2000–2010 | During 2010–2019 |
|---|---|---|
| Decreasing growth rate | Yantian District, Duanzhou District, Shunde District, Southern Group in Zhongshan | |
| Mean value of the SLOPEs is −0.0211 | ||
| Slowest growth rate | Futian District, Longmen County, Haizhu District, Dinghu District, Yantian District, Liwan District, Yuexiu District, Luohu District, Jianghai District, Guangning County, Huaiji County, Fengkai County, Deqing County | Jianghai District, Guangning County, Huaiji County, Fengkai County, Deqing County, Huadu District, Sanshui District, Northeast Group in Zhongshan, Eastern Group in Zhongshan, Chancheng District, Gaoming District, Pengjiang District, Pengjiang District, Nanhai District, Northwest Group in Zhongshan, Southeast Area in Dongguan, Sihui City |
| Mean SLOPE value = 0.0701 | Mean SLOPE value = 0.0193 | |
| Slower growth rate | Tianhe District, Nanshan District, Pingshan District, Enping City, Duanzhou District, Kaiping City, Guangming District, Longhua District, Chancheng District | Liwan District, Yuexiu District, Luohu District, Nansha District, Kaiping City, Heshan City, Central Group in Zhongshan, Eastern Industrial Park Area in Dongguan, Water Township New Town Area in Dongguan, Doumen District |
| Mean SLOPE value = 0.1601 | Mean SLOPE value = 0.0581 | |
| Medium growth rate | Urban area in Dongguan, Conghua District, Jinwan District, Gaoyao District, Bao’an District, Southern Group in Zhongshan, Heshan City, Water Township New Town Area in Dongguan, Doumen District, Huangpu District, Xiangzhou District, Taishan City, Huidong County, Northeast Group in Zhongshan, Eastern Group in Zhongshan, Gaoming District, Pengjiang District, Sihui City | Futian District, Longmen County, Boluo County, Haizhu District, Tianhe District, Nanshan District, Pingshan District, Enping City, Dinghu District, Urban Area in Dongguan, Conghua District, Jinwan District, Gaoyao District |
| Mean SLOPE value = 0.3176 | Mean SLOPE value = 0.1022 | |
| Fast growth rate | Longgang District, Central Group in Zhongshan, Eastern Industrial Park Area in Dongguan, Songshan Lake Area in Dongguan, Baiyun District, Panyu District, Xinhui District, Northwest Group in Zhongshan, Southeast Area in Dongguan | Binhai Area, Songshan Lake Area in Dongguan, Baiyun District, Huangpu District, Panyu District, Zengcheng District, Xinhui District, Guangming District, Huicheng District, Longhua District, Xiangzhou District, Taishan City, Huidong County |
| Mean SLOPE value = 0.4888 | Mean SLOPE value = 0.1925 | |
| Rapid growth rate | Boluo County, Huiyang District, Shunde District, Nansha District, Zengcheng District, Huicheng District, Huadu District, Sanshui District, Nanhai District | Baoan District, Longgang District, Huiyang District |
| Mean SLOPE value = 0.7873 | Mean SLOPE value = 0.3671 |
| Factors | Variables | Variable Interpretation Instructions |
|---|---|---|
| Population urbanization | Urbanization (UPOP) | Size of permanent urban population in each district and county (unit: 10,000) |
| Economic development | Economic density (DGDP) | The ratio of GDP of each district and county to each district and county area (unit: yuan/km2) |
| Economic globalization | Foreign direct investment (FDI) | The actual amount of foreign direct investment used in each district and county (unit: 10,000 USD) |
| Foreign trade (TEXIM) | Total amount of import and export trade of each district and county (unit: 100 million CNY) | |
| Land use | Construction land (UAREA) | Total area of construction land in each district and county (unit: km2) |
| Road density (DROAD) | The ratio of the total mileage of the road network of each district and county to the area of the district and county (unit: km/km2) | |
| Household consumption | Total retail sales of consumer goods (TRSCG) | Total retail sales of consumer goods per capita in each district or county (unit: CNY/person) |
| Investment in fixed assets | Investment in fixed assets (FAI) | Investment in fixed assets of each district or county (unit: 10,000 CNY) |
| Government expenditure | Local government expenditure (GPBE) | Local government expenditure of each district or county (unit: 10,000 CNY) |
| Variables | Explanatory Power (q Value) | ||
|---|---|---|---|
| 2010 | 2015 | 2019 | |
| UPOP | 0.359 *** | 0.533 *** | 0.541 *** |
| DGDP | 0.245 *** | 0.259 *** | 0.284 *** |
| UAREA | 0.886 *** | 0.896 *** | 0.898 *** |
| DROAD | 0.313 *** | 0.285 *** | 0.252 ** |
| TRSCG | 0.279 * | 0.309 *** | 0.404 *** |
| FDI | 0.461 *** | 0.241 * | 0.348 ** |
| TEXIM | 0.343 *** | 0.386 *** | 0.343 ** |
| FAI | 0.423 *** | 0.466 *** | 0.548 *** |
| GPBE | 0.506 *** | 0.495 *** | 0.368 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Wang, C.; Lin, X.; Li, Z.; Sun, C. County-Level Spatiotemporal Dynamics and Driving Mechanisms of Carbon Emissions in the Pearl River Delta Urban Agglomeration, China. Land 2024, 13, 1829. https://doi.org/10.3390/land13111829
Wang F, Wang C, Lin X, Li Z, Sun C. County-Level Spatiotemporal Dynamics and Driving Mechanisms of Carbon Emissions in the Pearl River Delta Urban Agglomeration, China. Land. 2024; 13(11):1829. https://doi.org/10.3390/land13111829
Chicago/Turabian StyleWang, Fei, Changjian Wang, Xiaojie Lin, Zeng Li, and Changlong Sun. 2024. "County-Level Spatiotemporal Dynamics and Driving Mechanisms of Carbon Emissions in the Pearl River Delta Urban Agglomeration, China" Land 13, no. 11: 1829. https://doi.org/10.3390/land13111829
APA StyleWang, F., Wang, C., Lin, X., Li, Z., & Sun, C. (2024). County-Level Spatiotemporal Dynamics and Driving Mechanisms of Carbon Emissions in the Pearl River Delta Urban Agglomeration, China. Land, 13(11), 1829. https://doi.org/10.3390/land13111829





