Estimating Rainfall Erosivity in North Korea Using Automated Machine Learning: Insights into Regional Soil Erosion Risks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data Collection
2.2. Calculation of Monthly Rainfall Erosivity in South Korea
2.3. Application of TPOT for Monthly Rainfall Erosivity Estimation
2.4. Rainfall Erosivity Estimation and Spatial Distribution
3. Results and Discussion
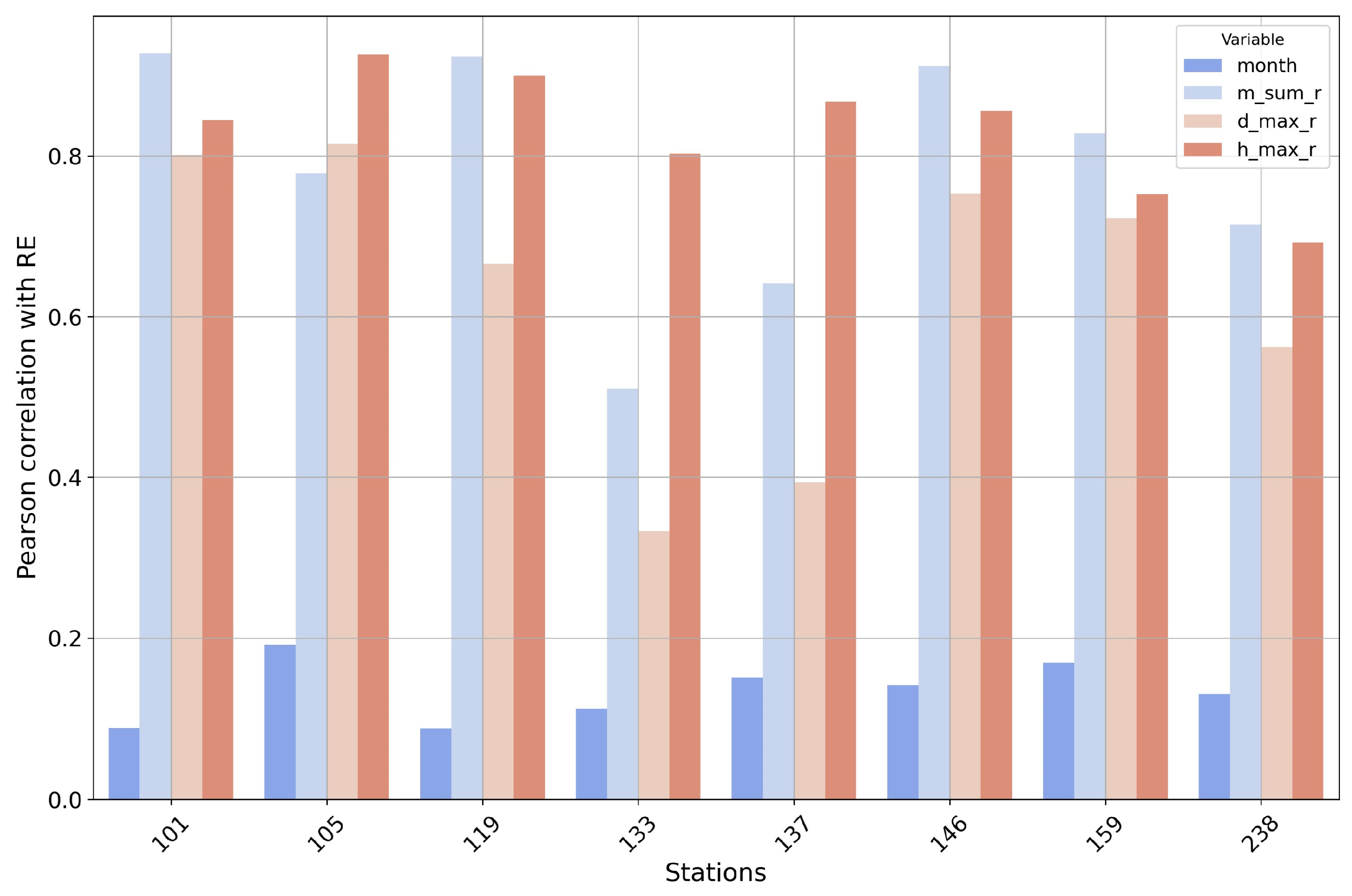
3.1. Correlation Analysis Between Input Features and RE
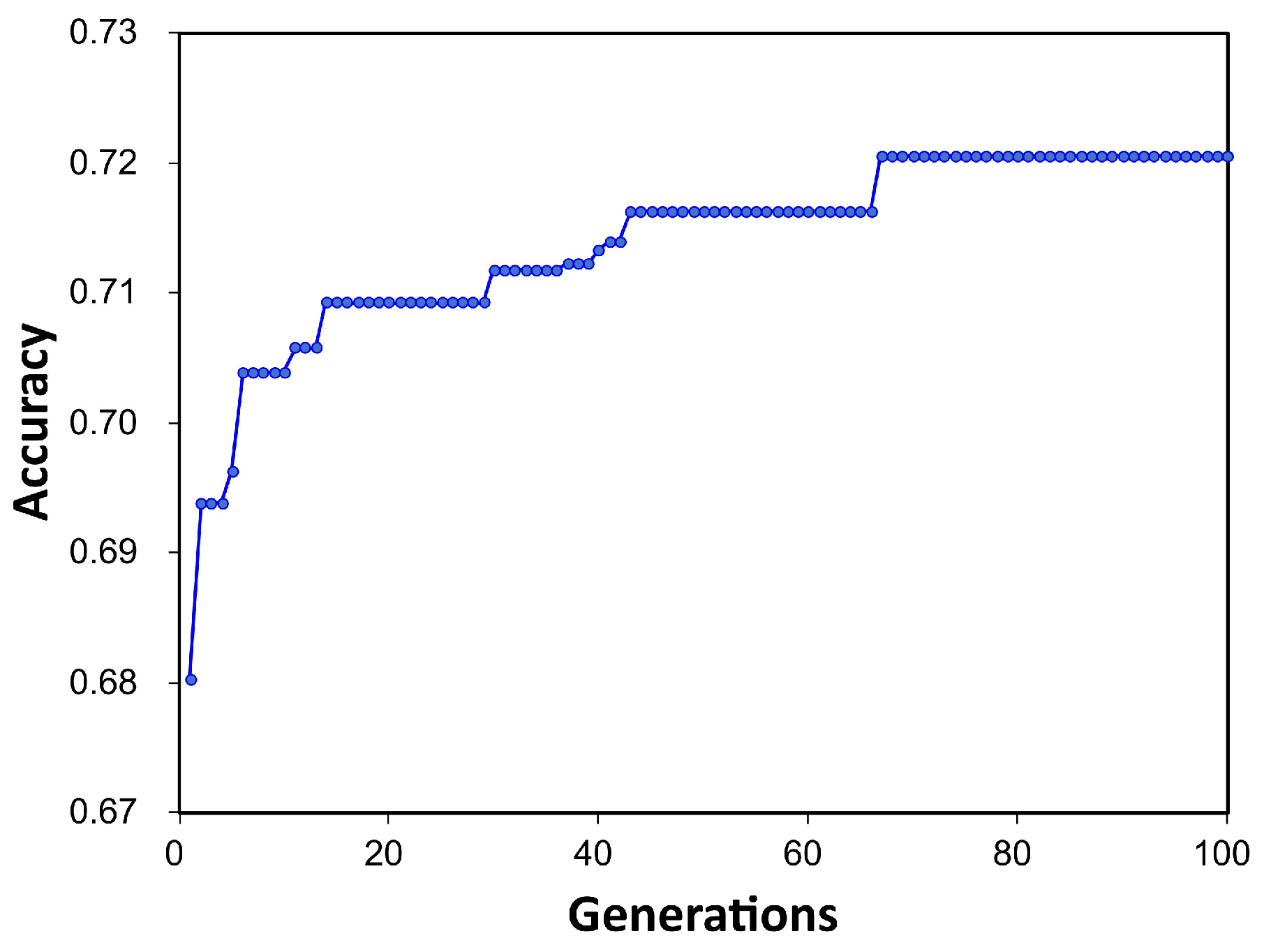
3.2. Best Model Algorithm and Pipeline Selected by TPOT
3.3. Model Validation on Estimated Rainfall Erosivity in South Korea
3.4. Estimated Rainfall Erosivity in North Korea
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kum, D.; Jang, C.H.; Shin, M.H.; Choi, J.; Kim, B.; Jeong, G.-C.; Won, C.H.; Lim, K.J. Determination of Model Parameters of Surface Cover Materials in Evaluation of Sediment Reduction and Its Effects at Watershed Scale Using SWAT. J. Korean Soc. Water Environ. 2012, 28, 923–932. [Google Scholar]
- Guerra, C.A.; Maes, J.; Geijzendorffer, I.; Metzger, M.J. An Assessment of Soil Erosion Prevention by Vegetation in Mediterranean Europe: Current Trends of Ecosystem Service Provision. Ecol. Indic. 2016, 60, 213–222. [Google Scholar] [CrossRef]
- Issaka, S.; Ashraf, M.A. Impact of Soil Erosion and Degradation on Water Quality: A Review. Geol. Ecol. Landsc. 2017, 1, 1–11. [Google Scholar] [CrossRef]
- He, J.; Xu, J. Is There Decentralization in North Korea? Evidence and Lessons from the Sloping Land Management Program 2004–2014. Land Use Policy 2017, 61, 113–125. [Google Scholar] [CrossRef]
- Lee, E.; Ahn, S.; Im, S. Estimation of Soil Erosion Rate in the Democratic People’s Republic of Korea Using the RUSLE Model. Forest Sci. Technol. 2017, 13, 100–108. [Google Scholar] [CrossRef]
- Lim, C.-H.; Choi, Y.; Kim, M.; Jeon, S.W.; Lee, W.-K. Impact of Deforestation on Agro-Environmental Variables in Cropland, North Korea. Sustainability 2017, 9, 1354. [Google Scholar] [CrossRef]
- Jin, Y.; Zhu, J.; Cui, G.; Yin, Z.; Zhu, W.; Lee, D.K. Characterization of Two Main Forest Cover Loss Transitions in North Korea from 1990 to 2020. Forests 2023, 14, 1966. [Google Scholar] [CrossRef]
- Korea Development Bank. The North Korea’s Industry, 2nd ed.; Korea Development Bank: Seoul, Republic of Korea, 2020. [Google Scholar]
- Engler, R.; Teplyakov, V.; Adams, J.M. An Assessment of Forest Cover Trends in South and North Korea, From 1980 to 2010. Environ. Manag. 2014, 53, 194–201. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised Universal Soil Loss Equation. J. Soil. Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Renard, K.G. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); US Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1997; ISBN 0160489385.
- Rutebuka, J.; De Taeye, S.; Kagabo, D.; Verdoodt, A. Calibration and Validation of Rainfall Erosivity Estimators for Application in Rwanda. CATENA 2020, 190, 104538. [Google Scholar] [CrossRef]
- Nearing, M.A.; Yin, S.; Borrelli, P.; Polyakov, V.O. Rainfall Erosivity: An Historical Review. CATENA 2017, 157, 357–362. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1978. [Google Scholar]
- Bonilla, C.A.; Vidal, K.L. Rainfall Erosivity in Central Chile. J. Hydrol. 2011, 410, 126–133. [Google Scholar] [CrossRef]
- Wu, L.; Liu, X.; Ma, X. Spatiotemporal Distribution of Rainfall Erosivity in the Yanhe River Watershed of Hilly and Gully Region, Chinese Loess Plateau. Environ. Earth Sci. 2016, 75, 315. [Google Scholar] [CrossRef]
- Ferro, V.; Porto, P.; Yu, B. A Comparative Study of Rainfall Erosivity Estimation for Southern Italy and Southeastern Australia. Hydrol. Sci. J. 1999, 44, 3–24. [Google Scholar] [CrossRef]
- Muhire, I.; Ahmed, F.; Abd Elbasit, M.M.M. Spatio-Temporal Variations of Rainfall Erosivity in Rwanda. J. Soil Sci. Environ. Manag. 2015, 6, 72–83. [Google Scholar]
- Arnoldus, H.M.J. Methodology Used to Determine the Maximum Potential Average Annual Soil Loss Due to Sheet and Rill Erosion in Morocco. FAO Soilds Bull. 1977, 34, 39–48. [Google Scholar]
- Li, X.; Li, Z.; Lin, Y. Suitability of TRMM Products with Different Temporal Resolution (3-Hourly, Daily, and Monthly) for Rainfall Erosivity Estimation. Remote Sens. 2020, 12, 3924. [Google Scholar] [CrossRef]
- Moreira, L.L.; Novais, R.R.; Schwamback, D.; de Carvalho Júnior, S.M. Spatial–Temporal Dynamics of Rainfall Erosivity in the State of Espírito Santo (Brazil) from Remote Sensing Data. World J. Sci. Technol. Sustain. Dev. 2020, 17, 297–309. [Google Scholar] [CrossRef]
- Lee, S.; Bae, J.H.; Hong, J.; Yang, D.; Panagos, P.; Borrelli, P.; Yang, J.E.; Kim, J.; Lim, K.J. Estimation of Rainfall Erosivity Factor in Italy and Switzerland Using Bayesian Optimization Based Machine Learning Models. CATENA 2022, 211, 105957. [Google Scholar] [CrossRef]
- Jeong, Y.-S.; Park, C.-S.; Jeong, P.-K.; Im, J.-N.; Shin, J.-S. Estimation of R-Factor for Universal Soil Loss Equation with Monthly Precipitation Data in North Korea. Korean J. Soil Sci. Fert. 2002, 35, 87–92. [Google Scholar]
- Teixeira, D.B.d.S.; Cecílio, R.A.; Moreira, M.C.; Pires, G.F.; Fernandes Filho, E.I. Recent Advancements in Rainfall Erosivity Assessment in Brazil: A Review. CATENA 2022, 219. [Google Scholar] [CrossRef]
- Beguería, S.; Serrano-Notivoli, R.; Tomas-Burguera, M. Computation of Rainfall Erosivity from Daily Precipitation Amounts. Sci. Total Environ. 2018, 637–638, 359–373. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, K.A.; Chen, W.; Lin, B.-S.; Seeboonruang, U. Using Machine Learning-Based Algorithms to Analyze Erosion Rates of a Watershed in Northern Taiwan. Sustainability 2020, 12, 2022. [Google Scholar] [CrossRef]
- Chakrabortty, R.; Pal, S.C.; Sahana, M.; Mondal, A.; Dou, J.; Pham, B.T.; Yunus, A.P. Soil Erosion Potential Hotspot Zone Identification Using Machine Learning and Statistical Approaches in Eastern India. Nat. Hazards 2020, 104, 1259–1294. [Google Scholar] [CrossRef]
- de Souza, C.M.P.; Veloso, G.V.; de Mello, C.R.; Ribeiro, R.P.; da Silva, L.A.P.; Leite, M.E.; Fernandes Filho, E.I. Spatiotemporal Prediction of Rainfall Erosivity by Machine Learning in Southeastern Brazil. Geocarto Int. 2022, 37, 11652–11670. [Google Scholar] [CrossRef]
- Vantas, K.; Sidiropoulos, E.; Evangelides, C. Rainfall Erosivity and Its Estimation: Conventional and Machine Learning Methods. In Soil Erosion—Rainfall Erosivity and Risk Assessment; IntechOpen: London, UK, 2019; p. 19. [Google Scholar]
- Olson, R.S.; Bartley, N.; Urbanowicz, R.J.; Moore, J.H. Evaluation of a Tree-Based Pipeline Optimization Tool for Automating Data Science. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, USA, 20–24 July 2016; pp. 485–492. [Google Scholar]
- North Korea Information Portal. Available online: https://nkinfo.unikorea.go.kr/ (accessed on 28 September 2024).
- Korea Development Bank. The North Korea’s Industry; Korea Development Bank: Seoul, Republic of Korea, 2015. [Google Scholar]
- ECMWF|Advancing Global NWP through International Collaboration. Available online: https://www.ecmwf.int/ (accessed on 28 September 2024).
- Korea Meteorological Administration. Available online: https://data.kma.go.kr/cmmn/main.do (accessed on 28 September 2024).
- Brown, L.; Foster, G. Storm Erosivity Using Idealized Intensity Distributions. Trans. ASAE 1987, 30, 379. [Google Scholar] [CrossRef]
- Foster, G.R. User’s Reference Guide: Revised Universal Soil Loss Equation (RUSLE2); US Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 2004.
- Olson, R.S.; Moore, J.H. TPOT: A Tree-Based Pipeline Optimization Tool for Automating Machine Learning. In Proceedings of the Workshop on Automatic Machine Learning, PMLR, New York, NY, USA, 24 June 2016; 2016; pp. 66–74. [Google Scholar]
- Alqahtani, A.; Shah, M.I.; Aldrees, A.; Javed, M.F. Comparative Assessment of Individual and Ensemble Machine Learning Models for Efficient Analysis of River Water Quality. Sustainability 2022, 14, 1183. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Martinez-Espana, R.; Casalí, J.; Pérez-Sánchez, J.; Senent-Aparicio, J. A Comparison of Performance of SWAT and Machine Learning Models for Predicting Sediment Load in a Forested Basin, Northern Spain. CATENA 2022, 212, 105953. [Google Scholar] [CrossRef]
- Chen, J.-L.; Liu, H.-B.; Wu, W.; Xie, D.-T. Estimation of Monthly Solar Radiation from Measured Temperatures Using Support Vector Machines—A Case Study. Renew. Energy 2011, 36, 413–420. [Google Scholar] [CrossRef]
- Waseem, M.; Mani, N.; Andiego, G.; Usman, M. A Review of Criteria of Fit for Hydrological Models. Int. Res. J. Eng. Technol. 2017, 4, 1765–1772. [Google Scholar]
- Environmental Systems Research Institute (Esri). ArcGIS Desktop: Release 10.3; Environmental Systems Research Institute (Esri): Redlands, CA, USA, 2014. [Google Scholar]
- Lee, J.; Lee, S.; Hong, J.; Lee, D.; Bae, J.H.; Yang, J.E.; Kim, J.; Lim, K.J. Evaluation of Rainfall Erosivity Factor Estimation Using Machine and Deep Learning Models. Water 2021, 13, 382. [Google Scholar] [CrossRef]
- Lee, J.-H.; Heo, J.-H. Estimation of Rainfall Erosivity in North Korea Using Modified Institute of Agricultural Sciences. J. Soil Sci. Fert. 2011, 44, 1004–1009. [Google Scholar]
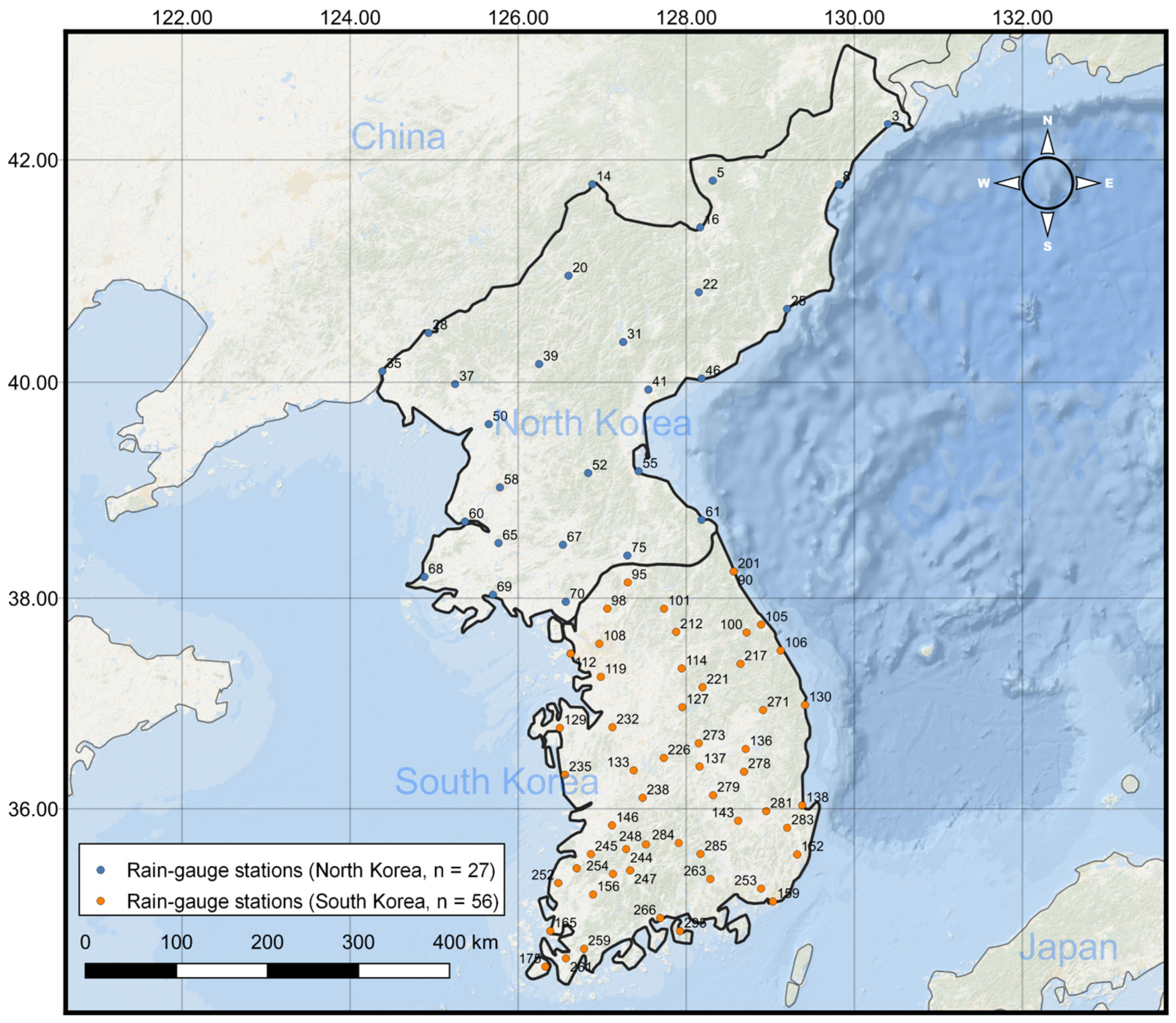

| ID | Station | Latitude | Longitude | Elevation | Average Annual Precipitation |
|---|---|---|---|---|---|
| 3 | Sonbong | 42.3167 | 130.4000 | 3 m | 775 mm |
| 5 | Samjiyon | 41.8167 | 128.3167 | 1386 m | 1092 mm |
| 8 | Cheongjin | 41.7833 | 129.8167 | 43 m | 1135 mm |
| 14 | Chunggang | 41.7833 | 126.8833 | 332 m | 999 mm |
| 16 | Hyesan | 41.4000 | 128.1667 | 714 m | 873 mm |
| 20 | Kanggye | 40.9667 | 126.6000 | 306 m | 1170 mm |
| 22 | Pungsan | 40.8167 | 128.1500 | 1206 m | 999 mm |
| 25 | Kimchaek | 40.6667 | 129.2000 | 23 m | 963 mm |
| 28 | Supung | 40.4500 | 124.9333 | 83 m | 1081 mm |
| 31 | Changjin | 40.3667 | 127.2500 | 1081 m | 1305 mm |
| 35 | Sinuiju | 40.1000 | 124.3833 | 7 m | 1011 mm |
| 37 | Kusong | 39.9833 | 125.2500 | 99 m | 1327 mm |
| 39 | Huichon | 40.1667 | 126.2500 | 155 m | 1290 mm |
| 41 | Hamhung | 39.9333 | 127.5500 | 38 m | 1245 mm |
| 46 | Sinpo | 40.0333 | 128.1833 | 19 m | 962 mm |
| 50 | Anju | 39.6167 | 125.6500 | 27 m | 1250 mm |
| 52 | Yangdok | 39.1667 | 126.8333 | 279 m | 1272 mm |
| 55 | Wonsan | 39.1833 | 127.4333 | 36 m | 1369 mm |
| 58 | Pyongyang | 39.0333 | 125.7833 | 38 m | 1076 mm |
| 60 | Nampo | 38.7167 | 125.3667 | 47 m | 1000 mm |
| 61 | Jangjeon | 38.7333 | 128.1833 | 35 m | 1268 mm |
| 65 | Sariwon | 38.5167 | 125.7667 | 52 m | 1016 mm |
| 67 | Singye | 38.5000 | 126.5333 | 100 m | 1273 mm |
| 68 | Yongbyon | 38.2000 | 124.8833 | 5 m | 1026 mm |
| 69 | Haeju | 38.0333 | 125.7000 | 81 m | 1115 mm |
| 70 | Kaesong | 37.9667 | 126.5667 | 70 m | 1244 mm |
| 75 | Pyeonggang | 38.4000 | 127.3000 | 371 m | 1447 mm |
| Variable | Correlation Coefficient |
|---|---|
| month | 0.13 |
| m_sum_r | 0.8 |
| d_max_r | 0.65 |
| h_max_r | 0.79 |
| Case ID | Stations | RMSE (MJ mm ha−1 h−1) | MAE (MJ mm ha−1 h−1) | R2 | Data Period |
|---|---|---|---|---|---|
| 101 | Chuncheon | 265.12 | 88.52 | 0.96 | 2013–2019 |
| 105 | Gangneung | 205.88 | 89.94 | 0.98 | 2013–2019 |
| 119 | Suwon | 221.35 | 71.74 | 0.98 | 2013–2019 |
| 133 | Daejeon | 326.46 | 117.78 | 0.89 | 2013–2019 |
| 137 | Sangju | 173.38 | 75.07 | 0.92 | 2013–2019 |
| 146 | Jeonju | 123.80 | 62.78 | 0.96 | 2013–2019 |
| 159 | Busan | 820.41 | 276.69 | 0.71 | 2013–2019 |
| 238 | Guemsan | 344.72 | 116.12 | 0.67 | 2013–2019 |
| Case ID | Stations | Annual Precipitation (mm) | Average Annual RE (MJ mm ha−1 h−1) | CV (%) | ||
|---|---|---|---|---|---|---|
| Mean | Min | Max | Mean | |||
| 3 | Sonbong | 775 | 299 | 1259 | 612 | 39 |
| 5 | Samjiyon | 1092 | 347 | 863 | 586 | 21 |
| 8 | Cheongjin | 1135 | 357 | 2462 | 909 | 53 |
| 14 | Chunggang | 999 | 354 | 2121 | 760 | 47 |
| 16 | Hyesan | 873 | 282 | 1119 | 468 | 37 |
| 20 | Kanggye | 1170 | 433 | 2454 | 1006 | 50 |
| 22 | Pungsan | 999 | 335 | 1616 | 747 | 47 |
| 25 | Kimchaek | 963 | 375 | 2361 | 849 | 57 |
| 28 | Supung | 1081 | 390 | 3222 | 1168 | 56 |
| 31 | Changjin | 1305 | 460 | 3514 | 1129 | 54 |
| 35 | Sinuiju | 1011 | 404 | 3920 | 1339 | 58 |
| 37 | Kusong | 1327 | 650 | 6859 | 2242 | 62 |
| 39 | Huichon | 1290 | 426 | 5270 | 1421 | 69 |
| 41 | Hamhung | 1245 | 409 | 3499 | 1328 | 46 |
| 46 | Sinpo | 962 | 311 | 2193 | 919 | 55 |
| 50 | Anju | 1250 | 491 | 5201 | 1778 | 62 |
| 52 | Yangdok | 1272 | 388 | 6195 | 1667 | 65 |
| 55 | Wonsan | 1369 | 470 | 4560 | 1558 | 59 |
| 58 | Pyongyang | 1076 | 583 | 3941 | 1406 | 54 |
| 60 | Nampo | 1000 | 410 | 3654 | 1294 | 59 |
| 61 | Jangjeon | 1268 | 495 | 4554 | 1529 | 56 |
| 65 | Sariwon | 1016 | 390 | 4154 | 1446 | 64 |
| 67 | Singye | 1273 | 583 | 4207 | 2006 | 52 |
| 68 | Yongbyon | 1026 | 355 | 4895 | 1424 | 64 |
| 69 | Haeju | 1115 | 319 | 4206 | 1898 | 51 |
| 70 | Kaesong | 1244 | 537 | 4777 | 2222 | 48 |
| 75 | Pyeonggang | 1447 | 713 | 5240 | 2238 | 52 |
| - | Average | 1133 | 428 | 3641 | 1331 | 53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Lee, S. Estimating Rainfall Erosivity in North Korea Using Automated Machine Learning: Insights into Regional Soil Erosion Risks. Land 2024, 13, 2038. https://doi.org/10.3390/land13122038
Han J, Lee S. Estimating Rainfall Erosivity in North Korea Using Automated Machine Learning: Insights into Regional Soil Erosion Risks. Land. 2024; 13(12):2038. https://doi.org/10.3390/land13122038
Chicago/Turabian StyleHan, Jeongho, and Seoro Lee. 2024. "Estimating Rainfall Erosivity in North Korea Using Automated Machine Learning: Insights into Regional Soil Erosion Risks" Land 13, no. 12: 2038. https://doi.org/10.3390/land13122038
APA StyleHan, J., & Lee, S. (2024). Estimating Rainfall Erosivity in North Korea Using Automated Machine Learning: Insights into Regional Soil Erosion Risks. Land, 13(12), 2038. https://doi.org/10.3390/land13122038






