Territorial Functional Pattern Reconstruction Integrating Set-Theoretic and Functional Mappings with Game-Theoretic Analysis to Reconcile Development and Conservation in China
Abstract
1. Introduction
2. Literature Review
2.1. TSFC Coordination: Methodological Evolution from Static Identification to Dynamic Response
2.2. Coordinated Achievement of Economic Development and Ecological Protection: From Conceptual Advocacy to Indicator Integration in Practice
2.3. Understanding Human–Land Relationships in TSF Utilisation: From Human Dominance to Harmonious Coexistence
2.4. Explicit Expression of TSFP Reconstruction Models: From Conceptual Frameworks to Deeper Mathematical Abstraction
3. Methods
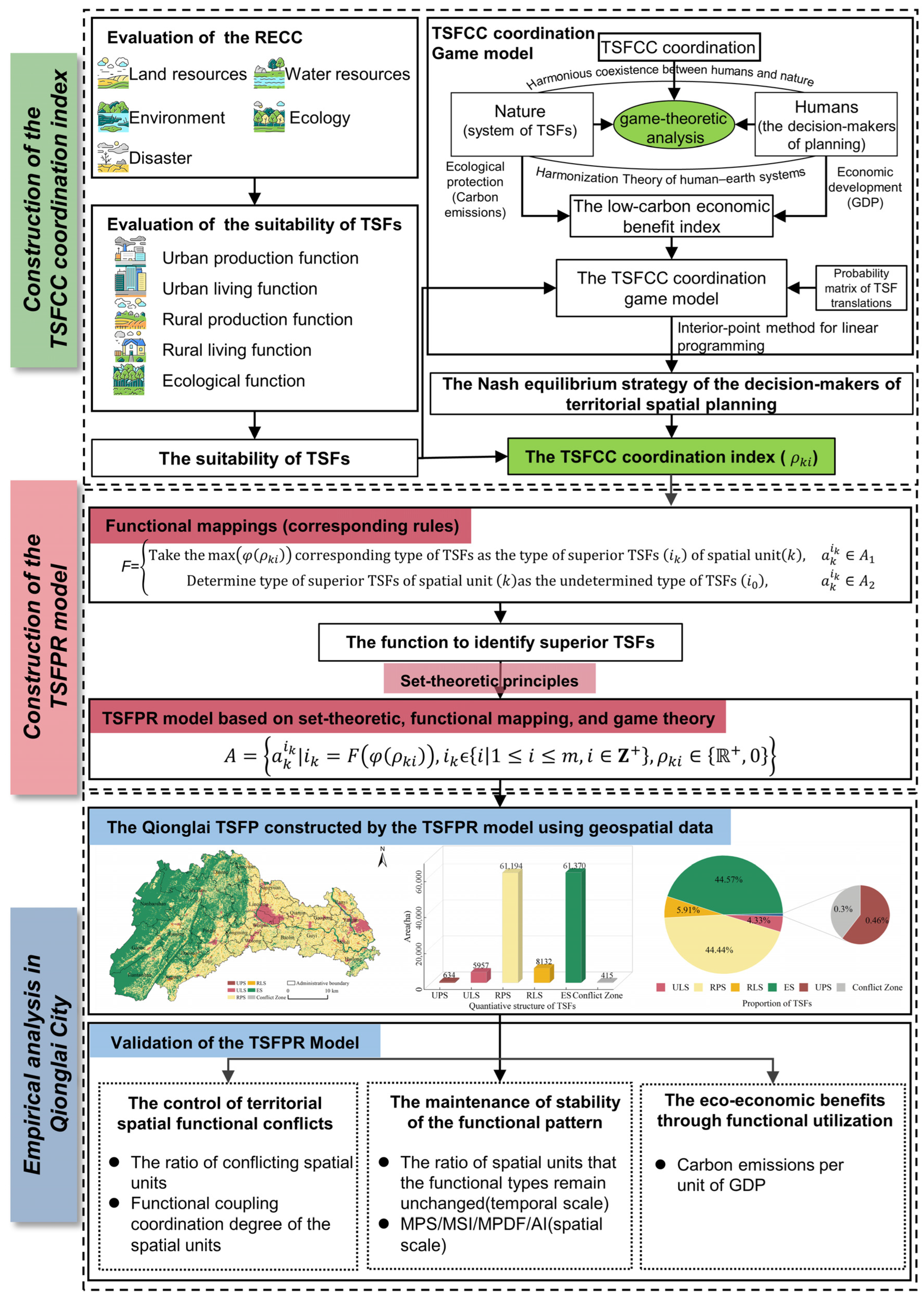
3.1. Research Methodology Framework
3.2. TSFPR Model Based on Set-Theoretic, Functional Mapping, and Game Theory
3.2.1. Construction of the TSFC Coordination Index Based on Game Theory
- (1)
- TSFC coordination Game model
- (2)
- A solution method for coordinating functional conflicts in TSFs
3.2.2. Construction of Corresponding Rules of Identification Function of Superior TSFs of Spatial Units
3.3. Evaluation of the Reconstruction Effect of TSFPs
3.3.1. Comparison and Validation of Coordination Degree of TSFCs
3.3.2. Comparison and Validation of Stability of TSFP
| Indicators | Formula | Explanation of Parameters | |
|---|---|---|---|
| Patch type level | Mean patch size index | is mean patch size index; is the total area of all patches in the landscape; is the total number of patches. | |
| Mean shape index | is mean shape index; , are the perimeter and area of the -th patch in the -th landscape class, respectively; is the number of all patches in the -th TSF types [85]. | ||
| Landscape level | Mean patch fractal dimension Index | is the mean patch fractal dimension index, is the perimeter of patch , is the area of patch , is the number of all patches in the landscape [85]. | |
| Aggregation Index | is aggregation index; is the number of similar adjacent patches of the corresponding landscape type [86]. | ||
3.3.3. Comparison and Validation of Eco-Economic Benefits of Functional Utilization
4. Application in the Study Area
4.1. Study Area and Data
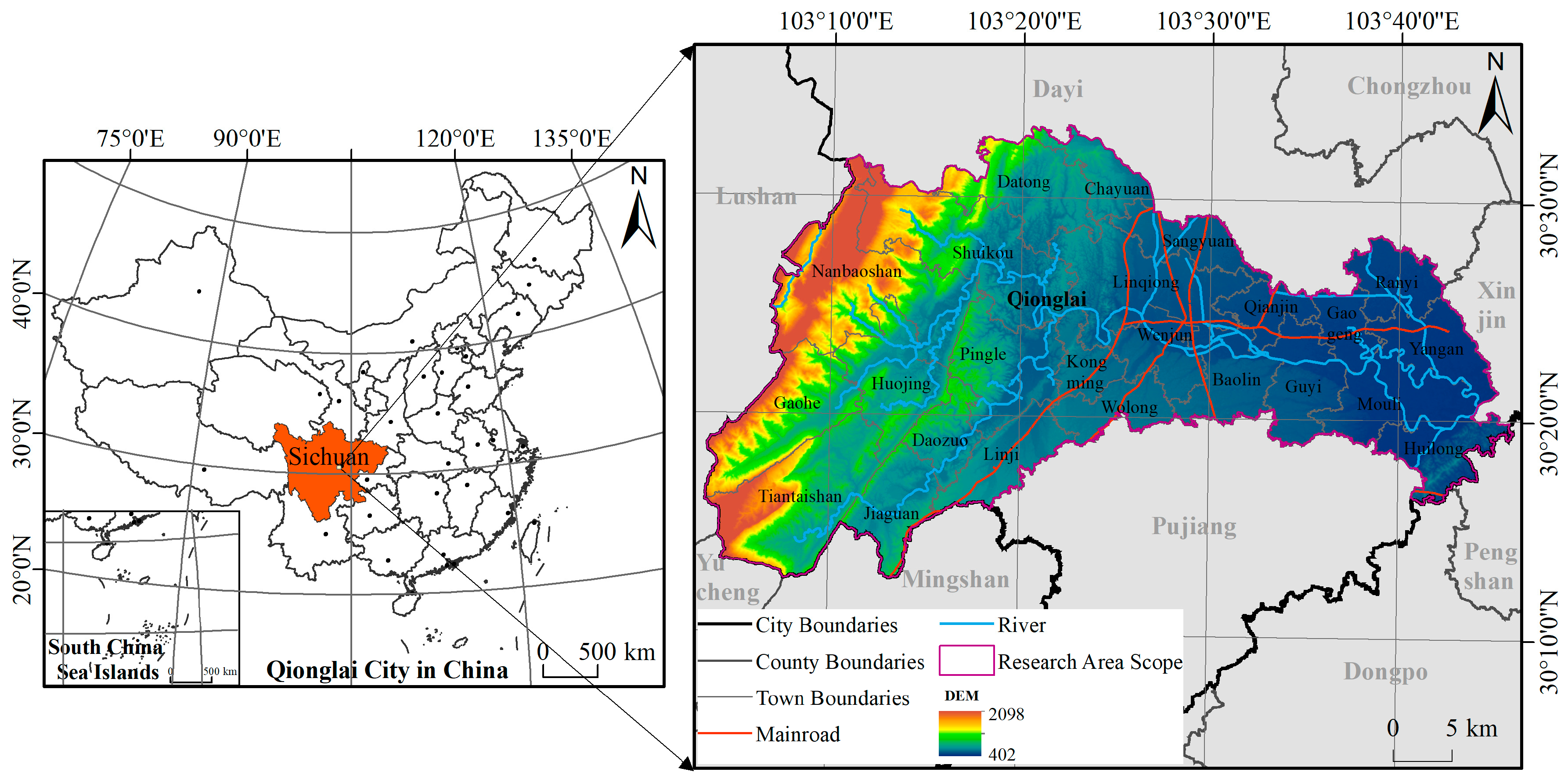
4.1.1. Case Study Area
4.1.2. Data Sources and Processing
4.2. Realization of Calculation Method of the TSFC Coordination Index
4.2.1. Realization of the TSFC Coordination Game Model
- (1)
- Calculation of eco-economic benefits of utilization of TSFs
- (2)
- The implementation process and results of the evaluation method for the suitability of TSFs are shown in Supplementary Materials S2 and S3 (Refs. [17,92,93,94] have been cited in the Supplementary Materials S2; Refs. [17,92,93,94,95,96] have been cited in the Supplementary Materials S3).
- (3)
- Prediction of the transfer probability matrix of TSFs
4.2.2. Realization of the Solution Method of TSFC Coordination Game Model
4.3. Realization of the Construction Method of the Corresponding Rules of Identification Function of Superior TSFs of Spatial Units
4.4. Validation of the TSFPR Model
5. Results and Analysis
5.1. Model Empirical Results and Analysis
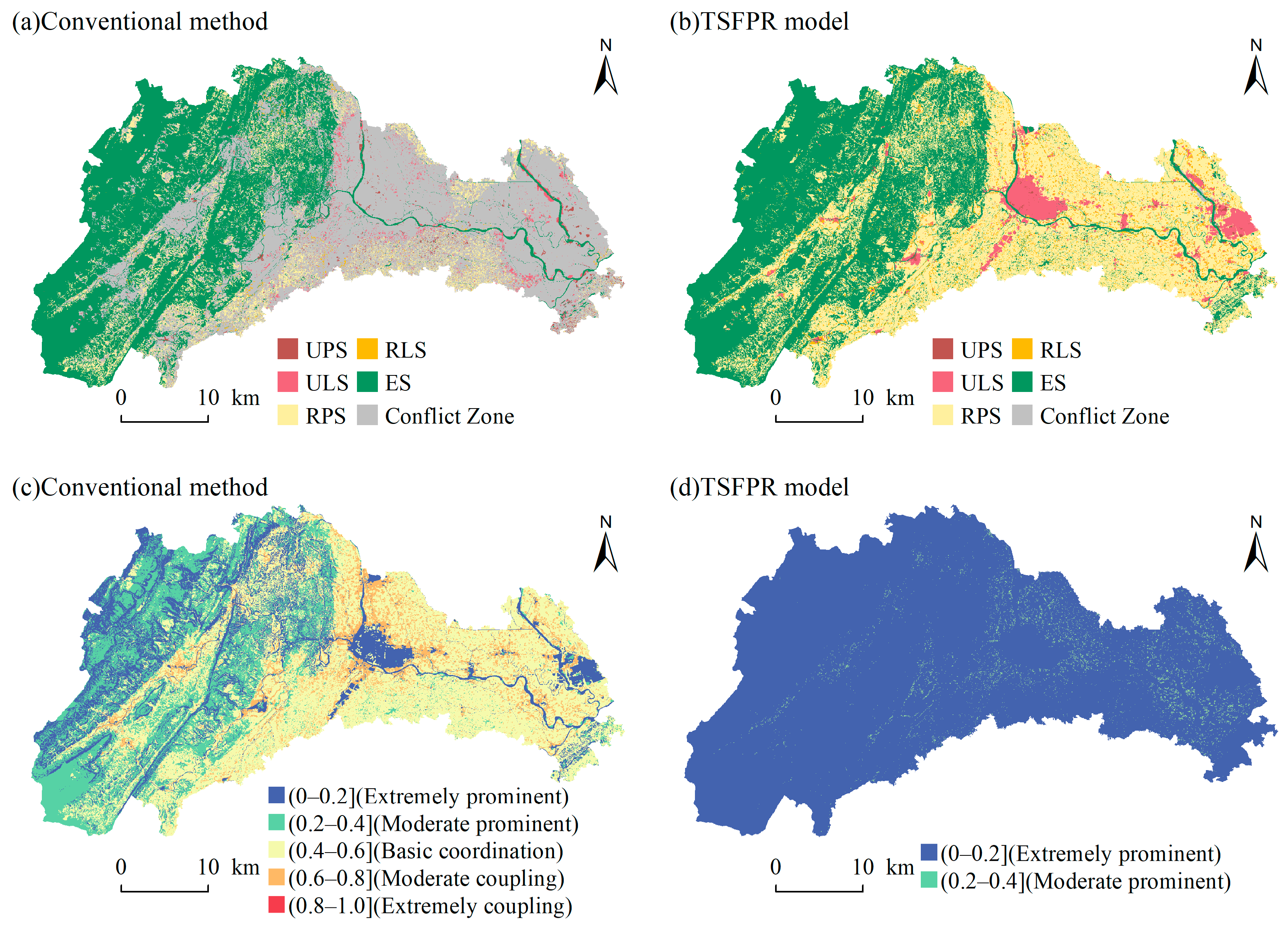
5.1.1. Results and Analysis of the Quantitative Structure of TSFs
5.1.2. Results and Analysis of the Spatial Distribution of TSFs
5.2. Model Validation and Analysis
5.2.1. Comparative Analysis of Coordination Degree of TSFC in Reconstruction Results
5.2.2. Comparative Analysis of Stability of TSFP of Reconstruction Results
5.2.3. Comparative Analysis of the Eco-Economic Benefits of Functional Utilization from Reconstruction Results
6. Discussion
6.1. Enhancing the Theoretical Universality and Cross-Regional Applicability of Methods for Reconstructing TSFP
6.2. Resolved the Spatial Conflict in Establishing a TSFP Based on Functional Suitability
6.2.1. Solved the Spatial Conflict Problem in Establishing TSFPs Based on Functional Suitability
6.2.2. Resolved the Weakness in Stability When Establishing TSFP Based on Functional Suitability
6.2.3. Solved the Problem of Neglecting Both Ecological and Economic Benefits in TSFP Established Solely on the Basis of Functional Suitability
6.3. Policy Implications
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Zhou, Y. Territory spatial planning and national governance system in China. Land Use Policy 2021, 102, 105288. [Google Scholar] [CrossRef]
- Wang, Z.; Deng, W.; Zhang, S.; Zhang, H. Improved trade-off model of land use functions: Differentiated objective setting by territory spatial planning. Ecol. Indic. 2024, 160, 111881. [Google Scholar] [CrossRef]
- Jiang, S.; Meng, J.; Zhu, L.; Cheng, H. Spatial-temporal pattern of land use conflict in China and its multilevel driving mechanisms. Sci. Total Environ. 2021, 801, 149697. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Li, W.; Wang, L. How should rural development be chosen? The mechanism narration of rural regional function: A case study of Gansu Province, China. Heliyon 2023, 9, e20485. [Google Scholar] [CrossRef]
- Hong, C.; Burney, J.A.; Pongratz, J.; Nabel, J.E.M.S.; Mueller, N.D.; Jackson, R.B.; Davis, S.J. Global and regional drivers of land-use emissions in 1961–2017. Nature 2021, 589, 554–561. [Google Scholar] [CrossRef]
- Baude, M.; Meyer, B.C.; Schindewolf, M. Land use change in an agricultural landscape causing degradation of soil based ecosystem services. Sci. Total Environ. 2019, 659, 1526–1536. [Google Scholar] [CrossRef]
- Peng, J.; Yang, Y.; Liu, Y.; Hu, Y.; Du, Y.; Meersmans, J.; Qiu, S. Linking ecosystem services and circuit theory to identify ecological security patterns. Sci. Total Environ. 2018, 644, 781–790. [Google Scholar] [CrossRef]
- Hui, E.C.M.; Bao, H. The logic behind conflicts in land acquisitions in contemporary China: A framework based upon game theory. Land Use Policy 2013, 30, 373–380. [Google Scholar] [CrossRef]
- Hoegh-Guldberg, O.; Jacob, D.; Taylor, M.; Guillén Bolaños, T.; Bindi, M.; Brown, S.; Camilloni, I.A.; Diedhiou, A.; Djalante, R.; Ebi, K.; et al. The human imperative of stabilizing global climate change at 1.5 °C. Science 2019, 365, eaaw6974. [Google Scholar] [CrossRef]
- Li, X.; Du, J.; Long, H. Theoretical framework and formation mechanism of the green development system model in China. Environ. Dev. 2019, 32, 100465. [Google Scholar] [CrossRef]
- Fang, C.; Wang, Z.; Liu, H. Beautiful China initiative: Human-nature harmony theory, evaluation index system and application. J. Geogr. Sci. 2020, 30, 691–704. [Google Scholar] [CrossRef]
- Abbass, K.; Qasim, M.Z.; Song, H.; Murshed, M.; Mahmood, H.; Younis, I. A review of the global climate change impacts, adaptation, and sustainable mitigation measures. Environ. Sci. Pollut. Res. 2022, 29, 42539–42559. [Google Scholar] [CrossRef]
- Anderson, R.; Bayer, P.E.; Edwards, D. Climate change and the need for agricultural adaptation. Curr. Opin. Plant Biol. 2020, 56, 197–202. [Google Scholar] [CrossRef]
- Gomez-Zavaglia, A.; Mejuto, J.C.; Simal-Gandara, J. Mitigation of emerging implications of climate change on food production systems. Food Res. Int. 2020, 134, 109256. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Rogelj, J.; Séférian, R.; Wartenburger, R.; Allen, M.R.; Cain, M.; Millar, R.J.; Ebi, K.L.; Ellis, N.; Hoegh-Guldberg, O.; et al. The many possible climates from the Paris Agreement’s aim of 1.5 °C warming. Nature 2018, 558, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Ou, D.; Gao, X.; Yang, Z.; Zhong, Y.; Yang, W.; Wu, J.; Yang, Y.; Liu, Y.; Sun, J.; et al. Synergizing economic growth and carbon emission reduction in China: A path to coupling the MFLP and PLUS models for optimizing the territorial spatial functional pattern. Sci. Total Environ. 2024, 929, 171926. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Dong, X.; Su, D.; Jiang, G.; Ma, W. How to balance protection and development? A comprehensive analysis framework for territorial space utilization scale, function and pattern. J. Environ. Manag. 2023, 336, 117670. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Li, J. Spatial suitability and multi-scenarios for land use: Simulation and policy insights from the production-living-ecological perspective. Land Use Policy 2022, 119, 106219. [Google Scholar] [CrossRef]
- Jiang, Z.; Wu, H.; Lin, A.; Shariff, A.R.M.; Hu, Q.; Song, D.; Zhu, W. Optimizing the spatial pattern of land use in a prominent grain-producing area: A sustainable development perspective. Sci. Total Environ. 2022, 843, 156971. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, Y.; Ma, X.; Wang, Y.; Yang, G.; Zhu, L. Evaluation of resources and environmental carrying capacity of 36 large cities in China based on a support-pressure coupling mechanism. Sci. Total Environ. 2019, 688, 838–854. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Liu, J.; Chai, J.; Wei, C. Selection of targeted poverty alleviation policies from the perspective of land resources-environmental carrying capacity. J. Rural Stud. 2022, 93, 318–325. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Lin, N.; Lin, Y.; Yuan, S.; Zhang, L.; Zhu, J.; Wang, K.; Gan, M.; Zhu, C. Spatial identification and trade-off analysis of land use functions improve spatial zoning management in rapid urbanized areas, China. Land Use Policy 2022, 116, 106058. [Google Scholar] [CrossRef]
- Yang, H.; Zhai, G.; Zhang, Y. Ecological vulnerability assessment and spatial pattern optimization of resource-based cities: A case study of Huaibei City, China. Hum. Ecol. Risk Assess. Int. J. 2020, 27, 606–625. [Google Scholar] [CrossRef]
- Zhang, Y.; Long, H.; Tu, S.; Ge, D.; Ma, L.; Wang, L. Spatial identification of land use functions and their tradeoffs/synergies in China: Implications for sustainable land management. Ecol. Indic. 2019, 107, 105550. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, Y. Synergy/trade-offs and differential optimization of production, living, and ecological functions in the Yangtze River Economic Belt, China. Ecol. Indic. 2023, 147, 109925. [Google Scholar] [CrossRef]
- Yang, Y.; Bao, W.; Liu, Y. Coupling coordination analysis of rural production-living-ecological space in the Beijing-Tianjin-Hebei region. Ecol. Indic. 2020, 117, 106512. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Chen, X.; Wang, L.; Zhao, M. Coupling coordination degree of production, living and ecological spaces and its influencing factors in the Yellow River Basin. J. Clean. Prod. 2021, 298, 126803. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, L.; Zhou, P.; Zhu, X.; Cudjoe, D. Coordination between Economic Growth and Carbon Emissions: Evidence from 178 Cities in China. Econ. Anal. Policy 2023, 81, 164–180. [Google Scholar] [CrossRef]
- Liu, C.; Sun, W.; Li, P.; Zhang, L.; Li, M. Differential characteristics of carbon emission efficiency and coordinated emission reduction pathways under different stages of economic development: Evidence from the Yangtze River Delta, China. J. Environ. Manag. 2022, 327, 116819. [Google Scholar] [CrossRef]
- Sheng, P.; Li, J.; Zhai, M.; Huang, S. Coupling of economic growth and reduction in carbon emissions at the efficiency level: Evidence from China. Energy 2020, 213, 118747. [Google Scholar] [CrossRef]
- Cao, X.; Wang, H.; Song, Y.; Zeng, H.; Zhang, B. An optimization-simulation modeling framework for exploring the dynamic correlation between the coordinated development of the human-nature nexus and land use under uncertainty. Sustain. Cities Soc. 2024, 110, 105995. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, Y.; Wang, L.; Cheng, Z.; Wu, X. Obstacle indicators diagnosis and advantage functions zoning optimization based on “Production-Living-Ecological” functions of national territory space in Jilin Province. Sustainability 2022, 14, 4215. [Google Scholar] [CrossRef]
- Han, B.; Jin, X.; Zhao, Q.; Chen, H. Spatiotemporal patterns and mechanisms of land-use conflicts affecting high-quality development in China. Appl. Geogr. 2023, 155, 103093. [Google Scholar] [CrossRef]
- Huang, C.; Zhao, D.; Liu, C.; Liao, Q. Integrating territorial pattern and socioeconomic development into ecosystem service value assessment. Environ. Impact Assess. Rev. 2023, 101, 107236. [Google Scholar] [CrossRef]
- Liao, G.; He, P.; Gao, X.; Lin, Z.; Huang, C.; Zhou, W.; Deng, O.; Xu, C.; Deng, L. Land use optimization of rural production–living–ecological space at different scales based on the BP–ANN and CLUE–S models. Ecol. Indic. 2022, 139, 108911. [Google Scholar] [CrossRef]
- Fu, B.; Wu, X.; Wang, Z.; Wu, X.; Wang, S. Coupling human and natural systems for sustainability: Experiences from China’s Loess Plateau. Earth Syst. Dyn. Discuss. 2022, 13, 795–808. [Google Scholar] [CrossRef]
- Tan, J.; Duan, Q.; Xiao, C.; He, C.; Yan, X. A brief review of the coupled human-Earth system modeling: Current state and challenges. Anthr. Rev. 2023, 10, 664–684. [Google Scholar] [CrossRef]
- Li, S.; Zhao, X.; Pu, J.; Miao, P.; Wang, Q.; Tan, K. Optimize and control territorial spatial functional areas to improve the ecological stability and total environment in karst areas of Southwest China. Land Use Policy 2021, 100, 104940. [Google Scholar] [CrossRef]
- Li, Y.; Ma, X.; Zhao, J.; Zhang, S.; Liu, C. Spatio-Temporal Evolution and Conflict Diagnosis of Territorial Space in Mountainous–Flatland Areas from a Multi-Scale Perspective: A Case Study of the Central Yunnan Urban Agglomeration. Land 2025, 14, 703. [Google Scholar] [CrossRef]
- Rossi, C.; Kneubühler, M.; Schütz, M.; Schaepman, M.; Haller, R.; Risch, A. From local to regional: Functional diversity in differently managed alpine grasslands. Remote Sens. Environ. 2020, 237, 111522. [Google Scholar] [CrossRef]
- Schneider, F.D.; Morsdorf, F.; Schmid, B.; Petchey, O.L.; Hueni, A.; Schimel, D.S.; Schaepman, M.E. Mapping functional diversity from remotely sensed morphological and physiological forest traits. Nat. Commun. 2017, 8, 1441. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, W.; He, J.; Liu, Y.; Ai, T.; Liu, D. A land-use spatial optimization model based on genetic optimization and game theory. Comput. Environ. Urban Syst. 2015, 49, 1–14. [Google Scholar] [CrossRef]
- Maleki, J.; Masoumi, Z.; Hakimpour, F.; Coello, C.A.C. A spatial land-use planning support system based on game theory. Land Use Policy 2020, 99, 105013. [Google Scholar] [CrossRef]
- Hilbe, C.; Simsa, S.; Chatterjee, K.; Nowak, M. Evolution of cooperation in stochastic games. Nature 2018, 559, 246–249. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Y.; Wang, C.; Chen, T.; Jin, F.; Zhang, W.; Li, L.; Xu, Y.; Dai, E.; Tao, A.; et al. Reshaping the sustainable geographical pattern: A major function zoning model and its applications in China. Earth’s Future 2018, 7, 25–42. [Google Scholar] [CrossRef]
- Wang, J.; Hu, Y.; Song, R.; Wang, W. Research on the optimal allocation of ecological land from the perspective of human needs—Taking Hechi City, Guangxi as an example. Int. J. Environ. Res. Public Health 2022, 19, 12418. [Google Scholar] [CrossRef]
- Gao, M.; Hu, Y.; Bai, Y. Construction of ecological security pattern in national land space from the perspective of the community of life in mountain, water, forest, field, lake and grass: A case study in Guangxi Hechi, China. Ecol. Indic. 2022, 139, 108867. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, L. Development and synergetic evolution of the water–energy–food nexus system in the Yellow River Basin. Environ. Sci. Pollut. Res. 2022, 29, 65549–65564. [Google Scholar] [CrossRef]
- Sun, Q.; Wang, J.; Zhang, J.; Xing, Z. Selecting reservoir reconstruction schemes from an ecological-economic trade-off perspective: Model building and case study. J. Clean. Prod. 2022, 370, 133468. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, M. Optimization of land use structure integrating ecosystem service function and economic development—A case study in Dongting Lake Ecological and Economic Zone, China. Environ. Sustain. Indic. 2025, 19, 100387. [Google Scholar] [CrossRef]
- Niu, M.; Wang, Y. Greening the economy: How territorial spatial planning policy promotes ecological and economic integration. Environ. Impact Assess. Rev. 2025, 105, 107338. [Google Scholar] [CrossRef]
- Chen, G.; Wang, S. Evaluation of Urban Resource Environmental Carrying Capacity and Land Spatial Development Suitability in a Semiarid Area of the Yellow River Basin. Sustainability 2023, 15, 12411. [Google Scholar] [CrossRef]
- Deco, G.; Kringelbach, M.; Arnatkevičiūtė, A.; Oldham, S.; Sabaroedin, K.; Rogasch, N.; Aquino, K.; Fornito, A. Dynamical consequences of regional heterogeneity in the brain’s transcriptional landscape. Sci. Adv. 2020, 6, eabc5539. [Google Scholar] [CrossRef] [PubMed]
- Ghodsvali, M.; Dane, G.; de Vries, B. An integrated decision support system for the urban food-water-energy nexus: Methodology, modification, and model formulation. Comput. Environ. Urban Syst. 2023, 100, 101940. [Google Scholar] [CrossRef]
- Sadooghi, S.E.; Taleai, M.; Abolhasani, S. Simulation of urban growth scenarios using integration of multi-criteria analysis and game theory. Land Use Policy 2022, 120, 106267. [Google Scholar] [CrossRef]
- Liang, T.; Yang, F.; Luo, Y.; Fang, M.; Huang, X.; Zhang, Z.; Wen, C.; Ren, X. The Synchronous Development Pattern and Type Division of Functional Coupling Coordination and Human Activity Intensity Based on the “Production–Living–Ecological” Space Perspective: A Case Study of Wanzhou District. Land 2022, 11, 1897. [Google Scholar] [CrossRef]
- Ellis, E.C.; Pascual, U.; Mertz, O. Ecosystem services and nature’s contribution to people: Negotiating diverse values and trade-offs in land systems. Curr. Opin. Environ. Sustain. 2019, 38, 86–94. [Google Scholar] [CrossRef]
- Brander, L.; Beukering, P.V.; Nijsten, L.; McVittie, A.; Baulcomb, C.; Eppink, F.; Cado van der Lelij, J.A. The global costs and benefits of expanding Marine Protected Areas. Mar. Policy 2020, 116, 103953. [Google Scholar] [CrossRef]
- Drechsler, M. Flexibility trade-offs in conservation offsets. Conserv. Biol. 2023, 38, e14144. [Google Scholar] [CrossRef]
- Alger, J. The Political Economy of Protected Area Designations: Commercial Interests in Conservation Policy. Glob. Environ. Politics 2023, 23, 54–73. [Google Scholar] [CrossRef]
- Krueger, J.I.; Heck, P.R.; Evans, A.M.; DiDonato, T.E. Social game theory: Preferences, perceptions, and choices. Eur. Rev. Soc. Psychol. 2020, 31, 222–253. [Google Scholar] [CrossRef]
- Prodanović, V.; Bach, P.M.; Stojković, M. Urban nature-based solutions planning for biodiversity outcomes: Human, ecological, and artificial intelligence perspectives. Urban Ecosyst. 2024, 27, 1795–1806. [Google Scholar] [CrossRef]
- Huber, J.; Newig, J.; Loos, J. Participation in protected area governance: A systematic case survey of the evidence on ecological and social outcomes. J. Environ. Manag. 2023, 336, 117593. [Google Scholar] [CrossRef]
- Tilman, A.R.; Plotkin, J.B.; Akçay, E. Evolutionary games with environmental feedbacks. Nat. Commun. 2020, 11, 915. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Qin, Y.; Yu, R.; Wu, Q. Optimization of Chinese land spatial pattern in the transformation process of resource-based cities: A case study in Tongling City, China. Sci. Rep. 2024, 14, 6092. [Google Scholar] [CrossRef] [PubMed]
- Zamberletti, P.; Papaïx, J.; Gabriel, E.; Opitz, T. Markov random field models for vector-based representations of landscapes. Ann. Appl. Stat. 2021, 15, 1801–1822. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, L.; Liang, Y.; Wen, Q. Scientific cognition and research framework of territorial space function in the New Era. J. Nat. Resour. 2022, 37, 3060–3072. [Google Scholar] [CrossRef]
- Ou, D.; Wu, N.; Li, Y.; Ma, Q.; Zheng, S.; Li, Q.; Yu, D.; Tang, H.; Gao, X. Delimiting Ecological Space and Simulating Spatial-temporal Changes in Its Ecosystem Service Functions based on a Dynamic Perspective: A Case Study on Qionglai City of Sichuan Province, China. J. Resour. Ecol. 2022, 13, 1128–1142. [Google Scholar] [CrossRef]
- Zhang, R.; Tian, G.; Borowiak, K.; Lisiak-Zielińska, M.; Lei, Y.; Yang, M.; Tian, Y.; Zhao, R.; Yan, J.; Mu, B. Measuring the evolutionary game process among three functional space types at the county scale in Henan Province, China. Cities 2023, 142, 104654. [Google Scholar] [CrossRef]
- Qu, Y.; Wang, S.; Tian, Y.; Jiang, G.; Zhou, T.; Meng, L. Territorial spatial planning for regional high-quality development—An analytical framework for the identification, mediation and transmission of potential land utilization conflicts in the Yellow River Delta. Land Use Policy 2023, 125, 106462. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Burbano-Moreno, A.A.; Mayrink, V.D. Spatial functional data analysis: Irregular spacing and bernstein polynomials. Spat. Stat. 2024, 60, 100832. [Google Scholar] [CrossRef]
- Su, C.; Hu, X.; Meng, Q.; Zhang, L.; Shi, W.; Zhao, M. A multimodal fusion framework for urban scene understanding and functional identification using geospatial data. Int. J. Appl. Earth Obs. Geoinf. 2024, 127, 103563. [Google Scholar] [CrossRef]
- Wang, X.; Wang, D.; Wu, S.; Yan, Z.; Han, J. Cultivated land multifunctionality in undeveloped peri-urban agriculture areas in China: Implications for sustainable land management. J. Environ. Manag. 2023, 325, 116500. [Google Scholar] [CrossRef] [PubMed]
- Cococcioni, M.; Fiaschi, L.; Lambertini, L. Non-Archimedean zero-sum games. J. Comput. Appl. Math. 2021, 393, 113483. [Google Scholar] [CrossRef]
- Wu, D.; Lisser, A. Using CNN for solving two-player zero-sum games. Expert Syst. Appl. 2022, 204, 117545. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Turner, M.G. Landscape ecology: The effect of pattern on process. Annu. Rev. Ecol. Syst. 1989, 20, 171–197. [Google Scholar] [CrossRef]
- Luck, M.; Wu, J. A Gradient Analysis of Urban Landscape Pattern: A Case Study from the Phoenix Metropolitan Region, Arizona, USA. Landsc. Ecol. 2002, 17, 327–339. [Google Scholar] [CrossRef]
- Cabral, A.I.; Costa, F.L. Land Cover Changes and Landscape Pattern Dynamics in Senegal and Guinea Bissau Borderland. Appl. Geogr. 2017, 82, 115–128. [Google Scholar] [CrossRef]
- Wu, J. Landscape sustainability science: Ecosystem services and human well-being in changing landscapes. Landsc. Ecol. 2021, 36, 639–664. [Google Scholar] [CrossRef]
- McGarigal, K.; Marks, B.J. FRAGSTATS: Spatial Pattern Analysis Program for Quantifying Landscape Structure; General Technical Report PNW-GTR-351; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1995. [CrossRef]
- Gustafson, E.J. Quantifying Landscape Spatial Pattern: What Is the State of the Art? Ecosystems 1998, 1, 143–156. [Google Scholar] [CrossRef]
- Li, H.; Reynolds, J.F. On definition and quantification of heterogeneity. Oikos 1995, 73, 280–284. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, W.; Zheng, H.; Ren, Z.; Zhai, C.; Tang, Z.; Shen, G.; He, X. Effects of urbanization intensity on forest structural-taxonomic attributes, landscape patterns and their associations in Changchun, Northeast China: Implications for urban green infrastructure planning. Ecol. Indic. 2017, 80, 286–296. [Google Scholar] [CrossRef]
- Xie, Z.; Han, Y.; Sun, L.; Ping, J. Analysis of land cover evolution within the built-up areas of provincial capital cities in northeastern China based on nighttime light data and Landsat data. PLoS ONE 2020, 15, e0239371. [Google Scholar] [CrossRef] [PubMed]
- Ou, D.; Zhang, Q.; Wu, Y.; Qin, J.; Xia, J.; Deng, O.; Gao, X.; Bian, J.; Gong, S. Construction of a territorial space classification system based on spatiotemporal heterogeneity of land use and its superior territorial space functions and their dynamic coupling: Case study on Qionglai City of Sichuan Province, China. Int. J. Environ. Res. Public Health 2021, 18, 9052. [Google Scholar] [CrossRef]
- Ou, D.; Zhang, Q.; Qin, J.; Gong, S.; Wu, Y.; Zheng, Z.; Xia, J.; Bian, J.; Gao, X. Classification system for county-level territorial space using spatiotemporal heterogeneity and dynamic coupling of land use and functionality. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2021, 37, 284–296. [Google Scholar] [CrossRef]
- IPCC (Intergovernmental Panel on Climate Change). 2006 IPCC Guidelines for National Greenhouse Gas Inventories, Prepared by the National Greenhouse Gas Inventories Programme; Eggleston, H.S., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., Eds.; IPCC: Hayama, Japan, 2006. Available online: https://www.osti.gov/etdeweb/biblio/20880391 (accessed on 1 October 2025).
- IPCC (Intergovernmental Panel on Climate Change). 2019 Refinement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Calvo Buendia, E., Tanabe, K., Kranjc, A., Baasansuren, J., Fukuda, M., Ngarize, S., Osako, A., Pyrozhenko, Y., Shermanau, P., Federici, S., Eds.; IPCC: Geneva, Switzerland, 2019; Available online: https://www.ipcc-nggip.iges.or.jp/public/2019rf/index.html (accessed on 1 October 2025).
- Wang, X.; Ou, D.; Shu, C.; Liu, Y.; Yan, Z.; La, M.; Xia, J. How Can We Achieve Carbon Neutrality During Urban Expansion? An Empirical Study from Qionglai City, China. Land 2025, 14, 1689. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; You, X.Y.; Shan, M.M. A novel approach for failure mode and effects analysis using combination weighting and fuzzy VIKOR method. Appl. Soft Comput. 2015, 28, 579–588. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Li, A.J.; Fung, T. Using GIS and multi-criteria decision analysis for conflict resolution in land use planning. Procedia Environ. Sci. 2012, 13, 2264–2273. [Google Scholar] [CrossRef]
- Xu, H.; Ma, C.; Lian, J.; Xu, K.; Chaima, E. Urban flooding risk assessment based on an integrated k-means cluster algorithm and improved entropy weight method in the region of Haikou, China. J. Hydrol. 2018, 563, 975–986. [Google Scholar] [CrossRef]
- Luo, W.; Ren, Y.; Shen, L.; Zhu, M.; Jiang, Y.; Meng, C.; Zhang, P. An evolution perspective on the urban land carrying capacity in the urbanization era of China. Sci. Total Environ. 2020, 744, 140827. [Google Scholar] [CrossRef]
- Zhu, W.; Pan, Y.; Zhang, J. Estimation of net primary productivity of Chinese terrestrial vegetation based on remote sensing. J. Plant Ecol. 2007, 31, 413–424. [Google Scholar] [CrossRef]
- Ma, S.; Wen, Z. Optimization of land use structure to balance economic benefits and ecosystem services under uncertainties: A case study in Wuhan, China. J. Clean. Prod. 2021, 311, 127537. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D.; Chen, J.; Wang, C.; Shen, M. The mixed pixel effect in land surface phenology: A simulation study. Remote Sens. Environ. 2018, 211, 338–344. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S. Is energy transition promoting the decoupling economic growth from emission growth? Evidence from the 186 countries. J. Clean. Prod. 2020, 260, 120768. [Google Scholar] [CrossRef]
- Wang, Q.; Su, M. The effects of urbanization and industrialization on decoupling economic growth from carbon emission—A case study of China. Sustain. Cities Soc. 2019, 51, 101758. [Google Scholar] [CrossRef]
- Wu, Y.; Tam, V.W.Y.; Shuai, C.; Shen, L.; Zhang, Y.; Liao, S. Decoupling China’s economic growth from carbon emissions: Empirical studies from 30 Chinese provinces (2001–2015). Sci. Total Environ. 2019, 656, 576–588. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.Q.; Huang, X.J.; Zhong, T.Y.; Cui, X.W. Carbon effect evaluation and low-carbon optimization of regional land use structure. J. Agric. Eng. 2013, 29, 220–229. [Google Scholar] [CrossRef]
- Zhu, E.; Deng, J.; Zhou, M.; Gan, M.; Jiang, R.; Wang, K.; Shahtahmassebi, A. Carbon emissions induced by land-use and land-cover change from 1970 to 2010 in Zhejiang, China. Sci. Total Environ. 2019, 646, 930–939. [Google Scholar] [CrossRef]
- Zhao, R.; Huang, X.; Liu, Y.; Zhong, T.; Ding, M.; Chuai, X. Carbon emission of regional land use and its decomposition analysis: Case study of Nanjing City, China. Chin. Geogr. Sci. 2015, 25, 198–212. [Google Scholar] [CrossRef]
- Zhao, R.; Huang, X.; Peng, B. Research on carbon cycle and carbon balance of Nanjing urban system. Acta Geogr. Sin. 2012, 67, 758–770. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Philippe, C.; Philippe, P.; Huang, Y.; Stephen, S.; Wang, T. The carbon balance of terrestrial ecosystems in China. Nature 2009, 458, 1009–1013. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Kang, G.; Tsuruta, H.; Mosier, A. Estimate of CH4 emissions from year-round flooded rice fields during rice growing season in China. Pedosphere 2005, 15, 66–71. [Google Scholar]
- He, Y.; Dan, L.; Dong, W.; Ji, J.; Qin, D. The terrestrial NPP simulations in China since Last Glacial Maximum. Chin. Sci. Bull. 2005, 50, 2074–2079. [Google Scholar] [CrossRef]
- Fang, J.; Guo, Z.; Pu, S.; Chen, A. Terrestrial vegetation carbon sinks in China, 1981–2000. Sci. China Ser. D 2007, 50, 1341–1350. [Google Scholar] [CrossRef]
- Duan, X.N.; Wang, X.K.; Lu, F.; Ouyang, Z.Y. Carbon sequestration and its potential by wetland ecosystems in China. Acta Ecol. Sin. 2008, 28, 463–469. [Google Scholar] [CrossRef]
- Lai, L.; Huang, X.J.; Wang, H.; Dong, Y.H.; Xiao, S.S. Estimation of environmental costs of chemical fertilizer application in China. Acta Pedol. Sin. 2009, 46, 63–69. [Google Scholar] [CrossRef]
- Baggio, R.; Sainaghi, R. Complex and chaotic tourism systems: Towards a quantitative approach. Int. J. Contemp. Hosp. Manag. 2011, 23, 840–861. [Google Scholar] [CrossRef]
- Guan, Y.; Shan, Y.; Huang, Q.; Chen, H.; Wang, D.; Hubacek, K. Assessment to China’s recent emission pattern shifts. Earth’s Future 2021, 9, e2021EF002241. [Google Scholar] [CrossRef]
- Zhai, Y.; Zhai, G.; Chen, Y.; Liu, J. Research on regional terrestrial carbon storage based on the pattern-process-function. Ecol. Inform. 2024, 78, 102497. [Google Scholar] [CrossRef]
- Zou, L.; Liu, Y.; Wang, J.; Yang, Y. An analysis of land use conflict potentials based on ecological-production-living function in the southeast coastal area of China. Ecol. Indic. 2021, 122, 107229. [Google Scholar] [CrossRef]
- Bao, W.; Yang, Y.; Zou, L. How to reconcile land use conflicts in mega urban agglomeration? A scenario-based study in the Beijing-Tianjin-Hebei region, China. J. Environ. Manag. 2021, 294, 112995. [Google Scholar] [CrossRef]
- Fang, Y.-T.; Ai, D.-Y.; Yang, Y.; Sun, W.; Zu, J. Multi-Objective Spatial Suitability Evaluation and Conflict Optimization Considering Productivity, Sustainability, and Livability in Southwestern Mountainous Areas of China. Sustainability 2021, 14, 371. [Google Scholar] [CrossRef]
- Palmer, M.A.; Bernhardt, E.S.; Allan, J.D.; Lake, P.S.; Alexander, G.; Brooks, S.; Carr, J.; Clayton, S.; Dahm, C.N.; Follstad Shah, J.; et al. Standards for ecologically successful river restoration. J. Appl. Ecol. 2005, 42, 208–217. [Google Scholar] [CrossRef]
- Franco, M.A.; Rizzo, L.V.; Teixeira, M.J.; Artaxo, P.; Azevedo, T.; Lelieveld, J.; Nobre, C.A.; Pöhlker, C.; Pöschl, U.; Shimbo, J.; et al. How climate change and deforestation interact in the transformation of the Amazon rainforest. Nat. Commun. 2025, 16, 7944. [Google Scholar] [CrossRef] [PubMed]
- Zhukov, Y.M.; Byers, J.S.; Davidson, M.; Kollman, K. Integrating data across misaligned spatial units. Political Anal. 2023, 31, 267–285. [Google Scholar] [CrossRef]
- Jahan, F.; Kennedy, D.W.; Duncan, E.W.; Mengersen, K. Evaluation of spatial Bayesian Empirical Likelihood models in analysis of small area data. PLoS ONE 2022, 17, e0268130. [Google Scholar] [CrossRef]
- Ding, S.; Liu, S.; Chang, M.; Lin, H.; Lv, T.; Zhang, Y.; Zeng, C. Spatial Optimization of Land Use Pattern toward Carbon Mitigation Targets—A Study in Guangzhou. Land 2023, 12, 1903. [Google Scholar] [CrossRef]
- Shah, P.; Peterson, R.; Jones, S.L.; Ferguson, A.J. Things are not always what they seem: The origins and evolution of intragroup conflict. Adm. Sci. Q. 2020, 65, 1112–1152. [Google Scholar] [CrossRef]
- Luo, B.; Yang, Y.; Liu, D. Policy Iteration Q-Learning for Data-Based Two-Player Zero-Sum Game of Linear Discrete-Time Systems. IEEE Trans. Cybern. 2020, 50, 728–739. [Google Scholar] [CrossRef] [PubMed]
- Sun, J. Two-Person Zero-Sum Stochastic Linear-Quadratic Differential Games. SIAM J. Control Optim. 2020, 58, 1710–1735. [Google Scholar] [CrossRef]
- Govindan, S.; Wilson, R. A global Newton method for computing Nash equilibria. J. Econ. Theory 2003, 110, 65–86. [Google Scholar] [CrossRef]
- Wright, S.J. Primal-Dual Interior-Point Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997. [Google Scholar] [CrossRef]
- Nesterov, Y.; Nemirovskii, A. Interior-Point Polynomial Algorithms in Convex Programming; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar] [CrossRef]
- Forsgren, A.; Gill, P.E.; Wright, M.H. Interior methods for nonlinear optimization. SIAM Rev. 2002, 44, 525–597. [Google Scholar] [CrossRef]
- Roos, C.; Terlaky, T.; Vial, J.-P. Interior Point Methods for Linear Optimization, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Peng, B.; Sheng, X.; Wei, G. Does environmental protection promote economic development? From the perspective of coupling coordination between environmental protection and economic development. Environ. Sci. Pollut. Res. 2020, 27, 27980–27993. [Google Scholar] [CrossRef]
- Hossin, M.A.; Abudu, H.; Sai, R.; Agyeman, S.; Wesseh, P.K. Examining sustainable development goals: Are developing countries advancing in sustainable energy and environmental sustainability? Environ. Sci. Pollut. Res. 2023, 31, 1–19. [Google Scholar] [CrossRef]
- Liang, C.; Zhang, R.-C.; Zeng, J. Optimizing ecological and economic benefits in areas with complex land-use evolution based on spatial subdivisions. Landsc. Urban Plan. 2023, 233, 104701. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, B.; Hu, W. Study on Territorial Spatial Equilibrium Based on Ecosystem Service Value: A Case Study of the Southwest Guangxi Karst–Beibu Gulf, China. Land Degrad. Dev. 2024, 36, 900–918. [Google Scholar] [CrossRef]
- Song, W.; Cao, S.; Du, M.; He, Z. Aligning territorial spatial planning with sustainable development goals: A comprehensive analysis of production, living, and ecological spaces in China. Ecol. Indic. 2024, 158, 113393. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, M.; Zhao, B.; Lu, Z.; Sun, X.; Zhang, Z. Spatially explicit carbon emissions from land use change: Dynamics and scenario simulation in the Beijing-Tianjin-Hebei urban agglomeration. Land Use Policy 2025, 137, 107001. [Google Scholar] [CrossRef]
- Wang, S.; Liu, C.; Zhou, Z. Government-enterprise green collaborative governance and urban carbon emission reduction: Empirical evidence from green PPP programs. Environ. Res. 2024, 246, 119484. [Google Scholar] [CrossRef] [PubMed]
- Bodin, Ö. Collaborative environmental governance: Achieving collective action in social-ecological systems. Science 2017, 357, eaan1114. [Google Scholar] [CrossRef] [PubMed]
- Mi, Z.; Coffman, D. The sharing economy promotes sustainable societies. Nat. Commun. 2019, 10, 1214. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lu, Z. Exploring the balance between ecosystem services and economic benefits via multi-objective land use optimization. Land 2025, 14, 920. [Google Scholar] [CrossRef]
- Zheng, W.; Ke, X.; Xiao, B.; Zhou, T. Optimising land use allocation to balance ecosystem services and economic benefits: A case study in Wuhan, China. J. Environ. Manag. 2019, 251, 109613. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Z.; Saito, Y.; Liu, J.P.; Sun, X.; Wang, Y. Stepwise decreases of the Huanghe (Yellow River) sediment load (1950–2005): Impacts of climate change and human activities. Glob. Planet. Change 2007, 57, 331–354. [Google Scholar] [CrossRef]
- Miao, C.; Ni, J.; Borthwick, A.G.L.; Yang, L. A preliminary estimate of human and natural contributions to the changes in water discharge and sediment load in the Yellow River. Glob. Planet. Change 2011, 76, 196–205. [Google Scholar] [CrossRef]
- Balakrishnan, K.; Dey, S.; Gupta, T.; Dhaliwal, R.S.; Brauer, M.; Cohen, A.J.; Stanaway, J.D.; Beig, G.; Joshi, T.K.; Aggarwal, A.N.; et al. The impact of air pollution on deaths, disease burden, and life expectancy across the states of India: The Global Burden of Disease Study 2017. Lancet Planet. Health 2019, 3, e26–e39. [Google Scholar] [CrossRef]
- Kehoe, L.; Romero-Muñoz, A.; Polaina, E.; Estes, L.; Kreft, H.; Kuemmerle, T. Biodiversity at risk under future cropland expansion and intensification. Nat. Ecol. Evol. 2017, 1, 1129–1135. [Google Scholar] [CrossRef]


| Data Type | Data Name | Time Section (Year) | Spatial Resolution | Data Source |
|---|---|---|---|---|
| Geospatial data | Remote sensing imagery | 2010–2020 | 10 m | Earth engine data catalog (https://developers.google.com/earth-engine/datasets, accessed on 28 September 2025) |
| Land use data | 2010–2020 | 1: 5000 | Land survey results (Key laboratory of investigation, monitoring, protection and utilization of cropland resources, MNR, PRC) | |
| NDVI | 2010–2020 | 500 m | United States Geological Survey (USGS) (https://www.usgs.gov/, accessed on 27 September 2025) | |
| DEM | 2020 | 12.5 m | 91 satellite map assistant (https://www.91weitu.com/, accessed on 28 September 2025) | |
| Electronic maps (point, line, and area data for healthcare, education, and commercial services) | 2010–2020 | 1: 10,000 | Geographical information Monitoring Cloud Platform (http://www.dsac.cn/, accessed on 27 September 2025), 91 satellite map assistant (https://www.91weitu.com/, accessed on 28 September 2025) | |
| Monitoring data | Temperature, rainfall | 2010–2020 | County level (62 stations) | Resource and environmental science data platform (https://www.resdc.cn/, accessed on 30 September 2025) |
| Radiation dose | 2010–2020 | County level | Meteorological science knowledge service system (https://k.data.cma.cn/, accessed on 28 September 2025) | |
| Soil organic matter content, organic phosphorus content, available potassium content, alkali-hydrolyzable nitrogen content | 2020 | 921 sample points | Soil quality monitoring and evaluation project for crop rotation and fallow areas in Sichuan province (Sichuan provincial department of agriculture and rural affairs) | |
| Soil particle composition | 2020 | 1000 m | Geographical information Monitoring Cloud Platform (http://www.dsac.cn/, accessed on 30 September 2025) | |
| Panel data | Statistical data on national economic and social development | 2010–2020 | Township level, county level | Qionglai Statistical Yearbook |
| Energy statistics data | 2010–2020 | Municipal level, provincial level | Chengdu Statistical Yearbook China Energy Statistical Yearbook |
| Type of Territorial Functions | Conventional Method | TSFPR Model | ||
|---|---|---|---|---|
| GDP (100 Million Yuan) | Net Carbon Emissions (10,000 Tonnes) | GDP (100 Million Yuan) | Net Carbon Emissions (10,000 Tonnes) | |
| Urban production space | 673.72 | 29.14 | 322.24 | 13.94 |
| Urban living space | 194.27 | 17.38 | 152.89 | 13.68 |
| Rural production space | 87.08 | 93.39 | 92.10 | 98.77 |
| Rural living space | 5.63 | 16.33 | 4.43 | 12.87 |
| Ecological space | 14.50 | −3.50 | 14.78 | −3.56 |
| Total | 975.20 | 152.75 | 586.44 | 135.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, D.; Cheng, X.; Yan, Z.; Ruan, K.; Huang, Q.; Zhao, Z.; Yang, Z.; Qin, J.; Xia, J. Territorial Functional Pattern Reconstruction Integrating Set-Theoretic and Functional Mappings with Game-Theoretic Analysis to Reconcile Development and Conservation in China. Land 2025, 14, 2060. https://doi.org/10.3390/land14102060
Ou D, Cheng X, Yan Z, Ruan K, Huang Q, Zhao Z, Yang Z, Qin J, Xia J. Territorial Functional Pattern Reconstruction Integrating Set-Theoretic and Functional Mappings with Game-Theoretic Analysis to Reconcile Development and Conservation in China. Land. 2025; 14(10):2060. https://doi.org/10.3390/land14102060
Chicago/Turabian StyleOu, Dinghua, Xiaofan Cheng, Zijia Yan, Kun Ruan, Qingyan Huang, Zhi Zhao, Ziheng Yang, Jing Qin, and Jianguo Xia. 2025. "Territorial Functional Pattern Reconstruction Integrating Set-Theoretic and Functional Mappings with Game-Theoretic Analysis to Reconcile Development and Conservation in China" Land 14, no. 10: 2060. https://doi.org/10.3390/land14102060
APA StyleOu, D., Cheng, X., Yan, Z., Ruan, K., Huang, Q., Zhao, Z., Yang, Z., Qin, J., & Xia, J. (2025). Territorial Functional Pattern Reconstruction Integrating Set-Theoretic and Functional Mappings with Game-Theoretic Analysis to Reconcile Development and Conservation in China. Land, 14(10), 2060. https://doi.org/10.3390/land14102060







