The Influence of Non-Landslide Sample Selection Methods on Landslide Susceptibility Prediction
Abstract
:1. Introduction
2. Study Area
3. Material and Methods
3.1. Data Source
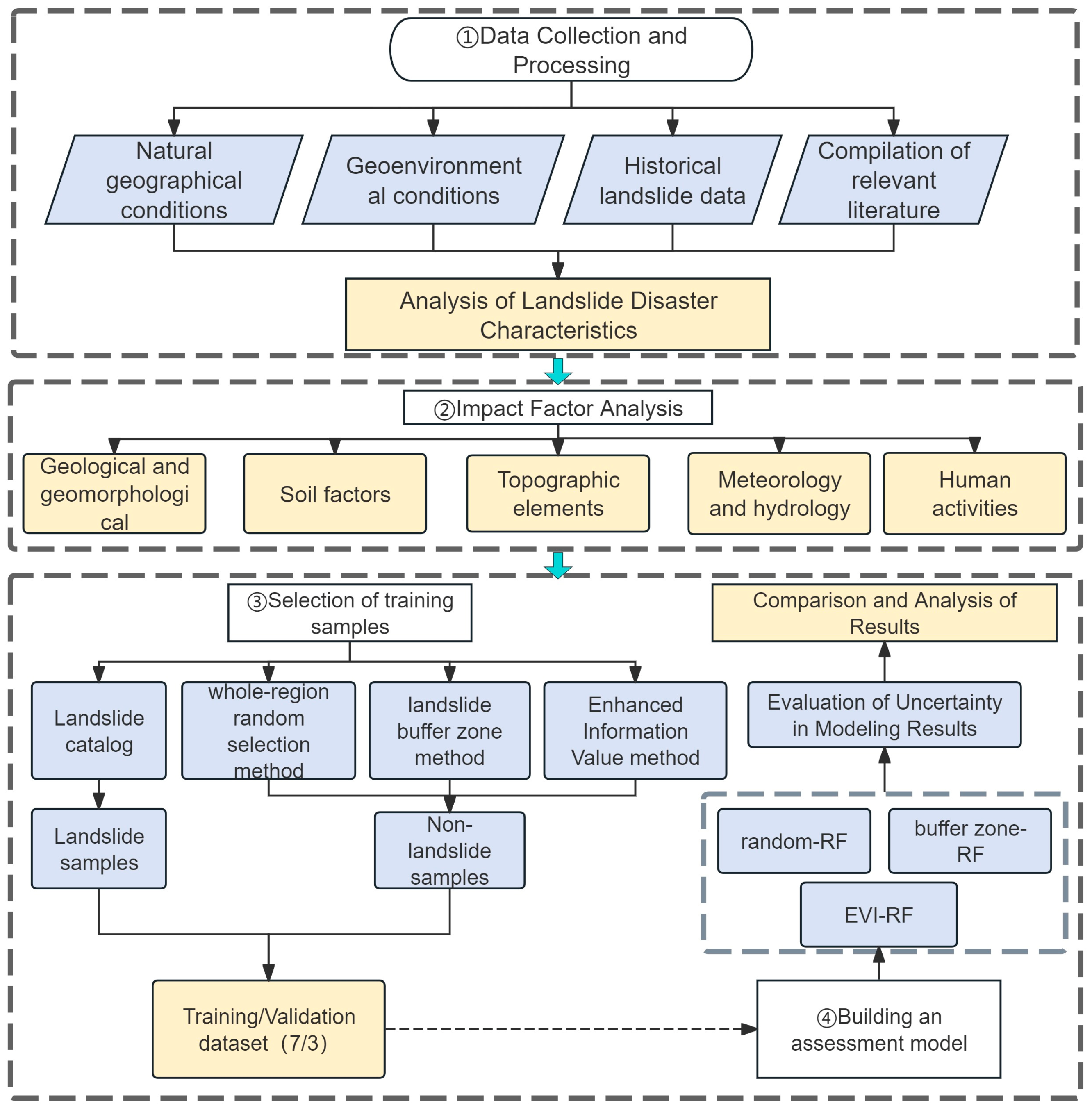
3.2. Modelling Procedure
3.3. Recursive Feature Elimination
3.4. Non-Landslide Sampling Methods
3.4.1. Whole-Region Random Sampling Method
3.4.2. Landslide Buffer Zone Method
3.4.3. Enhanced Information Value (EIV) Method
3.5. Random Forest (RF) Model
3.6. Model Uncertainty Assessment
3.6.1. Accuracy Analysis Based on ROC Curves
3.6.2. Accuracy Evaluation Based on Confusion Matrix
4. Results
4.1. Selection of Landslide Impact Factors
4.2. Selection of Non−Landslide Samples
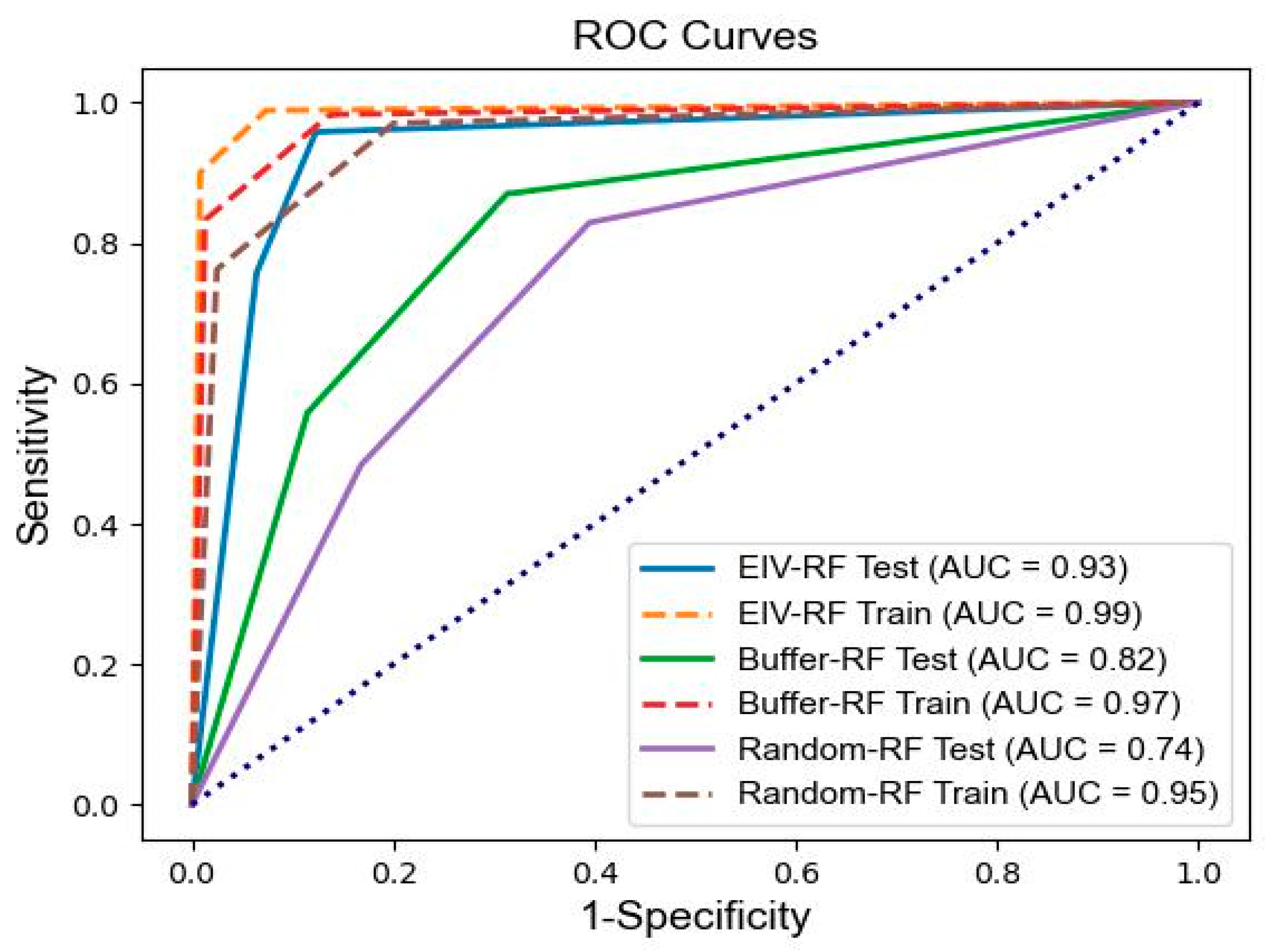
4.3. Model Comparison and Evaluation
4.4. Impact of Non-Landslide Sampling Strategies
4.4.1. Difference in Non-Landslide Sample Distribution
4.4.2. Difference in Model Accuracy
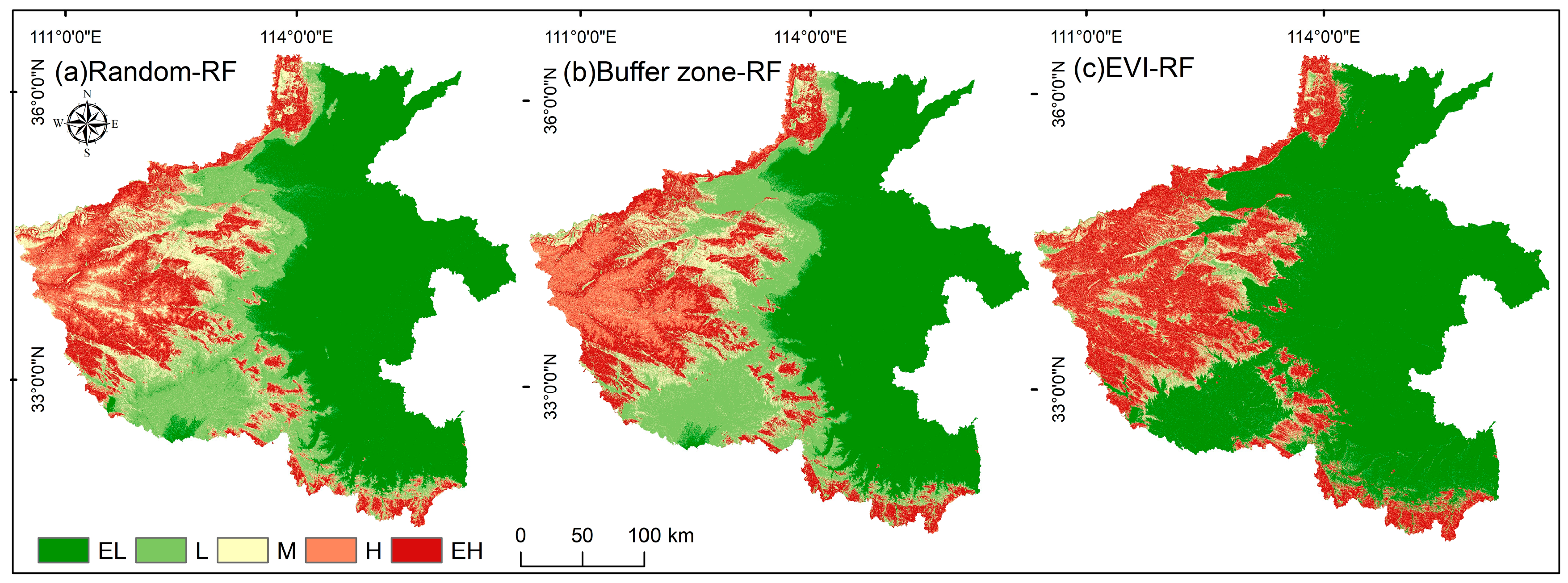
4.4.3. Difference in Landslide Susceptibility Distribution
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaudhary, M.T.; Piracha, A. Natural disasters—Origins, impacts, management. Encyclopedia 2021, 1, 1101–1131. [Google Scholar] [CrossRef]
- Cao, W.; Pan, D.; Xu, Z.; Zhang, W.; Ren, Y.; Nan, T. Landslide Disaster Vulnerability Mapping Study in Henan Province: Comparison of Different Machine Learning Models. Bull. Geol. Sci. Technol. 2025, 44, 101–111. [Google Scholar]
- China Natural Resources News Agency. Excerpts from the China Natural Resources Bulletin 2023. Resour. Hum. Settl. Environ. 2024, 2024, 6–10. [Google Scholar] [CrossRef]
- Nath, S.K.; Sengupta, A.; Srivastava, A. Remote sensing GIS-based landslide susceptibility & risk modeling in Darjeeling–Sikkim Himalaya together with FEM-based slope stability analysis of the terrain. Nat. Hazards 2021, 108, 3271–3304. [Google Scholar]
- Deng, X.; Zeng, M.; Xu, D.; Qi, Y. Why do landslides impact farmland abandonment? Evidence from hilly and mountainous areas of rural China. Nat. Hazards 2022, 113, 699–718. [Google Scholar] [CrossRef]
- Gizzi, F.T.; Antunes, I.M.H.R.; Reis, A.P.M.; Giano, S.I.; Masini, N.; Muceku, Y.; Pescatore, E.; Potenza, M.R.; Corbalán Andreu, C.; Sannazzaro, A.; et al. From Settlement Abandonment to Valorisation and Enjoyment Strategies: Insights through EU (Portuguese, Italian) and Non-EU (Albanian) ‘Ghost Towns’. Heritage 2024, 7, 3867–3901. [Google Scholar] [CrossRef]
- Pradhan, B. Landslide susceptibility mapping of a catchment area using frequency ratio, fuzzy logic and multivariate logistic regression approaches. J. Indian Soc. Remote Sens. 2010, 38, 301–320. [Google Scholar] [CrossRef]
- Huang, F.; Zeng, S.; Yao, C.; Xiong, H.; Fan, X.; Huang, J. Uncertainties of landslide susceptibility prediction modeling: Influence of different selection methods of “non-landslide samples”. Adv. Eng. Sci. 2024, 56, 169–182. [Google Scholar]
- Barik, M.G.; Adam, J.C.; Barber, M.E.; Muhunthan, B. Improved landslide susceptibility prediction for sustainable forest management in an altered climate. Eng. Geol. 2017, 230, 104–117. [Google Scholar] [CrossRef]
- Chao, Z.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from Longju in the Three Gorges Reservoir area, China. Comput. Geosci. 2018, 112, 23–37. [Google Scholar]
- Azarafza, M.; Ghazifard, A.; Akgun, H.; Asghari-Kaljahi, E. Landslide susceptibility assessment of South Pars Special Zone, southwest Iran. Environ. Earth Sci. 2018, 77, 805. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M. Landslide susceptibility mapping using GIS-based statistical models and Remote sensing data in tropical environment. Sci. Rep. 2015, 5, 9899. [Google Scholar] [CrossRef] [PubMed]
- Du, G.L.; Zhang, Y.S.; Iqbal, J.; Yang, Z.H.; Yao, X. Landslide susceptibility mapping using an integrated model of information value method and logistic regression in the Bailongjiang watershed, Gansu Province, China. J. Mt. Sci. 2017, 14, 249–268. [Google Scholar]
- Zhang, P.; Deng, H.; Zhang, W.; Xve, D.; Wu, X.; Zhuo, W. Landslide susceptibility evaluation based on Information Value model and Machine Learning method: A case study of Lixian County, Sichuan Province. Sci. Geogr. Sin. 2022, 42, 1665–1675. [Google Scholar] [CrossRef]
- Nsengiyumva, J.B.; Luo, G.; Amanambu, A.C.; Mind, R.; Habiyaremye, G.; Karamage, F.; Ochege, F.U.; Mupenzi, C. Comparing probabilistic and statistical methods in landslide susceptibility modeling in Rwanda/Centre-Eastern Africa. Sci. Total Environ. 2019, 659, 1457–1472. [Google Scholar] [CrossRef]
- Eker, A.M.; Dikmen, M.; Cambazoğlu, S.; Düzgün, Ş.H.B.; Akgün, H. Evaluation and comparison of landslide susceptibility mapping methods: A case study for the Ulus district, Bartın, northern Turkey. Int. J. Geogr. Inf. Sci. 2015, 29, 132–158. [Google Scholar] [CrossRef]
- Bueechi, E.; Klime, J.; Frey, H.; Huggel, C.; Strozzi, T.; Cochachin, A. Regional-scale landslide susceptibility modelling in the Cordillera Blanca, Peru—A comparison of different approaches. Landslides 2019, 16, 395–407. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide Susceptibility Assessment in Vietnam Using Support Vector Machines, Decision Tree, and Naive Bayes Models. Math. Probl. Eng. 2012, 2012, 1–26. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar]
- Guo, R. Henan. In Regional China: A Business and Economic Handbook; Palgrave Macmillan: London, UK, 2013; pp. 130–141. [Google Scholar]
- Wang, N.; Cheng, W.; Wang, B.; Liu, Q.; Zhou, C. Geomorphological regionalization theory system and division methodology of China. J. Geogr. Sci. 2020, 30, 212–232. [Google Scholar] [CrossRef]
- Wang, J.A.; Liang, S.; Shi, P. Topography and landforms. In The Geography of Contemporary China; Springer International Publishing: Cham, Switzerland, 2022; pp. 63–84. [Google Scholar]
- Wu, W.; Wang, C.; Guan, H.; Huang, M.; Qiao, W. Geological hazard vulnerability assessment in southern part of Tangkou fault based on GIS and weighted information value model. Sci. Technol. Eng. 2024, 24, 11121–11130. [Google Scholar]
- Li, J.; Liu, Y.; Cao, M.; Xue, B. Space-time characteristics of vegetation cover and distribution: Case of the Henan Province in China. Sustainability 2015, 7, 11967–11979. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Zhang, X.; Zhang, H.; Yang, L.; Lv, X.; Xi, X. A Harmony-Based Approach for the Evaluation and Regulation of Water Security in the Yellow River Water-Receiving Area of Henan Province. Water 2024, 16, 2497. [Google Scholar] [CrossRef]
- Zhang, F.; Peng, J.; Huang, X.; Lan, H. Hazard assessment and mitigation of non-seismically fatal landslides in China. Nat. Hazards 2021, 106, 785–804. [Google Scholar]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Zhou, J.W.; Cui, P.; Hao, M.H. Comprehensive analyses of the initiation and entrainment processes of the 2000 Yigong catastrophic landslide in Tibet, China. Landslides 2016, 13, 39–54. [Google Scholar] [CrossRef]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y.; et al. Landslide spatial modelling using novel bivariate statistical based Naïve Bayes, RBF Classifier, and RBF Network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar]
- Shahri, F.L.S.; Spross, J.; Johansson, F.; Larsson, S. Landslide susceptibility hazard map in southwest Sweden using artificial neural network. CATENA 2019, 183, 104225. [Google Scholar]
- Dao, D.V.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.; Moayedi, H.; Van Phong, T.; Ly, H.-B.; Le, T.-T.; Trinh, P.T.; et al. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility. CATENA 2020, 188, 104451. [Google Scholar] [CrossRef]
- Gizzi, F.T.; Bentivenga, M.; Lasaponara, R.; Danese, M.; Potenza, M.R.; Sileo, M. Natural Hazards, Human Factors, and “Ghost Towns”: A Multi-Level Approach. Geoheritage 2019, 11, 1533–1565. [Google Scholar] [CrossRef]
- Fiorucci, F.; Ardizzone, F.; Mondini, A.C.; Viero, A.; Guzzetti, F. Visual interpretation of stereoscopic NDVI satellite images to map rainfall-induced landslides. Landslides 2019, 16, 165–174. [Google Scholar] [CrossRef]
- Hürlimann, M.; Guo, Z.; Puig-Polo, C.; Medina, V. Impacts of future climate and land cover changes on landslide susceptibility: Regional scale modelling in the Val d’Aran region (Pyrenees, Spain). Landslides 2022, 19, 99–118. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.-T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar]
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide risk assessment and management: An overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B.; et al. Modeling flood susceptibility using data-driven approaches of naïve bayes tree, alternating decision tree, and random forest methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar]
- Xu, K.; Zhao, Z.; Chen, W.; Ma, J.; Liu, F.; Zhang, Y.; Ren, Z. Comparative study on landslide susceptibility mapping based on different ratios of training samples and testing samples by using RF and FR-RF models. Nat. Hazards Res. 2024, 4, 62–74. [Google Scholar]
- Awad, M.; Fraihat, S. Recursive feature elimination with cross-validation with decision tree: Feature selection method for machine learning-based intrusion detection systems. J. Sens. Actuator Netw. 2023, 12, 67. [Google Scholar] [CrossRef]
- Imtiaz, I.; Umar, M.; Latif, M.; Ahmed, R.; Azam, M. Landslide susceptibility mapping: Improvements in variable weights estimation through machine learning algorithms—A case study of upper Indus REIVer Basin, Pakistan. Environ. Earth Sci. 2022, 81, 112. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Miao, Y.; Zhu, A.; Yang, L.; Bai, S.; Liu, J.; Deng, Y. Sensitivity of BCS for Sampling Landslide Absence Data in Landslide Susceptibility Assessment. Mt. Res. 2016, 34, 432–441. [Google Scholar] [CrossRef]
- Turner, A.K. Social and environmental impacts of landslides. Innov. Infrastruct. Solut. 2018, 3, 70. [Google Scholar] [CrossRef]
- Kainthura, P.; Sharma, N. Machine learning drEIVen landslide susceptibility prediction for the Uttarkashi region of Uttarakhand in India. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2021, 16, 570–583. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar]
- Zhang, S.; Tan, S.; Liu, L.; Ding, D.; Sun, Y.; Li, J. Slope Rock and Soil Mass Movement Geological Hazards Susceptibility Evaluation Using Information Quantity, Deterministic Coefficient, and Logistic Regression Models and Their Comparison at Xuanwei, China. Sustainability 2023, 15, 10466. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Predictive Performances of Ensemble Machine Learning Algorithms in Landslide Susceptibility Mapping Using Random Forest, Extreme Gradient Boosting (XGBoost) and Natural Gradient Boosting (NGBoost). Arab. J. Sci. Eng. 2022, 47, 7367–7385. [Google Scholar]
- Zali, M.; Shahedi, K. Landslide sensitivity assessment using fuzzy logic approach and GIS in Neka Watershed. Water Soil Manag. Model. 2021, 1, 67–80. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Ma, L.; Yu, B. Pronunciation quality evaluation based on the phoneme confusion matrix. Qinghua Daxue Xuebao/J. Tsinghua Univ. 2012, 52, 5–10. [Google Scholar]
- Turpeinen, O.M.; Garand, L.; Benoit, R.; Roch, M. Diabatic initialization of the Canadian Regional Finite-Element (RFE) Model Using Satellite Data. Part I: Methodology and Application to a Winter Storm. Mon. Weather. Rev. 1990, 118, 1381–1395. [Google Scholar] [CrossRef]
- Williamson, L.D.; Brookes, K.L.; Scott, B.E.; Graham, I.M.; Bradbury, G.; Hammond, P.S.; Thompson, P.M. Echolocation detections and digital video surveys provide reliable estimates of the relative density of harbour porpoises. Methods Ecol. Evol. 2016, 7, 762–769. [Google Scholar] [CrossRef]
- Gu, T.; Duan, P.; Wang, M.; Li, J.; Zhang, Y. Effects of non-landslide sampling strategies on machine learning models in landslide susceptibility mapping. Sci. Rep. 2024, 14, 7201. [Google Scholar]



| Landslide Impact Factors | Data Description | Data Source | Data Type |
|---|---|---|---|
| Landslide_site | Distribution data of geological disaster points in Henan Province | Geographic Remote Sensing Ecology Network (http://www.gisrs.cn, accessed on 3 January 2024) | Polygon |
| Elevation (m) | Henan Province 30 m precision DEM digital elevation data | Geospatial Data Cloud (http://www.gscloud.cn, accessed on 3 January 2024) | Grid |
| Slope (°) | Grid | ||
| Slope aspect (°) | Grid | ||
| Plane curvature (1/m) | Grid | ||
| Profile curvature (1/m) | Grid | ||
| Soil dataset (%) | Henan Province soil dataset | Global Soil Database (HWSD) | Grid |
| Rainfall (mm) | Henan Province 30 m precision rainfall, humidity, population density data. | Resource and Environmental Science Data Platform (http://www.resdc.cn, accessed on 3 January 2024) | Grid |
| Humidity (%) | Grid | ||
| Population density (people/km2) | Grid | ||
| NDVI | Normalized Difference Vegetation Index | MOD13A3 dataset (https://ladsweb.modaps.eosdis.nasa.gov, accessed on 3 January 2024) | Grid |
| Model | Accuracy | Precision | Kappa | Recall |
|---|---|---|---|---|
| Random-RF | 67.02% | 71.43% | 0.3227 | 0.4839 |
| Buffer zone-RF | 73.31% | 80.84% | 0.4524 | 0.5581 |
| EIV-RF | 85.31% | 91.09% | 0.7014 | 0.7581 |
| Model | Susceptibility Level | Random-RF | Buffer Zone-RF | EIV-RF |
|---|---|---|---|---|
| Total number of grid cells | Extremely Low | 9,313,872 | 9,084,133 | 12,498,894 |
| Low | 4,185,097 | 4,583,694 | 938,480 | |
| Medium | 2,367,277 | 1,921,630 | 1,294,850 | |
| High | 2,133,736 | 1,927,953 | 2,039,278 | |
| Extremely High | 2,472,152 | 2,954,724 | 3,700,615 | |
| Percentage of total grid cells (%) | Extremely Low | 45.50% | 44.37% | 61.05% |
| Low | 20.44% | 22.39% | 4.58% | |
| Medium | 11.56% | 9.39% | 6.32% | |
| High | 10.42% | 9.42% | 9.96% | |
| Extremely High | 12.08% | 14.43% | 18.08% | |
| Landslide count in the study area | Extremely Low | 1.67% | 0.98% | 2.06% |
| Low | 8.91% | 7.93% | 3.43% | |
| Medium | 17.24% | 16.26% | 7.15% | |
| High | 36.04% | 31.15% | 30.66% | |
| Extremely High | 36.14% | 43.68% | 56.71% | |
| Proportion of landslides (%) | Extremely Low | 1.67% | 0.98% | 2.06% |
| Low | 8.91% | 7.93% | 3.43% | |
| Medium | 17.24% | 16.26% | 7.15% | |
| High | 36.04% | 31.15% | 30.66% | |
| Extremely High | 36.14% | 43.68% | 56.71% | |
| Relative density D value | Extremely Low | 0.04 | 0.02 | 0.03 |
| Low | 0.44 | 0.35 | 0.75 | |
| Medium | 1.49 | 1.73 | 1.13 | |
| High | 3.46 | 3.31 | 3.08 | |
| Extremely High | 2.99 | 3.03 | 3.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Fan, Z.; Li, X.; Wang, P.; Sun, X.; Ren, Y.; Cao, W. The Influence of Non-Landslide Sample Selection Methods on Landslide Susceptibility Prediction. Land 2025, 14, 722. https://doi.org/10.3390/land14040722
Fu Y, Fan Z, Li X, Wang P, Sun X, Ren Y, Cao W. The Influence of Non-Landslide Sample Selection Methods on Landslide Susceptibility Prediction. Land. 2025; 14(4):722. https://doi.org/10.3390/land14040722
Chicago/Turabian StyleFu, Yu, Zhihao Fan, Xiangzhi Li, Pengyu Wang, Xiaoyue Sun, Yu Ren, and Wengeng Cao. 2025. "The Influence of Non-Landslide Sample Selection Methods on Landslide Susceptibility Prediction" Land 14, no. 4: 722. https://doi.org/10.3390/land14040722
APA StyleFu, Y., Fan, Z., Li, X., Wang, P., Sun, X., Ren, Y., & Cao, W. (2025). The Influence of Non-Landslide Sample Selection Methods on Landslide Susceptibility Prediction. Land, 14(4), 722. https://doi.org/10.3390/land14040722




