Estimation of Land Surface Evapotranspiration and Identification of Key Influencing Factors in the Zoige Forest–Grass Transition Zone
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Data Source
2.3. Research Methods
2.3.1. Model Accuracy Evaluation System
- The Bias formula is as follows:
- The R2 formula is as follows:
- The KGE formula is as follows:
2.3.2. MOD16-STM ET Algorithm
2.3.3. Assessing Model Drivers and LUCC Contributions
2.3.4. Geographical Detectors Analysis of External Environmental Factors
3. Results
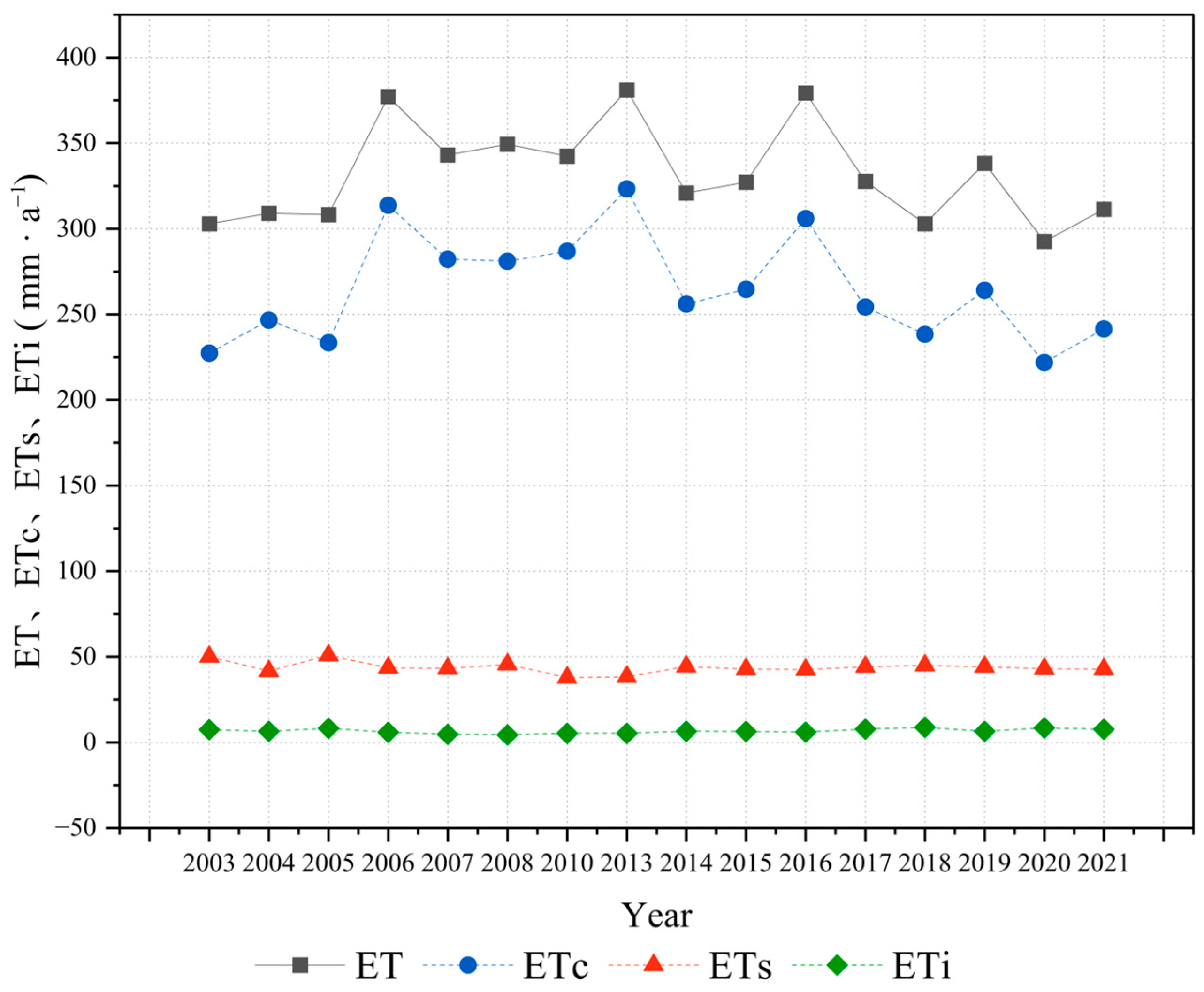
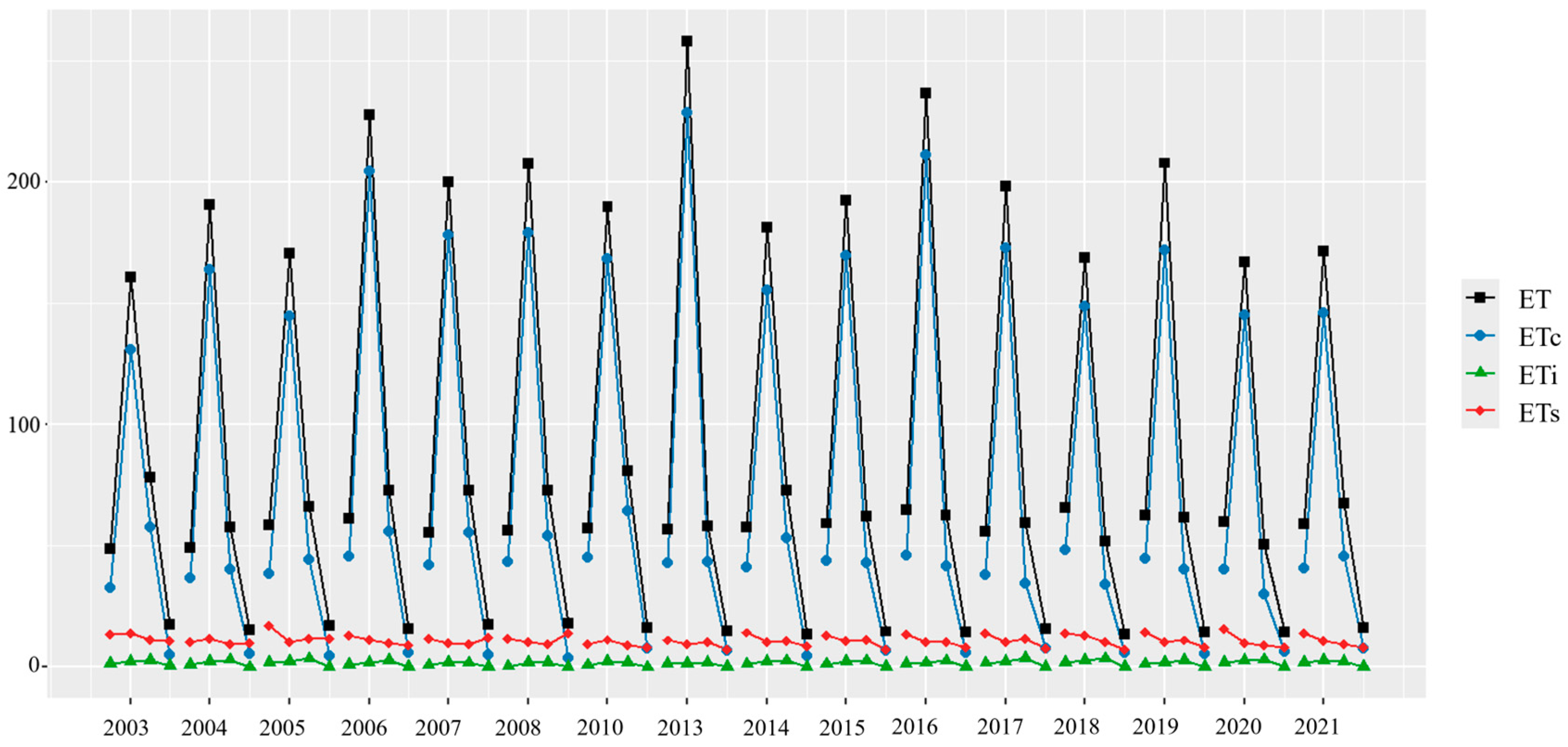
3.1. Assessment of ET Accuracy and Its Pattern of Temporal and Spatial Change
3.2. Effects of Environmental Factors on ET
3.2.1. Impact of Model Drivers on ET Trends
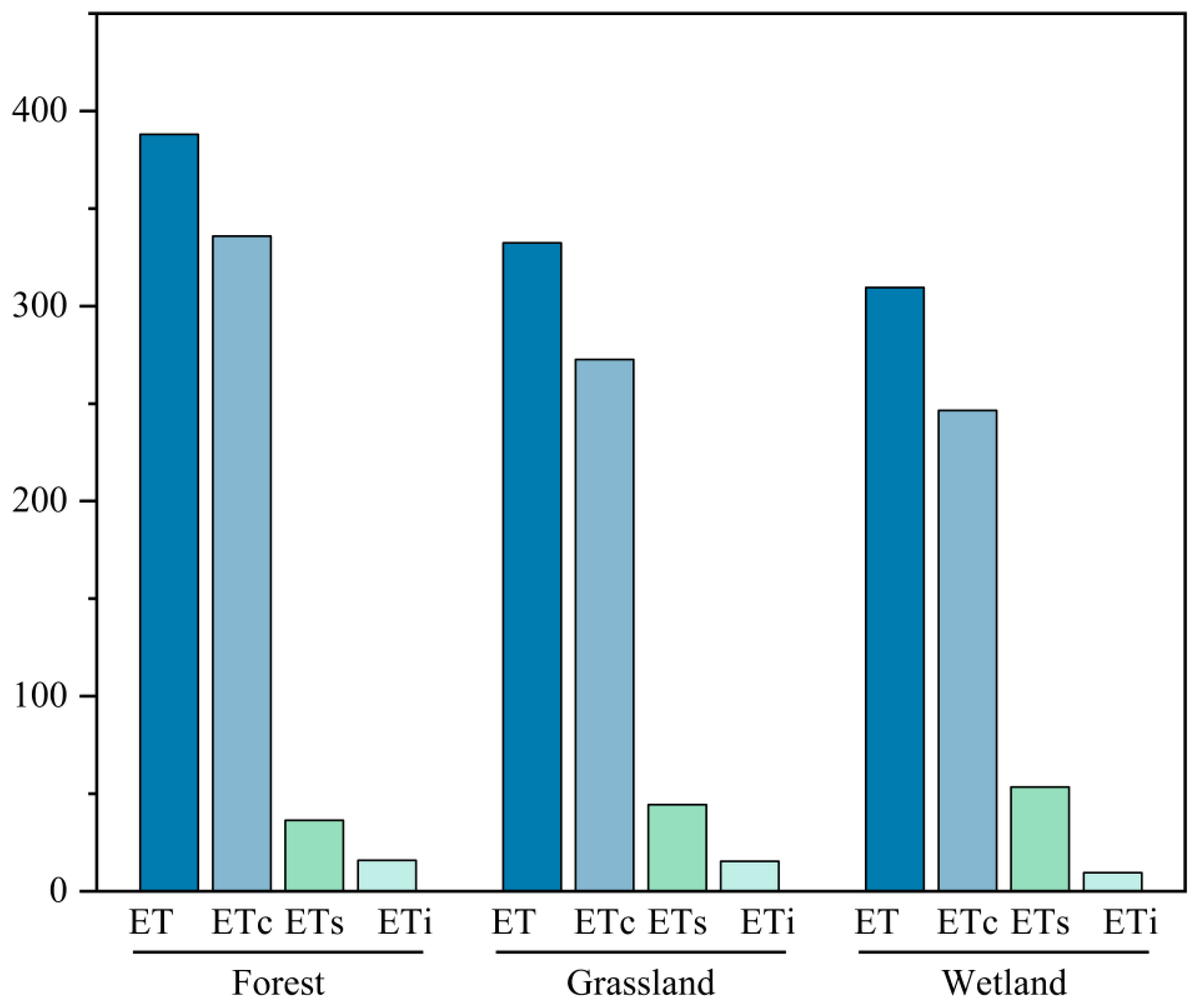
3.2.2. LUCC Impacts on ET
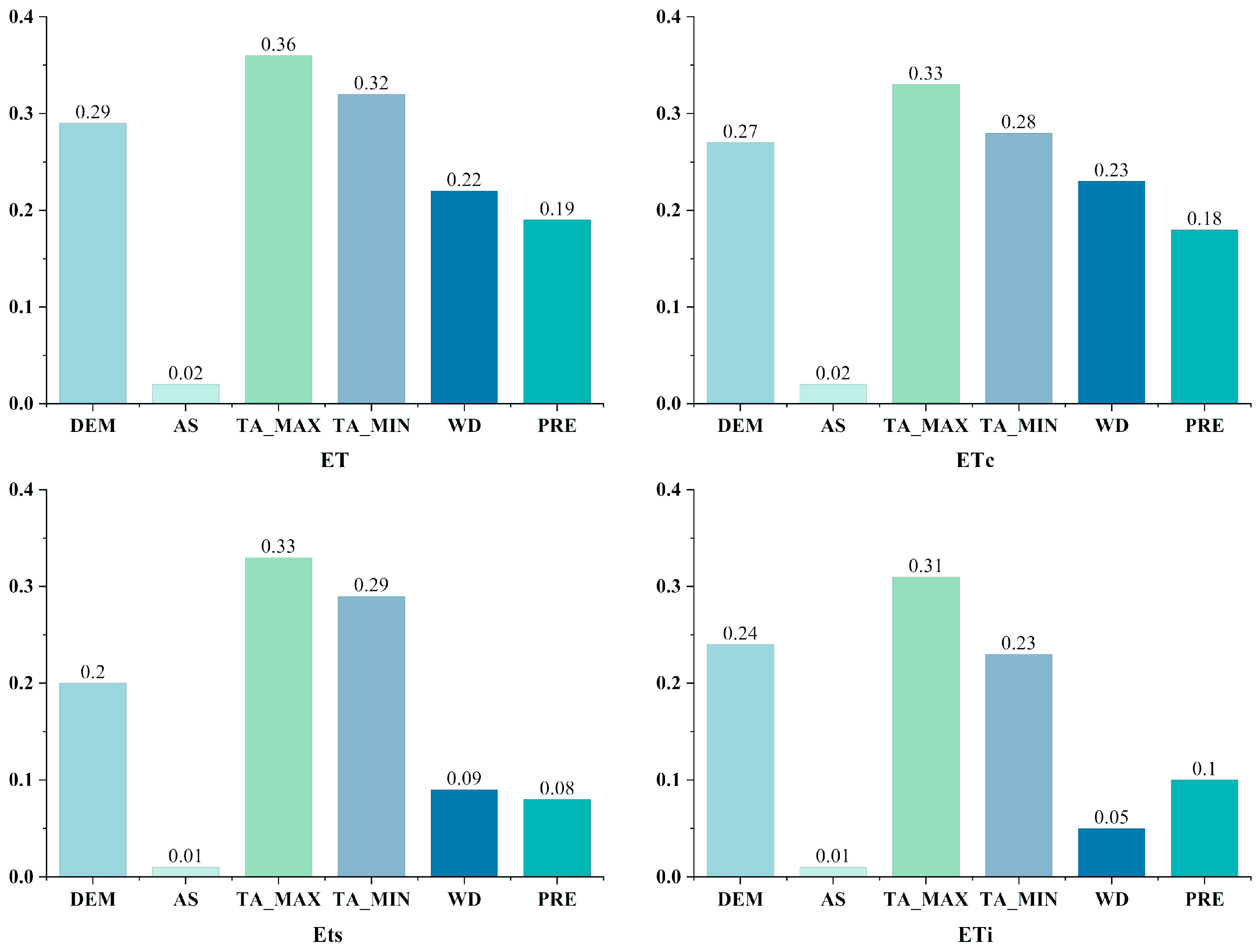
3.2.3. Impact of External Environmental Factors on ET
4. Discussion
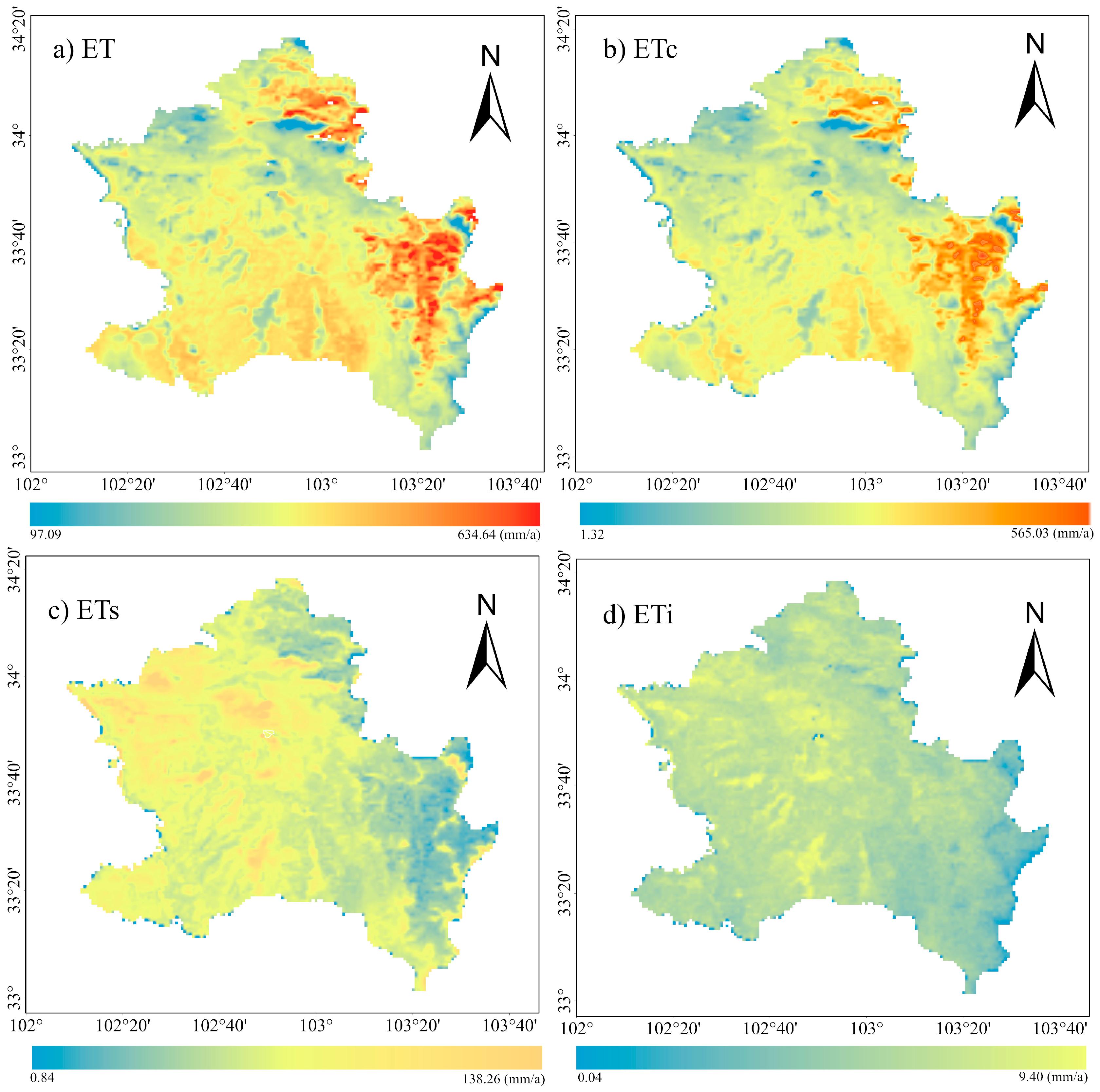
4.1. Interpretation of the ET Distribution
4.2. Interpretation of the ET Impact Factor
4.3. Sources of Uncertainty and Future Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Tong, R.; Yang, X.; Ren, L.; Liu, Y.; Ma, M. Temporal and spatial characteristics of evapotranspiration in the Yellow River Basin during 1961–2012 and analysis of its influence factors. Water Resour. Prot. 2015, 31, 16–21. [Google Scholar]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef]
- Bai, P.; Cai, C. Attribution analysis of changes in terrestrial evapotranspiration in China during 1982–2019. Acta Geogr. Sin. 2023, 78, 2750–2762. [Google Scholar]
- Lu, Q.; He, H.; Zhu, X.; Yu, G.; Wang, H.; Zhang, J.; Yan, J. Study on the Variations of Forest Evapotranspiration and Its Components in Eastern China. J. Nat. Resour. 2015, 30, 1436–1448. [Google Scholar]
- Gong, L.B.; Xu, C.Y.; Chen, D.L.; Halldin, S.; Chen, Y.Q.D. Sensitivity of the Penman-Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, C.; Liu, X.; Zheng, H. Sensitivity of the Potential Evapotranspiration to Key Climatic Variables in the Haihe River Basin. Resour. Sci. 2009, 31, 1470–1476. [Google Scholar]
- Zhang, Y.Q.; Pena-Arancibia, J.L.; McVicar, T.R.; Chiew, F.H.S.; Vaze, J.; Liu, C.M.; Lu, X.J.; Zheng, H.X.; Wang, Y.P.; Liu, Y.Y.; et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef]
- Jovanovic, N.; Mu, Q.Z.; Bugan, R.D.H.; Zhao, M.S. Dynamics of MODIS evapotranspiration in South Africa. Water SA 2015, 41, 79–90. [Google Scholar] [CrossRef]
- Sun, G.; Alstad, K.; Chen, J.Q.; Chen, S.P.; Ford, C.R.; Lin, G.H.; Liu, C.F.; Lu, N.; McNulty, S.G.; Miao, H.X.; et al. A general predictive model for estimating monthly ecosystem evapotranspiration. Ecohydrology 2011, 4, 245–255. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, R.; Zhang, Y. Temporal and Spatial Variation Characteristics and Impact Analysis of Evapotranspiration and Its Components in Poyang Lake Basin Based on SWH Dual-Source Model. China Rural Water Hydropower 2023, 11, 52–63. [Google Scholar]
- Bai, P. Comparison of remote sensing evapotranspiration models: Consistency, merits, and pitfalls. J. Hydrol. 2023, 617, 128856. [Google Scholar] [CrossRef]
- Feng, J.; Jing, Y.; Ran, C.; Sachini Kaushalya Dissanayake, S.D. Estimating High Spatial and Temporal Resolution MODIS Remote Sensing Evapotranspiration Data in Southern Red Soil Region Based on ESTARFM Model. Chin. J. Agrometeorol. 2024, 45, 953–967. [Google Scholar]
- Meng, Y.; Jiang, P.; Dong, W. Progress in the Evapotranspiration Estimation Using Remotely Sensed Data. Remote Sens. Technol. Appl. 2022, 37, 839–853. [Google Scholar]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev.-Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Ji, P.; Yuan, X. Modeling the evapotranspiration and its long-term trend over Northwest China using different machine learning models. Trans. Atmos. Sci. 2023, 46, 69–81. [Google Scholar]
- Jiang, F.X.; Xie, X.H.; Liang, S.L.; Wang, Y.B.; Zhu, B.W.; Zhang, X.T.; Chen, Y.C. Loess Plateau evapotranspiration intensified by land surface radiative forcing associated with ecological restoration. Agric. For. Meteorol. 2021, 311, 108669. [Google Scholar] [CrossRef]
- Tang, J.; Hu, B.; Yu, B.; Zou, Y.; Su, H. Spatio-temporal Variation of Guangxi Drought Based on the SPEI_PM and Its Correlation with ENSO. Chin. J. Agrometeorol. 2024, 45, 1067–1078. [Google Scholar]
- Mu, Q.Z.; Zhao, M.S.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Feng, F.; Li, X.L.; Yao, Y.J.; Liang, S.L.; Chen, J.Q.; Zhao, X.; Jia, K.; Pintér, K.; McCaughey, J.H. An Empirical Orthogonal Function-Based Algorithm for Estimating Terrestrial Latent Heat Flux from Eddy Covariance, Meteorological and Satellite Observations. PLoS ONE 2016, 11, e0160150. [Google Scholar] [CrossRef] [PubMed]
- Yuan, L.; Ma, Y.; Chen, X.; Wang, Y.; Li, Z. An Enhanced MOD16 Evapotranspiration Model for the Tibetan Plateau During the Unfrozen Season. J. Geophys. Res.-Atmos. 2021, 126, e2020JD032787. [Google Scholar] [CrossRef]
- Chen, X.L.; Yuan, L.; Ma, Y.M.; Chen, D.L.; Su, Z.B.; Cao, D.B. A doubled increasing trend of evapotranspiration on the Tibetan Plateau. Sci. Bull. 2024, 69, 1980–1990. [Google Scholar] [CrossRef]
- Bai, J.; Ouyang, H.; Cui, B.; Wang, Q.; Chen, H. Changes in landscape pattern of alpine wetlands on the Zoige Plateau in the past four decades. Acta Ecol. Sin. 2008, 28, 2245–2252. [Google Scholar]
- Tian, Y.; Xiong, M.; Song, G. Restoration succession of wetland soils and their changes of water and nutrient in Ruoergai Plateau. Chin. J. Ecol. 2005, 24, 21–25. [Google Scholar]
- Wu, R.N.; Ma, S.; Lan, L.; Tian, J.P.; Ding, W.; Zhou, Z.J.; Wang, M.D.; Bi, L.C.; Wang, L. Effects of Grazing on Soil Nitrogen Content in the Forest-steppe Ecotoneon the Southern Edge of the Greater Khingan Mountains. Terr. Ecosyst. Conserv. 2023, 3, 48–55. [Google Scholar]
- Shi, S.; Li, W.; Qu, C.; Yang, Z.-Y. Spatiotemporal Evolution and Quantitative Attribution Analysis of Vegetation NDVI in Greater Khingan Mountains Forest-Steppe Ecotone. Huan Jing Ke Xue = Huanjing Kexue 2024, 45, 248–261. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Jochheim, H.; Kersebaum, K.C.; Lischeid, G.; Nendel, C. Gradients of microclimate, carbon and nitrogen in transition zones of fragmented landscapes—A review. Agric. For. Meteorol. 2017, 232, 659–671. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.M.; Zhang, Y.Q.; Liu, C.M. Assessing the Impacts of Vegetation Greenness Change on Evapotranspiration and Water Yield in China. Water Resour. Res. 2020, 56, e2019WR027019. [Google Scholar] [CrossRef]
- Mo, X.; Liu, S.; Hu, S. Co-evolution of climate-vegetation-hydrology and its mechanisms in the source region of Yellow River. Acta Geogr. Sin. 2022, 77, 1730–1744. [Google Scholar]
- Li, X.; Yu, D. Progress on Evapotranspiration Estimation Methods and Driving Forces in Arid and Semiarid Regions. Arid Zone Res. 2020, 37, 26–36. [Google Scholar]
- Deng, X.; Liu, C.; Li, L.; Lu, H.; Li, N. Mechanism and Computational Modelling of the Erosion Process of Zoige Meadow-typeBending River. Adv. Eng. Sci. 2024, 1–15. [Google Scholar]
- Guo, J.; Li, G.P. Climate Change in Zoige Plateau Marsh Wetland and Its Impact on Wetland Degradation. Plateau Meteorol. 2007, 26, 422–428. [Google Scholar]
- Tian, Y. The Vegetation Type and Its Distribution Regularity under Different Habitats in Ruoergai Plateau. J. Yangtze Univ. Nat. Sci. Ed. 2005, 2, 1–5+103. [Google Scholar]
- Xiong, Y.; Wu, P.; Zhang, H.; Cui, L.; He, X. Dynamics of soil water conservation during the degradation process of the Zoige Alpine Wetland. Acta Ecol. Sin. 2011, 31, 5780–5788. [Google Scholar]
- Ma, X.L.; Li, C.E.; Chen, Q.G. Study on the method of GIS based spatial interpolation of climate factors in China. Pratacultural Sci. 2008, 25, 13–19. [Google Scholar]
- Ye, J.; Liu, H.; Li, W.; Cai, S.; Li, Y.; Cao, L. Estimation of the Net Radiation over Arid and Semiarid Areas Only Using MODIS Data for Clear Sky Days. Acta Sci. Nat. Univ. Pekin. 2010, 46, 942–950. [Google Scholar]
- Yang, J.; Huang, X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Jiang, W.; Shu, Z.G.; Lv, Y.H.; Su, X.K.; Wu, X.; Wang, C.; Wang, K.; Sun, S.Q.; Liu, G.H. Quantifying impacts of climate and land use changes on ecosystem services from statistic perspective. Ecol. Indic. 2025, 172, 113285. [Google Scholar] [CrossRef]
- Chen, Y.; Chai, S.; Chen, W.J.; Xia, J.Z. The Effects of Climate Change and Greening of Vegetation on Spatiotemporal Variation of Evapotranspiration in the Haihe River Basin, China. Ecol. Evol. 2025, 15, e71092. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- McCandless, T.; Gagne, D.J.; Kosovic, B.; Haupt, S.E.; Yang, B.; Becker, C.; Schreck, J. Machine Learning for Improving Surface-Layer-Flux Estimates. Bound.-Layer Meteorol. 2022, 185, 199–228. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J. The influence of land surface moisture retention on precipitation statistics. J. Clim. 1996, 9, 2551–2567. [Google Scholar] [CrossRef]
- Li, G.; Zhang, F.M.; Jing, Y.S.; Liu, Y.B.; Sun, G. Response of evapotranspiration to changes in land use and land cover and climate in China during 2001–2013. Sci. Total Environ. 2017, 596, 256–265. [Google Scholar] [CrossRef]
- Zheng, H.X.; Liu, X.M.; Liu, C.M.; Dai, X.Q.; Zhu, R.R. Assessing contributions to panevaporation trends in Haihe River Basin, China. J. Geophys. Res.-Atmos. 2009, 114, D24105. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar]
- Wang, J.F.; Hu, Y. Environmental health risk detection with GeogDetector. Environ. Model. Softw. 2012, 33, 114–115. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, H.; Yang, Y.; You, J.; Feng, Q. Analysis of driving factors and variation characteristics of vegetation NDVI in Zoige region from 1998 to 2020. Nat. Prot. Areas 2024, 4, 74–85. [Google Scholar]
- Zhao, Z.; Luo, Y.; Huang, j. Global warming and El Nino events. Progress. Inquisitiones Mutat. Clim. 2023, 19, 663–666. [Google Scholar]
- Yeh, S.W.; Kug, J.S.; Dewitte, B.; Kwon, M.H.; Kirtman, B.P.; Jin, F.F. El Nino in a changing climate. Nature 2009, 461, U511–U570. [Google Scholar] [CrossRef]
- Peng, H.; Zhao, C.; Liang, J. Daily variation of evapotranspiration rate of alpine grassland and analysis of its environmental factors in upper reach of Heihe River. J. Water Resour. Water 2016, 27, 46–53. [Google Scholar]
- Mei, J.; Sun, M.; Li, L. Variations of evapotranspiration and its components in alpine meadow on the Tibetan Plateau based on SWH model. Arid Land Geogr. 2022, 45, 1740–1751. [Google Scholar]
- Guo, X.; Wang, K.; Li, L.; Zhang, H.; Ma, L.; Yao, Z.; Zhang, W.; Hu, Z.; Zheng, X. Surface Energy Exchanges and Evapotranspiration of an Alpine Meadow on the Zoige Plateau. Chin. J. Agrometeorol. 2021, 42, 642–656. [Google Scholar]
- Li, X.Y.; Zou, L.; Xia, J.; Dou, M.; Li, H.W.; Song, Z.H. Untangling the effects of climate change and land use/cover change on spatiotemporal variation of evapotranspiration over China. J. Hydrol. 2022, 612, 128189. [Google Scholar] [CrossRef]
- Bronstert, A.; Niehoff, D.; Bürger, G. Effects of climate and land-use change on storm runoff generation:: Present knowledge and modelling capabilities. Hydrol. Process. 2002, 16, 509–529. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, D.; Zhang, X.; Tian, J.; Li, C. Impacts of vegetation changes on global evapotranspiration in the period 2003–2017. Acta Geogr. Sin. 2021, 76, 584–594. [Google Scholar]
- Xie, H. The Evapotranspiration and Its Response to Climate Change on the Tibetan Plateau (1970–2010). Doctoral Dissertation, Lanzhou University, Lanzhou, China, 2012. [Google Scholar]
- Lee, B.Y.; Yang, S.K.; Kwon, K.H.; Kim, J.B. The Effect of Evapotranspiration by Altitude and Observation of Lysimeter. J. Environ. Sci. Int. 2012, 21, 749–755. [Google Scholar] [CrossRef]
- Walter, M.T.; Wilks, D.S.; Parlange, J.Y.; Schneider, R.L. Increasing evapotranspiration from the conterminous United States. J. Hydrometeorol. 2004, 5, 405–408. [Google Scholar] [CrossRef]
- Ma, Z.; Fu, C. Basic facts about aridification in northern China, 1951–2004. Chin. Sci. Bull. 2006, 51, 2429–2439. [Google Scholar]
- Liu, K.; Jiang, D. Analysis of Dryness/Wetness over China Using Standardized Precipitation Evapotranspiration Index Based on Two Evapotranspiration Algorithms. Chin. J. Atmos. Sci. 2015, 39, 23–36. [Google Scholar]
- Yang, X.; Wang, G.; Pan, X.; Zhang, Y. Spatio-temporal variability of terrestrial evapotranspiration in Chinafrom 1980 to 2011 based on GLEAM data. Trans. Chin. Soc. Agric. Eng. 2015, 31, 132–141. [Google Scholar]
- Chang, B.; Liu, X.; Wang, S.; Zhang, Y.; Zhang, X.; Sun, Y. Study on grassland evapotranspiration at different slope orientation and its impact factors in Qilian Mountains. J. Cent. South Univ. For. Technol. 2014, 34, 90–95. [Google Scholar]
- Swenson, S.C.; Lawrence, D.M. Assessing a dry surface layer-based soil resistance parameterization for the Community Land Model using GRACE and FLUXNET-MTE data. J. Geophys. Res.-Atmos. 2014, 119, 10299–10312. [Google Scholar] [CrossRef]
- Chang, Y.; Qin, D.; Ding, Y.; Zhao, Q.; Zhang, S. A modified MOD16 algorithm to estimate evapotranspiration over alpine meadow on the Tibetan Plateau, China. J. Hydrol. 2018, 561, 16–30. [Google Scholar] [CrossRef]



| Data Type | Variable | Spatial Resolution | Data Source |
|---|---|---|---|
| Meteorological data | dew point temperature, air temperature, atmospheric pressure | - | https://www.noaa.gov/ (accessed on 25 March 2024) |
| Remote sensing data | Soil moisture Land use | 1 km 30 m | https://data.tpdc.ac.cn/ (accessed on 11 April 2024) http://gis5g.com/home (accessed on 4 November 2024) |
| NDVI, albedo, net shortwave radiation | 1 km | https://ladsweb.modaps.eosdis.nasa.gov/search/ (accessed on 15 April 2024) | |
| DEM maximum temperature, minimum temperature, precipitation, wind speed | 500 m 1 km | https://www.gebco.net/ (accessed on 10 November 2024) https://data.tpdc.ac.cn/ (accessed on 11 November 2024) | |
| Station data | Meteorological elements, measured ET | - | https://data.tpdc.ac.cn/ (accessed on 5 March 2024) |
| 2003 | 2021 | |||
|---|---|---|---|---|
| Forest | Grassland | Wetland | Other Land Types | |
| Forest | −1.8 | −2.6 | −3.6 | |
| Grassland | 0.8 | −1.4 | −3.2 | |
| Wetland | 3.3 | 2.2 | −1.6 | |
| Other land types | 3.7 | 3.5 | 2.3 | |
| Interaction | Sum of q-Values | Result | Impact |
|---|---|---|---|
| DEM ∩ AS = 0.32 | 0.31 | C > A + B | nonlinear enhancement |
| DEM ∩ TA_MAX = 0.56 | 0.65 | C < A + B | two-factor enhancement |
| DEM ∩ TA_MIN = 0.38 | 0.61 | C < A + B | two-factor enhancement |
| DEM ∩ WD = 0.38 | 0.51 | C < A + B | two-factor enhancement |
| DEM ∩ PRE = 0.34 | 0.48 | C < A + B | two-factor enhancement |
| AS ∩ TA_MAX = 0.41 | 0.38 | C > A + B | nonlinear enhancement |
| AS ∩ TA_MIN = 0.35 | 0.34 | C > A + B | nonlinear enhancement |
| AS ∩ WD = 0.25 | 0.24 | C > A + B | nonlinear enhancement |
| AS ∩ PRE = 0.24 | 0.21 | C > A + B | nonlinear enhancement |
| TA_MAX ∩ TA_MIN = 0.51 | 0.68 | C < A + B | two-factor enhancement |
| TA_MAX ∩ WD = 0.55 | 0.58 | C < A + B | two-factor enhancement |
| TA_MAX ∩ PRE = 0.52 | 0.55 | C < A + B | two-factor enhancement |
| TA_MIN ∩ WD = 0.41 | 0.54 | C < A + B | two-factor enhancement |
| TA_MIN ∩ PRE = 0.37 | 0.51 | C < A + B | two-factor enhancement |
| WD ∩ PRE = 0.40 | 0.41 | C < A + B | two-factor enhancement |
| DEM | AS | TA_MAX | TA_MIN | WD | PRE | |
|---|---|---|---|---|---|---|
| DEM | ||||||
| AS | Y | |||||
| TA_MAX | Y | Y | ||||
| TA_MIN | Y | Y | Y | |||
| WD | Y | Y | Y | Y | ||
| PRE | Y | Y | Y | Y | Y |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Shao, H.; Kan, Y.; Liu, S.; Du, C.; Shao, Q.; Duan, L.; Xiao, H. Estimation of Land Surface Evapotranspiration and Identification of Key Influencing Factors in the Zoige Forest–Grass Transition Zone. Land 2025, 14, 805. https://doi.org/10.3390/land14040805
Lu X, Shao H, Kan Y, Liu S, Du C, Shao Q, Duan L, Xiao H. Estimation of Land Surface Evapotranspiration and Identification of Key Influencing Factors in the Zoige Forest–Grass Transition Zone. Land. 2025; 14(4):805. https://doi.org/10.3390/land14040805
Chicago/Turabian StyleLu, Xinzhu, Huaiyong Shao, Yixi Kan, Shibin Liu, Chang Du, Qiufang Shao, Linsen Duan, and Huan Xiao. 2025. "Estimation of Land Surface Evapotranspiration and Identification of Key Influencing Factors in the Zoige Forest–Grass Transition Zone" Land 14, no. 4: 805. https://doi.org/10.3390/land14040805
APA StyleLu, X., Shao, H., Kan, Y., Liu, S., Du, C., Shao, Q., Duan, L., & Xiao, H. (2025). Estimation of Land Surface Evapotranspiration and Identification of Key Influencing Factors in the Zoige Forest–Grass Transition Zone. Land, 14(4), 805. https://doi.org/10.3390/land14040805







