Exploration of Dual-Carbon Target Pathways Based on Machine Learning Stacking Model and Policy Simulation—A Case Study in Northeast China
Abstract
1. Introduction
2. Literature Review
- By integrating the unique geographical position, climatic conditions, and energy structure of Northeast China, this study conducts a comprehensive and in-depth analysis of the region’s carbon emissions characteristics and influencing factors, laying a solid foundation for the development of a region-specific model.
- An innovative machine learning stacking model is developed and applied, integrating multiple driving factors and complex nonlinear relationships into the carbon emissions prediction framework. This model delves deeper into the dynamic interactions among influencing factors, improving the accuracy of carbon emissions trend forecasting. Additionally, interpretable SHAP (Shapley additive explanations) values are employed to evaluate the importance of each feature, offering valuable insights into the contributions of various factors to the carbon emissions prediction model.
- Within the framework of dual-carbon targets, policy scenarios are simulated to quantify low-carbon policy recommendations that are tailored to the specific conditions of Northeast China. This provides a scientific basis for policy-making and identifies key pathways to achieving dual-carbon goals, offering feasible guidance for the region’s low-carbon transition.
3. Data
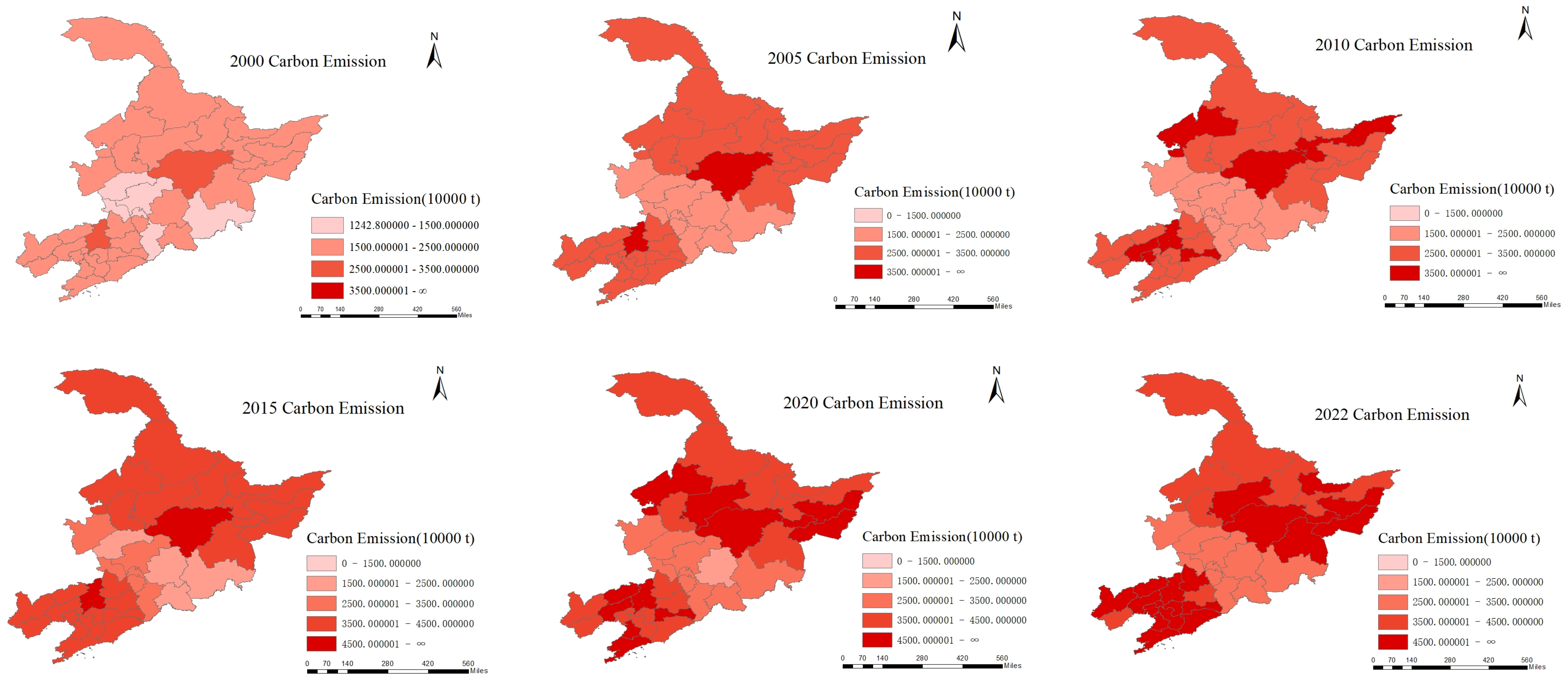
3.1. Data Collection
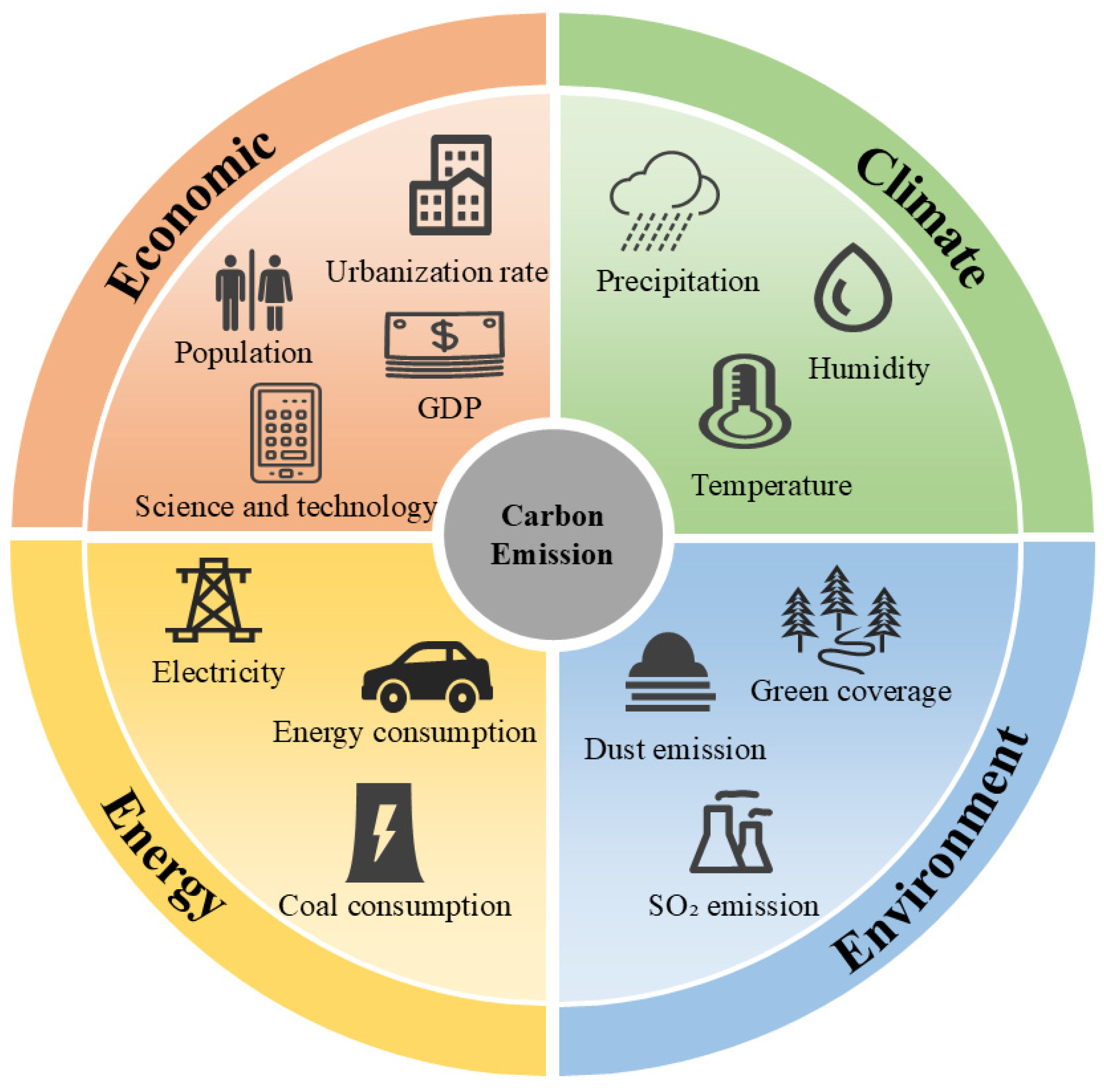
3.2. Variable Description
- GDP [65]: Gross domestic product (GDP) measures the total value of economic activities within a given region. It is commonly used to assess economic development levels and the accumulation of social wealth.
- Proportion of the primary industry [66]: The share of agriculture, forestry, animal husbandry, and fishery in the GDP. A higher proportion often indicates a resource-dependent economy.
- Proportion of the secondary industry [66]: The share of industrial and construction sectors in the GDP. A higher proportion is typically linked to increased energy use and emissions.
- Proportion of the tertiary industry [66]: The share of the service sector in the GDP. An increasing share often signifies a transition to a lower-carbon, higher-value economy.
- Permanent population [67]: The permanent population refers to the total number of residents who have lived in a specific region for an extended period. Population size influences total energy consumption, infrastructure demand, and carbon emissions levels.
- Total energy consumption [68]: This indicator measures the total amount of energy consumed in a region for all economic activities and residential use.
- Coal consumption ratio [68]: This represents the proportion of coal in total energy consumption. Given that coal combustion releases substantial amounts of carbon dioxide (CO2) and pollutants such as sulfur dioxide (SO2) and nitrogen oxides (NOx), a higher coal consumption ratio is generally associated with increased carbon emissions and environmental degradation.
- Total electricity consumption [69]: This refers to the total power consumption of all sectors and residential users within a region, serving as an indicator of economic development and industrial energy demand.
- Urbanization rate [70]: This metric represents the proportion of the population residing in urban areas. Urbanization significantly impacts energy consumption, transportation patterns, infrastructure development, and carbon emissions.
- Proportion of fiscal expenditure on science and technology (R&D spending) [71]: The share of local government spending on scientific research and technological innovation. Higher investment can facilitate low-carbon technologies and improve energy efficiency.
- Dust emissions [72]: This refers to the total particulate matter emitted from industrial activities, primarily from coal-fired power plants, steel manufacturing, and cement production. This indicator directly affects air quality and environmental health.
- Green coverage rate in built-up areas [73]: This measures the proportion of green space within urban built-up areas. A higher green coverage ratio enhances carbon sequestration, mitigates the urban heat island effect, and improves air quality.
- Sulfur dioxide emissions [72]: SO2 is a major pollutant generated by coal combustion, smelting, and chemical production. Excessive SO2 emissions contribute to acid rain and air pollution, posing threats to ecosystems and public health.
- Average humidity [74]: This represents the average level of atmospheric moisture over a given period. Variations in humidity influence air quality, ecosystem stability, and climate adaptation.
- Precipitation [74]: This denotes the total volume of precipitation over a specified period, which directly affects regional water resource availability, ecosystem stability, and agricultural productivity.
- Average temperature [74]: This refers to the mean temperature over a given period, which is significantly influenced by global climate change and can impact regional energy demand, agricultural production, and ecosystem dynamics.
4. Methodology
4.1. Feature Selection
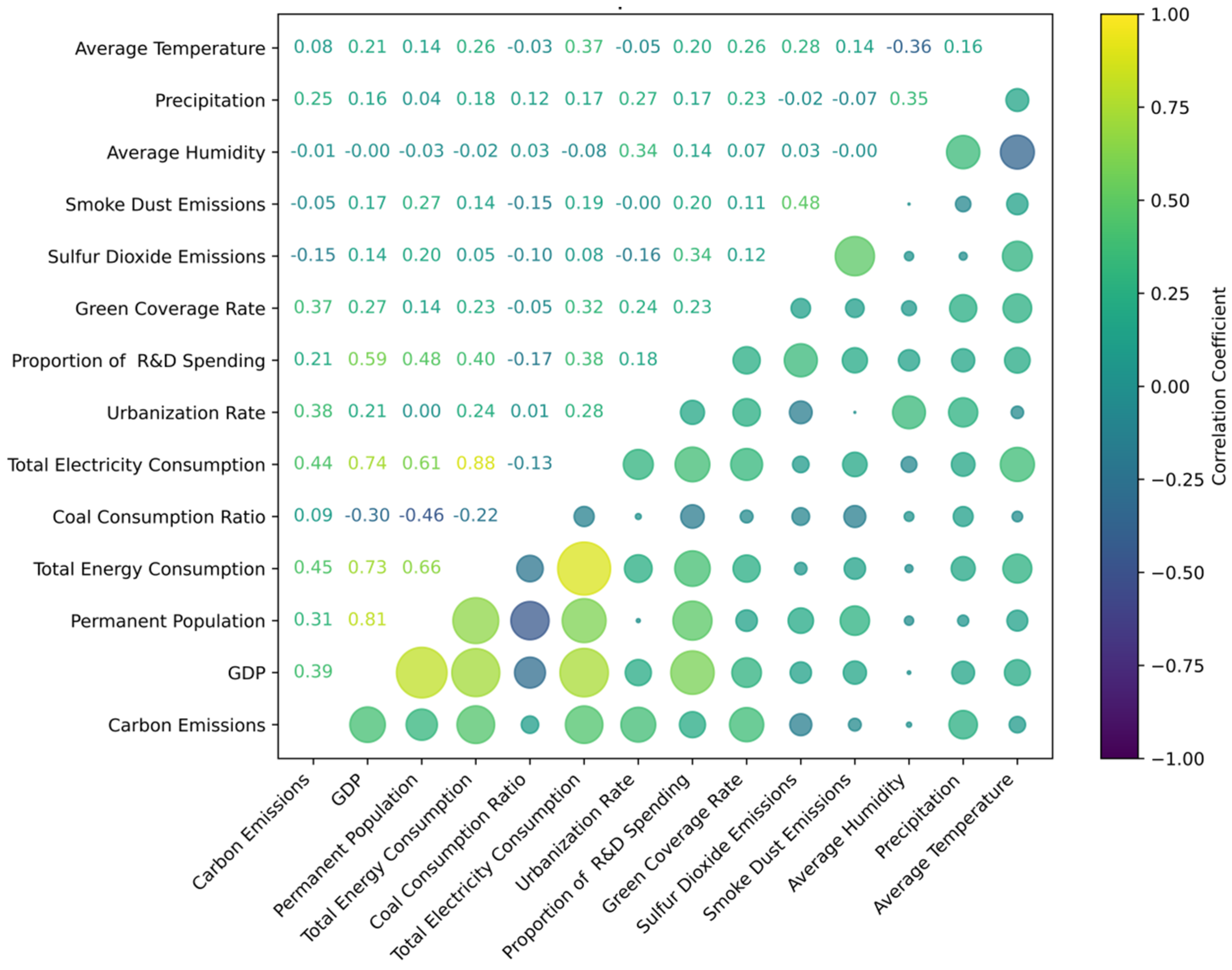
4.1.1. Correlation Analysis
4.1.2. Multicollinearity Testing
4.2. Machine Learning Algorithm
4.2.1. Support Vector Machine (SVM)
4.2.2. K-Nearest Neighbors (KNN)
4.2.3. Random Forest
4.2.4. eXtreme Gradient Boosting (XGBoost)
4.2.5. Ridge Regression
4.2.6. Lasso Regression
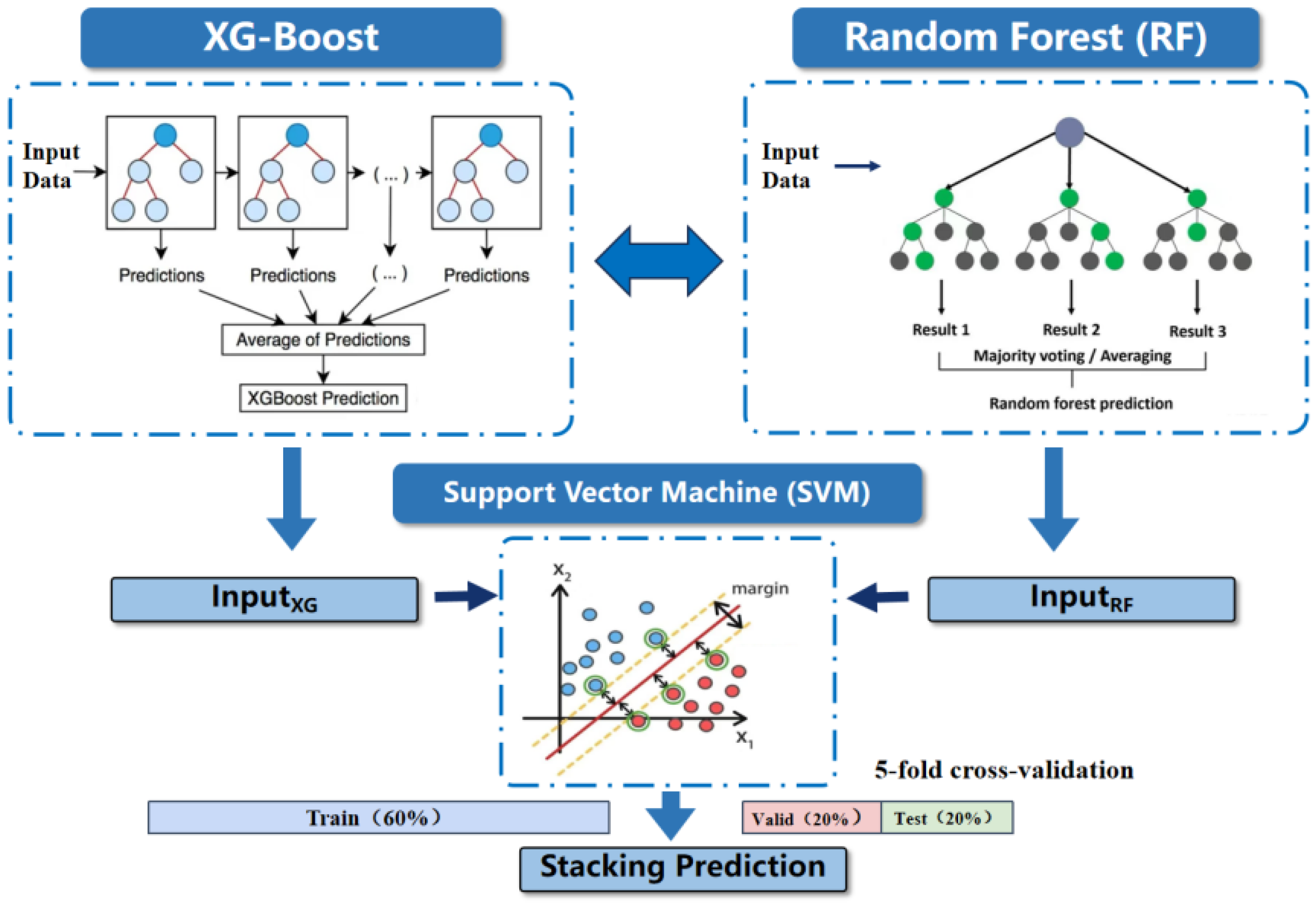
4.2.7. Stacking Regressor
4.3. Model Description and Evaluation
4.3.1. Model Description
4.3.2. Performance Evaluation
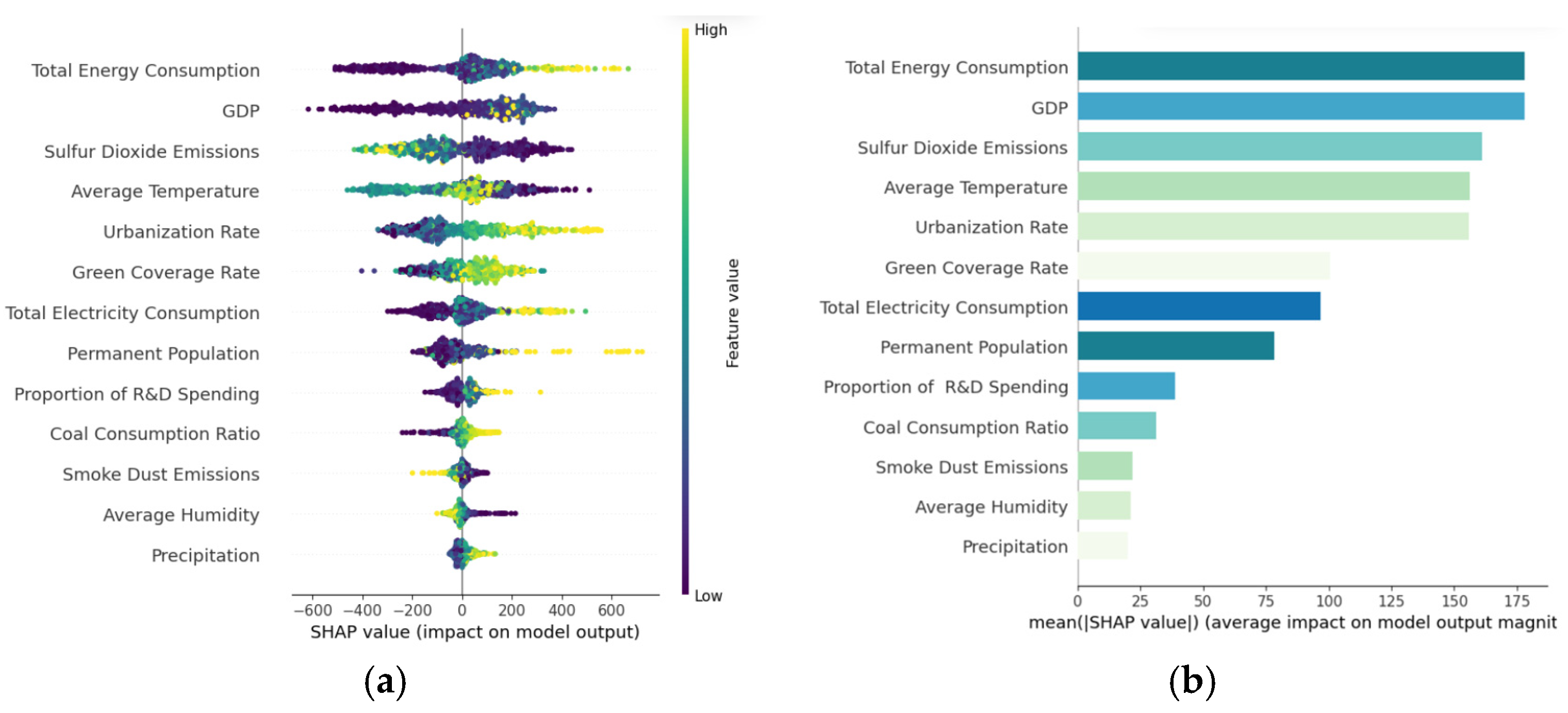
4.4. Feature Importance
4.5. Scenario Simulation
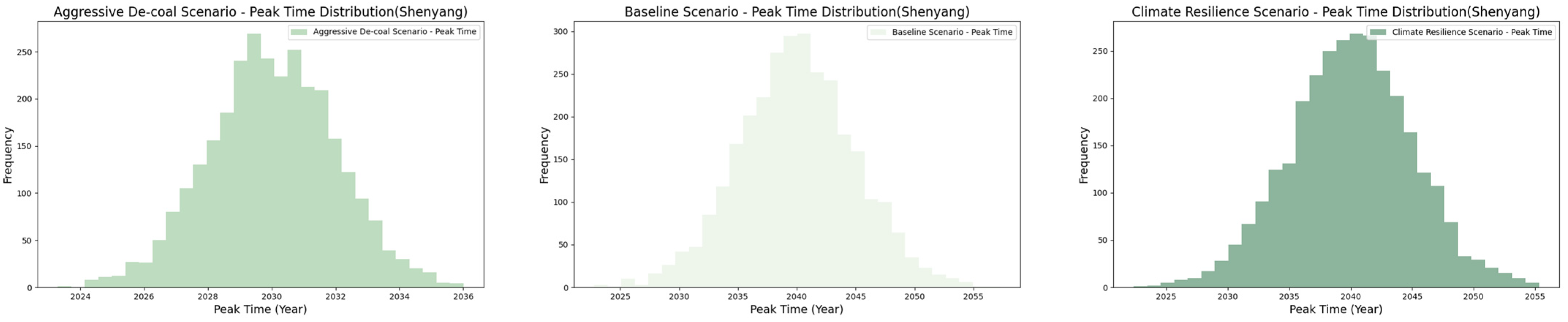
- Baseline Scenario (BS): This scenario represents the future development path under current policies and trends, without significant adjustments to the existing energy consumption structure, economic growth model, or climate change mitigation efforts. It typically represents a “business-as-usual” situation, characterized by a lack of major policy changes. The annual change rates for the variables—energy consumption, urbanization rate, coal consumption ratio, GDP, and average temperature—are set at 2%, 1%, −1%, 2%, and 0.4%, respectively.
- Aggressive De-coal Scenario (ADS): This scenario assumes more aggressive policy measures in the future to reduce coal dependence and lower carbon emissions. It involves significantly reducing coal usage and accelerating the energy structure transition, such as increasing the use of renewable energy and improving energy efficiency. The annual change rates for the variables—energy consumption, urbanization rate, coal consumption ratio, GDP, and average temperature—are set at 1%, 2%, −3%, 3%, and 0.8%, respectively.
- Climate Resilience Scenario (CRS): This scenario focuses on enhancing society’s ability to adapt to and build resilience against climate change, while promoting energy consumption and urbanization. It aims to control greenhouse gas emissions through strategies such as improving energy efficiency, increasing the use of renewable energy, and strengthening climate change adaptation strategies. The annual change rates for the variables—energy consumption, urbanization rate, coal consumption ratio, GDP, and average temperature—are set at 5%, 4%, 0%, 7%, and 0.2%, respectively.
5. Results and Discussion
5.1. Results of Feature Selection
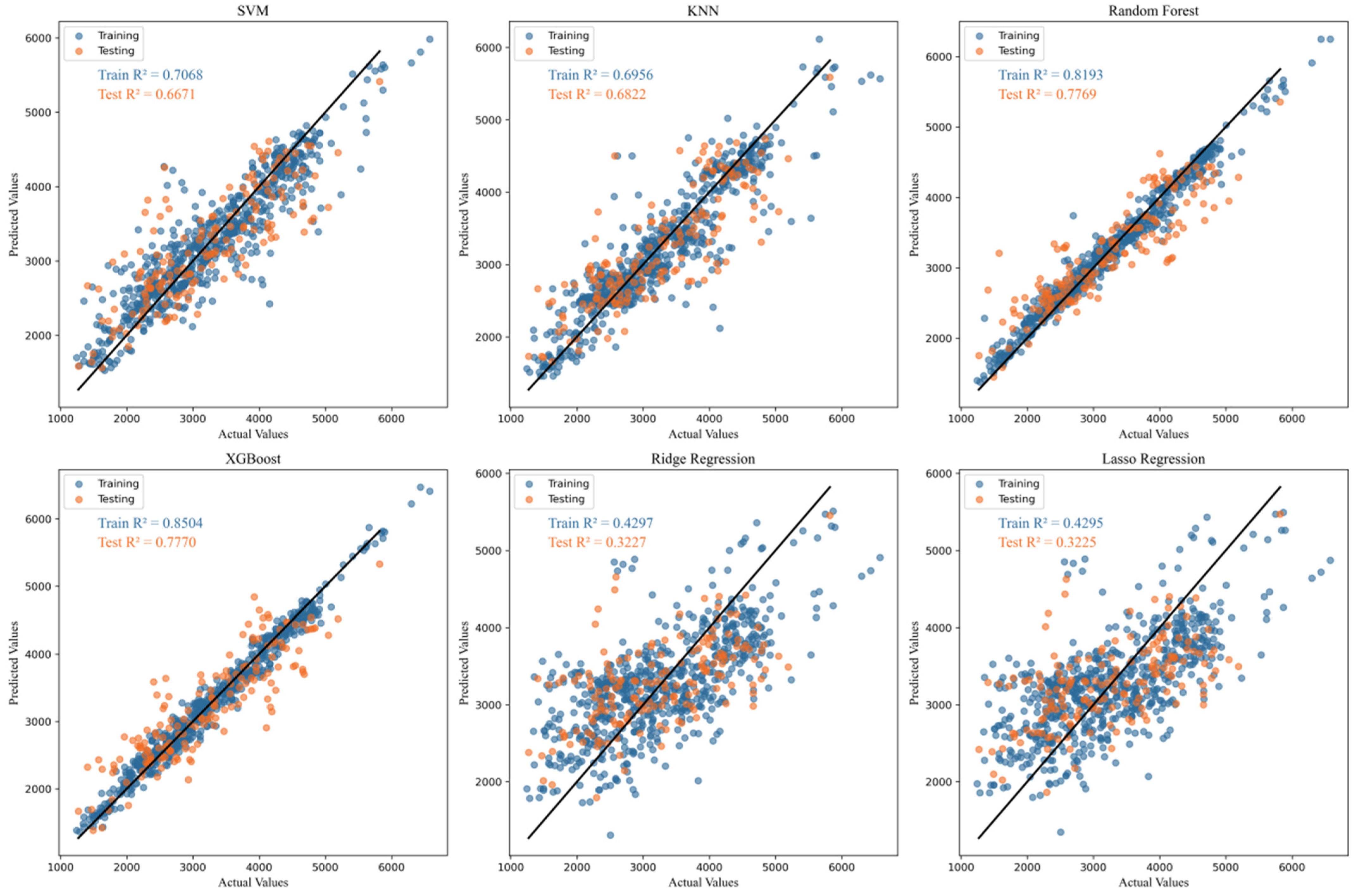
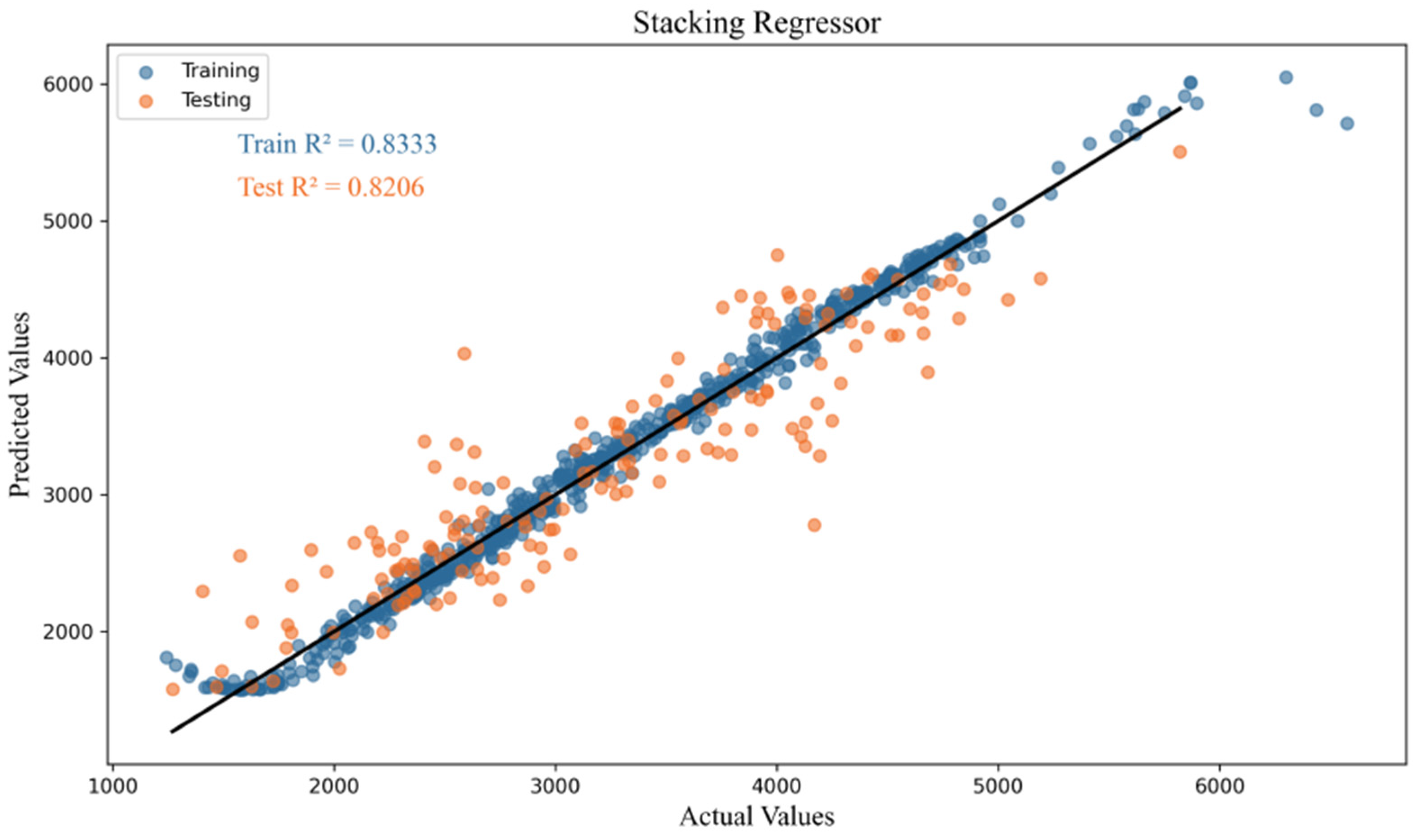
5.2. Regression of Carbon Emissions
5.3. Results of Feature Importance
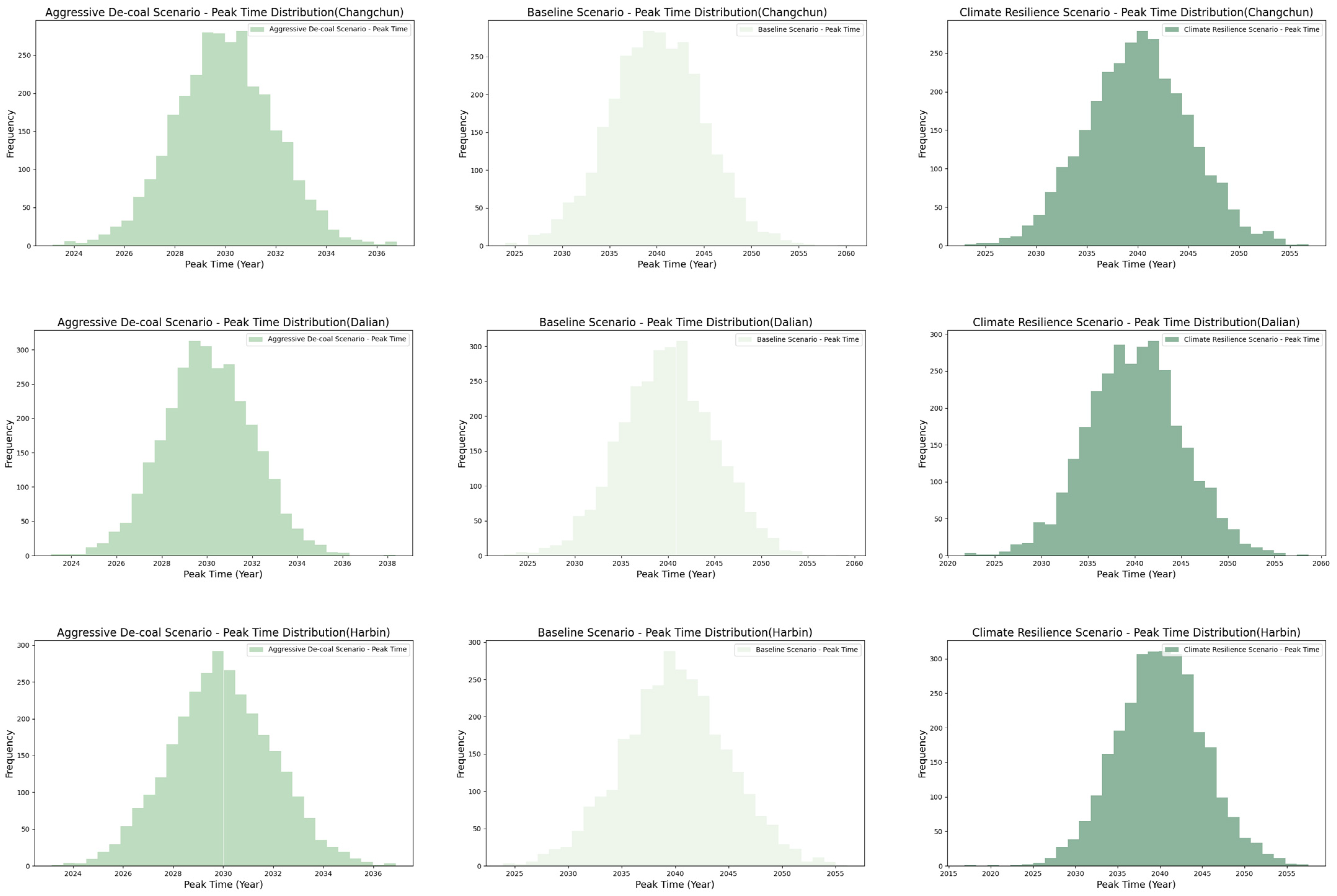
5.4. Results of Scenario Simulations
5.5. Policy Recommendations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, R.; Wang, Q.; Liu, Y.; Jiang, R. Per-capita carbon emissions in 147 countries: The effect of economic, energy, social, and trade structural changes. Sustain. Prod. Consum. 2021, 27, 1149–1164. [Google Scholar] [CrossRef]
- Khan, I.; Hou, F.; Le, H.P. The impact of natural resources, energy consumption, and population growth on environmental quality: Fresh evidence from the United States of America. Sci. Total Environ. 2021, 754, 142222. [Google Scholar] [CrossRef]
- Zhao, X.; Ma, X.; Chen, B.; Shang, Y.; Song, M. Challenges toward carbon neutrality in China: Strategies and countermeasures. Resour. Conserv. Recycl. 2022, 176, 105959. [Google Scholar] [CrossRef]
- Osman, A.I.; Chen, L.; Yang, M.; Msigwa, G.; Farghali, M.; Fawzy, S.; Rooney, D.W.; Yap, P.S. Cost, environmental impact, and resilience of renewable energy under a changing climate: A review. Environ. Chem. Lett. 2023, 21, 741–764. [Google Scholar] [CrossRef]
- Amin, M.; Shah, H.H.; Fareed, A.G.; Khan, W.U.; Chung, E.; Zia, A.; Rahman Farooqi, Z.U.; Lee, C. Hydrogen production through renewable and non-renewable energy processes and their impact on climate change. Int. J. Hydrogen Energy 2022, 47, 33112–33134. [Google Scholar] [CrossRef]
- Dong, F.; Li, Y.; Gao, Y.; Zhu, J.; Qin, C.; Zhang, X. Energy transition and carbon neutrality: Exploring the non-linear impact of renewable energy development on carbon emission efficiency in developed countries. Resour. Conserv. Recycl. 2022, 177, 106002. [Google Scholar] [CrossRef]
- Ou, Y.N.; Iyer, G.; Clarke, L.; Edmonds, J.; Fawcett, A.A.; Hultman, N.; McFarland, J.R.; Binsted, M.; Cui, R.; Fyson, C.; et al. Can updated climate pledges limit warming well below 2 °C?; Increased ambition and implementation are essential. Science 2021, 374, 693–695. [Google Scholar] [CrossRef]
- Zhou, W.; Fan, W.; Lan, R.; Su, W.; Fan, J.L. Retrofitted CCS technologies enhance economy, security, and equity in achieving carbon zero in power sector. Appl. Energy 2025, 378, 124803. [Google Scholar] [CrossRef]
- Chen, L.; Msigwa, G.; Yang, M.; Osman, A.I.; Fawzy, S.; Rooney, D.W.; Yap, P.-S. Strategies to achieve a carbon neutral society: A review. Environ. Chem. Lett. 2022, 20, 2277–2310. [Google Scholar] [CrossRef]
- Meinshausen, M.; Lewis, J.; McGlade, C.; Gütschow, J.; Nicholls, Z.; Burdon, R.; Cozzi, L.; Hackmann, B. Realization of Paris Agreement pledges may limit warming just below 2 °C. Nature 2022, 604, 304–309. [Google Scholar] [CrossRef]
- Abbasi, K.R.; Shahbaz, M.; Zhang, J.; Irfan, M.; Alvarado, R. Analyze the environmental sustainability factors of China: The role of fossil fuel energy and renewable energy. Renew. Energy 2022, 187, 390–402. [Google Scholar] [CrossRef]
- Larsen, K.; Pitt, H.; Grant, M.; Houser, T. China’s greenhouse gas emissions exceeded the developed world for the first time in 2019. Rhodium Group, 6 May 2021. [Google Scholar]
- Liu, L.; Chen, C.; Zhao, Y.; Zhao, E. China׳ s carbon-emissions trading: Overview, challenges and future. Renew. Sustain. Energy Rev. 2015, 49, 254–266. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, S.; Wang, P. Key areas and pathways for carbon emissions reduction in Beijing for the “Dual Carbon” targets. Energy Policy 2022, 164, 112873. [Google Scholar] [CrossRef]
- Zou, C.; Xue, H.; Xiong, B.; Zhang, G.; Pan, S.; Jia, C.; Wang, Y.; Ma, F.; Sun, Q.; Guan, C. Connotation, innovation and vision of “carbon neutrality”. Nat. Gas Ind. B 2021, 8, 523–537. [Google Scholar] [CrossRef]
- Hao, J.; Gao, F.; Fang, X.; Nong, X.; Zhang, Y.; Hong, F. Multi-factor decomposition and multi-scenario prediction decoupling analysis of China’s carbon emission under dual carbon goal. Sci. Total Environ. 2022, 841, 156788. [Google Scholar] [CrossRef]
- Dong, F.; Li, X.; Long, R.; Liu, X. Regional carbon emission performance in China according to a stochastic frontier model. Renew. Sustain. Energy Rev. 2013, 28, 525–530. [Google Scholar] [CrossRef]
- Wang, K.; Wu, M.; Sun, Y.; Shi, X.; Sun, A.; Zhang, P. Resource abundance, industrial structure, and regional carbon emissions efficiency in China. Resour. Policy 2019, 60, 203–214. [Google Scholar] [CrossRef]
- Yuan, D.; Dong, J. Research on ecological restoration and its impact on society in coal resource-based areas: Lessons from the Ruhr area in Germany and the Liulin area in China. Geoforum 2024, 154, 104038. [Google Scholar] [CrossRef]
- Dimanchev, E.G.; Paltsev, S.; Yuan, M.; Rothenberg, D.; Tessum, C.W.; Marshall, J.D.; Selin, N.E. Health co-benefits of sub-national renewable energy policy in the US. Environ. Res. Lett. 2019, 14, 085012. [Google Scholar] [CrossRef]
- Gao, Z.; Li, S.; Cao, X.; Li, Y. Carbon emission intensity characteristics and spatial spillover effects in counties in northeast China: Based on a spatial econometric model. Land 2022, 11, 753. [Google Scholar] [CrossRef]
- Cheng, H.; Dong, S.; Li, F.; Yang, Y.; Li, S.; Li, Y. Multiregional input-output analysis of spatial-temporal evolution driving force for carbon emissions embodied in interprovincial trade and optimization policies: Case study of northeast industrial district in China. Environ. Sci. Technol. 2018, 52, 346–358. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Zhang, Y.; Yang, Y.; Gao, H. Carbon Peak Scenario Simulation of Manufacturing Carbon Emissions in Northeast China: Perspective of Structure Optimization. Energies 2023, 16, 5227. [Google Scholar] [CrossRef]
- Chen, J.S.; Li, H.R.; Tian, Y.G.; Deng, P.P.; Oladele, O.P.; Bai, W.; Dang, Y.P.; Zhao, X.; Zhang, H.L. Greenhouse gas emissions and mitigation potential of crop production in Northeast China. Eur. J. Agron. 2024, 161, 127371. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Q. The confrontation and symbiosis of green and development: Coupling coordination analysis between carbon emissions and spatial development in urban agglomerations of China. Sustain. Cities Soc. 2024, 106, 105391. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, Y.; Wang, J.; Gao, W.; Liu, D.; Yang, M.; Chen, X.; Xie, H.; He, H.; Zhang, X.; et al. Greenhouse gas emissions from the growing season are regulated by precipitation events in conservation tillage farmland ecosystems of Northeast China. Sci. Total Environ. 2024, 948, 174716. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Sun, Y.; Kuramae, E.E.; Zhang, S.; Wang, E.; Yao, Z.; Nasir, F.; Tian, L.; Gao, Q.; Tian, C. Positive effect of carbohydrate-metabolizing bacteria determines increasing soil organic carbon during long-term fertilization and straw returning in the black soil region of China. Pedosphere 2024, 34, 853–864. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, H.; Deng, Y.; Yi, C. Effects of Conservation Tillage on Agricultural Green Total Factor Productivity in Black Soil Region: Evidence from Heilongjiang Province, China. Land 2024, 13, 1212. [Google Scholar] [CrossRef]
- Wang, B.; Niu, X.; Xu, T. Identifying the Full Carbon Sink of Forest Vegetation: A Case Study in the Three Northeast Provinces of China. Sustainability 2023, 15, 10396. [Google Scholar] [CrossRef]
- Wang, H.; Wu, J.; Lin, W.; Luan, Z. Carbon Footprint Accounting and Influencing Factors Analysis for Forestry Enterprises in the Key State-Owned Forest Region of the Greater Khingan Range, Northeast China. Sustainability 2023, 15, 8898. [Google Scholar] [CrossRef]
- Wang, H.; Jin, H.; Li, X.; Zhou, L.; Qi, Y.; Huang, C.; He, R.; Zhang, J.; Yang, R.; Luo, D.; et al. Changes in carbon stock in the Xing’an permafrost regions in Northeast China from the late 1980s to 2020. GIScience Remote Sens. 2023, 60, 2217578. [Google Scholar] [CrossRef]
- Wang, X.; Song, C.; Chen, N.; Qiao, T.; Wang, S.; Jiang, J.; Du, Y. Gas storage of peat in autumn and early winter in permafrost peatland. Sci. Total Environ. 2023, 898, 165548. [Google Scholar] [CrossRef] [PubMed]
- Es-sakali, N.; Zoubir, Z.; Kaitouni, S.I.; Mghazli, M.O.; Cherkaoui, M.; Pfafferott, J. Advanced predictive maintenance and fault diagnosis strategy for enhanced HVAC efficiency in buildings. Appl. Therm. Eng. 2024, 254, 123910. [Google Scholar] [CrossRef]
- Narayan, P.K.; Saboori, B.; Soleymani, A. Economic growth and carbon emissions. Econ. Model. 2016, 53, 388–397. [Google Scholar] [CrossRef]
- Alam, M.M.; Murad, M.W.; Noman, A.H.M.; Ozturk, I. Relationships among carbon emissions, economic growth, energy consumption and population growth: Testing Environmental Kuznets Curve hypothesis for Brazil, China, India and Indonesia. Ecol. Indic. 2016, 70, 466–479. [Google Scholar] [CrossRef]
- Ghosh, S. Examining carbon emissions economic growth nexus for India: A multivariate cointegration approach. Energy Policy 2010, 38, 3008–3014. [Google Scholar] [CrossRef]
- Jin, T.; Kim, J. What is better for mitigating carbon emissions–Renewable energy or nuclear energy? A panel data analysis. Renew. Sustain. Energy Rev. 2018, 91, 464–471. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, T.; Wang, Y.; Shi, Z. Research on impacts of population-related factors on carbon emissions in Beijing from 1984 to 2012. Environ. Impact Assess. Rev. 2015, 55, 45–53. [Google Scholar] [CrossRef]
- Gelenbe, E.; Caseau, Y. The impact of information technology on energy consumption and carbon emissions. Ubiquity 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Tian, X.; Geng, Y.; Zhong, S.; Wilson, J.; Gao, C.; Chen, W.; Yu, Z.; Hao, H. A bibliometric analysis on trends and characters of carbon emissions from transport sector. Transp. Res. Part D Transp. Environ. 2018, 59, 1–10. [Google Scholar] [CrossRef]
- Jiang, M.; An, H.; Gao, X. Adjusting the global industrial structure for minimizing global carbon emissions: A network-based multi-objective optimization approach. Sci. Total Environ. 2022, 829, 154653. [Google Scholar] [CrossRef]
- Nässén, J.; Holmberg, J.; Wadeskog, A.; Nyman, M. Direct and indirect energy use and carbon emissions in the production phase of buildings: An input–output analysis. Energy 2007, 32, 1593–1602. [Google Scholar] [CrossRef]
- Jiang, M.; An, H.; Gao, X.; Jia, N.; Liu, S.; Zheng, H. Structural decomposition analysis of global carbon emissions: The contributions of domestic and international input changes. J. Environ. Manag. 2021, 294, 112942. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.; Benjamin, N.I. Influencing factors on carbon emissions in China transport industry. A new evidence from quantile regression analysis. J. Clean. Prod. 2017, 150, 175–187. [Google Scholar] [CrossRef]
- Huang, L.; Kelly, S.; Lv, K.; Giurco, D. A systematic review of empirical methods for modelling sectoral carbon emissions in China. J. Clean. Prod. 2019, 215, 1382–1401. [Google Scholar] [CrossRef]
- Chuai, X.; Huang, X.; Wang, W.; Wen, J.; Chen, Q.; Peng, J. Spatial econometric analysis of carbon emissions from energy consumption in China. J. Geogr. Sci. 2012, 22, 630–642. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, H.; Zikhali, P.; Lv, Y. Carbon emissions in China: A spatial econometric analysis at the regional level. Sustainability 2014, 6, 6005–6023. [Google Scholar] [CrossRef]
- Jin, Y.; Sharifi, A.; Li, Z.; Chen, S.; Zeng, S.; Zhao, S. Carbon emission prediction models: A review. Sci. Total Environ. 2024, 927, 172319. [Google Scholar] [CrossRef]
- Wen, L.; Cao, Y. Influencing factors analysis and forecasting of residential energy-related CO2 emissions utilizing optimized support vector machine. J. Clean. Prod. 2020, 250, 119492. [Google Scholar] [CrossRef]
- Fang, Y.; Lu, X.; Li, H. A random forest-based model for the prediction of construction-stage carbon emissions at the early design stage. J. Clean. Prod. 2021, 328, 129657. [Google Scholar] [CrossRef]
- Cui, X.; Shaojun, E.; Niu, D.; Chen, B.; Feng, J. Forecasting of carbon emission in China based on gradient boosting decision tree optimized by modified whale optimization algorithm. Sustainability 2021, 13, 12302. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, L.; Liu, H. Grey relational analysis, principal component analysis and forecasting of carbon emissions based on long short-term memory in China. J. Clean. Prod. 2019, 209, 415–423. [Google Scholar] [CrossRef]
- Lin, X.; Zhu, X.; Feng, M.; Han, Y.; Geng, Z. Economy and carbon emissions optimization of different countries or areas in the world using an improved Attention mechanism based long short term memory neural network. Sci. Total Environ. 2021, 792, 148444. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Zhang, Y.; Sun, H.; Wang, A. A real-time operational carbon emission prediction method for the early design stage of residential units based on a convolutional neural network: A case study in Beijing, China. J. Build. Eng. 2023, 75, 106994. [Google Scholar] [CrossRef]
- Pavlyshenko, B. Using stacking approaches for machine learning models. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; pp. 255–258. [Google Scholar]
- Wang, Z.; Li, Y.; Huang, G.; Gong, J.; Li, Y.; Zhang, Q. A factorial-analysis-based Bayesian neural network method for quantifying China’s CO2 emissions under dual-carbon target. Sci. Total Environ. 2024, 920, 170698. [Google Scholar] [CrossRef]
- Xu, G.; Schwarz, P.; Yang, H. Determining China’s CO2 emissions peak with a dynamic nonlinear artificial neural network approach and scenario analysis. Energy Policy 2019, 128, 752–762. [Google Scholar] [CrossRef]
- Han, Z.; Cui, B.; Xu, L.; Wang, J.; Guo, Z. Coupling LSTM and CNN neural networks for accurate carbon emission prediction in 30 Chinese provinces. Sustainability 2023, 15, 13934. [Google Scholar] [CrossRef]
- Wu, X.; Chen, L.; Zhao, J.; He, M.; Han, X. CNN-GRU-Attention Neural Networks for Carbon Emission Prediction of Transportation in Jiangsu Province. Sustainability 2024, 16, 8553. [Google Scholar] [CrossRef]
- Fragkos, P.; Tasios, N.; Paroussos, L.; Capros, P.; Tsani, S. Energy system impacts and policy implications of the European Intended Nationally Determined Contribution and low-carbon pathway to 2050. Energy Policy 2017, 100, 216–226. [Google Scholar] [CrossRef]
- Kang, Y.; Yang, Q.; Bartocci, P.; Wei, H.; Liu, S.S.; Wu, Z.; Zhou, H.; Yang, H.; Fantozzi, F.; Chen, H. Bioenergy in China: Evaluation of domestic biomass resources and the associated greenhouse gas mitigation potentials. Renew. Sustain. Energy Rev. 2020, 127, 109842. [Google Scholar] [CrossRef]
- Xiao, J.; Lu, J.; Niu, B.; Liu, X.; Hong, J.; Xu, Z. Ex-ante life cycle evaluation of spent lithium-ion battery recovery: Modeling of complex environmental and economic impacts. Environ. Sci. Ecotechnol. 2025, 23, 100490. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, S.; Lu, X.; Liu, Y.; Wang, T.; Zhang, B.; Li, Z.; Wang, W.; Kong, M.; Chen, K. Establish of air pollutants and greenhouse gases emission inventory and co-benefits of their reduction of transportation sector in Central China. J. Environ. Sci. 2025, 150, 604–621. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, X.; Jiang, Z.; Shao, S. How to achieve the 2030 CO2 emission-reduction targets for China’s industrial sector: Retrospective decomposition and prospective trajectories. Glob. Environ. Change 2017, 44, 83–97. [Google Scholar] [CrossRef]
- Georgescu, I.A.; Oprea, S.V.; Bâra, A. Investigating the relationship between macroeconomic indicators, renewables and pollution across diverse regions in the globalization era. Appl. Energy 2024, 363, 123077. [Google Scholar] [CrossRef]
- Balsalobre-Lorente, D.; Shahbaz, M.; Roubaud, D.; Farhani, S. How economic growth, renewable electricity and natural resources contribute to CO2 emissions? Energy Policy 2018, 113, 356–367. [Google Scholar] [CrossRef]
- Kasman, A.; Duman, Y.S. CO2 emissions, economic growth, energy consumption, trade and urbanization in new EU member and candidate countries: A panel data analysis. Econ. Model. 2015, 44, 97–103. [Google Scholar] [CrossRef]
- Liu, Z.; Guan, D.; Wei, W.; Davis, S.J.; Ciais, P.; Bai, J.; Peng, S.; Zhang, Q.; Hubacek, K.; Marland, G.; et al. Reduced carbon emission estimates from fossil fuel combustion and cement production in China. Nature 2015, 524, 335–338. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, W.Y. China’s Energy Transition Pathway in a Carbon Neutral Vision. Engineering 2022, 14, 64–76. [Google Scholar] [CrossRef]
- Wang, W.Z.; Liu, L.C.; Liao, H.; Wei, Y.M. Impacts of urbanization on carbon emissions: An empirical analysis from OECD countries. Energy Policy 2021, 151, 112171. [Google Scholar] [CrossRef]
- Chen, J.D.; Li, Y.Q.; Xu, Y.Y.; Vardanyan, M.; Shen, Z.Y.; Song, M.L. The impact of fiscal technology expenditures on innovation drive and carbon emissions in China. Technol. Forecast. Soc. Change 2023, 193, 122631. [Google Scholar] [CrossRef]
- Xing, P.; Wang, Y.; Ye, T.; Sun, Y.; Li, Q.; Li, X.; Li, M.; Chen, W. Carbon emission efficiency of 284 cities in China based on machine learning approach: Driving factors and regional heterogeneity. Energy Econ. 2024, 129, 107222. [Google Scholar] [CrossRef]
- Wang, X.P.; Li, Z.Y.; Kee, T. Spatial and temporal correlation between green space landscape pattern and carbon emission-Three major coastal urban agglomerations in China. Urban Clim. 2024, 58, 102222. [Google Scholar] [CrossRef]
- Liu, K.; Ren, G.X.; Dong, S.M.; Xue, Y.T. The synergy between pollution reduction and carbon reduction in Chinese cities and its influencing factors. Sustain. Cities Soc. 2024, 106, 105348. [Google Scholar] [CrossRef]
- Heaton, J. An empirical analysis of feature engineering for predictive modeling. In Proceedings of the SoutheastCon 2016, Norfolk, VA, USA, 30 March–3 April 2016; pp. 1–6. [Google Scholar]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Marcílio, W.E.; Eler, D.M. From explanations to feature selection: Assessing SHAP values as feature selection mechanism. In Proceedings of the 2020 33rd SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Porto de Galinhas, Brazil, 7–10 November 2020; pp. 340–347. [Google Scholar]
- Ray, R.L.; Singh, V.P.; Singh, S.K.; Acharya, B.S.; He, Y. What is the impact of COVID-19 pandemic on global carbon emissions? Sci. Total Environ. 2022, 816, 151503. [Google Scholar] [CrossRef] [PubMed]
| Method Type | Model Name | Characteristics | Reference |
|---|---|---|---|
| Traditional Statistical and Economic methods | Input–Output Analysis (IOA) | Emphasize interpretability and excel at revealing the linear relationships between carbon emissions driving factors. | [42] |
| Structural Decomposition Analysis (SDA) | [43] | ||
| Regression Models | [44] | ||
| Econometric Models | [46,47] | ||
| Machine Learning | Support Vector Machines (SVMs) | Data-driven at their core, enhancing prediction accuracy through flexible modeling, capable of handling nonlinear relationships and adapting to complex data. | [49] |
| Random Forests (RFs) | [50] | ||
| Gradient Boosting Decision Trees (GBDTs) | [51] | ||
| Deep Learning | Long Short-Term Memory (LSTM) | Through multi-layer neural network structures, automatically learn features, excelling at handling large-scale data and capturing complex nonlinear and high-dimensional features. | [52,53] |
| Convolutional Neural Networks (CNNs) | [54] |
| Model Name | Parameter Settings |
|---|---|
| SVM | |
| KNN | K = 5 Uniform weights |
| Random Forest | Number_estimators = 50 Min_samples_split = 5 |
| XGBoost | Number_estimators = 100 Learning_rate = 0.1 Max_depth = 4 |
| Ridge Regression | = 10 |
| Lasso Regression | = 0.01 |
| Feature | Unit | Min | Max | Mean | Standard Deviation | VIF Value |
|---|---|---|---|---|---|---|
| GDP | 100 million yuan | 56.210 | 8752.900 | 1061.620 | 1362.408 | 5.344 |
| Permanent Population | 10,000 people | 48.000 | 1028.171 | 245.381 | 212.315 | 5.109 |
| Total Energy Consumption | t | 58,074.360 | 11,515,049.072 | 1,169,979.757 | 1,341,811.011 | 7.304 |
| Coal Consumption Ratio | % | 0.594 | 0.998 | 0.858 | 0.090 | 1.509 |
| Total Electricity Consumption | 10,000 kWh | 30,325.770 | 9,207,800.000 | 785,520.990 | 905,994.339 | 7.970 |
| Urbanization Rate | % | 0.156 | 0.914 | 0.547 | 0.164 | 1.616 |
| Proportion of R&D Spending | % | 0.000 | 0.045 | 0.006 | 0.007 | 1.893 |
| Green Coverage Rate | % | 1.020 | 62.200 | 36.225 | 8.247 | 1.285 |
| Sulfur Dioxide Emissions | t | 589.909 | 446,181.000 | 32,042.967 | 30,646.727 | 1.819 |
| Smoke Dust Emissions | t | −1849.936 | 166,611.000 | 28,609.307 | 22,992.993 | 1.475 |
| Average Humidity | % | 49.124 | 74.047 | 64.296 | 4.522 | 1.714 |
| Precipitation | mm | 240.327 | 1824.655 | 722.280 | 238.220 | 1.516 |
| Average Temperature | °C | 0.509 | 11.902 | 6.630 | 2.690 | 2.119 |
| Model Name | _Train | MSE_Train | MAE_Train | _Test | MSE_Test | MAE_Test |
|---|---|---|---|---|---|---|
| SVM | 0.71 | 154,859.79 | 292.32 | 0.67 | 290,144.83 | 409.54 |
| KNN | 0.70 | 151,568.09 | 270.15 | 0.68 | 277,008.50 | 398.78 |
| Random Forest | 0.82 | 30,250.37 | 124.49 | 0.78 | 194,444.39 | 332.10 |
| XGBoost | 0.85 * | 21,642.81 | 113.23 | 0.78 | 194,346.00 | 344.66 |
| Ridge Regression | 0.43 | 514,570.67 | 584.64 | 0.32 | 590,337.84 | 614.38 |
| Lasso Regression | 0.43 | 518,243.79 | 589.33 | 0.32 | 590,466.85 | 617.63 |
| Stacking Regressor | 0.83 | 11,132.83 * | 78.23 * | 0.82 * | 156,376.61 * | 306.01 * |
| (10,000 t) | Mean (Shenyang) | Std (Shenyang) | Mean (Changchun) | Std (Changchun) | Mean (Dalian) | Std (Dalian) | Mean (Harbin) | Std (Harbin) |
|---|---|---|---|---|---|---|---|---|
| BS | 4741.07 | 10.24 | 2182.70 | 9.98 | 3549.32 | 10.12 | 4893.83 | 10.14 |
| ADS | 4741.14 | 5.04 | 2182.51 | 5.03 | 3549.67 | 4.96 | 4893.62 | 4.98 |
| CRS | 4740.26 | 9.96 | 2182.89 | 10.00 | 3549.51 | 10.16 | 4893.60 | 9.96 |
| Scenario | Key Parameter Settings (Average Annual Change Rate) | Projected Carbon Peak Time | Policy Implications |
|---|---|---|---|
| BS | Energy Consumption: +2%; Urbanization Rate: +1%; Coal Consumption Ratio: −1%; GDP: +2%; Average Temperature: +0.4% | 2039–2040 | Current policies continue. Moderate emissions reductions, but peak is delayed. Requires significant acceleration of efforts to meet the 2030 peak target. |
| ADS | Energy Consumption: +1%; Urbanization Rate: +2%; Coal Consumption Ratio: −3%; GDP: +3%; Average Temperature: +0.8% | 2030 | Rapid decarbonization driven by strong coal reduction policies. Achieves the 2030 peak target. Requires substantial investment in renewable energy, grid upgrades, and industrial transformation. Potential short-term economic adjustments. |
| CRS | Energy Consumption: +5%; Urbanization Rate: +4%; Coal Consumption Ratio: 0%; GDP: +7%; Average Temperature: +0.2% | 2039–2040 | Focus on adaptation and resilience, with high economic growth. Fails to significantly advance the carbon peak due to continued reliance on fossil fuels. Highlights the need for stronger emissions reduction measures in addition to adaptation. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Zhao, J.; Wang, S.; Zhang, C.; Zhang, H.; Wei, N. Exploration of Dual-Carbon Target Pathways Based on Machine Learning Stacking Model and Policy Simulation—A Case Study in Northeast China. Land 2025, 14, 844. https://doi.org/10.3390/land14040844
Ren X, Zhao J, Wang S, Zhang C, Zhang H, Wei N. Exploration of Dual-Carbon Target Pathways Based on Machine Learning Stacking Model and Policy Simulation—A Case Study in Northeast China. Land. 2025; 14(4):844. https://doi.org/10.3390/land14040844
Chicago/Turabian StyleRen, Xuezhi, Jianya Zhao, Shu Wang, Chunpeng Zhang, Hongzhen Zhang, and Nan Wei. 2025. "Exploration of Dual-Carbon Target Pathways Based on Machine Learning Stacking Model and Policy Simulation—A Case Study in Northeast China" Land 14, no. 4: 844. https://doi.org/10.3390/land14040844
APA StyleRen, X., Zhao, J., Wang, S., Zhang, C., Zhang, H., & Wei, N. (2025). Exploration of Dual-Carbon Target Pathways Based on Machine Learning Stacking Model and Policy Simulation—A Case Study in Northeast China. Land, 14(4), 844. https://doi.org/10.3390/land14040844








