Evaluating the Spatial Relationships Between Tree Cover and Regional Temperature and Precipitation of the Yucatán Peninsula Applying Spatial Autoregressive Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
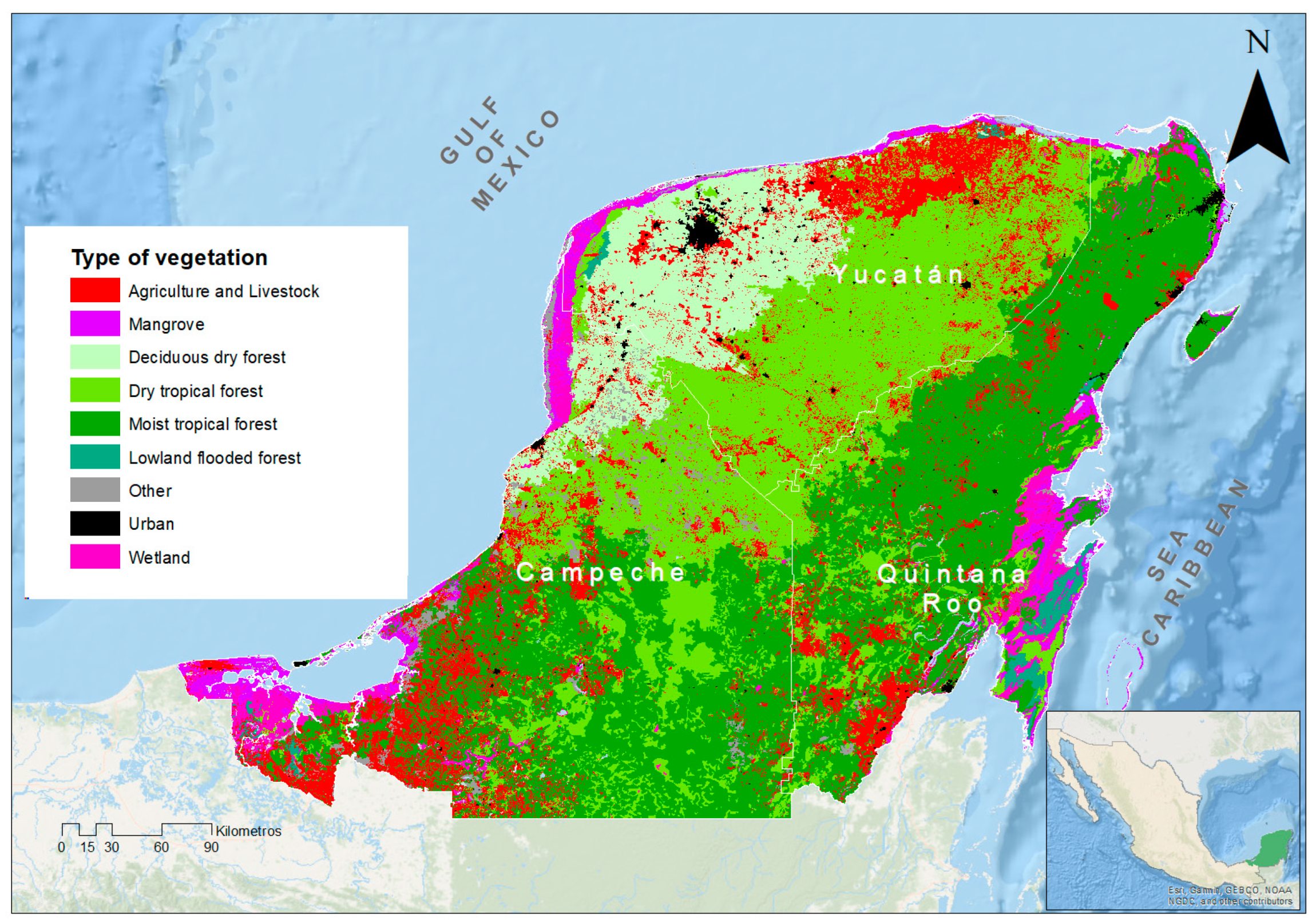
2.2. Spatial Data and Processing
2.3. Sampling Design
2.4. Statistical Analysis
- -
- Y is the dependent variable vector (e.g., mean annual temperature).
- -
- λ is the spatial autoregressive coefficient capturing the degree of spatial dependence in Y.
- -
- W is the spatial weights matrix defining the relationships between spatial units.
- -
- X is the matrix of independent variables.
- -
- β is the coefficient vector for X.
- -
- μ is the fixed effects capturing unobserved heterogeneity (i.e., forest cover category effects).
- -
- ε is the error term.
3. Results
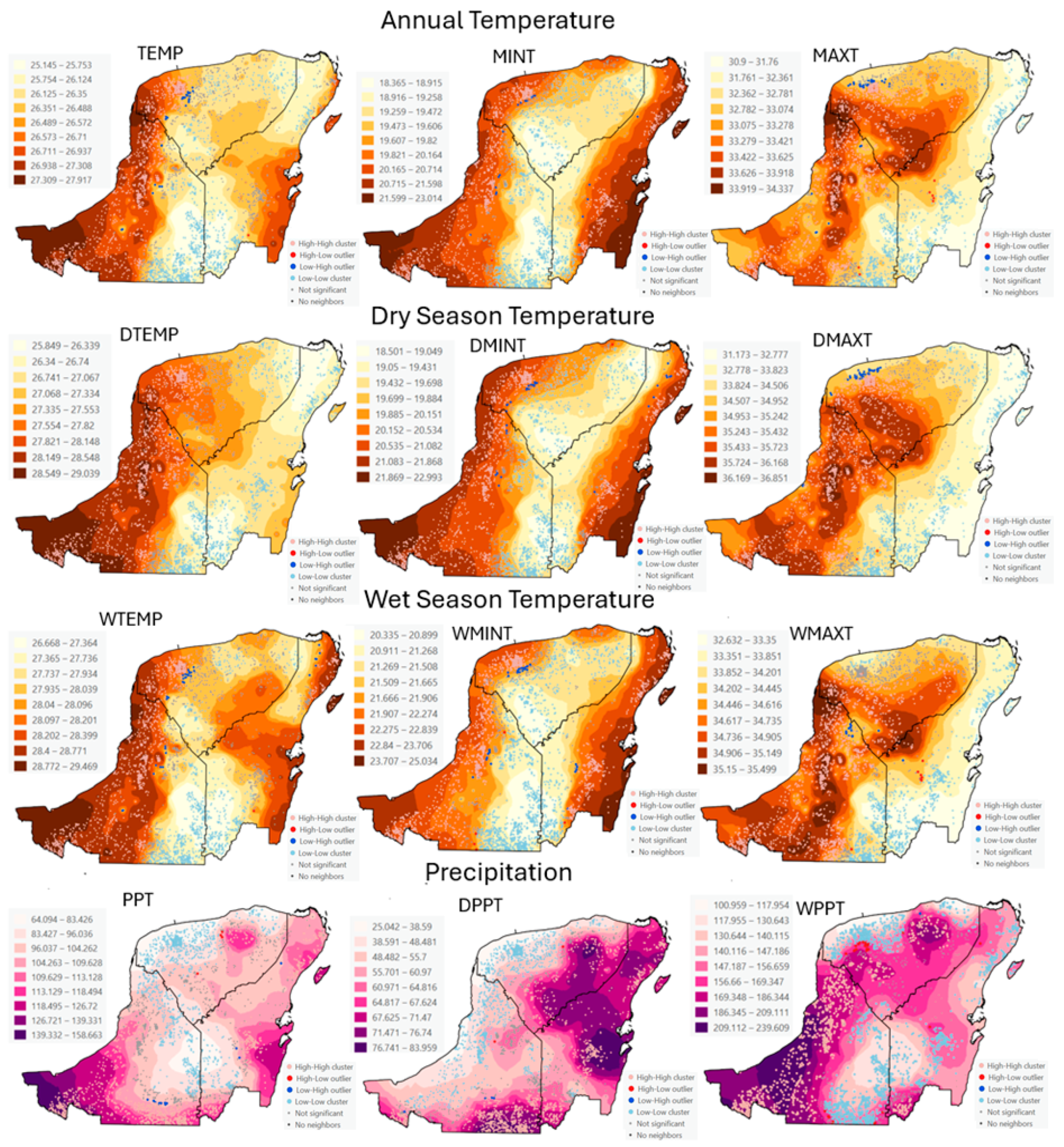
3.1. Spatial Distribution of Forest Cover and Climate
3.2. Spatial Relationship Between Forest Cover and Climate
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Houghton, R.A.J. Tropical deforestation as a source of greenhouse gas emissions. Trop. Deforestation Clim. Change 2005, 13, 13–21. [Google Scholar]
- Baccini, A.; Goetz, S.; Walker, W.; Laporte, N.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.; Dubayah, R.; Friedl, M. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Change 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Houghton, R.A.; Nassikas, A.A. Global and regional fluxes of carbon from land use and land cover change 1850–2015. Glob. Biogeochem. Cycles 2017, 31, 456–472. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M. CO2 Emissions. 2020. Available online: https://ourworldindata.org/co2-emissions (accessed on 1 October 2022).
- Ometto, J.; Kalaba, K.; Anshari, G.; Chacón, N.; Farrell, A.; Halim, S.; Neufeldt, H.; Sukumar, R.; Pörtner, H.; Roberts, D. Cross-chapter paper 7: Tropical forests. Clim. Change 2023, 14, 2369–2410. [Google Scholar] [CrossRef]
- de Albuquerque, F.S.; Benito, B.; Beier, P.; Assunção-Albuquerque, M.J.; Cayuela, L. Supporting underrepresented forests in Mesoamerica. Nat. Conserv. 2015, 13, 152–158. [Google Scholar] [CrossRef]
- Baccini, A.; Walker, W.; Carvalho, L.; Farina, M.; Sulla-Menashe, D.; Houghton, R.A. Tropical forests are a net carbon source based on aboveground measurements of gain and loss. Science 2017, 358, 230–234. Available online: https://www.science.org/doi/10.1126/science.aam5962 (accessed on 20 November 2022). [CrossRef] [PubMed]
- Skutsch, M.; Mccall, M.; Karky, B.; Zahabu, E.; Guarin, G. Case Studies on Measuring and Assessing Forest Degradation. Community Measurement of Carbon Stock Change for REDD; Forest Resources Assessment Working Paper; FAO: Rome, Italy, 2009; Available online: https://cybertracker.org/downloads/forestry/Forest_case_studies.pdf (accessed on 5 October 2024).
- Pearson, T.R.; Brown, S.; Murray, L.; Sidman, G. Greenhouse gas emissions from tropical forest degradation: An underestimated source. Carbon Balanc. 2017, 12, 3. [Google Scholar] [CrossRef]
- Mansourian, S.; Vallauri, D.; Dudley, N.; Hobley, M. The impacts of degradation and forest loss on human well-being and its social and political relevance for restoration. Forest Restoration in Landscapes: Beyond Planting Trees; Springer: Berlin/Heidelberg, Germany, 2005; pp. 22–30. [Google Scholar] [CrossRef]
- Budiharta, S.; Meijaard, E.; Erskine, P.D.; Rondinini, C.; Pacifici, M.; Wilson, K.A. Restoring degraded tropical forests for carbon and biodiversity. Environ. Res. Lett. 2014, 9, 114020. [Google Scholar] [CrossRef]
- Giam, X. Global biodiversity loss from tropical deforestation. Proc. Natl. Acad. Sci. USA 2017, 114, 5775–5777. [Google Scholar] [CrossRef]
- Varns, T.; Cortez, R.; Hovani, L.; Kingsbury, P. Yucatán Peninsula, Mexico: A Jurisdictional Approach to Conserving the Maya Forest; The Nature Conservancy: Arlington, VA, USA, 2018. [Google Scholar]
- Pacheco, P.; Mo, K.; Dudley, N.; Shapiro, A.; Aguilar-Amuchastegui, N.; Ling, P.; Anderson, C.; Marx, A.J.W. Deforestation Fronts: Drivers and Responses in a Changing World; WWF: Gland, Switzerland, 2021; p. 125. [Google Scholar]
- CONAFOR, Estimación de la Tasa de Deforestación Bruta en México Para el Periodo 2001–2018 Mediante el Método de Muestreo. Documento Técnico 2020, 28, 1–19. Available online: http://www.conafor.gob.mx:8080/documentos/docs/1/7767Resumen%20Ejecutivo%20Deforestaci%C3%B3n%202001-2018%20M%C3%A9xico.pdf (accessed on 5 October 2024).
- Ellis, E.A.; Navarro Martínez, A.; García Ortega, M.; Hernández Gómez, I.; Chacón Castillo, D. Forest cover dynamics in the Selva Maya of Central and Southern Quintana Roo, Mexico: Deforestation or degradation? J. Land. Use Sci. 2020, 15, 25–51. [Google Scholar] [CrossRef]
- Romero-Sanchez, M.E.; Ponce-Hernandez, R. Assessing and monitoring forest degradation in a deciduous tropical forest in Mexico via remote sensing indicators. Forests 2017, 8, 302. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, M.; Wang, J.; Ma, X.; Luo, J.; Yao, X. Diurnal variation characteristics of the surface sensible heat flux over the Tibetan Plateau. Atmosphere 2023, 14, 128. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Pörtner, H.-O.; Skea, J.; Zhai, P.; Roberts, D.; Shukla, P.R.; Buendía, E.C. Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; CGIAR: Montpellier, France, 2019. [Google Scholar]
- Nyawira, S.S.; Herold, M.; Mulatu, K.A.; Roman-Cuesta, R.M.; Houghton, R.A.; Grassi, G.; Pongratz, J.; Gasser, T.; Verchot, L. Pantropical CO2 emissions and removals for the AFOLU sector in the period 1990–2018. Mitig. Adapt. Strat. Glob. Change 2024, 29, 13. [Google Scholar] [CrossRef]
- Green Climate Fund, R. REDD+ Results-based Payments Pilot. Available online: https://www.greenclimate.fund/redd (accessed on 7 October 2024).
- Kramer, K.; Sheil, D. Restoring deforested drylands for a wetter future–harnessing trees for credits, climate and water. Front. For. Glob. Change 2024, 7, 1371117. [Google Scholar] [CrossRef]
- Watanabe, S. Impact of Deforestation on Regional Climate Patterns in Japan. Int. J. Clim. Stud. 2024, 3, 37–47. [Google Scholar] [CrossRef]
- Longobardi, P.; Montenegro, A.; Beltrami, H.; Eby, M. Deforestation induced climate change: Effects of spatial scale. PLoS ONE 2016, 11, 0153357. [Google Scholar] [CrossRef]
- Smith, C.; Robertson, E.; Chadwick, R.; Kelley, D.I.; Argles, A.P.; Coelho, C.A.; de Souza, D.C.; Kubota, P.Y.; Talamoni, I.L.; Spracklen, D.V. Observed and simulated local climate responses to tropical deforestation. Environ. Res. Lett. 2023, 18, 104004. [Google Scholar] [CrossRef]
- Prevedello, J.A.; Winck, G.R.; Weber, M.M.; Nichols, E.; Sinervo, B. Impacts of forestation and deforestation on local temperature across the globe. PLoS ONE 2019, 14, 0213368. [Google Scholar] [CrossRef]
- Luo, X.; Ge, J.; Guo, W.; Fan, L.; Chen, C.; Liu, Y.; Yang, L. The biophysical impacts of deforestation on precipitation: Results from the CMIP6 model intercomparison. J. Clim. 2022, 35, 3293–3311. [Google Scholar] [CrossRef]
- Wanderley, R.L.N.; Domingues, L.M.; Joly, C.A.; da Rocha, H.R. Relationship between land surface temperature and fraction of anthropized area in the Atlantic forest region, Brazil. PLoS ONE 2019, 14, 0225443. [Google Scholar] [CrossRef] [PubMed]
- Wan Mohd Jaafar, W.S.; Abdul Maulud, K.N.; Muhmad Kamarulzaman, A.M.; Raihan, A.; Md Sah, S.; Ahmad, A.; Saad, S.N.M.; Mohd Azmi, A.T.; Jusoh Syukri, N.K.A.; Razzaq Khan, W. The influence of deforestation on land surface temperature—A case study of Perak and Kedah, Malaysia. Forests 2020, 11, 670. [Google Scholar] [CrossRef]
- Lawrence, D.; Vandecar, K. Effects of tropical deforestation on climate and agriculture. Nat. Clim. Change 2015, 5, 27–36. [Google Scholar] [CrossRef]
- Muluneh, A.; van Loon, E.; Bewket, W.; Keesstra, S.; Stroosnijder, L.; Burka, A. Effects of long-term deforestation and remnant forests on rainfall and temperature in the Central Rift Valley of Ethiopia. For. Ecosyst. 2017, 4, 23. [Google Scholar] [CrossRef]
- Medvigy, D.; Walko, R.L.; Avissar, R. Effects of deforestation on spatiotemporal distributions of precipitation in South America. J. Clim. 2011, 24, 2147–2163. [Google Scholar] [CrossRef]
- Mu, Y.; Jones, C. An observational analysis of precipitation and deforestation age in the Brazilian Legal Amazon. Atmos. Res. 2022, 271, 106122. [Google Scholar] [CrossRef]
- Márdero, S.; Nickl, E.; Schmook, B.; Schneider, L.; Rogan, J.; Christman, Z.; Lawrence, D. Sequías en el sur de la península de Yucatán: Análisis de la variabilidad anual y estacional de la precipitación. Investig. Geográficas 2012, 78, 19–33. [Google Scholar] [CrossRef]
- Campo, J.; Merino, A.J.G.C.B. Variations in soil carbon sequestration and their determinants along a precipitation gradient in seasonally dry tropical forest. Ecosystems 2016, 22, 1942–1956. [Google Scholar] [CrossRef]
- Metcalfe, S.E.; Schmook, B.; Boyd, D.S.; De la Barreda-Bautista, B.; Endfield, G.E.; Mardero, S.; Manzon Che, M.; Medina Gonzalez, R.; Munguia Gil, M.T.; Navarro Olmedo, S. Community perception, adaptation and resilience to extreme weather in the Yucatan Peninsula, Mexico. Reg. Environ. Change 2020, 20, 25. [Google Scholar] [CrossRef]
- Andrew, M.E.; Wulder, M.A.; Nelson, T.A.; Coops, N.C.J.G.; Sensing, R. Spatial data, analysis approaches, and information needs for spatial ecosystem service assessments: A review. GIScience Remote. Sens. 2015, 52, 344–373. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Potapov, P.; Hansen, M.C.; Kommareddy, I.; Kommareddy, A.; Turubanova, S.; Pickens, A.; Adusei, B.; Tyukavina, A.; Ying, Q. Landsat analysis ready data for global land cover and land cover change mapping. Remote Sens. 2020, 12, 426. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.-P.; Feng, M.; Noojipady, P.; Anand, A.; Huang, C.; Kim, D.-H.; Collins, K.M.; Channan, S.; DiMiceli, C. Global, 30-m resolution continuous fields of tree cover: Landsat-based rescaling of MODIS vegetation continuous fields with lidar-based estimates of error. Int. J. Digit. Earth 2013, 6, 427–448. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Mermoz, S.; Bouvet, A.; Le Toan, T.; Carvalhais, N.; Rozendaal, D.; Herold, M.; Avitabile, V.; Quegan, S. GlobBiomass Global Above-Ground Biomass and Growing Stock Volume Datasets. 2018. Available online: https://globbiomass.org/products/global-mapping/ (accessed on 6 January 2022).
- Quegan, S.; Le Toan, T.; Chave, J.; Dall, J.; Exbrayat, J.-F.; Minh, D.H.T.; Lomas, M.; D’alessandro, M.M.; Paillou, P.; Papathanassiou, K. The European Space Agency BIOMASS mission: Measuring forest above-ground biomass from space. Remote Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef]
- Spawn, S.A.; Sullivan, C.C.; Lark, T.J.; Gibbs, H.K. Harmonized global maps of above and belowground biomass carbon density in the year 2010. Sci. Data 2020, 7, 112. [Google Scholar] [CrossRef]
- Vancutsem, C.; Achard, F.; Pekel, J.-F.; Vieilledent, G.; Carboni, S.; Simonetti, D.; Gallego, J.; Aragao, L.E.; Nasi, R. Long-term (1990–2019) monitoring of forest cover changes in the humid tropics. Sci. Adv. 2021, 7, eabe1603. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. A J. R. Meteorol. Soc. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Karger, D.N.; Lange, S.; Hari, C.; Reyer, C.P.; Conrad, O.; Zimmermann, N.E.; Frieler, K. CHELSA-W5E5: Daily 1 km meteorological forcing data for climate impact studies. Earth Syst. Sci. Data 2023, 15, 2445–2464. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Dee, D.; Horányi, A.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I. The ERA5 Global Atmospheric Reanalysis at ECMWF as a comprehensive dataset for climate data homogenization, climate variability, trends and extremes. In Geophysical Research Abstracts; EGU: Munich, Germany, 2019. [Google Scholar]
- Lu, M.; Zhang, Y.; Liang, F.; Wu, Y. Spatial relationship between land use patterns and ecosystem services value—Case study of Nanjing. Land 2022, 11, 1168. [Google Scholar] [CrossRef]
- da Silva, L.B.; Oliveira, G.L.; Frederico, R.G.; Loyola, R.; Zacarias, D.; Ribeiro, B.R.; Mendes-Oliveira, A.C. How future climate change and deforestation can drastically affect the species of monkeys endemic to the eastern Amazon, and priorities for conservation. Biodivers. Conserv. 2022, 31, 971–988. [Google Scholar] [CrossRef]
- Feeley, K.J.; Malhi, Y.; Zelazowski, P.; Silman, M.R. The relative importance of deforestation, precipitation change, and temperature sensitivity in determining the future distributions and diversity of Amazonian plant species. Glob. Change Biol. 2012, 18, 2636–2647. [Google Scholar] [CrossRef]
- Manchego, C.E.; Hildebrandt, P.; Cueva, J.; Espinosa, C.I.; Stimm, B.; Günter, S. Climate change versus deforestation: Implications for tree species distribution in the dry forests of southern Ecuador. PLoS ONE 2017, 12, e0190092. [Google Scholar] [CrossRef] [PubMed]
- Gomes, V.H.; Vieira, I.C.; Salomão, R.P.; ter Steege, H.J.N.C.C. Amazonian tree species threatened by deforestation and climate change. Nat. Clim. Change 2019, 9, 547–553. [Google Scholar] [CrossRef]
- Bertazzon, S.; Johnson, M.; Eccles, K.; Kaplan, G.G. Accounting for spatial effects in land use regression for urban air pollution modeling. Epidemiology 2015, 14, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Liu, Z.; Wang, P.; Liu, G.; Lu, F. Exploring the mechanisms of ecological land change based on the spatial autoregressive model: A case study of the Poyang Lake Eco-Economic Zone, China. Int. J. Environ. Res. Public. Health 2014, 11, 583–599. [Google Scholar] [CrossRef]
- Mets, K.D.; Armenteras, D.; Dávalos, L.M. Spatial autocorrelation reduces model precision and predictive power in deforestation analyses. Ecosphere 2017, 8, e01824. [Google Scholar] [CrossRef]
- Jeong, S.; Yoon, D. Examining vulnerability factors to natural disasters with a spatial autoregressive model: The case of South Korea. Sustainability 2018, 10, 1651. [Google Scholar] [CrossRef]
- INEGI. Anuario Estadístico y Geográfico por Entidad Federative; Instituto Nacional de Estadística y Geografía: Aguascalientes, México, 2023. [Google Scholar]
- INEGI. Estudio de Información Integrada del Acuífero Cárstico Península de Yucatán; Instituto Nacional de Estadística y Geografía: Aguascalientes, Mexico, 2016. [Google Scholar]
- Estrada Medina, H.; Jiménez Osornio, J.J.; Álvarez Rivera, O.; Barrientos Medina, R.C. El karst de Yucatán: Su origen, morfología y biología. Acta Univ. 2019, 29, 1–18. [Google Scholar] [CrossRef]
- Torrescano-Valle, N.; Folan, W.J. Physical Settings, Environmental History with an Outlook on Global Change. In Biodiversity and Conservation of the Yucatán Peninsula; Islebe, G.A., Calmé, S., León-Cortés, J.L., Schmook, B., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 9–37. [Google Scholar] [CrossRef]
- Vidal-Zepeda, R. Las Regiones Climáticas de México; Undiversified Nacional Autónoma de México, Instituto de Geografía: Coyoacán, Mexico, 2005; Volume 1, pp. 189–204. [Google Scholar]
- INEGI. Diccionario de Datos de Clima; Instituto Nacional de Estadística y Geografía: Aguascalientes, Mexico, 2021. [Google Scholar]
- Farfán, L.M.; D’Sa, E.J.; Liu, K.-b.; Rivera-Monroy, V.H. Tropical cyclone impacts on coastal regions: The case of the Yucatán and the Baja California Peninsulas, Mexico. Estuaries Coasts 2014, 37, 1388–1402. [Google Scholar] [CrossRef]
- Rivera-Monroy, V.H.; Farfán, L.M.; Brito-Castillo, L.; Cortés-Ramos, J.; González-Rodríguez, E.; D’Sa, E.J.; Euan-Avila, J.I. Tropical cyclone landfall frequency and large-scale environmental impacts along karstic coastal regions (Yucatan Peninsula, Mexico). Appl. Sci. 2020, 10, 5815. [Google Scholar] [CrossRef]
- Romero, D.; León-Cruz, J.F. Spatiotemporal changes in hurricane-force wind risk assessment in the Yucatan Peninsula, Mexico. Nat. Hazards 2024, 120, 4675–4698. [Google Scholar] [CrossRef]
- Mascorro, V.S.; Coops, N.C.; Kurz, W.A.; Olguín, M. Attributing changes in land cover using independent disturbance datasets: A case study of the Yucatan Peninsula, Mexico. Reg. Environ. Change 2016, 16, 213–228. [Google Scholar] [CrossRef]
- Romero, D.; Alfaro, E.; Orellana, R.; Hernandez Cerda, M.-E. Standardized drought indices for pre-summer drought assessment in tropical areas. Atmosphere 2020, 11, 1209. [Google Scholar] [CrossRef]
- Bautista, F.; Frausto, O.; Ihl, T.; Aguilar, Y. An update soil map of The Yucatan State, Mexico: Geomorphopedological approach and WRB. Ecosistemas Y Recur. Agropecu. 2015, 2, 303–315. [Google Scholar]
- Pineda-Martínez, L.F.; Carbajal, N.J.A. Climatic analysis linked to land vegetation cover of Mexico by applying multivariate statistical and clustering analysis. Atmósfera 2017, 30, 233–242. [Google Scholar] [CrossRef]
- Bonan, G.B.; Levis, S.; Sitch, S.; Vertenstein, M.; Oleson, K.W. A dynamic global vegetation model for use with climate models: Concepts and description of simulated vegetation dynamics. Glob. Change Biol. 2003, 9, 1543–1566. [Google Scholar] [CrossRef]
- Neilson, R.P. A model for predicting continental-scale vegetation distribution and water balance. Ecol. Appl. 1995, 5, 362–385. [Google Scholar] [CrossRef]
- Miranda, F.; Hernandez, X.E. The types of Mexican vegetation and their classification. Bol. Soc. Bot. 1963, 28, 29–179. [Google Scholar] [CrossRef]
- Sánchez, S.; Islebe, G.; Herrera, E. Flora representativa de Quintana Roo. In Enciclopedia de Quintana Roo; 1998; pp. 1–10. Available online: https://search.worldcat.org/title/Enciclopedia-de-Quintana-Roo/oclc/42861119 (accessed on 5 October 2024).
- Gasca Zamora, J.; Bustamante Lemus, C. El Tren Maya: Impactos en la Península de Yucatán; UNAM: Mexico City, Mexico, 2024. [Google Scholar]
- SIAP. Estadística de producción Agricola. Available online: http://infosiap.siap://nube.agricultura.gob.mx/gobmx/datosAbiertos.phpcierre_agricola/ (accessed on 5 October 2024).
- SIAP. Estadística de Producción Agricola; Servicio de infomación Agroalimentaria y Pesquera: Mexico City, Mexico, 2023. [Google Scholar]
- MREDD, T.-A. Proceso REDD+ SES (salvaguardas sociales y ambientales) en la Península de Yucatán: Reporte final y lecciones aprendidas. Alianza México para la Reducción de Emisiones por Deforestación y Degradación: 2015.1-152. Available online: http://www.monitoreoforestal.gob.mx/repositoriodigital/files/original/c45d61f57b33cc77afee94e08eceeeec.pdf (accessed on 5 October 2024).
- Ellis, E.A.; Gomez, U.H.; Romero-Montero, J.A. Los procesos y causas del cambio en la cobertura forestal de la Península Yucatán, México. Ecosistemas Y Recur. Agropecu. 2017, 26, 101–111. [Google Scholar] [CrossRef]
- Romero, E.M.; Olguín, L.G.E. Estudio de Caso: Deforestación en el Estado de Campeche. Causas Directas e Indirectas de la Principal Amenaza Sobre la Biodiversidad. Amenazas a la Biodiversidad: Caos de Studio, 2010, 573. Available online: https://d1wqtxts1xzle7.cloudfront.net/35203692/Biodiversidad_Campeche_baja-libre.pdf? (accessed on 12 October 2024).
- Esparza-Olguín, L.; Martínez Romero, E. Deforestación en Campeche: Causas y Efectos. Rev. Fomix Campeche 2011, 3, 6–11. [Google Scholar]
- Ramírez Cancino, L.; Rivera-Lorca, J. La ganadería en el contexto de la biodiversidad. In Biodiversidad y Desarrollo Humano en Yucatán; Mérida, Mexico, 2010; pp. 106–108. Available online: https://www.cicy.mx/documentos/CICY/Sitios/Biodiversidad/pdfs/Cap2/17%20La%20ganaderia.pdf (accessed on 5 October 2024).
- INEGI. Encuesta Nacional Agropecuaria (ENA). Available online: https://www.inegi.org.mx/programas/ena/2019/ (accessed on 5 October 2024).
- Porter-Bolland, L.; Sánchez González, M.C.; Ellis, E.A. La conformación del paisaje y el aprovechamiento de los recursos naturales por las comunidades mayas de La Montaña, Hopelchén, Campeche. Investig. Geográficas 2008, 66, 65–80. [Google Scholar]
- INEGI. Compendio de Información Geográfica Municipal; Instituto Nacional de Estadística y Geografía: Aguascalientes, México, 2010. [Google Scholar]
- Vargas, A.; Julián, M. Proceso de Urbanización en Chetumal Quintana Roo 1981–2015; Asociación Mexicana de Ciencias para el Desarrollo Regional A.C.: Mexico City, Mexico, 2016; Volume 23. [Google Scholar]
- Vargas Godínez, C.; García Ortega, M. Vulnerabilidad y sistemas agrícolas: Una experiencia menonita en el sur de México. Soc. Y Ambiente 2018, 16, 137–156. [Google Scholar] [CrossRef]
- Huacuja, F.E. Expansión de la soja en México y Exclusión Productiva de los Pequeños Agricultores de la Península de Yucatán. Papeles Geogr. 2020, 66, 68–84. [Google Scholar] [CrossRef]
- Rogan, J.; Bumbarger, N.; Kulakowski, D.; Christman, Z.; Runfola, D.; Blanchard, S. Improving Forest type discrimination with mixed lifeform classes using fuzzy classification thresholds informed by field observations. Can. J. Remote Sens. 2010, 36, 699–708. [Google Scholar] [CrossRef]
- Snook, L.K. Partnerships and Sustainable Forest Management: Towards Sustaining Mahogany (Swietenia Macrophylla) in the Maya Forest of Mexico and Belize; CIFOR: Bogor, Indonesia, 2003. [Google Scholar]
- Gomez-Pompa, A.; Kaus, A. Taming the wilderness myth. BioScience 1992, 42, 271–279. [Google Scholar]
- Romero-Duque, L.P.; Jaramillo, V.J.; Pérez-Jiménez, A. Structure and diversity of secondary tropical dry forests in Mexico, differing in their prior land-use history. For. Ecol. Manag. 2007, 253, 38–47. [Google Scholar] [CrossRef]
- Bray, D.B.; Ellis, E.A.; Armijo-Canto, N.; Beck, C.T. The institutional drivers of sustainable landscapes: A case study of the ‘Mayan Zone’in Quintana Roo, Mexico. Land. Use Policy 2004, 21, 333–346. [Google Scholar] [CrossRef]
- INEGI. Conjunto de datos vectoriales de uso de suelo y vegetación, serie VII (escala 1:250 000). Instituto Nacional de Estadística y Geografía. 2021. Available online: https://www.inegi.org.mx/app/biblioteca/ficha.html?upc=889463967220 (accessed on 6 January 2021).
- USGS. Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30 m (GFCC30TCv003). Available online: https://lpdaac.usgs.gov/products/gfcc30tcv003/ (accessed on 1 January 2023).
- Liu, L.; Zhang, X.; Gao, Y.; Chen, X.; Shuai, X.; Mi, J. Finer-resolution mapping of global land cover: Recent developments, consistency analysis, and prospects. J. Remote Sens. 2021, 1–38. [Google Scholar] [CrossRef]
- Sexton, J.O.; Noojipady, P.; Song, X.-P.; Feng, M.; Song, D.-X.; Kim, D.-H.; Anand, A.; Huang, C.; Channan, S.; Pimm, S.L. Conservation policy and the measurement of forests. Nat. Clim. Change 2016, 6, 192–196. [Google Scholar] [CrossRef]
- EarthData, N. GFCC Percent Tree Cover Data. Available online: https://search.earthdata.nasa.gov/search (accessed on 5 October 2024).
- Wunder, S.J.F. Forests without trees? A note on problematic forest definitions and change assessments. Forest 2003, 93, 100. Available online: https://www.fao.org/4/XII/0173-B1.htm (accessed on 6 November 2024).
- Estoque, R.C.; Johnson, B.A.; Gao, Y.; DasGupta, R.; Ooba, M.; Togawa, T.; Hijioka, Y.; Murayama, Y.; Gavina, L.D.; Lasco, R.D.; et al. Remotely sensed tree canopy cover-based indicators for monitoring global sustainability and environmental initiatives. Environ. Res. Lett. 2021, 16, 044047. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef] [PubMed]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. A J. R. Meteorol. Soc. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- INEGI. Instituto Nacional de Estadística y Geografía Descarga de Imagenes. Available online: https://www.inegi.org.mx/temas/ (accessed on 1 January 2022).
- Cartus, O.; Kellndorfer, J.; Walker, W.; Franco, C.; Bishop, J.; Santos, L.; Michel Fuentes, J.M.A. National, detailed map of forest aboveground carbon stocks in Mexico. Remote Sens. 2014, 6, 5559–5588. [Google Scholar] [CrossRef]
- CONABIO. Geoportal Temperatura y Precipitación. Available online: http://geoportal.conabio.gob.mx (accessed on 6 January 2022).
- Zhu, B.; Fu, Y.; Liu, J.; He, R.; Zhang, N.; Mao, Y. Detecting the priority areas for health workforce allocation with LISA functions: An empirical analysis for China. BMC Health Serv. Res. 2018, 18, 1–14. [Google Scholar] [CrossRef]
- Li, Q.; Song, J.; Wang, E.; Hu, H.; Zhang, J.; Wang, Y. Economic growth and pollutant emissions in China: A spatial econometric analysis. Stoch. Environ. Res. 2014, 28, 429–442. [Google Scholar] [CrossRef]
- Armaș, I.; Gavriș, A. Social vulnerability assessment using spatial multi-criteria analysis (SEVI model) and the Social Vulnerability Index (SoVI model)—A case study for Bucharest, Romania. Nat. Hazards Earth Syst. Sci. 2013, 13, 1481–1499. [Google Scholar] [CrossRef]
- Liu, D.; Liu, W.; He, Y. How Does the Intensive Use of Urban Construction Land Improve Carbon Emission Efficiency? Evidence from the Panel Data of 30 Provinces in China. Land 2024, 13, 2133. [Google Scholar] [CrossRef]
- Deb, P.; Norton, E.C.; Manning, W.G. Health Econometrics Using Stata; Stata Press: College Station, TX, USA, 2017; Volume 3. [Google Scholar]
- Butt, E.W.; Baker, J.C.; Bezerra, F.G.S.; von Randow, C.; Aguiar, A.P.; Spracklen, D.V. Amazon deforestation causes strong regional warming. Proc. Natl. Acad. Sci. USA 2023, 120, e2309123120. [Google Scholar] [CrossRef]
- Dumelle, M.; Higham, M.; Ver Hoef, J.M. Spmodel: Spatial statistical modeling and prediction in R. PLoS ONE 2023, 18, e0282524. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, X.; Huang, Y.; On Chan, T. Spatial patterns of childhood obesity prevalence in relation to socioeconomic factors across England. ISPRS Int. J. Geo-Inf. 2020, 9, 599. [Google Scholar] [CrossRef]
- Jun, S.; Jung, J. Urban Livability Assessment in South Korea: Incorporating Climate Change Vulnerability. Urban. Sci. 2024, 8, 181. [Google Scholar] [CrossRef]
- Ochoa, S.A.H.; Navarro-Martínez, A.; Ellis, E.A.; Gómez, I.U.H. Deforestación en el municipio de Bacalar, Quintana Roo, México durante el período 1993–2017. Madera Y Bosques 2022, 28, 1–13. [Google Scholar] [CrossRef]
- Boubekraoui, H.; Maouni, Y.; Ghallab, A.; Draoui, M.; Maouni, A. Deforestation drivers in northern Morocco: An exploratory spatial data analysis. Environ. Res. Commun. 2024, 6, 071005. [Google Scholar] [CrossRef]
- Dos Santos, A.M.; da Silva, C.F.A.; de Almeida Junior, P.M.; Rudke, A.P.; de Melo, S.N. Deforestation drivers in the Brazilian Amazon: Assessing new spatial predictors. J. Environ. Manag. 2021, 294, 113020. [Google Scholar] [CrossRef]
- Shirvani, Z.; Abdi, O.; Buchroithner, M.F.; Pradhan, B. Analysing spatial and statistical dependencies of deforestation affected by residential growth: Gorganrood Basin, Northeast Iran. Land. Degrad. Dev. 2017, 28, 2176–2190. [Google Scholar] [CrossRef]
- Hage, R.D.S.; Nunes e Silva, S.V.; Bohm, B.C.; Lima, J.V.; Bruhn, N.C.P.; Menezes, G.R.; Bruhn, F.R.P. Spatiotemporal relationship between agriculture, livestock, deforestation, and visceral leishmaniasis in Brazilian legal Amazon. Sci. Rep. 2024, 14, 21542. [Google Scholar] [CrossRef]
- dos Santos, D.D.A.; Lopes, T.R.; Damaceno, F.M.; Duarte, S.N. Evaluation of deforestation, climate change and CO2 emissions in the Amazon biome using the Moran Index. J. S. Am. Earth Sci. 2024, 143, 105010. [Google Scholar] [CrossRef]
- Majumdar, D.D.; Biswas, A. Quantifying land surface temperature change from LISA clusters: An alternative approach to identifying urban land use transformation. Landsc. Urban. Plan. 2016, 153, 51–65. [Google Scholar] [CrossRef]
- Das, D.N.; Chakraborti, S.; Saha, G.; Banerjee, A.; Singh, D. Analysing the dynamic relationship of land surface temperature and landuse pattern: A city level analysis of two climatic regions in India. City Environ. Interact. 2020, 8, 100046. [Google Scholar] [CrossRef]
- Hernández Gómez, I.U.; Ellis, E.A.J. Selective logging and shifting agriculture may help maintain forest biomass on the Yucatán peninsula. Land. Degrad. Dev. 2023, 34, 4456–4471. [Google Scholar] [CrossRef]
- Ellis, E.A.; Navarro-Martínez, A.; García-Ortega, M. Drivers of forest cover transitions in the Selva Maya, Mexico: Integrating regional and community scales for landscape assessment. Land. Degrad. Dev. 2021, 32, 3122–3141. [Google Scholar] [CrossRef]
- Wang, W.; Neuman, E.J.; Newman, D.A. Statistical power of the social network autocorrelation model. Soc. Netw. 2014, 38, 88–99. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhou, Q.; He, Y.; Wang, C.; Wang, X.; Wang, H. An optimized approach for extracting urban land based on log-transformed DMSP-OLS nighttime light, NDVI, and NDWI. Remote Sens. 2021, 13, 766. [Google Scholar] [CrossRef]
- Manoharan, V.S.; Welch, R.M.; Lawton, R.O. Impact of deforestation on regional surface temperatures and moisture in the Maya lowlands of Guatemala. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- De la Barreda, B.; Metcalfe, S.E.; Boyd, D.S. Precipitation regionalization, anomalies and drought occurrence in the Yucatan Peninsula, Mexico. Int. J. Climatol. 2020, 40, 4541–4555. [Google Scholar] [CrossRef]
- Wu, H.C.; Felis, T.; Scholz, D.; Giry, C.; Kölling, M.; Jochum, K.P.; Scheffers, S.R. Changes to Yucatán Peninsula precipitation associated with salinity and temperature extremes of the Caribbean Sea during the Maya civilization collapse. Sci. Rep. 2017, 7, 15825. [Google Scholar] [CrossRef]
- Marchi, M.; Sinjur, I.; Bozzano, M.; Westergren, M. Evaluating WorldClim Version 1 (1961–1990) as the Baseline for Sustainable Use of Forest and Environmental Resources in a Changing Climate. Sustainability 2019, 11, 3043. [Google Scholar] [CrossRef]
- Marínez Sánchez, J.N.; Cuéllar Rodríguez, L.G.; Yerena Yamallel, J.I.; Cavazos Pérez, M.T.; Gárate Escamilla, H.A. Comparación de bases de datos climáticos en la modelación de distribución potencial de Pinus cembroides Zucc. Rev. Mex. Cienc. For. 2023, 14, 135–158. [Google Scholar] [CrossRef]
- Bobrowski, M.; Weidinger, J.; Schickhoff, U. Is New Always Better? Frontiers in Global Climate Datasets for Modeling Treeline Species in the Himalayas. Atmosphere 2021, 12, 543. [Google Scholar] [CrossRef]
- Sugiarto, Y.; Atmaja, T.; Nurhasanah, S. Evaluation of the use of data reanalysis for climate regionalization. IOP Conf. Ser. Earth Environ. Sci. 2017, 187, 012062. [Google Scholar] [CrossRef]
- Longo, M.; Saatchi, S.; Keller, M.; Bowman, K.; Ferraz, A.; Moorcroft, P.R.; Morton, D.C.; Bonal, D.; Brando, P.; Burban, B. Impacts of degradation on water, energy, and carbon cycling of the Amazon tropical forests. J. Geophys. Res. Biogeosciences 2020, 125, e2020JG005677. [Google Scholar] [CrossRef] [PubMed]
- Mitchard, E.T. The tropical forest carbon cycle and climate change. Nat. Clim. Change 2018, 559, 527–534. [Google Scholar] [CrossRef]
- Kanae, S.; Oki, T.; Musiake, K. Impact of deforestation on regional precipitation over the Indochina Peninsula. J. Hydrometeorol. 2001, 2, 51–70. [Google Scholar] [CrossRef]
- Lima, L.S.; Coe, M.T.; Soares Filho, B.S.; Cuadra, S.V.; Dias, L.C.; Costa, M.H.; Lima, L.S.; Rodrigues, H.O. Feedbacks between deforestation, climate, and hydrology in the Southwestern Amazon: Implications for the provision of ecosystem services. Landsc. Ecol. 2014, 29, 261–274. [Google Scholar] [CrossRef]
- Vázquez-Luna, M.; Ellis, E.A.; Martínez, M.A.N.; Cabrera, C.R.C.; Ortiz-Ceballos, G.C. Percepción pública sobre el cambio climático en la península de Yucatán, México. Soc. Y Ambiente 2024, 27, 1–26. [Google Scholar] [CrossRef]
- O’Brien, K.L. Tropical deforestation and climate change: What does the record reveal? Prof. Geogr. 1998, 50, 140–153. [Google Scholar] [CrossRef]
- Fenzi, M.; Rogé, P.; Cruz-Estrada, A.; Tuxill, J.; Jarvis, D.J. Community seed network in an era of climate change: Dynamics of maize diversity in Yucatán, Mexico. Agric. Hum. Values 2022, 39, 339–356. [Google Scholar] [CrossRef]
- Pereira Corona, A.; Prezas Hernández, B.; Olivares Mendoza, J.A.; Fragoso Servón, P.; Niño Torres, C.A. Programa Estatal de Acción ante el Cambio Climático (Estado de Quintana Roo); Universidad de Quintana Roo: Chetumal, Mexico, 2013; Available online: https://risisbi.uqroo.mx/handle/20.500.12249/4571 (accessed on 10 November 2024).
- PEACCC. Programa Estatal ante el Cambio Climático Campeche, Visión 2015–2030; Gobierno del estado de Campeche: Campeche, Mexico, 2015; pp. 7–88. [Google Scholar]
- PEACCQ. Programa Estatal ante el Cambio Climático Quintana Roo; Gobierno del estado de Quintana Roo: Campeche, Mexico, 2013; pp. 1–102. [Google Scholar]
- PEACCY. Programa Especial de Acción ante el Cambio Climático Yucatán; Gobierno del estado de Yucatán: Campeche, Mexico, 2014; pp. 1–110. [Google Scholar]
- Griscom, B.W.; Adams, J.; Ellis, P.W.; Houghton, R.A.; Lomax, G.; Miteva, D.A.; Schlesinger, W.H.; Shoch, D.; Siikamäki, J.V.; Smith, P. Natural climate solutions. Proc. Natl. Acad. Sci. USA 2017, 114, 11645–11650. [Google Scholar] [CrossRef]
- Cook-Patton, S.C.; Drever, C.R.; Griscom, B.W.; Hamrick, K.; Hardman, H.; Kroeger, T.; Pacheco, P.; Raghav, S.; Stevenson, M.; Webb, C. Protect, manage and then restore lands for climate mitigation. Nat. Clim. Change 2021, 11, 1027–1034. [Google Scholar] [CrossRef]

| Variables | Symbol | Type of Variable | Description | Scale of Measurement |
|---|---|---|---|---|
| Temperature | TMP | Dependent | Mean annual temperature (2000–2015) | Continuous |
| Minimum Temperature | MINT | Dependent | Mean minimum annual temperature (2000–2015) | Continuous |
| Maximum Temperature | MAXT | Dependent | Mean maximum annual temperature (2000–2015) | Continuous |
| Dry Season Temperature | DTEMP | Dependent | Mean temperature during the dry season (December–May 2000–2015) | Continuous |
| Minimum Dry Season Temperature | DMINT | Dependent | Mean minimum temperature during the dry season (December–May 2000–2015) | Continuous |
| Maximum Dry Season Temperature | DMAXT | Dependent | Mean maximum temperature during the dry season (December–May 2000–2015) | Continuous |
| Wet Season Temperature | WTEMP | Dependent | Mean temperature during the wet season (June–November 2000–2015) | Continuous |
| Minimum Wet Season Temperature | WMINT | Dependent | Mean minimum temperature during the wet season (June–November 2000–2015) | Continuous |
| Maximum Wet Season Temperature | WMAXT | Dependent | Mean maximum temperature during the wet season (June–November 2000–2015) | Continuous |
| Annual Precipitation | PPT | Dependent | Mean annual precipitation (2000–2015) | Continuous |
| Dry Season Precipitation | DPPT | Dependent | Mean annual precipitation during the dry season (December–May 2000–2015) | Continuous |
| Wet Season Precipitation | WPPT | Dependent | Mean annual precipitation during the wet season (June–November 2000–2015) | Continuous |
| Forest Cover 2000–2015 | FOR | Fixed | Percent tree cover greater than 70% during years 2000, 2005, 2010, and 2015 | Categorical |
| Degradation 2000–2015 | DEGR | Fixed | Percent tree cover from 30% to 70% during years 2000, 2005, 2010, and 2015 | Categorical |
| Deforestation 2000–2015 | DEFOR | Fixed | Percent tree cover below 30% during years 2000, 2005, 2010, and 2015 | Categorical |
| Biomass | BIO | Covariate | Above ground biomass (kg ha−1) with 30 m resolution | Continuous value |
| Elevation | ELEV | Covariate | Elevation above sea level in meters with 15 m resolution | Continuous value |
| Urban Centers | URB | Covariate | Distance to main urban areas in meters | Continuous value |
| Water Bodies | WAT | Covariate | Distance to water bodies in meters | Continuous value |
| Roads | RDS | Covariate | Distance to roads in meters | Continuous value |
| Vegetation Type | VEG | Covariate | Vegetation type or ecosystem and land use | Integer value |
| Minimum Temperature Zones | ZMINT | Covariate | INEGI minimum temperature zones | Integer value |
| Maximum Temperature Zones | ZMAXT | Covariate | INEGI maximum temperature zones | Integer value |
| Precipitation Zones | ZPPT | Covariate | INEGI precipitation regions | Integer value |
| Variables | TEMP | MINT | MAXT |
|---|---|---|---|
| Coefficient (SE) | Coefficient (SE) | Coefficient (SE) | |
| DEGR | 0.007 (0.015) | 0.040 (0.027) | 0.044 (−0.023) |
| DEFOR | 0.062 ** (0.020) | 0.123 *** (0.035) | 0.044 (−0.030) |
| BIO | 1.21 × 10−3 * (6.13 × 10−4) | 2.78 ** (1.10 × 10−3) | −4.50 × 10−3 *** (−9.31 × 10−4) |
| ELEV | −3.25 × 10−3 *** (8.35 × 10−5) | −5.31 × 10−3 *** (1.423 × 10−4) | −1.06 × 10−3 *** (1.26 × 10−4) |
| URB | 0.0000014 (7.51 × 10−7) | 0.0000165 *** (1.37 × 10−6) | −3.73 × 10−6 *** (1.15 × 10−6) |
| WAT | −5.17 × 10−6 *** (5.29 × 10−7) | −0.000012 *** (1.00 × 10−6) | 1.41 × 10−6 (8.07 × 10−7) |
| RDS | −1.21 × 10−6 (1.35 × 10−6) | 7.86 × 10−6 ** (2.53 × 10−6) | −7.87 × 10−6 *** (2.07 × 10−6) |
| VEG | −1.1429 × 10−3 (1.79 × 10−3) | −0.0139 *** (3.13 × 10−3) | 0.015 *** (2.71 × 10−3) |
| ZMINT | 0.051 *** (3.46 × 10−3) | 0.151 *** (6.37 × 10−3) | −0.053 *** (5.27 × 10−3) |
| ZMAXT | 0.034 *** (3.89 × 10−3) | −0.061 *** (7.02 × 10−3) | 0.161 *** (5.94 × 10−3) |
| ZPPT | 1.37 × 10−4 *** (2.7 × 10−5) | 5.38 × 10−4 *** (4.45 × 10−5) | −8.65 × 10−5 * (4.12 × 10−5) |
| Constant | 24.601 *** (0.145) | 19.719 *** (0.259) | 28.052 *** (0.222) |
| Spatial Lag | −1.41 × 10−3 (1.21 × 10−3) | −0.011 *** (2.30 × 10−3) | 0.010 *** (1.46 × 10−3) |
| Spatial Error | 2.674 *** (0.034) | 3.542 *** (0.073) | 2.639 *** (0.032) |
| Model Parameters | n = 3000 Wald Chi2 (12) = 4710.16 Prob > Chi2 = 0.000 Pseudo R2 = 0.541 | n = 3000 Wald Chi2 (12) = 6989.23 Prob > Chi2 = 0.000 Pseudo R2 = 0.677 | n = 3000 Wald Chi2 (12) = 3188.45 Prob > Chi2 = 0.000 Pseudo R2 = 0.546 |
| Variables | DTEMP | DMINT | DMAXT |
|---|---|---|---|
| Coefficient (SE) | Coefficient (SE) | Coefficient (SE) | |
| DEGR | 0.114 *** (0.021) | 0.060 (0.033) | 0.229 *** (0.034) |
| DEFOR | 0.178 *** (0.027) | 0.167 *** (0.042) | 0.238 *** (0.044) |
| BIO | 7.22 × 10−4 (8.42 × 10−4) | 4.52 × 10−3 *** (1.31 × 10−3) | −5.54 × 10−3 *** (1.36 × 10−3) |
| ELEV | −2.58 × 10−3 *** (1.13 × 10−4) | −5.36 × 10−3 *** (1.72 × 10−4) | 1.76 × 10−4 (1.85 × 10−4) |
| URB | −1.42 × 10−6 (1.04 × 10−6) | 1.51 × 10−5 *** (1.64 × 10−6) | −1.04 × 10−5 *** (1.66 × 10−6) |
| WAT | −3.44 × 10−6 *** (7.31 × 10−7) | −0.0000135 *** (1.18 × 10−6) | 6.72 × 10−6 *** (1.17 × 10−6) |
| RDS | −5.69 × 10−6 ** (1.87 × 10−6) | 5.06 × 10−6 (2.99 × 10−6) | −1.34 × 10−5 *** (3.00 × 10−6) |
| VEG | −6.59 × 10−4 (2.44 × 10−3) | −0.019 *** (3.76 × 10−3) | 0.019 *** (3.96 × 10−3) |
| ZMINT | 0.038 *** (4.77 × 10−3) | 0.164 *** (7.60 × 10−3) | −0.092 *** (7.66 × 10−3) |
| ZMAXT | 0.108 *** (5.37 × 10−3) | −0.036 *** (8.47 × 10−3) | −1.26 × 10−4 * (5.98 × 10−5) |
| ZPPT | 1.199 × 10−4 *** (3.74 × 10−5) | 5.06 × 10−4 *** (5.63 × 10−5) | 1.199 × 10−4 ** (3.74 × 10−5) |
| Constant | 22.899 *** (0.201) | 18.761 *** (0.315) | 25.768 *** (0.322) |
| Spatial Lag | 0.013 *** (1.57 × 10−3) | 5.14 × 10−3 (2.90 × 10−3) | 0.021 *** (2.04 × 10−3) |
| Spatial Error | 2.621 *** (0.019) | 3.065 *** (0.047) | 2.509 *** (0.040) |
| Model Parameters | n = 3000 Wald Chi2 (12) = 4173.27 Prob > Chi2 = 0.000 Pseudo R2 = 0.484 | n = 3000 Wald Chi2 (12) = 4316.73 Prob > Chi2 = 0.000 Pseudo R2 = 0.559 | n = 3000 Wald Chi2 (12) = 3968.32 Prob > Chi2 = 0.000 Pseudo R2 = 0.603 |
| Variables | WTEMP | WMINT | WMAXT |
|---|---|---|---|
| Coefficient (SE) | Coefficient (SE) | Coefficient (SE) | |
| DEGR | 0.022 (0.015) | 0.0220 (0.025) | 0.057 * (0.023) |
| DEFOR | 0.072 *** (0.019) | 0.101 ** (0.033) | 0.056 (0.029) |
| BIO | 9.86 × 10−4 (5.84 × 10−4) | 2.536 × 10−3 * (1.02 × 10−3) | −2.5796 × 10−3 ** (9.12 × 10−4) |
| ELEV | −3.05 × 10−3 *** (7.82 × 10−5) | −5.59 × 10−3 *** (1.33 × 10−4) | −4.82 × 10−4 *** (1.23 × 10−4) |
| URB | 1.60 × 10−6 * (7.22 × 10−7) | 1.11 × 10−5 *** (1.27 × 10−6) | −3.05 × 10−6 ** (1.13 × 10−6) |
| WAT | −3.65 × 10−6 *** (5.09 × 10−7) | 6.72 × 10−6 *** (9.19 × 10−7) | −7.51 × 10−7 (7.93 × 10−7) |
| RDS | −3.19 × 10−6 ** (1.30 × 10−6) | 3.75 × 10−6 (2.32 × 10−6) | 8.01 × 10−6 *** (2.03 × 10−6) |
| VEG | −3.06 × 10−3 (1.69 × 10−3) | −0.0147 *** (2.91 × 10−3) | 0.011 *** (2.64 × 10−3) |
| ZMINT | 0.052 *** (3.32 × 10−3) | 0.133 *** (5.90 × 10−3) | −0.037 *** (5.18 × 10−3) |
| ZMAXT | 0.021 *** (3.73 × 10−3) | −0.083 *** (6.54 × 10−3) | 0.148 *** (5.83 × 10−3) |
| ZPPT | 1.732 *** (2.6 × 10−5) | 2.608 × 10−4 *** (4.29 × 10−5) | 7.18 × 10−5 (4.05 × 10−5) |
| Constant | 26.777 *** (0.140) | 23.010 *** (0.243) | 29.754 *** (0.218) |
| Spatial Lag | −7.34 × 10−3 *** (1.06 × 10−3) | −0.014 *** (2.06 × 10−3) | 2.19 × 10−5 (1.36 × 10−3) |
| Spatial Error | 2.630 *** (0.043) | 3.408 *** (0.062) | 2.641 *** (0.034) |
| Model Parameters | n = 3000 Wald Chi2 (12) = 6068.25 Prob > Chi2 = 0.000 Pseudo R2 = 0.504 | n = 3000 Wald Chi2 (12) = 8507.97 Prob > Chi2 = 0.000 Pseudo R2 = 0.693 | n = 3000 Wald Chi2 (12) = 2022.41 Prob > Chi2 = 0.000 Pseudo R2 = 0.390 |
| Variables | PPT | DPPT | WPPT |
|---|---|---|---|
| Coefficient (SE) | Coefficient (SE) | Coefficient (SE) | |
| DEGR | −0.546 (0.6720) | −3.174 *** (0.550) | 6.211 *** (1.220) |
| DEFOR | −0.358 (0.872) | −3.759 *** (0.7124) | 3.120 * (1.588) |
| BIO | 0.063 * (0.027) | −0.0148 (0.022) | 0.051 (0.049) |
| ELEV | −0.006 (0.004) | 0.055 *** (3.29 × 10−3) | −0.0671243 *** (0.0073214) |
| URB | 1.23 × 10−4 *** (3.21 × 10−5) | 1.48 × 10−4 *** (2.71 × 10−5) | −1.183 × 10−4 * (5.83 × 10−5) |
| WAT | 1.55 × 10−6 (2.27 × 10−5) | 7.87 × 10−5 *** (1.9 × 10−5) | 1.04 × 10−6 (4.12 × 10−5) |
| RDS | 0.0001211 * (0.0000587) | 1.04 × 10−4 * (4.9 × 10−5) | 5.48 × 10−5 (1.07 × 10−4) |
| VEG | −0.052 (7.96 × 10−2) | 0.0193 (0.064) | 0.329 * (0.145) |
| ZMINT | 0.195 (0.149) | −0.602 *** (0.125) | −1.394 *** (0.270) |
| ZMAXT | −0.781 *** 0.165 | −0.716 *** (0.138) | 3.105 *** (0.305) |
| ZPPT | 3.97 × 10−2 *** (1.11 × 10−3) | 0.023 *** (9.47 × 10−4) | 0.057 *** (2.017 × 10−3) |
| Constant | 84.296 *** (6.155) | 61.472 *** (5.245) | 8.383 (11.153) |
| Spatial Lag | −0.0252 (0.015) | 0.046 * (0.021109) | 0.029 (0.017) |
| Spatial Error | 2.535 *** (0.020) | 3.295 *** (0.068) | 2.499 *** (0.025) |
| Model Parameters | n = 3000 Wald Chi2 (12) = 1472.30 Prob > Chi2 = 0.000 Pseudo R2 = 0.557 | n = 3000 Wald Chi2 (12) = 3688.12 Prob > Chi2 = 0.000 Pseudo R2 = 0.454 | n = 3000 Wald Chi2 (12) = 1352.48 Prob > Chi2 = 0.000 Pseudo R2 = 0.468 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez-Luna, M.; Ellis, E.A.; Navarro-Martínez, M.A.; Cerdán-Cabrera, C.R.; Ortiz-Ceballos, G.C. Evaluating the Spatial Relationships Between Tree Cover and Regional Temperature and Precipitation of the Yucatán Peninsula Applying Spatial Autoregressive Models. Land 2025, 14, 943. https://doi.org/10.3390/land14050943
Vázquez-Luna M, Ellis EA, Navarro-Martínez MA, Cerdán-Cabrera CR, Ortiz-Ceballos GC. Evaluating the Spatial Relationships Between Tree Cover and Regional Temperature and Precipitation of the Yucatán Peninsula Applying Spatial Autoregressive Models. Land. 2025; 14(5):943. https://doi.org/10.3390/land14050943
Chicago/Turabian StyleVázquez-Luna, Mayra, Edward A. Ellis, María Angélica Navarro-Martínez, Carlos Roberto Cerdán-Cabrera, and Gustavo Celestino Ortiz-Ceballos. 2025. "Evaluating the Spatial Relationships Between Tree Cover and Regional Temperature and Precipitation of the Yucatán Peninsula Applying Spatial Autoregressive Models" Land 14, no. 5: 943. https://doi.org/10.3390/land14050943
APA StyleVázquez-Luna, M., Ellis, E. A., Navarro-Martínez, M. A., Cerdán-Cabrera, C. R., & Ortiz-Ceballos, G. C. (2025). Evaluating the Spatial Relationships Between Tree Cover and Regional Temperature and Precipitation of the Yucatán Peninsula Applying Spatial Autoregressive Models. Land, 14(5), 943. https://doi.org/10.3390/land14050943







