Kinematics Modeling and Analysis of Mid-Low Speed Maglev Vehicle with Screw and Product of Exponential Theory
Abstract
:1. Introduction
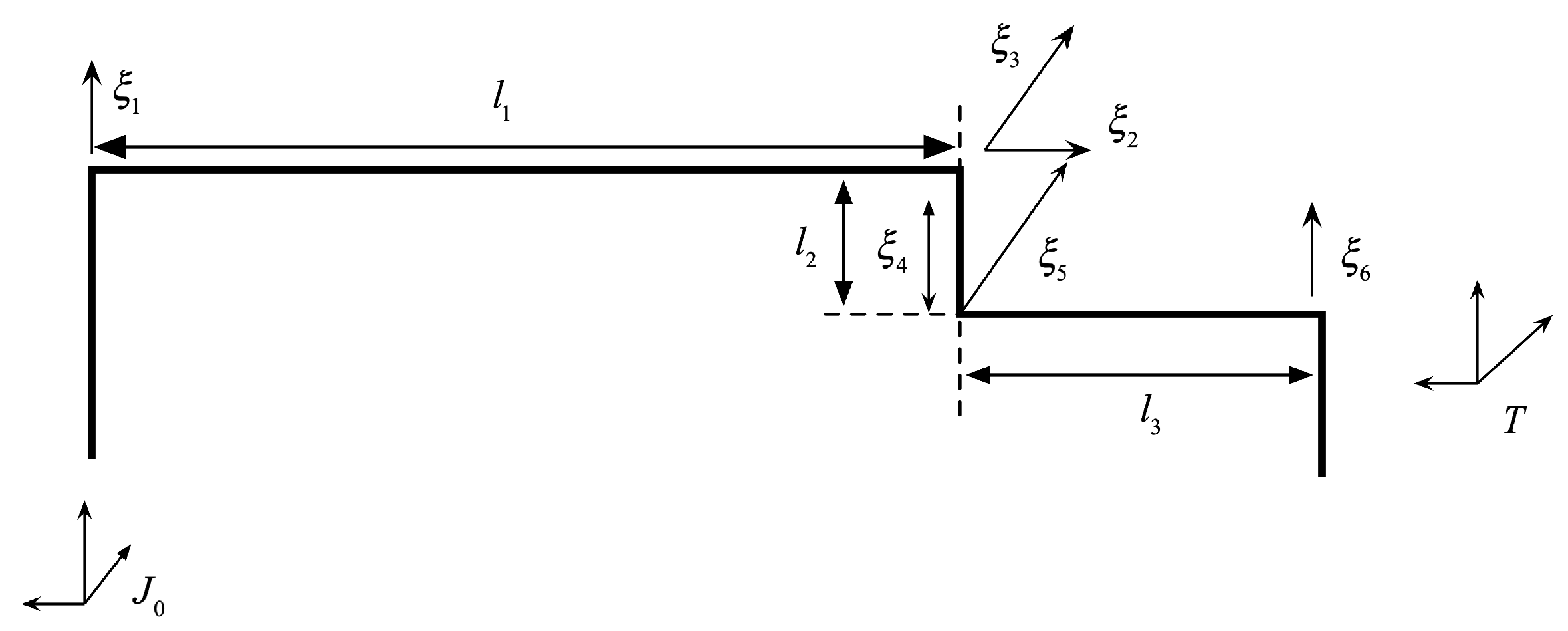
2. Forward Kinematics Modeling for a Mid-Low Speed Maglev Train
- (1)
- There is a rotational degree of freedom along the z-direction between base 0 and anti-roll beam 1, whose twist coordinate is . This degree of freedom can decouple the motion of the left and right modules of the suspension frame in the running direction.
- (2)
- The ball joint between the anti-roll beam 1 and the hanger rod 2, respectively, includes three rotational degrees of freedom along x, y, and z. Considering the constraint relationship between the two anti-roll beams, the rotational degree of freedom in the z-direction can be ignored. Thus, the rotational degrees of freedom in the x- and y-directions are just considered, and the twists of rotation are and , respectively.
- (3)
- The hanger rod 2 has a telescopic translational freedom, and its twist is .
- (4)
- The ball joint between the anti-roll beam 1 and the hanger 2 respectively includes three rotational degrees of freedom. The degree of freedom in the z-direction is ignored, and the rotational freedom in the x-direction is retained and the twist is .
- (5)
- There is a rotational degree of freedom in the z-direction between the anti-roll beam 3 and the right module 4, whose twist coordinates are .
3. Solution of Reverse Motion of a Mid-Low Speed Maglev Train
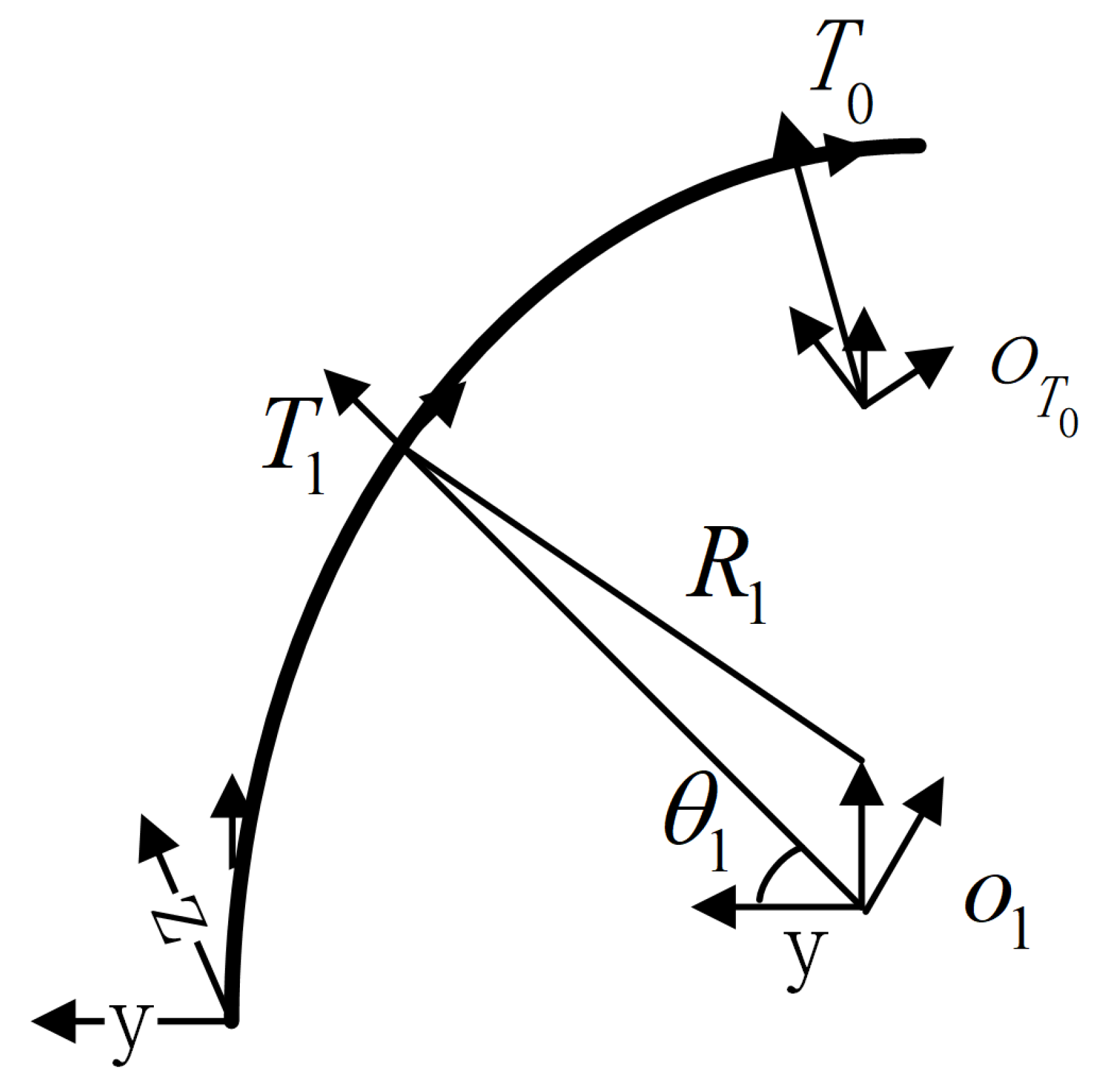
4. The Relationship of the Vehicle/Track Position–Posture on the Transition Curve Track
4.1. Parametric Description of the Transition Curve
4.2. The Track Coordinate System on the Transition Curve
4.3. The Posture Matrix of Train Reference System Relative to Track Reference System
5. The Motion Analysis of the Maglev Train
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Each Element in Equation (4)
References
- Youlun, X. Science of Robotics; China Machine Press: Beijing, China, 1992. [Google Scholar]
- Zixing, C. Robotics: Principles and Applications; South and Center University Press: Changsha, China, 1988. [Google Scholar]
- Murray, R.; Zexiang, L.; Sastry, S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Jingjun, D.; Xinjun, L.; Xilun, D. Mathematic Foundation of Mechanisms and Robotics, 2nd ed.; Machine Press: Beijing, China, 2016. [Google Scholar]
- Santolaria, J.; Aguilar, J.-J.; Yagüe, J.-A.; Pastor, J. Kinematic parameter estimation technique for calibration and repeatability improvement of articulated arm coordinate measuring machines. Precis. Eng. 2008, 32, 251–268. [Google Scholar] [CrossRef]
- Jie, L.; Tijian, S.; Kun, Z. Kinematical Analysis for the Second Suspension System of the Maglev Vehicle. J. China Railw. Soc. 2007, 29, 32–38. [Google Scholar]
- Fernandez-Gauna, B.; Lopez-Guede, J.M.; Zulueta, E.; Echegoyen, Z.; Graña, M. Basic results and experiments on robotic multi-agent system for hose deployment and transportation. Int. J. Artif. Intell. 2011, 6, 183–202. [Google Scholar]
- Takács, Á.; Kovács, L.; Rudas, I.; Precup, R.-E.; Haidegger, T. Models for force control in telesurgical robot systems. Acta Polytech. Hung. 2015, 12, 95–114. [Google Scholar]
- Jie, L.; Guanchun, L.; Kun, Z.; Peng, C.; Danfeng, Z. Kinematical Analysis for the Second Suspension System of the Mid-Low-Speed Maglev Vehicle. In Proceedings of the 2013 China Automation Congress(CAC), Changsha, China, 7–8 November 2013. [Google Scholar]
- Kun, Z.; Jie, L.; Wensen, C. Structure Decoupling Analysis of Maglev Train Bogie. Electr. Drive Locomot. 2005, 2005, 22–39. [Google Scholar]




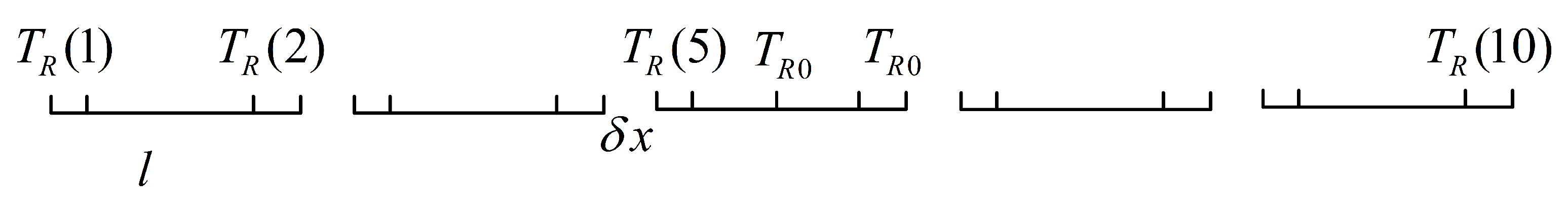

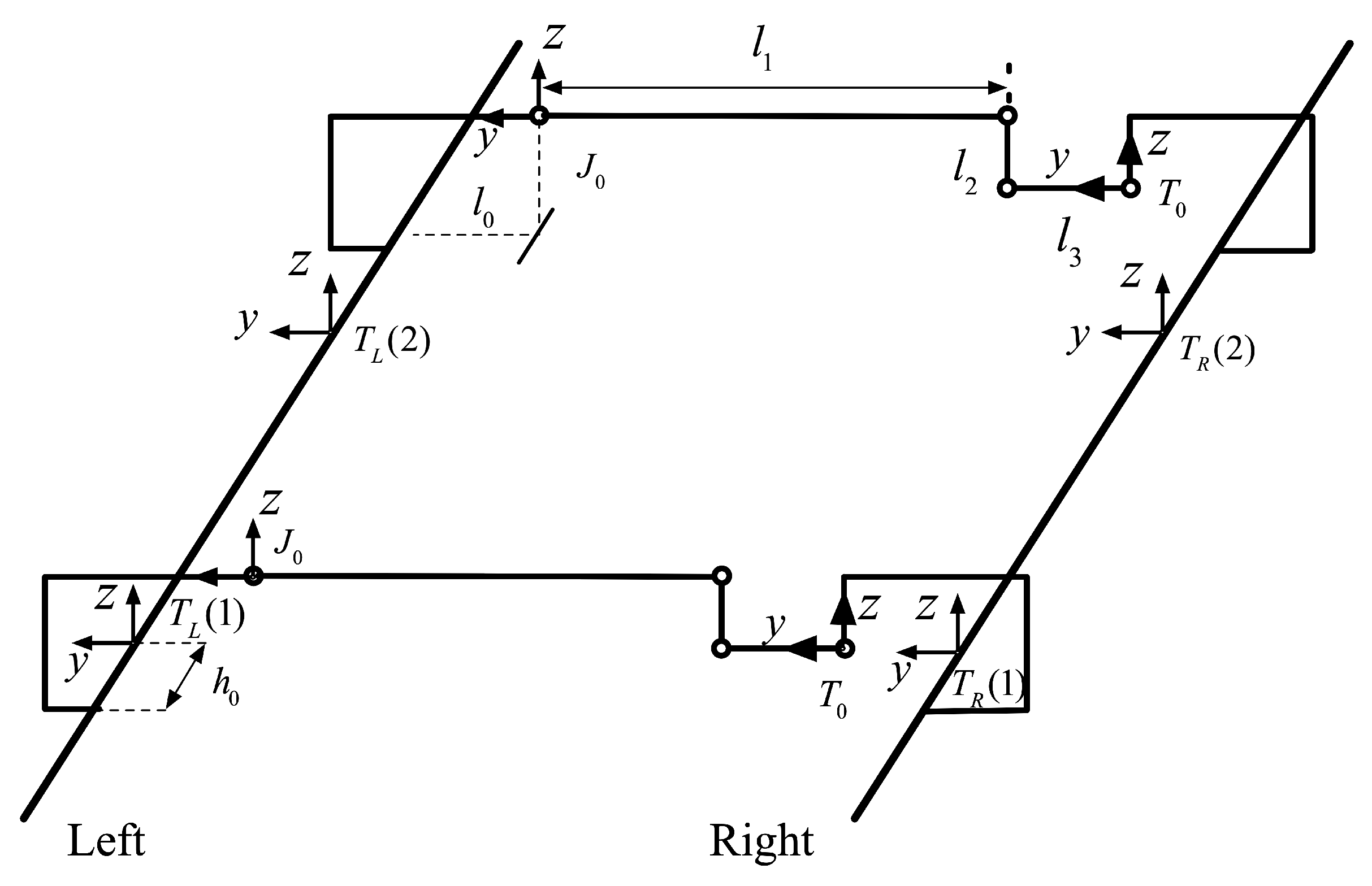
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Minimum Curve Radius | 1000 m | m | |
| Maximum transverse slope angle | m | ||
| Gauge D | 2 m | m | |
| The length of electromagnet l | m | m | |
| The distance between adjacent magnets | m | m | |
| The distance of the air spring on the same module | m | m | |
| The distance of adjacent air springs | m | The length of transition curve | 36 m |
| Number | (degree) | (degree) | (degree) | (mm) | (degree) | (degree) |
|---|---|---|---|---|---|---|
| 1 | 0.42 | −0.33 | −0.00 | −5.58 | 0.01 | −0.42 |
| 2 | −0.29 | −0.33 | 0.00 | 5.59 | −0.00 | 0.29 |
| 3 | 0.46 | −0.33 | −0.00 | −5.58 | 0.01 | −0.46 |
| 4 | −0.33 | −0.33 | −0.00 | 5.59 | −0.00 | 0.33 |
| 5 | 0.50 | −0.33 | −0.00 | −5.58 | 0.01 | −0.50 |
| 6 | −0.37 | −0.33 | −0.00 | 5.59 | −0.00 | 0.37 |
| 7 | 0.54 | −0.33 | −0.00 | −5.57 | 0.01 | −0.54 |
| 8 | −0.41 | −0.33 | −0.00 | 5.59 | −0.00 | 0.41 |
| 9 | 0.58 | −0.33 | −0.01 | −5.57 | 0.01 | −0.58 |
| 10 | −0.44 | −0.33 | −0.00 | 5.59 | −0.00 | 0.44 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, P.; Li, J.; Jin, Y. Kinematics Modeling and Analysis of Mid-Low Speed Maglev Vehicle with Screw and Product of Exponential Theory. Symmetry 2019, 11, 1201. https://doi.org/10.3390/sym11101201
Leng P, Li J, Jin Y. Kinematics Modeling and Analysis of Mid-Low Speed Maglev Vehicle with Screw and Product of Exponential Theory. Symmetry. 2019; 11(10):1201. https://doi.org/10.3390/sym11101201
Chicago/Turabian StyleLeng, Peng, Jie Li, and Yuxin Jin. 2019. "Kinematics Modeling and Analysis of Mid-Low Speed Maglev Vehicle with Screw and Product of Exponential Theory" Symmetry 11, no. 10: 1201. https://doi.org/10.3390/sym11101201
APA StyleLeng, P., Li, J., & Jin, Y. (2019). Kinematics Modeling and Analysis of Mid-Low Speed Maglev Vehicle with Screw and Product of Exponential Theory. Symmetry, 11(10), 1201. https://doi.org/10.3390/sym11101201






