1. Introduction
An extreme learning machine (ELM) is an innovative learning algorithm for the single hidden layer feed-forward neural networks (SLFNs for short), proposed by Huang et al [
1], that is characterized by the internal parameters generated randomly without tuning. In essence, the ELM is a special artificial neural network model, whose input weights are generated randomly and fixed, so as to get the unique least-squares solution of the output weight [
1], making the performance better [
2,
3,
4]. In the conventional model there is a lack of convergence ability, generalization, over-fitting, local minimum and parameter adjustment, all of which make the ELM superior [
1,
5]. Considering the learning process of the ELM, it is relatively simple. Firstly, some internal parameters of the hidden layer are generated randomly, such as input weights connecting the input layer and hidden layer, the number of hidden layer neurons, etc., which are fixed during the whole process. Secondly, the non-linear mapping function is selected to map the inputting data to the feature space, and through analyzing the real output results and expected output results, the key parameter (output weight connecting the hidden layer and the output layer) can be directly obtained, omitting iterative tuning. So, its training speed is considerably faster than that of the conventional algorithms [
6].
Due to the good performance of the ELM, it is used widely in regression and classification. For meeting higher requirements, researchers optimize and improve the ELM, and have proposed many better algorithms based on ELM. Di Wang et al. combined the local-weighted jackknife and RELM, proposed a novel conformal regressor (LW-JP-RELM), which complements ELM with interval predictions satisfying a given level of confidence [
7]. For improving the generalization performance, Ying Yin et al. proposed enhancing the ELM by a Markov boundary-based feature selection, based on the feature interaction and the mutual information to reduce the number of features, so as to construct more compact network, whose generalization was improved greatly [
8]. Ding et al. reformulated an optimization extreme learning machine to take a new regularization parameter, which is bounded between 0 and 1, and also easier to interpret as compared to the error penalty parameter
, it could achieve better generalization performance [
9]. For solving sensibility of ELM to the ill-conditioned data, Hasan et al. proposed two novel algorithms based on ELM, ridge regression and almost unbiased ridge regression, and also gave three criteria to select the regularization parameter, which improved the generalization and stability of the ELM greatly [
10]. Besides, there are more effective algorithms based on the ELM, such as Distributed Generalized Regularized ELM (DGR-ELM) [
11], Self-Organizing Map ELM (SOM-ELM) [
12], Data and Model Parallel ELM (DMP-ELM) [
13], Genetic Algorithm ELM (GA-ELM) [
14], Jaya optimization with mutation ELM (MJaya-ELM) [
15], et al.
Either with a simple ELM or more complex algorithms based on ELM one must find the optimal solution of the two key parameters in ELM essentially, the number of hidden layer neurons and the output weights. From input layer to the output layer, essentially ELM learns the output weights based on the least squares regression analysis [
16]. Therefore, many algorithms except those mentioned above are still proposed based on least squares regression, and their main work is to find an optimal transformation matrix, so as to minimize the error of sum-of-squares. Among these strategies [
17,
18], introducing orthogonal constraint into the optimization problem is required and also employed widely in the classification and subspace learning. Nie et al. showed that the performance of least squares discriminant and regression analysis after introducing orthogonal constraint is much better than those without orthogonal constraint [
19,
20]. After introducing orthogonal constraint into ELM, the optimization problem is seen as unbalanced procrustes problems, which is hard to be solved. Yong Peng et al. pointed out that the unbalanced procrustes problem can be transformed into a balanced procrustes problem, which is relatively simple [
16]. Motivated by this research, in this paper we focus on the output weight, a novel orthogonal optimizing method (NOELM) is proposed to solve the unbalanced procrustes problem, and its main contribution is that the optimization of complex matrix is decomposed into optimizing the single column vector of the matrix, reducing the complexity of the algorithm.
The remainder of the paper is organized as follows.
Section 2 reviews briefly the basic ELM model. In
Section 3, the model formulation and the iterative optimization method are detailed. The convergence and complexity analysis is presented in
Section 4. In
Section 5, the experiments are conducted to show the performances of NOELM. Finally,
Section 6 concludes the paper.
2. Extreme Learning Machine
Mathematically, given
discrete sample
, where
is the sample number,
is the input vector,
is the expected output vector, and the expected output of the
sample is
,
,
. For selected activation function, if the real output of the SLFNs is the same as the expected output
, the mathematical representation of SLFNs is as follows:
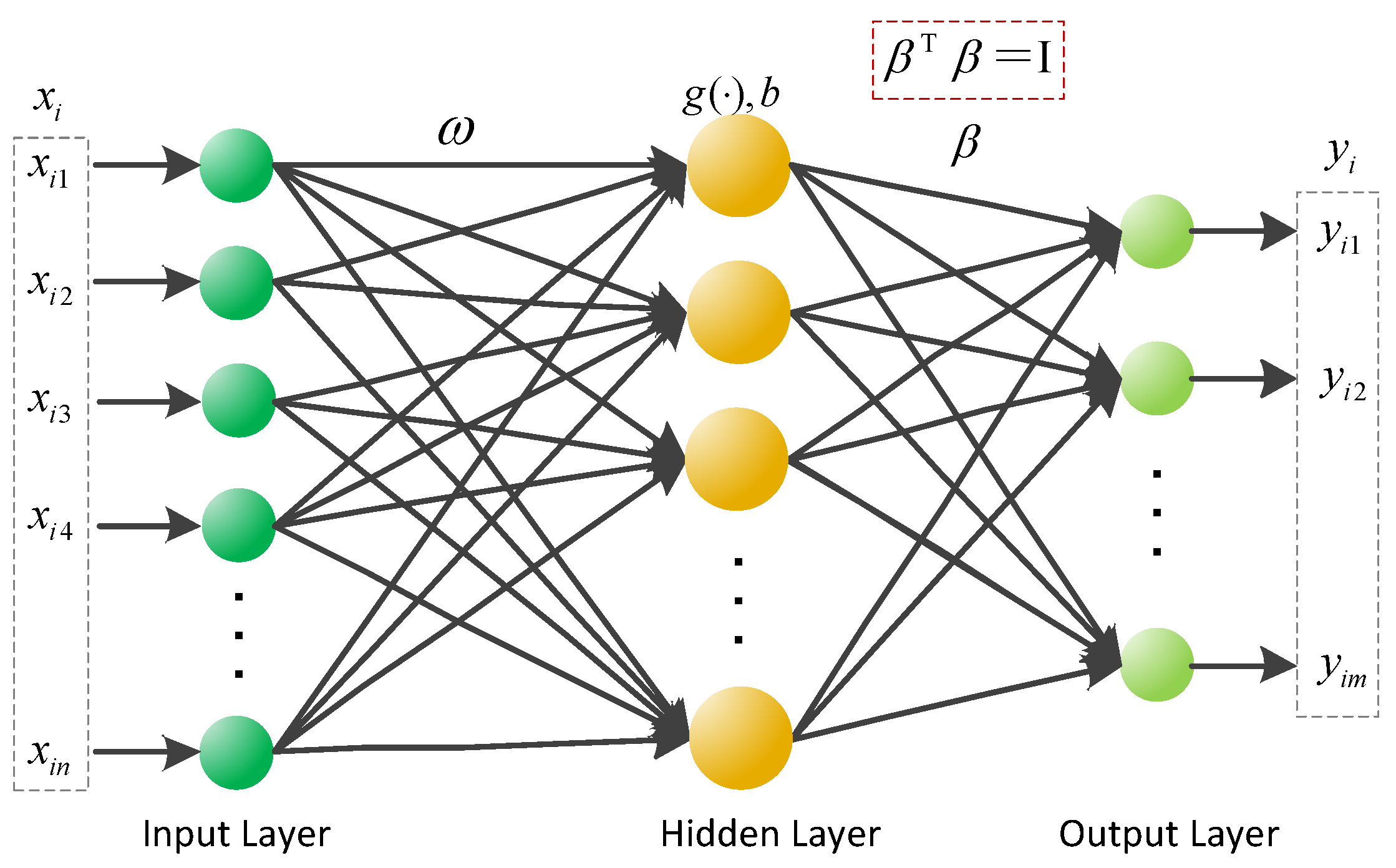
where
is the input weight connecting the input layer to the
hidden layer neuron,
is the basis of the
hidden layer neuron,
is the output weight connecting the
hidden layer neuron and the output layer, and
is the number of the hidden layer neurons, shown in
Figure 1.
Equation (1) can be compactly rewritten as
where
So, based on the theory of ELM, the optimal solution of Equation (2) is as follows,
where
is the Moore–Penrose inverse of the Matrix
,
. For further improving model precision, the regularization is introduced into ELM, the optimal problem is transformed as follows,
where
is the regularization parameter, which is used to balance the empirical risk and structural risk. Based on the Karush–Kuhn–Tucker condition, the optimal solution of
is obtained:
3. Novel Orthogonal Extreme Learning Machine (NOELM)
The orthogonal constraint is introduced into ELM, shown in
Figure 1, the optimal problem is transformed as follows,
where
,
is the output matrix and the output weight of the hidden layer,
. Because of the orthogonal constraint, the input samples are mapped into an orthogonal subspace, where their metric structure could be preserved.
Set
, so the problem (8) is an unbalanced orthogonal procrustes problem which is difficult to be resolved directly because of the orthogonal constraint [
16]. In this paper, an improved method is proposed to optimize the problem (8) based on the following lemma.
Lemma 1 [[
21], Theorem 3.1]
. If is the optimal solution for the problem (8) and its orthogonal complement is , then is positive, semi-definite and symmetric, andwhere , is the column vector of .
The proof of Lemma 1 is simple, which can be found in the literature [
21]. Motivated by Lemma 1, a local transformation is applied in the Equation (8), we relax the
column
(
and fix others,
, then the equation could be transformed into
If is the optimal solution of Equation (10), the approximation could be improved after replacing by , and obviously, the modified is also orthogonal.
To resolve the constrained problem (10) is a little difficult, so, the orthogonal complement
of
can be used to simplify the Equation (10). Set
, and it is known
, then
is the orthogonal complement of
. So, in the constrained problem (10), the condition
could be represented in another form,
,
is a unit vector. Thus, the problem (10) can be transformed into the following form with quadratic equality constraint:
Clearly, after get the optimal solution
of problem (11), the solution of problem (10) is
. If the orthogonal complement of
is
, then
,
is the orthogonal complement of
, and it can be constructed easily, using the Householder reflection
with
, which meets
,
is the first component of
. Indeed, partitioning
,
and
can be picked out from the following equation,
For resolving the problem (11), it first rewrites the Equation (11) in general form,
where
,
.
is transformed in the following form
Known from the Equations (13) and (14), the parameters
and
are fixed, the minimum problem of function
is transformed to the maximum of
approximately, showing by Equation (15), denoted by
.
Let Singular Value Decomposition of
be
where
,
,
,
,
,
and
are orthogonal.
As known above,
is a unit vector, partitioning
Because of
, then
Note that
is unit and orthogonal,
, then
, so based on the Equation (20), for the maximum, it can be deduced that
,
, then
,
, and
. Hence,
,
Based on the analysis above, the novel optimization to objective problem (8) is proposed in the position, its detail is as follows (Algorithm 1):
| Algorithm 1: Optimization to objective problem (8) |
| Basic Information: training samples |
| Initialization: Set threshold and |
| S1. | Generate the input weight layer and bas vector ; |
| S2. | Calculate the output matrix of the hidden layer based on Equation (3); |
| S3. | Calculate the orthogonal of span , and its orthogonal complement , then ; |
| S3. | While |
| S4. | Relax the column , from the matrix , separately, and fix the rest; |
| S5. | Set , then solve ; |
| S6. | Set , , then . By SVD, , so as to obtain and ; |
| S7. | Based on the Equation (21), ; |
| S8. | Calculate the vector , ; |
| S9. | Partition so as to obtain and , then replace of to obtain , and ; |
| | End While |
| S10. | Calculate , then if , terminate, otherwise, , is the new orthogonal complement of , go to step S3. |
4. Convergence and Complexity Analysis
Considering the convergence if the algorithm, Let be a sequence of generating during iteration, which converges to , so, its orthogonal complement also converges to , where is the iterating number, and is the operation of relaxing the column from original matrix, so, it follows converges to .
Based on the equations above, it is know that
is the optimal solution of Equation (10). If
, then for
is large enough,
and
meets
Set
,
, and
, then based on Equation (22), it has
Based on Equations (10) and (22), it has
Based on the Equations (23) and (24), it has
So, , based on the derivation of the inequality above, it can deduced that . By the same method and analysis, it also can be obtained that . So, it is , so the sequence is monotonically decreasing, and when , . In a word, after analysis above, the novel algorithm monotonically decreases the objective shown in Equation (8).
It is known that the complexity of ELM derives from the calculation of output weights
, or rather, it is mainly used to calculate the inverse of matrix
. In most cases, the number of hidden layer neurons
is much smaller than the training sample size
,
, thus the complexity is less than least square support vector machine (LS-SVM) and proximal support vector machine (PSVM), which need to calculate the inverse of
matrix [
16]. As we know, the complexity of ELM and OELM is
,
separately. As for the complexity of the novel algorithm proposed in the paper, its main calculation is from the loop. In each iteration,
relaxing from
, and during this, it needs to do SVD decomposition on the
matrix
, whose complexity is
, and then, the complexity of updating
once is
. So, the complexity of the proposed algorithm is
, where
is the number of updating
. In real application, regardless of classification or regression, the output dimension is much less than the number of hidden layer neurons and the training samples size.
As we know, , then . Considering the Euclidean distance between any two data points and , because of the orthogonal constraint , it has . It is known that is the point in the ELM feature space, is the distance in ELM space, and is the distance in the subspace. From this analysis, the novel ELM with orthogonal constraints is superior in maintaining the metric structure from first to last.
5. Performance Evaluation
For testing the performances of the novel algorithm proposed in the paper, it is compared with other learning algorithms on the classification problems (EMG for Gestures, Avila and Ultrasonic Flowmeter) and regression problems (Auto price, Breast cancer, Buston housing, etc.), which are from the University of California Irvine (UCI) machine learning repository [
22], shown in
Table 1. These learning algorithms include ELM [
1], OELM [
16] and I-ELM [
23,
24], their activation function is the sigmoid function, and the number of hidden layer neurons is set as three times as the input dimension. For I-ELM, the initial number of hidden layer neurons is set to zero. In the real experiments, the key parameters such as the input weights, the biases, etc., are generated randomly from
, and then, all samples are normalized into
, and the outputs of the regression problems are normalized into
[
25]. All simulations are done in Matlab R2016a environment.
In the classification problems, ELM and OELM are selected to compare with NOELM. The experimental results are shown in
Figure 2 and
Figure 3.
Figure 2 shows the convergence property of NOELM. At first, the convergence rate is larger, the objective value falls rapidly, when reaching about 0.8, it falls slowly, until stable. During the whole process, the number of iterations does not vary significantly, the maximum is not more than 20, and the minimum is only about 5, so in a word, the novel algorithm is a little more effective.
Figure 3 shows the comparison of the training time and classification rate. Due to the complexity above, the traditional ELM is low in complexity, and its training time is shortest. The complexity of NOELM is less than OELM, then its training time is shorter than OELM, and longer than that of ELM because of too many iterations, but the difference is not larger than 0.05. Although NOELM is not the best in terms of training time, its classification is better than the other two, the largest rate can reach 0.9.
In the regression problems, ELM, OELM and I_ELM are selected to compare with NOELM, the experimental results are shown in
Table 2. As mentioned above, the number of hidden layer neurons is determined based on the input dimension, so the hidden layer neurons of ELM, OELM and NOELM are fixed, and the others are dynamically increasing hidden layer neurons. Analyzing the information of
Table 2, compared with I_ELM, the network complexity of NOELM is a little lower, and its structure is more compact, but it is a little worse than I_ELM in some datasets, the difference is not large and fully acceptable. As for the accuracy of training and testing from
Table 3 and
Table 4, comparing with ELM and OELM, the performances of NOELM is better, it has better stability. Because of characteristics of I_ELM, it constructs a more compact network and is a little superior in the training and testing accuracy in some datasets, and this is just the weak point of NOELM and other related algorithms. However, by introducing the orthogonal constraints and improving the algorithm, NOELM can greatly narrow this gap, and its performance is also acceptable.