Adjusting Electric Field Intensity Using Hybridized Dielectric Metamolecule
Abstract
1. Introduction
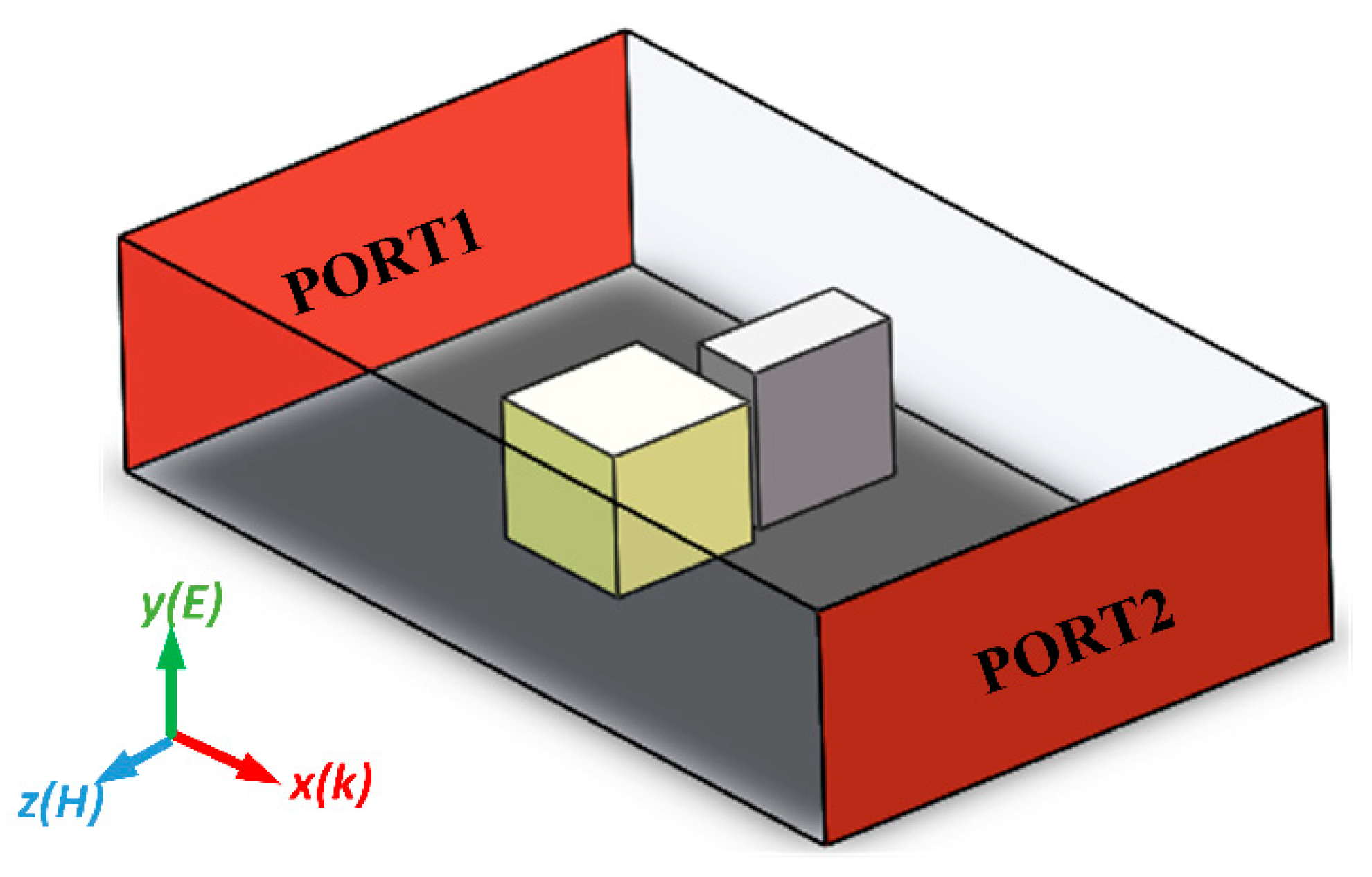
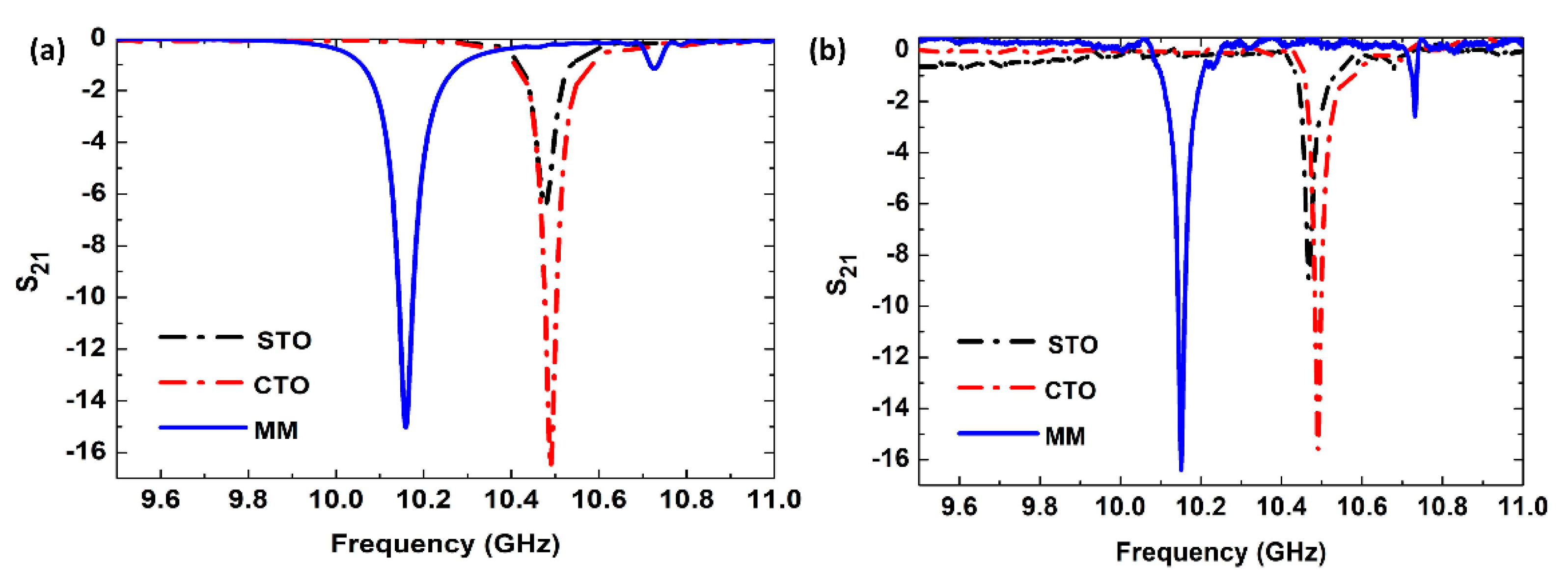
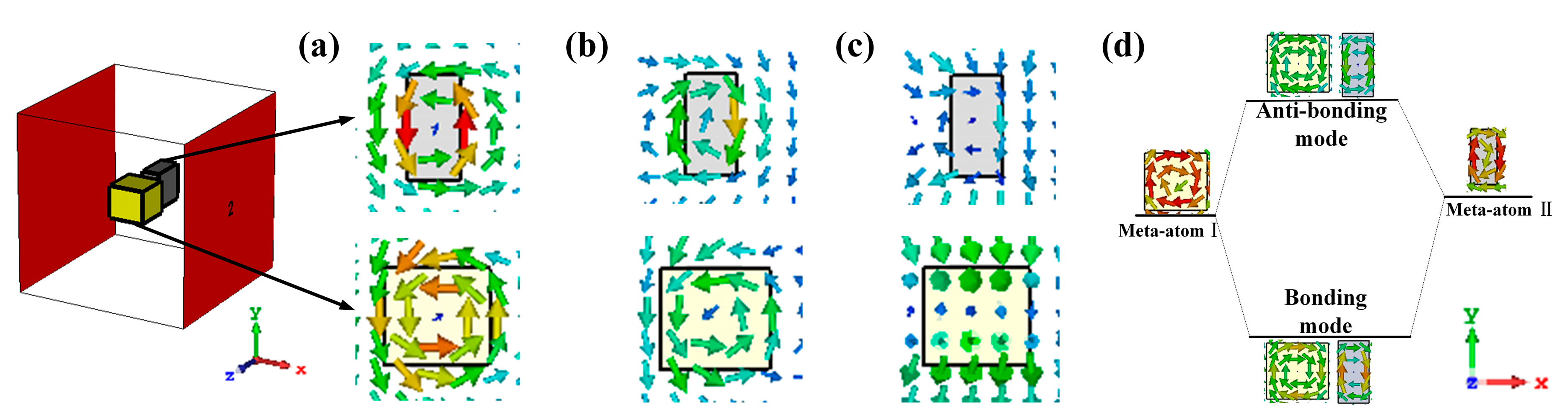
2. Design and Performance
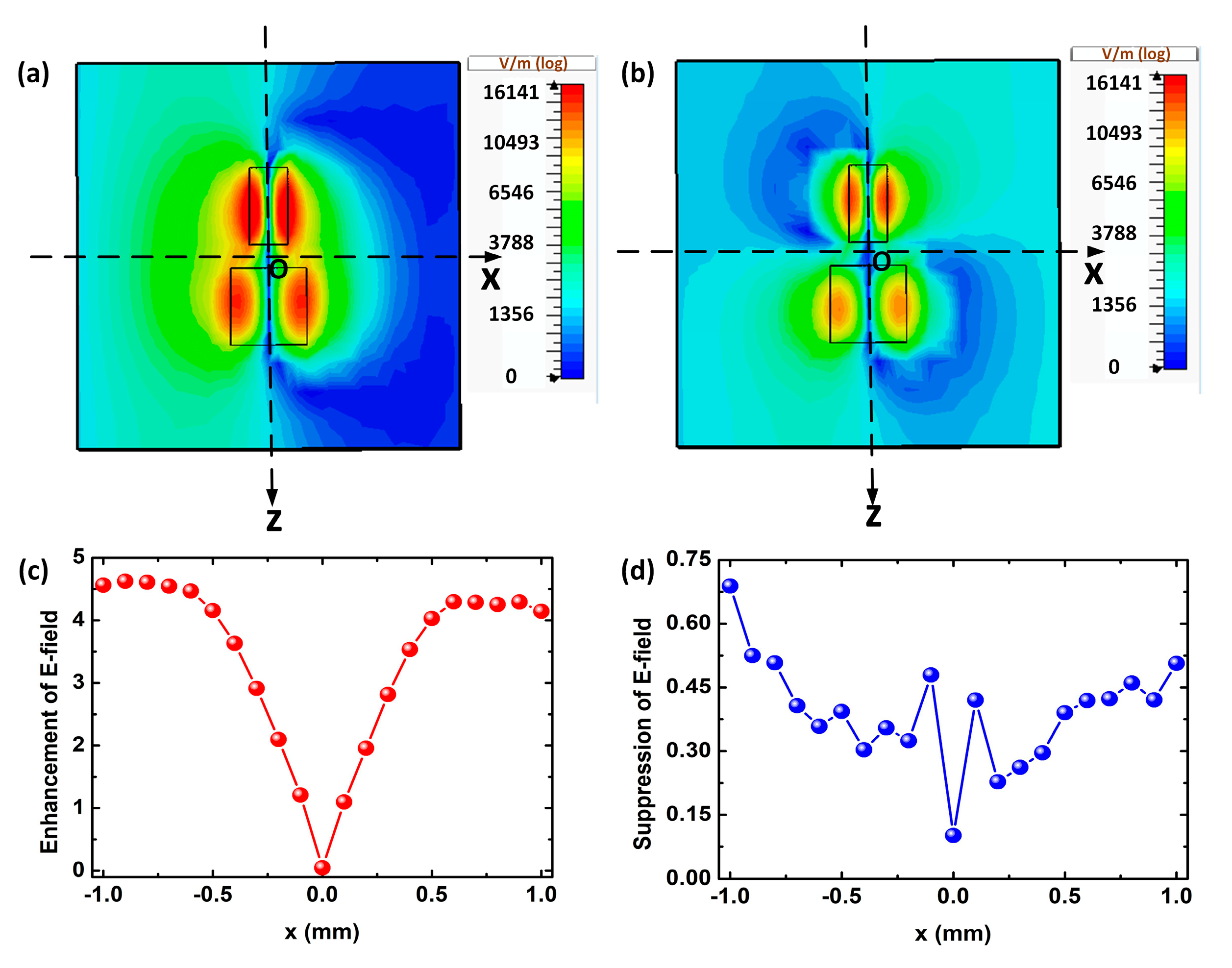
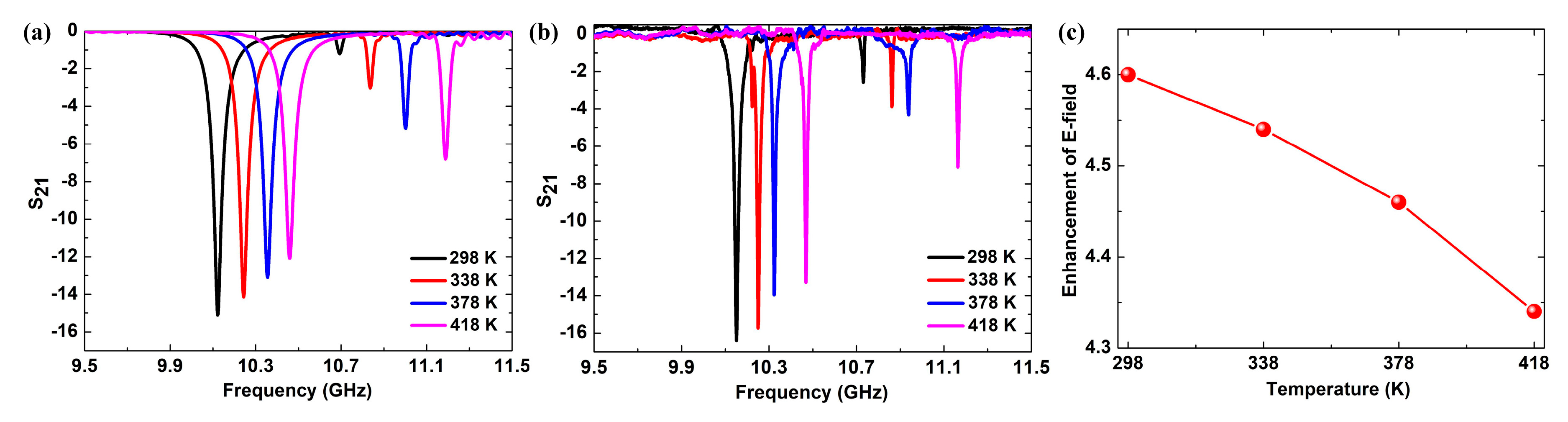
3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of isin and mu. Uspekhi Fizicheskii Nauk 1967, 92, 517–548. [Google Scholar] [CrossRef]
- Veselago, V.G. Electrodynamics of substances with simultaneously negative values of sigma and mu. Sov. Phys. Uspekhi Ussr 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Cui, T.J.; Qi, M.Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci. Appl. 2014, 3, e218. [Google Scholar] [CrossRef]
- Silva, A.; Monticone, F.; Castaldi, G.; Galdi, V.; Alu, A.; Engheta, N. Performing Mathematical Operations with Metamaterials. Science 2014, 343, 160–163. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. All-dielectric metasurface analogue of electromagnetically induced transparency. Nat. Commun. 2014, 5, 5753. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, S.D.; Ruostekoski, J.; Papasimakis, N.; Savo, S.; Zheludev, N.I. Many-Body Subradiant Excitations in Metamaterial Arrays: Experiment and Theory. Phys. Rev. Lett. 2017, 119, 053901. [Google Scholar] [CrossRef] [PubMed]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A hybridization model for the plasmon response of complex nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef]
- Funston, A.M.; Novo, C.; Davis, T.J.; Mulvaney, P. Plasmon Coupling of Gold Nanorods at Short Distances and in Different Geometries. Nano Lett. 2009, 9, 1651–1658. [Google Scholar] [CrossRef]
- Wu, D.J.; Liu, X.J. Tunable near-infrared optical properties of three-layered gold-silica-gold nanoparticles. Appl. Phys. B Lasers Opt. 2009, 97, 193–197. [Google Scholar] [CrossRef]
- Park, T.-H.; Nordlander, P. On the nature of the bonding and antibonding metallic film and nanoshell plasmons. Chem. Phys. Lett. 2009, 472, 228–231. [Google Scholar] [CrossRef]
- Kurter, C.; Tassin, P.; Zhang, L.; Koschny, T.; Zhuravel, A.P.; Ustinov, A.V.; Anlage, S.M.; Soukoulis, C.M. Classical Analogue of Electromagnetically Induced Transparency with a Metal-Superconductor Hybrid Metamaterial. Phys. Rev. Lett. 2011, 107, 043901. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Saliba, M.; Vogelgesang, R.; Giessen, H.; Alivisatos, A.P.; Liu, N. Transition from Isolated to Collective Modes in Plasmonic Oligomers. Nano Lett. 2010, 10, 2721–2726. [Google Scholar] [CrossRef] [PubMed]
- Aydin, K.; Pryce, I.M.; Atwater, H.A. Symmetry breaking and strong coupling in planar optical metamaterials. Opt. Express 2010, 18, 13407–13417. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Genov, D.A.; Wu, D.M.; Liu, Y.M.; Liu, Z.W.; Sun, C.; Zhu, S.N.; Zhang, X. Magnetic plasmon hybridization and optical activity at optical frequencies in metallic nanostructures. Phys. Rev. B 2007, 76, 073101. [Google Scholar] [CrossRef]
- Verellen, N.; Van Dorpe, P.; Huang, C.; Lodewijks, K.; Vandenbosch, G.A.E.; Lagae, L.; Moshchalkov, V.V. Plasmon Line Shaping Using Nanocrosses for High Sensitivity Localized Surface Plasmon Resonance Sensing. Nano Lett. 2011, 11, 391–397. [Google Scholar] [CrossRef]
- McPolin, C.P.T.; Marino, G.; Krasavin, A.V.; Gili, V.; Carletti, L.; De Angelis, C.; Leo, G.; Zayats, A.V. Imaging Electric and Magnetic Modes and Their Hybridization in Single and Dimer AlGaAs Nanoantennas. Adv. Opt. Mater. 2018, 6, 1800664. [Google Scholar] [CrossRef]
- Talley, C.E.; Jackson, J.B.; Oubre, C.; Grady, N.K.; Hollars, C.W.; Lane, S.M.; Huser, T.R.; Nordlander, P.; Halas, N.J. Surface-enhanced Raman scattering from individual Au nanoparticles and nanoparticle dimer substrates. Nano Lett. 2005, 5, 1569–1574. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, J.; Liu, Z.; Xu, G.; Fan, Y.; Zhong, H.; Cao, B.; Wang, C.; Xu, K. Strong-Field-Enhanced Spectroscopy in Silicon Nanoparticle Electric and Magnetic Dipole Resonance near a Metal Surface. J. Phys. Chem. C 2015, 119, 28127–28135. [Google Scholar] [CrossRef]
- Alonso-Gonzalez, P.; Albella, P.; Golmar, F.; Arzubiaga, L.; Casanova, F.; Hueso, L.E.; Aizpurua, J.; Hillenbrand, R. Visualizing the near-field coupling and interference of bonding and anti-bonding modes in infrared dimer nanoantennas. Opt. Express 2013, 21, 1270–1280. [Google Scholar] [CrossRef]
- Moradian, R.; Saliminasab, M. Surface-Enhanced Raman Scattering in Tunable Bimetallic Core-Shell. Plasmonics 2018, 13, 1143–1151. [Google Scholar] [CrossRef]
- Yang, H.; Yao, J.; Wu, X.-W.; Wu, D.-J.; Liu, X.-J. Strong Plasmon-Exciton-Plasmon Multimode Couplings in Three-Layered Ag-J-Aggregates-Ag Nanostructures. J. Phys. Chem. C 2017, 121, 25455–25462. [Google Scholar] [CrossRef]
- Park, J.-E.; Kim, S.; Son, J.; Lee, Y.; Nam, J.-M. Highly Controlled Synthesis and Super-Radiant Photoluminescence of Plasmonic Cube-in-Cube Nanoparticles. Nano Lett. 2016, 16, 7962–7967. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Liu, Y.M.; Li, T.; Wang, S.M.; Zhu, S.N.; Zhang, X. Coupled magnetic plasmons in metamaterials. Phys. Status Solidi (b) 2009, 246, 1397–1406. [Google Scholar] [CrossRef]
- Hao, F.; Nehl, C.L.; Hafner, J.H.; Nordlander, P. Plasmon resonances of a gold nanostar. Nano Lett. 2007, 7, 729–732. [Google Scholar] [CrossRef]
- Liu, N.; Giessen, H. Coupling Effects in Optical Metamaterials. Angew. Chem. Int. Ed. 2010, 49, 9838–9852. [Google Scholar] [CrossRef]
- Liu, X.; Lan, C.; Bi, K.; Li, B.; Zhao, Q.; Zhou, J. Dual band metamaterial perfect absorber based on Mie resonances. Appl. Phys. Lett. 2016, 109, 062902. [Google Scholar] [CrossRef]
- Guo, Y.; Liang, H.; Hou, X.; Lv, X.; Li, L.; Li, J.; Bi, K.; Lei, M.; Zhou, J. Thermally tunable enhanced transmission of microwaves through a subwavelength aperture by a dielectric metamaterial resonator. Appl. Phys. Lett. 2016, 108, 051906. [Google Scholar] [CrossRef]
- Bi, K.; Guo, Y.; Liu, X.; Zhao, Q.; Xiao, J.; Lei, M.; Zhou, J. Magnetically tunable Mie resonance-based dielectric metamaterials. Sci. Rep. 2014, 4, 7001. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, J.; Lan, C.; Guo, Y.; Bi, K. Microwave Memristive-like Nonlinearity in a Dielectric Metamaterial. Sci. Rep. 2014, 4, 5499. [Google Scholar] [CrossRef]
- Bi, K.; Huang, K.; Zeng, L.Y.; Zhou, M.H.; Wang, Q.M.; Wang, Y.G.; Lei, M. Tunable Dielectric Properties of Ferrite-Dielectric Based Metamaterial. PLoS ONE 2015, 10, e0127331. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, X.; Zhou, J. Adjusting Electric Field Intensity Using Hybridized Dielectric Metamolecule. Symmetry 2019, 11, 1285. https://doi.org/10.3390/sym11101285
Li H, Wang X, Zhou J. Adjusting Electric Field Intensity Using Hybridized Dielectric Metamolecule. Symmetry. 2019; 11(10):1285. https://doi.org/10.3390/sym11101285
Chicago/Turabian StyleLi, Haohua, Xiaobo Wang, and Ji Zhou. 2019. "Adjusting Electric Field Intensity Using Hybridized Dielectric Metamolecule" Symmetry 11, no. 10: 1285. https://doi.org/10.3390/sym11101285
APA StyleLi, H., Wang, X., & Zhou, J. (2019). Adjusting Electric Field Intensity Using Hybridized Dielectric Metamolecule. Symmetry, 11(10), 1285. https://doi.org/10.3390/sym11101285




