Numerical Investigation of Aligned Magnetic Flow Comprising Nanoliquid over a Radial Stretchable Surface with Cattaneo–Christov Heat Flux with Entropy Generation
Abstract
:1. Introduction
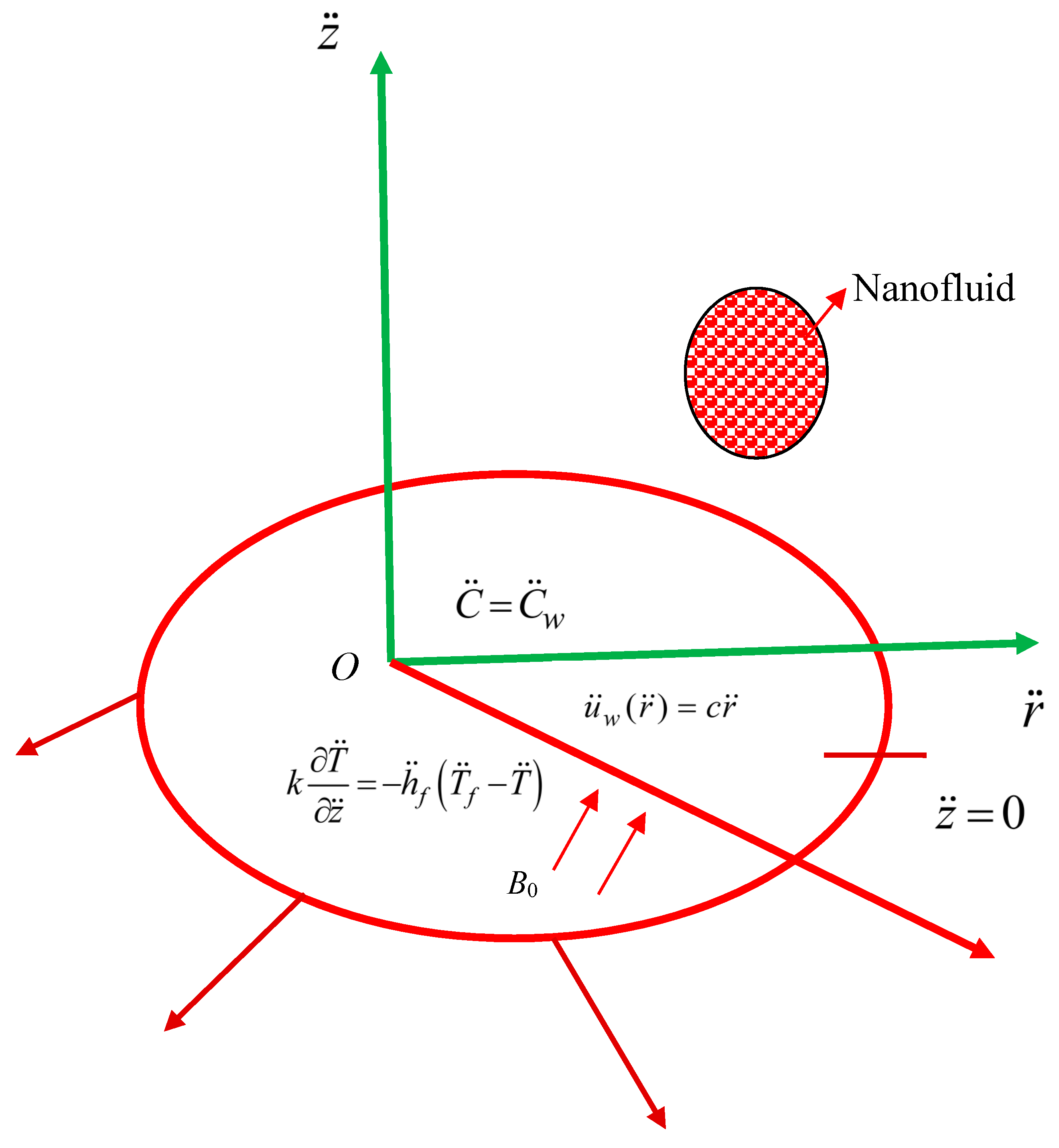
2. Problem Formulation
3. Analysis of Entropy Generation
4. Results and Discussion
5. Final Remarks
- The fluid flow velocity diminishes due to aligned angle, while the temperature and concentration of nanoparticles show escalating behavior.
- The velocity profile decays due to magnetic parameter, whereas concentration of nanoparticles and temperature display opposite behavior.
- The impacts of Brownian and thermophoresis parameter on temperature distribution are identical.
- The influences of motion of Brownian and thermophoresis on the volume fraction are opposite.
- Temperature distribution as well as the concentration of nanofluid improves due to convective parameter.
- Due to the thermal relaxation parameter, the temperature distribution declines.
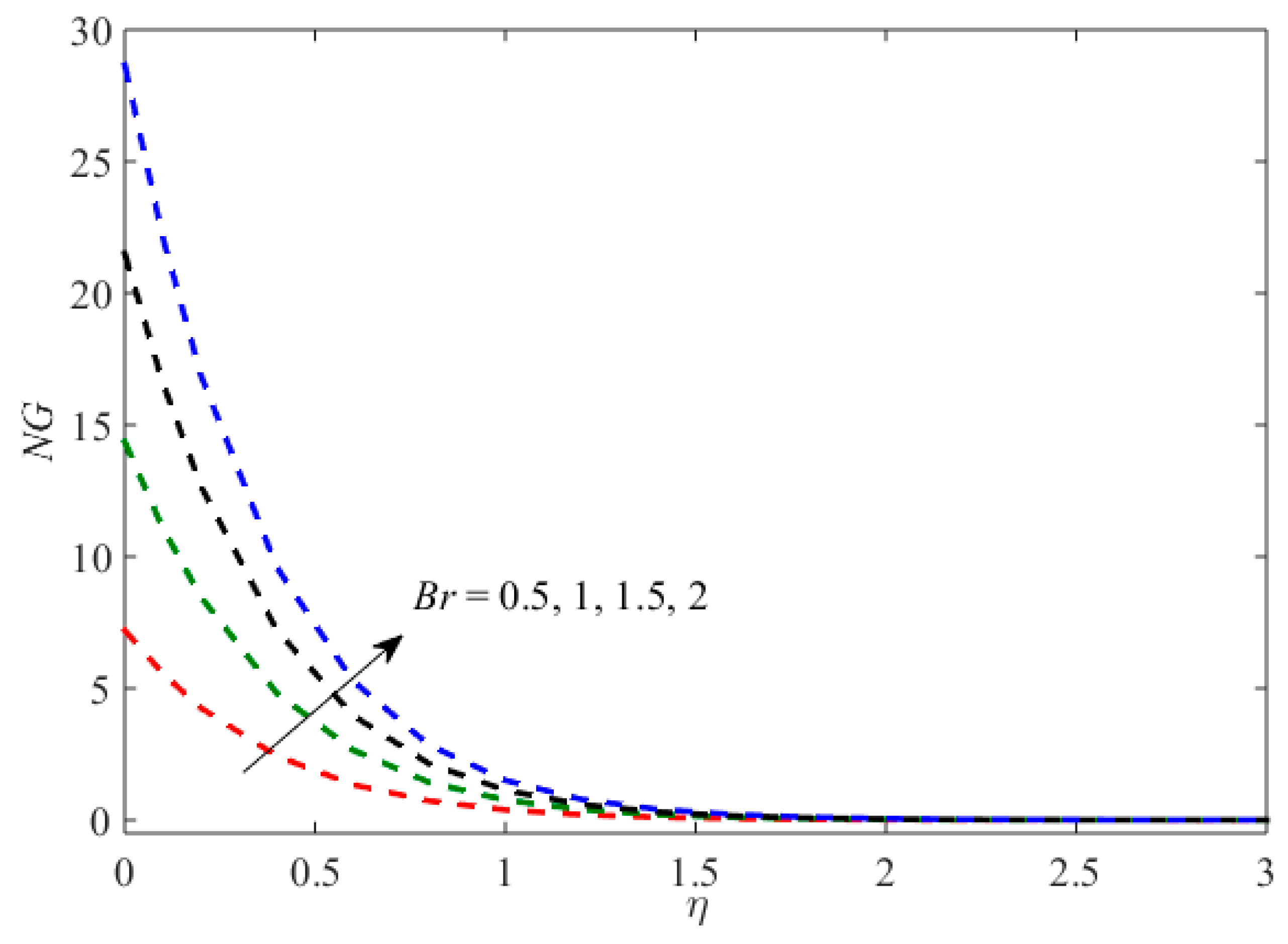
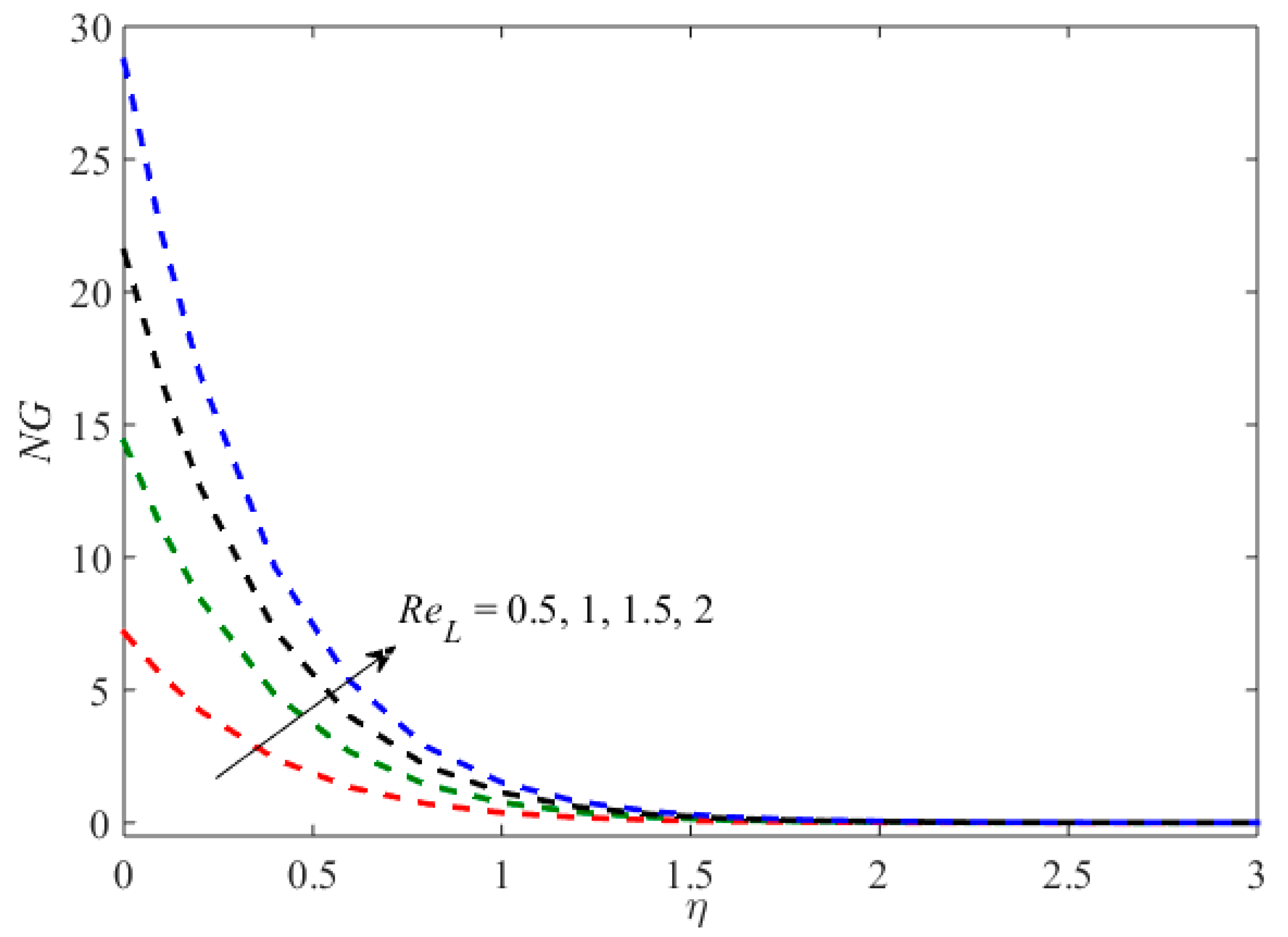
- An entropy profile becomes larger for bigger values of aligned angle, Reynolds number, magnetic parameter, the Brinkman number.
- The values of appreciably increase due to aligned angle, while the values of and decay.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Bejan number | |
| intensity of magnetic field | |
| Brinkman number | |
| positive constant | |
| skin friction coefficient | |
| concentration of nanoparticles | |
| ambient concentration of nanoparticles | |
| the Brownian constraint | |
| the thermophoresis diffusion | |
| heat transfer coefficient | |
| thermal conductivity | |
| characteristic length | |
| magnetic parameter | |
| mw | mass flux |
| Brownian parameter | |
| volumetric rate of entropy generation | |
| thermophoresis parameter | |
| Nusselt number | |
| Prandtl number | |
| qw | heat flux |
| local Reynolds number | |
| the characteristic length based Reynolds number | |
| Schmidt number | |
| generated entropy | |
| entropy generation characteristic | |
| temperature | |
| temperature of the hot liquid | |
| ambient temperature | |
| velocity components | |
| Cartesian coordinates | |
| Greek symbols | |
| thermal diffusivity | |
| time relaxation of heat flux | |
| convective parameter | |
| aligned acute angle | |
| diffusive constant | |
| dimensionless concentration of nanoparticle | |
| dimensionless temperature | |
| kinematic viscosity | |
| the density | |
| the electrical conductivity | |
| thermal relaxation parameter | |
| capacity ratio | |
| temperature difference | |
| shear stress | |
| stream function | |
| similarity variable | |
| Superscripts | |
| ‘ | derivative w.r.t. |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Fluids Eng. Div. 1995, 231, 99–105. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Analytical solutions of single and multi-phase models for the condensation of nanofluid film flow and heat transfer. Eur. J. Mech. B Fluids 2015, 53, 272–277. [Google Scholar] [CrossRef]
- Pour, M.S.; Nassab, S.A.G. Numerical investigation of forced laminar convection flow of nanofluids over a backward facing step under bleeding condition. J. Mech. 2012, 28, 7–12. [Google Scholar] [CrossRef]
- Goodarzi, M.; Safaei, M.R.; Vafai, K.; Ahmadi, G.; Dahari, M.; Kazi, S.N.; Jomhari, N. Investigation of nanofluid mixed convection in a shallow cavity using a two-phase mixture model. Int. J. Thermal Sci. 2014, 75, 204–220. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Analytical and numerical solutions for axisymmetric flow of nanofluid due to non-linearly stretching sheet. Int. J. Non Linear Mech. 2015, 71, 22–29. [Google Scholar] [CrossRef]
- Akbari, O.A.; Safaei, M.R.; Goodarzi, M.; Akbar, N.S.; Zarringhalam, M.; Ahmadi, G.; Shabani, S.; Dahari, M. A modified two-phase mixture model of nanofluid flow and heat transfer in a 3-D curved microtube. Adv. Powder Technol. 2016, 27, 2175–2185. [Google Scholar] [CrossRef]
- Khan, M.; Azam, M. Unsteady heat and mass transfer mechanisms in MHD Carreau nanofluid flow. J. Mol. Liq. 2017, 225, 554–562. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I. Microstructure and inertial characteristics of a magnetite ferrofluid over a stretching/shrinking sheet using effective thermal conductivity model. J. Mol. Liq. 2018, 255, 64–75. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sharif, E.S.M.; Nisar, K.S. Brownian motion and thermophoretic diffusion effects on micropolar type nanofluid flow with Soret and Dufour impacts over an inclined sheet: Keller-box simulations. Energies 2019, 12, 4191. [Google Scholar] [CrossRef] [Green Version]
- Yousefzadeh, S.; Rajabi, H.; Ghajari, N.; Sarafraz, M.M.; Akbari, O.A.; Goodarzi, M. Numerical investigation of mixed convection heat transfer behavior of nanofluid in a cavity with different heat transfer areas. J. Thermal Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Faraz, F.; Haider, S.; Imran, S.M. Study of magneto-hydrodynamics (MHD) impacts on an axisymmetric Casson nanofluid flow and heat transfer over unsteady radially stretching sheet. SN Appl. Sci. 2020, 2, 14. [Google Scholar] [CrossRef] [Green Version]
- Bagherzadeh, S.A.; Jalali, E.; Sarafraz, M.M.; Akbari, O.A.; Karimipour, A.; Goodarzi, M.; Bach, Q.-V. Effects of magnetic field on micro cross jet injection of dispersed nanoparticles in a microchannel. Int. J. Num. Meth. Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Tian, Z.; Etedali, S.; Afrand, M.; Abdollahi, A.; Goodarzi, M. Experimental study of the effect of various surfactants on surface sediment and pool boiling heat transfer coefficient of silica/DI water nano-fluid. Powder Technol. 2019, 356, 391–402. [Google Scholar] [CrossRef]
- Spasojević, M.D.; Janković, M.R.; Djaković, D.D. A new approach to entropy production minimization in diabatic distillation column with trays. Therm. Sci. 2010, 14, 317–328. [Google Scholar] [CrossRef]
- Abu-Nada, E. Investigation of entropy generation over a backward facing step under bleeding conditions. Energy Conver. Manag. 2008, 49, 3237–3242. [Google Scholar] [CrossRef]
- Komurgoz, G.; Arikoglu, A.; Ozkol, I. Analysis of the magnetic effect on entropy generation in an inclined channel partially filled with porous medium. Numer. Heat Transf. Part A Appl. 2012, 61, 786–799. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy effects in hydromagnetic free convection flow past a vertical plate embedded in a porous medium in the presence of thermal radiation. Eur. Phys. J. Plus 2013, 128, 51–55. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Kavyani, N.; Abelman, S. Investigation of entropy generation in MHD and slip flow over a rotating porous disk with variable properties. Int. J. Heat Mass Transf. 2014, 70, 892–917. [Google Scholar] [CrossRef]
- Goodarzi, M.; Safaei, M.R.; Oztop, H.F.; Karimipour, A.; Sadeghinezhad, E.; Dahari, M.; Kazi, S.N.; Jomhari, N. Numerical study of entropy generation due to coupled laminar and turbulent mixed convection and thermal radiation in an enclosure filled with a semitransparent medium. Sci. World J. 2014, 2014, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Chakraborty, S.; Jana, R.N.; Makinde, O.D. Entropy analysis of unsteady magneto-nanofluid flow past accelerating stretching sheet with convective boundary condition. Appl. Math. Mech. 2015, 36, 1593–1610. [Google Scholar] [CrossRef]
- Shateyi, S.; Motsa, S.S.; Makukula, Z. On spectral relaxation method for entropy generation on a MHD flow and heat transfer of a Maxwell fluid. J. App. Fluid Mech. 2015, 8, 21–31. [Google Scholar]
- Rehman, S.U.; Haq, R.U.; Khan, Z.H.; Lee, C. Entropy generation analysis for non-Newtonian nanofluid with zero normal flux of nanoparticles at the stretching surface. J. Taiwan Inst. Chem. Eng. 2016, 63, 226–235. [Google Scholar] [CrossRef]
- Almakki, M.; Dey, S.; Mondal, S.; Sibanda, P. On unsteady three-dimensional axisymmetric MHD nanofluid flow with entropy generation and thermo-diffusion effects on a non-linear stretching sheet. Entropy 2017, 19, 168. [Google Scholar] [CrossRef] [Green Version]
- Afridi, M.I.; Qasim, M.; Khan, I. Entropy generation minimization in MHD boundary layer flow over a slendering stretching sheet in the presence of frictional and Joule heating. J. Korean Phys. Soc. 2018, 73, 1303–1309. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.W.A.; Khan, M.I.; Alsaedi, A. Nonlinear radiative heat flux and heat source/sink on entropy generation minimization rate. Phys. B Phys. Cond. Matt. 2018, 538, 95–103. [Google Scholar] [CrossRef]
- Aghaei, A.; Sheikhzadeh, G.A.; Goodarzi, M.; Hasani, H.; Damirchi, H.; Afrand, M. Effect of horizontal and vertical elliptic baffles inside an enclosure on the mixed convection of a MWCNTs-water nanofluid and its entropy generation. Eur. Phys. J. Plus 2018, 133, 486. [Google Scholar] [CrossRef]
- El-Aziz, M.A.; Afify, A.A. MHD Casson fluid flow over a stretching sheet with entropy generation analysis and Hall influence. Entropy 2019, 21, 592. [Google Scholar] [CrossRef] [Green Version]
- Pordanjani, A.H.; Aghakhani, S.; Karimipour, A.; Afrand, M.; Goodarzi, M. Investigation of free convection heat transfer and entropy generation of nanofluid flow inside a cavity affected by magnetic field and thermal radiation. J. Thermal Anal. Calorim. 2019, 137, 997–1019. [Google Scholar] [CrossRef]
- Cattaneo, C. Sulla conduzionedelcalore. Atti Semin. Mat. Fis. Univ. Modena Reggio Emilia 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell-Cattaneo model of finite speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Straughan, B. Thermal convection with the Cattaneo-Christov model. Int. J. Heat Mass Transf. 2010, 53, 95–98. [Google Scholar] [CrossRef]
- Li, J.; Zheng, L.; Liu, l. MHD viscoelastic flow and heat transfer over a vertical stretching sheet with Cattaneo-Christov heat flux effects. J. Mol. Liq. 2016, 221, 19–25. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. Effects of MHD homogeneous-heterogeneous reactions on third grade fluid flow with Cattaneo-Christov heat flux. J. Mol. Liq. 2016, 223, 1284–1290. [Google Scholar] [CrossRef]
- Hayat; Khan, M. On Cattaneo–Christov heat flux model for Carreau fluid flow over a slendering sheet. Resul. Phys. 2017, 7, 310–319. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Alsaedi, A.; Khan, M.I. Thermally stratified stretching flow with Cattaneo-Christov heat flux. Int. J. Heat Mass Transf. 2017, 106, 289–294. [Google Scholar] [CrossRef]
- Ali, M.E.; Sandeep, N. Cattaneo-Christov model for radiative heat transfer of magnetohydrodynamic Casson-ferrofluid: A numerical study. Results Phys. 2017, 7, 21–30. [Google Scholar] [CrossRef] [Green Version]
- Babu, M.J.; Sandeep, N.; Saleem, S. Free convective MHD Cattaneo-Christov flow over three different geometries with thermophoresis and Brownian motion. Alex. Eng. J. 2017, 56, 659–669. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J.; Raju, C.S.K. Cattaneo-Christov heat flux on UCM nanofluid flow across a melting surface with double stratification and exponential space dependent internal heat source. Inform. Med. Unlock. 2017, 9, 26–34. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy analysis of magnetohydrodynamic flow and heat transfer over a convectively heated radially stretching surface. J. Taiwan Inst. Chem. Eng. 2014, 45, 1197–1203. [Google Scholar] [CrossRef]
- Soid, S.K.; Ishak, A. MHD flow and heat transfer over a radially stretching/shrinking disk. Chin. J. Phys. 2018, 56, 58–66. [Google Scholar] [CrossRef]















| Butt and Ali [42] | Mathematical Error | Soid et al. [43] | Mathematical Error | Present | |
|---|---|---|---|---|---|
| 0 | −1.17372 | 0.00002 | −1.17372088 | 0.00002088 | −1.1737 |
| 0.5 | −1.36581 | 0.00001 | −1.36581449 | 0.00001449 | −1.3658 |
| 1 | −1.53571 | 0.00001 | −1.53571052 | 0.00001052 | −1.5357 |
| 2 | −1.83049 | 0.00001 | −1.83048967 | 0.00001033 | −1.8305 |
| 3 | −2.08484 | 0.00004 | −2.08484656 | 0.00004656 | −2.0848 |
| 2 | 1.5357 | 0.2133 | 0.6329 | |
| 1.8305 | 0.2088 | 0.5763 | ||
| 2.3117 | 0.2014 | 0.4976 | ||
| 3 | 1.8972 | 0.2078 | 0.5643 | |
| 2.4172 | 0.1997 | 0.4827 | ||
| 3.2154 | 0.1882 | 0.3944 | ||
| 4 | 2.3117 | 0.2014 | 0.4976 | |
| 3.0560 | 0.1904 | 0.4090 | ||
| 4.1637 | 0.1764 | 0.3303 | ||
| 5 | 2.7551 | 0.1947 | 0.4404 | |
| 3.7198 | 0.1816 | 0.3561 | ||
| 5.1318 | 0.1667 | 0.2910 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaib, A.; Khan, U.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M. Numerical Investigation of Aligned Magnetic Flow Comprising Nanoliquid over a Radial Stretchable Surface with Cattaneo–Christov Heat Flux with Entropy Generation. Symmetry 2019, 11, 1520. https://doi.org/10.3390/sym11121520
Zaib A, Khan U, Khan I, Seikh AH, Sherif E-SM. Numerical Investigation of Aligned Magnetic Flow Comprising Nanoliquid over a Radial Stretchable Surface with Cattaneo–Christov Heat Flux with Entropy Generation. Symmetry. 2019; 11(12):1520. https://doi.org/10.3390/sym11121520
Chicago/Turabian StyleZaib, A., Umair Khan, Ilyas Khan, Asiful H. Seikh, and El-Sayed M. Sherif. 2019. "Numerical Investigation of Aligned Magnetic Flow Comprising Nanoliquid over a Radial Stretchable Surface with Cattaneo–Christov Heat Flux with Entropy Generation" Symmetry 11, no. 12: 1520. https://doi.org/10.3390/sym11121520
APA StyleZaib, A., Khan, U., Khan, I., Seikh, A. H., & Sherif, E.-S. M. (2019). Numerical Investigation of Aligned Magnetic Flow Comprising Nanoliquid over a Radial Stretchable Surface with Cattaneo–Christov Heat Flux with Entropy Generation. Symmetry, 11(12), 1520. https://doi.org/10.3390/sym11121520






