Solution Models Based on Symmetric and Asymmetric Information
Abstract
:1. Introduction
2. Contributions
3. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Turskis, Z.; Urbonas, K.; Daniūnas, A. A Hybrid Fuzzy Group Multi-Criteria Assessment of Structural Solutions of the Symmetric Frame Alternatives. Symmetry 2019, 11, 261. [Google Scholar] [CrossRef]
- Vinogradova, I.; Podvezko, V.; Zavadskas, E.K. The Recalculation of the Weights of Criteria in MCDM Methods Using the Bayes Approach. Symmetry 2018, 10, 205. [Google Scholar] [CrossRef]
- Schad, J.; Lewis, M.W.; Raisch, S.; Smith, W.K. Paradox research in management science: Looking back to move forward. Acad. Manag. Ann. 2016, 10, 5–64. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Selecting a contractor by using a novel method for multiple attribute analysis: Weighted Aggregated Sum Product Assessment with grey values (WASPAS-G). Stud. Inform. Control 2015, 24, 141–150. [Google Scholar] [CrossRef]
- Chalekaee, A.; Turskis, Z.; Khanzadi, M.; Ghodrati Amiri, G.; Keršulienė, V. A New Hybrid MCDM Model with Grey Numbers for the Construction Delay Change Response Problem. Sustainability 2019, 11, 776. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Khalifah, Z.; Jusoh, A.; Nor, K. Multiple criteria decision-making techniques in transportation systems: A systematic review of the state of the art literature. Transport 2016, 31, 359–385. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications—Two decades review from 1994 to 2014. Expert Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, S.C.; Oztaysi, B. Fuzzy Multicriteria Decision-Making: A Literature Review. Int. J. Comput. Intell. Syst. 2015, 8, 637–666. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Nor, K.M.D.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications—A review of the literature from 2000 to 2014. Econ. Res.-Ekon. Istraz. 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Antucheviciene, J.; Kala, Z.; Marzouk, M.; Vaidogas, E.R. Solving Civil Engineering Problems by Means of Fuzzy and Stochastic MCDM Methods: Current State and Future Research. Math. Probl. Eng. 2015, 2015, 362579. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Antucheviciene, J. Supplier evaluation and selection in fuzzy environments: A review of MADM approaches. Econ. Res.-Ekon. Istraz. 2017, 30, 1073–1118. [Google Scholar] [CrossRef]
- Mardani, A.; Nilashi, M.; Antucheviciene, J.; Tavana, M.; Bausys, R.; Ibrahim, O. Recent fuzzy generalisations of rough sets theory: A systematic review and methodological critique of the literature. Complexity 2017, 1608147. [Google Scholar] [CrossRef]
- Yazdanbakhsh, O.; Dick, S. A systematic review of complex fuzzy sets and logic. Fuzzy Sets Syst. 2018, 338, 1–22. [Google Scholar] [CrossRef]
- Rajab, S.; Sharma, V. A review on the applications of neuro-fuzzy systems in business. Artif. Intell. Rev. 2018, 49, 481–510. [Google Scholar] [CrossRef]
- Khan, M.; Son, L.H.; Ali, M.; Chau, H.T.M.; Na, N.T.N.; Smarandache, F. Systematic review of decision making algorithms in extended neutrosophic sets. Symmetry 2018, 10, 314. [Google Scholar] [CrossRef]
- Mardani, A.; Nilashi, M.; Zavadskas, E.K.; Awang, S.R.; Zare, H.; Jamal, N.M. Decision making methods based on fuzzy aggregation operators: Three decades review from 1986 to 2017. Int. J. Inf. Technol. Decis. Mak. 2018, 17, 391–466. [Google Scholar] [CrossRef]
- Turskis, Z.; Dzitac, S.; Stankiuviene, A.; Šukys, R. A Fuzzy Group Decision-making Model for Determining the Most Influential Persons in the Sustainable Prevention of Accidents in the Construction SMEs. Int. J. Comput. Commun. Control 2019, 14, 90–106. [Google Scholar] [CrossRef]
- Govindan, K.; Rajendran, S.; Sarkis, J.; Murugesan, P. Multi criteria decision making approaches for green supplier evaluation and selection: A literature review. J. Clean Prod. 2015, 98, 66–83. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K.; Khalifah, Z.; Nor, K.M. Application of multiple-criteria decision-making techniques and approaches to evaluating of service quality: A systematic review of the literature. J. Bus. Econ. Manag. 2015, 16, 1034–1068. [Google Scholar] [CrossRef]
- Shen, K.Y.; Zavadskas, E.K.; Tzeng, G.H. Updated discussions on “Hybrid multiple criteria decision-making methods: A review of applications for sustainability issues”. Econ. Res.-Ekon. Istraz. 2018, 31, 1437–1452. [Google Scholar] [CrossRef]
- Govindan, K.; Hasanagic, M. A systematic review on drivers, barriers, and practices towards circular economy: A supply chain perspective. Int. J. Prod. Res. 2018, 56, 278–311. [Google Scholar] [CrossRef]
- Govindan, K.; Soleimani, H. A review of reverse logistics and closed-loop supply chains: A Journal of Cleaner Production focus. J. Clean. Prod. 2017, 142, 371–384. [Google Scholar] [CrossRef]
- Correia, E.; Carvalho, H.; Azevedo, S.G.; Govindan, K. Maturity models in supply chain sustainability: A systematic literature review. Sustainability 2017, 9, 64. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K.; Kazemilari, M.; Ahmad, U.N.U.; Khalifah, Z. Application of multiple criteria decision making techniques in tourism and hospitality industry: A systematic review. Transform. Bus. Econ. 2016, 15, 192–213. [Google Scholar]
- Keshavarz Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Turskis, Z. Extended EDAS method for fuzzy multi-criteria decision-making: An application to supplier selection. Int. J. Comput. Commun. Control 2016, 11, 358–371. [Google Scholar] [CrossRef]
- Khanzadi, M.; Turskis, Z.; Ghodrati Amiri, G.; Chalekaee, A. A model of discrete zero-sum two-person matrix games with grey numbers to solve dispute resolution problems in construction. J. Civ. Eng. Manag. 2017, 23, 824–835. [Google Scholar] [CrossRef]
- Hashemkhani Zolfani, S.; Zavadskas, E.K.; Turskis, Z. Design of products with both International and Local perspectives based on Yin-Yang balance theory and SWARA method. Econ. Res. -Ekon. Istraživanja 2013, 26, 153–166. [Google Scholar] [CrossRef]
- Ruzgys, A.; Volvačiovas, R.; Ignatavičius, Č.; Turskis, Z. Integrated evaluation of external wall insulation in residential buildings using SWARA-TODIM MCDM method. J. Civ. Eng. Manag. 2014, 20, 103–110. [Google Scholar] [CrossRef]
- Sousa, J.P.; Xavier, J.P. Symmetry-based generative design and fabrication: A teaching experiment. Autom. Constr. 2015, 51, 113–123. [Google Scholar] [CrossRef]
- Jaganathan, S.; Nesan, L.J.; Ibrahim, R.; Mohammad, A.H. Integrated design approach for improving architectural forms in industrialized building systems. Front. Archit. Res. 2013, 2, 377–386. [Google Scholar] [CrossRef]
- Banginwar, R.S.; Vyawahare, M.R.; Modani, P.O. Effect of plans configurations on the seismic behaviour of the structure by response spectrum method. Int. J. Eng. Res. Appl. 2012, 2, 1439–1443. [Google Scholar]
- Balali, V.; Zahraie, B.; Roozbahani, A. A Comparison of AHP and PROMETHEE Family Decision Making Methods for Selection of Building Structural System. Am. J. Civ. Eng. Archit. 2014, 2, 149–159. [Google Scholar] [CrossRef]
- Ye, K.; Zeng, D.; Wong, J. Competition rule of the multi-criteria approach: What contractors in China really want? J. Civ. Eng. Manag. 2018, 24, 155–166. [Google Scholar] [CrossRef]
- De la Fuente, A.; Armengou, J.; Pons, O.; Aguado, A. Multi-criteria decision-making model for assessing the sustainability index of wind-turbine support systems: Application to a new precast concrete alternative. J. Civ. Eng. Manag. 2017, 23, 194–203. [Google Scholar] [CrossRef]
- Prascevic, N.; Prascevic, Z. Application of fuzzy AHP for ranking and selection of alternatives in construction project management. J. Civ. Eng. Manag. 2017, 23, 1123–1135. [Google Scholar] [CrossRef]
- Chen, C.J.; Juan, Y.K.; Hsu, Y.H. Developing a systematic approach to evaluate and predict building service life. J. Civ. Eng. Manag. 2017, 23, 890–901. [Google Scholar] [CrossRef]
- Shariati, S.; Abedi, M.; Saedi, A.; Yazdani-Chamzini, A.; Tamošaitienė, J.; Šaparauskas, J.; Stupak, S. Critical factors of the application of nanotechnology in construction industry by using ANP technique under fuzzy intuitionistic environment. J. Civ. Eng. Manag. 2017, 23, 914–925. [Google Scholar] [CrossRef]
- Štreimikienė, D.; Šliogerienė, J.; Turskis, Z. Multi-criteria analysis of electricity generation technologies in Lithuania. Renew. Energy 2016, 85, 148–156. [Google Scholar] [CrossRef]
- Kalibatas, D.; Kovaitis, V. Selecting the most effective alternative of waterproofing membranes for multifunctional inverted flat roofs. J. Civ. Eng. Manag. 2017, 23, 650–660. [Google Scholar] [CrossRef]
- Gardziejczyk, W.; Zabicki, P. Normalization and variant assessment methods in selection of road alignment variants–case study. J. Civ. Eng. Manag. 2017, 23, 510–523. [Google Scholar] [CrossRef]
- Bielinskas, V.; Burinskienė, M.; Podviezko, A. Choice of abandoned territories conversion scenario according to MCDA methods. J. Civ. Eng. Manag. 2018, 24, 79–92. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Giama, E.; Papadopoulos, A.M. Assessment tools for the environmental evaluation of concrete, plaster and brick elements production. J. Clean. Prod. 2015, 99, 75–85. [Google Scholar] [CrossRef]
- Van Kesteren, I.E.H. Product designers’ information needs in materials selection. Mater. Des. 2008, 29, 133–145. [Google Scholar] [CrossRef]
- Shen, L.; Tam, V.W.Y.; Tam, L.; Ji, Y. Project feasibility study: The key to successful implementation of sustainable and socially responsible construction management practice. J. Clean. Prod. 2010, 18, 254–259. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Bagočius, V. Multi-criteria selection of a deep-water port in the Eastern Baltic Sea. Appl. Soft Comput. 2015, 26, 180–192. [Google Scholar] [CrossRef]
- Dahooie, J.H.; Zavadskas, E.K.; Abolhasani, M.; Vanaki, A.; Turskis, Z. A novel approach for evaluation of projects using an Interval-Valued Fuzzy Additive Ratio Assessment (ARAS) Method: A case study of oil and gas well drilling projects. Symmetry 2018, 10, 45. [Google Scholar] [CrossRef]
- Hashemi, H.; Mousavi, S.M.; Zavadskas, E.K.; Chalekaee, A.; Turskis, Z. A New group decision model based on grey-intuitionistic fuzzy-ELECTRE and VIKOR for contractor assessment problem. Sustainability 2018, 10, 1635. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Turskis, Z.; Adeli, H. Hybrid multiple-criteria decision-making methods: A review of applications in engineering. Sci. Iran. 2016, 23, 1–20. [Google Scholar]
- Zavadskas, E.K.; Govindan, K.; Antucheviciene, J.; Turskis, Z. Hybrid multiple criteria decision-making methods: A review of applications for sustainability issues. Econ. Res.-Ekon. Istraz. 2016, 29, 857–887. [Google Scholar] [CrossRef]
- Keeney, R.L. Decision Analysis: An Overview. Oper. Res. 1982, 30, 803–838. [Google Scholar]
- Phillips, L.D. Decision Analysis in the 1990’s. In Tutorial Papers in Operational Research; Shahini, A., Stainton, R., Eds.; Operational Research Society: Birmingham, UK, 1989. [Google Scholar]
- Telles, R.C. Geometrical Information Flow Regulated by Time Lengths: An Initial Approach. Symmetry 2018, 10, 645. [Google Scholar] [CrossRef]
- Radović, D.; Stević, Ž.; Pamučar, D.; Zavadskas, E.K.; Badi, I.; Antuchevičiene, J.; Turskis, Z. Measuring Performance in Transportation Companies in Developing Countries: A Novel Rough ARAS Model. Symmetry 2018, 10, 434. [Google Scholar] [CrossRef]
- Namakin, A.; Najafi, S.E.; Fallah, M.; Javadi, M. A New Evaluation for Solving the Fully Fuzzy Data Envelopment Analysis with Z-Numbers. Symmetry 2018, 10, 384. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. An Extended Step-Wise Weight Assessment Ratio Analysis with Symmetric Interval Type-2 Fuzzy Sets for Determining the Subjective Weights of Criteria in Multi-Criteria Decision-Making Problems. Symmetry 2018, 10, 91. [Google Scholar] [CrossRef]
- Wang, J.; Wei, G.; Wei, Y. Models for Green Supplier Selection with Some 2-Tuple Linguistic Neutrosophic Number Bonferroni Mean Operators. Symmetry 2018, 10, 131. [Google Scholar] [CrossRef]
- Zhou, J.; Su, W.; Baležentis, T.; Streimikiene, D. Multiple Criteria Group Decision-Making Considering Symmetry with Regards to the Positive and Negative Ideal Solutions via the Pythagorean Normal Cloud Model for Application to Economic Decisions. Symmetry 2018, 10, 140. [Google Scholar] [CrossRef]
- Yan, Q.; Yang, L.; Baležentis, T.; Streimikiene, D.; Qin, C. Optimal Dividend and Capital Injection Problem with Transaction Cost and Salvage Value: The Case of Excess-of-Loss Reinsurance Based on the Symmetry of Risk Information. Symmetry 2018, 10, 276. [Google Scholar] [CrossRef]
- Kuantama, E.; Tarca, I.; Dzitac, S.; Dzitac, I.; Tarca, R. Flight Stability Analysis of a Symmetrically-Structured Quadcopter Based on Thrust Data Logger Information. Symmetry 2018, 10, 291. [Google Scholar] [CrossRef]

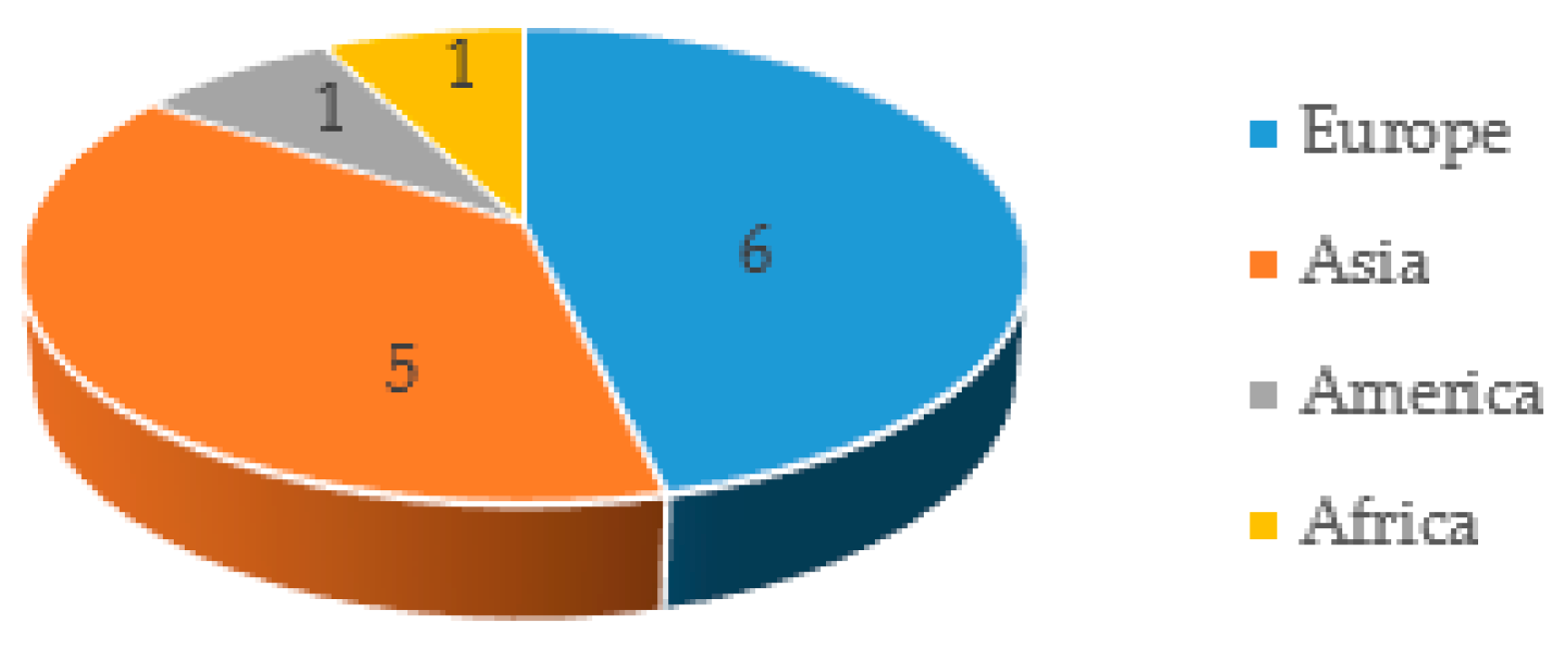



| Countries | Number of Papers |
|---|---|
| Brazil | 1 |
| Romania | 1 |
| China | 1 |
| Iran | 1 |
| Lithuania | 1 |
| China–Lithuania | 2 |
| Iran–Lithuania | 1 |
| Bosnia and Herzegovina–Serbia–Libya–Lithuania | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Solution Models Based on Symmetric and Asymmetric Information. Symmetry 2019, 11, 500. https://doi.org/10.3390/sym11040500
Zavadskas EK, Turskis Z, Antucheviciene J. Solution Models Based on Symmetric and Asymmetric Information. Symmetry. 2019; 11(4):500. https://doi.org/10.3390/sym11040500
Chicago/Turabian StyleZavadskas, Edmundas Kazimieras, Zenonas Turskis, and Jurgita Antucheviciene. 2019. "Solution Models Based on Symmetric and Asymmetric Information" Symmetry 11, no. 4: 500. https://doi.org/10.3390/sym11040500
APA StyleZavadskas, E. K., Turskis, Z., & Antucheviciene, J. (2019). Solution Models Based on Symmetric and Asymmetric Information. Symmetry, 11(4), 500. https://doi.org/10.3390/sym11040500







