An Information Entropy Based Event Boundary Detection Algorithm in Wireless Sensor Networks
Abstract
:1. Introduction
2. Related Work
3. Network Model and Assumptions
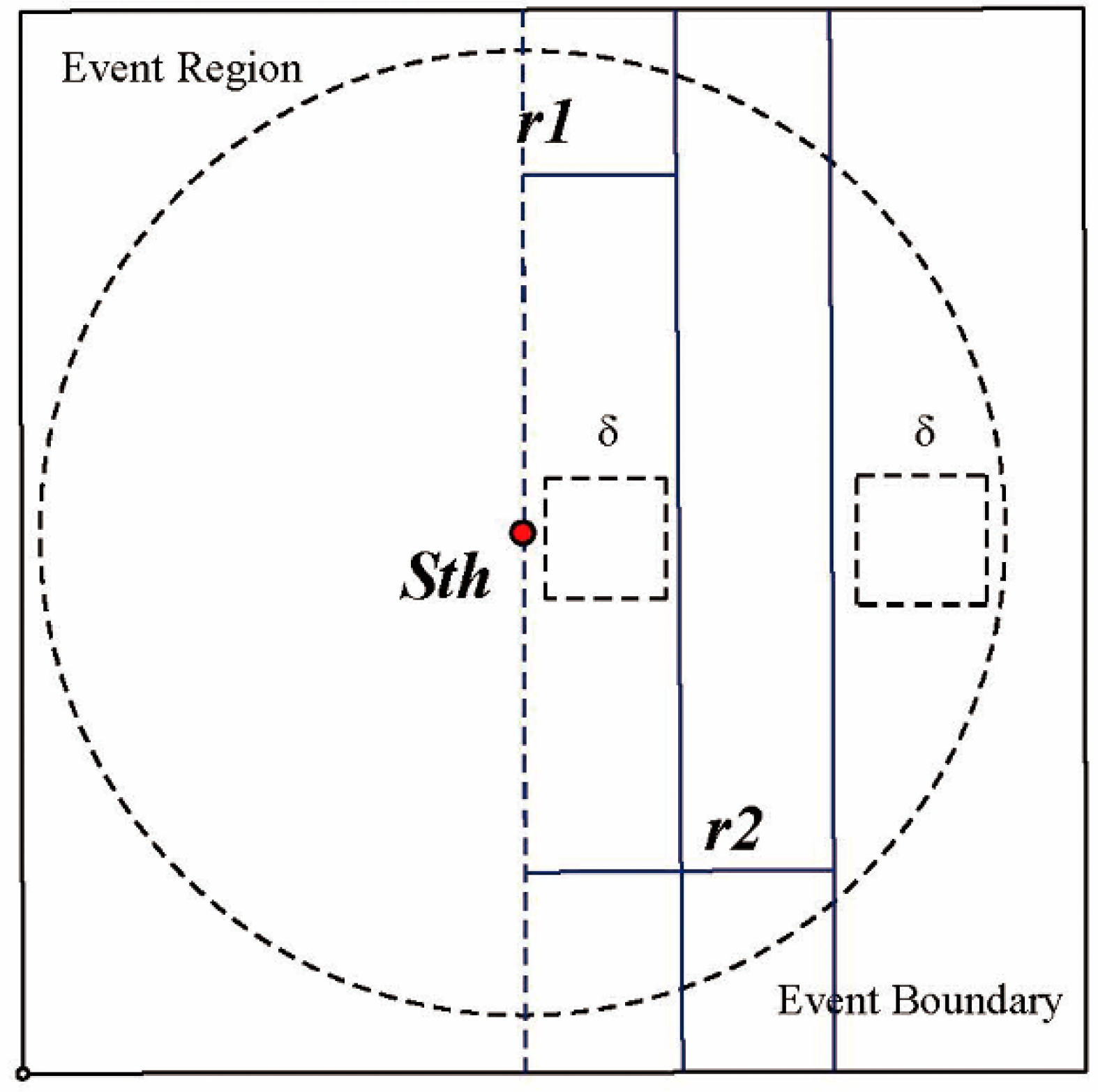
- The term sensor area, denoted as , not only refers to the geographical area covered by the WSN but also to the set of nodes in this area. We denote an event region as , which is the sub-region of covered by an event and is the remaining region. Thus, . Hence, a sensor node means it is an affected node while means it is a normal node.
- A sensor node with its location information, that is , is considered to be a boundary node when it is on the actual boundary. Let us consider a boundary width defined as the communication radius of the sensor according to [13]. Let denote the disk centred at node with the radius . Therefore is a boundary node if ≤ r where is the geographic distance between and B the actual boundary. Then the event boundary is the collection of such boundary nodes.
4. Proposed Algorithm
4.1. The Statistical Boundary Detection Model
- H = 0 if and only if all the but one are null. This means that all the neighbours of are entirely affected or absolutely normal. Otherwise, if H is positive, that is, node has the probability to be a boundary node. The higher the value of H is, the closer the node is to the actual boundary.
- When all the are equal (i.e., p = q), the value of H is the largest and is log 2. This is also intuitively the higher probability a node to be a boundary node.
- Any change towards equalization of the probabilities p, q increases H.
4.2. Determining Rules
| Algorithm 1: Entropy based Event Boundary Detection (EEBD) Algorithm |
| Input, node density ρ |
| Output: broadcast the ID if it is the real event boundary senor node |
| For each sensor node |
| ; |
| step 1; |
| Discover the affected sensor nodes |
| if |
| flag(i) ← 1 |
| else |
| flag(i) ← 0 |
| end |
| to its neighbour nodes |
| ifflag(i) == 1 |
| end |
| step 2; |
| Listen to its neighbour nodes |
| step 3 |
| if |
5. Simulation Results
5.1. Simulation Initialization
5.2. Simulation Results
5.3. Efficiency Evaluation
6. Conclusions
- (1)
- To further decrease the sensor nodes’ energy consumption and extend network lifespan under the condition of ensuring the accuracy of event boundary detection, the energy consumption model and the event reporting routing protocol need further research.
- (2)
- A complete event dataset is necessary before the boundary detection algorithm is executed. Due to the adverse conditions of the sea, the collected marine big data always experience a serious data loss phenomenon in WSNs [22]. To further improve the accuracy of event boundary detection, the missing data recovery of WSNs is an important research topic.
- (3)
- Real marine event boundary detection experiments and event boundary dynamic tracking are also key research directions for the future.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sheng, Z.; Mahapatra, C.; Zhu, C.; Leung, V.C. Recent Advances in Industrial Wireless Sensor Networks Toward Efficient Management in IoT. IEEE Access 2015, 3, 622–637. [Google Scholar] [CrossRef]
- Minhas, U.I.; Naqvi, I.H.; Qaisar, S.; Ali, K.; Shahid, S.; Aslam, M.A. A WSN for Monitoring and Event Reporting in Underground Mine Environments. IEEE Syst. J. 2018, 12, 485–496. [Google Scholar] [CrossRef]
- Wang, T.Y.; Yang, M.H.; Wu, J.Y. Distributed Detection of Dynamic Event Regions in Sensor Networks with a Gibbs Field Distribution and Gaussian Corrupted Measurements. IEEE Trans. Commun. 2016, 64, 3932–3945. [Google Scholar] [CrossRef]
- Sitanayah, L.; Datta, A.; Cardell-Oliver, R. Heuristic algorithm for finding boundary cycles in location-free low density wireless sensor networks. Comput. Netw. 2010, 54, 1630–1645. [Google Scholar] [CrossRef]
- Abani, N.; Braun, T.; Gerla, M. Proactive caching with mobility prediction under uncertainty in information-centric networks. In Proceedings of the 4th ACM Conference on Information-Centric Networking, Berlin, Germany, 26–28 September2017; pp. 88–97. [Google Scholar]
- Kundu, S.; Das, N. In-network area estimation and localization in Wireless Sensor Networks. In Proceedings of the GC’12 Workshop: The 7th IEEE International Workshop on Heterogeneous, Multi-Hop, Wireless and Mobile Networks, Anaheim, CA, USA, 3–7 December 2012; pp. 431–435. [Google Scholar]
- Li, X.; He, S.; Chen, J.; Liang, X.; Lu, R.; Shen, S. Coordinate-free distributed algorithm for boundary detection in wireless sensor networks. In Proceedings of the Global Telecommunications Conference (GLOBECOM 2011), Houston, TX, USA, 5–9 December 2011; pp. 1–5. [Google Scholar]
- Sadeq, M.J.; Duckham, M.; Worboys, M.F. Decentralized Detection of Topological Events in Evolving Spatial Regions. Comput. J. 2013, 56, 1417–1431. [Google Scholar] [CrossRef]
- Ding, M.; Cheng, X. Robust event boundary detection in sensor networks—A mixture model based approach. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 2991–2995. [Google Scholar]
- Liao, P.; Chang, M.; Kuo, C. Distributed edge detection with composite hypothesis test in wireless sensor networks. In Proceedings of the IEEE Global Telecommunications Conference, 2004, GLOBECOM ’04, Dallas, TX, USA, 29 November–3 December 2004; pp. 129–133. [Google Scholar]
- Kundu, S.; Das, N.; Roy, S.; Saha, D. Irregular-Shaped Event Boundary Estimation in Wireless Sensor Networks. In Progress in Intelligent Computing Techniques: Theory, Practice and Applications; Springer: Singapore, 2018; pp. 423–435. [Google Scholar]
- Sajida, I.; Young-Bae, K. A Continuous Object Boundary Detection and Tracking Scheme for Failure-Prone Sensor Networks. Sensors 2017, 17, 361. [Google Scholar]
- Duh, D.; Li, S.; Cheng, W. Distributed Fault-Tolerant Event Region Detection of Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2013, 5, 286–291. [Google Scholar] [CrossRef]
- Ren, K.; Zeng, K.; Lou, W. Secure and fault-tolerant event boundary detection in wireless sensor networks. IEEE Trans. Wirel. Commun. 2008, 7, 354–363. [Google Scholar] [CrossRef]
- Dogandzic, A.; Zhang, B. Distributed Estimation and Detection for Sensor Networks Using Hidden Markov Random Field Models. IEEE Trans. Signal Process. 2006, 54, 3200–3215. [Google Scholar] [CrossRef] [Green Version]
- Chu, W.C.; Ssu, K.F. Location-free boundary detection in mobile wireless sensor networks with a distributed approach. Comput. Netw. 2014, 70, 96–112. [Google Scholar] [CrossRef]
- Shukla, S.; Misra, R.; Prasad, A. Efficient disjoint boundary detection algorithm for surveillance capable WSNs. J. Parallel Distrib. Comput. 2017, 109, 245–257. [Google Scholar] [CrossRef]
- Ding, M.; Chen, D.; Xing, K.; Cheng, X. Localized fault-tolerant event boundary detection in sensor networks. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM 2005), Miami, FL, USA, 13–17 March 2005; pp. 902–913. [Google Scholar]
- Senouci, M.R.; Mellouk, A.; Assnoune, K. Localized Movement-Assisted Sensor Deployment Algorithm for HoleDetection and Healing. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1267–1277. [Google Scholar] [CrossRef]
- Ouyang, W.; Liu, Y.T.; Lin, Y.W.; Chen, Y.H. Entropy-Based Distributed Fault-Tolerant Event Boundary Detection Algorithm for Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Ubiquitous Intelligence & Computing and, International Conference on Autonomic & Trusted Computing, Fukuoka, Japan, 4–7 September 2012; pp. 882–887. [Google Scholar]
- Mitsche, D.; Resta, G.; Santi, P. The random waypoint mobility model with uniform node spatial distribution. Wirel. Netw. 2014, 20, 1053–1066. [Google Scholar] [CrossRef]
- Wu, H.; Xian, J.; Wang, J.; Khandge, S.; Mohapatra, P. Missing data recovery using reconstruction in ocean wireless sensor networks. Comput. Commun. 2018, 132, 1–9. [Google Scholar] [CrossRef]
















© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Meng, Q.; Xian, J.; Mei, X.; Claramunt, C.; Cao, J. An Information Entropy Based Event Boundary Detection Algorithm in Wireless Sensor Networks. Symmetry 2019, 11, 537. https://doi.org/10.3390/sym11040537
Wu H, Meng Q, Xian J, Mei X, Claramunt C, Cao J. An Information Entropy Based Event Boundary Detection Algorithm in Wireless Sensor Networks. Symmetry. 2019; 11(4):537. https://doi.org/10.3390/sym11040537
Chicago/Turabian StyleWu, Huafeng, Qingshun Meng, Jiangfeng Xian, Xiaojun Mei, Christophe Claramunt, and Junkuo Cao. 2019. "An Information Entropy Based Event Boundary Detection Algorithm in Wireless Sensor Networks" Symmetry 11, no. 4: 537. https://doi.org/10.3390/sym11040537
APA StyleWu, H., Meng, Q., Xian, J., Mei, X., Claramunt, C., & Cao, J. (2019). An Information Entropy Based Event Boundary Detection Algorithm in Wireless Sensor Networks. Symmetry, 11(4), 537. https://doi.org/10.3390/sym11040537






