Hydrodynamical Study of Micropolar Fluid in a Porous-Walled Channel: Application to Flat Plate Dialyzer
Abstract
:1. Introduction
- the fluid flowing in the channel was assumed to be Newtonian in nature,
- the no-slip condition was assumed to be held at the permeable wall,
- a seepage velocity of a constant, linear, or exponential type at the porous wall was assumed in advance.
- The constitutive equation of the micropolar fluid model can be reduced to the Newtonian fluid model as a special case when certain parameters in this model are set to zero. Thus, a variety of industrial and biological non-Newtonian fluids along with the previously-studied Newtonian fluid can be investigated by the current results.
- Results for the no-slip flow can be recovered from our obtained solutions when the slip parameter approaches zero.
- The obtained solution also reveals that for particular values of parameters, a uniform, linear, and exponentially-decaying flow rate can be deduced from the results of the current article, which were assumed in advance in the previous studies.
2. Basic Equations
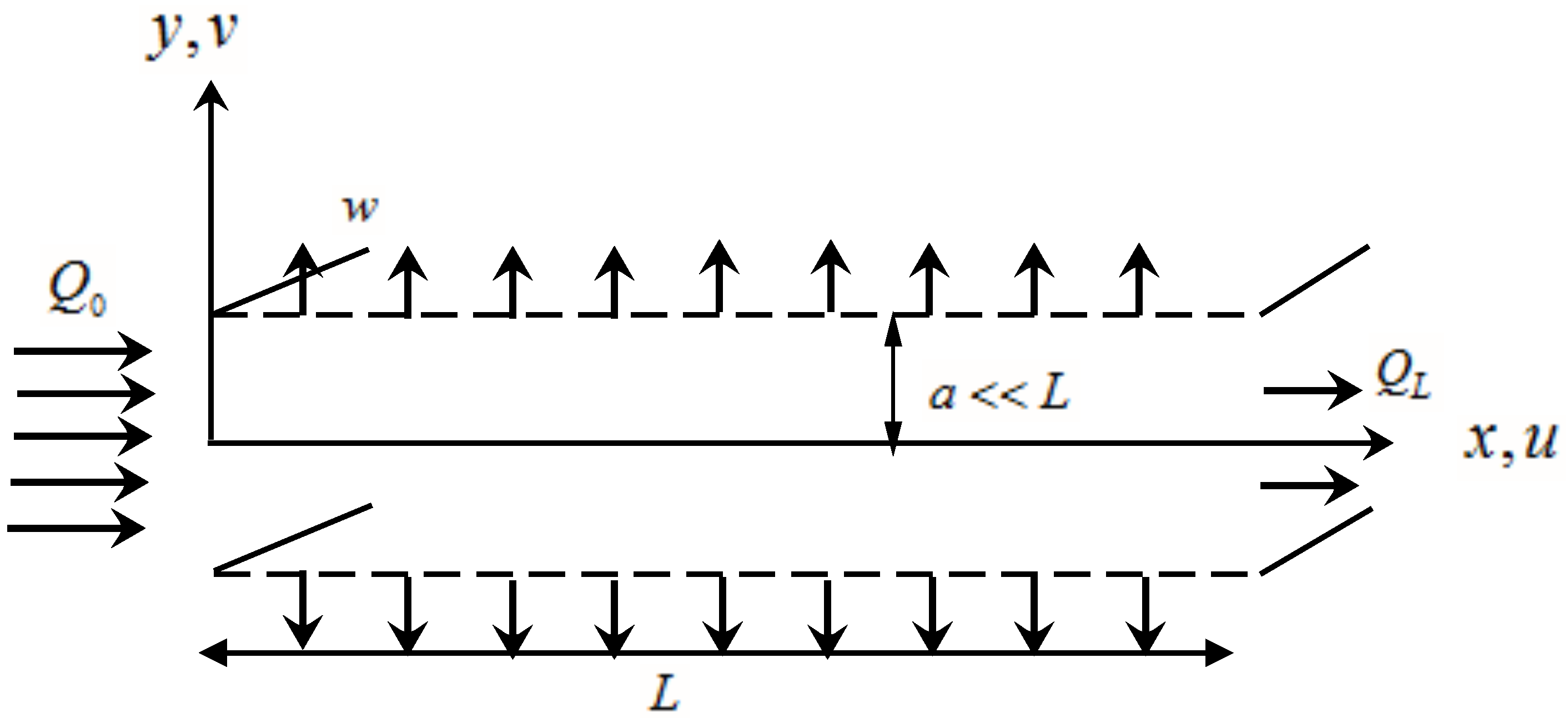
3. Problem Statement
4. Dimensionless Formulation and Solution
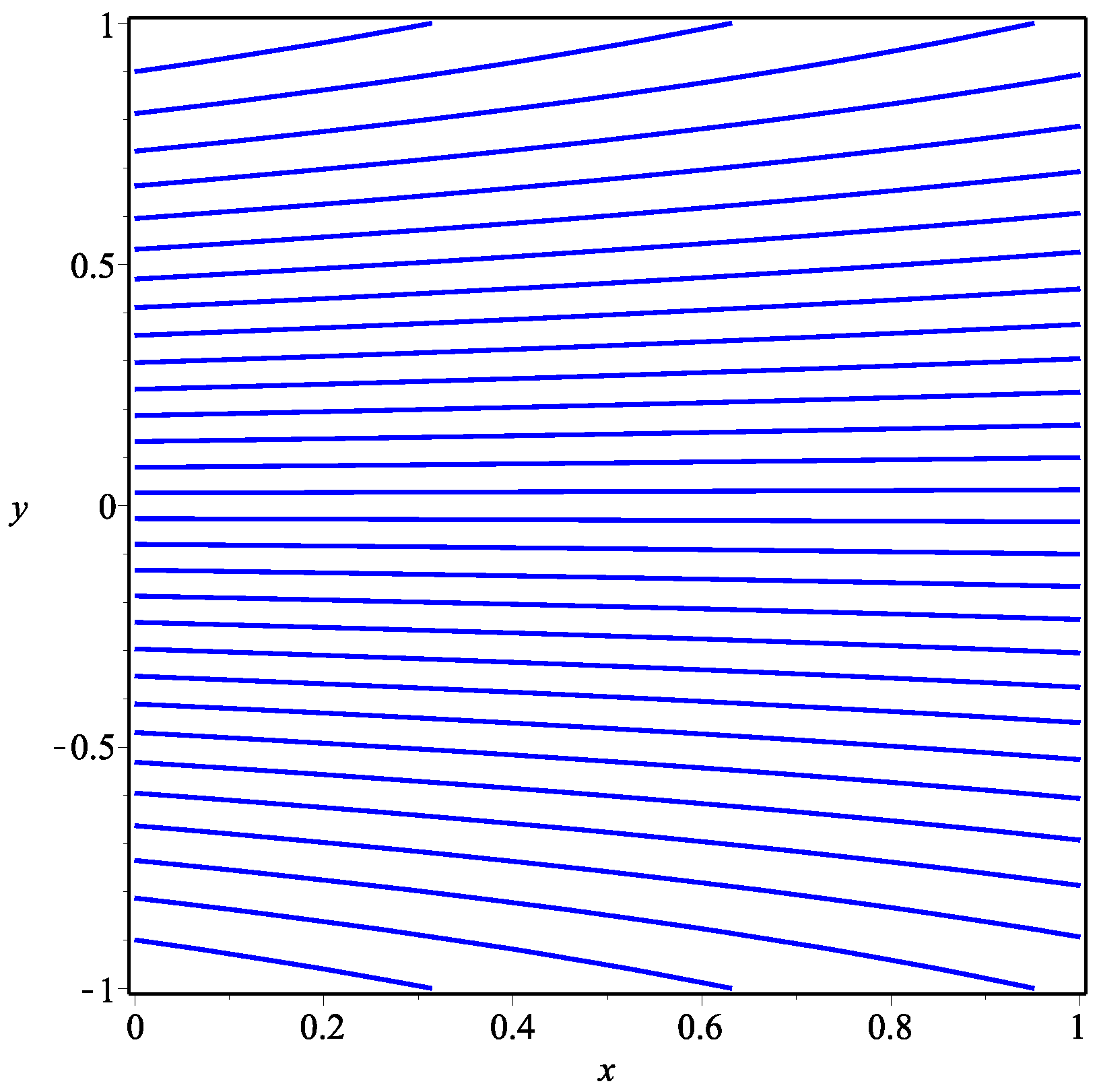
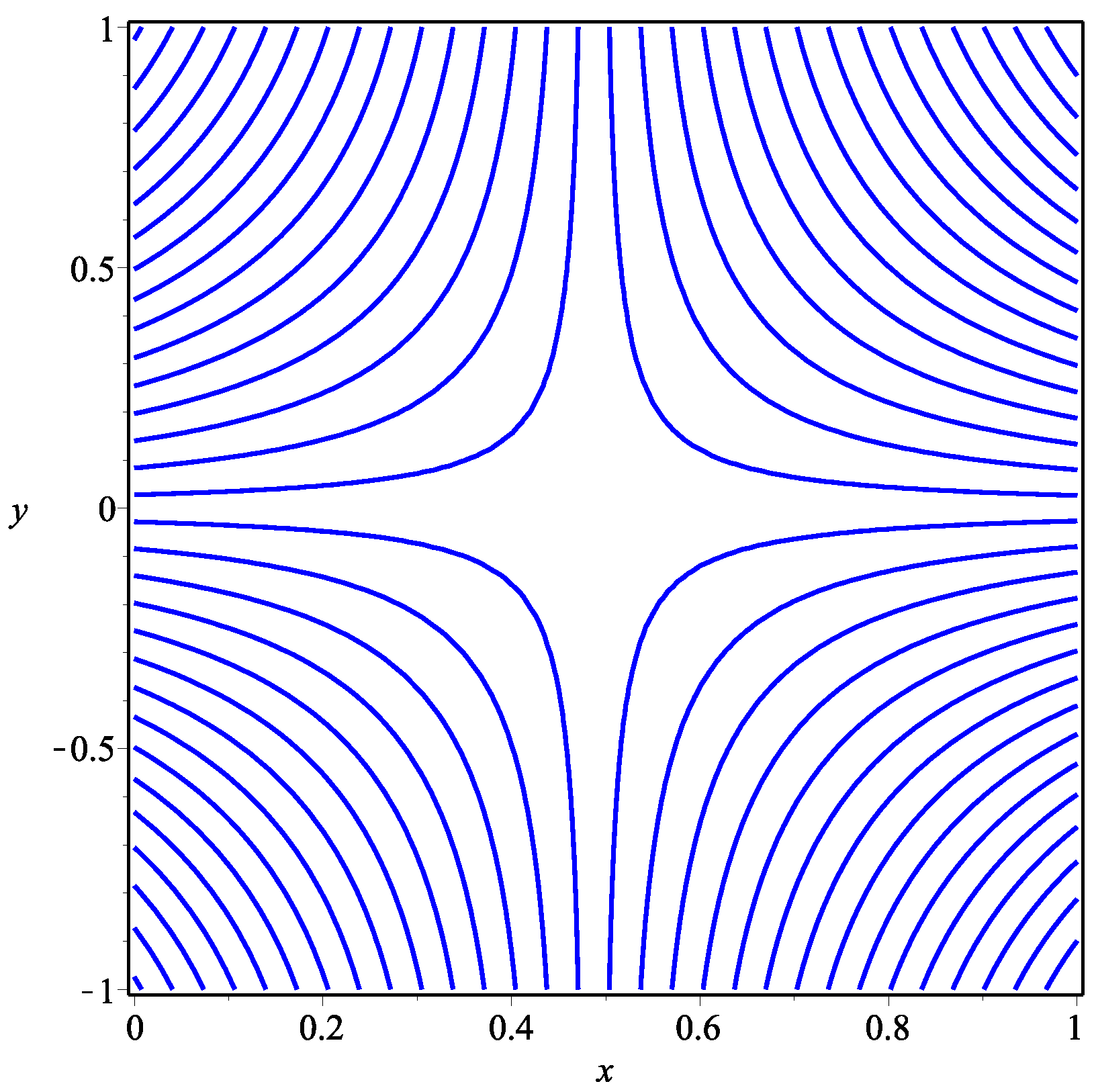
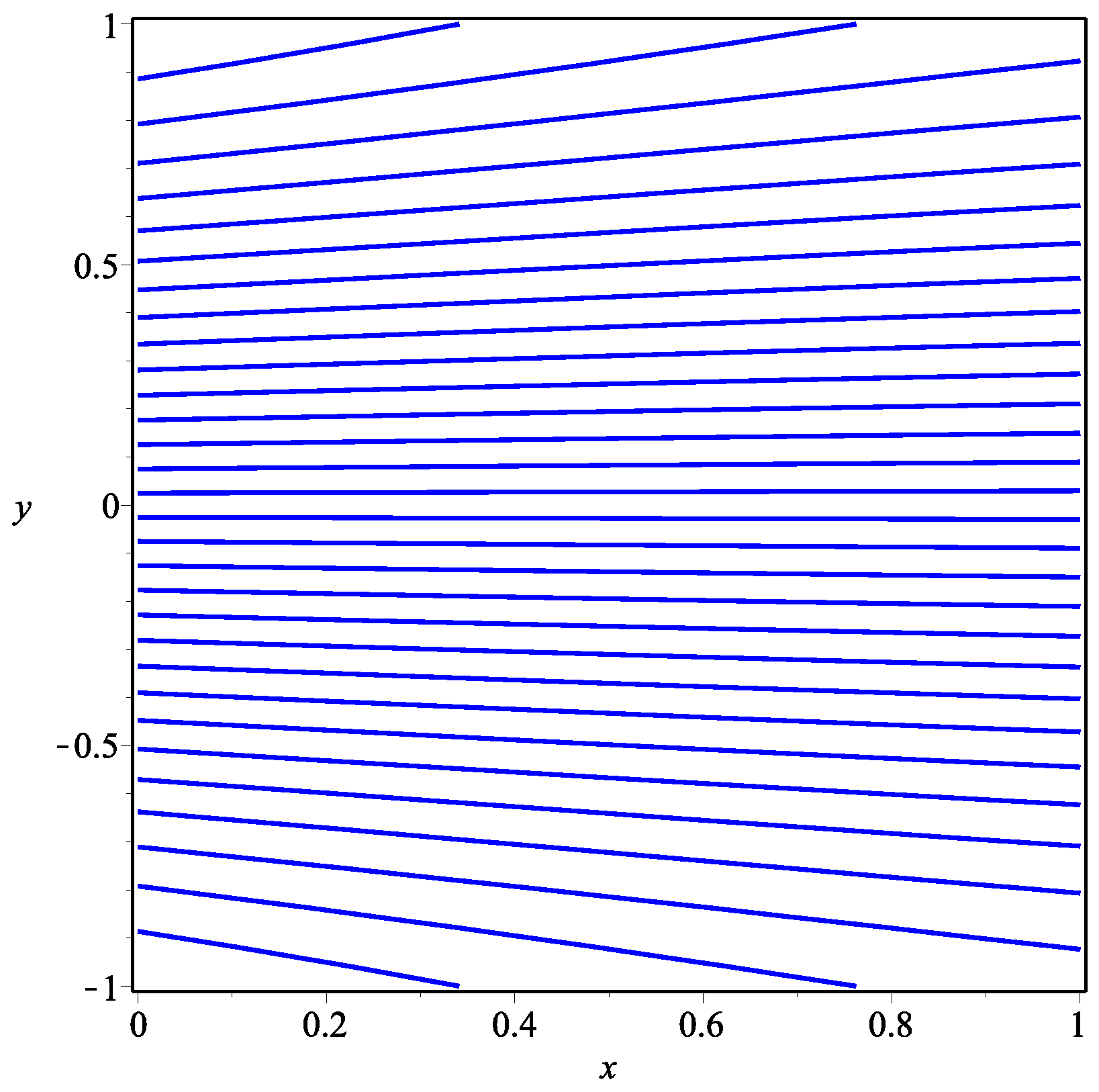
5. Numerical Results and Discussion
6. Application to a Flat Plate Dialyzer
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FPD | Flat plate dialyzer |
| Fluid density | |
| Coefficient of viscosity | |
| Coefficient of the micro-rotation viscosity | |
| Viscosity coefficients of the angular velocity | |
| Micro-inertia coefficient | |
| u | Dimensionless tangential velocity component |
| v | Dimensionless transverse velocity component |
| Dimensionless microrotation velocity | |
| Inlet flow rate | |
| Inlet pressure | |
| Ratio of the channel width to its length | |
| Coupling number | |
| Micropolar fluid parameter | |
| K | Dimensionless wall filtration coefficient |
| W | Channel width to height ratio |
| Dimensionless wall slip parameter | |
| Dimensionless ultrafiltration rate | |
| Dimensionless mean pressure drop |
References
- Voutchkov, N. Desalination Engineering: Planning and Design; McGraw Hill: New York, NY, USA, 2012. [Google Scholar]
- Macey, R.I. Pressure flow patterns in a cylinder with reabsorbing walls. Bull. Math. Biophys. 1963, 25, 303–312. [Google Scholar] [CrossRef]
- Macey, R.I. Hydrodynamics in the renal tubule. Bull. Math. Biophys. 1965, 27, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Marshall, E.A.; Trowbridge, E.A. Flow of a Newtonian fluid through a permeable tube: The application to the proximal renal tubule. Bull. Math. Biophys. 1974, 25, 457–476. [Google Scholar] [CrossRef]
- Marshall, E.A.; Trowbridge, E.A.; Aplin, A.J. Flow of a Newtonian fluid between parallel flat permeable plates—The application to a flat-plate hemodialyzer. Math. Biophys. 1975, 27, 119–139. [Google Scholar] [CrossRef]
- Sadeghi, R.; Shadloo, M.S.; Hirschler, M.; Hadjadj, H.A.; Nieken, U. Three-dimensional lattice Boltzmann simulations of high density ratio two-phase flows in porous media. Comput. Math. Appl. 2018, 75, 2445–2465. [Google Scholar] [CrossRef]
- Hirschler, M.H.; Shadloo, M.S.; Nieken, U. Viscous fingering phenomena in the early stage of polymer membrane formation. J. Fluid Mech. 2019, 864, 97–140. [Google Scholar] [CrossRef]
- Kozinski, A.A.; Schmidt, F.P.; Lightfoot, E.N. Velocity profiles in porous-walled ducts. Ind. Eng. Chem. Fundam. 1970, 9, 502–505. [Google Scholar] [CrossRef]
- Papanastasiou, T.C. Viscous Fluid Flow; CRC Press LLC: Florida, FA, USA, 2000. [Google Scholar]
- Berman, A.S. Laminar flow in channels with porous walls. J. Appl. Phys. 1953, 24, 1232–1235. [Google Scholar] [CrossRef]
- Berman, A.S. Laminar flow in an annulus with porous walls. J. Appl. Phys. 1958, 29, 71–75. [Google Scholar] [CrossRef]
- Yuan, S.W.; Finkelstein, A.B. Laminar Pipe Flow With Injection and Suction Through a Porous Wall. Trans. ASME 1956, 78, 719–724. [Google Scholar]
- Haroon, T.; Siddiqui, A.M.; Shahzad, A. Creeping Flow of Viscous Fluid through a Proximal Tubule with Uniform Reabsorption: A Mathematical Study. Appl. Math. Sci. 2016, 10, 795–807. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Haroon, T.; Shahzad, A. Hydrodynamics of viscous fluid through porous slit with linear absorption. Appl. Math. and Mech. 2016, 37, 361–378. [Google Scholar] [CrossRef]
- Byron, B.R. Dynamics of Polymeric Liquids; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1965, 1, 1–18. [Google Scholar]
- Cowin, S.C. Polar fluids. Phys. Fluids 1968, 35, 1919–1927. [Google Scholar] [CrossRef]
- Beavers, G.S.; Joseph, D.D. Boundary conditions at a naturally permeable wall. J. Fluid Mech. 1967, 30, 197–207. [Google Scholar] [CrossRef]
- Saffman, P.G. On the boundary condition at the surface of a porous medium. Stud. Appl. Math. 1971, 50, 93–101. [Google Scholar] [CrossRef]
- Darcy, H.P.G. Dètermination des Lois D’ècoulement de L’eau à Travers le Sable; Victor Dalamont: Paris, France, 1856. [Google Scholar]
- Siddiqui, A.M.; Haroon, T.; Kahshan, M. MHD flow of newtonian fluid in a permeable tubule. Magnetohydrodynamics 2015, 51, 655–672. [Google Scholar]
- Kahshan, M.; Siddiqui, A.M.; Haroon, T. A micropolar fluid model for hydrodynamics in the renal tubule. Eur. Phys. J. Plus 2018, 133, 546. [Google Scholar] [CrossRef]
- Oka, S.; Murata, T. A theoretical study of the flow of blood in a capillary with permeable wall. Jpn. J. Appl. Phys. 1970, 9, 345. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Haroon, T.; Kahshan, M.; Iqbal, M.Z. Slip Effects on the Flow of Newtonian Fluid in Renal Tubule. J. Comput. Theor. Nanosci. 2015, 12, 4319–4328. [Google Scholar] [CrossRef]
- Maple 18; Waterloo Maple Inc.: Waterloo, ON, Canada, 1981–2014.
- Drukker, W.; Parsons, F.M.; Maher, J.F. Replacement of Renal Function by Dialysis: A Textbook of Dialysis; Springer Science & Business Media: Hingham, MA, USA, 2012. [Google Scholar]
- Funck-Brentano, J.L.; Sausse, A.; Vantelon, J.; Granger, A.; Zingraff, J.; Man, N.K. A new disposable plate-kidney. ASAIO J. 1969, 15, 127–130. [Google Scholar]
- Muthu, P.; Ratish, R.K.; Chandra, P. A study of micropolar fluid in an annular tube with application to blood flow. J. Mech. Med. Biol. 2008, 8, 561–576. [Google Scholar] [CrossRef]
- Kiran, G.R.; Radhakrishnamcharya, G.; Bég, O.A. Peristaltic flow and hydrodynamic dispersion of a reactive micropolar fluid-simulation of chemical effects in the digestive process. J. Mech. Med. Biol. 2017, 17, 1750013. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Kimiaeifar, A.; Bagheri, D. Series solution for heat transfer of continuous stretching sheet immersed in a micropolar fluid in the existence of radiation. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 289–304. [Google Scholar] [CrossRef]
- Funck-Brentano, J.L. Studies of intramembrane transport: A phenomenological approach. AIChE J. 1968, 14, 110–117. [Google Scholar]
- Malinow, M.R.; Korzon, W. An experimental method for obtaining an ultrafiltrate of the blood. Transl. Res. 1947, 12, 461–471. [Google Scholar]
- McDonald, J.R.; Harold, P. An automatic peritoneal dialysis machine: Preliminary report. J. Urol. 1966, 96, 397–401. [Google Scholar] [CrossRef]
- Brown, H.W.; Schreiner, G.E. Prolonged hemodialysis with bath refrigeration: The influence of dialyzer membrane thickness, temperature and other variables on performance. Trans Am. Soc. Artif. Intern. Organs 1962, 8, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Kelman, R.B. A theoretical note on exponential flow in the proximal part of the mammalian nephron. Bull. Math. Biol. 1962, 24, 303–317. [Google Scholar] [CrossRef]
- Radhakrishnamacharya, G.; Chandra, P.; Kaimal, M.R. A hydrodynamical study of the flow in renal tubules. Bull. Math. Biol. 1981, 43, 151–163. [Google Scholar] [CrossRef] [PubMed]
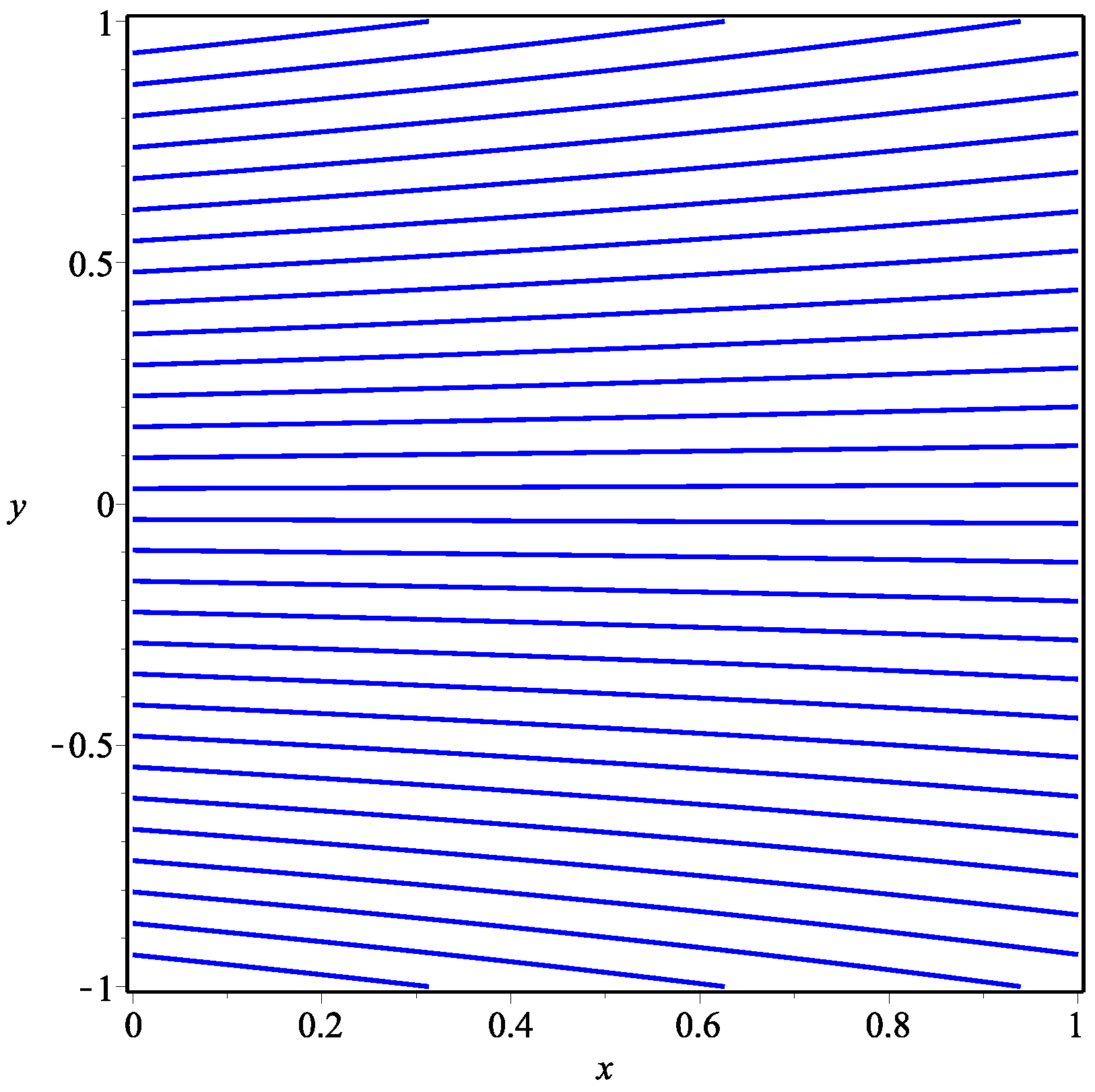
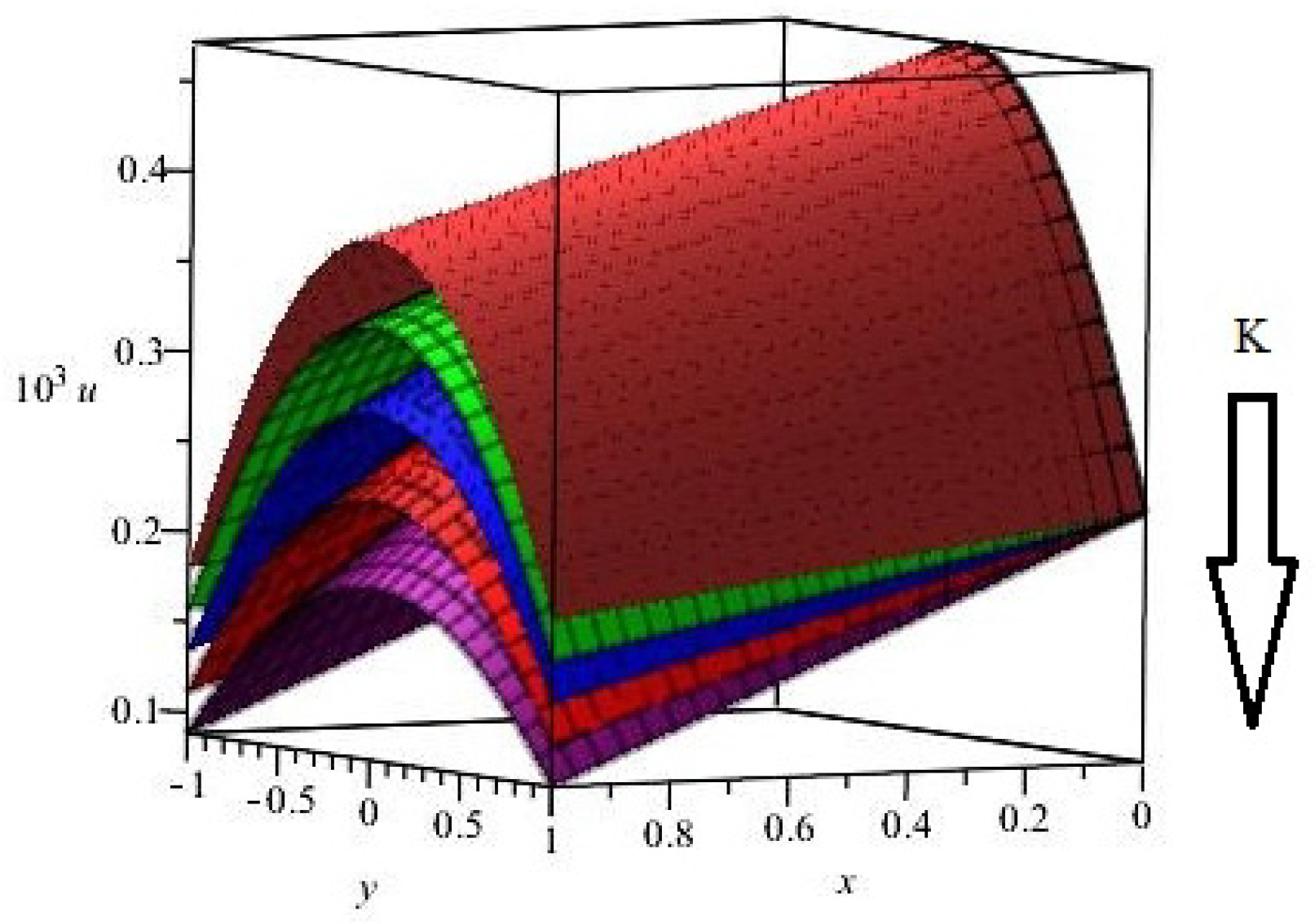
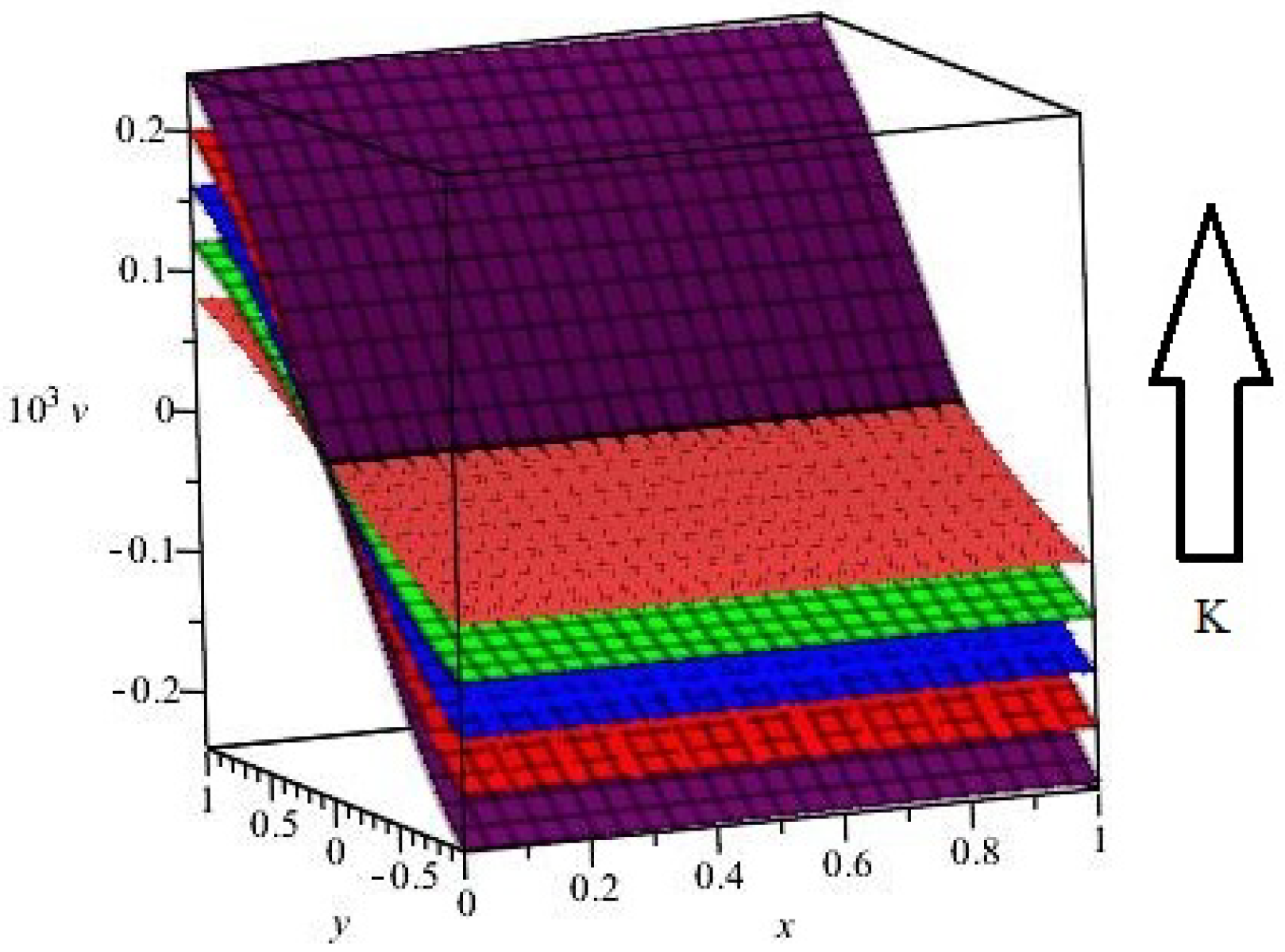
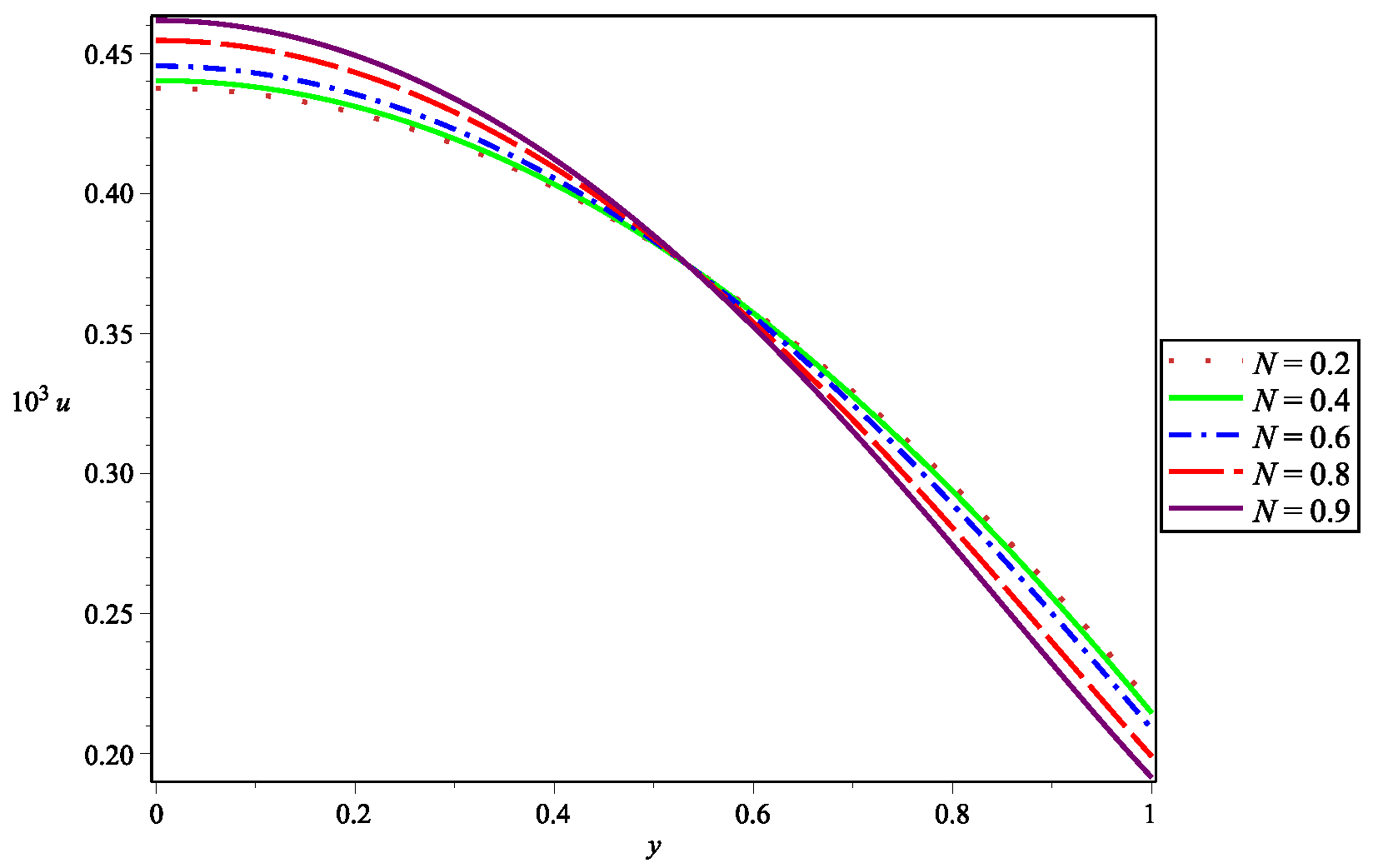
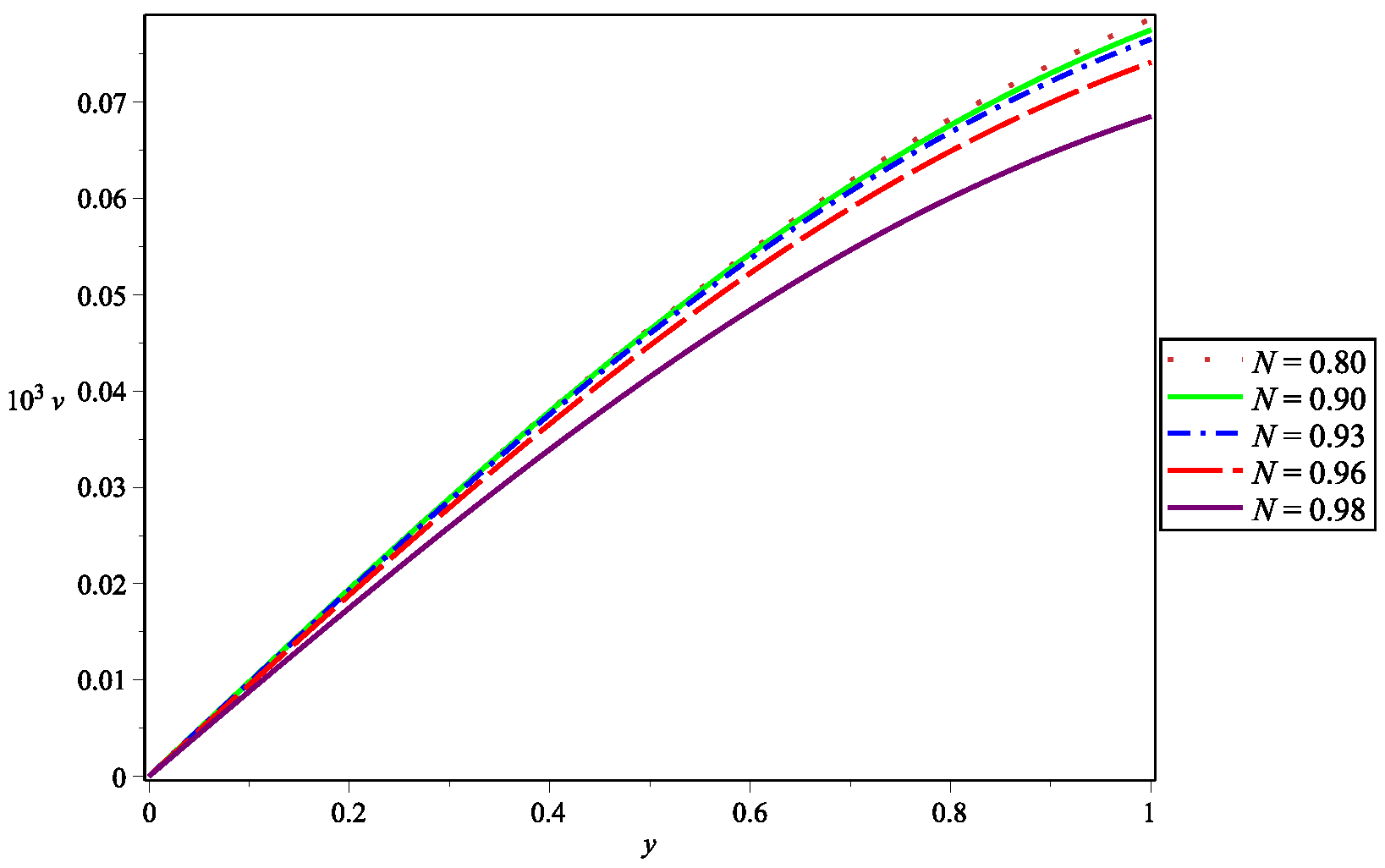
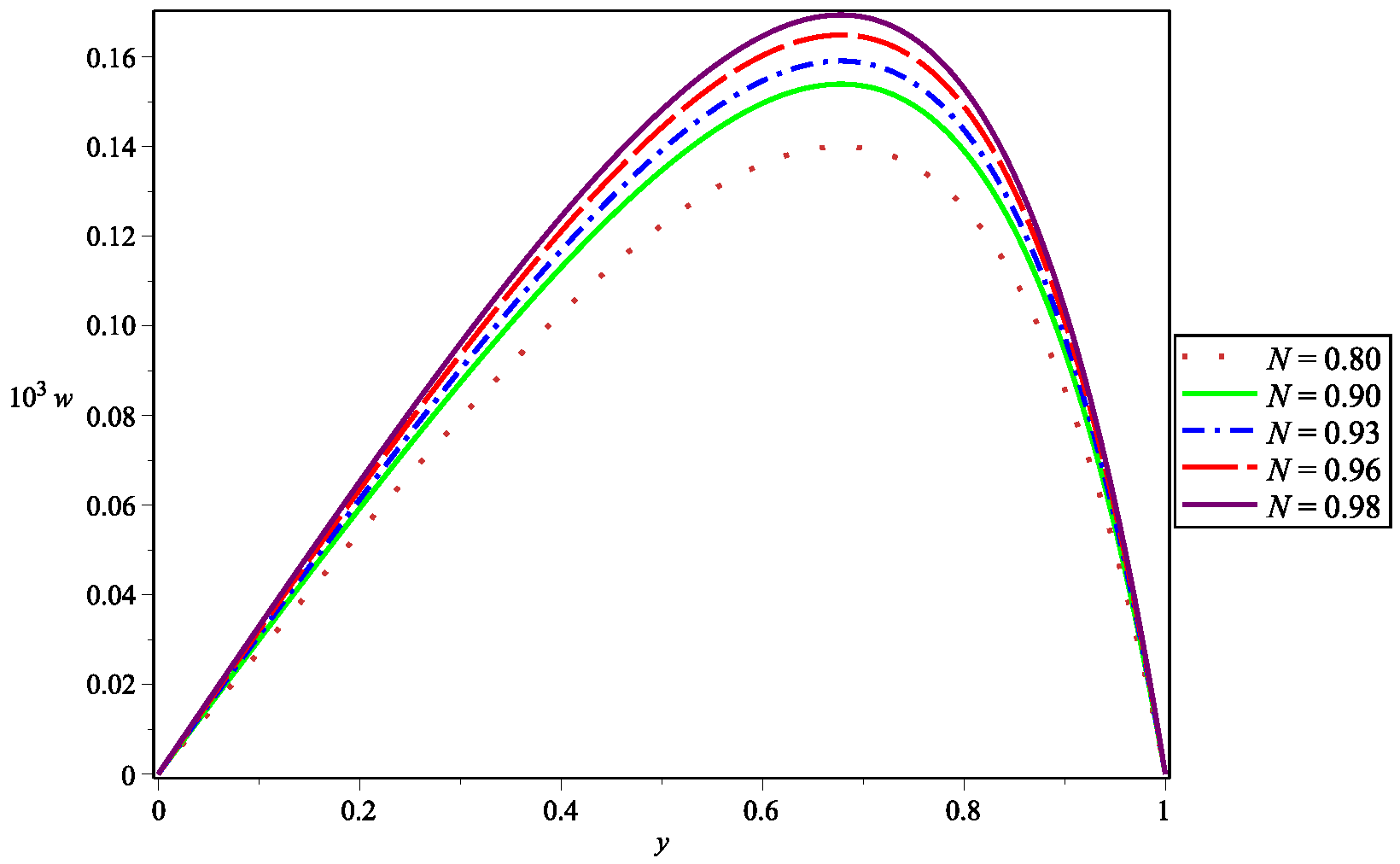

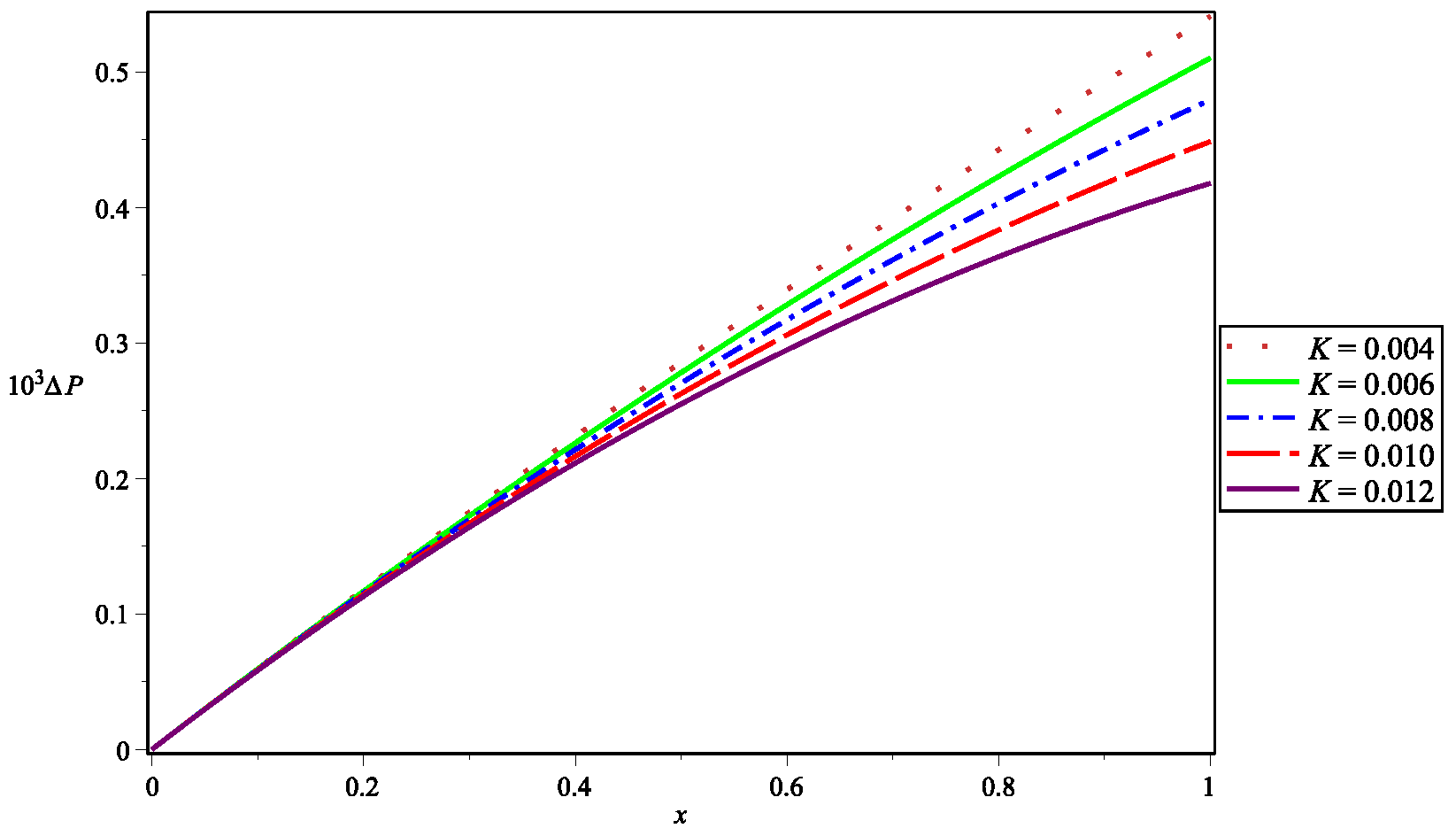


| Parameter | Abbreviation | Numerical Value |
|---|---|---|
| Number of blood | 8 | |
| compartments | ||
| Membrane length | L | 42 cm |
| Membrane width | w | cm |
| Membrane thickness | t | cm |
| Blood half channel | a | cm |
| height | ||
| Fluid viscosity | dynes-s/cm | |
| Transmembrane | ||
| pressure difference | 150 mm Hg | |
| at the entrance | ||
| Total ultrafiltration | 200 mL/h | |
| rate | ||
| Total entrance | 160 mL/min | |
| volume flow rate |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, D.; Kahshan, M.; Siddiqui, A.M. Hydrodynamical Study of Micropolar Fluid in a Porous-Walled Channel: Application to Flat Plate Dialyzer. Symmetry 2019, 11, 541. https://doi.org/10.3390/sym11040541
Lu D, Kahshan M, Siddiqui AM. Hydrodynamical Study of Micropolar Fluid in a Porous-Walled Channel: Application to Flat Plate Dialyzer. Symmetry. 2019; 11(4):541. https://doi.org/10.3390/sym11040541
Chicago/Turabian StyleLu, Dianchen, Muhammad Kahshan, and A. M. Siddiqui. 2019. "Hydrodynamical Study of Micropolar Fluid in a Porous-Walled Channel: Application to Flat Plate Dialyzer" Symmetry 11, no. 4: 541. https://doi.org/10.3390/sym11040541
APA StyleLu, D., Kahshan, M., & Siddiqui, A. M. (2019). Hydrodynamical Study of Micropolar Fluid in a Porous-Walled Channel: Application to Flat Plate Dialyzer. Symmetry, 11(4), 541. https://doi.org/10.3390/sym11040541







